Isotropic resolution diffusion tensor imaging with whole brain acquisition in a clinically acceptable time

Abstract

Our objective was to develop a diffusion tensor MR imaging pulse sequence that allows whole brain coverage with isotropic resolution within a clinically acceptable time. A single‐shot, cardiac‐gated MR pulse sequence, optimized for measuring the diffusion tensor in human brain, was developed to provide whole‐brain coverage with isotropic (2.5 × 2.5 × 2.5 mm) spatial resolution, within a total imaging time of approximately 15 min. The diffusion tensor was computed for each voxel in the whole volume and the data processed for visualization in three orthogonal planes. Anisotropy data were further visualized using a maximum‐intensity projection algorithm. Finally, reconstruction of fiber‐tract trajectories i.e., ‘tractography’ was performed. Images obtained with this pulse sequence provide clear delineation of individual white matter tracts, from the most superior cortical regions down to the cerebellum and brain stem. Because the data are acquired with isotropic resolution, they can be reformatted in any plane and the sequence can therefore be used, in general, for macroscopic neurological or psychiatric neuroimaging investigations. The 3D visualization afforded by maximum intensity projection imaging and tractography provided easy visualization of individual white matter fasciculi, which may be important sites of neuropathological degeneration or abnormal brain development. This study has shown that it is possible to obtain robust, high quality diffusion tensor MR data at 1.5 Tesla with isotropic resolution (2.5 × 2.5 × 2.5 mm) from the whole brain within a sufficiently short imaging time that it may be incorporated into clinical imaging protocols. Hum. Brain Mapping 15:216–230, 2002. © 2002 Wiley‐Liss, Inc.

INTRODUCTION

MRI diffusion tensor imaging (DTI), developed by Basser et al. [1994], provides a means of completely characterizing the random (Brownian) motion or ‘diffusivity’ of water molecules in vivo. The apparent diffusivity of water molecules within certain regions of the brain (predominantly the white matter) is strongly dependent on the direction in which it is measured [Chenevert et al., 1990; Doran et al., 1990; Moseley et al., 1990; Turner et al., 1990]. This is attributable to the anisotropic nature of the tissue in these regions, with movement of the diffusing molecules being less hindered along the long‐axis of a group of highly ordered fibers than perpendicular to it.

Basser et al. [1994] showed how, by acquiring a set of MR images with diffusion‐weighting applied along different orientations, the diffusion tensor, which completely characterizes diffusion in anisotropic systems, can be estimated within each voxel of the image. This provides a rotationally invariant estimate of diffusivity [Basser et al., 1994], various measures of diffusion anisotropy [Basser et al., 1994; Basser and Pierpaoli, 1996; Pierpaoli and Basser, 1996] that reflect the degree of tissue structure, and the orientation of the tensor [Basser and Pierpaoli, 1995], which has been shown to be parallel to the dominant orientation of anisotropic structures in vivo.

DTI has found application in a wide‐range of clinical situations including cerebral ischemia [Chabriat et al., 1999; Jones et al., 1999a; Mukherjee et al., 1999, 2000; Sorenson et al., 1999; Zelaya et al., 1999], multiple sclerosis [Horsfield et al., 1998; Scanderberg et al., 2000; Tievsky et al., 1999; Werring et al., 1999], amyotrophic lateral sclerosis (ALS) [Ellis et al., 1999a,b], schizophrenia and Alzheimer disease [Buchsbaum et al., 1998, Foong et al., 2000; Lim et al., 1999; Pfefferbaum et al., 1999; Steel et al., 2000], as well as tumors [Bastin et al. 1999; Inglis et al., 1999; Simmons et al., 1998; Wieshmann et al., 1999, 2000], head trauma [Jones et al., 2000; Werring et al., 1998] and in developmental studies [Baratti et al., 1999; Huppi et al., 1998; Klingberg et al., 1999].

In some situations, a priori information about the most likely site of pathology may be available and hence the selection of both the optimal imaging plane and region of the brain from which to acquire data can be accurately prescribed. In many cases, however, the location of pathology may be unknown, or widespread, and therefore the optimal choice of imaging plane and the region of the brain from which to acquire data is less clear. Further, the fasciculi that constitute cerebral white matter are not adequately visualized in a single plane for more than a small part of their pathways through the brain. In such situations, it is clearly desirable to acquire data from the entire brain and to have the ability to reformat and view the data in any arbitrary orientation.

Data from lesioned subjects, PET, functional MRI and electrophysiological studies consistently suggest that most cognitive processes (both higher and lower) require a substantial neuronal network for optimal performance [Horwitz et al., 1995; McIntosh, 1999]. Therefore the ability to acquire data from the whole brain allows investigation of the whole network integral to a particular function.

Another advantage of using a DTI sequence that allows whole‐head coverage but which has a sufficiently short acquisition time that it can be well tolerated by all subjects, is that a common DTI protocol can be used for all subjects. This facilitates grouping of data from different individuals to establish a normative database so that pathological variants can readily be identified. Furthermore, to perform group analysis of DTI data [Davatzikos et al., 2000; Hedehus et al., 1999; Pütz and Auer, 2000], it is necessary to co‐register the data sets either to one another or to a ‘template’ image. Such registration is much more robust if the data is acquired from the whole brain. This is also true for co‐registration of DTI with image data sets obtained with different contrast mechanisms (e.g., T ₁‐weighted ‘structural’ images, perfusion‐weighted images, BOLD fMRI images).

Some important diffusion tensor derived measures, such as indices of diffusion anisotropy, are highly sensitive to the signal to noise ratio (SNR) of the input data [Pierpaoli and Basser, 1996] and it is therefore usual to acquire more than the minimum number of images required to estimate the tensor, to improve precision, which results in longer scan times. Furthermore, one of the emerging ‘hot topics’ in the field of diffusion tensor imaging is that of fiber‐tracking or ‘tractography’ [Basser 1998; Basser et al., 2000; Conturo et al., 1999; Jones et al., 1998, 1999b; Mori et al., 1999; Poupon et al., 1999, 2000]. The aim of tractography is to reconstruct white matter tracts in three dimensions. This is generally done by following a continuous path of greatest diffusivity (i.e., the direction parallel to the eigenvector associated with the largest eigen‐value) through the brain from an initial set of seedpoints. The technique is dependent on accurate estimation of the orientation of the tensor within each voxel, which requires optimal signal to noise ratio while retaining the highest possible spatial resolution. As a consequence, scan times in excess of those that are likely to be acceptable for inclusion in a standard clinical protocol have generally been reported for tractography. For example, Conturo et al. [1999] reported near full brain coverage (45–51 axial slices, 2.5 mm thick) within a total scan time of 29 min. Poupon et al. [1999] and Basser et al. [2001] report scan times for tractography of 37 min and 30 to 40 min, respectively. Although such scan times may be tolerated by healthy or motivated individuals, they are not within the limits of clinical acceptability for many neurologic or psychiatric patients. Therefore, unless the scan time for whole brain DTI can be reduced to within patient tolerable limits, it is unlikely that tractography will be employed as a clinical tool.

From our personal experience of scanning some 20,000 psychiatric or neurologic patients, we have found that most subjects (including adolescents diagnosed with ADHD), who enter the magnet, are capable of lying still for an individual scan for approximately 15 min.

In this study, we detail an MR acquisition scheme that allows collection of isotropic resolution DTI data from the whole brain in 15 min or less, and allows production of high quality images of indices derived from the diffusion tensor. Thus, by carefully selecting the imaging parameters to maximize the precision of the diffusion tensor measurement, the total imaging time for robust DTI is brought within the limit tolerated by most patients.

MATERIALS AND METHODS

All subjects involved in this study gave written informed consent and the study was approved by The Bethlem and Maudsley NHS Trust Research Ethics Committee.

MR imaging

The diffusion tensor MR imaging sequence was developed in‐house on a 1.5 T GE Signa NV/i LX system (General Electric, Milwaukee, WI) with actively shielded magnetic field gradients (maximum amplitude 40 mT m⁻¹). A standard quadrature birdcage head coil was used for both RF transmission and NMR signal reception.

The pulse sequence was a single‐shot pulsed gradient spin‐echo pulse sequence with echo planar read‐out, in which the diffusion encoding gradients were placed asymmetrically about the 180° refocusing pulse to provide maximum temporal separation of the gradients for a given echo time. The pulse sequence parameters were optimized for precise estimation of the diffusion tensor, in accordance with the detailed theoretical description by Jones et al. [1999c,d] summarized below.

Echo time and diffusion gradient timing

The pulse sequence timings (echo time, duration and separation of the diffusion encoding gradients) were chosen to provide maximum precision in the estimates of the unique elements of the diffusion tensor matrix, by simultaneously considering the effects of attenuation due to both diffusion and transverse (T ₂) relaxation [Jones et al., 1999d]. Briefly, due to the finite gradient strengths that are achievable, increasing the diffusion sensitivity (quantified by the b‐factor [Le Bihan and Breton, 1985] or, more correctly, ‘b‐matrix’ [Basser et al., 1994; Matiello et al., 1997]) of a pulse sequence generally requires an increase in the echo time that in turn leads to increased T ₂ relaxation and thus a poorer signal‐to‐noise ratio. When these two effects are considered simultaneously [Jones et al., 1999d], the optimal diffusion weighting for normal adult brain is found to be approximately 75–80% (at 1.5 T) of the ‘optimal’ diffusion weighting calculated when transverse relaxation is ignored, giving an optimal diffusion weighting of 1,300 sec mm⁻².

The pulse sequence was designed to minimize the echo time for a given b‐factor (i.e., by minimizing any periods during which no gradients were applied). Thus, the optimal echo time was automatically determined to be 106.9 msec by optimizing the b‐factor. The expression for obtaining the echo time from the b‐factor can be found in equation (16) of Jones et al. [1999d].

Repetition time

The introduction of diffusion encoding gradient pulses to an imaging pulse sequence, renders the image sensitive to both microscopic and macroscopic motion. Poncelet et al. [1992] and Enzmann and Pelc [1992] have demonstrated intrinsic pulsatile motion of the brain linked to the cardiac cycle, leading to spatial velocity gradients within the parenchyma. Such motion manifests as variable increases in signal attenuation in diffusion‐weighted images leading to imprecise and inaccurate measurements of diffusivity. Thus, even with rapid imaging techniques such as EPI, the reliability of diffusion measurements is substantially improved if the acquisition is gated to the cardiac cycle [Conturo et al., 1995; Turner et al., 1990; Wieshmann et al., 1998]. To minimize this source of uncertainty, image acquisition was triggered to the cardiac cycle using a peripheral gating device placed on the subject's forefinger.

Number of measurements made with different diffusion weightings

Several groups [Bito et al., 1995; Eis and Hoehn‐Berlage, 1995; Jones et al., 1999c,d; Pell et al., 1997; Xing et al., 1997], have demonstrated that increased precision in estimates of diffusivity can be obtained by optimization of the ratio of measurements made with the higher diffusion weighting (N _high) to the number made with the lower diffusion weighting (N _low). Further, it has been shown [Jones et al., 1999d] how this optimal ratio of measurements (N _high/N _low) is strongly influenced by the transverse (T ₂) relaxation time in the range of T ₂ values found in the human brain. Following the approach of Jones et al. [1999d], and assuming the mean diffusivity to be 0.7 × 10⁻⁶ mm²s⁻¹ [Pierpaoli et al., 1996] and T ₂ of normal human white matter to be 80 msec [Whittall et al., 1997] at 1.5 T, the optimal value of N _high/N _low was determined through simultaneous minimization of the sum of the error variances of the estimates of the individual tensor elements, σ ${}_{\mathit{\text{D}}{}_{\mathit{\text{ij}}}}$ ² _(est) , with respect to the maximum b‐factor (b ₂) and the number of measurements made at the low b‐factor (N _L), for a given total number of measurements, i.e., by solution of the two simultaneous equations:

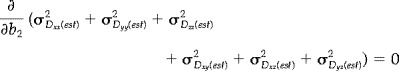(1)

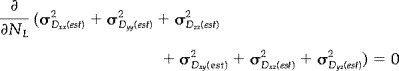(2)

In this way, the optimal value of N _high/N _low was found to be 9.1:1.

Diffusion encoding gradient orientations

Finally, it has been suggested [Jones et al., 1999c,d; Papadakis et al., 1999a,b; Skare et al., 2000a; Skare and Nordell, 1999, Poonawalla et al., 2000] that the precision of estimation of the diffusion tensor can be improved if the orientations of the diffusion encoding gradient vectors are arranged uniformly in space. Recent studies by Skare et al. [2000a,b] have compared several gradient orientation schemes proposed for DTI [Conturo et al., 1996; Jones et al., 1999c,d; Muthupallai et al., 1999; Papadakis et al., 1999b; Skare et al., 1999], and concluded that, in the presence of noise, rotational variance in the estimate of the diffusion tensor is minimized when using the gradient orientation strategy described in the paper by Jones et al. [1999d], and implemented here for this study.

Scan time, number of averages and resolution

As stated earlier, we have found that patients, particularly those with neuropsychiatric disorders, are not willing to tolerate the requirement to remain still for a single MR scan for periods in excess of 20 min, whereas our ‘success’ rate, in terms of patient motion and compliance, for DTI lasting in the region of 15 min is high. Based on this timing constraint, the requirement for isotropic voxels and the volume of brain to cover (a maximal superior‐inferior extent of the brain of 15 cm was assumed), consideration and measurement of signal to noise ratios with different voxel dimensions resulted in a decision to use a voxel dimension of 2.5 mm × 2.5 mm × 2.5 mm. This resolution was obtained with a field of view of 240 mm × 240 mm, an acquisition matrix of 96 × 96 and a slice thickness of 2.5 mm. Full brain (near‐axial orientation) coverage in the superior‐inferior direction necessitated acquisition of data from 60 slice locations. Because the sequence was prospectively peripherally gated to the cardiac cycle, an effective TR was selected that allowed at least 180 msec per image (sufficient time to collect, reconstruct and save each slice). For example, if the heart rate of the patient was 60 bpm, we used an effective TR of 12 R‐R intervals, with five slices per R‐R interval. If the heart rate was 70 bpm, we used an effective TR of 15 R‐R intervals (4 slices per R‐R interval). If the heart rate was 90 bpm, an effective TR of 20 R‐R intervals was used (with three slices per R‐R interval). Because these repetition times are much longer than the T₁‐relaxation times found in the brain, there were no problems due to variations in spin saturation. Depending on the heart rate, actual scan times varied between 13.5 minutes and 15.75 min. The ‘odd’ numbered slice locations (i.e., the first, third, fifth… and so on) were acquired first followed by the ‘even’ numbered slices. This strategy, together with the long sequence repetition time, meant that it was unnecessary to introduce any gap between image slices, which is often required with shorter TRs to minimize cross‐talk between adjacent slices.

Our calculations indicated that approximately 70 images would be required at each slice location to provide acceptable signal to noise ratios and precision in the estimates of the diffusion tensor. Because the optimal value of N _high/N _low had previously been determined to be approximately 9.1:1, the number of measurements made without diffusion gradients applied (N _low) was set to 7 and the number with diffusion gradients applied (N _high) was set to 64 giving a total of 71 images per slice location and a ratio N _high/N _low of 9.14:1. The 64 diffusion encoding gradient vectors were arranged uniformly in space using an algorithm based on an analogy with electrostatic repulsion, described by Jones et al. [1999d]. The imaging parameters, determined according to the optimization procedures described above are summarized in Table I. The configuration of diffusion encoding gradients used to approximate the optimal value of N _high/N _low of 9.1:1, is given in Table II. The amplitude of the diffusion gradient applied on each of the three axes for any particular image is given by multiplying the vector component in the table by the maximum gradient amplitude of 40 mT m⁻¹.

Table I.

Summary of acquisition parameters for DTI pulse sequence

Parameter
Echo time	107 ms
Repetition time	15 R‐R intervals
Duration of diffusion gradients	17.3 ms
Separation of diffusion gradients	49 ms
Amplitude of diffusion gradients	40 mT m−1
Maximum diffusion weighting	1300 s mm−2
# Measurements without diffusion gradients (per slice location)	7
# Measurements with diffusion gradients applied (per slice location)	64
Field of view	24 cm × 24 cm
Acquisition matrix	96 × 96
Slice thickness/gap	2.5 mm/0 mm
Number of slice locations	60

Table II.

List of diffusion gradient vectors applied for each of the 71 images collected at each slice location

Image	X	Y	Z	Image	X	Y	Z
1	0.000	0.000	0.000	37	0.888	0.417	0.193
2	0.000	0.000	0.000	38	−0.562	0.232	−0.794
3	0.000	0.000	0.000	39	−0.381	0.143	0.914
4	0.000	0.000	0.000	40	−0.306	−0.199	−0.931
5	0.000	0.000	0.000	41	−0.332	−0.130	0.934
6	0.000	0.000	0.000	42	−0.963	−0.265	0.044
7	0.000	0.000	0.000	43	−0.959	0.205	0.193
8	1.000	0.000	0.000	44	0.453	−0.889	0.068
9	0.000	1.000	0.000	45	−0.773	0.628	0.088
10	−0.026	0.649	0.760	46	0.709	0.408	0.575
11	0.591	−0.766	0.252	47	−0.693	0.024	0.721
12	−0.236	−0.524	0.818	48	0.682	0.529	−0.506
13	−0.893	−0.259	0.368	49	−0.142	−0.725	0.674
14	0.796	0.129	0.591	50	−0.740	0.388	0.549
15	0.234	0.930	0.284	51	−0.103	0.822	0.560
16	0.936	0.140	0.324	52	0.584	−0.596	0.551
17	0.506	−0.845	−0.175	53	−0.088	−0.335	0.938
18	0.346	−0.847	−0.402	54	−0.552	−0.792	0.259
19	0.457	−0.631	−0.627	55	0.838	−0.458	−0.296
20	−0.487	−0.389	0.782	56	0.363	−0.561	0.744
21	−0.618	0.673	0.407	57	−0.184	0.392	−0.901
22	−0.577	−0.105	−0.810	58	−0.721	−0.693	0.009
23	−0.827	−0.521	0.213	59	0.433	0.682	−0.589
24	0.894	−0.040	−0.447	60	0.502	0.690	0.521
25	0.290	−0.541	−0.789	61	−0.171	−0.509	−0.844
26	0.116	−0.963	−0.245	62	0.463	0.423	0.779
27	−0.800	0.403	−0.444	63	0.385	−0.809	0.444
28	0.514	0.840	0.174	64	−0.713	−0.247	0.656
29	−0.789	0.153	−0.596	65	0.260	0.885	−0.387
30	0.949	−0.233	0.211	66	0.001	0.077	−0.997
31	0.233	0.783	0.577	67	0.037	−0.902	0.430
32	−0.021	−0.188	−0.982	68	0.570	−0.303	−0.763
33	0.217	−0.956	0.199	69	−0.282	0.145	−0.948
34	0.774	−0.604	0.190	70	0.721	0.608	0.332
35	−0.161	0.356	0.921	71	0.267	0.960	−0.085
36	−0.147	0.731	−0.666

Subjects

We present here results in detail from two typical subjects, a 39‐year‐old male volunteer (Subject A) and an 80‐year‐old male volunteer (Subject B), both in good health and free of neuro‐psychiatric symptoms. Image data were acquired from 60 near‐axial slice locations parallel to the AC‐PC line. During scanning the subject's head was comfortably secured in the head‐coil by means of foam padding and a restraining strap stretched across the forehead.

Analysis

Data were analyzed on an independent workstation (Sun Sparcstation Ultra 140, Sun Microsystems, Mountain View, CA). The diffusion‐weighted images were initially corrected for the effects of eddy‐current induced distortion using in‐house software. For each data set, a reference image was first constructed by calculating the mean intensity in each voxel from all the non‐diffusion‐weighted images. Next, for each diffusion‐weighted image the downhill simplex method [Press et al., 1992] was used to select the optimal magnification, shear and displacement of the diffusion‐weighted images to give the best registration with the reference image. The ‘mutual information’ [Studholme et al., 1997] was used to assess the registration between the ‘reference’ image and the corrected image.

After correction of image distortion, the data were then masked from the background using a semi‐automated thresholding procedure and the diffusion tensor calculated for each voxel using multi‐variate linear regression after logarithmic transformation of the signal intensities [Basser et al., 1994]. The tensor matrix at each voxel was subsequently diagonalized to compute the eigen‐values, and images of the tensor trace and fractional anisotropy [Basser and Pierpaoli, 1996] were created.

The fractional anisotropy is one of a range of possible anisotropy indices [Basser and Pierpaoli, 1996], but was chosen because it is a) rotationally invariant; b) an intra‐voxel measure (as opposed to an inter‐voxel measure such as those proposed in Basser and Pierpaoli [1996] and Pierpaoli and Basser [1996] that tend to ‘smooth’ the data to improve robustness to noise); and c) does not require ordering of the eigen‐values according to their size, which has been shown to bias measurements [Pierpaoli and Basser, 1996]. A study by Papadakis et al. [1999c] that compared three rotationally invariant indices of anisotropy, namely fractional anisotropy, relative anisotropy and volume ratio [Basser and Pierpaoli, 1996], concluded that the fractional anisotropy index mapped diffusion anisotropy with the greatest signal to noise ratio and with the greatest detail. The volume ratio provided strongest contrast between regions of low and high anisotropy (albeit at the expense of SNR and lower detail), and relative anisotropy provided intermediate detail. For these reasons, fractional anisotropy was chosen to satisfy our primary remit of optimal visualization of fiber tracts in the human brain.

The dispim image display program (David Plummer, Medical Physics Dept., University College Hospital, London – http://www.medphys.ucl.ac.uk) was used to visualize and further analyze the data in axial orientation. The image processing package, Analyze (Biomedical Imaging Resource, Mayo Foundation, Rochester, MN), was then used to reformat the data into coronal and sagittal orientations and permit simultaneous viewing of all three orthogonal planes, using the ‘Fly’ facility.

After masking the anisotropy image data from the background noise, maximum intensity projections (MIP) of the 3D fractional anisotropy volume were computed using the MIP facility in Analyze (Biomedical Imaging Resource, Mayo Foundation). MIPs were created for a range of orientations to allow full appreciation of the anisotropic structures and for viewing in a cine loop.

White matter fiber trajectories were reconstructed and visualized in three dimensions by ‘tractography.’ Sets of voxels were selected manually in a) the cortico‐spinal tracts, and b) the body of the corpus callosum to act as seedpoints for the tracking process. Fiber tracts were then reconstructed using the method originally suggested by Basser [1998]. In brief, at each point the eigen‐vector associated with the largest eigen‐value (i.e., the direction of greatest diffusivity) was treated as being tangential to the trajectory of the tract. Each fiber trajectory was reconstructed by propagating a streamline bi‐directionally from an initial seedpoint in the direction of the principal eigen‐vector for 0.5 mm and then recomputing the principal eigen‐vector at the next location. The tracking process continued until the fractional anisotropy fell below a fixed threshold. For this purpose, a fractional anisotropy threshold of 0.15 was used. This was the threshold that appeared to consistently differentiate between white and grey matter when windowing the fractional anisotropy image. Once the trajectories were computed, they were displayed as surface rendered constant radius tubes using the mathematical software package MATLAB (The Mathworks, Natick, MA) along with three orthogonal cut planes showing fractional anisotropy to act as a frame of reference. The use of ‘streamtubes’ for visualizing white matter tract trajectories in this way was first suggested by Zhang et al. [2000].

RESULTS

The pulse sequence and requirement to remain still for 15 min were well tolerated by patients, and the image data were not affected by subject movement during scanning. This single‐shot EPI strategy allows pausing of acquisition and subsequent co‐registration of images, if necessary, without the requirement for further sophisticated correction of time‐domain data, as would be the case if movement occurred before completion of the desired k‐space trajectory [Atkinson et al., 2000].

The optimization of acquisition parameters resulted in high quality images of tensor‐derived indices, with clear definition of anisotropic structures throughout the entire brain. Figure 1 shows every third slice from the 60 slice fractional anisotropy image data set acquired from Subject A. The complete data set can be viewed at a website set up to accompany this study (http://www.mridiffusion.com).

Figure 1.

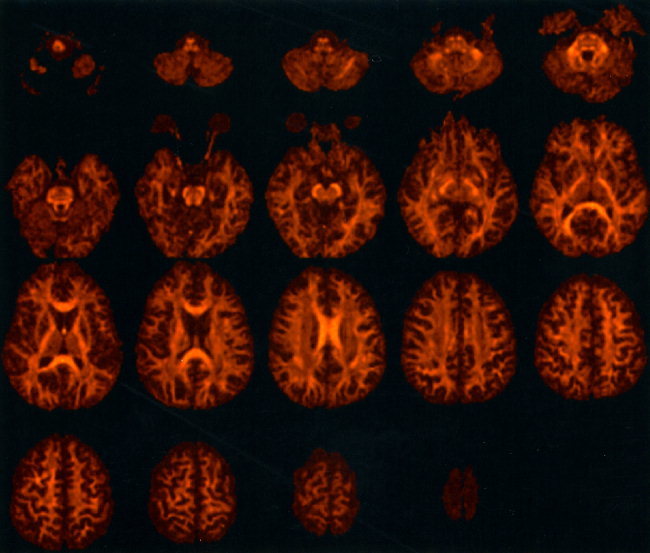
Fractional anisotropy data obtained from subject A in axial orientation. Every third slice is presented from the 60 slice data set. The data have been masked from the background.

In their article describing the optimization of DTI, Jones et al. [1999d] presented data acquired with a slice thickness of 5 mm. In this study, Figure 2 shows the advantage of reducing the slice thickness to 2.5 mm. Note that the edges of anisotropic structures, such as the splenium of the corpus callosum, are much more sharply defined when imaging with thinner slices due to a reduction in partial volume effects.

Figure 2.

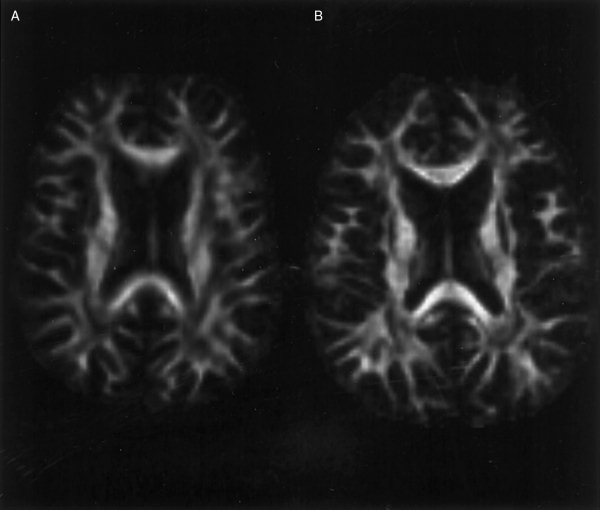
Demonstration of the effect of reducing slice thickness from (A) 5 mm to (B) 2.5 mm on image sharpness for Subject A. Note that the edges of anisotropic structures are more sharply defined in (B), due to a reduction in the partial volume effect.

Figure 3 shows examples of reformatting the data from Figure 1 into coronal and sagittal orientations. Note the absence of reformatting artifacts in the superior‐inferior direction, which is attributable to inter‐slice cross‐talk being negligible due to the long repetition time of the sequence.

Figure 3.

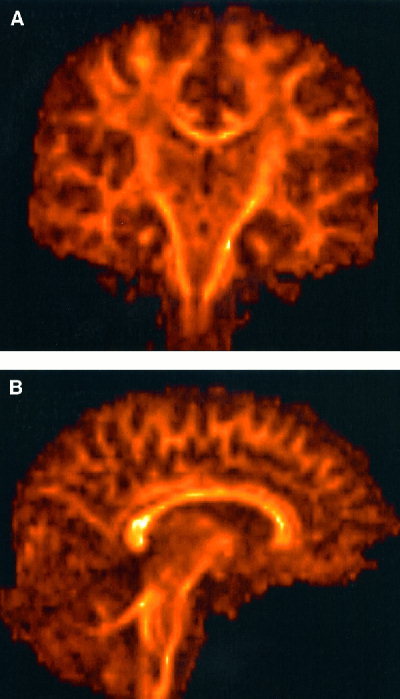
Results of reformatting the axially acquired data presented in Figure 1 into coronal plane (A) and sagittal plane (B). Note the absence of artifacts in the original slice‐selection direction (superior‐inferior), which is due to minimal slice cross‐talk resulting from a long TR.

Figure 4 shows the fractional anisotropy data obtained from Subject B. Again, the entire data set can be visualized at the accompanying website. The enlarged lateral ventricles and rarefaction of white matter due to the normal ageing process are clear. Note the exquisite depiction of tract thinning or depletion of the whole corpus callosum when compared to the younger volunteer.

Figure 4.

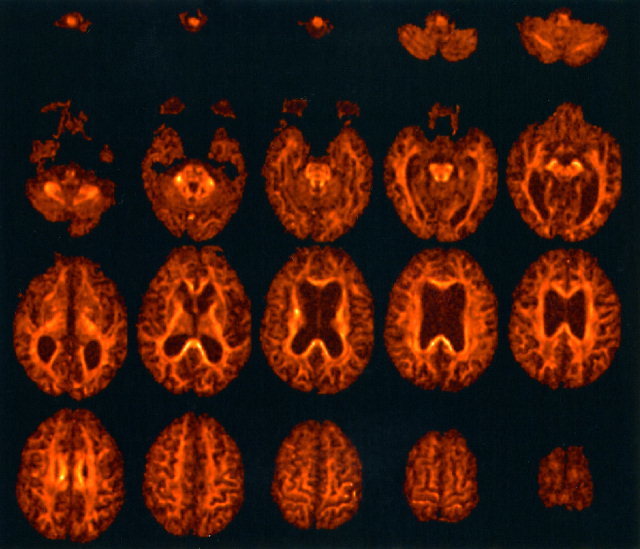
Fractional anisotropy data obtained from Subject B. Note the enlarged ventricles and reduction in white matter volume when compared to the data obtained from Subject A in Figure 1.

Figure 5 shows an example of the simultaneous visualization of anisotropy data in three orthogonal planes, using the ‘fly’ facility in Analyze. Space prohibits us from presenting such visualization for the entire brain volume here, but the data sets can be viewed interactively at the website mentioned above.

Figure 5.

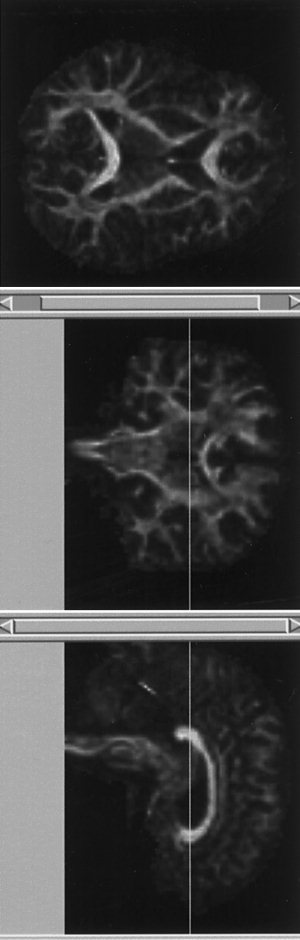
Examples of simultaneous visualization of fractional anisotropy obtained from Subject A in three orthogonal planes. The benefits of visualization in this format are best appreciated at http://www.mridiffusion.com

Figure 6 shows the result of performing the maximum intensity projection (MIP) on the data from Subject A. Cinematic MIP visualization of the whole head allows better visualization of entire tracts than is afforded by conventional 2D presentation. The cine loops can be viewed at http://www.mridiffusion.com. Furthermore, our 3D MIPs presented here accentuate the global white matter rarefaction seen in Subject B (when compared to Subject A) due to normal ageing.

Figure 6.

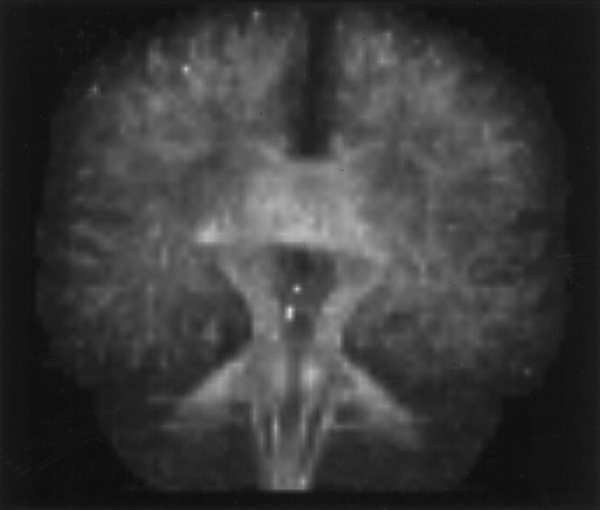
Maximum intensity projection reconstruction of the fractional anisotropy data obtained from Subject A. Cine loops of this data can be viewed at http://www.mridiffusion.com

Figure 7 shows an example of the tractography results obtained from Subject A. Fiber tract trajectories initiated from seedpoints placed within the cortico‐spinal tracts are displayed using red tubes, whereas those initiated from seedpoints in the body of the corpus‐callosum are displayed in green. Three orthogonal intersecting planes showing fractional anisotropy have also been included, to act as a frame of reference for the tract trajectories. The reconstructed trajectories are consistent with known anatomy, with tracts branching posteriorly from the cortico‐spinal tracts toward the cerebellum (red tubes) and tracts crossing the body of the corpus callosum in parallel fashion before arching upwards to the cortex (green tubes).

Figure 7.

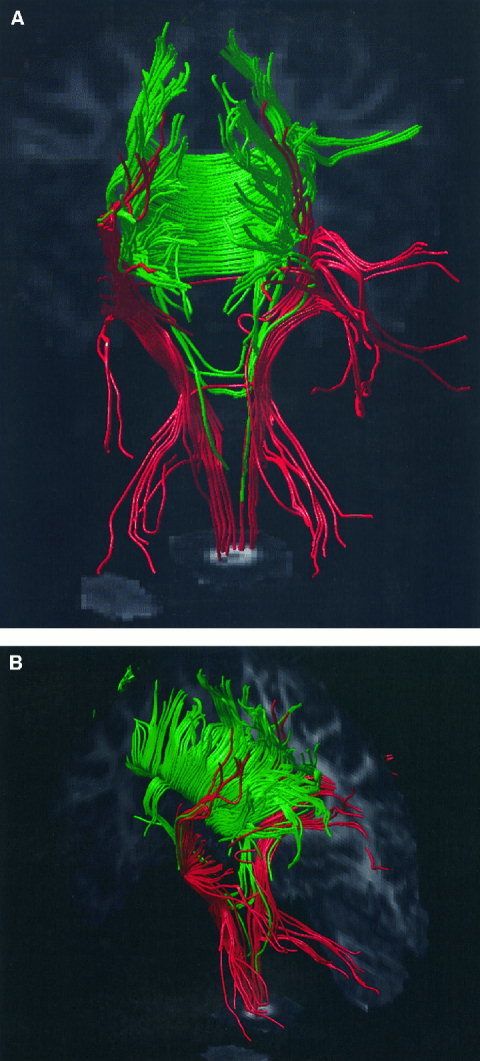
Two different views of white matter tract trajectories reconstructed from the DTI data obtained from Subject A. The pathways of reconstructed white matter tract trajectories are displayed using tubes of constant radius. Trajectories initiated from seedpoints placed in the cortico‐spinal tracts are shown in red, and those initiated from seedpoints placed in the body of the corpus callosum are shown in green. The three intersecting planes show the fractional anisotropy and serve as a useful frame of reference when viewing the reconstructed fiber tract trajectories.

DISCUSSION

This study has demonstrated that it is possible to obtain high quality diffusion tensor images from the whole adult brain, with isotropic resolution, within a time that could be tolerated by patients in a clinical setting. Through careful optimization of the imaging parameters we have been able to achieve the same precision in the tensor with much fewer images than would be required using non‐optimized DTI sequences. This allows either higher spatial resolution for the same total scan time, more slice locations, or both.

To date, we have obtained DT‐MRI data from over 90 subjects with this protocol including a wide range of healthy controls (n = 30), schizophrenic subjects (n = 30) and subjects with limb and bulbar onset amyotrophic lateral sclerosis (n = 30). The success rate, in terms of subject tolerance and obtaining a complete data set without corruptions due to subject motion, has been over 80%. We do not, of course, envisage that this protocol will be tolerated by all subject groups, for example actively psychotic patients or patients within 24 hr of an acute stroke. The applicability to a wider range of subjects than was previously possible with longer scan times should be enhanced, however, by using this protocol.

At our institution, we have chosen most commonly an axial or near‐axial orientation for MR data acquisition, because this orientation results in the least number of slices required to cover the whole brain and, for our system, minimizes the level of Nyquist ghost artifacts for echo planar imaging. By using isotropic resolution, however, and thus providing the ability to reformat into any plane, this pulse sequence is applicable to any neurological or psychiatric application. For example, in amyotrophic lateral sclerosis a coronal orientation is preferable for visualization of the motor tracts [Ellis et al. 1999a,b], whereas, for example, periventricular white matter disease or sclerotic plaques are often best viewed in axial orientation [Jones et al. 1999a; Werring et al., 1999]. Furthermore, the ability to reformat an isotropic data set into any plane means that the initial plane of acquisition can be selected for maximal signal to ghost ratio, i.e., it is very rare that any clinical system yields comparable temporal stability and signal to ghost ratio for all principal axes.

Acquiring data with whole brain coverage and isotropic voxels should make inter‐subject co‐registration of DTI data sets and serial intra‐subject co‐registration during progressive white matter degenerative processes easier. This should also be true for cross‐modality registration and mapping the data into a standard template ‘atlas’, such as the atlas of Tailarach and Tournoux [1988].

We have demonstrated that it is possible to reconstruct fiber tract trajectories with diffusion tensor MR data acquired in 15 min. This therefore potentially allows tractography to be employed as a clinical investigative tool, rather than it remaining as a research tool. Although the result presented in Figure 7 has some features in common with known neuroanatomy (parallel fibers across the body of the corpus callosum and tracts running to the cerebellum for example), there are other features that are not consistent. For example, the lateral connections of the cortico‐spinal tracts (shown in red) were not expected. Furthermore, the ‘streamline’ approach employed here does not allow the ‘inter‐digitation’ of fibers of the corpus callosum and internal capsule to be portrayed. The anatomical meaning of a result such as that presented in Figure 7 therefore needs to be treated with caution, and is the subject of future research.

Some groups have suggested that in certain regions in the brain where fibers cross or splay within a voxel, a single tensor model, which assumes Gaussian diffusion, is insufficient to fully characterize diffusion [Frank, 2001; Tuch et al., 1999; Wedeen et al., 2000]. This has led to the concept of ‘diffusion spectrum imaging’ [Wedeen et al., 2000] that aims to reconstruct the diffusion displacement profile by sampling diffusion over a wide range of angles. Frank [2001] has also shown how multiple fiber bundles within a voxel can be inferred by analysis of the diffusivity profile, again by sampling over a large range of angles. Such information may well help to resolve some of the discrepancies observed between known neuroanatomy and tractography results obtained using a single tensor model (Tuch et al. 2000).

The data acquisition strategies for these approaches are similar to the work presented here, in that they sample diffusion over a wide range of angles. They benefit from much higher diffusion weighting than was employed here, however, and would require a different optimization approach to that presented here. Although these approaches offer exciting prospects for resolution of complex fiber architecture, they are currently beyond the scope of most clinical investigations.

CONCLUSION

We have developed a diffusion tensor imaging protocol that allows high precision estimates of the diffusion tensor to be obtained from the entire adult brain in vivo in 15 min. The ability to acquire data from the whole brain and reformat in any plane means that the same sequence can be used for all subjects, thereby facilitating analysis and comparisons with a common database of control data.

The reduction in scan time should mean that more studies can incorporate DTI into the battery of imaging sequences, and the high quality of the images should mean that clinically useful diffusion tensor imaging data can be obtained from a wider group of patients.