Abstract
Neuroimaging studies of learning focus on brain areas where the activity changes as a function of time. To circumvent the difficult problem of model selection, we used a data‐driven analytic tool, cluster analysis, which extracts representative temporal and spatial patterns from the voxel‐time series. The optimal number of clusters was chosen using a cross‐validated likelihood method, which highlights the clustering pattern that generalizes best over the subjects. Data were acquired with PET at different time points during practice of a visuomotor task. The results from cluster analysis show practice‐related activity in a fronto‐parieto‐cerebellar network, in agreement with previous studies of motor learning. These voxels were separated from a group of voxels showing an unspecific time‐effect and another group of voxels, whose activation was an artifact from smoothing. Hum. Brain Mapping 15:135–145, 2002. © 2002 Wiley‐Liss, Inc.
Keywords: multivariate analysis, generalization error, cross‐validation, positron emission tomography, functional neuroimaging
INTRODUCTION
Data from most published studies are analyzed voxel‐by‐voxel, or region‐by‐region, fitting an a priori model to the recorded signal and highlighting brain regions where this model explains the variation in neural activity. For tasks with a complex interplay of sensation, movement, memory and attention, e.g., learning paradigms, the selection of an appropriate model is complicated, because the relation between time and neural activity is difficult to predict and varies from region to region [Toni et al., 1998].
Functional imaging studies of learning record cerebral activity at different time points over practice trials and identify brain regions where the activity changes as a function of time. Some studies contrast ‘early’ and ‘late’ stages of learning by comparing the first and the last scans [Jenkins et al., 1994; Jueptner et al., 1997; Krebs et al., 1998; Van Horn et al., 1998; van Mier et al., 1998], other assume a linear relation between the neural activity and time, fitting a linear function to data [Deiber et al., 1997; Grafton et al., 1992, 1994; Hazeltine et al., 1997; Toni and Passingham, 1999] or use the variation of an index of performance as regressor for the neural activity [Honda et al., 1998]. Recently, flexible models that fit combinations of basis functions to data have been applied to look at the neurophysiological correlate of learning [Toni et al., 1998]. The strength of this approach is that it allows for differential responses in different brain areas and models both linear and nonlinear dependencies. The type (e.g., cosine, polynomial, Taylor expansions) and the number of basis functions in a set, however, must be decided in advance [Buchel et al., 1996].
This study demonstrates the use of a data‐driven approach, cluster analysis, as an alternative tool for the analysis of temporally varying signals collected during experiments of motor learning. This method is based on a different set of assumptions and has complementary advantages to the traditional methods of data analysis. Cluster analysis extracts the main patterns in time and the corresponding spatial profiles and, in this way, summarizes all the data collected during an experiment. Because it does not depend on an a priori hypothesis about how the signal will vary over time, the analysis may reveal unexpected temporal signals. As a data‐driven multivariate method, cluster analysis is analogous to principal component analysis (PCA) [Friston et al., 1993; for an application in a neuroimaging study of motor learning see Frutiger et al, 2000] or independent component analysis (ICA) [McKeown et al., 1998], but unlike those approaches it does not impose orthogonality or statistical independence conditions on the spatio‐temporal patterns.
MATERIALS AND METHODS
Cluster analysis
Functional imaging data consist of a large number of voxel‐time series, each defining a waveform. The principle of the method is to partition the dataset by grouping similarly shaped waveforms together. The analysis returns a number of spatial patterns, the clusters, and their representative time series, the cluster centers. This principle has been implemented in various clustering techniques, most of them used previously in neuroimaging applications: fuzzy c‐means [Baumgartner et al., 1997], hierarchical clustering [Goutte et al., 1999], K‐means [Ding et al., 1994, 1996], mixture models [Ashburner et al., 1996], and dynamical clustering [Baune et al., 1999] being some examples.
We used the K‐means algorithm [MacQueen, 1967] with a low computational cost and fast convergence [Bottou and Bengio, 1995]. For a given number K of clusters, a set of initial cluster centers is chosen randomly from the data. The K‐means algorithm assigns vectors or voxel time‐series to the nearest cluster center, as measured by a similarity metric. When all vectors in the data have been assigned, the new cluster centers are calculated by averaging over cluster members, and the procedure is repeated until no data vectors change class between two iterations. A more detailed description of the K‐means method, including a discussion of the role of the similarity measure, is available in Goutte et al. [1999].
Optimizing the number of clusters
One of the key problems in clustering is to decide the optimal number of clusters (K). Here, we used a probabilistic approach designed to optimize the generalization of the clustering solution to independent data generated by the same statistical process [Hansen and Larsen, 1996; Goutte et al., 2001]. To generalize, the cluster structure must at the same time capture the full complexity of the data and avoid focusing on non‐generic details. With increasing K, the time series within the clusters are better characterized by the cluster centers as the within‐cluster variance decreases, but the resulting cluster structure becomes more dependent on the particular dataset.
The time series are assumed to be independent samples from an underlying mixture of K normal distributions. The parameters of this distribution, K vectors of mean values and a variance, are computed on data from all but one subject. Then, an error function, expressing the likelihood of data from the left‐out subject given the estimated model is calculated. To make the calculations independent on the specific choice of the data in the two subsets, the procedure is repeated for all possible partitionings of the data, and the error is averaged over these partitionings. This procedure is known as “blocked” leave‐one‐out cross validation in which data from one subject is treated like one item of data [see e.g., Bishop, 1995] or v‐fold cross‐validation with v = 18 [Smyth, 1996]. The optimal K corresponds to the model with the lowest generalization error. Details of the calculations are given in the Appendix.
Subjects
The subjects consisted of 18 paid healthy volunteers (median age: 24 years; range 22–29 years; 8 female, 10 male). All of them were right handed [Oldfield, 1971]. None of the subjects had past or present neurologic or psychiatric disorders or active use of medication or recreational drugs. Informed consent was obtained according to the Declaration of Helsinki II and the study was approved by the local ethics committee of Copenhagen (J. nr. (KF) 01‐194/97).
Experimental design
The subjects lay supine on a PET scanner bed, with their left hand on a mouse (FELIX) controlled by their index finger. They viewed a six‐pointed star generated on a computer screen placed at approximately 1‐meter in front of their eyes. The star subtended a visual angle of 10 degrees, the ratio of the width of the star‐shaped path to star diameter being 0.11. Using the mouse, the subjects moved a cursor (0.56 degrees visual angle) along the star‐shaped path. Each trial lasted for 90 sec. At the start of each trial the subjects positioned the cursor within the left‐most horizontal tip of the star. After 30 sec the cursor changed from an arrow to a red filled circle and the subjects traced the path in counterclockwise direction for 60 sec. They were instructed to work through the star‐shaped path as fast as possible and to avoid tracing outside the path. The position of the cursor in x and y direction was sampled every 0.03 sec. During the task of interest, mirror tracing, the position of the cursor was shown up‐down mirrored around the center of the screen. During the baseline task, tracing, the position of the cursor was not inverted. The subjects had 11 trials of tracing, then the cursor was inverted and the subjects were given 15 trials to practice this novel task. Eleven PET‐scans were conducted, starting after the fifth trial of tracing. Data was acquired only during even trials, giving a total of three tracing scans and eight mirror tracing scans (Fig. 1).
Figure 1.
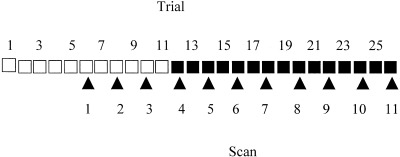
Diagram showing the course of the experiment. Tracing trials (□). Mirror tracing trials (▪). Scanned trials (arrow points).
The reason for scanning the last trials of the baseline task was to be able to isolate time‐effects in the data, in the form of monotonic increases or decreases of activity over the scan session. The tracing scans were placed at the beginning rather than interleaved as usually recommended [Petersson et al., 1999] to avoid interaction effects between the two tasks.
Data acquisition
PET scans were obtained with an 18‐ring GE‐Advance scanner (General Electric Medical Systems, Milwaukee, WI) operating in 3D‐acquisition mode, producing 35 image slices with an interslice distance of 4.25 mm. The total axial field of view was 15.2 cm with an approximate in‐plane resolution of 5 mm. The technical specifications have been described elsewhere [DeGrado et al., 1994; Lewellen et al., 1999]. PET scans were reconstructed with a 4.0 mm Hanning filter transaxially and axially with an 8.5 mm Ramp filter. Head movements were limited by head‐holders constructed by molded foam.
Every subject received 11 intravenous bolus injections of 400 MBq of H2 15O with an interscan interval of approximately 9 min. The isotope was administered in an antecubital intravenous catheter concomitantly with the trial onset, and a 90‐sec scan was triggered when the radioactivity reached the brain. Assuming a 45 sec delay for the radioactive bolus to reach the brain, the subjects were actively performing the task during the first 45 sec of image acquisition. After tracing the subjects lay still, with closed eyes. Emission scans were attenuation corrected with a 10 min transmission scan collected before the activation session.
Preprocessing
The images were realigned on a voxel‐by‐voxel basis using a 3D automated six‐parameter rigid body transformation (AIR software 3.08) [Woods et al., 1992] and transformed into the standard space of the atlas of Talairach and Tournoux [1988] as defined by Montreal Neurological Institute (MNI) [Evans et al., 1994], based on intra‐individual average PET images (SPM96) [Friston et al., 1995]. For this transformation a reference template PET image already conforming to the standard space was used. The stereotaxically normalized images consisted of 68 planes of 2 × 2 × 2 mm voxels. Images were smoothed with a 16‐mm isotropic Gaussian filter to increase the signal‐to‐noise ratio and accommodate the residual variation in morphological and topographical anatomy that was not accounted for by the stereotaxic normalization process.
All scans were scaled to have the same global activity. The global activity was estimated independent of changes in local activity, according to Andersson [1998].
To discard the voxels with no overall effect of the 11 conditions, an F‐statistic was computed for each voxel, and the data to enter the subsequent analysis was thresholded at P < 0.05 (SPM96, multisubject study, 11 conditions). 42% of the voxels survived the threshold, giving a total of 177,585 voxels to be clustered. The time series were extracted from the XA.mat matrix of the SPM96 output, which contained activity values adjusted for subject effects. For each voxel the time series was averaged over the subjects and centered, to classify different time series independent on the regional differences in the baseline activity levels.
Cluster analysis
The analysis was run for increasing values of K from 2 to 20 using the K‐means algorithm from the publicly available “lyngby” toolbox [Hansen et al., 2000, http://hendrix.imm.dtu.dk/software/lyngby]. For each of the 18 partitionings of the dataset, the voxel‐time series were averaged over 17 subjects used for estimating the model. The similarity measure was the Euclidean distance between the time series. We initialized the mean for each cluster with a set of K time series chosen randomly from the data, as proposed initially by MacQueen [1967]. This method is free of any assumption about the relative position of the ‘true’ cluster centers in the dataset, at the expense of being more sensitive to outliers than other methods proposed in the literature [Al'Daoud and Roberts, 1996; Lloyd, 1982]. To limit this risk, we performed 10 clusterings using different random initializations, and averaged the generalization error over these clusterings. Figure 2 shows the error calculated on data from the remaining one subject, averaged over 18 possible partitionings. The minimum of the error function at K = 6 indicates that a model with six clusters generalizes best across subjects. To assess the effect of random initialization on the generalization error, the standard deviation of the generalization error over 10 different random initializations was calculated, then averaged over 18 partionings of the dataset. For all K, this average standard deviation was small (<2.5 × 10−4), suggesting that for this dataset the choice of the initial centers for the clusters is not critical for the result of the analysis.
Figure 2.
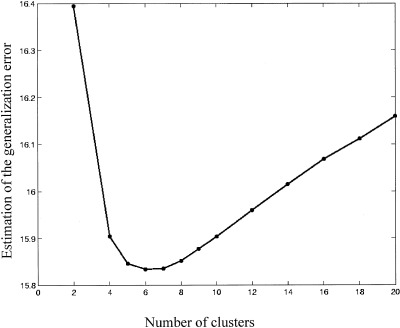
Generalization error calculated on data from one ‘left‐out’ subject, given the mixture model estimated on data from the other subjects. The error was calculated for increasing number of clusters up to K = 20 and averaged over 180 replications (18 possible partitionings of the dataset × 10 random initializations of the cluster centers).
Subsequently, the data from all subjects was pooled and clustered into six clusters. The initial cluster centers were six time series chosen randomly from the data, the number of clusters was set at K = 6 for which the generalization error function was lowest. To characterize voxels within the clusters further, regionally specific positive correlations (Pearson's r) between the voxel‐time series and the cluster center were calculated.
RESULTS
Task performance
Performance was indexed by velocity in terms of the cycles completed during a trial and accuracy as time spent outside the path relative to the tracing time. Figure 3 shows the decrease in speed and accuracy in the first mirror tracing trial and the fast improvement in performance with practice across trials.
Figure 3.
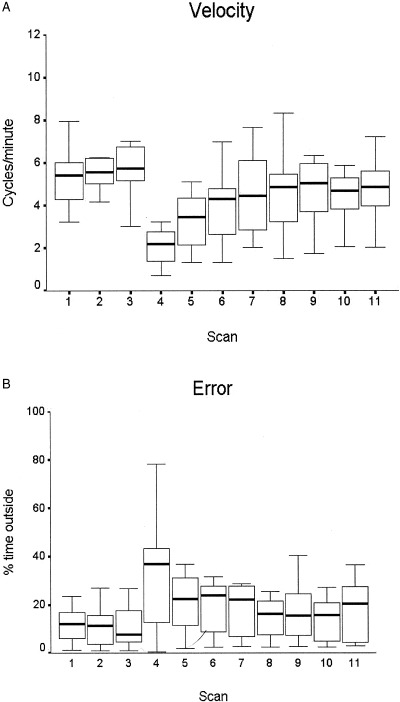
Behavioral data. A: Velocity of tracing, calculated as number of completed cycles around the star path in each trial of 60 sec. Median, interquartile interval and range are shown. The median for velocity in the eleven trials were significantly different (Kruskal‐Wallis test H = 37.893, P < 0.001 calculated from the chi‐square distribution with 10 degrees of freedom). Tracing scans: 1–3. Mirror tracing scans: 4–11. B: Error calculated as percentage of the tracing time in which the cursor was outside the path, with the same conventions as in (A). The difference between trials was not significant (P = 0.238, Kruskal‐Wallis test).
PET data
An overview of the six spatial patterns, the clusters, and their representative time series, the cluster centers, is given in Figure 4.
Figure 4.
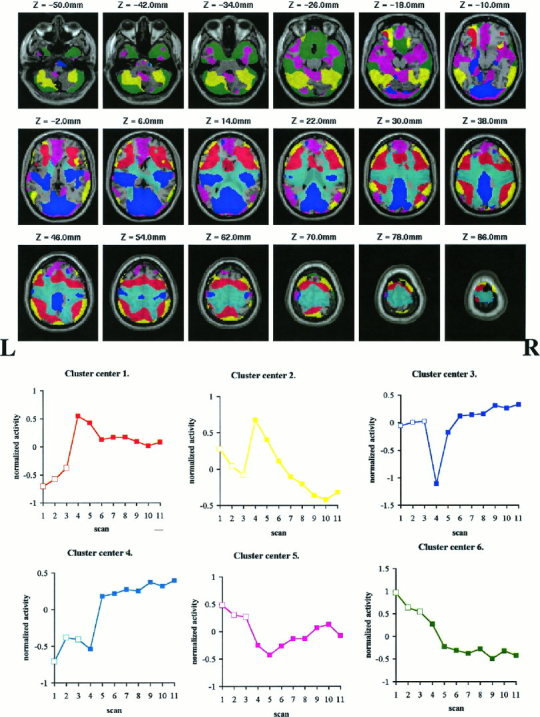
Overview over the spatial clusters (top) and the corresponding temporal patterns of activity, the cluster center (bottom), calculated as the average of time series from the individual voxels within a cluster. The spatial extent of each cluster and the cluster center are shown in the same color. The voxels assigned to the clusters are superposed on a single MRI template, in coregistration with the standard anatomical space; z is the vertical displacement relative to the AC–PC line (–below this line). The activity of the time series was normalized to 0 mean. Tracing scans (□). Mirror tracing scans (▪).
Some of the cluster voxels lie within the ventricles or white matter because of the 16 mm FWHM smoothing of the functional images. Most of the voxels, though, including those that correlate highest with the cluster center correspond to the cerebral sulci and gyri.
The time series forming the center of Cluster 4 is nearly the sum of the time series of the first and the third cluster centers. Anatomically, Cluster 4 is located between Clusters 1 and 3. Smoothing the signal in two regions separated by less than the FWHM can generate an artifactual signal in between, whose magnitude is the sum of the two individual signals. This cluster is probably such a smoothing artifact, its activity signal being a spillover from the adjacent voxels. The biological significance of the activity signal in Cluster 4 will therefore not be discussed further.
The similarity of the voxel‐time series to the cluster centers as a measure of the homogeneity of the clusters is shown in Figure 5 using the correlation coefficient between the voxel‐time series within a cluster and the cluster center.
Figure 5.
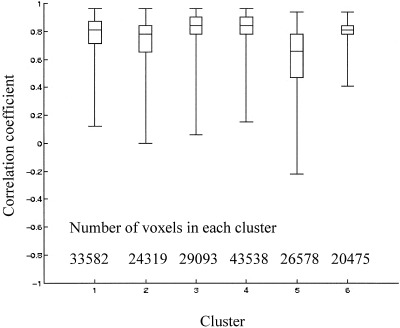
The correlation coefficient (Pearson's r) between the activity time series at each voxel and the cluster center for each of the 6 clusters is shown as a measure of the variance within the cluster. The median, range, and the 75th centile are shown. The cluster center is the average of the time series of the individual voxels within a cluster.
A summary of the anatomical location of the foci of high correlation with the cluster center (r > 0.9) for the Clusters 1, 2, 3, 5 and 6 is given in Table I.
Table I.
Local maxima of positive correlation with the representative time‐series in each cluster*
| Region | Cluster | ||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 5 | 6 | |
| R medial frontal gyri (BA6,9) | X | ||||
| L medial frontal gyri (BA6,9) | X | X | |||
| R lateral frontal cortex (6,9,44,45,46) | X | X | |||
| L lateral frontal cortex (6,9,44,45,46) | X | X | |||
| R anterior insula | X | ||||
| L anterior insula | X | ||||
| R anterior cingulate (BA24, 32) | X | X | |||
| L anterior cingulate (BA24, 32) | X | X | |||
| R frontal pole (BA10,11) | X | ||||
| L frontal pole (BA10,11) | X | ||||
| R basal forebrain | X | ||||
| L basal forebrain | X | ||||
| R post‐/precentral gyrus (BA4,3,2,1) | X | X | |||
| L post‐/precentral gyrus (BA4,3,2,1) | X | ||||
| R inferior parietal lobule (BA40) | X | X | X | ||
| L inferior parietal lobule (BA40) | X | X | X | ||
| R superior parietal lobule (BA40) | X | ||||
| L superior parietal lobule (BA40) | X | ||||
| R precuneus (BA7) | X | ||||
| L precuneus (BA7) | X | ||||
| R posterior cingulate (BA23,29,31) | X | ||||
| L posterior cingulate (BA23,29,31) | X | X | |||
| R cuneus (BA17,18) | X | ||||
| L cuneus (BA17,18) | X | ||||
| R lingual gyrus (BA18,19) | X | ||||
| L lingual gyrus (BA18,19) | X | ||||
| R lat occipital lobe (BA19,37) | X | X | |||
| L lat occipital lobe (BA19,37) | |||||
| R posterior insula | X | ||||
| L posterior insula | X | ||||
| R superior temporal lobe (BA21,22) | X | X | |||
| L superior temporal lobe (BA21,22) | X | X | |||
| R middle, inferior temporal gyri | X | X | X | ||
| L middle, inferior temporal gyri | X | X | |||
| R cerebellum‐lateral hemisphere | X | X | |||
| L cerebellum lateral hemisphere | X | X | |||
| R pallidum | X | ||||
| L pallidum | X | ||||
| Number of foci with correlation r > 0.90 | 23 | 18 | 27 | 13 | 37 |
The anatomical distribution of the local maxima of positive correlation between the voxel‐time series within the clusters and the cluster center. X, the occurrence of at least one focus with a correlation coefficient r > 0.9 in a brain region. The cluster center is the representative time series for a cluster, calculated as the average of the time series assigned to the cluster. The approximate Brodmann areas (BA) were found using the stereotactic atlas of Talairach and Tournoux (1988) (http://ric.uthscsa.edu/projects/talairachdaemon.html), after transforming the MNI coordinates into Talairach coordinates (http://www.mrc-cbu.cam.ac.uk/Imaging/mnispace.html). L, left; R, right.
Because the difference between the values of the generalization error for K = 6 and K = 7 was small, the results for the analysis with K = 7 were inspected for any notable difference from the analysis with K = 6. No such difference was found: six of the temporal patterns from the clustering with K = 7 reproduced almost exactly the patterns from K = 6, the remaining cluster resembled Cluster 4 in terms of both temporal pattern and anatomical location.
DISCUSSION
Activation patterns
Cluster 1
The voxels assigned to Cluster 1 had a maximum of activity in the first mirror tracing trial. Anatomically, the foci of maximum correlation for this clusters were distributed bilaterally in the frontal lobe anterior to the precentral sulcus and in the posterior parietal cortex.
Decreases of activity in the premotor and posterior parietal areas with practice have been observed over a wide range of motor tasks: reaching to visually displaced targets [Inoue et al., 2000], conditional motor learning [Deiber et al., 1997], tactile maze tracing [van Mier et al., 1998], motor sequence learning with auditory [Jenkins et al., 1994; Jueptner et al., 1997] or visual feed‐back [Toni et al., 1998]. These authors associate the activity in these areas to visuomotor transformations or to executive processes like working memory or attention to action.
Cluster 2
Cluster 2 was similar to the first cluster with respect to both time course and anatomical distribution. Unlike the first cluster though, it extended into the cerebellum, the foci of maximum correlation located posteriorly in the cerebellar hemisphere. The decrease in activity over practice trials in the cerebellar hemisphere is also in agreement with previous studies of skill acquisition [Frutiger et al., 2000; Jenkins et al., 1994; Jueptner et al., 1997; Toni et al., 1998; van Mier et al., 1998]. The posterior part of the cerebellum is thought to be involved in monitoring and controlling movement using sensory feedback [Jueptner and Weiller, 1998].
Cluster 3
Cluster 3 was characterized by an increase of activity over practice trials, mainly in the visual and sensorimotor cortices on both sides. The increase of activity with practice in these visual and somatosensory areas could reflect the improvement in hand and eye kinematics [Blinkenberg et al., 1996; Paus et al., 1995] or learning effects as described previously for the motor cortex [Grafton et al., 1992; Hazeltine et al., 1997].
Cluster 5
The voxels in cluster 5 were located in the frontal pole, cingulate gyrus and inferior in the temporal lobe on both sides. The biological significance of this cluster is not straightforward. It might represent noise, i.e., brain activity without a simple connection to the experimental task.
Cluster 6
Cluster 6 was spatially distributed in the cerebellum, basal forebrain and temporal lobes. The recorded activity decreased monotonically over the scan session, suggesting habituation with the experimental setting or decreasing levels of arousal [Rajah et al., 1998] as possible explanations. Cluster analysis can identify and separate such effects and is thus an alternative to the existing analytical and design‐related methods [Petersson et al., 1999]. Alternatively, given the location of the cluster at the edges of the volume, where registration errors are typically prominent, it is possible that this pattern of activity is a motion artifact.
Cluster analysis approach
With no a priori knowledge about the variation of the brain activity over time, we were able to detect learning effects in the brain that paralleled the adaptation at behavioral level.
The anatomical distribution of these changes was in line with previous studies of motor learning, reporting decreases of activity over time in a fronto‐parieto‐cerebellar network. In addition, the analysis showed an increase of activity in the visual and sensorimotor areas, probably related to increasing speed of hand and eye movement with practice. These signals were separated from non‐specific time effects and from a smoothing artifact.
Limitations of the generalization error approach
To decide on the number of clusters we have used the generalization error method, which optimizes the number of clusters according to a predictability criterion. From a biological point of view there is probably no ‘optimal’ number of clusters: increasing the number of clusters will increase the homogeneity of the functional connectivity networks. The resolution of the method and the noise in the data, however, limits the number of meaningful clusters. Assuming that the signal will generalize over subjects, whereas the noise will not, the cross‐validated likelihood approach used here allows to compare different clustering structures and choose one that predicts best new data, in the limits of the assumed Gaussian mixture model of the data set.
Several methods have been proposed for estimating the number of clusters in a likelihood framework, some examples being the Information Criterion proposed by Akaike [Goutte et al., 2001], the Bayesian Information Criterion [Fraley and Raftery, 1998; Smyth, 1996], the Integrated Completed Likelihood of Biernacki et al. [2000] and cross‐validated likelihood [Hansen and Larsen, 1996; Smyth, 1996, 1998]. These criteria lead usually to different clustering models [Goutte et al., 2001]. Direct comparison of the structures chosen by these criteria against the true structure of the data indicates that the performance of these methods depends on the natural structure [Smyth, 1996] and the size [Celeux, 2001] of the dataset. The cross‐validated likelihood method performs reasonably well at recovering the structure of real data from standard data sets such as iris, diabetes or vowel [Smyth, 1996]. Yet, on simulated data this method has been shown to overestimate the number of clusters [Smyth, 1996; Biernacki et al., 2000].
An inherent limitation of the generalization error approach to estimating the number of clusters is that it treats potentially interesting intersubject differences in the clustering structure as noise. Another limitation of the present model is that it constrains the Gaussian distributions that constitute the mixture to have isotropic and identical variances. For larger datasets, more flexible models have been shown to give a better estimate of the data, and thus to generalize best for independent data [see e.g., Mørch et al., 1997].
Despite its limitations, we adopted this solution to decide the number of clusters because it identifies predictive models for the structure of the data. Additionally, it offers the advantage of being automatic and in this way less subjective than a scheme of clustering based on manual selection.
Significance of the cluster centers
A neuroimaging dataset as acquired with PET or fMRI consists of a large number of time series, with a continuous gradation from one pattern in time to another. The purpose of applying cluster analysis to such a dataset was to identify its main temporal modes of variation in the form of the cluster centers. To attain this purpose, the cluster centers must summarize the voxel‐time series within the clusters well, that is the variance within each cluster must be small. The K‐means algorithm returns the clustering structure with minimal intra‐class variance and calculates the cluster centers as the average of the time series assigned to a cluster. In this way the cluster centers approximate the main temporal patterns in the data. The goodness of this approximation is given by the homogeneity of the clusters. Although some of the voxels in the current dataset have weak‐ to no‐correlation with the cluster center, the majority of the voxels in all clusters, are positively and highly correlated with the cluster centers. Figure 5 shows that over 75% of the voxels assigned to each of the Clusters 1–4 and 6, the functional clusters we attempt to interpret, have a correlation with the cluster center above 0.5.
Within each cluster, the similarity between the voxel‐time series and the cluster center varies across the assigned voxels. The clear anatomical borders between the clusters depicted in Figure 4 result from a hard clustering algorithm, which returns a simplified model of the data. For a more flexible model one could use a soft clustering technique, like fuzzy clustering [Bezdek, 1974; Dunn, 1974] instead of K‐means. The price for using a more flexible model is computational time and further assumptions, for instance the degree of fuzziness [Scarth et al., 1995].
Functional connectivity
The voxels within a cluster have similar patterns of activity over time, presumably reflecting direct synaptic connection or common afferents [Friston, 1997].
Functionally connected structures are likely to share a common function, which can be identified in the context of the studies that link brain locations to sensory, motor and cognitive processes. Cluster analysis can thus shed light on how a complex task is split into parallel processes in the brain. The reduced number of observations for each voxel in this experiment, however, limited the detail of the classification. Clustering on longer time series such as obtained with fMRI, electroencephalography or magnetoencephalography or on various features of the hemodynamic response, such as strength or delay extracted from cross‐correlation [Goutte, 2001], could uncover more specific functional connectivity structures.
In summary, we have demonstrated the use of a data‐driven approach for the analysis of functional imaging data. Its main strength is that it can be used exploratively, when prior knowledge about the task‐related brain activity is lacking. This might be useful for complex paradigms, for instance learning studies.
Acknowledgements
Karin Stahr and the staff at the PET center at Rigshospitalet, Copenhagen, are acknowledged for their participation. Furthermore the John and Birthe Meyer Foundation is gratefully acknowledged for the donation of the Cyclotron and PET scanner.
For k‐means [Celeux and Govaert, 1992; Goutte et al., 2001], the underlying density for a d‐dimensional data vector u j ∈ ℝd can be expressed as :
a mixture of K equally weighted Gaussian distributions with mean μk and common variances σ2. In our notation, M contains all the means μk for the K clusters. The mean is the cluster center for each cluster C k and the variance is the within‐cluster variance:
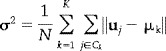 |
where N is the number of voxel time series. The likelihood of an independent dataset X is:
The generalization error is the negative logarithm of the likelihood:
REFERENCES
- Al'Daoud BM, Roberts, AS (1996): New methods for initialization of clusters. Pattern Recognit Lett 17: 451–455. [Google Scholar]
- Andersson JLR (1998): How to estimate global activity independent of changes in local activity. Neuroimage 6: 237–244. [DOI] [PubMed] [Google Scholar]
- Ashburner J, Haslam J, Taylor C, Cunningham VJ, Jones T (1996): A cluster analysis approach for the characterization of dynamic PET‐data In: Myers R, Cunningham VJ, Bailey D, Jones T, editors. Quantification of brain function using PET. San Diego: Academic Press; p 301–306. [Google Scholar]
- Baumgartner R, Scarth G, Teichtmeister C, Somorjai R, Moser E (1997): Fuzzy clustering of gradient‐echo functional MRI in the human visual cortex. Part I: reproducibility. J Magn Reson Imaging 7: 1094–1101. [DOI] [PubMed] [Google Scholar]
- Baune A, Sommer FT, Erb M, Wildgruber D, Kardatzki B, Palm G, Grodd W (1999): Dynamical cluster analysis of cortical fMRI activation. Neuroimage 9: 477–489. [DOI] [PubMed] [Google Scholar]
- Bezdek JC (1974): Cluster validity with fuzzy sets. J Cybernetics 3: 58–72. [Google Scholar]
- Biernacki C, Celeux G, Govaert G (2000): Assessing a mixture model for clustering with the integrated completed likelihood. IEEE Trans Pattern Analysis Machine Intelligence 22: 719–725. [Google Scholar]
- Bishop CM (1995): Neural networks for pattern recognition. Oxford: Clarendon Press; 375 p. [Google Scholar]
- Blinkenberg M, Bonde C, Holm S, Svarer C, Andersen J, Paulson OB, Law I (1996): Rate dependence of regional cerebral activation during performance of a repetitive motor task: a PET study. J Cereb Blood Flow Metab 16: 794–803. [DOI] [PubMed] [Google Scholar]
- Bottou L, Bengio Y (1995): Convergence properties of the K‐means algorithm In: Advances in neural information processing systems Cambridge: MIT Press; vol 7 pp 585–592. [Google Scholar]
- Büchel C, Wise RJ, Mummery CJ, Poline JB, Friston KJ (1996): Nonlinear regression in parametric activation studies. Neuroimage 4: 60–66. [DOI] [PubMed] [Google Scholar]
- Celeux G, Govaert, G (1992): A classification EM algorithm for clustering and two stochastic versions. Comput Stat Data Anal 14: 315–332. [Google Scholar]
- Celeux G (2001): Different points of view for choosing the number of components in a mixture model In: Govaert G, Janssen J, Limnios N, editors. Proceedings ASMDA. Compiégne; p 21–28. [Google Scholar]
- DeGrado TR, Turkington TG, Williams JJ, Stearns CW, Hoffman JM, Coleman RE (1994): Performance characteristics of a whole‐body PET scanner. J Nucl Med 35: 1398–1406. [PubMed] [Google Scholar]
- Deiber MP, Wise SP, Honda M, Catalan MJ, Grafman J, Hallett M (1997): Frontal and parietal networks for conditional motor learning: a positron emission tomography study. J Neurophysiol 78: 977–991. [DOI] [PubMed] [Google Scholar]
- Ding X, Tkach J, Ruggeri P, Masaryk T (1994): Analysis of the time‐course functional MRI data with clustering methods without use of reference signal. Proceedings of the Society of Magnetic Resonance. San Francisco: ISMRM; p 630. [Google Scholar]
- Ding X, Tkach J, Ruggeri P., Masaryk T (1996): Detection of activation patterns in dynamic functional MRI with clustering technique. Proceedings of the International Society for Magnetic Resonance in Medicine. New York: ISMR; p 1798. [Google Scholar]
- Dunn JC (1974): A fuzzy relative of the ISODATA process and its use in detecting compact, well‐separated clusters. J Cybernetics 3: 32–57. [Google Scholar]
- Evans AC, Kamber M, Collins DL, McDonald D (1994): An MRI‐based probabilistic atlas of neuroanatomy In: Shorvon S, Fish D, Andermann F, Bydder GM, Stephan H, editors. Magnetic resonance scanning and epilepsy. NATO ASI Series A, Life Sciences Volume 264 New York: Plenum Press; p 263–274. [Google Scholar]
- Fraley C, Raftery AE (1998): How many clusters? Which clustering method? Answers via model‐based cluster analysis. Comput J 41: 578–588. [Google Scholar]
- Friston KJ (1997): Analyzing brain images: principles and overview In: Frackowiak RSJ, Friston KJ, Frith CD, Dolan RJ, Mazziotta JC, editors. Human brain function. San Diego: Academic Press; p 25–41. [Google Scholar]
- Friston KJ, Ashburner J, Frith CD, Poline JB, Heather JD, Frackowiak RSJ (1995): Spatial registration and normalization of images. Hum Brain Mapp 3: 165–189. [Google Scholar]
- Friston KJ, Frith CD, Liddle PF, Frackowiak RS (1993): Functional connectivity: the principal‐component analysis of large (PET) data sets. J Cereb Blood Flow Metab 13: 5–14. [DOI] [PubMed] [Google Scholar]
- Frutiger SA, Strother SC, Anderson JR, Sidtis JJ, Arnold JB, Rottenberg DA (2000): Multivariate predictive relationship between kinematic and functional activation patterns in a PET study of visuomotor learning. Neuroimage 12: 515–527. [DOI] [PubMed] [Google Scholar]
- Goutte C, Toft P, Rostrup E, Nielsen FA, Hansen LK (1999): On clustering fMRI time series. Neuroimage 9: 298–310. [DOI] [PubMed] [Google Scholar]
- Goutte C, Hansen LK, Liptrott MG, Rostrup E (2001): Feature space clustering for fMRI meta‐analysis. Hum Brain Mapp 13: 165–183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grafton ST, Hazeltine E, Ivry RB (1998): Abstract and effector‐specific representations of motor sequences identified with PET. J Neurosci 18: 9420–9428. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grafton ST, Mazziotta JC, Presty S, Friston KJ, Frackowiak RS, Phelps ME (1992): Functional anatomy of human procedural learning determined with regional cerebral blood flow and PET. J Neurosci 12: 2542–2548. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grafton ST, Woods RP, Tyszka M (1994): Functional imaging of procedural motor learning: relating cerebral blood flow with individual subject performance. Hum Brain Mapp 1: 221–234. [DOI] [PubMed] [Google Scholar]
- Hansen LK, Larsen J (1996): Unsupervised learning and generalization. In: Proceedings of the IEEE International Conference on Neural Networks. Washington DC: IEEE Press; p 25–30. [Google Scholar]
- Hansen LK, Nielsen Få, Liptrot MG, Goutte C, Strother SC, Lange N, Gade A, Rottenberg DA, Paulson OB (2000): “lyngby”—A modeler's Matlab toolbox for spatio‐temporal analysis of functional neuroimages. Neuroimage 11: S917. [Google Scholar]
- Hazeltine E, Grafton ST, Ivry R (1997): Attention and stimulus characteristics determine the locus of motor‐sequence encoding. A PET study. Brain 120: 123–140. [DOI] [PubMed] [Google Scholar]
- Honda M, Deiber MP, Ibanez V, Pascual Leone A, Zhuang P, Hallett M (1998): Dynamic cortical involvement in implicit and explicit motor sequence learning. A PET study. Brain 121: 2159–2173. [DOI] [PubMed] [Google Scholar]
- Inoue K, Kawashima R, Satoh K, Kinomura S, Sugiura M, Goto R, Ito M, Fukuda H (2000): A pet study of visuomotor learning under optical rotation. Neuroimage 11: 505–516. [DOI] [PubMed] [Google Scholar]
- Jenkins IH, Brooks DJ, Nixon PD, Frackowiak RS, Passingham RE (1994): Motor sequence learning: a study with positron emission tomography. J Neurosci 14: 3775–90. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jueptner M, Stephan KM, Frith CD, Brooks DJ, Frackowiak RS, Passingham RE (1997): Anatomy of motor learning. I. Frontal cortex and attention to action. J Neurophysiol 77: 1313–1324. [DOI] [PubMed] [Google Scholar]
- Jueptner M, Weiller C (1998): A review of differences between basal ganglia and cerebellar control of movements as revealed by functional imaging studies. Brain 121: 1437–1449. [DOI] [PubMed] [Google Scholar]
- Krebs HI, Brashers Krug T, Rauch SL, Savage CR, Hogan N, Rubin RH, Fischman AJ, Alpert NM (1998): Robot‐aided functional imaging: application to a motor learning study. Hum Brain Mapp 6: 59–72. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lewellen TK, Miyaoka RS, Swan WL. 1999. PET imaging using dual‐headed gamma cameras: an update. Nucl Med Commun 20: 5–12. [DOI] [PubMed] [Google Scholar]
- Lloyd SP (1982): Least square quantization in PCM. IEEE Transactions on Information Theory 28: 129–137. [Google Scholar]
- MacQueen J (1967): Some methods for classification and analysis of multivariate observations. Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability. Berkeley: University of California Press; vol 1 pp 281–297. [Google Scholar]
- McKeown MJ, Makeig S, Brown GG, Jung TP, Kindermann SS, Bell AJ, Sejnowski TJ (1998): Analysis of fMRI data by blind separation into independent spatial components. Hum Brain Mapp 6: 160–188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mørch N, Hansen LK, Strother SC, Svarer C, Rottenberg DA, Lautrup B, Savoy R, Paulson OB (1997): Nonlinear vs. linear models in functional neuroimaging: learning curves and generalization crossover In: Duncan J, Gindi G, editors. Proceedings of the 15th International Conference on Information Processing in Medical Imaging Volume 1230 Berlin: Springer Verlag; p 259–270. [Google Scholar]
- Oldfield RC (1971): The assessment and analysis of handedness: the Edinburgh inventory. Neuropsychologia 9: 97–113. [DOI] [PubMed] [Google Scholar]
- Paus T, Marrett S, Worsley KJ, Evans AC (1995): Extraretinal modulation of cerebral blood flow in the human visual cortex: implications for saccadic suppression. J Neurophysiol 74: 2179–83. [DOI] [PubMed] [Google Scholar]
- Petersson KM, Elfgren C, Ingvar M (1999): Learning‐related effects and functional neuroimaging. Hum Brain Mapp 7: 234–243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rajah MN, Hussey D, Houle S, Kapur S, McIntosh AR (1998): Task‐independent effect of time on rCBF. Neuroimage 7: 314–325. [DOI] [PubMed] [Google Scholar]
- Scarth G, McIntyre M, Wowk B, Somorjai R (1995): Detection of novelty in functional images using fuzzy clustering. Nice: ISMRM; p 238. [Google Scholar]
- Smyth P (1996): Clustering using Monte Carlo cross‐validation. Proceedings of the 2nd international Conference on Knowledge Discovery and Data Mining. Portland: AAAI Press; p 126–133. [Google Scholar]
- Smyth P (2000): Model selection for probabilistic clustering using cross‐validated likelihood. Stat Comput 10: 63–72. [Google Scholar]
- Talairach J, Tournoux P (1988): Co‐planar stereotaxic atlas of the human brain. 3‐Dimensional proportional system: an approach to cerebral imaging. Stuttgart: Thieme. [Google Scholar]
- Toni I, Krams M, Turner R, Passingham RE (1998): The time course of changes during motor sequence learning: a whole‐brain fMRI study. Neuroimage 8: 50–61. [DOI] [PubMed] [Google Scholar]
- Toni I, Passingham RE (1999): Prefrontal‐basal ganglia pathways are involved in the learning of arbitrary visuomotor associations: a PET study. Exp Brain Res 127: 19–32. [DOI] [PubMed] [Google Scholar]
- Van Horn JD, Gold JM, Esposito G, Ostrem JL, Mattay V, Weinberger DR, Berman KF (1998): Changing patterns of brain activation during maze learning. Brain Res 793: 29–38. [DOI] [PubMed] [Google Scholar]
- van Mier H, Tempel LW, Perlmutter JS, Raichle ME, Petersen SE (1998): Changes in brain activity during motor learning measured with PET: effects of hand of performance and practice. J Neurophysiol 80: 2177–2199. [DOI] [PubMed] [Google Scholar]
- Woods RP, Cherry SR, Mazziotta JC. 1992. Rapid automated algorithm for aligning and reslicing PET images. J Comput Assist Tomogr 16: 620–633. [DOI] [PubMed] [Google Scholar]


