Spatial mixture modeling of fMRI data

Abstract

Recently, Everitt and Bullmore [1999] proposed a mixture model for a test statistic for activation in fMRI data. The distribution of the statistic was divided into two components; one for nonactivated voxels and one for activated voxels. In this framework one can calculate a posterior probability for a voxel being activated, which provides a more natural basis for thresholding the statistic image, than that based on P‐values. In this article, we extend the method of Everitt and Bullmore to account for spatial coherency of activated regions. We achieve this by formulating a model for the activation in a small region of voxels and using this spatial structure when calculating the posterior probability of a voxel being activated. We have investigated several choices of spatial models but find that they all work equally well for brain imaging data. We applied the model to synthetic data from statistical image analysis, a synthetic fMRI data set and to visual stimulation data. Our conclusion is that the method improves the estimation of the activation pattern significantly, compared to the nonspatial model and to smoothing the data with a kernel of FWHM 3 voxels. The difference between FWHM 2 smoothing and our method were more modest. Hum. Brain Mapping 11:233–248, 2000. © 2000 Wiley‐Liss, Inc.

INTRODUCTION

In the literature on analysis of functional magnetic resonance imaging (fMRI) data, the focus is primarily on the temporal aspect. Perhaps the most common analysis scheme is to treat voxel time series separately, and estimate the activation level voxel by voxel. This framework ranges from simple t‐tests and correlation methods to more detailed models for the haemodynamic response, and models that account for correlated noise. The latter encompasses generalized linear models and time series models. A few articles that fall in this category are Bandettini et al. [1993], Bullmore et al. [1996], Worsley and Friston [1995], and Lange and Zeger [1997], but we refer to an overview article such as Lange et al. [1999] for the long list of references that should be cited in this context.

The spatial properties of the data are rarely modeled with the same care as is given the temporal ones: Common approaches are either to assume spatial independence or to smooth data spatially with a Gaussian kernel. The latter approach has been studied primarily by Keith Worsley in a series of articles (see, e.g., Worsley et al., 1996). Smoothing the data spatially is in fact equivalent to using a nonparametric model for the spatial activation pattern, assuming only smoothness of the latter [Müller, 1988]. It should hence be viewed as an estimation procedure that is optimal in this model, but there is no general statistical reason for smoothing. On the contrary, smoothing may produce a biased estimate by displacing activation peaks and underestimating the height of the latter [Descombes et al., 1998; Hartvig, 1999].

Even if explicit spatial models are rare, the value of including spatial information in the analysis has been recognized for many years. Commonly this is achieved by assessing significance of activation by the size of suprathreshold clusters. This was first suggested by Poline and Mazoyer [1993] and later studied from a theoretical point of view [Friston et al., 1994; Poline et al., 1997] using Monte Carlo methods [Forman et al., 1995] and permutation methods [Bullmore et al., 1999]. In our minds the important distinction here is that of a spatial model and the inference made in this. Even if cluster size is used as a measure of significance, the estimated pattern is still a product of the underlying model used to produce the clusters. Also in this context, the nonparametric smoothing model seems to be the typical choice.

Recently, Descombes et al. [1998] proposed a Markov random field model for the spatio‐temporal activation pattern and used this for estimation of the latter. Their assumption is that the activation pattern is spatially coherent, yet may possess sharp boundaries between different regions, and the model introduces this explicitly in the estimation procedure. Assessment of uncertainty and significance is not straightforward in this framework as it requires simulations of the posterior distribution of the spatio‐temporal activation pattern. In principle this may be done with Markov chain Monte Carlo (MCMC) techniques [Gilks et al., 1996], but because the state space of the spatio‐temporal activation pattern is enormous, it is a time‐consuming and far from trivial task. Instead the authors suggested to use the procedure only as a preprocessing step, and did not use the model for making explicit inference on the activation.

The dimensionality of the activation pattern is much reduced in Hartvig [1999] where stronger assumptions are made. Specifically, the activation is modeled as a collection of centres with Gaussian shape but with unknown extent and height. This enables inclusion of prior information directly in the model, and simulation of the posterior distribution is possible by MCMC. However, also in this context the need to perform lengthy simulations is a limitation of the method.

The problems of the two last approaches perhaps explain the lack of spatial models: 1) It is somewhat difficult to formulate the general idea of coherency of activated regions in a specific model, which is still general enough to model the range of patterns observed in brain data. 2) Most spatial models are analytically intractable, and statistical inference must rely on simulation methods, which are time consuming and often require a lot of user interaction. The latter makes them less suitable for routine use. In this article we try to bridge the gap between formulating a spatial model, which has some realistic properties, and the computational feasibility, which makes it applicable in a routine analysis. The idea is to formulate the model through the marginal distribution on a small grid of voxels, for instance a 3 × 3 region in the slice.

Though the model may be used as the spatial part of a spatio‐temporal model, we will only consider the problem of estimating the activation pattern based on a single summary image (or volume) of voxel‐wise activation estimates, also known as a statistical parametric map (SPM). Let {x _i } denote the latter, where i indexes the voxels. Recently, Everitt and Bullmore [1999] (henceforth denoted EB) suggested a marginal analysis of such an image. Let A _i be the indicator for voxel i being activated. The approach of EB is to calculate the conditional probability P(A _i = 1|x _i) for each voxel, and use the latter to estimate the activated areas. In order to calculate this, they specify the distribution of activated and nonactivated voxels, i.e. the conditional distributions p(x _i |A _i = 1) and p(x _i |A _i = 0), as well as the probability P(A _i = 1). The method does not use any spatial properties of the data.

What we propose in this article is to keep the simplicity of the approach in EB, but to extend it in such a way that spatial interaction is partly taken into account. Instead of using P(A _i = 1|x _i) we suggest to use P(A _i = 1|x ${}_{\mathit{\text{C}}{}_{\mathit{\text{i}}}}$), where C _i is voxel i together with the neighbouring voxels. The idea is that activated areas tend to constitute a group of at least a few voxels, hence voxel i has a higher chance of being activated if both voxel i and some of its neighbours have high values. Conversely, the activation probability is small if x _i is high, but all the neighbours have small values. The main problem in this approach becomes the specification of the marginal probabilities of the activation A ${}_{\mathit{\text{C}}{}_{\mathit{\text{i}}}}$ in the region C _i. We propose three different models for these probabilities, ranging from a very simple one to a more realistic one. Common to all is that the probability of a voxel being activated has a simple expression, which can be easily calculated.

THEORY

In the two first subsections we present an overview of the method and the spatial models for the activation pattern. The third subsection is on estimation of parameters in the model and is more technical than the two first. The reader who is most interested in the general concept and examples of application of the model may skip this third subsection on a first reading.

Overview of the Mixture Model

As mentioned in the introduction, we assume that a statistical parametric map {x _i } is given, and we wish to derive a posterior probability that a voxel is activated using this map. In the following we will describe how a local model for the activation pattern around a voxel i can be used to incorporate spatial information in the posterior probability. In order to simplify notation we will drop the voxel index i from the notation.

Suppose we consider k neighbours around voxel i. Typically these would be the 8 neighbours in a 3 × 3 square in the slice or the 26 neighbours in a 3 × 3 × 3 cube in a volume of slices with voxel i in the centre. We will let C denote the set of k + 1 voxels given by voxel i together with the k neighbours.

We will let A be an indicator for the event that voxel i is activated, in the sense that A = 0 means that there is no activation in voxel i and A = 1 means that the voxel is activated. Likewise, we will let A ¹, …, A ^k be a vector of indicators for activation in the k neighbours. We index the As by a superscript to avoid confusion with the usual voxel subscript. Finally A _C = (A, A ¹, …, A ^k) is the vector of all activation indicators in C. We will consider this as a vector of unobserved stochastic variables and formulate a model for its distribution. Thus for each vector a _C = {0, 1}^k+1 we specify the prior probability P(A _C = a _C) that the activation configuration takes a particular value. Different choices of models, which reflect the idea that activated areas tend to constitute a cluster of voxels, are proposed in the next section.

Rather than observing A _C, we observe x _C = (x, x ¹, …, x ^k), the values of the test statistic for activation in the different voxels. Like before x is the value for voxel i, and x ¹, …, x ^k are the values for the neighbours. The usual hypothesis testing approach assumes a specific model for x given that the voxel is not activated, for instance that this is a normal variable with zero mean and unit variance. In our setup, we require that one can also specify the alternative distribution, i.e., the distribution of x given A = 1. In EB the statistics are fundamental power quotients (FPQ), which have respectively a central and a noncentral χ²‐distribution under the two activation states. In our Example 3, the test statistics are the estimated activity level from a regression analysis, and it is natural to take (x|A = 0) ∼ N(0, σ²). When the voxel is activated, A = 1, it is not so clear what the proper distribution is. We find that the range of different activation levels are described well by a Gamma distribution, (x|A = 1) ∼ Γ(λ, β). Denote the distribution of x _C given A _C = a _C by the density f(x _C |a _C).

When these two parts of the model are specified it is straightforward to calculate the posterior probability of an activation configuration a _C given the data x _C, since, by Bayes rule, this is given by

Thus the posterior probability that the activation pattern A _C equals a _C is simply proportional to the likelihood of observing x _C given A _C = a _C times the prior probability of A _C = a _C. In particular, one may calculate the probability that voxel i is active or not, irrespectively of the neighbours, by summing over the neighbouring states,

(1)

where a _C = (a, a ¹, …, a ^k). The constant of proportionality can be determined from the fact that the probabilities P(A = 0|x _C) and P(A = 1|x _C) must sum to one.

The problem with using this approach in practice is the calculation of the sum in (1), which has 2^k terms. In the situation with a 3 × 3 × 3 neighbourhood cube, the sum thus has 2²⁶ or about 67 million terms, and since we must calculate this for each voxel in the volume, we are facing an order of 10¹³ iterations. Even though the computations may be performed in parallel, this is of course hopelessly too many in practice. The main contribution of our method is that we propose models for P(A _C = a _C), which are able to model clustered activation, but where the sum may be calculated analytically. Thus we obtain a simple, closed form expression for the posterior probability that a voxel is activated, which may be calculated almost instantly. These are given for each of the three models in the following sections, see equations (4), (16), and (19).

We will assume in the following that the statistics x _C are independent given the true activation pattern A _C. Thus the density of x _C given A _C can be written as,

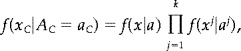where f(x|a) is the density of x given A = a.

Models for the Marginal Probabilities

In this section we give three choices for the marginal probabilities P(A _C = a _C), a _C = (a, a ¹, …, a ^k) ∈ {0, 1}^k+1. For an activation configuration a _C, we will let s = a + a ¹ + ⋮ a ^k, that is the number of ones in a _C.

Model 1

Perhaps the most simple choice is to take

(2)

Since there are 2^k+1 values of a _C we must have q ₀ = 1 − (2^k+1 − 1)q ₁ in order that the probabilities sum to one. Thus this distribution has only one parameter and a natural way of interpreting this parameter is through the probability p of a voxel being activated. This gives p = q ₁2^k or

(3)

Notice that in the model there is equal probability of observing a configuration with all ones and one with only ones in a corner of the region C, for instance. If we expected the activated areas to be large coherent regions, the former probability should be larger than the second, whereas if we expected the areas to be of moderate size but with long boundaries, the second probability should be larger than the first. The above model hence represents the situation that we neither believe that activated regions consist of single voxels nor that they are very large.

We will illustrate in this simple situation how the posterior probability in (1) may be calculated. We shall be using the equality

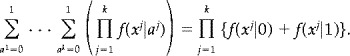Let η denote the above product. When a = 0 the expression in (1) is

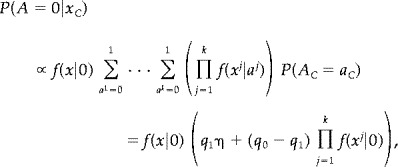and when a = 1 we simply get

Since the two probabilities must sum to one, we find,

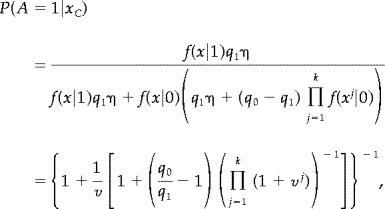(4)

where

(5)

Notice that v is the likelihood ratio for the voxel being active vs. not active. The formula (4) thus effectively combine the likelihood ratios from voxel i together with those of its neighbours to calculate the posterior probability of activation. The formula shows in a direct way the difference to the approach in EB. If all the neighbours are nonactivated then (4) will typically be of the order

whereas if at least one neighbour is activated the order is typically

For illustration let us consider the case where p = 0.02 and k = 8. Then q ₀/q ₁ = 12289, and if f(x|0)/f(x|1) ≈ exp(−8) then the first term is 0.20 whereas the second expression is 0. 9997.

Model 2

Another simple choice of P(A _C = a _C) is

(6)

Here γ = 1 gives back the model 1 in (2), whereas the restriction α = γ/(1 + γ)^k+1 corresponds to the model where the voxels are independent and the probability of a voxel being activated is γ/(1 + γ). The latter is equivalent to the model in EB.

The model may be parametrized by the probability p of a voxel being active, which is given as p = α(1 + γ)^k, and by γ. The latter is a measure of correlation of neighbouring activation sites. The last parameter q ₀ is given by the constraint that the probabilities must sum to one. The posterior probability of activation may be derived in the same way as in model 1, the expression is given in (16) in the appendix.

Model 3

Finally, we will consider a model of the form (6), but being more symmetric with respect to activated and nonactivated voxels. We will consider the model

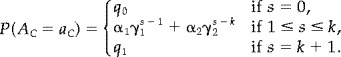(7)

The model may be parametrized by the probability p of a voxel being active, and 4 other parameters describing the correlation between voxels. The relation between parameters may be found in the, as may the expression for the probability that a voxel is active (18).

Estimation of Parameters

For estimation purposes, we will now study the whole volume of voxels, v, rather than just a single voxel. For this reason, we will let the notation depend explicitly on the voxel index. Rather than just using x _C, we will let x ${}_{\mathit{\text{C}}{}_{\mathit{\text{i}}}}$ denote the vector of observations in the region C _i around voxel i. The elements of the vector are denoted by x ${}_{\mathit{\text{C}}{}_{\mathit{\text{i}}}}$ = (x ${}_{\text{0}}^{\text{i}}$ , x ${}_{\text{1}}^{\text{i}}$ , …, x ${}_{\text{k}}^{\text{i}}$), thus x ${}_{\text{0}}^{\text{i}}$ refers to the statistic x _i in voxel i, and x ${}_{\text{1}}^{\text{i}}$ , …, x ${}_{\text{k}}^{\text{i}}$ to the statistic in the k neighbours of i. Similarly A _C is changed to A ${}_{\mathit{\text{C}}{}_{\mathit{\text{i}}}}$ = (A ${}_{\text{0}}^{\text{i}}$ , A ${}_{\text{1}}^{\text{i}}$ , …, A ${}_{\text{k}}^{\text{i}}$) and the likelihood ratios (5) are denoted v${}_{\text{j}}^{\text{i}}$, where

Within the model we can calculate the marginal density of x ${}_{\mathit{\text{C}}{}_{\mathit{\text{i}}}}$. We denote this by f(x ${}_{\mathit{\text{C}}{}_{\mathit{\text{i}}}}$; ϕ, ψ), where ϕ parametrizes the conditional distribution of x ${}_{\mathit{\text{C}}{}_{\mathit{\text{i}}}}$ given A ${}_{\mathit{\text{C}}{}_{\mathit{\text{i}}}}$, and ψ parametrizes the marginal distribution of A ${}_{\mathit{\text{C}}{}_{\mathit{\text{i}}}}$. Thus

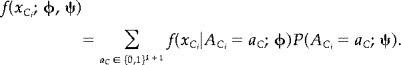A possibility for estimating the parameters (ϕ, ψ) is to maximize the contrast function

(8)

This is related to maximum likelihood estimation, in particular the estimators will be asymptotically normal distributed under conditions where the maximum likelihood estimators are. For model 2, and hence also for model 1 by setting γ = 1, we get

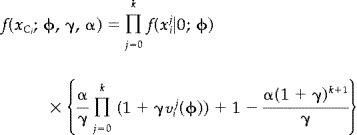(9)

The formula for model 3 is given in (19) in the.

Usually, though, we will take a more simple approach instead of using (8). We propose to use only the marginal distribution of x _i to estimate ϕ and the fraction of activated voxels p. The marginal density of x _i is a mixture density

(10)

We thus maximize the contrast function

(11)

to estimate ϕ and p. Under model 1 all parameters have been estimated this way.

When P(A ${}_{\mathit{\text{C}}{}_{\mathit{\text{i}}}}$ = a ${}_{\mathit{\text{C}}{}_{\mathit{\text{i}}}}$) is given by model 2 we still estimate p = α(1 + γ)^k from (11). The remaining parameter γ may then be estimated from the empirical covariance of {x _i }: Suppose, for example, that (x|A = 0) ∼ N(0, σ²), and (x|A = 1) ∼ N(1, σ²). Then the covariance of x _i and x _j is given by

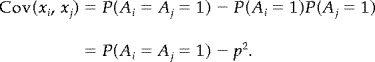(12)

If j is a neighbour to i, say neighbour number 1, we may derive the first probability as

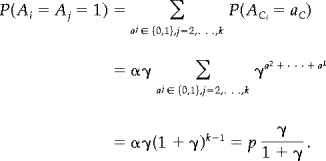(13)

Notice that the two expressions above do not depend on the position of the neighbour j. Suppose an estimate Cˆ of the covariance Cov(x _i, x _j) is given. This may be combined with the estimate pˆ of p to form an estimate of γ by the equations above,

(14)

Since the covariance is the same for all neighbours, we may combine estimates of the covariance at different spatial lags within the neighbourhood, to form the estimate Cˆ. In practice in our examples (where we consider respectively 3 × 3 and 5 × 5 neighbourhoods) we have used the eight nearest neighbours to estimate the covariance,

Here Cˆ _l is the correlogram for the spatial lag l [Cressie, 1991],

where V denotes the set of brain voxels, N _l is the number of terms in the sum, and x̄. is the average of the x _i 's.

Notice that the probability in (13) only depends on the model for A _C, and hence applies whenever model 2 is considered. This is not true for the covariance in (12), which depends on the distribution of x given A. In the setup above we have considered a statistic which is distributed as (x|A = 0) ∼ N(0, σ²) and (x|A = 1) ∼ N(1, σ²). When more generally (x|A = 1) ∼ N(μ, σ²) where μ > 0, we obtain the setup above by scaling x by μ⁻¹. When the distribution of x is not normal, we need to calculate the covariance in (12) for the distribution considered. A general formula, which applies whenever x _i and x _j are conditionally independent given A _i and A _j, is given by

Usually it is straightforward to calculate the right‐hand side above. This is the approach used in Example 3, where x _i has a Gamma distribution when A _i = 1.

As for the model 3, this has 4 free parameters when p is given. Moment estimators may be derived for these as above, but we will refrain from this since the equations get more complicated. Instead we will estimate the remaining parameters from (8).

In our examples below we have used the simplex method to maximize the contrast functions [Press et al., 1992]. The standard errors of the maximum contrast estimators may be obtained by general asymptotic theory, see for instance Heyde [1997]. Cressie [1991] provides formulas for the standard error of Cˆ _l. Presently we have no formal way of including the uncertainty of the parameters in the analysis; it is, however, our experience that the posterior probability maps were quite robust to the observed variations in the parameters. In fact, as we will show in Examples 2 and 3, they are quite robust to the choice of model.

SIMULATIONS AND APPLICATIONS

We will illustrate the method by applying it to two synthetic data sets (where the truth is known) and a visual stimulation data set. For the synthetic data, we may quantify results by classification error, statistical power or true positive rate (TPR), and level of significance or false positive rate (FPR). For a given threshold, the classification error is estimated as the number of misclassified voxels (either type I or type II errors), divided by the total number of voxels. The TPR is estimated as the number of active voxels classified as active, divided by the total number of active voxels. The FPR is estimated as the number of nonactive voxels that are classified as active, divided by the total number of nonactive voxels.

Example 1: Image Restoration Data

We will apply the models to a classical problem in statistical image analysis, namely the restoration of an unknown true image based on a degraded version of it. Techniques for achieving this are applied in many areas where images are recorded or transmitted with noise, including remote sensing images, satellite images, and medical images. In functional brain imaging the problem is more complex than in the setting above: It is not as evident what the “true scene” is or which geometric characteristics it has, and the noise sources are far more complex than in image restoration problems. It still serves a purpose, however, to study how the models perform in this more simple problem, in order to understand the characteristics of the models, before moving on to more complex data.

We will consider two images. The first (denoted Image I) is the 64 × 64 binary image of an ‘A’ by Greig et al. [1989], see Figure 1. The image is corrupted with binary noise, where a pixel A _i with probability q is replaced by 1 − A _i. The probability densities of the degraded pixel X _i given the true value A _i are then

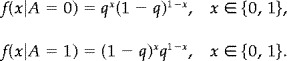The error rate q was set to 25%. Five independently corrupted images were produced, in order to assess the variability of the estimates. The results are summarized in Table I and some of the image estimates are displayed in Figure 1.

Figure 1.

Comparison of spatial mixture models. Top row: Image I and degraded version. Middle row: Estimates of the true image based on model 1, 2, and 3 applied to a 3 × 3 pixel region. Bottom row: Same as above, but with the models defined on a 5 × 5 region.

Table I.

Estimated classification errors for the three models and the ICM and MAP estimates*

Model	Classification error
	Image I	Image II
1, 3 × 3	10.0 (0.3)	14.6 (0.3)
1, 5 × 5	9.4 (0.2)	12.2 (0.2)
2, 3 × 3	7.6 (0.3)	9.0 (0.4)
2, 5 × 5	5.9 (0.8)	6.4 (0.2)
3, 3 × 3	7.6 (0.3)	9.0 (0.4)
3, 5 × 5	6.1 (0.3)	6.2 (0.3)
MAP	5.2 (0.2)	5.5 (0.2)
ICM	6.3 (0.4)	6.4 (0.1)

^*Based on 5 independent simulations of the degraded image. Image I refers to the true image in Figure 1, degraded with binary noise. Image II refers to the image in Figure 4a in Besag [1986], degraded with Gaussian noise. All figures are in percent; standard errors of estimates are given in parentheses.

The second image (Image II) is the binary image displayed in Figure 4a of Besag [1986]. The image was corrupted by adding white Gaussian noise with standard deviation 0. 9105. In this setting the densities of a pixel X _i given A _i are

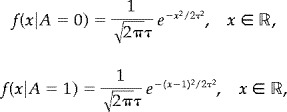where τ = 0. 9105. We produced five independent noisy images to assess the variability of estimates. The results are given in Table I.

Figure 4.

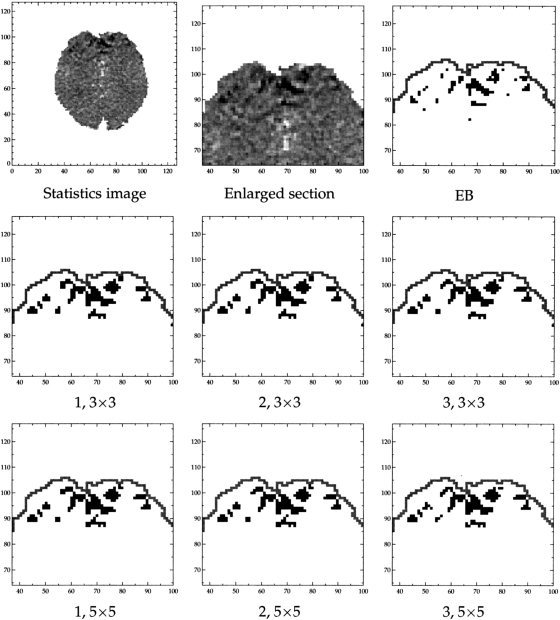
Comparison of estimated activation patterns for the different mixture models of the visual stimulation data. Top left and middle: Raw image of t‐statistics and an enlarged section of this. The remaining panels are posterior probability images thresholded at 0.5. Top right: nonspatial mixture model. Middle and last row: Models 1, 2, and 3 defined on respectively a 3 × 3 voxel region (middle row) and 5 × 5 voxel region (last row).

For each model, the parameters were estimated both by maximizing the contrast function (8) and, for model 1 and 2, by the simple estimators described earlier. As the results were almost similar, we give only the figures for the maximum‐constrast estimates. In practice we recommend that the simple estimators should be used when possible, since they are much easier to obtain, and give almost as good results.

We calculated the posterior probability of A = 1 given X _C in each pixel, and the estimate of the true image was obtained by thresholding the probability image at 0.5. The estimates for one of the noisy versions of image I can be seen in Figure 1.

The estimated classification error and its standard error are listed in the second and third column of Table I. The first column lists the models used in this example. The models 1, 2, and 3 were applied, respectively, defined on a 3 × 3 pixel region and on a 5 × 5 region. For comparison, we have reproduced the classification errors of the maximum a posteriori (MAP) estimate and the iterated conditional modes (ICM) estimate, which can be found in Greig et al. [1989]. These two estimates are based on the same global model for the true image, but only the local properties of the model are used with ICM.

The table shows that model 1 performs worse than model 2 and 3, which is also clear from Figure 1. It is also clear that the 5 × 5 region models are superior in this setting, which is not surprising as the true images are quite regular with large patches of either black or white. We might suspect that the 3 × 3 models will be more appropriate in brain imaging, where the true scene is not as regular. Model 2 and 3 perform almost equally well, hence we prefer model 2, since this only has two parameters.

Model 2 performs well compared to the ICM and MAP methods also. There are several practical differences between these and our model: First, it is more computationally intensive to obtain the ICM and MAP estimates than our posterior probability images. The latter are calculated in closed form while the ICM and MAP procedures require iterative algorithms. Second, the MAP and ICM procedures depend on a smoothing parameter that, especially for the MAP estimate, is crucial for the reconstructed image. In this case, the value of the smoothing parameter was based on the true image, which is of course not possible in practice. On the contrary, the parameters of model 2 are estimated directly from the observed image. Seen in this light, our model seems to be an attractive alternative to the traditional methods. It is however not as flexible as the ICM approach, which can be generalized for instance to multicolour settings.

Example 2: Simulated fMRI Data

In order to study the performance on data, which are closer related to brain imaging problems than the ones in Example 1, we have applied the methods to a synthetic fMRI data set. We used the data set of Lange et al. [1999], which was generated from 72 baseline EPI scans that were temporally resampled to 384 scans.1 We refer to the article for a full description of the data, but will repeat the basic properties here. A region of 24 × 12 voxels is considered, and in each voxel the time series is linearly detrended. Denote the residual time series by Y _it, where i indexes voxels i = 1, …, V and t indexes scan t = 1, …, T. Here V = 288 and T = 384. Artificial activation was added to obtain the actual data Z _it, say, by the model

where the magnitude of activation b _i is given by

Here s ${}_{\text{2}}^{\text{Y,i}}$ is an estimate of σ${}_{\text{2}}^{\mathit{\text{i}}}$, the variance of Y _it, given by

The temporal activation pattern x _t is a simple binary function, where x _t = 0 when off and x _t = 1 when on, for t = 1, …, T. The function is periodic with 8 runs, each of length 48 scans with 12 scans off, 24 on and 12 off. The ratio m of the activation magnitude to standard deviation was chosen to be positive and constant in the two connected regions of size 25 and 37 voxels depicted in Figure 2, and zero elsewhere. According to Lange et al. [1999], a value of m = 0.15 was chosen in the activated areas, however when estimating m directly from the data by a regression analysis (when the true activation pattern is known), we obtain m̂ = 0.43 with a standard error of 0.015. The value of m is not important for the present study, however.

Figure 2.

Activation images for the first of four subsets of the synthetic dataset. Top left and middle: True binary activation image and observed t‐statistics image. The remaining are thresholded posterior probability images for the different models. EB: Everitt and Bullmore's mixture model. 1, 2, and 3: Models 1, 2, and 3 defined on a 3 × 3 region or a 5 × 5 region. The images were thresholded at posterior probability 0.5.

In order to make the estimation problem a bit harder than in the article, we divided the data into 4 subsets, each of length 96 scans. We estimated the spatial activation pattern from a single subset at a time and used the empirical variation over the four subsets to evaluate the uncertainty of our results.

Consider a voxel time series at voxel i, Z _it, for t = 1, …, T ₀, T ₀ = 96. We tested for activation by a t‐test. More specifically, the estimate of the activation level is given by

and the variance of Z _it is estimated by

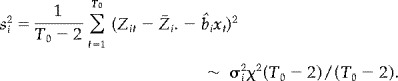Here χ²(f) denotes the χ²‐distribution with f degrees of freedom. Then the statistic

has a t‐distribution with T ₀ − 2 = 94 degrees of freedom, if the voxel is not activated. Since the degrees of freedom are quite large, it is reasonable to make the approximation that the variance estimates are exact, s ${}_{\text{2}}^{\text{Y,i}}$ = s ${}_{\text{2}}^{\text{i}}$ = σ ${}_{\text{2}}^{\text{i}}$ , whence we get a normal distribution for X _i,

where μ = m 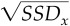. The image of test statistics {X _i } hence follows a mixture distribution, where the mean is positive when the voxel is activated and zero when not, and the setup is as in the Overview of the Mixture Model section with

We have assumed here that the temporal correlation is zero, which is necessarily an optimistic assumption. Temporal correlation will affect the variance of bˆ _i, but not the mean, and will lead to a higher variance of the statistic X _i, than stated above.

Figure 2 displays the image of t‐statistics for the first of the four subdata sets. The posterior probability that a voxel is activated was calculated using the simple mixture model without spatial interaction, i.e., the setup of EB, and the models 1, 2, and 3. The image of posterior probabilities was thresholded at 0.5, which is a natural level when specifying a neutral balance between type I and II errors. The thresholded activation images are displayed in Figure 2. Clearly the spatial models (1, 2, 3) represent the true activation pattern much more closely than the simple mixture model. When using the latter, we effectively threshold the raw t‐statistic image at a certain level, while at the spatial models we use information in neighbouring voxels, when classifying a voxel.

In Table II the models are compared quantitatively by their ability to classify voxels correctly, and by the TPR at a given level of significance (FPR). The threshold was adjusted to yield an empirical FPR of 5% and 1%, respectively, in each image, and the TPR of this level was calculated. While the TPR estimates provide an idea of the strength of the classification test, they are mainly of theoretical interest, since the threshold used was calculated given the true activation pattern. On the contrary to this, the classification error measures reproducibility of the true pattern, when a practical and objective threshold is applied.

Table II.

Comparison of models for the synthetic fMRI data in Figure 2, *

Model	Class. error	TPR (level 5%)	TPR (level 1%)
EB	11.0 (0.7)	66.1 (2.3)	46.8 (5.0)
1, 3 × 3	6.3 (0.5)	88.3 (0.8)	65.7 (4.0)
1, 5 × 5	7.0 (0.3)	85.1 (2.0)	57.7 (6.3)
2, 3 × 3	6.3 (0.8)	90.7 (1.4)	72.5 (2.4)
2, 5 × 5	6.6 (0.8)	84.3 (2.9)	74.6 (3.5)
3, 3 × 3	6.3 (0.7)	87.5 (2.3)	66.5 (3.5)
3, 5 × 5	7.4 (0.3)	82.7 (3.0)	51.6 (7.6)

^*From left to right are estimates of classification error for the thresholded images and TPR for images thresholded at a FPR of 5% and at 1% respectively. All figures are in percent. Standard errors of estimates, expressing the variability over the four sub‐datasets, are given in parentheses.

The table confirms the impression from Figure 2: The simple mixture model has the worst classification error and the lowest power. The three spatial models perform almost equally well, and a grid of 3 × 3 voxels gives the best result for this data. If the activated areas were larger than these, the 5 × 5 model might be more suitable; however, this activation pattern seems reasonably representative for real data, and hence we recommend the 3 × 3 model to be used in practice. When considering the power, model 2 is slightly superior to the models 1 and 3, though this is not significant. Models 1 and 2 are furthermore preferable to model 3, since they have only 1 and 2 parameters, respectively.

We may conclude that model 2 applied to a 3 × 3 neighbourhood is preferable in this situation: The statistical power is more than 90% at a significance level of 5%, and the misclassification is reduced by more than 40% compared to the simple mixture model.

We will compare the performance of model 2 with a nonparametric model, where the activation is estimated by smoothing the data spatially with a Gaussian kernel of full width at half maximum (FWHM) 2 and 3 voxels, respectively, before calculating the t‐statistic image. This is perhaps the most common way of including spatial information in the analysis of fMRI data, and usually the smooth t‐image is thresholded using the random fields theory [Worsley et al., 1996]. Voxels may then be classified either on the basis of peak height or on cluster size. However, our aim here is not to compare results from thresholding based on random fields theory with that based on posterior probabilities. We think this is difficult as the underlying principles and assumptions are fundamentally different. Rather we wish to compare the estimates of spatial activation pattern obtained by the two models. For this reason, we have thresholded the activation images in a comparable way, namely at the level which yields an actual FPR of 5% and 1%, respectively, based on the true activation pattern. Figure 3 displays the estimated activation patterns.

Figure 3.

Activation images for the first of four subsets of the synthetic dataset. From left to right: Model 2 defined on a 3 × 3 region and the nonparametric model with FWHM 2 and 3 voxels, respectively. Top row: Original activation images. Below: Images thresholded at empirical FPR 5% (middle) and 1% (bottom).

From the first row, we see that the distinction between noise and activation is dramatically different on the posterior probability scale compared to the t‐image scale. EB made similar observations when comparing p‐values and posterior probabilities. The two last rows show that the nonparametric model yields estimates which are smoother than the true regions, while the regions of model 2 are more irregular and have more holes. The estimated TPR for the nonparametric model are given in Table III. By comparing this with Table II, we see that model 2 reproduces the true activation best, as it has the highest TPR for each level of FPR. The difference is only significant for FWHM 3.

Table III.

Estimates of TPR for nonparametric activation images in Figure 3, *

Model	TPR (level 5%)	TPR (level 1%)
NP, FWHM 2	89.5 (2.0)	66.9 (2.8)
NP, FWHM 3	78.6 (3.4)	46.0 (6.7)

^*Thresholded at a FPR of 5% and at 1%, respectively. All figures are in percent. Standard errors of estimates are given in parentheses.

Example 3: Visual Stimulation fMRI Data

We finally considered a visual stimulation data set acquired with T ${}_{\text{*}}^{\text{2}}$‐weighted EPI on a 1.5 T scanner at the MR Research Centre, Aarhus University Hospital in Denmark. The data consist of 90 128 × 128 scans (5 × 1.875 × 1.875 mm voxels) for each slice, with a TR of 2 sec. Five oblique slices were acquired in axial‐coronal direction through the visual cortex. The stimulus was a 7 Hz flashing light, which was presented in a blocked paradigm of 10 scans off, 10 scans on, etc., starting an ending with an off period. The first 5 scans were discarded, and we selected one of the slices for this analysis.

The scans were realigned by minimizing the squared distance of each scan to a reference scan under rotations and translations. Next we log‐transformed the data and masked 4389 brain‐voxels out. A linear model was fitted individually to each voxel time series. The mean value space was spanned by a linear trend and a model for the haemodynamic response function given by a convolution of the paradigm with a Gaussian function with mean 6 sec. and variance 9 sec². The estimated activation amplitude was divided by its standard error to yield an image of t‐statistics. The latter is displayed in the first panel in Figure 4.

We did not account for correlation in the time series, whence we expect the variance of the statistics to be larger than the theoretical variance of the t‐distribution. We investigated the empirical distribution of the set {x _i } of 4,389 statistics and found that a mixture of three components fitted well to this. Two of these were Gamma distributions, modeling respectively positive and negative BOLD effects, and one was a Normal distribution modeling the noise. The fitted density was

(15)

where f _N ( ·; μ, σ²) denotes the density of a normal distribution with mean μ and variance σ² > 0, and f _Γ( ·; λ, β) is the density of a Gamma distribution with mean λ/β and variance λ/β²,

With the requirement that p ₀ + p ₊ + p ₋ = 1, there are 7 free parameters, which were estimated by maximizing the likelihood function under the restriction that

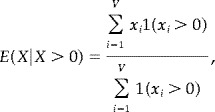i.e., the mean of X given that it is positive, must equal the empirical mean of the positive x _i 's. It is well known that the likelihood function may be unbounded in mixture models, and the latter restriction was imposed to reduce the parameter space to finite likelihood values. The estimates are given in Table IV.

Table IV.

Parameter estimates for the distribution (15) of {x _i}

σˆ = 1. 5160	pˆ + = 0. 0502	pˆ − = 0. 0081
λˆ+ = 6. 2349	λˆ− = 56.923
βˆ+ = 0. 9433	βˆ− = 10.253

We are only interested in detecting positive activation in this example. Therefore we write f(x) as

where

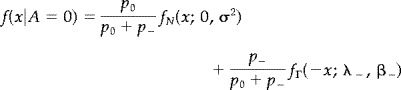is the null distribution and

is the distribution of x, given that the voxel is positively activated.

The setup is hence as given previously, only here the null distribution represents both no activation and negative BOLD effects. As an alternative to the Gamma distribution for positive activation, one could consider the sum of a Gamma and a Normal distribution, to account for the fact that the activation level is observed with noise. The density of the latter is, however, not available in closed form, and because the distributions are very similar at the present noise level, we have chosen a single Gamma.

Figure 4 shows the image of statistics {x _i } and enlarged sections of thresholded posterior probability maps for the nonspatial mixture model (EB), and for models 1, 2, and 3. The images were thresholded at 0.5. Like in the previous section, there is hardly any difference between the different spatial models, but there is a striking difference between the EB model and the others. In general the activated areas are larger with the spatial models and small (i.e., single voxel) areas are suppressed. Clearly we can only speculate whether these estimates are more accurate. However, the simulated data of the previous section suggest that for activated areas of a certain size, the spatial model gives a significantly improved estimate. The idea that activation should have a certain spatial extent is the rationale behind spatial smoothing and other filtering techniques, and hence also this methodology.

In Figure 5 we have displayed the estimate one gets by smoothing the original data before calculating the statistical image. We have no directly comparable way of thresholding this image, instead we have thresholded the image at three different levels. The mixture model estimates have some similarities with these activation patterns, but clearly the latter are much smoother. Again we can only speculate what is most accurate. It is, however, well known [Müller, 1988] that a kernel smoothing estimate will be biased, in the sense that the estimate will be smoother than the underlying signal. This is a likely explanation for the difference in smoothness.

Figure 5.

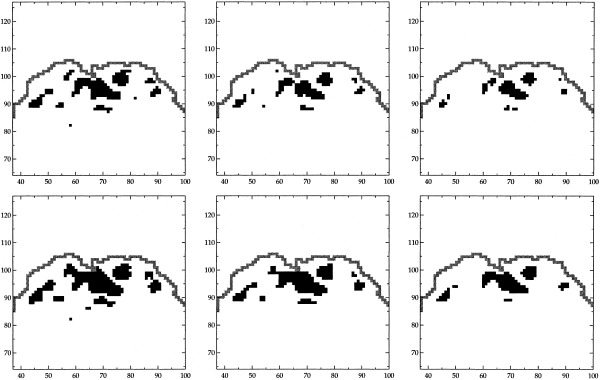
Images of t‐statistics based on the visual stimulation data smoothed spatially with a Gaussian kernel of FHWM 2 voxels (top row) and 3 voxels (bottom row). The images are thresholded at 5.0 (left), 6.0 (middle), and 7.0 (right).

DISCUSSION

Conceptual Summary

We have proposed a spatial mixture model for a statistical parametric map {x _i }. The idea is to model the distribution of x _i both when the voxel is not active and when it is. Typically the nonactivated distribution is known, this is the usual null distribution of the SPM. The activation distribution might either be a simple noncentral version of the null distribution, as in Example 2, or a completely different distribution, which models the range of different activation strengths observed in the data, as in Example 3. The activation pattern is described by an unobserved volume of binary indicators, {A _i }. We suggest three different prior models for this pattern, which reflect the property that activation tends to occur in clusters rather than individual pixels. By formulating the models locally on a small region of pixels, it is possible to obtain a closed form expression for the posterior probability that a voxel is activated, given the values of the SPM in a region around the voxel.

To use the method in practice all one needs to specify are the two distributions of the test statistic. As in an ordinary analysis, the choice of test statistic influences the sensitivity, but there are no restrictions on the class of statistics that may be employed: the only requirement is that one can specify parametric distributions for the two activation states.

The proposed models account to some extent for the spatial structure of the underlying activation pattern. We found that the three different models worked almost equally well on synthetic and real fMRI data. In fact we tested two more advanced models also, but they gave similar results. (The models are described in a research report by the authors.) We recommend model 2 to be used in practice: It has only two parameters, with natural interpretations: One is p, the probability of a voxel being activated. An estimate of p is a global measure of the fraction of activated voxels, which is of interest in itself. The other is γ, which is a measure of the correlation of the true activation field. The parameters may be estimated directly from the data.

When modeling only a single slice with 1.9 mm voxels, we found that a 3 × 3 neighbourhood worked well. When a volume of slices is considered, the neighbourhood could be extended with the two voxels directly below and above the centre or to a 3 × 3 × 3 cube. This should of course depend on the interslice distance.

Comparison with Existing Methods

The methodology extends that of EB, who proposed a nonspatial mixture model. In fact, the EB model is a special case of our analysis scheme, as it is contained in model 2. We found significant improvements in sensitivity on synthetic fMRI data compared to the non‐spatial mixture model: The sensitivity increased from 66% to 91% at a FPR of 5%, and the misclassification rate of the 0.5‐thresholded images was reduced from 11% to 6%. The analysis of visual stimulation data indicated similar improvements.

When applied to synthetic fMRI data, our method was more sensitive than smoothing the data with a kernel of FWHM 3 voxels, but the sensitivity of the FWHM 2 smoothing was similar to ours. However the nonparametric smoothing model seems to produce estimates which are more smooth, than the ones obtained with our method. As mentioned in Example 3, this could be explained by the bias in the kernel smoothing estimate. One argument used for smoothing data is the Matched Filter Theorem [Rosenfeld and Kak, 1982]. This states that in order to maximize signal‐to‐noise ratio at a specific point in an image, one should convolve the image with a kernel that has the same shape as the signal at that point. This is a statement about detecting a signal. When one wants to estimate the signal or some features of it, this is not necessarily an optimal strategy because of the bias introduced. On the contrary, a parametric model, if correct, yields estimates that are less biased and more efficient. Clearly, our model is not “correct,” but we would like to emphasize the difference between parametric and nonparametric modeling. Furthermore, the choice of the smoothing parameter, i.e., the FWHM of the kernel, is always a critical point in nonparametric estimation. It seems that for fMRI data, this parameter is often chosen in an ad hoc manner. With our method, the “smoothing parameter” (such as the parameter γ of model 2) is estimated directly from the data itself.

The assumptions underlying mixture modeling seem more natural and transparent to us than those underlying the random fields theory. We expect a priori to find basically two different types of voxels, activated and nonactivated, and a model for the data should reflect this. The inference in the model is fundamentally different from the usual hypothesis testing framework. In the latter, what is really an estimation problem, is answered by a hypothesis test [Worsley, 1997]. The main problem is then the protection against false positives, with the large number of tests performed. In our approach we estimate the proportion of active voxels p, and use this to determine the posterior probability that a voxel is activated. As may be seen from (3) and (4) the probability that A = 1 tends to 0 as p tends to 0. This may be regarded as our way of handling multiple comparisons: If the size of the volume is increased, but the number of active voxels is fixed, p will decrease, and hence so will the posterior probability that a voxel is activated. For a fixed amount of activation, a larger search volume hence yields a more conservative analysis than a small.

Another advantage compared to the random fields framework is the robustness to misspecification of the model. To illustrate this, we replaced the normal distribution in Example 3 with a t‐distribution with 20 degrees of freedom. The thresholded activation images were almost identical, with only a few voxels changing state. This is not surprising, as the two distributions are almost equivalent for our purposes. On the contrary, the random field theory relies on the extreme tail of the distribution, whence there is nonnegligible difference between a t(20) distribution and the normal distribution in this framework.

The method may be particularly relevant in applications where signal estimation is more important than signal detection. This is the case for instance when fMRI is used for presurgical planning, where the protection against false negatives is more important than false positives. Another example is when the results of an fMRI study are combined with data from other modalities, such as to regularize the inverse problem of MEG/EEG [Liu et al., 1998].

During the review process of this article, we realized that the idea of using local models for the true image in restoration problems is not new. Meloche and Zamar [1994] used an approach similar to ours, and they also derived moment estimators for parameters of the true image model. Meloche and Zamar considered a more general framework, where they estimated the probabilities P(A _C = a _C) nonparametrically in a very elegant way. We restrict our attention to parametric models, which are realistic from a brain imaging point of view, and this gives us the big advantage of being able to calculate the posterior probability in closed form. As mentioned earlier, this point is crucial for the applicability of the method in practice. Furthermore Meloche and Zamar only consider models of the form (x|A = 0) ∼ N(0, σ²) and (x|A = 1) ∼ N(1, σ²), where our setup is completely general.

We have assumed throughout the article that the observations are uncorrelated given the true activation pattern. Some spatial correlation can be detected in the noise in fMRI data, and hence this assumption will often be violated. The correlation of the signal is, however, much larger than that of the noise, and we have accounted for most of the correlation in the data by the model for the activation pattern. In some models, one may extend the methodology to correlated noise by estimating the spatial correlation first, and incorporating this in the expression for f(x _C |a _C). Assuming stationarity of the correlation, this may be estimated from the residual time series, see for instance Hartvig [1999]. Clearly the computations get more complicated then, as the closed form expression for the posterior probability is lost.

From a mathematical point of view, a natural question is whether there exist global models for the whole set of voxels, which have marginal distributions given by the models in this article. This is in fact the case, since all three models have the property, that the structure of the model is maintained when reducing to marginal distributions. Considering model 2, for instance, this means that if we formulate the model on the whole set of voxels, the marginal distribution of a 3 × 3 region will be the same as that obtained by formulating the model on this region only. This also means that edge effects may be handled in a rigorous way by simply reducing the number of neighbours k when calculating the probability of activation in boundary voxels.

CONCLUSION

We have formulated a simple mixture model for fMRI data that captures most of the spatial structure of the underlying activation pattern. The spatial model has two parameters, which are directly interpretable and may be estimated from the data. The expression for the posterior probability that a voxel is activated is given in closed form. Rather than the usual hypothesis testing, the focus of the method is estimation of the activation, which seems more natural in many applications.

In order to use this method, one needs only specify the null distribution and the distribution of activated voxels. These can be any distributions. The resulting activation image is a posterior probability image, which may be thresholded in an intuitive way without the need for correcting for multiple comparisons. Alternatively, one may display the unthresholded probability map, which shows a clear distinction between estimated activation and baseline.

We derive the formulas for the posterior probability that a voxel is activated in model 2 and model 3 in the following.

Model 2

For given p and γ, q ₀ is determined by

Using the same technique as in model 1, we find

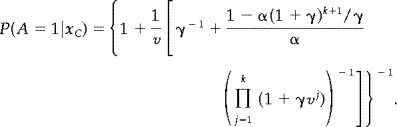(16)

Model 3

In this model we have

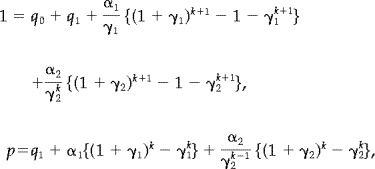(17)

where p is the probability of a voxel being activated. Instead of (16) we find

(18)

where

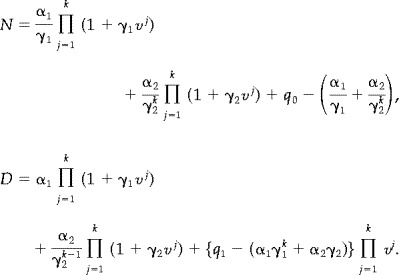For model 3 the marginal density of x ${}_{\mathit{\text{C}}{}_{\mathit{\text{i}}}}$, used in the constrast function (8), is

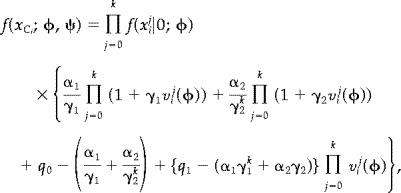(19)

with ψ = (α₁, α₂, γ₁, γ₂, q ₁) and q ₀ given by the constraint in (17).