Image registration using a symmetric prior—in three dimensions

Abstract

This paper describes a Bayesian method for three‐dimensional registration of brain images. A finite element approach is used to obtain a maximum a posteriori estimate of the deformation field at every voxel of a template volume. The priors used by the MAP estimate penalize unlikely deformations and enforce a continuous one‐to‐one mapping. The deformations are assumed to have some form of symmetry, in that priors describing the probability distribution of the deformations should be identical to those for the inverses (i.e., warping brain A to brain B should not be different probablistically from warping B to A). A gradient descent algorithm is presented for estimating the optimum deformations. Hum. Brain Mapping 9:212–225, 2000. © 2000 Wiley‐Liss, Inc.

INTRODUCTION

Two brain images from the same subject can be coregistered using a six‐parameter rigid body transformation that simply describes the relative position and orientation of the images. However, for matching brain images of different subjects (or the brain of the same subject that may have changed shape over time) [Freeborough and Fox, 1998], it is necessary to estimate a deformation field that also describes the relative shapes of the images. Many parameters are required to describe the shape of a brain precisely, and estimating these parameters can be very prone to error. The error can be reduced by ensuring that the deformation fields are internally consistent. For example, suppose a deformation that matches brain A to brain B is estimated, and also a deformation that matches brain B to brain A. If the registration is perfect, then one deformation should be the inverse of the other. If there are internal inconsistencies in the registration, then it is very unlikely that this will be the case.

This paper is about achieving consistent estimates of deformation fields, and is a direct extension of our previous work [Ashburner et al., 1999] where we described a high‐dimensional method of image registration for two‐dimensional images. The theory behind the two‐dimensional approach still holds for three dimensions, but the computational overhead required for the priors would be prohibitive for use on the current generation of desktop workstations. In this paper, we derive an approximation to the priors used previously that can be computed much more quickly. The optimization algorithm has been modified slightly to increase its efficiency and stability.

The remainder of the paper is divided into three main sections. The theory section describes the Bayesian principles behind the registration, which is essentially an optimization procedure that simultaneously minimizes the likelihood function (i.e., the sum of squared differences between the images), and a penalty function that relates to the prior probability of obtaining the deformations. A number of examples of registered images are provided in the next section. The final section discusses the validity of the method, and includes a number of suggestions for future work.

THEORY

Registering one image volume to another involves estimating a vector field (deformation field) that maps from coordinates of one image to those of the other. In this work, we consider one image (the template image) to be fixed, and estimate the mapping to the second image (the source image). The intensity of the ith voxel of the template is denoted by g(x _i ), where x _i is a vector describing the coordinates of the voxel. The vector field spanning the domain of the template is donated by y(x _i ) at each point, and the intensity of the source image at this mapped point by f(y(x _i )). The source image is transformed to match the template by resampling it at the mapped coordinates.

This section begins by describing how the deformation fields are parameterized as piecewise affine transformations within a finite element mesh. The registration is achieved by matching the images while simultaneously trying to maximize the smoothness of the deformations. Bayesian statistics are used to incorporate this smoothness into the registration, and a method of optimization is presented for finding the maximum a posteriori (MAP) estimate of the parameters. A suitable form for the smoothness priors is presented.

Deformation Fields

Our previous work [Ashburner et al., 1999] described a method of two‐dimensional image registration, where the deformations consisted of a patchwork of triangles. The situation is more complex when working with three‐dimensional deformations. In this work, the volume of the template image is divided into a mesh of irregular tetrahedra, where the vertices of the tetrahedra are centered on the voxels. This is achieved by considering groups of eight voxels as little cubes. Each of these cubes is divided into five tetrahedra: one central one having 1/3 of the cube's volume, and four outer ones, each having 1/6 of the cube's volume [Guéziec and Hummel, 1995]. There are two possible ways of dividing a cube into five tetrahedra. Alternating between the two conformations in a three‐dimensional checkerboard pattern ensures that the whole template volume is uniformly covered (see Fig. 1). A deformation field is generated by treating the vertices of the tetrahedra as control points. These points are moved iteratively until the best match is achieved. The deformations are constrained to be locally one‐to‐one by ensuring that a tetrahedron never occupies the same volume as its neighbors. When the deformations are one‐to‐one, it is possible to compute their inverses (see Appendix).

Figure 1.

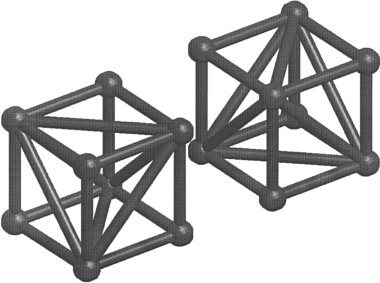
The volume of the template image is divided into a mesh of irregular tetrahedra, where the vertexes of the tetrahedra are centered on the voxels. Groups of eight voxels are considered as little cubes. The volume of each cube is divided into five tetrahedra, in one of the two possible arrangements shown here. A face of a cube that is divided according to one arrangement, opposes with the face of a cube that has been divided the other way. Because of this, it is necessary to arrange the two conformations in a three‐dimensional checkerboard pattern.

The algorithm can use one of two possible boundary conditions. The simplest is when the vertices of tetrahedra that lie on the boundary remain fixed in their original positions (Dirichlet boundary condition). Providing that the initial starting estimate for the deformations is globally one‐to‐one, then the final deformation field will also satisfy this constraint [Christensen et al., 1995]. The other boundary condition allows the vertices on the surface to move freely (analogous to the Neumann boundary condition). It is possible for the global one‐to‐one constraints to be broken in this case, because the volumes of nonneighboring tetrahedra can now overlap. The examples shown in this paper use the free boundary condition.

Bayesian Framework

We describe an approach for three‐dimensional image registration that estimates the required spatial transformation at every voxel, and therefore requires many parameters. For example, to register two volumes of size 256 × 256 × 108 voxels, needs 21,233,664 parameters. The number of parameters describing the transformations exceeds the number of voxels in the data. Because of this, it is essential that priors or constraints are imposed on the registration. We use Bayesian statistics to incorporate a prior probability distribution into the warping model [Amit et al., 1991; Gee et al., 1995a,b; Miller et al., 1993].

Bayes rule can be expressed as:

where p(Y) is the a priori probability of parameters of Y, p(b|Y) is the likelihood of observing data b given the parameters Y, and p(Y|b) is the a posteriori probability of Y given the data b. Here, Y are the parameters describing the deformation, and b are the images to be matched. The estimate that we determine here is the MAP estimate, which is the value of Y that maximizes p(Y|b). A probability is related to its Gibbs form [Christensen, 1999a; Gee and Bajcsy, 1999] by:

Therefore, the MAP estimate is identical to the parameter estimate that minimizes the Gibbs potential of the posterior distribution (H(Y|b)), where:

where c is a constant. The registration is therefore a nonlinear optimization problem, whereby the cost function to be minimized is the sum of the likelihood potential (H(b|Y)) and the prior potential (H(Y)).

Optimization

The images are matched by estimating the set of parameters (Y) that maximizes their a posteriori probability. This involves beginning with a set of starting estimates, and repeatedly making tiny adjustments such that the a posteriori potential is decreased. In each iteration, the positions of the control points (nodes) are updated in situ, by sequentially scanning through the template volume. During one iteration, the looping may work from inferior to superior (most slowly), posterior to anterior, and left to right (fastest). In the next iteration, the order of the updating is reversed (superior to inferior, anterior to posterior, and right to left). This alternating sequence is continued until there is no longer a significant reduction to the posterior potential, or for a fixed number of iterations.

In the updating, each node is moved along the direction that most rapidly decreases the a posteriori potential (a gradient descent method). Moving a node in the mesh influences the Jacobian matrices of the tetrahedra that have a vertex at that node, so the rate of change of the posterior potential is equal to the rate of change of the likelihood plus the rate of change of the prior potentials from these local tetrahedra. Approximately half of the nodes form a vertex in eight neighboring tetrahedra, whereas the other half are vertices of 24 tetrahedra. If a node is moved too far, then the Jacobian determinant associated with one or more of the neighboring tetrahedra may become negative. This would mean a violation of the one‐to‐one constraint in the mapping (because neighboring tetrahedra would occupy the same volume), so it is prevented by a bracketing procedure. The initial attempt moves the node by a small distance ϵ. If any of the determinants become negative, then the value of ϵ is halved and another attempt made to move the node the smaller distance from its original location. This continues for the node until the constraints are satisfied. A similar procedure is then repeated whereby the value of ϵ continues to be halved until the new potential is less than or equal to the previous value. By incorporating this procedure, the potential will never increase as a node is moved, therefore ensuring that the potential over the whole image will decrease with every iteration. Because of the inherent stability, larger initial values for ϵ can be used, leading to a more rapid convergence than for the optimization strategy described previously [Ashburner et al., 1999].

At first sight, it would appear that optimizing the millions of parameters that describe a deformation field would be an impossible task. It should be noted that these parameters are all related to each other because the regularization tends to preserve the shape of the image, and so reduces the effective number of parameters. The limiting case would be to set the regularization parameter λ to infinity. Providing that the boundary conditions allowed it, this would theoretically reduce the dimensionality of the problem to a six‐parameter rigid body transformation (although the current optimization algorithm would be unable to cope with a λ of infinity).

Prior Potentials (H(Y))

Within each tetrahedron, the deformation is considered as a uniform affine transformation. If the coordinates of the vertices of an undeformed tetrahedron are (x ₁₁, x ₂₁, x ₃₁), (x ₁₂, x ₂₂, x ₃₂), (x ₁₃, x ₂₃, x ₃₃), and (x ₁₄, x ₂₄, x ₃₄), and if they map to coordinates (y ₁₁, y ₂₁, y ₃₁), (y ₁₂, y ₂₂, y ₃₂), (y ₁₃, y ₂₃, y ₃₃), and (y ₁₄, y ₂₄, y ₃₄), respectively, then the 4 × 4 affine mapping within the tetrahedron (M) can be obtained by:

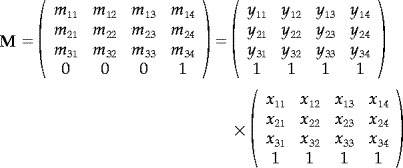The Jacobian matrix (J) of this affine mapping is simply obtained from matrix M by:

A penalty is applied to each of the tetrahedra that constitute the volume covered. For each tetrahedron, it is the product of a penalty per unit volume, and the total volume affected by the tetrahedron. The affected volume is the volume of the undeformed tetrahedron in the template image, plus the volume that the deformed tetrahedron occupies within the source image (v(1 + |J|), where v is the volume of the undeformed tetrahedron).

The penalty against deforming each tetrahedron is derived from its Jacobian matrix. Using singular value decomposition (SVD), J can be decomposed into two unitary matrixes (U and V) and a diagonal matrix (S), such that J = USV ^T. The penalty is based on the singular values from the diagonal of matrix S, which represent relative stretching in orthogonal directions. Matrixes U and V represent rotations, and can be ignored.

A good penalty per unit volume for image registration is based on the singular values of the Jacobian matrices at every point in the deformation being drawn from a lognormal distribution. Unfortunately, the use of conventional methods for computing the SVD of a 3 × 3 matrix is currently too slow to be used within an image registration procedure. C code for an analytic form for computing the singular values of a 3 × 3 matrix was developed using the Symbolic Toolbox of Matlab (The MathWorks, Natick, MA, USA), and also a function describing the rates of change of the singular values with respect to changes to the Jacobian matrix. Unfortunately, the functions were very susceptible to severe rounding errors—particularly for matrices close to the identity matrix. This instability, and the complexity of computing a SVD meant that an alternative method was required.

Using the SVD regularization, the penalty per unit volume is ∑${}_{\text{3}}^{\mathit{\text{i}}\text{=1}}$ log(s _ii )², where s _ii is the ith singular value of the Jacobian matrix. This function is equivalent to ∑${}_{\text{3}}^{\mathit{\text{i}}\text{=1}}$ log(s _ii )²/4. By using an approximation that log(s)² ≃ s + 1/s − 2 for values of s very close to one, we now have the function ∑${}_{\text{3}}^{\mathit{\text{i}}\text{=1}}$ (s ${}_{\text{2}}^{\text{ii}}$ + 1/s ${}_{\text{2}}^{\text{ii}}$ − 2)/4. This function is relatively simple to evaluate because the sum of squares of the singular values of a matrix is equivalent to the sum of squares of the individual matrix elements. This derives from the facts that the trace of a matrix is equal to the sum of its eigenvalues, and the eigenvalues of J ^TJ are the squares of the singular values of J. The trace of J ^TJ is equivalent to the sum of squares of the individual elements of J. Similarly, the sum of squares of the reciprocals of the singular values is identical to the sum of squares of the elements of the inverse matrix. The singular values of the matrix need not be calculated, and there is no longer a need to call the log function (which is slow to compute, but could be tabulated for more speed). The penalty function for each of the tetrahedra is now:

(1)

where tr is the trace operation, I is a 3 × 3 identity matrix, v is the volume of the undeformed tetrahedron (either 1/6 or 1/3), and λ is a regularization constant (see section on “The Priors”). The prior potential (H(Y)) for the whole image is the sum of these penalty functions over all tetrahedra. Figure 2 shows a comparison of the potential based on the original (log(s _ii ))² cost function, and the potential based on (s ${}_{\text{2}}^{\text{ii}}$ + s ${}_{\text{−2}}^{\text{ii}}$ − 2)/4.

Figure 2.

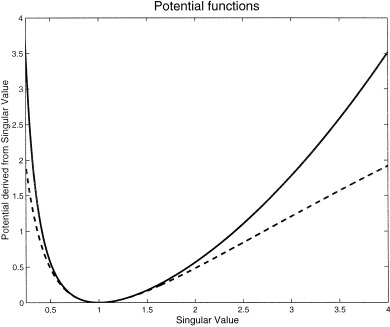
A comparison of the different cost functions. The dotted line shows the potential estimated from (log(s _ii ))², where s _ii is the ith singular value of a Jacobian matrix. The solid line shows the new potential, which is based on (s ${}_{\text{2}}^{\text{ii}}$ + s ${}_{\text{−2}}^{\text{ii}}$ − 2)/4. For singular values very close to one, the potentials are almost identical.

For the optimization, the rate of change of the penalty function for each tetrahedron with respect to changes in position of one of the vertices is required. The Matlab Symbolic Toolbox (The MathWorks, Natick, MA, USA) was used to derive expressions for analytically computing these derivatives, but space prohibits us from giving these formulae here. The ideas presented here assume that the voxel dimensions are isotropic, and the same for both images. Modifications to the method that are required to account for the more general cases are trivial.

Likelihood Potentials (H(b|Y))

The registration deforms an source image (f) to match a template image (g). It assumes that one is simply a spatially transformed version of the other (i.e., there are no intensity variations between them), where the only intensity differences are because of uniform additive Gaussian noise. The Gibbs potential is simply based upon the sum of squared differences between the images, sampled at each voxel of the template image:

(2)

where g(x _i ) is the ith voxel value of g and f(y(x _i )) is the corresponding voxel value of f. The variance (σ²) is assumed to be constant for all voxels, and is estimated from the residual sum of squared difference from the previous iteration. The potential is computed by sampling I discrete voxels within the template image, and equivalent points within the source image are sampled using trilinear interpolation. Gradients of the trilinearly interpolated source image are required for the registration, and these are computed using a finite difference method.

EXAMPLES

Two sets of examples are provided in this section. The first set is based on a single pair of brains. The second set of examples explores the iterative construction of an average shaped brain image based on six individual images.

Registering a Pair of Images

Differences in size and orientation between a pair of brain images are first removed by performing a 12‐parameter affine registration [Ashburner et al., 1997]. Most of the remaining measurable shape differences are low frequency, and are estimated using a basis function approach [Ashburner and Friston, 1999], whereby the deformations are described by 1176 parameters. The combination of these two methods provides a good starting point for estimating the optimum high‐dimensional deformation field. A value of one is used for λ, and 40 iterations of the algorithm are used. This takes about 15½ hr to estimate the 21,233,664 parameters on one of the processors of a SPARC Ultra 2 (Sun Microsystems, USA). 94.5 Mbytes of memory were required by the program (6.75 Mbytes for each of the 8‐bit images, and 81 Mbytes for a single precision floating point representation of the deformation field). This meant that all the data could be stored in random access memory. Figure 3 shows an example of two brain images that have been registered in this way. The corresponding deformation fields are shown in Figure 4.

Figure 3.

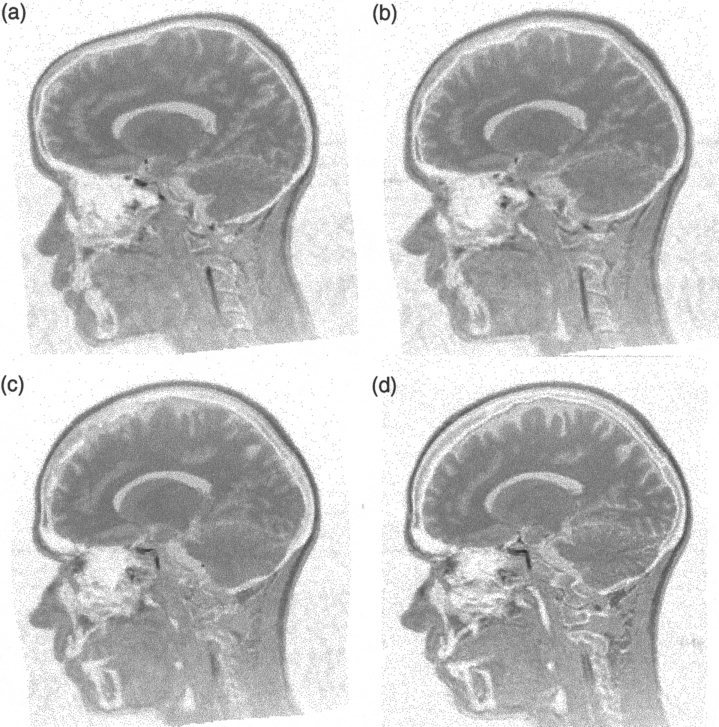
A sagittal plane from two images registered together. The template (reference) image is shown in (d). (a) shows the source image after affine registration to the template image. The source image after the basis function registration is shown in (b), and the final registration result is in (c). The deformation fields are shown in Figure 4.

Figure 4.

The deformation fields corresponding to the images in Figure 3. Two components (vertical and horizontal translations) of the field following affine and basis function registration are shown on the left, whereas the final deformation field is shown on the right.

The symmetry of the registration process was examined by repeating the registration, but swapping the source and template images. This gives us a second deformation field, which, if the registration procedure is symmetric, should be the inverse of the first. To do the comparisons, the inverses of the two deformation fields were computed as described in the Appendix. An example of part of a deformation field computed both ways is shown in Figure 5. The average absolute discrepancy between the first and the inverse of the second deformation, and between the second and the inverse of the first was found to be 1.36 and 1.37 mm. Part of the error is because the likelihood function is not symmetric, as it uses only the gradient of one of the images. A fully symmetric likelihood function [Christensen, 1999b] would be required to make the transformations more consistent.

Figure 5.

A deformation computed by warping the first image to the second (left), and by taking the inverse of the deformation computed by warping the second to the first (right).

Registering to an Average

One of the themes of this paper is about achieving internal consistency in the estimated warps. So far, only mappings between pairs of images have been discussed. When a number of images are to be registered to the same stereotactic space, then there are many possible ways in which this can be achieved. The different routes that can be taken to achieve the same goal may not always produce consistent results [Le Briquer and Gee, 1997; Woods et al., 1998]. To achieve consistency in the warps, we suggest that the images should all be registered to a template image that is some form of average of all the individual images. A mapping between any pair of brains can then be obtained by combining the transformation from one of the brains to the template, with the inverse of the transformation that maps from the other brain to the template.

Here we attempt to compute an image that is the average of six normal subjects brains. The image is an average not only in intensity, but also in shape. We began by estimating the approximate deformations that map each of the images to a reference template, using a 12‐parameter affine registration [Ashburner et al., 1997] followed by the basis function approach [Ashburner and Friston, 1999] (see Figs. 6 and 7). Following the registration, each of the images were transformed according to the estimated parameters. The transformed images contained 121 × 145 × 121 voxels, with a resolution of approximately 1.5 × 1.5 × 1.5 mm. The first estimate of the new template was computed as the average of these images. The estimated 4 × 4 affine transformation matrices and basis function coefficients were used to generate starting parameters for estimating the high dimensional deformation fields.

Figure 6.

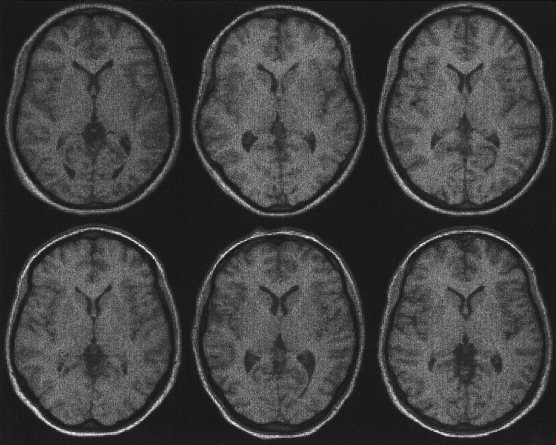
Images of six subjects registered using a 12‐parameter affine registration (see also Figs. 7 and 8). The affine registration matches the positions and sizes of the images.

Figure 7.

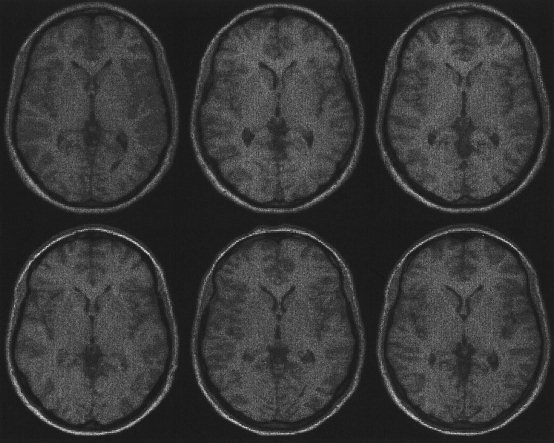
Six subjects brains registered with both affine and basis function registration (see also Figs. 6 and 8). The basis function registration estimates the global shapes of the brains, but is not able to account for high spatial frequency warps.

For each of the six images, ten iterations of the current algorithm were used to bring the images slightly more in register with the template. A value of four was used for λ. The spatially transformed images were averaged again to obtain a new estimate for the template, following which the images were again registered to the template using a further ten iterations. This process continued for a total of four times. A plane from each of the spatially transformed images is shown in Figure 8.

Figure 8.

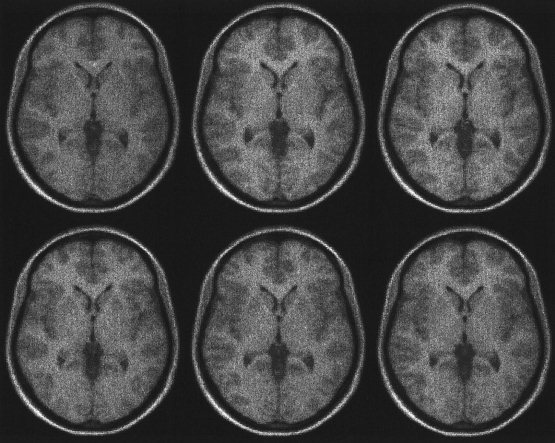
The images of the six brains following affine and basis function registration, followed by high‐dimensional image registration using the methods described in this paper (see also Figs. 6 and 7). The high‐dimensional transformations are able to model high frequency deformations that cannot be achieved using the basis function approach alone.

Visually, the images appear very similar. This is not always a good indication of the quality of the registration (but it does confirm that the optimization algorithm has reduced the likelihood potentials). In theory, the wrong structures could be registered together, but distorted so that they look identical. For the examples shown here, the mapping between the images appeared satisfactory for brain structures that are consistently present and identifiable.

The brain surfaces of the original images were extracted using the tools within SPM99. This involved a crude segmentation of the grey and white matter [Ashburner and Friston, 1997] on which morphological operations were performed to remove the small amounts of none‐brain tissue that remained. The surfaces were then rendered using the tools within Matlab 5.3 (The MathWorks, Natick, MA, USA). A number of points were selected that were near the surface of the template brain (the average of the spatially transformed images). The points did not refer to any particular distinctive features, but were randomly selected from coronal slices spaced approximately 20 mm apart. By using the computed spatial transformations, these points were projected on to the closest corresponding location on the rendered brain surfaces. Figure 9 shows the rendered surfaces. Note that the large amount of cortical variability means that it is very difficult to objectively identify homologous locations on the surfaces of the different brains. The shapes of the internal brain structures are less variable, so the method is able to estimate the transformations much more precisely.

Figure 9.

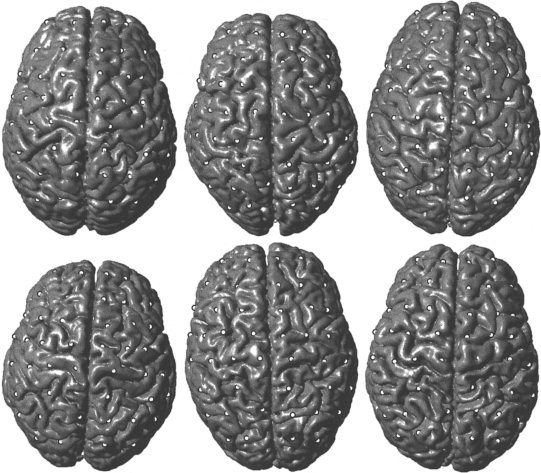
Rendered surfaces of the original six brains. The white markers correspond to equivalent locations on the brain surfaces as estimated by the registration algorithm.

Although the deformation fields contain a mapping from the average shaped template image to each of the individual images, it is still possible to compute the mapping between any image pair. This is done by combining a forward deformation that maps from the template image to the first image, with an inverse deformation (computed as described in the Appendix) that maps from the second image to the template. Figure 10 shows five images that have been transformed in this way to match the same image.

Figure 10.

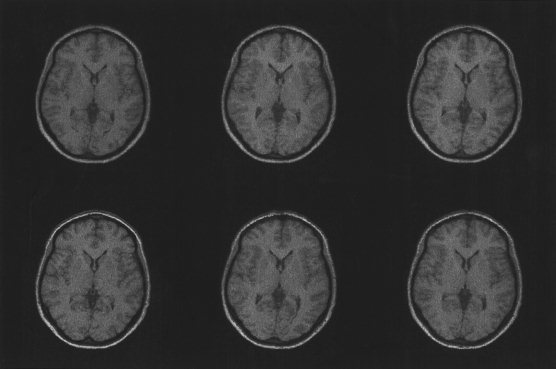
By combining the warps, it is possible to compute a mapping between any pair of images. In this example, the remaining images were all transformed to match the one shown at the lower left.

ISSUES OF VALIDITY

The validity the registration method is dependent on four main elements: the parameterization of the deformations, the matching criteria, the constraints or priors describing the nature of the warps, and the algorithm for estimating the spatial transformations.

Parameterizing the Deformations

The deformations are parameterized using regularly arranged piecewise affine transformations. The same principles described in this paper can also be applied to more irregular arrangements of tetrahedra. Since much of an estimated deformation field is very smooth, whereas other regions are more complex, it would be advantageous in terms of speed to arrange the tetrahedra more efficiently. The layout of the tetrahedra described in this paper is relatively simple, and it does have the advantage that no extra memory is required to store the original coordinates of vertices. It also means that some of the calculations required to determine the Jacobian matrices (part of a matrix inversion) can be precomputed and stored efficiently.

An alternative to using the linear mappings would be to use piecewise nonlinear mappings such as those described by Goshtasby [1987]. However, such mappings would not easily fit into the framework we describe. The main reason for this is that there is no suitable simple expression for the Gibbs potential for each of the patches of deformation field.

In terms of speed, our method does not compare favorably with some other high‐dimensional intensity‐based registration algorithms [Thirion, 1995]; and, in this paper, we have not concentrated on describing ways of making the algorithm more efficient. One way of achieving this would be to use an increasing density of nodes. For the early iterations, when estimating smoother deformations, less nodes are required to adequately define the deformations. The number of parameters describing the deformations is equal to three times the number of nodes, and a faster convergence should be achieved using fewer parameters. It is worth noting that a coarse to fine scheme for the arrangement of the nodes is not necessary in terms of the validity of the method. A coarse to fine approach (in terms of using smoother images and deformations for the early iterations) can still be achieved even when the deformation field is described by an equally large number of nodes from start to finish.

The Matching Criterion

The matching criterion described here is fully automatic, and produces reproducible and objective estimates of deformations that are not susceptible to bias from different investigators. It also means that relatively little user time is required to perform the registrations. However, this does have the disadvantage that human expertise and understanding (that is extremely difficult to encode into an algorithm) is not used by the registration. More accurate results may be possible if the method was semiautomatic, by also allowing user identified features to be matched.

The current matching criterion involves minimizing the sum of squared differences between the source image (which is transformed) and a template (or reference) image. This same criterion is also used by many other intensity based nonlinear registration methods and assumes that one image is just a spatially transformed version of the other, but with white Gaussian noise added. It should be noted that this is not normally the case. After matching a pair of brain images, the residual difference is never purely uniform white noise, but tends to have a spatially varying magnitude. For example, the residual variance in background voxels is normally much lower than that in gray matter. A better approximation than the simple model would involve using a nonstationary variance map.

The validity of the matching criterion depends partly upon the validity of the template image. If the contrast of the template image is different from the contrast of the source image, then the validity of the matching will be impaired because the correlations introduced into the residuals are not accounted for by the model. Pathology is another case where the validity of the registration is compromised. This is because there is no longer a one‐to‐one correspondence between the features of the two images. An ideal template image should contain a “canonical” or average shaped brain. On average, registering a brain image to a canonical template requires smaller (and therefore less error prone) deformations than would be necessary for registering to an unusual shaped template.

The Priors

Consider the transformations mapping between images A and B. By combining the transformation mapping from image A to image B, with the one that maps image B to image A, a third transformation can be obtained that maps from A to B and then back to A. Any nonuniformities in this resulting transformation represent errors in the registration process. The priors adopted in this paper attempt to reduce any such inconsistencies in the deformation fields. The extreme case of an inconsistency between a forward and inverse transformation is when the one‐to‐one mapping between the images breaks down. Unlike many Bayesian registration methods that use linear priors [Amit et al., 1991; Bookstein, 1989, 1997; Gee et al., 1997; Miller et al., 1993], the Bayesian scheme here uses a penalty function that approaches infinity if a singularity begins to appear in the deformation field. This is achieved by considering both the forward and inverse spatial transformations at the same time. For example, when the length of a structure is doubled in the forward transformation, it means that the length should be halved in the inverse transformation. Because of this, the penalty function we have adopted is identical for both the forward and inverse of a given spatial transformation. We believe that the ideal form for this function is that which we previously described [Ashburner et al., 1999], but the more rapidly computed function used in the current paper is a close enough approximation.

The penalty function is invariant to the relative orientations of the images. It does not penalize rotations in isolation, only rotations relative to the orientation of neighboring voxels. To rotate a voxel relative to its neighbors, it is necessary to introduce shearing into the affine transformations, and this shearing is penalized. Similarly, translations are not penalized, but translations relative to neighboring voxels are. This is because relative translations require some voxels to be stretched or shrunk. Zooming of voxels is penalized.

We have stated only the form of the prior potential, and said little about its magnitude relative to the likelihood potential. This is because we do not yet know what the relative magnitudes of the two sets of potentials should be. λ relates to our belief in the amount of brain structural variability that is likely to be observed in the population. A relatively large value for λ results in the deformations being more smooth, at the expense of a higher residual squared difference between the images, whereas a small value for λ will result in a lower residual squared difference, but less smooth deformations. The prior distributions described in this paper are stationary (because λ is constant throughout). In reality, the true amount of brain structural variability is very likely to be different from region to region, so a set of nonstationary priors should, in theory, produce more valid MAP estimates. Much of the nonstationary variability will be higher in some directions than others. A more precise encoding of this directional variability could be in the form of a tensor field, where the directions of variability are specified relative to the axes of a canonical template image. A possible form for this cost function would be something like:

where T is a matrix representing the variability for a particular tetrahedron (Eq. 1). Estimating the normal amount of structural variability is not straightforward. Registration methods could be used to do this by registering a large number of brain images to a canonical template. However, the estimates of structural variability will be heavily dependent upon the priors used by the algorithm. A “chicken and egg” situation arises, whereby the priors are needed to estimate the optimum deformation fields, and the deformation fields are needed to estimate the correct priors. It may be possible to overcome this problem using some form of restricted maximum likelihood estimation (REML) [Harville, 1974] approach. REML algorithms are normally used for fitting weighted linear least squares models where the weights are also treated as unknown hyperparameters. This is a similar situation to that described here, because we have unknown hyperparameters (i.e., σ² and λ) describing the relative importance of the likelihoods v. the priors.

The Optimization Algorithm

The method searches for the MAP solution, which is the single most probable realization of all possible deformation fields. The steepest descent algorithm that is used does not guarantee that the globally optimum MAP solution will be achieved, but it does mean that a local optimum solution can be reached. Robust optimization methods that almost always find the globally optimum solution would take an extremely long time to run with a model that uses millions of parameters. These methods are simply not feasible for routine use on problems of this scale. Even if the true MAP estimate is achieved, there will be other potential solutions that have similar probabilities of being correct. Also, because there is no one‐to‐one match between the small structures (especially gyral and sulcal patterns) of any two brains, it is not possible to obtain a single objective high frequency match, however good an algorithm is for determining the best MAP estimate. Because of this, registration using the minimum variance estimate (MVE) may be more appropriate. Rather than searching for the single most probable solution, the MVE is the average of all possible solutions, weighted by their individual probabilities of being correct. Although Miller et al. [1993] and Christensen [1994] have derived a useful approximation, this estimate is still difficult to achieve in practice because of the enormous amount of computing power required.

If the starting estimates are sufficiently close to the global optimum, then the algorithm is more likely to find the true MAP solution. Therefore, the choice of starting parameters can influence the validity of the final registration result. An error surface based only on the prior potential does not contain any local minima. However, there may be many local minima when the likelihood potential is added to this. Therefore, if the a posteriori potential is dominated by the likelihood potential, then it is much less likely that the algorithm will achieve the true MAP solution. If very high‐frequency deformations are to be estimated, then the starting parameters must be very close to the true optimum solution.

One method of increasing the likelihood of achieving a good solution is to gradually reduce the value of λ relative to 1/σ² over time. This has the effect of making the registration fit the lower frequency deformations before fitting the higher frequencies. Most of the spatial variability is low frequency, so the algorithm can get reasonably close to a good solution using a relatively high value for lambda. This also reduces the number of local minima for the early iterations. The images should also be smoother for the earlier iterations to reduce the amount of confounding information and the number of local minima.

A value for σ² is used that is based on the residual squared difference between the images following the previous iteration. σ² is larger for the early iterations, so the posterior potential is based more on the priors. It decreases over time, thus decreasing the influence of the priors and allowing higher frequency deformations to be estimated. Similarly, for the example where images were registered to their average, the template image was smoothest at the beginning. Each time the template was recreated, it was slightly crisper than the previous version. High‐frequency information that would confound the registration in the early iterations is gradually reintroduced to the template image as it is needed.

CONCLUSIONS

We have developed a method for high‐dimensional registration of brain images, where the deformations are represented by piecewise affine transformations. Unlikely deformations are penalized using a Bayesian framework that incorporates a set of symmetric priors that preserve a locally one‐to‐one mapping between the image volumes. Currently, execution of the registration algorithm is time consuming, but this should become less of an issue as desktop computers become faster.

ACKNOWLEDGMENTS

Many thanks are due to Keith Worsley for some very useful discussions.

APPENDIX. INVERTING THE DEFORMATION FIELD

The current method estimates a deformation field that describes a mapping from points in the template volume to those in the source volume. Each point within the template maps to exactly one point within the source image, and every point within the source maps to a point in the template. For this reason, a unique inverse of the spatial transformation exists. To invert the deformation field, it is necessary to find the mapping from the voxels in the source image to their equivalent locations in the template.

The template volume is covered by a large number of contiguous tetrahedra. Within each tetrahedron, the mapping between the images is described by an affine transformation. Inverting the transformation involves sequentially scanning through all the deformed tetrahedra to find any voxels of the source image that lie inside. The vertices of each tetrahedron are projected onto the space of the source volume, and so form an irregular tetrahedron within that volume. All voxels within the source image (over which the deformation field is defined) should fall into one of these tetrahedra. Once the voxels within a tetrahedron are identified, the mapping to the template image is achieved simply by multiplying the coordinates of the voxels in the source image by the inverse of the affine matrix M for the tetrahedron (from section on “Prior Potentials”).

The first problem is to locate the voxels of the source image that lie within a tetrahedron, given the locations of the four vertices. This involves finding locations where the x, y, and z coordinates assume integer values within the tetrahedral volume. First of all, the vertices of the tetrahedron are sorted into increasing z coordinates. Planes where z takes an integer value are identified between the first and second, the second and third, and the third and fourth vertices. Between the first and second vertices, the cross‐sectional shape of a tetrahedron (where it intersects a plane where z is an integer) is triangular. The corners of the triangle are at the locations where lines connecting the first vertex to each of the other three vertices intersect the plane. Similarly, between the third and fourth vertices, the cross‐section is again triangular, but this time the corners are at the intersects of the lines connecting the first, second and third vertices to the fourth. Between the second and third vertex, the cross‐section is a quadrilateral, and this can be described by two triangles. The first can be constructed from the intersects of the lines connecting vertices one to four, two to four, and two to three. The other is from the intersects of the lines connecting vertices one to four, one to three, and two to three. The problem has now been reduced to the more trivial one of finding coordinates within the area of each triangle for which x and y are both integer values (see Fig. 11).

Figure 11.

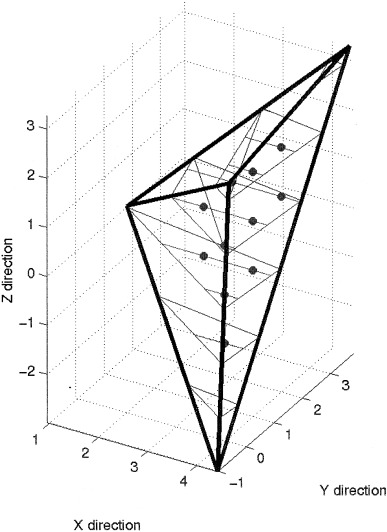
An illustration of how voxels are located within a tetrahedron.

The procedure for finding points within a triangle is broken down into finding the ends of line segments in the triangle where y takes an integer value. To find the line segments, the corners of the triangle are sorted into increasing y coordinates. The triangle is divided into two smaller areas, separated by a line at the level of the second vertex. The method for identifying the ends of the line segments is similar to the one used for identifying the corners of the triangles. The voxels are then simply located by finding points on each of the lines where x is integer.