Tonotopic cortical representation of periodic complex sounds

Abstract

Most of the sounds that are biologically relevant are complex periodic sounds, i.e., they are made up of harmonics, whose frequencies are integer multiples of a fundamental frequency (Fo). The Fo of a complex sound can be varied by modifying its periodicity frequency; these variations are perceived as the pitch of the voice or as the note of a musical instrument. The center frequency (CF) of peaks occurring in the audio spectrum also carries information, which is essential, for instance, in vowel recognition. The aim of the present study was to establish whether the generators underlying the 100m are tonotopically organized based on the Fo or CF of complex sounds. Auditory evoked neuromagnetic fields were recorded with a whole‐head magnetoencephalography (MEG) system while 14 subjects listened to 9 different sounds (3 Fo × 3 CF) presented in random order. Equivalent current dipole (ECD) sources for the 100m component show an orderly progression along the y‐axis for both hemispheres, with higher CFs represented more medially. In the right hemisphere, sources for higher CFs were more posterior, while in the left hemisphere they were more inferior. ECD orientation also varied as a function of the sound CF. These results show that the spectral content CF of the complex sounds employed here predominates, at the latency of the 100m component, over a concurrent mapping of their periodic frequency Fo. The effect was observed both on dipole placement and dipole orientation. Hum. Brain Mapping 20:71–81, 2003. © 2003 Wiley‐Liss, Inc.

INTRODUCTION

The term “tonotopy” describes the topographical organization of neural populations according to their sensitivity to respond to specific frequencies of an acoustic stimulus. In humans, empirical evidence supports the existence of tonotopy in the cochlea (Von Békésy, 1960) and in the auditory cortex (e.g., Liégeois‐Chauvel et al., 1991; Romani et al., 1982). As in animal studies (Kosaki et al., 1997; Merzenich and Brugge, 1973), even multiple tonotopic maps have been described in the supratemporal plane (Cansino et al., 1994; Pantev et al., 1995; Talavage, 2000). Classical tonotopic studies have in common that simple “pure tones”, i.e., sine‐waves, have been employed as stimuli.

Sine‐wave sounds can easily be produced by means of electroacoustical equipment. However, neither the human voice nor musical instruments produce these “pure tones.” Because of non‐linear movement patterns occurring in mechanical objects, waveforms associated with physical vibrations are usually far from sinusoidal. If a vibration is sustained by a continuous energy source (e.g., by lung pressure in the vowels of the human voice or by the movement of the bow in a violin), Fourier's theorem (Fourier, 1822) stipulates that it is equivalent to a series of sine‐waves. This series is made up of a fundamental frequency (Fo), which reflects the “periodicity pitch” of the wave, and of harmonics, which are multiples of Fo, and account for the wave shape complexity. Fo is perceived as the musical note on which the sound is produced. The spectrum, i.e., the distribution of harmonic amplitude with frequency, may be modified if some frequencies in the spectrum are made to be predominant. A band‐pass filter can select a region between two frequencies f1 and f2, where harmonics are emphasized. The “Central Frequency” (CF) of this filter can be defined as CF = sqrt (f1 × f2). In the case of spoken vowels, the mouth cavity forms narrow band‐pass filters, called “formants” (Peterson and Barney, 1952) that can also be characterized by their central or main resonant frequencies CFs. These allow vowels to be differentiated, independently from the periodicity pitch Fo at which the vocal cords vibrate. The independence between CF and Fo enables different words to be sung in the same melody and vice versa.

Tonotopy in the auditory cortex has been demonstrated in classical studies (e.g., Cansino et al., 1994; Howard III et al., 1996; Kuriki and Murase, 1989; Pantev et al., 1988; Romani et al., 1982; Yamamoto et al., 1992) using sine‐wave stimuli in which Fo and CF are the same. In a simple sine‐wave stimulus, the frequency spectrum is limited to a single spectral line that corresponds to the pitch itself, and therefore the pitch and spectrum dimensions are confounded. Because of this, they cannot reveal whether neural tonotopy represents the actual fundamental component (periodicity), or the spectrum of complex tones. In other words, the question is: does the frequency map on the cortex represent the Fo or the CF of the sounds?

This question was tackled by Crottaz‐Herbette and Ragot (2000) in an electroencephalography (EEG) study demonstrating that these sounds were represented on the cortex according to their spectral CF structure, since it was observed that equivalent dipole source (ECD) orientations varied as a function of CF, while their fundamental pitch was reflected by N1 latency variations. Langner et al. (1997) studied 100‐msec responses elicited by sine‐wave tones and by periodic sounds of different harmonic contents, which elicited a pitch corresponding to each of their pure tone frequencies. They reported an orthogonal representation of frequency and periodicity in the auditory cortex: the sources for the 100‐msec component varied from superior to inferior positions with higher frequencies, and from posterior to anterior positions with higher pitches. However, this study does not allow for disentangling the independent effects of pitch and spectrum of complex sounds, because dipole source position comparisons were conducted between pitch of complex sounds and frequency of pure tones, in which, as we have seen, Fo and CF are confounded.

EEG studies with pure tones have mainly reported differences in dipole orientation as a function of frequency (Bertand et al., 1991; Giard et al., 1994; Verkindt et al., 1995), whereas MEG experiments have demonstrated differences in source localization (Cansino et al., 1994; Elberling et al., 1982; Pantev et al., 1988). Variations in source position and orientation apparently occur simultaneously; however, each imaging technique is predominantly sensitive to one of these variations. Indeed, as stated in a study by Pantev et al. (1995, p 27), in which EEG and MEG data were recorded from the same subjects: “The frequency‐dependent dipole orientation, which can be more accurately estimated from electric than from magnetic recordings, agrees with the frequency‐dependent depth changes of the N1m equivalent source.” Variations in source localization and orientation can thus occur simultaneously, the latter being due to curvatures in the folium.

The purpose of the present experiment was to investigate with the MEG technique whether it is possible to detect source position differences as a function of the spectrum content of the stimulus, since only dipole orientation variations with CF were reported in the Crottaz‐Herbette and Ragot (2000) study. The question was addressed by setting an experimental paradigm in which spectrum and periodicity are directly compared, as in Crottaz‐Herbette and Ragot (2000). Nine complex auditory stimuli, for which the pitch and spectrum dimensions were independently varied, were constructed to make up a square design in which three different Fos (62.5, 125, and 250 Hz) were combined with three different CFs (“LOW,” “MID,” and “HIGH”; Fig. 1). These values of Fo and CF are typical for the spoken human voice. This 3×3 experimental design has been used in a series of psychophysical studies on the perception of complex sounds (Shackleton and Carlyon, 1994).

Figure 1.

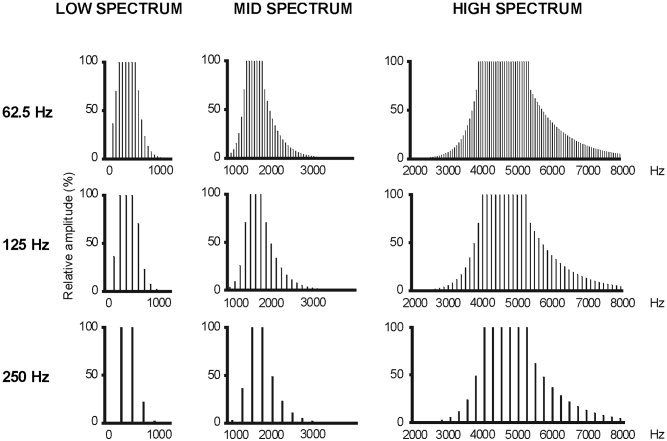
The nine types of stimuli employed in the experiment: 3 fundamental pitches (Fo) combined with 3 spectral envelopes (CF).

SUBJECTS AND METHODS

Subjects

Subjects were 14 paid male university students. Following medical examination by a neurologist, they were screened for auditory deficits and excluded from the study if an abnormal hearing loss was detected in the 125‐Hz to 8‐kHz band. They were fully informed of the methods and technique of non‐invasive MEG recordings before signing a written agreement to participate in the experiment. The experimental paradigm and procedures had been approved by the French Ethical Committee for Human Research (CCPPRB). The data from two subjects were excluded from the analysis because of the large amount of blinking and movement artifacts. Mean age of the 12 remaining subjects was 26.1 years (range 23–30).

Stimuli

Stimuli were constructed by Fourier additive synthesis of sine waves to make up nine different types of sounds: three different fundamental pitches (Fo) combined with three different spectra (Fig. 1). The three values for Fo were 62.5, 125, and 250 Hz. The three spectral windows (specified at −3 dB down point) were: from 125 to 625 Hz (“LOW” spectrum, CF = 280 Hz); from 1,375 to 1,875 Hz (“MID” spectrum, CF = 1,600 Hz); and from 3,900 to 5,400 Hz (“HIGH” spectrum, CF = 4,600 Hz). The stimulus intensity of all stimuli was adjusted to present the same amplitude of 78 dB ± 1 dB sound pressure level (SPL) at earphone output, using a sound level meter (type 2203; Brüel and Kjoer, Norway). Sounds were stored in digital format, generated by an electrostatic high‐fidelity transducer (S‐001 MK2 and driver unit; Stax, Japan), and presented monaurally through an anatomically‐shaped ear insert (Doc's Promold; International Aquatic Trades, USA). A graphic equalizer (GE 10 M; Yamaha, USA) inserted in the signal path was used to correct the frequency response of the whole system, making it flat from 100 Hz to 7 kHz ± 3 dB. A background pink noise of 60 dB SPL was presented continuously during the experiment, in order to eliminate low‐order distortion products. Tone duration was 400 msec, with a 5‐msec rise and fall time. Onset‐to‐onset interstimulus interval varied randomly from 800 to 1,200 msec. Stimuli were presented in 10 sequences of 3‐min duration for each ear with pauses between sequences allowing subjects to rest and blink at will. The first stimulated ear was counter‐balanced across subjects. In each sequence, the nine stimuli were presented 20 times each in random order, but the same stimulus was never presented twice in succession to avoid repetition effects. Each stimulus type was presented 200 times to each ear.

Procedure

Neuromagnetic measurements were carried out within a magnetically shielded room. Subjects were lying flat on their back, with their head immobilized in the Dewar with soft padding. They were asked to keep their eyes open, to keep their gaze fixed on a black cross on the ceiling, and to attend sounds in a passive manner, i.e., not to pay particular attention to the sounds. An audio–video system allowed for auditory and visual communication with the subject throughout the experiment. Brain magnetic activity was recorded with a whole‐head 151‐channel squid magnetometer (CTF systems, Canada) with third‐order gradiometers. Head position was measured between each sequence of stimuli with 3 coils placed on the nasion and on the right and left mastoids. Stimulus‐related epochs of 790‐msec duration (including a 200‐msec prestimulus baseline) were recorded with a sample rate of 625 Hz. The output of each sensor was lowpass‐filtered on line at 100 Hz.

Data Analysis

Epochs contaminated by muscle or eye blink artifacts with amplitude variations of more than 3 pT in any channel were rejected from the averaging procedure. Signals recorded for each type of stimulus were averaged together. Mean trial number was 165, SD = 14, range 149–190. The averaged epochs were adjusted relative to the mean amplitude in the 200‐msec prestimulus period to remove DC‐offset. Two distinct field extrema were observed over each side of the head, where the fields emerging from the head and returning to the head are stronger. The main response observed at each of these locations consisted of a peak between 70 and 140 msec after stimulus onset. In accordance with previous studies (Hari et al., 1980), this field pattern is associated with activity in the auditory cortex; therefore, this peak is denoted the 100m component, where the 100 expresses its approximate latency, and the “m” indicates a magnetic measurement.

The sources of the 100m component were modeled separately as a single equivalent current dipole (ECD) for each hemisphere. We employed a one‐dipole model because the existence of two distinct extrema on each hemisphere indicates that the neural activity can be modeled more reliably by a single current dipole when short time segments are analyzed (for a review see Hari, 1990). There is empirical evidence for the existence of two or more 100m equivalent sources (Cansino et al., 1994; Lu et al., 1992; Moran et al., 1993). However, the magnetic field produced at the surface of a sphere by one dipole differed subtly from that produced by more than one current dipole (Nunez, 1986; Okada, 1985). Indeed, more than one single dipole has been detected using specific experimental conditions as long inter‐stimulus intervals (Cansino et al., 1994; Lu et al., 1992) or by employing specific analysis as finite difference field mapping (Moran et al., 1993). The ECDs were calculated with a spherical conductor model, which can cause errors in the absolute placement of source dipole localization. However, this lack of absolute precision does not interfere with the purpose of this work, which is to study variations in dipole placement or orientation associated with changes in stimulus characteristics. Source dipoles were fit on magnetic signals recorded with the sensors located on the hemisphere contralateral to the stimulated ear, because auditory neuromagnetic field patterns are stronger for contralateral than for ipsilateral stimulation (Cansino and Williamson, 1997; Pantev et al., 1986).

Dipole fits were computed independently for data of each subject and separately for each hemisphere. Stationary ECDs were estimated on averaged signal data for each of the 9 experimental conditions: three fundamental pitches (62.5, 125, and 250 Hz) combined with three spectra (“LOW,” “MID,” and “HIGH”). First, the latency of the 100m component was determined for each condition by means of the root mean square (RMS) amplitudes calculated between 50 and 150 msec after the onset of the stimulus. Subsequently, ECDs were searched for in a 50‐msec period, 25 msec before and after the peak latency of the 100m component. The time point within the 50‐msec period that provided the best least‐squares fit between the forward solution and the measured signals was selected to determine the locations and orientations of the ECDs for each condition. All statistical analyses were carried out separately for data of the left and right hemispheres. The position and orientation values of the ECD were submitted to a 3 × 3 (pitch × spectrum) repeated measures analysis of variance (ANOVA). The same 3 × 3 (pitch × spectrum) repeated measures ANOVA was used to evaluate the 100m latencies. There was a 5‐msec delay in the tube linking the sound transducer to the ear. This measured delay remained constant from 100 to 7 KHz. Reported results of average 100m latencies have been corrected for this and represent latency in response to the sound presented to the ear. Degrees of freedom were corrected with the Greenhouse‐Geisser procedure. Original degrees of freedom, the Greenhouse‐Geisser coefficient (ϵ) and corrected probability levels are reported. Post hoc comparisons were computed with paired two‐tailed t tests with a significance level of P < 0.05.

It is important to notice that the between‐subjects variation in source location due to head dimension differences did not affect the ANOVA results reported below. This was tested by computing a second set of ANOVAs with data corrected for head dimension variations. For each subject the x, y, and z coordinates were realigned to an average‐size head model, which was obtained by averaging the individual head coordinates separately for each axis and both polarities. The ANOVA results with realigned data were identical to those obtained with raw dipole positions. In order to present realistic source locations and for the sake of clarity, only results with raw data are reported. Positions of deduced neural sources are expressed by a Cartesian coordinate system (Williamson and Kaufman, 1989), whose origin lies midway between the left and right periauricular landmarks. The positive x axis is defined as the line that extends from the origin to the nasion. The positive z axis passes upward from the origin, directed perpendicular to the plan containing the x axis and the line joining the two periauricular landmarks. The positive y axis is perpendicular to both the x and z axes, extending from the origin to emerge from the left side of the head.

RESULTS

Mean error source solutions was 11.23% (SD = 2.63) across conditions and subjects. The ANOVAs for ECD positions of the 100m component recorded on the left hemisphere were significant only for the factor spectrum, independently of stimulus pitch, along the y axis [F(2,22)= 8.36, ϵ = 0.96, P = 0.002] and the z axis [F(2,22)= 4.91, ϵ = 0.83, P = 0.02]. Post hoc analyses of the y axis data revealed that sources for the LOW and MID spectra were significantly more lateral than for the HIGH spectra (t = 3.74, P = 0.003 and t = 3.53, P = 0.005, respectively). Along the z axis, ECD positions differed between LOW and HIGH spectra (t = 2.71, P = 0.02): sources for stimulus with HIGH spectrum content had a more inferior position. Mean positions of ECD sources in both hemispheres as a function of stimulus spectrum are depicted in Table I.

Table I.

Positions for each axis and each hemisphere as a function of spectrum

	Left hemisphere			Right hemisphere
	x	y *	z *	x *	y *	z
LOW	−0.01 (.23)	5.34 (.11)	5.95 (.20)	0.87 (.22)	−5.02 (.11)	5.58 (.23)
MID	−0.07 (.21)	5.29 (.10)	5.78 (.17)	0.70 (.22)	−4.94 (.14)	5.56 (.16)
HIGH	−0.03 (.19)	5.08 (.09)	5.70 (.16)	0.38 (.27)	−4.77 (.15)	5.52 (.18)

Values are expressed in cm as mean (SE).

^*Axes with significant ANOVA.

For the 100m responses recorded on the right hemisphere, the ANOVAs revealed a significant spectrum effect on ECD positions measured along the x axis [F(2,22) = 9.95, ϵ = 0.83, P = 0.002] and y axis [F(2,22) = 4.26, ϵ = 0.70, P = 0.046]. Post hoc t test on the x axis data revealed that sources for the 100m elicited by LOW and MID spectra were significantly more anterior than those to the HIGH spectrum (t = 3.65, P = 0.004 and t = 3.09, P = 0.01, respectively). For dipole positions along the y axis, the LOW and HIGH spectra were significantly different (t = −2.26, P = 0.045), ECD positions were located more medially for stimuli with HIGH spectrum. In the y axis the interaction between spectrum and pitch was also significant [F(4,44) = 5.11, ϵ = 0.60, P = 0.01]. Post hoc analyses revealed that when the frequency periodicity was of 62.5 Hz, ECD positions for the MID (mean = −5.09 cm, SE = 0.15) spectrum were significantly more lateral than for the HIGH (mean = −4.67 cm, SE = 0.17) spectrum (t = −3.21, P = 0.008); while sources for the LOW (mean = −5.13 cm, SE = 0.11) spectrum were more lateral than for the MID (mean = −4.93 cm, SE = 0.13) and HIGH (mean = −4.87 cm, SE = 0.13) spectra (t = −3.08, P = 0.01 and t = −2.82, P = 0.02, respectively) when the periodicity pitch was 250 Hz but source positions did not vary as a function of pitch. Figure 2 shows the mean source positions for each type of stimulus across subjects, and Figure 3 exhibits, in a 3‐D space, the dipole positions collapsed across Fo and CF values.

Figure 2.

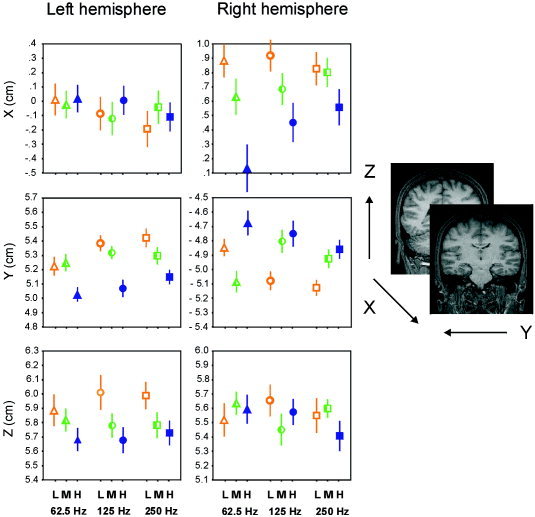
Source location as a function of stimulus spectrum (empty bullets for LOW [L], half‐filled bullets for MID [M], and filled bullets for HIGH [H]) and stimulus pitch (triangles for 62.5 Hz, circles for 125 Hz, and squares for 250 Hz). Data averaged across subjects. Positive x values for anterior positions, positive y values for left positions, and positive z values for superior positions. Lines represent the standard error.

Figure 3.

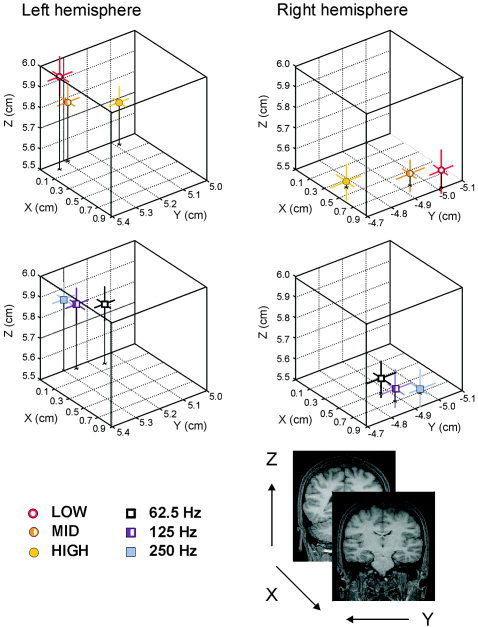
3‐D portrayal from a back view with Fo data collapsed to show source positions for each spectrum (LOW, MID, and HIGH) (top) and with CFs collapsed to show source locations for each pitch (62.5, 125, and 250 Hz) (bottom). The lines represent the standard errors in each of the axes.

Normalized orientation values were converted to degree values in order to make them more comprehensible. Dipole orientations were measured in the axial (x–y), coronal (y–z), and sagittal (z–x) planes. Positive angular values indicate that the dipoles turn counter‐clockwise with reference to the x, y, and z axes, respectively, in each of the planes mentioned above, while negative values denote that they turn clockwise. In spherical models for the head, only current dipoles that flow tangential to the surface are detectable outside the scalp (Kaufman and Williamson, 1982), thus the dipole moment y component is weaker compared with the x and z components. There was a main effect of spectrum along the z–x dipole orientation plane for data from both the left (F(2, 22) = 12.20, ϵ = 0.57, P = 0.003) and right hemisphere (F(2, 22) = 8.06, ϵ = 0.88, P = 0.004; see Table II). Post hoc analyses of the left hemisphere data revealed that dipole orientations significantly differed among stimuli: LOW and MID (t = −2.44, P = 0.03), MID and HIGH (t = −5.50, P = 0.0002), and LOW and HIGH (t = −4.08, P = 0.002); while analyses of the right hemisphere data showed that dipole orientations elicited by LOW spectrum significantly differed from dipole orientations elicited by MID and HIGH spectra (t = −2.62, P = 0.02 and t = −3.41, P = 0.006, respectively). Sources for stimuli with HIGH spectrum content were more superiorly oriented in both hemispheres. There were no significant main effects or interactions of spectrum and pitch periodicity along either the x–y or the y–z planes. Figure 4 shows dipole orientations as a function of Fo and CF across subjects.

Table II.

Dipole orientations for each plane and each hemisphere as a function of spectrum

	Left hemisphere			Right hemisphere
	x–y	y–z	z–x *	x–y	y–z	z–x *
LOW	81 (34)	−80 (4)	−132 (3)	−125 (29)	−103 (7)	−124 (4)
MID	79 (41)	−74 (6)	−122 (5)	−149 (19)	−102 (10)	−118 (3)
HIGH	80 (36)	−73 (7)	−114 (5)	−82 (39)	−103 (9)	−114 (3)

Values are expressed in degrees as mean (SE).

^*Axes with significant ANOVA.

Figure 4.

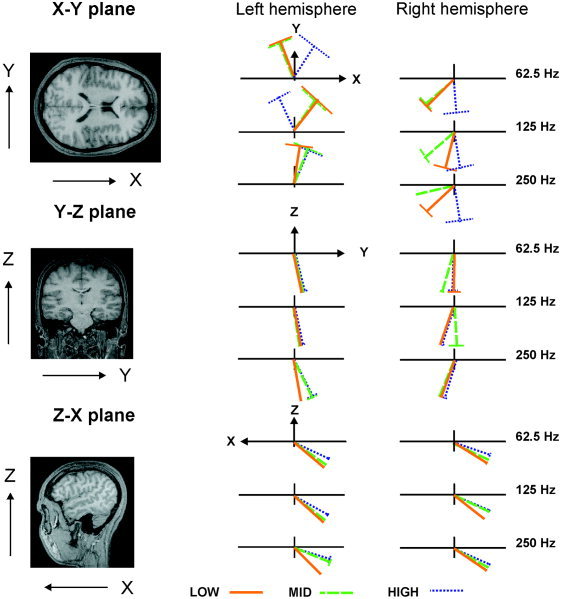
Source orientation variations as a function of stimulus spectrum and stimulus pitch. Data averaged across subjects. x–y plane view from top, y–z plane view from front, and z–x view from left. The perpendicular lines represent the standard errors.

The latency of the 100m component varied as a function of periodicity pitch on data from both left (F(2, 22) = 40.08, ϵ = 0.90, P = 0.0000002) and right (F(2, 22) = 18.39, E = 0.76, P = 0.0001) hemispheres. Post hoc analyses revealed that, for the left hemisphere, latencies varied significantly among stimuli: 62.5 Hz (mean = 134 msec, SE = 0.003) and 125 Hz (mean = 129 msec, SE = 0.002) (t = 3.59, P = 0.004), 125 and 250 Hz (mean = 118 msec, SE = 0.002) (t = 5.54, P = 0.0002), and 62.5 and 250 Hz (t = 8.00, P = 0.00001); while for the right hemisphere, differences were significant between the 62.5 Hz (mean = 134 msec, SE = 0.004) and the 250 Hz (mean = 120 msec, SE = 0.003) stimuli (t = 7.40, P = 0.00001), and between the 125 Hz (mean = 129 msec, SE = 0.005) and the 250 Hz stimuli (t = 4.09, P = 0.002). In both hemispheres, shorter latencies correspond to higher frequencies.

DISCUSSION

The present study provides evidence for a tonotopic organization in the auditory cortex based on the spectral content of sounds (CF). This finding does not preclude topographical organization in auditory cortex based on Fo. There is evidence for multiple maps in human auditory cortex, and these maps may contribute differentially to the various components of the auditory evoked potentials. Even multiple generators can contribute to the production of N1 and 100m components (Näätänen and Picton, 1987). Parvalbumin immunoreactivity studies have revealed two distinct tonotopic representations in the supratemporal plane of macaque monkeys, which reversed directions in terms of high vs. low frequency positioning (Kosaki et al., 1997). EEG and MEG techniques have the added advantage that they allow discriminating such possible different maps on the basis of their latency. Pantev et al. (1995) observed a tonotopic mapping to pure tones for the magnetic Pam and electrical Pa components (latency about 30 msec), which are reverse‐mapped with respect to that of the N1m and N1 components. It is possible that such mapping at this latency might truly reflect Fo rather than CF. A 50‐msec component was indeed observed in the present experiment, but its small amplitude did not allow for reliable dipole modeling. Let us stress then that the present results are valid for the mapping of magnetic sources eliciting maximum response at a latency between 118 and 134 msec. Picton et al. (1999) modeled sound‐elicited electrical components occurring around 105 and 140 msec with dipoles placed in the same location in the supratemporal plane but oriented differently. Attempts to model several generators for the 100m in each hemisphere in the present study, led to generator positioning inconsistency, which did not allow for studying the respective effects of CF and Fo reliably. At the latencies where the presently reported peaks occur, it cannot be excluded that several sources may contribute to the observed peaks, but data are consistent with a predominant generator located in the supratemporal plane. Present results must, therefore, be specified as reflecting the effect of CF and Fo on the main cortical source eliciting the 100m component.

Similar results have been previously reported in monkey studies. Schwarz and Tomlinson (1990) recorded single‐unit responses in the auditory cortex of the rhesus monkey to pure and harmonic complex sounds, and their results showed that neural responses were determined by the spectral content of the stimulus. Similarly, Fishman et al. (1998) reported a study with macaque monkeys where they measured single‐unit firing patterns and synchronized activity of neuronal populations. Their results demonstrated that population responses in primary auditory cortex reflected the spectral content of the stimulus rather than their pitch.

Few human studies have tested the effect of spectrum shape on ECD positions or orientations. Langner et al. (1997) compared pure tones with complex harmonic sounds. However, in only two harmonic sounds was the spectrum shape varied by using stimuli with the same pitch periodicity while changing the low cut‐off frequency from 400 to 800 Hz. Their results showed a superior‐inferior shift in dipole positions from lower to higher cut‐off frequency stimuli. In the present study, a similar shift was observed as the spectrum CF changed from LOW to HIGH. Langner et al. (1997) also reported an orthogonal representation of frequency and periodicity. In contrast, in the present experiment, the representation of spectral content was completely predominant, casting some doubt on the existence of a possible representation of such sound periodicity. It is worth noticing that Langner et al. (1997), rather than using an experimental paradigm in which Fo and CF varied independently, conducted the statistical analysis of dipole source positions between the pitch of complex sounds and the frequency of pure tones, in which Fo and CF are confounded. Diesch and Luce (2000) have also provided some evidence of the effect of spectral content on ECD positions by means of MEG. However, instead of using complex harmonic sounds, these authors employed vowel formants. Four of them were single vowel formants with 200‐, 400‐, 800‐, and 2,600‐Hz formant frequencies. As described, the spectrum shape expresses the main information that allows spoken vowels to be differentiated. Diesch and Luce (2000) found that the 100m sources were located more posterior for high frequency formants than for low frequency formants. The same spectral effect on source positions was observed in the present study.

Crottaz‐Herbette and Ragot (2000) tested whether the human cortical tonotopy represents the Fo of complex sound or their CF by electrophysiological recordings, and they also provided evidence of a sound mapping in the auditory cortex based on their spectral profiles rather than their frequency periodicity. The negative ERP component elicited by dipole sources was more frontally oriented as CF increased. In the present study, an orientation shift was observed in the z–x plane. Considering that a positive dipole source oriented backwards causes frontal negativity, the more backwards the dipole (as CF increases), the more frontal the negativity. Thus, the present results corroborate the above‐mentioned EEG data. Likewise, EEG (Bertrand et al., 1991; Verkindt et al., 1995) and MEG (Tiitinen et al., 1993) tonotopic studies with pure tones found an equivalent source orientation shift as frequency increased. The present experiment reveals that both position and orientation source variations are detectable by MEG. Orientation shifts might be due to the fact that a substantial portion of the auditory cortex lies in the Sylvian fissure on the upper surface of the temporal lobe, which is characterized for being an extremely folded region of the brain (Galaburda and Sanides, 1980).

The findings of the present experiment do not contradict results reported by classic tonotopic experiments with pure tones (e.g., Cansino et al., 1994; Kuriki and Murase, 1989; Pantev et al., 1988; Romani et al., 1982; Yamamoto et al., 1992;). In these studies, the tonotopic representation was associated to the fundamental frequency of stimuli rather than to their central frequency because simple sine waves do not allow distinguishing the effect of these two sound dimensions. In the present experiment, spectral content effects were observed in both hemispheres on the y axis. ECD sources were located more laterally for LOW spectral stimuli and more medially for HIGH spectral stimuli. The same distribution has been consistently observed with tone bursts (e.g., Cansino et al., 1994; Kuriki and Murase, 1989; Pantev et al., 1988; Romani et al., 1982; Yamamoto et al., 1992): sources for high frequencies are located deeper than sources for low frequencies.

Furthermore, in this study spectral effects were observed on the superior‐inferior axis of the left hemisphere and in the posterior–anterior axis of the right hemisphere. Sources for the 100m component were located more superiorly for stimuli with LOW CFs than HIGH CFs. Langner et al. (1997) also showed a superior‐inferior shift for pure tones as Fo increased, though in the right and not in the left hemisphere. In the posterior‐anterior axis, sources for stimuli with HIGH spectral content were located more posteriorly than sources for stimuli with LOW spectral content. Tonotopic representations along the x axis have been reported in the same direction by Pantev et al. (1988), Elberling et al. (1982), and Howard III et al. (1996), and in the opposite direction by Tuomisto et al. (1983) and Pelizzone et al. (1984). Nevertheless, most studies have not found a consistent effect on this axis (Cansino et al., 1994; Kuriki and Murase, 1989; Liégeois‐Chauvel et al., 2001; Pantev et al., 1995; Romani et al., 1982; Yamamoto et al., 1992).

Together, these results indicate that the tonotopic representation of the auditory cortex is represented predominantly over the lateral‐medial axis in both hemispheres with HIGH CF spectral sounds evoking responses lying deeper within the sulcus than LOW CF spectral sounds. This tonotopic organization has a distinctive spatial distribution in each hemisphere. Over the left hemisphere, sources evoked for HIGH CFs were located more inferior while in the right hemisphere, they were more posterior. Additionally, the current dipoles representing the 100m sources are more anterior in the right than in the left hemisphere, as previously noted by Elberling et al. (1982), Kuriki and Murase (1989) and Cansino et al. (1994). Galaburda and Sanides (1980) have described the gross anatomical asymmetries of the auditory region between the left and right hemisphere, where the degree and pattern of folding are extremely variable between brains and between the hemispheres of each brain. Functional and anatomic hemisphere asymmetries might explain the different hemisphere tonotopic representation observed in the present study. However, further research is necessary in order to test whether this asymmetry along the superior‐inferior and anterior‐posterior axes can be replicated.

Moreover, the tonotopic mapping for LOW, MID, and HIGH spectral contents observed in the present experiment, while showing a clear source displacement according to spectral changes from LOW to HIGH, reveals that this source displacement was not always significant between LOW and MID stimuli. This might be due to the fact that, despite the selection of stimuli to avoid overlapping spectral windows, the CF differences between LOW to MID, and MID to HIGH might not be represented at equivalent distances on the cortical maps. Therefore, further research with spectral CFs representing systematic variations is necessary to establish the minimum CF change capable of producing a visible dipole source displacement in the human auditory tonotopic representation.

The question can be raised as to whether tonotopic CF effects could be due to perceived loudness, which varies with frequency. This variation is large at low intensity levels, and much smaller for louder sounds (Fletcher and Munson, 1933). At the 78 dB SPL used in the present experiment, perceived loudness varies less than ±5 dB in the range of harmonics presented (between 125 Hz and 5.4 kHz), making it less likely for the observed effect to be caused by perceived loudness. In addition, the effect of frequency on perceived loudness is in the shape of a U‐curve (perceived loudness is lower at low and high frequencies). If the effects of CF on the variation of dipole source orientations and positions were due to such a loudness effect, they should reflect a U‐curve and not the linear trend that is presently observed.

The latency of the 100m component decreased as the periodicity pitch increased, independently of the CF of the complex sound. This finding replicates previous results with complex sounds (Crottaz‐Herbette and Ragot, 2000; Langner, 1997; Ragot and Lepaul‐Ercole, 1996) and with pure tones (Stufflebeam et al., 1998; Verkindt et al., 1995; Woods et al., 1993). Thus, Fo appears to be coded temporally instead of spatially.

In brief, the data of this study provide evidence for the following points: (1) 100m dipole positions vary with the spectral content of sounds, not with their periodicity. This indicates that the mapping for spectral contents (which accounts for vowels and timbre of sounds) predominates over a possible periodicity map; (2) equivalent current dipole increased in depth beneath the scalp with increasing CF of complex sounds. In the left hemisphere, a superior‐inferior shift was observed as CF increased, while in the right hemisphere there was a posterior‐anterior shift; (3) 100m dipole orientations vary as a function of the spectral dimension of the sound. This shows that MEG, like EEG, is capable of mapping dipole orientations. In addition, the fact that variations in dipole location were observed with MEG but not with EEG (Crottaz‐Herbette and Ragot, 2000) with the same experimental paradigm, suggests that MEG is more accurate in mapping dipole positions; and (4) the latency of the 100m component varies with periodicity, and not with the spectral content of sounds.