Abstract
This paper presents a new approach to functional magnetic resonance imaging (FMRI) data analysis. The main difference lies in the view of what comprises an observation. Here we treat the data from one scanning session (comprising t volumes, say) as one observation. This is contrary to the conventional way of looking at the data where each session is treated as t different observations. Thus instead of viewing the v voxels comprising the 3D volume of the brain as the variables, we suggest the usage of the vt hypervoxels comprising the 4D volume of the brain‐over‐session as the variables. A linear model is fitted to the 4D volumes originating from different sessions. Parameter estimation and hypothesis testing in this model can be performed with standard techniques. The hypothesis testing generates 4D statistical images (SIs) to which any relevant test statistic can be applied. In this paper we describe two test statistics, one voxel based and one cluster based, that can be used to test a range of hypotheses. There are several benefits in treating the data from each session as one observation, two of which are: (i) the temporal characteristics of the signal can be investigated without an explicit model for the blood oxygenation level dependent (BOLD) contrast response function, and (ii) the observations (sessions) can be assumed to be independent and hence inference on the 4D SI can be made by nonparametric or Monte Carlo methods. The suggested 4D approach is applied to FMRI data and is shown to accurately detect the expected signal. Hum. Brain Mapping 13:185–198, 2001. © 2001 Wiley‐Liss, Inc.
Introduction
Functional magnetic resonance imaging (FMRI) is one of the main tools used to investigate the functions of the human brain. The most commonly employed strategy is to investigate how the blood oxygenation level dependent (BOLD) signal changes as a function of stimuli and/or tasks [Bandettini et al., 1992; Frahm et al., 1992; Kwong et al., 1992; Ogawa et al., 1992]. One of the aims of these types of studies is to localize the regions of the brain that become activated during certain stimuli and/or tasks. There are several different methods for FMRI data analysis described in the literature that accomplish this [see Petersson et al., 1999a, b, for a general discussion of these methods, and Lange et al., 1999, for a comparative analysis]. Common to most of these proposed methods is the view of the data as a set of voxels observed at a number of consecutive time points. This set of voxels usually spans a 3D volume covering the whole, or parts, of the brain. Thus, for each voxel in the brain and each scanning session a time‐series is obtained. In the standard approach to FMRI data analysis, a statistical model, often a variant of the general linear model, is fitted to these many time‐series. Hypotheses are subsequently tested on the estimated parameters, resulting in an image that contains a statistic for each voxel (e.g., a correlation coefficient), a so‐called statistical image (SI). Finally, statistical inference is made on the SI, taking into consideration the many nonindependent observations made.
Difficulties faced by 3D methods
There are several difficulties inherent in this standard approach to FMRI data analysis. Temporal correlations between adjacent time points makes model estimation difficult. Spatial correlation between adjacent voxels makes it difficult to obtain accurate solutions to the multiple comparison problem. A straightforward Bonferroni correction would usually be too conservative. Another difficulty, particularly in so‐called event‐related studies [see Rosen et al., 1998, for a review], is related to the fact that the nature of the coupling between neuronal activity and the observed BOLD signal is partly unknown.
Temporal autocorrelations
It is well known that observations from adjacent time points are correlated [e.g., Friston et al., 1994a; Zarahn et al., 1997; Purdon and Weisskoff, 1998]. The observed temporal autocorrelation is believed to have several causes. The slow time course of the BOLD response is one [Friston et al., 1994a], other causes could be model misspecifications, head movements, physiological noise (heartbeat and respiratory effects [Jezzard, 1999]), and machine drifts [Smith et al., 1999]. The temporal autocorrelation is a nuisance because it invalidates the usage of standard linear model estimates if not taken into account. Several approaches to FMRI time‐series modeling have been suggested that take the temporal autocorrelation into consideration (e.g., by autoregressive‐moving average models; Bullmore et al. [1996]; Locascio et al. [1997], or by adjusting the degrees of freedom [Worsley and Friston, 1995]. A common assumption in these approaches is that the autocorrelation is stationary. However, this is not necessarily the case; the temporal autocorrelations introduced by physiological noise, e.g., heartbeat and respiratory related effects, can be nonstationary. Furthermore, even if the autocorrelation is stationary, the properties of the model estimates are usually known only asymptotically [Brockwell and Davis, 1991, chap. 8]. If the temporal autocorrelation is not properly dealt with the model estimates will be biased, potentially leading to either a loss of sensitivity or a loss of specificity [Zarahn et al., 1997]. Thus, the partly unknown and possibly nonstationary temporal‐autocorrelation makes the statistical modeling of FMRI data a challenging task.
Spatial autocorrelation
Spatial correlations can be introduced by the many transformations usually applied to the data (image reconstruction, realigning, anatomically normalizing, and spatially low‐pass filtering). Moreover, there is also evidence that the data coming directly from the scanner shows a spatial autocorrelation. Biswal and colleagues [Biswal et al., 1995] demonstrated that voxels in resting‐state FMRI data are correlated both with neighboring voxels and more distant voxels. Zarahn et al. [1997] showed that data only corrected for motion artifacts (but without any interpolations) shows frequency dependent spatial correlation, i.e., the spatial dependency varies as a function of temporal frequency. Statistical methods that take the spatial correlations into consideration have been developed for PET data [e.g., Friston et al., 1991; Worsley et al., 1992; Friston et al., 1994b], and have been successfully applied also to FMRI data [Friston et al., 1994a]. These methods assume that the spatial autocorrelation is stationary (however, the method suggested by Locascio et al. [1997] does not need this assumption, see also Worsley et al. [1999] for a method to deal with local nonstationarities). To the extent that the autocorrelation is caused by image transformations, this assumption seems to be a reasonable approximation (note however that nonlinear algorithms often used for the anatomical normalization might introduce local nonstationarities). However, other sources of spatial autocorrelations, physiological or machine related (shape distortions and ghosting [Cohen, 1999]), might invalidate the stationarity assumption. Not properly accounting for spatial autocorrelation leads to flawed estimates of the probability distributions of the statistics used, thus causing either a loss of sensitivity or specificity. Thus the partly unknown and possibly nonstationary spatial autocorrelation further increases the difficulty in modeling FMRI data and making statistical inference.
The BOLD signal response
The purpose of using a statistical model for the observed FMRI time‐series data is to detect the signal introduced by the stimulus/task. In general, to detect a signal in a background of noise in an optimal way, an idea of the spatial and temporal properties of the signal is needed. However, the neuronal activity is only observable through the filter of the hemodynamic effects underlying the BOLD contrast. The mechanisms behind the coupling between neuronal activity and the observed BOLD signal are not completely known. It is generally believed that changes in deoxyhemoglobin (HbR) content, mainly in the small veins, causes changes in the magnetic susceptibility difference between the blood and surrounding tissue, which in turn leads to changes in the magnetic field distortions in and around the blood vessels. The water protons in the vessels and surrounding tissue are affected by these changes in the magnetic field and this is detected as changes in the signal intensity of T2 *‐weighted MR images [Ogawa et al., 1990, 1992, 1998]. However, the mechanism behind the coupling between neuronal activity and changes in HbR content is still a matter of debate [see, e.g., Jueptner and Weiller, 1995; Magistretti and Pellerin, 1999; and Villringer, 1999, for a general discussion on this topic, Buxton and Frank, 1997; Hyder et al., 1998, for biophysical models of the relationship between blood flow and HbR, Buxton et al., 1998; Hoge et al., 1999a, for models of the coupling between blood flow and BOLD signal, Woolsey et al., 1996; Malonek and Grinvald, 1996; Malonek et al., 1997; Yang et al., 1997; Vanzetta and Grinvald, 1999; Silva et al., 1999, and Silva et al., 2000, for detailed empirical characterization of this coupling].
There have been several attempts to model the BOLD signal response, both phenomenological models [e.g., Friston et al., 1994a; Boynton et al., 1996] and biophysical [e.g., Buxton et al., 1998] all showing a good fit to data. However, it has been observed that the BOLD signal response to the same stimulus varies between subjects [Aguirre et al., 1998b], within subjects over time [Aguirre et al., 1998b], as well as between brain regions [Buckner et al., 1998; Kastrup et al., 1999] and that the BOLD signal response to different stimuli within the same brain region also varies [Hoge et al., 1999b]. Thus it seems difficult to find a single model of the BOLD signal response that can be used in all situations. One way around this difficulty is to measure the BOLD response at a separate occasion and then to use the measured BOLD response to model the signal. However, considering the within‐ and between‐subject variability, this implies that the BOLD response should be measured separately for each subject and brain region of interest. The problem of not fully knowing the characteristics of the signal is a problem of model selection. To use a bad model for the data might lead to an underestimation of the experimentally induced effect and, more seriously, to the introduction of false positives. Thus the partly unknown nature of the coupling between neuronal activity and the BOLD response poses further difficulties for the FMRI data modeler.
The 4D approach
In this paper, we propose an alternative method of analyzing FMRI data that does not require an explicit model of the BOLD signal response. Further, the suggested method takes temporal and spatial autocorrelations into consideration without requiring stationarity. By adopting a 4D view of the data we let the time‐course of the signal “speak for itself,” and by using nonparametric or Monte Carlo methods in making inference, we avoid the potential pitfalls of nonstationary autocorrelations.
Instead of viewing the FMRI data obtained in one session as a 3D volume observed at a number of points in time, we view it as a 4D hypervolume. Thus, each session represents one observation. By varying the stimulus/task between sessions, we introduce stimulus/task‐specific effects in the 4D hypervolumes. Instead of long sessions repeated few times, we suggest the use of short sessions repeated many times. Depending on the study design, the 4D approach can be used to study the responses to prolonged as well as brief stimulus/task events. To model the experimentally introduced effects we use the general linear model, and to the extent that the sessions can be assumed to be independent, standard parameter estimates apply. In testing hypotheses on the model parameters, 4D statistical images are generated, in contrast to the 3D SIs generated by other methods. Thus the generated SIs have three spatial dimensions and one temporal dimension. Any relevant test statistic can be applied to the 4D SIs. What is considered a relevant statistic will vary depending on the application. For example, the 4D cluster size statistic, one of the statistics described in this paper, is designed to find regions of connected voxels, extended both in time and space. These 4D clusters thus describe the spatial as well as the temporal characteristics of the BOLD signal response without the need for an explicit model. Given the assumption of independence between sessions, statistical inference about the chosen statistic can be made by nonparametric methods [Holmes et al., 1996] or by a 4D generalization of a Monte Carlo approach recently described [Ledberg, 2000]. These approaches are not dependent on any stationarity assumptions and can therefore be used for FMRI data.
In the next section the main steps of the 4D approach are described. In the subsequent section the 4D method is applied to FMRI data.
Theory
Notation
Let “scan” (also called “image”) denote the data obtained in one single volume acquired at a given time point and “session” a set of scans obtained in a sequence. Let boldface uppercase letters denote matrices and boldface lowercase vectors. Let ⊗ denote the Kronecker product, A − a generalized inverse of A, and N(m, v) the normal distribution with mean m and variance v. Let ε(·) and Cov(·) denote expectation and covariance, respectively. Let v 1×v be a vector containing the voxel values from one scan (v is the number of voxels). Let t denote the number of scans in one session (we assume that all sessions have the same number of scans) and n the number of sessions.
A linear model for the data
The usual way of modeling the data obtained in a FMRI experiment is by fitting a linear model to the data matrix
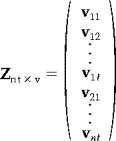 |
where v ij denotes the j‐th scan obtained in the i‐th session. Note that for FMRI data, the rows of Z will have a statistical dependency as it is known that scans acquired in succession are correlated. Instead, we suggest the formation of a data matrix
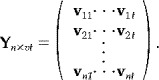 |
Thus the rows of Y represents the sessions and the columns the 4D‐voxels over sessions.1 Note that the rows in Y can be assumed to be independent because they represent different sessions. Now, let X n×p be a known design matrix, then a linear model for the data is then given by
| (1) |
where B is a p × vt matrix of the model parameters and E is a n × vt matrix of error terms. As a simple example, consider data from one subject obtained under two different conditions (TEST and CONTROL). Then, if there are 30 sessions alternating between TEST and CONTROL, an appropriate design matrix is given in Figure 1. If we assume that ε(E) = 0, Cov(e [j]) = σj2I, where e [j] denotes the j‐th column of E and that h p×1 is an estimatable1 contrast, then the best2 linear unbiased estimate (BLUE) of h t B is given by
| (2) |
[Christensen, 1991, chap. 1].
is an unbiased estimate of the variance of h t B̂ [Sen and Srivastava, 1990]. Here R = Y − XB̂ is the residuals, γ = n − rank(X) the degrees of freedom of the model and diag(·) is a matrix operation that puts all nondiagonal elements to zero. To generate a SI, t say, we divide h t B̂ with the square root of its variance:
Thus t is a 1 × vt vector, the values of which represents the linear combination of the parameter estimates, as determined by the contrast, divided with their standard deviation. This is just the ordinary univariate t‐test statistic in a matrix setting. Under quite weak assumptions,4 each element of t will be distributed as Student's t with parameter γ. Statistical images derived in this way will therefore be called “t images.” Let T be the t × v matrix containing the same data as t but arranged so that the voxel values from the same temporal position within the session in t are represented as a row in T. Thus, each row in T can be viewed as a 3D t image and T as a 4D t image. The columns of T are the (3D) voxel t values over time. It is important to notice that the rows of T will usually be dependent.
Figure 1.

The design matrix for the 4D example case. The columns refer to the mean value and the task factor (two columns). Black color indicates 1 and white 0.
Thus, given a set of MR data we generate a 4D t image that reflects the differences between conditions. How to make inference on this 4D image is the issue of the next section.
Inference on the 4D t images
The first thing to consider is which test statistic to use. In the case of a 3D t image, there are several test statistics currently in use [see, e.g., Friston et al., 1996]. The most commonly used are the global maxima and cluster size statistics. We have extended these statistics to 4D images as will be described below.
The maximum 4D cluster size statistic
Given a threshold s, a 4D cluster is a set of connected 4D voxels in T that are all above s. The maximum 4D cluster size statistic is the size (i.e., the number of voxels) of the largest of these clusters. Thus the 4D cluster size statistic is a straightforward generalization of the cluster size statistic for 3D images [e.g., Poline and Mazoyer, 1993; Roland et al., 1993]. Note that the clusters will have spatial as well as temporal extent, i.e., they represent spatio‐temporal objects. In the current implementation we have used eight connectivity, i.e., each voxel has six neighbors in space (connected by sides) and two in time (two voxels from adjacent time points are neighbors if they are located at the same spatial position). Note that with this statistic, inference is made on the level of 4D clusters. That is, it is regions in the 4D space that will be significant.
The maximum 4D voxel statistic
This statistic is simply the maximum value of all 4D voxels in the 4D SI. With this statistic, inference is made at the 4D‐voxel level.
Null probability distributions
To estimate the probability distributions of these two statistics, under the null hypothesis of no difference between conditions, we have applied both a nonparametric approach based on permutations [Holmes et al., 1996; Ledberg et al., 1998; Ledberg, 2000] and a 4D version of the Monte Carlo method recently described [Ledberg, 2000]. The permutation approach is implemented by generating new models for the data by permuting the design matrix. The data is then fitted to these new models, 4D t images are generated as described above, and from these images values of the two statistics are sampled. In the Monte Carlo approach we generate a large set of images that are of the same dimensions as T and have a distribution very similar to what T would have had under the null hypothesis. For each of these images we apply the two statistics described above and thus get an estimate of their probability distributions. The method described in Ledberg [2000] was implemented for 3D PET data, but because no assumptions about the stationarity of the variance–covariance structure is made, it is straightforward to extend it to 4D. The purpose of using two different methods to generate the null distributions is both to compare them and to illustrate the generality of the 4D approach.
Assumptions
For linear model estimation
For the model estimates in Eq. (2) to be the BLUEs, we need to assume that the expected value of the error matrix in Eq. (1) is zero (ε(E) = 0) and that the variance‐covariance of each voxel can be described as Cov(e [i]) = σi2I [Sen and Srivastava, 1990]. The first assumption is basically that the mean structure of the data should be described by the assumed model. With a careful choice of model this should be the case. The assumption about the variance‐covariance structure can be formulated as follows: the sessions should be independent and the voxels should have the same variance between sessions. Independence between sessions should be obtained if enough time elapses between them. We suggest a between‐session interval of 1 min. This should be sufficient to remove any physiological or machine‐related correlations. Note that this is the only assumption made about the BOLD response: that it operates on a time scale shorter than the between‐session interval. That sessions should have the same variance should also be the case under most circumstances. However, if data from different subjects is modeled with the same linear model, this assumption might not be valid anymore.
For nonparametric inference
If the permutation approach is used to make inference, the only assumption that is needed is that the distribution of the data matrix Y, under the null hypothesis, is invariant under the permutations applied [Lindgren, 1993]. If the rows of Y are independent and the model carefully chosen, this will be the case. Usually, there are too many possible permutations to actually calculate them all. Instead we use a random sample of the possible permutations. As long as the sample is relatively large (in the order of 1,000), it will be a good approximation of the true permutation distribution [Edgington, 1980].
For Monte Carlo based inference
The assumption(s) needed for the Monte Carlo approach to be valid is that the data matrix Y in Eq. (1) is distributed as N(XB, I ⊗ Σ). This means that, under the null hypothesis, the sessions should be independent and that the data from each session should be multivariate normal with the same variance‐covariance matrix. That data are normally distributed, voxel by voxel, has been shown to be a reasonable assumption [Aguirre et al., 1998a]. That data are multivariate normal with the same variance‐covariance matrix is more difficult to verify. The normality assumption can probably be relaxed to any distribution invariant under orthogonal transformations [Ledberg, 2000]. That the variance‐covariance matrix should be the same for all sessions seems likely under the null hypothesis and the method seems to be robust against departures from this assumption as shown for PET data by Ledberg [2000]. Note that this is an assumption also needed by most other approaches to inference as well [e.g., Friston et al., 1994a; Worsley and Friston, 1995]. The assumption of a distribution of a type N(XB, I ⊗ Σ) implies that the mean value is XB, where X is a design matrix. Normally the true X is not known, and if the design matrix chosen for the statistical model departs a lot from the true design matrix the Monte Carlo method will give flawed (most likely conservative) estimates of the null distributions.
Application to FMRI data
To illustrate the usage of the 4D method we applied it to FMRI data from one subject.
Experimental setup
Four horizontal slices overlying the occipital cortex were acquired in a 1.5 Tesla GE‐Signa scanner using a single‐shot gradient echo EPI sequence: slice thickness 6 mm, FOV = 240 mm × 240 mm, matrix size 64 × 64, TR = 1,000 ms, TE = 60 ms, flip angle 50°. Fifty sessions of 50 sec each were acquired under two experimental conditions (VIS and CONT). During both conditions the subject fixated on a small cross on a dark background presented through the goggles of a MR compatible visualization system (Resonance Technology Inc., Northridge, CA). The only difference between the conditions was that in VIS a flashing checkerboard was presented for 5 sec starting at scan number 11, whereas in CONT there was no such stimulus. The between‐session interval was at least 1 min.
The 4D method applied
The first and last five scans were removed before the analysis, leaving 40 scans for each session. This was done to remove T1 saturation effects and reduce the amount of data. High‐frequency noise was removed, for each session separately, by fitting a regression model containing a high‐frequency component to the voxel time‐series and subtracting away the high frequencies. The sessions during VIS were compared to those during CONT using a linear model with one factor (experimental condition) having two levels (VIS and CONT). The threshold used for the 4D cluster size statistic was 2.68 (corresponding to a voxel‐wise P value of 0.005). Four thousand permutations and simulations were made to estimate the probability distributions of the maximum 4D voxel statistic and the 4D cluster size statistic. Figure 2 shows the result of these estimations. The two methods of estimating the null distributions of the two statistics gives very similar results. That the permutation gives slightly lower thresholds might be because these are made on a smaller volume (activations removed). Voxels having a value above 5.8 and clusters with a size larger than 11 (4D) voxels are significant at the 0.05 level.
Figure 2.
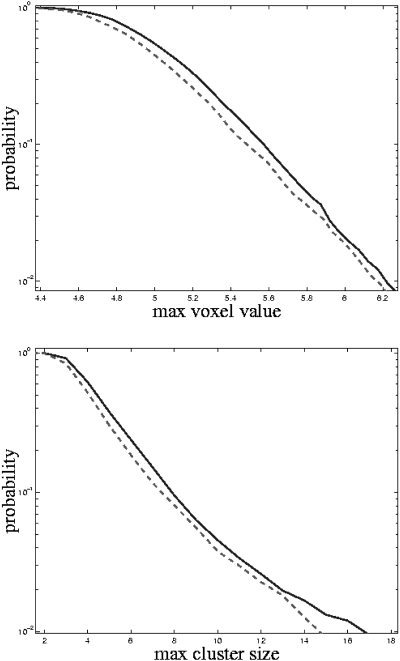
Estimated probabilities for the maximum voxel statistic (top) and maximum 4D cluster size statistic (bottom). The solid line refers to the Monte Carlo method and the dashed to the permutation method.
Results
Figures 3 and 4 shows the significant activations for the cluster and voxel based statistics respectively. The two statistics give very similar results. The cluster‐based statistic is however more sensitive than the voxel based in the sense of number of voxels occupied by activated regions. The activity starts around 3 sec after stimulus onset and persists for 11 sec. The first parts of the brain to become activated are located in the depth of the calcarine sulcus. The activity then spreads to surrounding regions of striate and extrastriate visual cortex before disappearing. Figure 5 shows an example of voxels activated early and late and their time courses. There is a striking difference in the location of the early and late voxels. Also their respective time courses are different.
Figure 3.
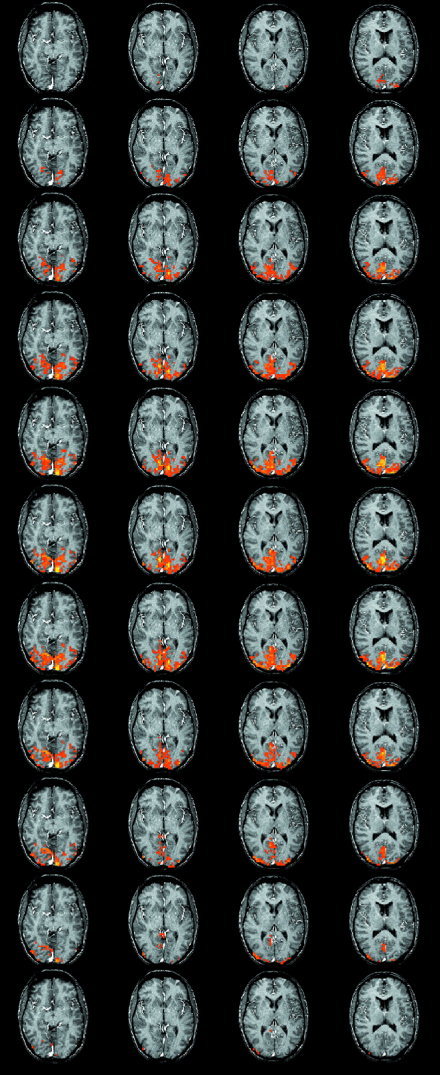
Significant differences between VIS and CONT as determined by the maximum 4D cluster size statistic shown superimposed on an T1‐weighted anatomical image. Starting at the top, the rows show the activations over time with each row representing a time step of 1 sec. The first row shows the images 3 sec after stimulus onset. Only the time points showing significant activations are shown.
Figure 4.
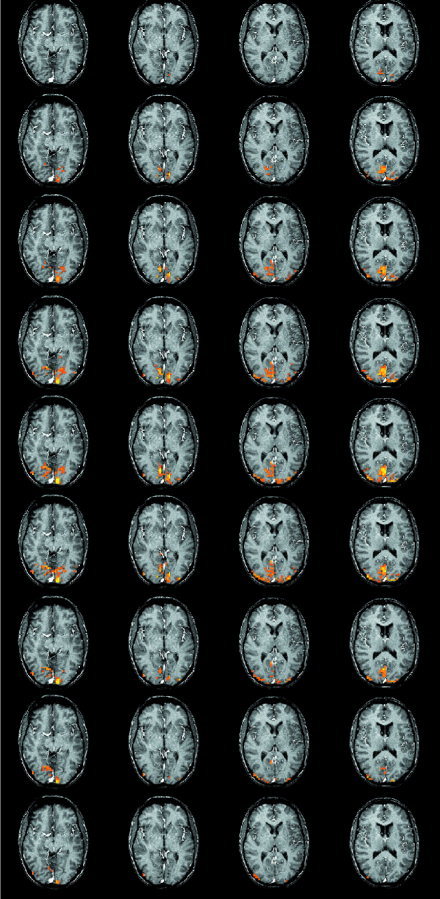
Significant differences between VIS and CONT as determined by the maximum voxel statistic shown superimposed on an T1‐weighted anatomical image. Starting at the top, the rows show the activations over time with each row representing a time step of 1 sec. The first row shows the images 4 sec after stimulus onset. Only the time points showing significant activations are shown.
Figure 5.
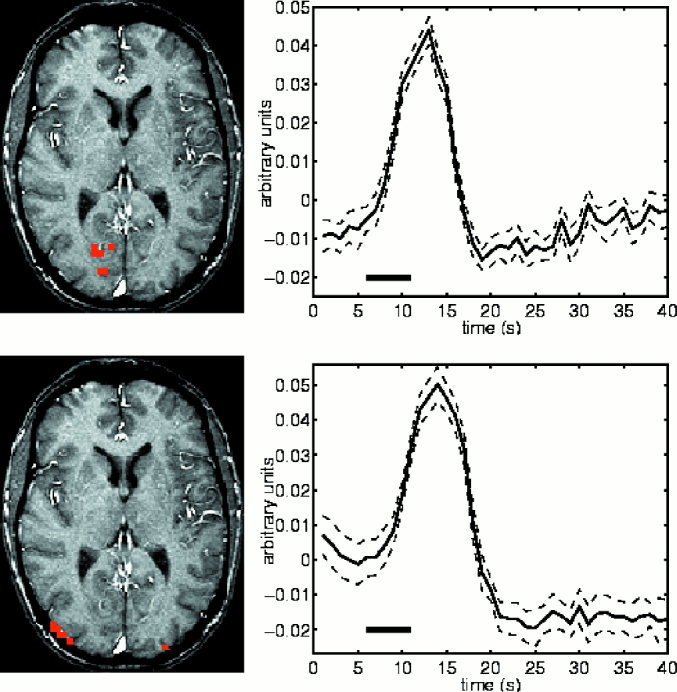
Early and late activations and their time courses. The top row shows the voxels activated 4 sec after stimulus onset. The graph on the right represents the average value of these voxels over the 25 sessions of VIS. The dashed lines represent the 95% confidence interval of this average. The black bar indicate the time and duration of the stimulus. The bottom row shows the voxels activated still 11 sec after the stimulus onset. The graph to the right shows the average time course of these voxels. Activations are based on the maximum voxel statistic. The time course of the late activated voxels has a somewhat slower onset and the peak occurs around 2 sec after the peak of the time course of the early voxels. This could indicate a difference in the underlying tissue. Indeed it seems that the late voxels are in the vicinity of large blood vessels.
Comparison with a 3D method
For comparison, the data was also analyzed with a “conventional” 3D method. SPM99 (http://www.fil.ion.bpmf.ac.uk/spm/) was used for this purpose. Because the inference used in SPM requires the data to be smooth, the data was smoothed by a Gaussian kernel with a full width at half max (FWHM) of 12 mm. The data was temporally smoothed with a Gaussian kernel with a FWHM of 4‐sec and temporal autocorrelation was modeled by an AR(1) model. A high‐pass filter was applied to remove temporal trends. A fixed effect linear model was fitted to the 25 sessions containing the visual stimulus. A regressor with alternating 1 and −1 was included in the model to remove high‐frequency noise observed in the data. The signal was modeled as a boxcar function convolved with the “hemodynamic response function.” Activated regions were determined at the voxel level at an omnibus P < 0.05.
To be able to compare the two methods of analysis the 4D method was also applied to the spatially smoothed data. Activations were detected by the maximum voxel statistic at an omnibus P < 0.05. The detected activations were projected onto three dimensions. This was done by labeling a (3D) voxel in the brain space as activated if it was active at any time point in the 4D data set. The activations of the 3D and 4D methods could then be compared voxel by voxel.
The patterns of activation, as determined by the two methods, was very similar. The 4D method gave somewhat larger activations than the 3D method. The overlap of the activated voxels detected by the two methods was 99% of the volume of the 3D activations, and 74% of the volume of the 4D activations. This means that 99% of the activations detected by the 3D method were also detected by the 4D method, and 74% of the activations detected by the 4D method were also detected by the 3D method.
Discussion
In this paper we have described a novel approach to FMRI data analysis. The main difference compared to previously described methods is that all data obtained in one session is used as the dependent variable. Thus we view the FMRI data as 4D spatio‐temporal objects observed under different conditions/sessions. This change of perspective, compared to the usual 3D view, provides several benefits, as described below.
Benefits of the 4D approach
The first benefit concerns the multitude of hypotheses that can be investigated with the 4D approach. By testing hypotheses on the 4D SIs we test hypotheses on the spatio‐temporal structure of the signal. By using either of the two test statistics described here we can investigate variations in the signal, both in time and space, to a given stimulus/task. Depending on the experimental setup the 4D approach can be used to investigate changes in brain activity caused by static as well as dynamic stimulus/task conditions. For example, if the only difference between sessions occurs during a very brief time period, the 4D approach can provide similar information as that obtained in event‐related FMRI studies [Buckner et al., 1996; Dale and Buckner, 1997; Josephs et al., 1997; for a review, see Rosen et al., 1998] in which the BOLD signal response to single events of short duration is studied. However, the 4D approach does not depend on any specific assumptions about the form of the BOLD signal response, except that it should operate on a time scale shorter than the between‐session interval. By selecting a specific model for the BOLD response there is always a danger of introducing bias. On the other hand, the price of using unbiased methods is usually lower sensitivity, i.e., more scans are needed to detect the signal. If the difference between sessions occurs during a prolonged time period, the 4D approach is more like a “blocked design” experiment. For example, if there are two conditions (A and B) and the question of interest is what areas are activated by A and not by B and vice versa, the 4D approach could be used with few scans per session (sps) and where sessions are alternating between the two conditions. In this case one can also, by starting the experiment some 10 seconds before the scanning, make sure to acquire data only during the “plateau” phase of the BOLD signal response, thus maximizing the signal‐to‐noise ratio.
Thus, the 4D approach allows the integration of blocked and event‐related designs in the same framework for statistical analysis.
A second benefit of the 4D approach is that, given the assumption of independence between sessions, standard least‐square estimates can be used to solve the equations in the linear model and to derive the SIs. This is not the case for the 3D methods (see Introduction).
A third benefit is that, given the independence of the sessions, nonparametric methods [Holmes et al., 1996] or a 4D version of the Monte Carlo method of Ledberg [2000] can be used in making inference. These methods do not rely on any stationarity assumptions and have been shown to work properly in the presence of nonstationary spatial autocorrelation [Ledberg, 2000]. In the 3D case it is more difficult to use nonparametric and Monte Carlo methods to make inference as the assumptions needed for these methods are not fulfilled.
There are other benefits as well. For example, by using much shorter sessions (depending on TR and number of sps, the length of a session can be as short as 10–20 sec), the within‐session variability (e.g., caused by head movements and variation in performance) seems likely to be reduced. Furthermore, the extra dimension of the SIs gives greater flexibility in the choice of test statistic.
Drawbacks of the 4D approach
The major drawback with the 4D approach is that the time in the scanner for each subject is prolonged compared to a more conventional design with relatively few and long sessions. This is because by using many short sessions and requiring them to be sufficiently separated in time, the between‐session intervals might add up to a considerable amount of time. For example, to acquire 600 scans with a TR of 1 sec takes 10 min if they are acquired in one session, dividing them into 60 sessions of 10 scans each, and assuming a between session interval of 1 min, will instead take 70 min, because of the intervals between sessions.
Another potential drawback is loss of sensitivity compared to 3D methods. Because the search space is enlarged by a factor t, the 4D method might be less sensitive than a standard 3D method for some experimental designs and test statistics. However, as the comparison with a “standard” 3D method showed, the reverse situation might also occur. In this comparison the 4D method detected “more” activations than did the 3D method, and almost all voxels detected by the 3D method were detected by the 4D method. Note however that twice as much data was used in the 4D analysis than in the 3D analysis, as the CONT scans were not included in the latter analysis. The discrepancy between the two methods could perhaps be reduced by allowing a more general form of the signal shape in the 3D analysis.
Issues concerning the implementation
In this paper we have used the 4D approach in connection with the maximum voxel and 4D cluster size statistics. To make inference we have used both a 4D generalization of the Monte Carlo method of Ledberg [2000] and a nonparametric permutation approach. However, the 4D approach can be combined with any relevant test statistic and any statistical inference procedure of which the necessary assumptions are met.
Choice of test statistic
The cluster‐ and voxel‐based statistics gave similar results (Fig. 3 and 4). The cluster‐based statistic was more sensitive (in terms of number of voxels occupied by “activations”) than the voxel based. This is expected given that activations occur in spatio‐temporally extended regions. If the resolution given by the clusters of voxels is sufficient to investigate a specific question, the 4D cluster size statistic should be the statistic of choice. The voxel‐based statistic on the other hand gives a much finer resolution, inference being made at the 4D‐voxel level. So if a detailed characterization of the spatio‐temporal properties of the signal is desired this is the statistic of choice.
Choice of inference method
The two methods for statistical inference used in this paper gave similar results (Fig. 2). This is in line with previous findings [Ledberg, 2000]. The nonparametric approach is very good in that it requires very weak assumptions about the data. However, in the presence of extended and strong activations, a step‐down approach is needed or a loss of sensitivity will result [Holmes et al., 1996; Ledberg et al., 1998; Ledberg, 2000]. The step‐down approach is readily implemented but increases the computational burden. In the 4D generalization of the Monte Carlo approach of Ledberg [2000], the signal is taken away before the null distribution is estimated. If data are behaving according to the assumptions, this method will be faster than the permutation approach and give very similar result. However, if the assumptions are violated, for example, by a bad model for the data, the Monte Carlo approach might give flawed estimates of the probability distributions.
To run the permutations/simulations in the FMRI data set used in this paper took around 24 hours on a 400 MHz PC.
How many sessions are needed?
In the 4D approach the sessions are the dependent variables, which means that more sessions will lead to better power to detect activations. How many sessions are needed then? This is a question of signal‐to‐noise ratio, the statistic used and the number of sps. In the example from real data we used 50 sessions and 40 sps. This was sufficient to detect the anticipated response in the visual cortex. If the 4D cluster size statistic is used, fewer sessions can probably be used without a large loss of sensitivity. Forty sps is probably more than enough in most cases. For studies where a detailed characteristic of the signal is of secondary importance, 10 or less sps should suffice, and this would imply fewer sessions.
Other areas of application
The 4D approach presented here could be useful in other areas of functional neuroimaging as well where spatio‐temporal signals are observed, such as EEG and optical imaging.
Conclusion
We have described a 4D approach to FMRI data analysis. This approach provides a general framework where hypotheses can be tested and statistical inference can be made circumventing some of the complications of more common 3D methods. Application to FMRI data showed that the 4D approach is sufficiently sensitive to be of practical use. Thus, the 4D approach is a useful complement to existing methods for statistical analysis of FMRI data.
Acknowledgements
A.L. was supported by a EU grant (QLRT‐1999‐00677). K.M.P. was supported by grants from the Stockholm County Council and the Swedish Society of Medicine. K.M.P. and P.F. were supported by Medicinska Forsknings Rädet (MFR) grant 8276. We would like to thank Rita Almeida for useful comments and suggestions, Martin Ingvar for making the MR facilities readily available, and Per E. Roland for his support of this work. Software for the 4D analysis was implemented in C++, and is available for Sun Solaris and Linux operative systems upon request from A.L. (Anders.Ledberg@neuro.ki.se).
Edited by: Karl Friston, Associate Editor
Footnotes
h t = a t X for some a n×1.
Best in the sense of minimum variance.
ht = a t X for some a n×1.
It suffices that Y has a left spherical (also sometimes called orthogonally invariant) distribution [Kariya and Sinha, 1988].
REFERENCES
- Aguirre GK, Zarahn E, D'Esposito M (1998a): A critique of the use of the Kolmogorov‐Smirnov statistic for the analysis of fMRI data. Magn Reson Med 39: 500–505. [DOI] [PubMed] [Google Scholar]
- Aguirre GK, Zarahn E, D'Esposito M (1998b): The variability of human, hemodynamic responses. Neuroimage 8: 360–369. [DOI] [PubMed] [Google Scholar]
- Bandettini PA, Wong EC, Hinks RS, Tikofsky RS, Hyde JS (1992): Time course of human brain function during task activation. Magn Reson Med 25: 390–397. [DOI] [PubMed] [Google Scholar]
- Biswal B, Yetkin FZ, Haughton VM, Hyde JS (1995): Functional connectivity in the motor cortex of resting human brain using echo‐planar. Magn Reson Med 34: 537–541. [DOI] [PubMed] [Google Scholar]
- Boynton GM, Engel SA, Glover GH, Heeger DJ (1996): Linear systems analysis of functional magnetic resonance imaging in human V1. J Neurosci 16: 4207–4221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brockwell PJ, Davis RA (1991): Time series: theory and methods. 2nd ed. New York: Springer. [Google Scholar]
- Buckner RL, Bandettini PA, O'Craven KM, Savoy RL, Petersen SE, Raichle ME, Rosen BR (1996): Detection of cortical activation during averaged single trials of a cognitive task using functional magnetic resonance imaging. Proc Natl Acad Sci U S A 93: 14878–14883. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buckner RL, Koutstaal W, Schacter DL, Dale AM, Rotte M, Rosen BR (1998): Functional‐anatomic study of episodic retrieval. Selective averaging of event‐related fMRI trials to test the retrieval success hypothesis. Neuroimage 7: 163–175. [DOI] [PubMed] [Google Scholar]
- Bullmore E, Brammer M, Williams SC, Rabe‐Hesketh S, Janot N, David A, Mellers J, Howard R, Sham P (1996): Statistical methods of estimation and inference for functional image analysis. Magn Reson Med 35: 261–277. [DOI] [PubMed] [Google Scholar]
- Buxton RB, Frank LR (1997): Model for the coupling between cerebral blood flow and oxygen metabolism during neural stimulation. J Cereb Blood Flow Metab 17: 64–72. [DOI] [PubMed] [Google Scholar]
- Buxton RB, Wong EC, Frank LR (1998): Dynamics of blood flow and oxygenation changes during brain activation: the balloon model. Magn Reson Med 39: 855–864. [DOI] [PubMed] [Google Scholar]
- Christensen R (1991): Linear models for multivariate, time series and spatial data. New York: Springer. [Google Scholar]
- Cohen MS (1999): Echo‐planar imaging and functional MRI In: Moonen C, Bandettini P, editors. Functional MRI. Berlin: Springer. [Google Scholar]
- Dale AM, Buckner RL (1997): Selective averaging of rapidly presented individual trials using fMRI. Hum Brain Mapp 5: 329–340. [DOI] [PubMed] [Google Scholar]
- Edgington ES (1980): Randomization tests. New York: Dekker. [Google Scholar]
- Frahm J, Bruhn H, Merboldt KD, Hanicke W (1992): Dynamic imaging of human brain oxygenation during rest and photic stimulation. J Magn Reson Imaging 2: 501–505. [DOI] [PubMed] [Google Scholar]
- Friston KJ, Frith CD, Liddle PF, Frackowiak RS (1991): Comparing functional brain images: the assessment of significant change. J Cereb Blood Flow Metab 11: 690–609. [DOI] [PubMed] [Google Scholar]
- Friston KJ, Jezzard P, Turner R (1994a): Analysis of functional MRI time series. Hum Brain Mapp 1: 45–53. [Google Scholar]
- Friston KJ, Worsley KJ, Frackowiak RSJ, Mazziotta JC, Evans AC (1994b): Assessing the significance of focal activations using their spatial extent. Hum Brain Mapp 1: 210–220. [DOI] [PubMed] [Google Scholar]
- Friston KJ, Holmes A, Poline JB, Price CJ, Frith CD (1996): Detecting activations in and fMRI: levels of inference and power. Neuroimage 4: 223–235. [DOI] [PubMed] [Google Scholar]
- Hoge RD, Atkinson J, Gill B, Crelier GR, Marrett S, Pike GB (1999a): Investigation of signal dependence on cerebral blood flow and oxygen consumption: the deoxyhemoglobin dilution model. Magn Reson Med 42: 849–863. [DOI] [PubMed] [Google Scholar]
- Hoge RD, Atkinson J, Gill B, Crelier GR, Marrett S, Pike GB (1999b): Stimulus‐dependent and perfusion dynamics in human V1. Neuroimage 9: 573–585. [DOI] [PubMed] [Google Scholar]
- Holmes AP, Blair RC, Watson JD, Ford I (1996): Nonparametric analysis of statistic images from functional mapping experiments. J Cereb Blood Flow Metab 16: 7–22. [DOI] [PubMed] [Google Scholar]
- Hyder F, Shulman RG, Rothman DL (1998): Model for the regulation of cerebral oxygen delivery. J Appl Physiol 85: 554–564. [DOI] [PubMed] [Google Scholar]
- Jezzard P (1999): The physical basis of spatial distortions in magnetic resonance images In: Moonen C, Bandettini P, editors. Functional MRI. Berlin: Springer. [Google Scholar]
- Josephs O, Turner R, Friston K (1997): Event‐related fMRI. Hum Brain Mapp 5: 264–272. [DOI] [PubMed] [Google Scholar]
- Jueptner M, Weiller C (1995): Review: does measurement of regional cerebral blood flow reflect synaptic activity? Implications for and fMRI. Neuroimage 2: 148–156. [DOI] [PubMed] [Google Scholar]
- Kariya T, Sinha BK (1988): Robustness of statistical tests. Boston: Academic Press. [Google Scholar]
- Kastrup A, Kruger G, Glover GH, Neumann‐Haefelin T, Moseley ME (1999): Regional variability of cerebral blood oxygenation response to hypercapnia. Neuroimage 10: 675–681. [DOI] [PubMed] [Google Scholar]
- Kwong KK, Belliveau JW, Chesler DA, Goldberg IE, Weisskoff RM, Poncelet BP, Kennedy DN, Hoppel BE, Cohen MS, Turner R, Cheng H‐M, Brady TJ, Rosen BR (1992): Dynamic magnetic resonance imaging of human brain activity during primary sensory stimulation. Proc Natl Acad Sci U S A 89: 5675–5679. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lange N, Strother SC, Anderson JR, Nielsen FA, Holmes AP, Kolenda T, Savoy R, Hansen LK (1999): Plurality and resemblance in fMRI data analysis. Neuroimage 10: 282–303. [DOI] [PubMed] [Google Scholar]
- Ledberg A (2000): Robust estimation of the probabilities of 3D clusters in functional brain images: application to data. Hum Brain Mapp 9: 143–155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ledberg A, Akerman S, Roland PE (1998): Estimation of the probabilities of 3D clusters in functional brain images. Neuroimage 8: 113–128. [DOI] [PubMed] [Google Scholar]
- Lindgren BW (1993): Statistical theory. 4th ed. New York: Chapman & Hall. [Google Scholar]
- Locascio JJ, Jennings PJ, Moore CT, Corkin S (1997): Time series analysis in the time domain and resampling methods for studies of functional magnetic resonance brain imaging. Hum Brain Mapp 5: 168–193. [DOI] [PubMed] [Google Scholar]
- Magistretti PJ, Pellerin L (1999): Cellular mechanisms of brain energy metabolism and their relevance to functional brain imaging. Philos Trans R Soc Lond B Biol Sci 354: 1155–1163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malonek D, Grinvald A (1996): Interactions between electrical activity and cortical microcirculation revealed by imaging spectroscopy: implications for functional brain mapping. Science 272: 551–554. [DOI] [PubMed] [Google Scholar]
- Malonek D, Dirnagl U, Lindauer U, Yamada K, Kanno I, Grinvald A (1997): Vascular imprints of neuronal activity: relationships between the dynamics of cortical blood flow, oxygenation, and volume changes following sensory stimulation. Proc Natl Acad Sci U S A 94: 14826–14831. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ogawa S, Lee TM, Kay AR, Tank DW (1990): Brain magnetic resonance imaging with contrast dependent on blood oxygenation. Proc Natl Acad Sci U S A 87: 9868–9872. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ogawa S, Tank DW, Menon R, Ellermann JM, Kim SG, Merkle H, Ugurbil K (1992): Intrinsic signal changes accompanying sensory stimulation: functional brain mapping with magnetic resonance imaging. Proc Natl Acad Sci U S A 89: 5951–5955. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ogawa S, Menon RS, Kim SG, Ugurbil K (1998): On the characteristics of functional magnetic resonance imaging of the brain. Annu Rev Biophys Biomol Struct 27: 447–474. [DOI] [PubMed] [Google Scholar]
- Petersson KM, Nichols TE, Poline JB, Holmes AP (1999a): Statistical limitations in functional neuroimaging. Non‐inferential methods and statistical models. Philos Trans R Soc Lond B Biol Sci 354: 1239–1260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petersson KM, Nichols TE, Poline JB, Holmes AP (1999b): Statistical limitations in functional neuroimaging. Signal detection and statistical inference. Philos Trans R Soc Lond B Biol Sci 354: 1261–1281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poline JB, Mazoyer BM (1993): Analysis of individual positron emission tomography activation maps by detection of high signal‐to‐noise‐ratio pixel clusters. J Cereb Blood Flow Metab 13: 425–437. [DOI] [PubMed] [Google Scholar]
- Purdon PL, Weisskoff RM (1998): Effect of temporal autocorrelation due to physiological noise and stimulus paradigm on voxel‐level false‐positive rates in fMRI. Hum Brain Mapp 6: 239–249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roland PE, Levin B, Kawashima R, Åkerman S (1993): Three‐dimensional analysis of clustered voxels in 15O‐butanol activation images. Hum Brain Mapp 1: 3–19. [Google Scholar]
- Rosen BR, Buckner RL, Dale AM (1998): Event‐related functional: past, present, and future. Proc Natl Acad Sci U S A 95: 773–780. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sen A, Srivastava M (1990): Regression analysis. Theory, methods, and applications. 1st ed. New York: Springer. [Google Scholar]
- Silva AC, Lee SP, Yang G, Iadecola C, Kim SG (1999): Simultaneous blood oxygenation level‐dependent and cerebral blood flow functional magnetic resonance imaging during forepaw stimulation in the rat. J Cereb Blood Flow Metab 19: 871–879. [DOI] [PubMed] [Google Scholar]
- Silva AC, Lee SP, Iadecola C, Kim SG (2000): Early temporal characteristics of cerebral blood flow and deoxyhemoglobin changes during somatosensory stimulation. J Cereb Blood Flow Metab 20: 201–206. [DOI] [PubMed] [Google Scholar]
- Smith AM, Lewis BK, Ruttimann UE, Ye FQ, Sinnwell TM, Yang Y, Duyn JH, Frank JA (1999): Investigation of low frequency drift in fMRI signal. Neuroimage 9: 526–533. [DOI] [PubMed] [Google Scholar]
- Vanzetta I, Grinvald A (1999): Increased cortical oxidative metabolism due to sensory stimulation: implications for functional brain imaging. Science 286: 1555–1558. [DOI] [PubMed] [Google Scholar]
- Villringer A (1999): Physiological changes during brain activation In: Moonen C, Bandettini P, editors. Functional MRI. Berlin: Springer. [Google Scholar]
- Woolsey TA, Rovainen CM, Cox SB, Henegar MH, Liang GE, Liu D, Moskalenko YE, Sui J, Wei L (1996): Neuronal units linked to microvascular modules in cerebral cortex: response elements for imaging the brain. Cereb Cortex 6: 647–660. [DOI] [PubMed] [Google Scholar]
- Worsley KJ, Friston KJ (1995): Analysis of fMRI time‐series revisited—again. Neuroimage 2: 173–181. [DOI] [PubMed] [Google Scholar]
- Worsley KJ, Evans AC, Marrett S, Neelin P (1992): A three‐dimensional statistical analysis for activation studies in human brain. J Cereb Blood Flow Metab 12: 900–918. [DOI] [PubMed] [Google Scholar]
- Worsley KJ, Andermann M, Koulis T, MacDonald D, Evans AC (1999): Detecting changes in nonisotropic images. Hum Brain Mapp 8: 98–101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang X, Hyder F, Shulman RG (1997): Functional signal coincides with electrical activity in the rat whisker barrels. Magn Reson Med 38: 874–847. [DOI] [PubMed] [Google Scholar]
- Zarahn E, Aguirre GK, D'Esposito M (1997): Empirical analyses of fMRI statistics. Spatially unsmoothed data collected under null‐hypothesis conditions. Neuroimage 5: 179–197. [DOI] [PubMed] [Google Scholar]


