Abstract
We introduce a hybrid method for functional magnetic resonance imaging (fMRI) activation detection based on the well‐developed split–merge and region‐growing techniques. The proposed method includes conjoining both of the spatio‐temporal priors inherent in split–merge and the prior information afforded by the hypothesis‐led component of region selection. Compared to the fuzzy c‐means clustering analysis, this method avoids making assumptions about the number of clusters and the computation complexity is reduced markedly. We evaluated the effectiveness of the proposed method in comparison with the general linear model and the fuzzy c‐means clustering method conducted on simulated and in vivo datasets. Experimental results show that our method successfully detected expected activated regions and has advantages over the other two methods. Hum. Brain Mapping 22:271–279, 2004. © 2004 Wiley‐Liss, Inc.
Keywords: fMRI time series, split‐merge, region growing, Kendall's coefficient of concordance
INTRODUCTION
Since the discovery of functional magnetic resonance imaging (fMRI) [Ogawa et al., 1990], fMRI activation detection has been an active field of research. One challenge is that there are many confounds presented in fMRI data such as subject movements, heartbeat, respiration, trend, and noise. Several methods have been proposed for activation detection, which we can classify into two categories: hypothesis‐led and data‐led methods. Hypothesis‐led methods usually rely on some model (assumptions) about the paradigm and the hemodynamic response function (modeled by combination of basis functions). A typical hypothesis‐led method is the general linear model (GLM) [Friston et al., 1995b]. The GLM is a framework that includes simple t‐test, analysis of variance (ANOVA), ANCOVA, and multiple regressions. Data‐led methods postpone the usual assumptions and allow the data itself to reveal its underlying structure. Typical data‐led methods are cluster analysis [Baumgartner et al., 1997; Filzmoser et al., 1999; Goutte et al., 1999; Scarth et al., 1995], principal component analysis (PCA) [Hansen et al., 1999; Lai and Fang, 1999], and independent component analysis (ICA) [Calhoun et al., 2001; Jung et al., 2001; McKeown et al., 1998].
We have adopted an established procedure in clustering, namely split–merge, and applied it in the novel context of fMRI data analysis. We have finessed this approach by a region‐selection component that draws on the benefits of hypothesis‐led analyses. In our implementation this involves identification of clusters that conform to a linear model of anticipated activation. In this sense, our procedure is a hybrid between a data‐led approach and a hypothesis‐led approach [Penny et al., 2003]. The benefits of this can be seen from two perspectives. First, from the point of view of conventional hypothesis‐led analyses, using the GLM, we are able to embody prior knowledge about the spatial contiguity of evoked blood oxygenation level‐dependent (BOLD) responses by looking for local homogeneity in the temporal responses. This extends the simple temporal analysis used by voxel‐based GLMs to a quasi‐spatiotemporal characterization. Second, from the point of view of conventional clustering algorithms, the split–merge procedure, in conjunction with region growing, allows us to eschew any prior assumptions about the number of activated clusters. In short, our hybrid approach offers potential advantages over extant clustering and conventional analysis. We demonstrate the increased power that results from using receiver‐operating characteristic (ROC) analysis. Here, simulated and in vivo datasets are presented, and methodologies of the split–merge and region‐growing techniques are reviewed. We also describe the split–merge‐based region‐growing method for fMRI activation detection. The sensitivities of GLM, the fuzzy c‐means clustering analysis (FCA) method, and the proposed method are compared using the simulated data, and using in vivo fMRI data. We present computation complexity, robustness, and sensitivity from the viewpoint of basic assumptions.
MATERIALS AND METHODS
Data Sets
Null experiment
Imaging was acquired on a 1.5‐T scanner (SIEMENS Sonata) equipped with high‐speed gradients. The technical parameters were as follows: 2,000/60 msec (TR/TE), 20 slices, 64 × 64 matrix, 90‐degree flip angle, 22‐cm field of view (FOV), 5‐mm thickness, and 2‐mm gap. The null dataset consisted of 180 volumes, and the latter 160 scans were selected for the simulated data. During acquisition the subject was instructed to rest and perform no specific cognitive task. We used actual baseline instead of computer‐simulated data because the former matches more closely the noise structure of real fMRI data. Simulated activations were then added to the null datasets.
Auditory experiment
This dataset was from the Wellcome Department of Cognitive Neurology and was used with the permission of the FIL (Functional Imaging Laboratory) methods group. The experiment was a study on auditory bi‐syllabic stimulation. A modified 2‐T SIEMENS scanner system was used to acquire the whole brain BOLD/EPI images with TR = 7 sec. The volume size was 64 × 64 × 64, with the voxel size 3 mm × 3 mm × 3 mm. The paradigm design started with rest, and alternated between rest and stimulation. In total, 96 acquisitions were made and 84 scans were selected (due to T1 effects, it is advisable to discard the first few scans). Because both the rest and stimulation blocks were 42 sec (6 scans), in total there were 84/12 = 7 cycles. The volume size of the structure image was 256 × 256 × 54, with the voxel size 1 mm × 1 mm × 1 mm.
Preprocessing of the Auditory Experimental Dataset
Images were first realigned with the least‐squares approach and a six‐parameter rigid transformation [Friston et al., 1995a] to reduce the effect of head motion. A spatial smoothing was then applied to improve the signal‐to‐noise ratio with an isotropic Gaussian filter, in which the full‐width half‐maximum (FWHM) was set to 6 mm. Lastly, the time series were detrended using the first‐order polynomial detrending method [Bandettini et al., 1993].
Simulated Data
Simulated activations were added to a single slice of the null experimental data. This way, the number and shape of simulated activated clusters was known before. We considered five kinds of shapes for activated clusters: square, ellipse, circular, rectangular, and triangular. Image size of the simulated dataset was 64 × 64 and the sizes of the presumed five activated clusters are shown in Figure 1. The time series of the area assumed to be activated was defined as a boxcar (starting with rest and alternating between rest and simulation; 10 sample points for both rest and stimulation for 8 cycles) convolved with a hemodynamic response function (HRF, a combination of two gamma functions) [Friston et al., 1998]. Five simulated datasets were generated with the contrast‐to‐noise ratio (CNR) [Lange, 1995] varied among 0.2, 0.4, 0.6, 0.8, and 1.0. The corresponding amplitude of activations (the ratio of the mean amplitude [strength] of activation to the value of the baseline) was slightly smaller than was a typical signal change observed in the BOLD contrast [Bandettini et al., 1992; Fadili et al., 2000; Filzmoser et al., 1999; Kwong et al., 1992]. Before analysis, a spatial smoothing was applied to the simulated data with an isotropic Gaussian filter in which the FWHM was set to 4 mm.
Figure 1.
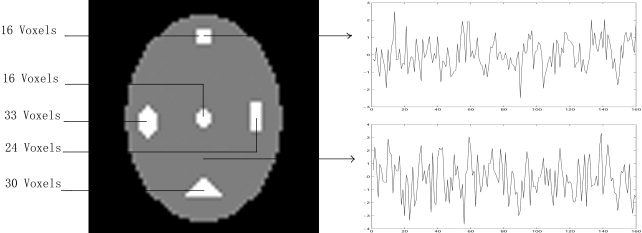
Simulated fMRI data. The white box represents sites of artificial activated regions. The top right‐hand graph depicts the time series of an activated voxel, and the bottom right‐hand graph displays the time series of a non‐activated voxel.
Split–Merge‐Based Region‐Growing Method
Overview of the split‐merge and region‐growing methods
The split–merge and region‐growing methods are well‐developed techniques for image segmentation [Morel et al., 1995]. They postulate that neighboring pixels within the same region have similar intensity values. The idea of split–merge is to break the image into a set of disjoint uniform regions. Its basic procedure comprises the following steps:
-
1
Initially consider the entire image as a single region
-
2
Pick a region R, if the homogeneity criterion H(R) is FALSE, then split the region into four subregions
-
3
Consider any two or more neighboring subregion R 1, R 2, …R n if H(R1∪R 2∪ …∪,R n) is TRUE, then merge the n regions into a single region
-
4
Repeat Steps 2–3 until no further splits and merges are possible.
For the region‐growing method, the basic idea is to group pixels with the same or similar intensities into a single maximally uniform region. This approach comprises the following steps:
-
1
Start by choosing a seed pixel (region) and compare it with neighboring pixels
-
2
Region is grown from the seed pixel (region) by adding in neighboring pixels according to the growth criterion
-
3
When the region can not be grown any further, stop
-
4
Choose another seed pixel (region) and repeat Steps 2–3.
Split–merge‐based region‐growing method
It is known that for an in vivo fMRI experiment, the true neural activation typically tends to occur in a functional cluster [Katanoda et al., 2002; Tononi et al., 1998]. In other words, true fMRI activation is more likely to occur in clusters of spatially connected voxels than in a single voxel. Intuitively, based on this feature, we can utilize the idea of split–merge and region‐growing methods for fMRI activation detection. The proposed split–merge‐based region‐growing method (SMRG) method is divided into three procedures: split–merge, region selection, and region growing. In the split–merge procedure, the homogeneous clusters in the image space are found. In the region‐selection procedure, some task‐related or interested clusters are selected based on the results of split‐merge procedure. In the region‐growing procedure, the selected clusters are set as the initial seeds and its neighboring voxels are grouped according to the growth criterion.
Split–merge
As applied in this study, the split–merge consists of a region‐splitting phase and agglomerative merging phase. In the region‐splitting phase, the fMRI data F = {f xyzt}MNOT is considered initially as a 4‐D block with a Kendall's coefficient of concordance (see Appendix) [for more details see Baumgartner et al., 1999; Kendall and Gibbons, 1990]. Where (x, y, z) are the spatial 3‐D coordinates of brain voxels, and t is the time index, M × N × O denotes the total number of brain voxels in an image scan, T represents the total number of image scans, and f xyzt indicates the image intensity of the brain voxel (x, y, z) at the tth instance of time. The block is split into eight sub‐blocks [B 1, B 2, …, B 8] of equal size, each of which is a 4‐D array, characterized by vectors of Kendall's coefficient of concordance [K ,K ,…,K ]. To define homogeneity, we consider a threshold T SM for Kendall's coefficient of concordance. It is specified in advance and kept constant in the splitting phase. Block B i is homogeneous if the homogeneity criterion K > T SM, i = 1,2,…,8 is satisfied. Otherwise, B i is heterogeneous. Heterogeneous sub‐blocks are split recursively until homogeneity occurs or a minimal block size is reached. Each application of the splitting process is followed by a merging step. In the merging phase, adjacent blocks are merged if the combined new block meets the homogeneity criterion. The above splitting and merging process can be described with an octree data structure. Each non‐terminal node in the tree has at most eight descendants, although it may have less due to merging. Final results of the split‐merge procedure are p clusters C i with volume size S i, i = 1, 2, …P The number P is far smaller than M × N × O.
Region selection
In this procedure, we extract the task‐related clusters from the obtained P clusters. To this end, there are two steps:
-
Step 1
Cluster size‐based constraint. We have known that random noise in the image space will not form a homogeneity region. In the procedure of split‐merge, if a higher T SM is specified the cluster size of noise will be small. Based on this fact, only the clusters with a cluster size greater than T s1 are reserved. Where T s1 is the predefined threshold, the left clusters will not be considered and the number of survived clusters is far smaller than P.
-
Step 2
A priori knowledge‐based constraint. As is known, not all the survived clusters from Step 1 are task related because there are some other homogeneous regions. If the paradigm information can be utilized, one could test for the significant periodicity via Fourier transform methods (for periodic paradigm) or for the significant correlation to the predefined reference [Fadili et al., 2000]. If the paradigm information can't be utilized, some a priori neurophysiologic and anatomic knowledge must be employed. In this study, a test of significant correlation was utilized, i.e., Pearson correlation was calculated between the predefined reference and each cluster's average time series. Only those with correlation coefficients greater than the predefined threshold T s2 are considered task related.
Region growing
Initially, each surviving region A i from the region‐selection procedure is specified as the initial seed. For each A i, we can define a set E as the unassigned voxels that are boundary points of A i
where N(q) is the set of neighbors (6‐connected, 18‐connected, or 26‐connected neighborhood in the three orthogonal directions can be considered) of voxel q. For each voxel p in E, if the predefined growth criterion is satisfied, voxel p is added to region A i. This growing procedure is repeated until no more voxels are assigned to region A i. In this study, the growth criterion is defined as
where f xyz: is the time series of voxel (x, y, z), M i is the average time series of the pre‐merged region A i, corr(0,0) is the Pearson correlation coefficient, and T RG is the predefined threshold.
In summary, the role of the split–merge procedure is to detect the homogeneous area in the image space based on the homogeneity criterion. Its accuracy and sensitivity is therefore not urgent. We pay more attention to its robustness, i.e., we hope the split–merge will not lose any homogeneous region; therefore, a high T SM should be specified. The role of the region‐selection procedure is to extract the task‐related clusters. To achieve this goal, there are two parameters, T s1 and T s2, that should be specified. In fact, the selection of T s1 and T s2 depend on the property of true data. Typically, according to our practical experience, T s1 and T s2 are selected from 4–8 and 0.5–0.8, respectively. In contrast to the above, the role of the region‐growing procedure is to ensure the accuracy and sensitivity of the task‐related clusters. The T RG parameter is analogous, but not equivalent to selecting a significance level of a statistical test.
Analysis of Simulated Data
We utilize the ROC analysis on the simulated data to evaluate the effectiveness of the SMRG method. In addition, GLM and FCA are compared to SMRG. Because GLM and FCA are typical hypothesis‐led and data‐led methods, respectively [Friston et al., 1997; Nicolino et al., 2001], the comparison is convincing. To give the ROC analysis, the true positive ratio in the activated region and the false positive ratio in the non‐activated region were first calculated. An ROC curve was then calculated by plotting the true‐positive ratio on the false‐positive ratio. The curve corresponding to a certain method closest to the upper left corner should be the best. Finally, as the conventional ROC analysis, the area under the ROC curve was taken as the detectability measure of different methods. For the three methods, only the clusters larger than 2 voxels were considered significant. The clusters left were regarded as random noise.
In the implementation of GLM, the design matrix is the simulated activated time series without mixing noise. In the implementation of FCA, the fuzziness exponent weight is set to 2 based on the previous work of Fadili and colleagues [2000]. There is no theory to determine the number of clusters before FCA. To find the optimal cluster number for each of the five simulated datasets, a number between 2–30 was set as the candidate (30 is a value used typically for FCA [Baumgartner et al., 2000] in a real fMRI dataset). The number that obtained the maximal area under the ROC curve was selected as the appropriate cluster number. Furthermore, the distance measure was the hyperbolic correlation measure [Golay et al., 1998]. To obtain the task‐related clusters, Pearson correlation coefficients were calculated between a predefined reference and the centroid of each cluster. The clusters with a correlation coefficient greater than the predefined threshold T FCA (it was set as 0.25 for simulated data) were considered to be task related. In the implementation of SMRG, T SM = 0.25, T s1 = 2, T s2 = 0.25 (this corresponding to T FCA = 0.25). The specification of threshold values for T SM = 0.25 and T FCA = T s2 = 0.25 was based on a priori knowledge of the simulated activated clusters. For both FCA and SMRG, the reference time series is the simulated activated time series without mixing Gaussian noise.
Analysis of In Vivo Data
The auditory dataset was analyzed with the three methods mentioned above. For the three methods, only brain voxels obtained from a low‐level threshold estimated from the histogram were considered. In addition, only the clusters larger than 4 voxels were considered significant. Because the fMRI activation is generally to occur in clusters, as conventional practice [Arfanakis et al., 2000], the clusters smaller than 4 voxels were regarded as noise and hence will not be considered. For GLM, the design matrix was set as the convolving result of fixed response (boxcar) with the canonical HRF. Before FCA, to overcome the ill‐balanced data problem, noisy pixels were removed by preprocessing (for each time series, we calculated their 1‐lag‐shifted autocorrelation function, and P = 0.01 was selected as the significance level [for details please refer see Somorjai et al., 2000]). The fuzziness exponent weight was set to 2, the cluster number was set to 30 (this is a value typically utilized for FCA [Baumgartner et al., 2000]), and the hyperbolic correlation measure was utilized as the distance measure. Furthermore, T FCA was set as 0.5. For SMRG, T SM = 0.85, T s1 = 4, and T s2 = 0.5 (this corresponding to T FCA = 0.5). Because the split–merge stage was to find the homogeneity region in the fMRI data space, a relatively high value, 0.85, was specified for T SM. Although specification of threshold values for T FCA = T s2 = 0.5 was empirical, the emphasis here was to make a fair comparison between SMRG and FCA.
These methods were compared both qualitatively and quantitatively. Quantitative comparison was carried out as follows: (1) a common activation area obtained by GLM was set as the reference area (because GLM is the most popular method for fMRI activation detection, we set the result of GLM as the benchmark); (2) the thresholds of FCA and SMRG were adjusted by keeping the same cluster volume for the reference area; and (3) the volume size and the average time series of the non‐reference area were taken as measures of effectiveness and sensitiveness for different methods.
RESULTS
Simulated Data
Figure 2 shows the area under the ROC curve for each of the three statistical models. Areas under the ROC curves were taken as the detectability index of the three methods. From Figure 2, it is easy to conclude that SMRG outperformed GLM and FCA. To clarify further the increased sensitivity of SMRG, we examined a particular case, with CNR at 0.4. ROC curves of the three methods are depicted in Figure 3a. The ROC curve of the SMRG approached the top left corner primely, whereas the ROC curves of the other two methods were farther. In Figure 3a, points x, y, and z are those points closest to the optimal classification (false positive rates = 0, true positive rates = 1) in the respective ROC curves. Figure 3c–e illustrates the best result of GLM, FCA, and SMRG, respectively. Compared to GLM and FCA, SMRG revealed more true‐positive and fewer false‐positive voxels. The computation complexities of the three methods are reported in Table I. Computations were carried out on a 1.8 GHz PC, and SMRG, GLM, and FCA were all coded in MatLab (MathWorks, Inc.).
Figure 2.
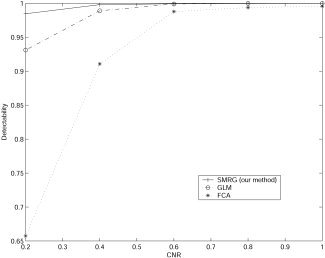
Performance of SMRG, GLM, and FCA for the simulated dataset.
Figure 3.
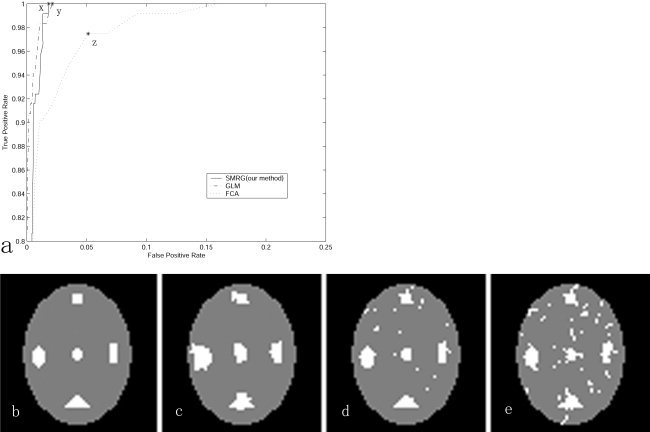
a: ROC curves corresponding to the case of CNR = 0.4 for the simulated data. b: presumed activation. c: Results of SMRG. d: Results of GLM. e: Results of FCA.
Table I.
Computation time for the three different methods in simulated dataset with different CNR
| Method | CNR | ||||
|---|---|---|---|---|---|
| 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | |
| GLM | <6 | <6 | <6 | <6 | <6 |
| FCA | 776 | 792 | 723 | 645 | 738 |
| SMRG | 19 | 20 | 19 | 25 | 23 |
Computation time in seconds for the three different methods in simulated dataset with different CNR. FCA is calculated in the optimal cluster and SMRG is calculated with the T RG value that corresponds to the optimal classification point. CNR, contrast‐to‐noise ratio; GLM, general linear model; FCA, fuzzy c‐means clustering analysis.
In Vivo Data
Right auditory cortex in the 29th slice was set as the reference area. For GLM, four thresholds were selected, corresponding to the P values of 10−7, 10−6, 10−5, and 10−4. The corresponding threshold T FCA of FCA was 0.19, 0.1, 0.06, and 0.03, respectively, and the corresponding threshold T RG of SMRG was 0.73, 0.71, 0.67, and 0.62, respectively. Results of the three methods are shown in Figure 4. From the viewpoint of qualitative analysis, each method could detect successfully the activated areas such as Brodmann's area (BA) 42 (primary auditory cortex) and BA 22 (auditory association area).
Figure 4.
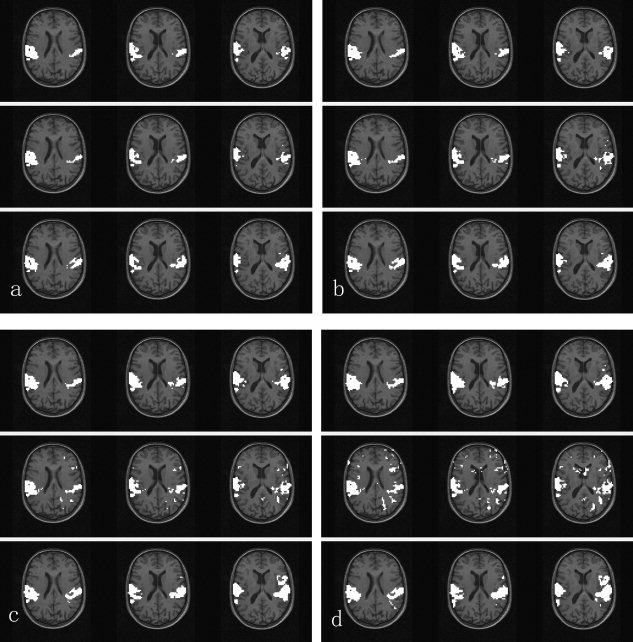
Activation maps revealed by each of the three methods, i.e., GLM, FCA, and SMRG, shown from the top row to the bottom of the figure. Three slices (29–31 of 64 slices) involved in the auditory experiment are shown. Left side corresponds to right hemisphere. a–d: are results of the three methods corresponding to GLM thresholded at the voxel‐wise significance level of P < 10−7, P < 10−6, P < 10−5, and P < 10−4, respectively.
Compared to FCA, the activated areas detected by SMRG were larger and more continuous, e.g., the activation in the left auditory cortex. In addition, there were less false‐positive clusters scattered throughout the brain in the SMRG results than in the FCA results. In Figure 4d, for instance, there were some false‐positive clusters in the FCA results.
Compared to GLM, quantitatively speaking, the activated area detected by SMRG was more continuous. In Figure 4d, in the left auditory cortex activated area, there were 216 voxels that activated in both SMRG and GLM; the average time series of these 216 voxels is shown in Figure 5a. In SMRG, there were 125 voxels activated that were not activated in GLM. The average time series of these 125 voxels is shown in Figure 5b. The correlation coefficient between this two average time series is 0.75; therefore, the 125 voxels were all meaningful activated voxels. In the right auditory cortex activated region there were 294 activated voxels in both SMRG and GLM; however, 35 voxels that were activated in GLM were not activated in SMRG. In other words, the detected activation in SMRG was smaller than that in GLM.
Figure 5.
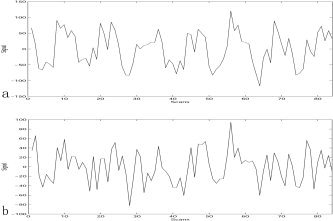
a: Average time series of the 216 voxels that activated in GLM and SMRG in the left auditory cortex. b: Average time series of the 125 voxels that activated in SMRG but did not activate in GLM in the left auditory cortex.
DISCUSSION
Split–merge is appropriate primarily for cubic images with dimensions that are a power of 2, such as 64 × 64 × 64 or 128 × 128 × 128. These images can be divided until the blocks are as small as 1 × 1 × 1. If the split–merge is applied to an image whose dimension is not a power of 2, at some point the blocks cannot be divided further. For instance, if an image is 48 × 48 × 48, it can be divided into blocks with size of 24 × 24 × 24, 12 × 12 × 12, 6 × 6 × 6, and finally, 3 × 3 × 3. No further division beyond 3 × 3 × 3 is possible. As for fMRI data, the image size of a single slice is typically 64 × 64. The number of slices is variable. To keep the precision of split–merge, there are two feasible schemes. The first would be to apply the split–merge procedure to each single slice. Each heterogeneous block should be split into four sub‐blocks, and the resulting data structure would be a regular quadtree. The second scheme would be to resample the original image to a cubic image whose dimensions are a power of 2. For instance, if the original image size is 64 × 64 × 14, the resulting image after interpolation should be 64 × 64 × 64.
For fMRI activation detection, each method has its unique characteristics such as basic assumptions, computation complexity, robustness, and sensitivity. Method selection for fMRI activation detection is an explorative procedure under the characteristics of candidate methods and the property of actual data. From our point of view, in addition to sensitivity comparison between different methods, the comparison of basic assumptions, computation complexity, and robustness are also meaningful.
From the viewpoint of basic assumptions, compared to GLM, SMRG has two advantages: (1) it combines hypothesis‐led and data‐led approaches; and (2) SMRG can utilize the information of neighboring voxels; however, GLM doesn't utilize it, hence, it is hindered from the clustered activation feature. Compared to FCA, SMRG has three advantages: (1) it is not sensitive to the ill‐balanced data problem; therefore, SMRG can minimize the risk of discarding possibly activated voxels; (2) because SMRG doesn't need the predefined cluster number, it is exempt from the “cluster validity” problem; and (3) FCA ignores the spatially clustered aspect of activations, whereas SMRG can utilize the spatial neighboring information of clustered activation. From the viewpoint of computation complexity, for the in vivo dataset, the computation time of GLM, FCA, and SMRG was 19, 8,676, and 636 sec, respectively (the thresholds for each method correspond to the result of Fig. 5d). GLM was fastest due to its hypothesis‐led property. SMRG was a sequence algorithm, whereas FCA was an iterative optimal algorithm; therefore, the computation speed of SMRG was faster. For large datasets, especially when a large cluster number was specified for FCA, predominance of SMRG was evident. The robustness of GLM depended on the model selected. Selecting the most appropriate model without additional assumptions was difficult, however, especially when the hemodynamic response to stimulus was complicated. For FCA, the robustness relies upon two factors: (1) the optional robust statistics in the normalization procedure; and (2) specification of an appropriate cluster number. This open “cluster validity” problem remains unsolved. For SMRG, the robustness also depends on two factors: (1) the homogeneity criterion in the split‐merge procedure (in the present study, Kendall's coefficient of concordance, which is a robust statistic, was selected as the homogeneity criterion); and (2) the inherent ability of the split–merge to find all homogeneous areas. Because task‐related clusters are homogeneous areas, the split–merge will not lose any task‐related clusters. Combined with the region‐selection procedure, the robustness of SMRG is ensured. From the viewpoint of sensitivity, the reason that the split and merge procedure out‐performs both FCA and voxel‐wise GLM is because our procedure harnesses spatiotemporal priors inherent in cluster analysis and the prior information afforded by the hypothesis‐led component of region selection. Conjoining these two sources of prior information allows our approach to detect with greater sensitivity the spatially extended activation clusters that conform to the GLM adopted.
Recently, attention has been focused on brain regions in which neural activity during the resting state [Biswal et al., 1995; Michael et al., 2003] and experimental task state [Liu et al., 1999]. Our method may helpful in detecting functional cluster [Tononi et al., 1998] in the brain. For instance, to study functional connectivity on the coherent networks in the human brain, one might want to find the homogeneous brain regions in the resting state or in a particular experimental condition. The split–merge and region‐growing procedure can be utilized to find homogeneous brain regions without any prior knowledge about the experimental design. Future effort will focus on the detection of functional cluster in the brain by utilizing our method.
In summary, a new method has been proposed for fMRI activation detection. ROC analysis on simulated datasets has demonstrated its effectiveness and faster computation speed. Furthermore, its usefulness has been confirmed by applying it to real data. Compared to the other two methods, SMRG has two advantages: (1) the activated clusters are more continuous; and (2) there are fewer small, scattered clusters. Experimental results demonstrate that the proposed method can serve as a reliable new method suited to the nature of fMRI data analysis.
Acknowledgements
We thank Professor K. Friston for kindly permitting the use of the in vivo datasets.
Kendall's Coefficients of Concordance
The 4‐D fMRI data F = {f xyzt}MNOT is first reshaped to a matrix X(T,Q) where T is the number of time instances and Q = M × N × O is the number of voxels in the fMRI data.
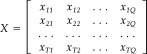 |
where x ij is the ith time instance of the jth time series. Then rank each column from 1 to T.
is the Kendall's coefficient of concordance. In which SR i is the sum of ranks for each row of X, and SR = {(T + 1) × Q} is the mean of the SR i values. Kendall's coefficient of concordance is a measure that characterizes the overall concordance of the group of time series. Its value is between 0 and 1 (0 indicates no concordance and 1 means a perfect match).
REFERENCES
- Arfanakis K, Cordes D, Haughton VM, Moritz CH, Quigley MA, Meyerand ME (2000): Combining independent component analysis and correlation analysis to probe interregional connectivity in fMRI task activation datasets. Magn Reson Imaging 18: 921–930. [DOI] [PubMed] [Google Scholar]
- Bandettini PA, Jesmanowicz A, Wong EC, Hyde JS (1993): Processing strategies for time‐course data sets in functional MRI of the human brain. Magn Reson Med 30: 161–173. [DOI] [PubMed] [Google Scholar]
- Bandettini PA, Wong EC, Hinks RS, Tikofsky RS, Hyde JS (1992): Time course EPI of human brain function during task activation. Magn Reson Med 25: 390–397. [DOI] [PubMed] [Google Scholar]
- Baumgartner R, Ryner L, Richter W, Summers R, Jarmasz M, Somorjai R (2000): Comparison of two exploratory data analysis methods for fMRI: fuzzy clustering vs. principal component analysis. Magn Reson Imaging 18: 89–94. [DOI] [PubMed] [Google Scholar]
- Baumgartner R, Scarth G, Teichtmeister C, Somorjai R, Moser E (1997): Fuzzy clustering of gradient‐echo functional MRI in the human visual cortex. Part I: Reproducibility. J Magn Reson Imaging 7: 1094–1101. [DOI] [PubMed] [Google Scholar]
- Baumgartner R, Somorjai R, Summers R, Richter W (1999): Assessment of cluster homogeneity in fMRI data using Kendall's coefficient of concordance. Magn Reson Imaging 17: 1525–1532. [DOI] [PubMed] [Google Scholar]
- Biswal MJ, Mock BJ, Sorenson JA (1995): Functional connectivity in the motor cortex of resting human brain using echo‐planar MRI. Magn Reson Med 34: 537–541. [DOI] [PubMed] [Google Scholar]
- Calhoun VD, Adali T, Pearlson GD, Pekar JJ (2001): Spatial and temporal independent component analysis of functional MRI data containing a pair of task‐related waveforms. Hum Brain Mapp 13: 43–53. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fadili MJ, Ruan S, Bloyet D, Mazoyer B (2000): A multistep unsupervised fuzzy clustering analysis of fMRI time series. Hum Brain Mapp 10: 160–178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Filzmoser P, Baumgartner R, Moser E (1999): A hierarchical clustering method for analyzing functional MR images. Magn Reson Imaging 17: 817–826. [DOI] [PubMed] [Google Scholar]
- Friston KJ, Ashburner J, Frith CD, Poline JB, Heather JD, Frackowiak RS (1995a): Spatial registration and normalization of images. Hum Brain Mapp 2: 165–189. [Google Scholar]
- Friston KJ, Fletcher P, Josephs O, Holmes A, Rugg MD, Turner R (1998): Event‐related fMRI: characterizing differential responses. Neuroimage 7: 30–40. [DOI] [PubMed] [Google Scholar]
- Friston KJ, Holmes AP, Worsley KJ, Poline JP, Frith CD, Frackowiak RS (1995b): Statistical parametric maps in functional imaging: a general linear approach. Hum Brain Mapp 2: 189–210. [Google Scholar]
- Friston KJ, et al. (1997): SPM course notes. Online at http://www.fil.ion.ucl.ac.uk/spm/course/notes.html.
- Golay X, Kollias S, Stoll G, Meier D, Valavanis A, Boesiger P (1998): A new correlation‐based fuzzy logic clustering algorithm for fMRI. Magn Reson Med 40: 249–260. [DOI] [PubMed] [Google Scholar]
- Goutte C, Toft P, Rostrup E, Nielsen FA, Hansen LK (1999): On clustering fMRI time series. Neuroimage 9: 3: 298–310. [DOI] [PubMed] [Google Scholar]
- Hansen LK, Larsen J, Nielsen FA, Strother SC, Rostrup E, Savoy R, Lange N, Sidtis J, Svarer C, Paulson OB (1999): Generalizable patterns in neuroimaging: how many principal components? Neuroimage 9: 534–544. [DOI] [PubMed] [Google Scholar]
- Jung TP, Makeig S, Mckeown MJ, Bell AJ, Lee TW, Sejnowski TJ (2001): Imaging brain dynamics using independent component analysis. Proc IEEE 89: 1107–1122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Katanoda K, Matsuda Y, Sugishita M (2002): A spatial‐temporal regression model for the analysis of functional MRI data. Neuroimage 17: 1415–1428. [DOI] [PubMed] [Google Scholar]
- Kendall M, Gibbons JD (1990): Rank correlation methods. Oxford: Oxford University Press. [Google Scholar]
- Kwong KK, Belliveau JW, Chesler DA, Goldberg IE, Weisskoff RM, Poncelet BP, Kennedy DN, Hoppel BE, Cohen MS, Turner R, Cheng HM, Brady TJ, Rosen BR (1992): Dynamic magnetic resonance imaging of human brain activity during primary sensory stimulation. Proc Natl Acad Sci USA 89: 5675–5679. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lai SH, Fang M (1999): A novel local PCA‐based method for detecting activation signals in fMRI. Magn Reson Imaging 17: 827–836. [DOI] [PubMed] [Google Scholar]
- Lange N (1996): Statistical approaches to human brain mapping by functional magnetic resonance imaging. Stat Med 15: 389–428. [DOI] [PubMed] [Google Scholar]
- Liu Y, Gao JH, Liotti M, Pu Y, Fox PT (1999): Temporal dissociation of parallel processing in the human subcortical outputs. Nature 400: 364–367. [DOI] [PubMed] [Google Scholar]
- McKeown MJ, Makeig S, Brown GG, Jung TP, Kindermann SS, Bell AJ, Sejnowski TJ (1998): Analysis of fMRI data by blind separation into independent spatial components. Hum Brain Mapp 6: 160‐188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Michael DG, Ben K, Allan LR, Vinod M (2003): Functional connectivity in the resting brain: A network analysis of the default mode hypothesis. Proc Natl Acad Sci USA 100: 253–258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morel JM, Solimini S (1995): Variational methods in image segmentation. Boston: Birkhäuser Publishing. [Google Scholar]
- Nicolino JP, Rodrigo AV, Somorjai RL (2001): Evident: a functional magnetic resonance image analysis system. Artif Intell Med 21: 263–269. [DOI] [PubMed] [Google Scholar]
- Ogawa S, Lee TM, Ray AR, Tank DW (1990): Brain magnetic resonance imaging with contrast dependent on blood oxygenation. Proc Natl Acad Sci USA 87: 9868–9872. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Penny W, Friston K (2003): Mixtures of general linear models for functional neuroimaging. IEEE Trans Med Imaging 22: 504–514. [DOI] [PubMed] [Google Scholar]
- Scarth G, Somorjai R, Alexander M, Wowk B, Wennerberg A, McIntyre M (1995): Cluster analysis of functional brain images. Proceedings of the First International Conference on Functional Mapping of the Human Brain. Hum Brain Mapp 1 (Suppl.): 158.
- Somorjai RL, Jarmasz M, Baumgartner R (2000): Evident: a two‐stage strategy for the exploratory analysis of functional MRI data by fuzzy clustering. Technical Report #37, Institute for Biodiagnostics .
- Tononi G, McIntosh AR, Russell DP, Edelman GM (1998): Functional clustering: identifying strongly interactive brain regions in neuroimaging data. Neuroimage 7: 133–149. [DOI] [PubMed] [Google Scholar]


