Coupling of regional activations in a human brain during an object and face affect recognition task

Abstract

Magnetic field tomography (MFT) was used to extract estimates for distributed source activity from average and single trial MEG signals recorded while subjects identified objects (including faces) and facial expressions of emotion. Regions of interest (ROIs) were automatically identified from the MFT solutions of the average signal for each subject. For one subject the entire set of MFT estimates obtained from unaveraged data was also used to compute simultaneous time series for the single trial activity in different ROIs. Three pairs of homologous areas in each hemisphere were selected for further analysis: posterior calcarine sulcus (PCS), fusiform gyrus (FM), and the amygdaloid complex (AM). Mutual information (MI) between each pair of the areas was computed from all single trial time series and contrasted for different tasks (object or emotion recognition) and categories within each task. The MI analysis shows that through feed‐forward and feedback linkages, the “computation” load associated with the task of identifying objects and emotions is spread across both space (different ROIs and hemispheres) and time (different latencies and delays in couplings between areas)—well within 200 ms, different objects separate first in the right hemisphere PCS and FG coupling while different emotions separate in the right hemisphere FG and AM coupling, particularly at latencies after 200 ms. Hum. Brain Mapping 11:77–92, 2000. © 2000 Wiley‐Liss, Inc.

INTRODUCTION

Neuroimaging data have consistently shown that the brain activity for specialised operations is segregated to distinct regions. In recent years much research effort has been devoted to the identification of neural correlates of operations, which must inevitably bring the results within segregated areas together and give rise to a unitary and unique perception and self‐awareness. If one wishes to study how segregation and integration are implemented in the brain one must extract quantitative measures of connectivity from measurements of brain activity at spatial and temporal scales that are likely to be relevant. The choice of method ranges from single and few unit recordings to mass measures of activity such as Positron Emission Tomography (PET), functional Magnetic Resonance Imaging (fMRI) and electrophysiological measures, i.e., Electroencephalography (EEG) and Magnetoencephalography (MEG).

In principle, single or few unit recordings are the gold standard, but in practice they fall far short of this ideal—they provide only a partial view in the strict locality where the needle has ended, and they are not available for studies with normal human subjects. This is a huge limitation if one wishes to relate the measured brain activity to states of conscious awareness. Elaborate training of animals provides valuable clues, but this is a poor substitute to the exquisite communicative skills endowed to humans by their language capabilities.

For PET the sampling time is long, at least many seconds, and the haemodynamic processes that underpin the production of PET images are far too slow to reveal changes in activity occurring at a small fraction of a second, which is the characteristic timescale for many processes in the brain. The same problem remains in the case of fMRI—a fast sampling rate of as low as 40 ms is feasible, but again the bulk of the effect that gives rise to the signal relies on the slow heamodynamic responses, introducing a temporal blurring of a second or two.

The raw MEG signal contains strong contributions from external sources and biological activity that do not relate directly to the brain (e.g., the heart, muscles, and eyes); these however can be removed reliably by a variety of methods. The remaining signal is a direct macromeasure of neuronal activity—the signal reflects instantaneous changes in electrical activity and propagates from the point of generation in the brain to the sensors with the speed of light. With modern helmet‐shaped probes, the magnetic field around the head can be mapped millisecond by millisecond. Any variability that is encountered in the clean signal when identical stimuli are repeatedly presented is due to variability at the level of neuronal activity, and whenever possible it must be described and explained accordingly, and not confused with external or system noise or relegated to the ambivalent notion of brain noise. We used MFT to extract estimates of local activations: MFT can produce reliable estimates of brain activity from the measured magnetic field for each millisecond snapshot of MEG signals [Ioannides et al., 1990]. These estimates are analogical and computed completely independently for each timeslice, they are therefore available for further post‐MFT processing [Ioannides et al., 1995]. When the millisecond by millisecond MFT estimates from different regions are studied together they provide a unique view of the formation, evolution, and final disintegration of functional clusters, determining in each case the mean duration and variance for each subprocess. We are thus able to test the hypothesis that the variability in brain activity one encounters when each region is studied in isolation is not some random background noise, but it is a consequence of focusing on just one part of a complex system.

Having identified the relevant timescales and the appropriate imaging technique for measuring brain activity we also need to define some appropriate quantification of the integrative function. The functional link between two neuronal populations can be quantified in terms of the “information transfer” from one group to another. Then we can define functional dependencies among regions through estimates of the amount of information that is common to all the signals at a specific instant of time. This provides a simple notion of functional interactivity. Recently Tononi et al. [1998] proposed a stronger condition, defining a functional cluster as a set of regions strongly correlated to each other but weakly correlated to the rest of the brain. They applied this analysis to PET data obtained from normal and schizophrenic subjects performing a set of cognitive tasks and the analysis appeared to differentiate between the two sets of subjects.

It is perfectly feasible to pursue the same analysis replacing the PET or fMRI second‐by‐second estimates of activity with our MFT millisecond by millisecond estimates, extracted from average MEG data. The average signal is smooth, reflecting the recurring events that are time locked to the stimulus onset; these events are also likely to contribute to the PET and fMRI signal. However, even a cursory look at single trial MFT reconstructions or the MEG raw signal itself reveals changes in activity a few milliseconds apart that are not likely to average well across trials because they are not precisely time locked to the stimulus. It is these more transient events (together with the ones contributing to the average signal) that this work probes through direct computations of the MI of pairs of time series; each time series in the pair is the activation within a well‐circumscribed ROI extracted by MFT from the MEG signal of a single trial.

Single trial analysis has been avoided because the volume of data involved and the large computational effort that it demands and the lingering notion that single trial signal is dominated by noise. It is for historical rather than scientific reasons that methods like heavy filtering and averaging originally developed for processing early noisy EEG data were adopted and are still widely used to remove what was inappropriately termed as “brain noise” in the MEG signal processing [Ioannides, 1994]. Earlier single trial MFT analysis [Liu et al. 1996; Liu et al., 1998a] has shown glimpses of what is eliminated by averaging, and large single trial intersubject variability. We have therefore focused our introduction of MI to the analysis of single trial MFT time series to just one subject to limit what was already a huge computational task and to avoid the layer of complications that intersubject variability would have brought. Speeding up the computations and using as much information as possible from other neuroimaging modalities are obvious extensions of the work. We have in fact used information from other modalities indirectly, through the choice of experiment and the selection of areas to include in the analysis. We have settled on three ROIs in each hemisphere: PCS, FG, and AM. Activity in each of these three areas has been identified in numerous PET and fMRI studies and has shown correlation with different task requirements: general activation by visual stimuli and involvement in low level visual processing (PCS), object and especially face selectivity (FG), and activity induced by emotions or simply by the recognition of emotion, specifically, fear (AM). Our MI analysis shows that segregation of function extends across space and time—different tasks (e.g., the recognition of objects versus emotions) and the individual processing for each category are segregated to different time periods within areas and different delay windows in the linkage of activity between areas.

MATERIALS AND METHODS

Experimental setup

Two experiments using the same protocol were performed. Experiment 1 used the BTi twin MAGNES system (2 × 37 channels) with lateral dewar positions and five subjects. Experiment 2 used the BTi whole head system (148 channels) with one of the five subjects. Both experiments were performed at the MEG laboratory in Jülich Research Center, Germany. Optical fibres brought the visual stimuli into the magnetically shielded room and back‐projected images on a screen placed about 45 cm in front of the subject (the visual angle was about 6 × 4°). The experiment included two tasks in three runs. Task 1: object recognition—30 different black and white images for each object category—front views of lorries, chairs, horse heads, birds, flowers and faces (Fig. 1a). Task 2: facial emotion recognition—same 30 faces as task 1; five images for each one of the six basic emotions—happiness, fear, anger, surprise, disgust, and sadness (Fig. 1b). Task 1 was used in run 1 and task 2 was used in runs 2 and 3 (run 3 was a duplicate of run 2). The experiment procedure is shown in Figure 1c: each image was presented for a short period of time (500 ms), followed by the option list 1 sec later to avoid automatic processing, especially for emotions. The subject was asked to name the object or emotion verbally as soon as the option list appeared, and the response was recorded by an operator for later analysis. The MEG signal was recorded in epoch mode as a 1.2 sec‐long segment beginning 200 ms before the onset of each image.

Figure 1.

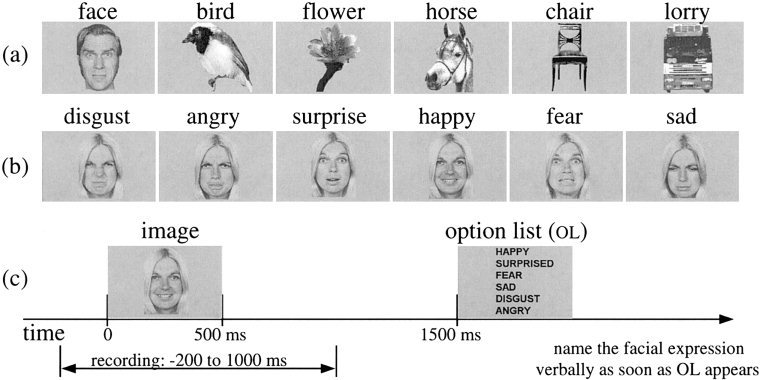
Examples of stimuli used for object (a) and face affect (b) recognition. The experimental procedure is shown in (c).

Signal processing

We reported elsewhere the details of the protocol and the signal processing of the data from the twin MAGNES [Streit et al., 1999] and the whole‐head probe [Liu et al., 1999]. We outline here the main procedures: the contamination of heart and eye movements was first removed from the MEG signal using an optimised reference noise cancellation software specifically developed for this task [Barnes and Ioannides, 1996]. Separate averages were constructed for each object and emotion category and both the average and single trial signals were then bandpass filtered from 1 to 45 Hz. All remaining single trial signals were visually reexamined and trials suspected of artefacts were rejected further. For run 1, 27 trials of faces, 26 of chairs, 28 of horses, and 29 each of birds, flowers, and lorries remained. For runs 2 and 3, trials for which the subject did not name the emotion correctly were also excluded, leaving 7 (4/3) trials of disgust from run 2/3, 7 (3/4) of anger, 7 (3/4) of surprise, 9 (4/5) of happiness, 8 (4/4) of fear, and 5 (2/3) of sadness for further single trial analysis.

MFT analysis, ROI selection, and activation curves

All the average and single trial signals were analyzed using MFT (−100 to 600 ms, at a step of 1.97 ms). Separate MFT computations were used for the left and right hemisphere: 50 channels from each hemisphere (covering the subject's temporal and parietal areas well) were used with hemispherical source spaces, one for the left and one for the right hemisphere (Fig. 2). For each timeslice the MFT analysis yields a continuous estimate of the current density in the left and right hemisphere source space. For purely practical reasons the solutions are stored in a 3D array with grid distance of 1 cm. The time sequence of activity can therefore be treated as a recording with a set of “virtual electrodes” placed in the brain. Tests with computer generated data from point sources and validation tests with implanted dipoles in humans [Ioannides et al., 1993] invariably produced very focal MFT activations; MFT analysis of actual data usually result in more extended estimates. We take the conservative view that the time courses for ROIs we label as PCS, FG, and AM may also include contributions from activity in some neighbouring areas. Having sounded this cautionary message it is also worth pointing out that the trial‐by‐trial comparison of activity shows remarkable similarity in the responses, which are highly variable in latency, however. The temporal jitter in the response gets progressively larger at long latencies and as one moves away from the primary sensory areas. In the case of the FG as well as other extended structures, the MFT estimates mirrors rather well the shape of the structure itself.

Figure 2.

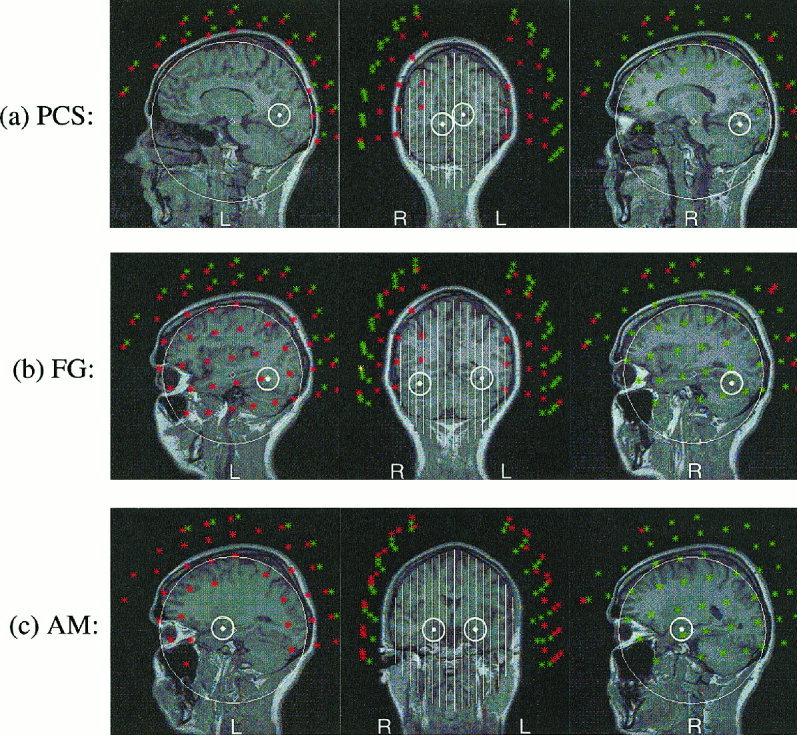
Sagittal and coronal views of the ROIs for PCS, FG and AM superimposed on the MRI of the subject. A dot and a small circle mark the centre and boundary of each ROI respectively. White lines and big circles show cuts through hemispherical source spaces. Sensors within 1 and 3 cm of the displayed slice are shown in red and green respectively.

The MFT and MI analysis were performed on all the single trial data of Experiment 2. In total nearly 200,000 3D images of vector fields were generated and used in the MI analysis. An automatic program was used to scan through the MFT solutions and identify areas of strong focal independent activity and to group such activations across latencies and trials into clusters. The centers of these clusters were taken as the centers of ROIs, each defined as a spherical region with a radius of 1.2 cm. These functionally defined ROIs (28 ROIs in each hemisphere) were then labeled according to their anatomical location. We have confined the MI analysis to the minimum necessary to provide examples of linkage across regions involved in the object recognition (run 1) and face affect recognition (runs 2 and 3). With many recent studies with PET and fMRI as guidance we have selected three regions in each hemisphere that were strongly activated and identified in both the present and in our previous analysis with the full set of subjects using the twin MAGNES system. Figure 2 shows the location of these three areas on the subject's MRI and Table I gives the Talairach coordinates. The first region we considered was PCS, which includes V1 and V2 and possibly V3 areas and is the primary cortical recipient of the visual signal from the retina. FG was the second area considered; it has been identified by many studies as an area specialised in the processing of faces [Allison et al., 1994; Halgren et al., 1994; McCarthy et al., 1997; Kanwisher et al., 1997; Puce et al., 1998]. AM was the third area selected for the analysis; it has been associated with the processing of emotions, particularly fear, in animal studies [LeDoux, 1996], lesion work [Adolphs et al., 1996], and more recently with the judgement of affect in facial expressions [Morris et al., 1996].

Table I.

Talairach coordinates for the three ROIs*

ROI	Left hemisphere			Right hemisphere
	x	y	z	x	y	z
PCS	−16	−61	4	5	−63	−8
FG	−35	−49	−11	29	−58	−19
AM	−24	−4	−15	20	−7	−17

^*Brain atlas coordinates are in millimeters along left‐right (right, positive x), anterior‐posterior (anterior, positive y), and superior‐inferior (superior, positive z) axes [Talairach and Tournoux, 1988].

It is worth reiterating once more that the averaged and single trial data at each timeslice is processed separately, each producing an independent probabilistic estimate for the (nonsilent) primary current density vector J ^P(r, t). The activation curves M(t) for the ROIs

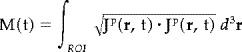can then be computed and plotted as a function of time [Ioannides et al., 1995], and from these the temporal sequence and their statistical properties can be studied without assumptions relying on repeatability across trials with very small jitter in latency.

In an earlier work [Liu et al., 1999], the Kolmogorov‐Smirnov test was used to identify time segments for which FG and AM showed significantly different activations for object and emotion recognition. In this work we use MI to describe in a quantitative way how the activity across individual pairs of regions depends on latency and category.

Mutual information

The fundamental quantity from the information theoretic point of view is the Shannon entropy. Consider a signal X with values that can be assigned to a number of bins, and let p(i) be the probability of recording a value for X which falls in the i ^th bin (Σ_i p(i) = 1), the entropy is defined as the mean amount of information about the system that is expected from a single measurement of X and explicitly given by:

The generalisation for two or more signals is straightforward. Consider first two signals, X ₁ and X ₂. In general we can sample these two signals either simultaneously or the second with a time delay τ. For any given value of τ the joint distribution can be partitioned into bins so that the probability of finding a value for X ₁ in the i ^th range and simultaneously a (τ shifted) value for X ₂ in the j ^th range is p(i, j; τ). Then the obvious generalisation for the combined entropy, i.e. the mean information about the system that is expected from a single simultaneous measurement of X ₁ and X ₂ is:

The above joint entropy is zero if and only if the two signals are statistically independent while in all other cases it is nonzero.

Consider the case when two signals are present, with known statistical properties and hence individual and combined entropies, we can still quantify our mean knowledge for X ₂ given a single measurement of X ₁using the concept of mutual information (MI):

The MI provides a natural criterion of independence of signals: if two signals are statistically independent their MI is zero, otherwise it is positive. The advantage of using MI is that it is sensitive to both linear and nonlinear correlations between two signals. If one replaces the Shannon entropy with

Then, after an obvious generalisation of symbols for the two distributions, one obtains the Renyi generalized mutual information [Renyi, 1970].

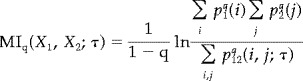The standard definition assigns equal weight to all couplings, while the generalised version assigns different weights to different components of the set of probabilities p(i). A reasonable starting point would be to emphasise the strongest couplings between areas of the brain by choosing q > 1. We have carried out computations with different values of q, but for the sake of consistency we will display results for q = 4 throughout, and based on this understanding we will drop the subscript q from MI hereafter. We used all valid repetitions (trials) available to compute a measure of MI at each point in the (t, τ) plane from segments of equal length 2 ΔT, where X ₁ ranges from t – ΔT to t + ΔT and X ₂ ranges from t + τ – ΔT to t + τ+ ΔT. We computed the MI from a very short time window (20 timeslices, 39.4 ms, ΔT = 19.7 ms) by scanning the time series with a step of 2 timeslices (3.94 ms). The resolution in time is directly related to a shift of the window (3.94 ms) and affected by the ΔT value used. A shorter ΔT will improve resolution at the expense of confidence in the MI value. With the above choices we have a reliable computation for the MI and a resolution in time around 5 ms.

Display of results

Displays of MI maps appear too abstract at first. Like any map they become informative when the key defining what the map describes is given and saliency is ascribed to easily recognizable geometric properties of the primitives (points, lines, and surface patches). The primitives in our case are islands of high MI in the (t, τ) plane, which we label as a linked activity period segment (LAPS) or L for short. We first distinguish three kinds of LAPS each describing a different facet of linkage between the two areas.

A conjunctive linked activity period segment (C‐LAPS or L_c) is an island in the (t, τ) plane with MI values above a prespecified threshold for every category. We will consistently use a heavy (white or black) line to delineate the contour with the prespecified threshold of C‐LAPS. An average linked activity period segment (A‐LAPS or L_a) is an island in the (t, τ) plane containing high MI values, averaged across all categories. An A‐LAPS can be delineated by the contour line corresponding to some prespecified threshold in the average MI. Colour can also be used to code different values of average MI. For an A‐LAPS, not all categories need be active above the threshold, only enough to give an average MI value that exceeds the threshold value. It is therefore useful to superimpose an A‐LAPS and a C‐LAPS using colour‐coded contours for A‐LAPS and a heavy contour for C‐LAPS. Finally we define category specific (say category x) linked activity period segment (S‐x‐LAPS or L${}_{\text{x}}^{\text{s}}$). The S‐x‐LAPS can be plotted with a different colour for each category and a heavy contour can be superimposed on the same plot to show either islands of high average MI (A‐LAPS) or islands in the (t, τ) plane where all categories have MI values above a threshold (C‐LAPS). If different categories are expressed by different neuronal populations or engage the brain at varying degree then the respective values at MI peak may be very different. Since we are concerned with the question when linkage is established between regions (which will show up as a peak in the MI plot of each category) we have adjusted each category so that its maximum is unity in our displays. For completeness, the actual range of the absolute values of MI for each category is also printed in the figures.

Different processes produce characteristic shapes and distributions of LAPS in the (t, τ) plane which are easy to identify once they are described. Figure 3 is an artificial example showing patterns in the (t, τ) plane corresponding to distinct linkage types between two areas. The reader can think of the display as showing any one of the LAPS between two regions. The horizontal axis labels the latency t for the first time series (i.e., the latency with respect to the stimulus for the activity in ROI₁ and the vertical axis labels the delay τ of the second time series, X ₂ i.e., the latency difference between ROI₁ and ROI₂). The upper half of the figure contains events for which the activity in ROI₁ leads, while the lower figure contains events where the activity in ROI₁ lags. The horizontal line with τ = 0 is the locus of simultaneous events in two regions. A zero delay LAPS occurring about 100 ms after stimulus onset is shown by A, where no preference is evident in the order of activation in the two areas. It is important to note that the MI bulge represents a spread of positive and negative delays of 20 ms, which corresponds to either simultaneous co‐activations or bidirectional activations. In contrast LAPS B (C) shows a sharp linkage of activations, where activity in ROI₁ leads (lags) the activity ROI₂ by a few milliseconds, consistent with monosynaptic transmission of information. Event D (E) is also an event where ROI₁ leads (lags) ROI₂ but the delay is much larger than the time it takes for activity to move by one synapse and lasts for a reasonable time. We also distinguish directions in the (t, τ) plane. The vertical stripe (F) corresponds to a fixed latency of 100 ms for ROI₁ with a variable delay and hence connects events where the time in ROI₁ is fixed (around 100 ms), while the latency in ROI₂ varies from 20 to 70 ms (negative delay from −80 to −30 ms). The horizontal LAPS G (E) corresponds to a sequence of events where activity in ROI₁ leads by 10 ms (lags by 50 ms) the activity in ROI₂. The slanted LAPS H represents events where the activity in ROI₂ is fixed, but that of ROI₁ varies. The dashed line through H corresponds to events at fixed latency for ROI₂. It is clear that even if we had considered the activity in single trials of ROI₁ and ROI₂ but only separately, the distinct nature of events contributing to LAPS E and H would not be differentiated. The much broader perspective of MI analysis shows that events E and H correspond to different processes.

Figure 3.

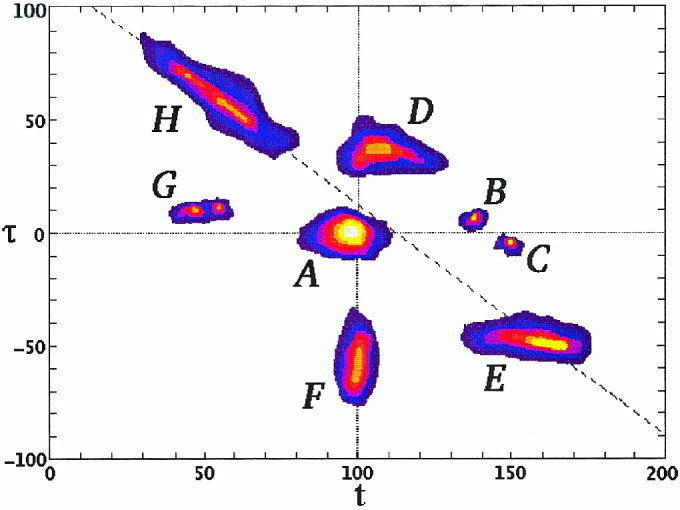
A display to demonstrate different cases of MI maps between two ROIs (see text for details).

Statistics, significance, and relevance

In our earlier work [Kwapien et al., 1998] we compared the standard definition for MI with the Renyi generalization for various q values, demonstrating that the generalised version with higher q values (e.g. q = 4 or 8) provides a much more sensitive amplification of the peaks of MI compared to the standard version. The increased sensitivity comes at a cost—the already difficult problem of assigning statistical significance to a given MI value becomes worse as some of the “nice” properties of the standard MI (like nonnegative values) are sacrificed for the extra sensitivity to the strong correlations.

Surrogate analysis provides some measure of merit and it can be performed in a number of ways. In our earlier study [Kwapien et al., 1998] we shuffled the time series so that the computation of the MI was performed from time series belonging to different single trials. In this work we have tested shuffling the phase of the Fourier coefficients and found that the resulting maximum MI values are typically 10 to 20% lower than the ones in the real data; the maxima are spread more uniformly in the (t, τ) plane and less reproducibly across runs. We have also used the test statistic Z_H on some of the data to confirm that most prominent maxima with of MI are significant in the case of ordinary MI (q = 1), which unfortunately does not extrapolate to the generalised MI [Roulston, 1997]. These tests, together with the earlier MI computations for the simpler comparison between left and right auditory cortex for five subjects [Kwapien et al., 1998], provide some guidance about the values of MI that are likely to be significant. Using the auditory examples as guidance and allowing for the use of the Renyi generalization (q = 4) we arrive at a value of 0.4 as a reasonable threshold for significance provided we have 25 or more single trials available for the MI computation. In all the results we will display we have used 0.45 as the minimum threshold while emphasizing cases with many single trials.

For an intuitive understanding of the problem consider the MI computation for a pair of areas computed from small segments drawn from one time series from each area. Let us assume that the activity in each area is completely independent of the activity in the other, and that on average there is just one event occurring randomly within each time series. As we move the segments relative to each other, the two events will be captured in one or more paired segments (depending on the relative temporal sizes of events and segments) and for the corresponding (t, τ) region(s) a very high MI value will be computed. The use of more time series will introduce new random artificial linkages but increasingly more evenly spread across the (t, τ) plane with corresponding reduction of the maximum MI. In contrast, and ignoring effects due to habituation and plasticity, LAPS reflecting true linkage with well‐defined underlying processes will converge to islands of high MI values with well‐defined boundaries. The net effect of using more time series will be the reduction of the size of spurious LAPS until eventually the background settles to a uniform level. Therefore, a sufficiently high threshold will completely eliminate the uniform background generated by random coincidences of events and leave only the LAPS corresponding to true linkages riding above the background. In the case of MI values for objects where each computation draws from about 30 separate trials for each object, and especially in the case of conjunctive LAPS where common areas of high MI are identified in the (t, τ) plane, the chance occurrence of even tiny islands of high mutual information is very small, and therefore even tiny LAPS are significant. We will use this later to extract information about feed‐forward and feedback activity from the time ordering of C‐LAPS of small size and even from the shape details of the dominant C‐LAPS. In contrast, the significance of any one island of high MI in the case of individual emotions is limited because there are only a few single trials available for each emotion. Although one should not assign too much importance to individual S‐LAPS, the presence of ordered pattern in the overall distribution might be significant. Chance coincidences will produce random coverage of the (t, τ) plane, which is distinctly different from the ordered arrangement of LAPS in Figure 3, which were designed with physiological plausibility in mind.

RESULTS

Behavioural data

In Experiment 1 all subjects accomplished task 1 accurately without any difficulty, but the accuracy for task 2 was much lower. The range of correct responses from the four subjects was between 60% and 93%. This is considerably higher than the chance level 16.7% of a six‐alternative task, showing that the subjects were really engaged in the task. The subject used in the MI analysis scored 64% and 78% in experiments 1 and 2 respectively. The subject had therefore reasonably stable responses across the MEG systems and was typical among the subjects used for the experiment.

Earlier average and single trial analysis

The analysis of the average data from the four subjects studied with the twin system (Experiment 1) has been reported elsewhere [Streit et al., 1997, 1999]. A precise identification of areas was not attempted because of the limited sensor coverage. The cortical folding may differ from subject to subject so the placement of the 37‐channel dewar could only be estimated to be optimal for any one given region. Regions in the superior temporal cortex (an area covered well in Experiment 1) were identified in all four subjects, which were activated more for faces than for other objects in run 1. Temporal and frontal areas were identified which responded stronger to faces in runs 2 and 3 (when the judgement of facial expressions was required) than in run 1. Despite the limitations endowed by the limited sensor coverage, the areas identified were broadly consistent across the four subjects in terms of their spatial location and even more so in terms of the timing of activations.

An accurate localisation was possible for a much wider area in Experiment 2, thanks to the whole head system. The automatic identification of ROIs was applied to the MFT solutions of the average signals from different conditions, producing 28 ROIs in each hemisphere. For each of these 28 ROIs, activation curves were computed for both the average and single trial signals. The single trial activation curves show that in single trials the stimulus induced activity in each ROI is only a small part of ongoing activity, which agrees with our earlier work in the auditory system [Liu et al., 1998a]. Averaging separates out aspects of the evoked responses time‐locked to the onset of the stimulus, but a lot more information contained in the activations of single trials is lost in the process. Statistical methods specifically developed for single trial MEG analysis [Liu et al., 1998b] have been applied to the set of single trials from a given ROI obtained from the whole head system [Liu et al., 1999]. This area‐by‐area single trial analysis revealed no face‐specific area as such but instead, areas like the FG were significantly activated by all complex objects at roughly similar latencies and varying strengths. The amygdala activity was significantly different between 150 and 180 ms for fearful expression, and even earlier for happy expression. The analysis showed further that in the fear condition the AM activation after 100 ms interfered with the FG activation, which was delayed until the AM activity subsided. Understanding regional interactions requires the analysis of relations between time series rather than the analysis of single trials from each ROI separately. The MI study to be described next considers pairs of activations and it is therefore the first step in this direction.

Mutual information

Figure 4 shows plots for the MI between PCS and FG; for run 1, all trials from the same object are pooled together in one category (a,b), and for runs 2 and 3, all trials from each emotion are pooled together in one category (c,d). Colour is used to code the average MI values (averaged across categories), which produce a L_a map in the (t, τ) plane. In the same figure the boundary of L_c common to all categories is marked by a white thick solid contour. The ranges of the MI values for each category are printed in the lower left part of each figurine. The negative values are a consequence of using Renyi parameter q = 4. For the computation of the L_a and L_c, only positive values were considered and renormalised so that the maximum of each category was unity. The same category normalisation procedure was adopted for all figures. The threshold levels for the average were 0.45 (blue) and 0.6 (red). The threshold for the L_c contour was set to 0.45, i.e., all categories had value at least 0.45 the maximum (positive) value of the category. In terms of the usual MI definition (q = 1) the threshold level for each category would correspond to 0.8–0.9 of the maximum of each category.

Figure 4.

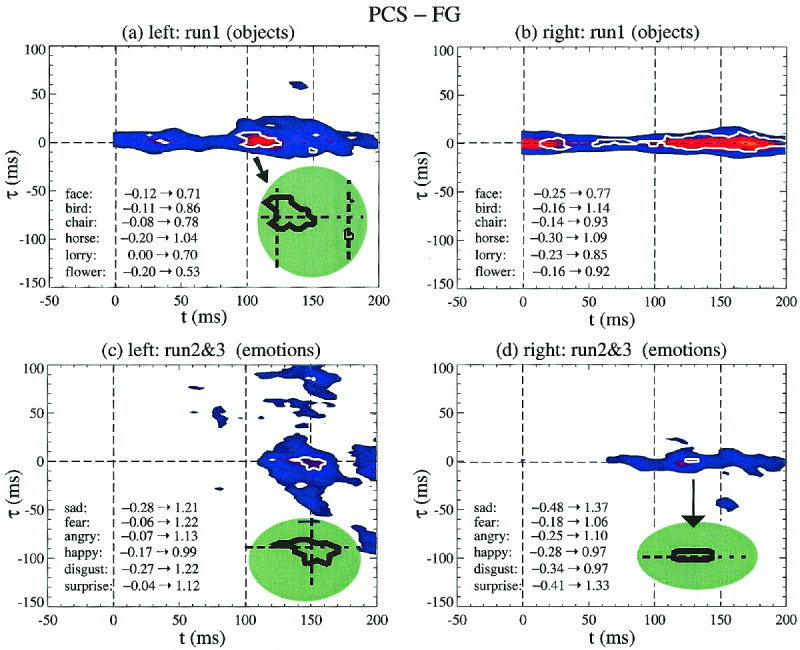
LAPS displays between PCS and FG: L_a is shown as colour‐coded averages of MI across categories with a thick white contour showing the boundary for the much smaller L_c. Objects are shown in (a,b) and emotions in (c,d), with left hemisphere on the left (a,c) and right hemisphere on the right (b,d). In a, c and d, the green‐shaded insert shows a magnified copy of the dominant L_c.

For objects the blue L_a contour corresponding to the lower threshold value (0.45) extends over all latencies within a latency delay window of 10–15 ms on either side of zero; there is a slight bias for positive values (PCS leading) in the left hemisphere. The strongest average MI values are encountered after 100 ms, from about 100 to 180 ms on the left and from 110 to 190 ms on the right. The L_c contour is distinctly different in the two hemispheres. On the right the L_c for objects extends over the entire latency range, except for a small period between 30 and 60 ms, with no clear directional preference. In contrast on the left, there is one main island of high L_c values from about 90–25 ms. A closer look (green‐shaded insert in Fig. 4a) shows that at the early part of the main L_c lies more in the upper (t, τ) plane suggesting an early feed‐forward flow of information from PCS to FG; at 150 ms the small L_c island is firmly in the lower half of the (t, τ) plane, indicating a top‐down activation from FG to PCS. In each case the peaks are at delays of 5–10 ms, consistent with monosynaptic transmission of information.

For emotions the main region of high average MI on the left hemisphere (Fig. 4c) is in the latency range from 110 to 160 ms, with a delay spread that is symmetric early on (110–130 ms) but becoming more biased toward negative delays (FG leading PCS) for moderate delays (below 50 ms). Positive delays above 50 ms are also encountered (PCS leading FG). On the right hemisphere the L_a extends from 70 ms to the end of the shown range (200 ms). There is one main L_c island from 130 to 160 ms and one much smaller L_c region on the right (around 130 ms). The green shaded inserts in Figure 4c and 4d show, respectively, blowups of the main L_c islands on the left and right hemisphere. Once again we observe the same distinctly different behaviour on the left and right hemisphere: on the left the main L_c island begins as a feed‐forward linkage turning round to a feedback linkage by 150 ms, while on the right no change is observed to an initial small feed‐forward bias.

The shape and location of the L_a and L_c islands in the (t, τ) plane suggest that two types of processes are in operation in this period. The first is near coactivation that spans long periods, present in both the left and right hemisphere and best seen in the low threshold L_a bands around the zero delay axis in the object runs (Fig. 4a,b). The second type of process is a cascade of activity anchored around the main L_c island and in the cases shown confined to the left hemisphere. The best example is furnished by the blue (low threshold) L_a bands of the emotions run in Figure 4c: the vertical band (fixed PCS latency around 150 ms) is a predominantly feed‐forward linkage (denser part of the band in the upper half of the (t, τ) plane), while the diagonal band (fixed FG latency around 125 ms) is primarily a feedback linkage (denser part of the band in the lower half of the (t, τ) plane). We have also computed the MI for all other pairs of regions for run 1, but no other L_c or even L_a has been identified at the threshold levels used above. The category‐specific LAPS between the PCS and FG for objects (not shown) show a separation of different objects in the right hemisphere—a diagonal band (fixed FG latency of about 160 ms) in the S‐LAPS begins with L${}_{\text{faces}}^{\text{s}}$ at PCS latency of 110 ms (PCS leads FG by 50 ms), with S‐LAPS for all other objects separated in the lower half of the (t, τ) plane, i.e., via a feedback linkage from FG to PCS.

Figure 5 shows category specific L_s and L_a displays for face affect recognition (runs 2 and 3), with both thresholds set to 0.6. LAPS with very high average MI values between PCS‐FG across emotions occupy a small part of the (t, τ) plane and are shifted to slightly later latencies compared to the simpler task of object recognition of run 1. Further, for PCS‐FG no clear separation of emotions is observed. The overlap is greater in the left hemisphere. In contrast for FG‐AM vertical and diagonal bands are evident in L_s corresponding respectively to constant latencies for FG or AM. The different emotions are still not very well separated on the left, while on the right the separation is almost complete. No region of high average MI value is seen for FG‐AM even if the threshold is reduced to 0.4. The small number of trials for each emotion reduces the significance of any individual L_s island. The clustering of the islands along vertical and diagonal bands on the other hand is unlikely to be the product of random coincidences of (lagged) events in the two areas.

Figure 5.

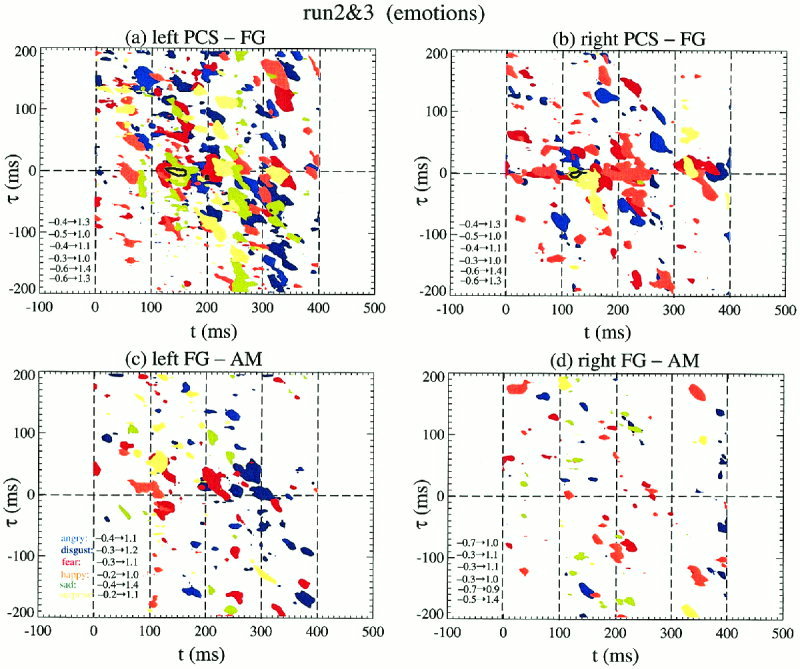
L_s and L_a displays for the face affect recognition runs 2 and 3. The results for PCS‐FG are shown in (a,b) and for FG‐AM in (c,d). Each emotion in the L_s display is allocated a different colour and the heavy black contour delineates the islands with high L_a values (only present in PCS‐FG).

The task specificity for faces is explored in Figure 6, through the L_a and L_c maps produced by pooling together into one category for each run all trials with faces. The results for PCS‐FG are in parts (a–d) and for FG‐AM in (e–h). We display in parts (a, b, e, and f) the L_a and L_c maps obtained from both tasks (runs 1, 2, and 3) and in the rest (c, d, g, and h) we pool together only the more demanding face‐affect recognition task (runs 2 and 3). The PCS‐FG linkage is very robust across the two tasks, with almost complete identity between the L_c maps on the right hemisphere. Overall in the left hemisphere the peaks in MI values are found in the same places across the two tasks, but the extend and actual peak values increase for the emotion recognition task. In contrast comparing the object and face affect recognition task on the right hemisphere peaks are encountered at new regions in the (t, τ) plane and the actual overall MI maximum value does not consistently increase for the emotion task. In fact, for some cases the overall MI maximum is considerably lower.

Figure 6.

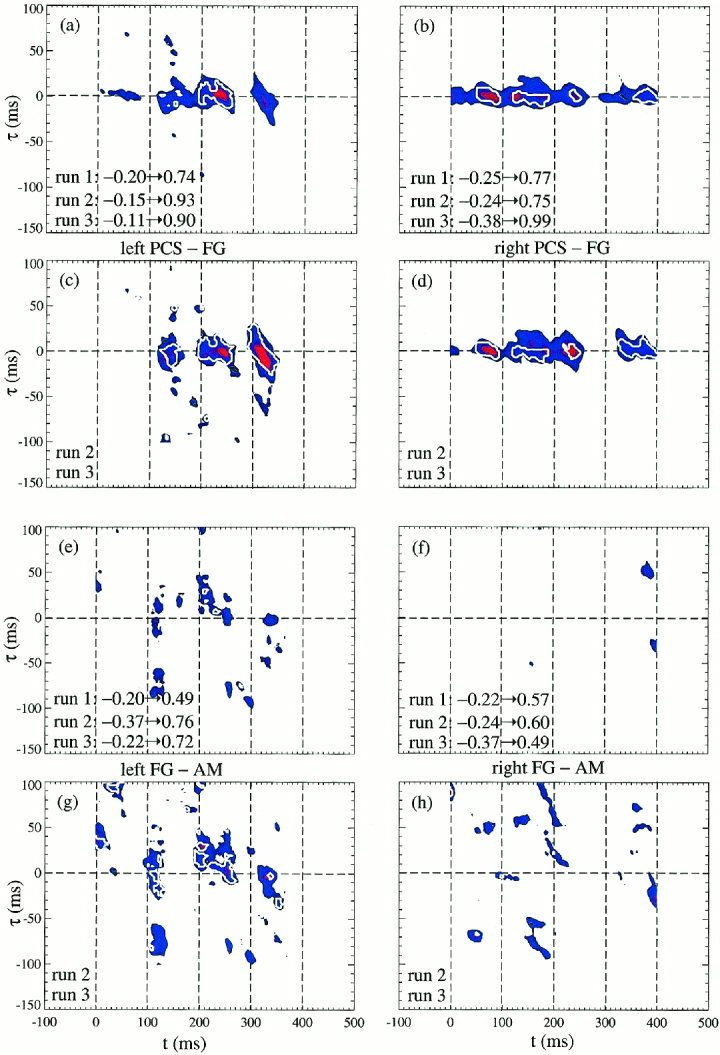
L_a (colour‐coded) and L_c (white thick contour) displays for all face stimuli grouped as one category for each run. The top quartet (a–d) shows the PCS‐FG results, while the lower quartet (e–h) shows the FG‐AM results. In each quartet the top pair uses the results of all runs. The lower pair in each quartet uses only the face‐affect recognition runs 2 and 3. The MI analysis has identified processes with short delays, just a few milliseconds, consistent with monosynaptic connectivity.

DISCUSSION

In recent years the discussion about how the information from specialised areas is pooled together has been dominated by the search for the big center or the key oscillation. It has been argued that the integration/awareness process may involve specialised neurons that although may be spread over the cortex [Crick and Koch, 1990, 1995] they must eventually project to executive regions in the frontal lobe. It has also been argued on theoretical grounds [von der Malsburg and Schneider, 1986] and experimental evidence that the “binding” of different regions is achieved by gamma band oscillations [Llinas, 1990; Singer and Gray, 1995] or synchronous bursting activity [Lisman, 1997].

We prefer as others have done recently [Dehaene et al., 1998] to address the same broad questions without explicit reference to consciousness and binding at this stage. We have employed a two‐step approach: first we used MFT to disentangle the activations in distinct cortical regions from the single trial MEG signal and to estimate the activation traces in each region. Second we computed the mutual information for pairs of activation curves, establishing a quantitative estimate of linkage with solid theoretical foundation.

Before discussing further the implications of our results we must address some legitimate concerns regarding the analysis methods and the reliance on data from a single subject. It is well known that the biomagnetic inverse problem has no unique solution. It may therefore appear presumptuous to develop an edifice founded on localisations of activity from single trial MEG signals. We have addressed this problem already [Ioannides, 1994; Liu et al., 1998a] showing that although the nonuniqueness problem looms large in the theoretical arena, in practice the remaining uncertainty after introducing reasonable constraints is small. There is ample empirical support provided by MFT analysis of computer generated data and numerous experiments, including one with implanted dipoles in humans [Ioannides et al., 1993]. Support directly relevant to the work presented here is provided by the earlier region‐by‐region MFT analysis of the same data using average [Streit et al., 1997, 1999] and single trial signals [Liu et al., 1999]. Both studies identified activity in the same regions as seen in similar PET and fMRI studies and at latencies consistent with results from animal experiments. From the theoretical point of view it has been recently shown that MFT possesses the expected properties for localized distributed sources [Taylor et al., 1999]. The purist who is still unconvinced can think of MFT estimates as a signal transformation describing the activity in a specific region much better than any one MEG channel.

The other criticism that might be levied against this study is that only one subject has been used. The data presented in this paper are from a subject who was not exceptional in any way we could trace on the basis of comparisons of performance, average signal and MFT estimates across subjects, and experiments in our earlier works; this is a minimum requirement but not a fully satisfying response to this very justifiable concern. In practical terms the single subject nature of the study was dictated by the demands of the computation—the analysis even for a single subject has been a computational mammoth task. The MFT and activation curves for all single trials and ROIs had to be computed before the equally computationally expensive MI analysis was carried out. There is also a methodological defense based on an expectation that the details of the dynamic interchanges between regions are unlikely to be replayed unchanged in every subject. It is likely that the patterns of MI distribution for different categories on the (t, τ) plane might depend on each individual's genetic makeup and biological and psychological history. If this is so, measures are needed with appropriate statistical analysis to encapsulate the commonality of the dynamics as revealed by our MI analysis. It is easier to identify some of the relevant properties through thorough single subject study, avoiding the extra complication which intersubject variability will no doubt introduce. The necessary extension to many subjects is then easier to make after some of the key features to look for are identified and targeted. This we have achieved: we anticipate that at least some of the systematic linkage we have identified in this one subject, like the feed‐forward and feedback sequences and the separation of object and emotion categories in the different linkages, will also be encountered in other subjects.

The MI analysis has identified a twin elaboration of processing—a spatially based segregation into specialized areas and a coupled separation of processing of different categories in the time characterizing strong linkage of activity between areas. The first observation is in agreement with what has been reported in numerous recent studies. Early processing in the primary and association visual areas is followed by activation of the fusiform gyrus, which in both this and our earlier analysis [Liu et al., 1999] is seen to be activated in a similar way both for complex objects in general and faces in particular. Face specificity is observed in the interval 100–200 ms if one makes a direct comparison between the FG activations elicited by single trials for faces and the corresponding activations for all other objects [Liu et al., 1999]. Face specificity in terms of our MI analysis shows up as the only feed‐forward branch of the first main band in the PCS‐FG LAPS of the right hemisphere, a strong hint for an early, automatic face‐specific processing.

The MI analysis has identified processes with short delays, just a few milliseconds, consistent with monosynaptic connectivity; these are best seen in the C‐LAPS of the left hemisphere, where the main L_c island is characterised by an initial feed‐forward monosynaptic linkage turning to a feedback monosynaptic linkage a few tens of millisecond later. Linkages with long delays, many tenths of milliseconds, are best seen as vertical and diagonal bands in the low threshold L_a contours. Category separation is seen on the right hemisphere, in the PCS‐FG linkage for objects and in the FG‐AM linkage for emotions. We note also that the analysis of the behavioural data of this subject showed that sadness wrongly labeled as fear was the most common mistake during the face affect recognition task. In displays of category (with no renormalisation to unity for each category), the same two emotions, fear and sadness, had overlapping peaks. The statistical analysis of the activation curves of each area has also revealed similar activation in the amygdala for fear and sad condition [Liu et al., 1999].

In an earlier study, analysis of the average signals demonstrated a reactivation of the FG in the more demanding task of recognizing the facial expression [Streit et al., 1997, 1999]. The more extensive single‐subject, single‐trial studies suggest that such a reactivation might be a refinement in processing accomplished by reorganization of activations within and between areas. Figure 6 is consistent with the notion that an increase in task complexity induces augmented linkage between areas already predisposed and at times already identified in the simpler tasks.

What appears as a noisy pattern when a single channel or a single area activation is observed from trial to trial, is seen to be less so when the activations between regions, across single trials, are examined for a given subject. Instead, a spectrum of dynamic activity is revealed, ranging from changes in specific areas to reorganization of the sequencing of activations and a novel spread of specialization in space and time. Function is segregated within areas at well‐defined but not too rigid windows. Across these areas, linked activity emerges fairly early (100–200 ms after stimulus onset), which initially is coincident (within a few milliseconds) in areas receiving direct sensory input and their immediate neighbors. Away from the primary sensory areas linked activity extends to longer latencies and it involves increasingly longer delays. The dispersion in time is not random, it seems to provide an ingenious way of elaborating cortical processing. It is evident that much of this dynamic organization can not survive averaging of signals across repeated trials or time. It is unclear what a grand average across subjects achieves, beyond highlighting the temporal contingencies imposed by anatomical invariance and associated constraints.

In our experiment, it seems likely that the average picture of the spatiotemporal evolution of events has missed an aspect of task‐specific directed attention, perhaps related to successful performance. Even if alternative interpretations of this phenomenon are plausible, its appearance in all the trials examined highlights the need for single‐trial analysis. The statistical confidence which multi‐trial averaging engenders can be bought at the expense of understanding the significant neural correlates of task‐specific processes. By focusing on the responses of one normal subject (eliminating concerns about varying anatomy and strategy in different individuals) in detail, we have been able to study the spatiotemporal evolution of brain activity throughout an entire cognitive task. In so much as both task‐specific and trial‐specific brain processes can emerge in such single trial analysis, this approach may move us closer to a genuine appreciation of how a real brain operates from moment to moment to achieve a given aim.