Functional connectivity as revealed by spatial independent component analysis of fMRI measurements during rest

Abstract

Cortical functional connectivity, as indicated by the concurrent spontaneous activity of spatially segregated regions, is being studied increasingly because it may determine the reaction of the brain to external stimuli and task requirements and it is reportedly altered in many neurological and psychiatric disorders. In functional magnetic resonance imaging (fMRI), such functional connectivity is investigated commonly by correlating the time course of a chosen “seed voxel” with the remaining voxel time courses in a voxel‐by‐voxel manner. This approach is biased by the actual choice of the seed voxel, however, because it only shows functional connectivity for the chosen brain region while ignoring other potentially interesting patterns of coactivation. We used spatial independent component analysis (sICA) to assess cortical functional connectivity maps from resting state data. SICA does not depend on any chosen temporal profile of local brain activity. We hypothesized that sICA would be able to find functionally connected brain regions within sensory and motor regions in the absence of task‐related brain activity. We also investigated functional connectivity patterns of several parietal regions including the superior parietal cortex and the posterior cingulate gyrus. The components of interest were selected in an automated fashion using predefined anatomical volumes of interest. SICA yielded connectivity maps of bilateral auditory, motor and visual cortices. Moreover, it showed that prefrontal and parietal areas are also functionally connected within and between hemispheres during the resting state. These connectivity maps showed an extremely high degree of consistency in spatial, temporal, and frequency parameters within and between subjects. These results are discussed in the context of the recent debate on the functional relevance of fluctuations of neural activity in the resting state. Hum. Brain Mapp. 22:165–178, 2004. © 2004 Wiley‐Liss, Inc.

Abbreviations.

COI

component of interest

CoM

center of mass

GLM

general linear model

ICA s‐/cb‐

independent component analysis spatial‐/cortex‐based

MP‐RAGE

magnetization prepared rapid gradient echo

NoV

number of voxels

PCA

principal component analysis

pCC

posterior cingulate cortex

preC

precuneus

SMC

sensorimotor cortex

SPC

superior parietal cortex

TE

echo time

TR

time of repetition

VOI

volume of interest

INTRODUCTION

Functional neuroimaging is being applied increasingly to issues of connectivity and communication between distant areas of the brain. Whereas functional connectivity refers to the correspondence over time between spatially distinct neurophysiological events without implying any notion of directionality, effective connectivity refers to the influence one brain region exerts over another [Friston, 1996]. Functional connectivity can be assessed by cognitive or motor tasks [Friston, 1996; Goebel et al., 1998], but can be extracted also from spontaneous activity of the resting brain. In the latter case, a network of functional communication between areas is revealed when their ongoing activity is not altered through task or cognitive demand. Compared to task‐related functional connectivity, resting state connectivity patterns probably depend more on a common neural modulator (e.g., thalamic input into cortical regions) or inherent neurophysiological properties of cortico‐cortical interaction (e.g., synchronized spontaneous neural firing). With electroencephalography (EEG) [Tucker et al., 1986] and direct neuronal recording [Fries et al., 2001; Leopold et al., 2003], it has been documented that during resting states, cortical neurons belonging to specific but spatially separated functional clusters show correlated patterns of spontaneous activity over time. Distinctive spatial distributions of correlated interhemispheric activity have been found for motor, auditory, and visual cortices [e.g., Shen et al., 1999; Tucker et al., 1986]. Such functional connectivity maps may provide insights into the anatomical‐functional relations that are not modulated by cognitive or motor task performance [Greicius et al., 2003].

The functional connectivity of the resting brain has also been studied with functional magnetic resonance imaging (fMRI). The blood oxygen level‐dependent (BOLD) signal of fMRI has been confirmed to reflect neural activity [Logothetis et al., 2001], which is a prerequisite for the assumption that BOLD signal functional connectivity maps may represent correlated neural activity of spatially segregated brain regions [Leopold et al., 2003]. Caution is needed, however, when interpreting functional connectivity in fMRI because many other metabolic processes and local hemodynamic properties at various time scales may contribute to the structure of BOLD signal fluctuations [Mitra et al., 1997].

The traditional method to assess functional connectivity maps for a specific region of interest in fMRI is the “seed voxel” approach. One or a small cluster of voxels is chosen, whose (averaged) time course serves as a reference model for cross‐correlation analysis with the remaining brain voxels, yielding a spatial zero‐lag cross‐correlation map [Biswal et al., 1995; Goebel et al., 1998]. The seed voxel can be selected using anatomical (e.g., gyral or sulcal landmarks) or functional knowledge (e.g., centre of mass of clusters of statistical maps). Using this approach, functional connectivity maps depicting bilateral auditory [Biswal et al., 1996], visual [Lowe et al., 1998], and motor cortex [Cordes et al., 2001; Lowe et al., 1998; Xiong et al., 1999] that match statistical maps of sensory or motor tasks have been obtained and replicated. In addition, it has been reported that low‐frequency oscillations in the range of 0.1 Hz or lower contributed most to the temporal structure of the auditory, visual, and sensorimotor functional connectivity maps [Cordes et al., 2001].

The seed voxel approach has some inherent caveats. Firstly, the cross‐correlation map obtained depends highly on the strategies for choosing the seed voxel, which determine the reference model. In addition, for resting state analyses, the chosen model will contain a high but unknown degree of noise‐related fluctuations. Secondly, as an instance of the univariate GLM [Friston, 1996] the cross‐correlations are computed on a voxel‐by‐voxel basis, thus pairing one independent (seed voxel time course) and one dependent (time course of a remaining voxel) variable. This approach thus ignores the relations between multiple voxels.

Several multivariate, model‐independent methods have been applied to resting state data to circumvent the problems of the seed voxel approach. These methods do not depend on the choice of any seed voxel reference, but rather use the covariance matrix of all implicated voxel time courses as the starting point for analysis. Many of these methods, however, use a subset of cortical voxels to estimate functional connectivity networks. In this sense, hierarchical clustering has been used in resting state measurements to assess networks of functional connectivity [Cordes et al., 2002]. Clustering techniques generate clusters of variables based upon an index of similarity or difference that can represent absolute (e.g., Euclidean distance) or relative units (e.g., Pearson correlation). Unlike other clustering techniques, hierarchical clustering does not depend on a predefined number of clusters to be estimated. In the study by Cordes et al. [2002], clusters of interest were chosen according to low‐frequency contributions to the time course of the cluster centre, which yielded connectivity maps similar to those found with the seed voxel approach. Another approach to assess functional connectivity is principal component analysis [Friston et al., 1993]. PCA estimates a number of orthogonal components from the covariance structure that together explain a large part of the variance of the data. Although these methods could replicate the functional connectivity maps obtained with the seed voxel approach, they have some limitations. First, often a subset of brain voxels is chosen from which the covariance matrix is estimated, thus potentially biasing the analysis. Second, PCA considers only second order (and not higher order) relations between voxels and the time courses of the components are constrained to be orthogonal. A useful candidate method to circumvent these drawbacks is independent component analysis (ICA), a data‐driven, multivariate signal processing approach [Comon, 1994]. In the applications of ICA to fMRI data, the observed 4‐D signals are usually modeled as linear mixtures of unknown, spatially independent processes (e.g., BOLD fluctuations, head movements, artifacts, etc.), each contributing to the dataset with an unknown time profile [spatial ICA or sICA; McKeown et al., 1998; McKeown and Sejnowski, 1998]. The time series are decomposed into spatial components or modes (ICs) that each have a unique time course (TC). The decomposition process, for which different algorithms have been developed [Bell and Sejnowski, 1995; Hyvärinen, 1999], maximizes the spatial statistical independence of the components. It is important to note that the spatial independence of the components is a much stronger criterion than if the spatial maps, or eigenimages, were merely constrained to be orthogonal (as in PCA). In this sense, sICA can be considered as a generalization of PCA, with the other prominent distinction that sICA, in contrast to PCA, does not constrain the time courses of the components to be mutually orthogonal.

Spatial ICA has been applied to resting state data of anesthetized child patients by Kiviniemi et al. [2003]. These authors were able to identify components in sensory and motor cortices and large vessels. The frequency analysis of parenchymal time courses showed a dominant peak at 0.03 Hz. ICA has also been applied to resting state data of the adult human brain [Biswal and Ulmer, 1999], but no thorough analysis of functional connectivity patterns was reported. We apply this method to fMRI data of healthy adults to study resting state functional connectivity of the non‐anesthetized human brain. We show that spatial ICA can be used to assess functional connectivity within and across hemispheres in sensory and motor cortices, as well as in several parietal and frontal regions. In addition, we assess the degree of reproducibility of these functional connectivity maps within and between subjects, by analyzing their spatial layout and their temporal profile.

SUBJECTS AND METHODS

Subjects

Seven healthy subjects with no history of neurological or psychiatric disorder participated in the study (four men; mean age, 28.6 years; age range, 22–39 years). Two subjects were predominantly left‐handed, the remaining were predominantly right‐handed, as assessed using the Edinburgh Handedness Inventory [Raczkowski et al., 1974]. The aim of the study was explained to the subjects and all subjects gave written informed consent before measurement. Before functional and anatomical measurements, the subjects were told to relax but remain awake, keep their eyes open and just to “let your thoughts go as they come.” Subjects were asked between and after sessions whether they were awake during the previous session. All subjects confirmed that they were.

Imaging Sequences and Parameters

Functional and anatomical measurements were conducted on a 1.5 T Magnetom Vision MRI Tomograph (Siemens, Erlangen, Germany) using an echo‐planar imaging (EPI) sequence for functional imaging (1 volume = 12 axial slices, number of volumes = 400, TR/TE = 1,500/60 msec, field of view = 220 × 220 mm², voxel size = 3.2 × 3.2 × 6.0 mm³). Each functional session lasted 10 min. For each subject, a T1‐weighted MP‐RAGE sequence was run to obtain an anatomical reference (voxel size = 1.0 × 1.0 × 1.0 mm³, field of view = 256 × 256 mm²), which lasted approximately 5 min. To prevent large head movements, the subject's head was fixed by placing foam pads on each side of the head within the head cage. For each subject, the session began with one functional measurement of resting state, followed by an anatomical measurement, which was followed by a second functional measurement. Functional imaging was carried out in complete darkness, and subjects were told they should keep their eyes open to prevent them from falling asleep during the measurements. Subjects were also instructed explicitly to move as little as possible.

Functional Connectivity Analysis

Analysis of the measured BOLD signals was carried out using the BrainVoyager 2000 v. 4.8 analysis software (online at http://www.brainvoyager.com). The first four volumes of each functional dataset were discarded from analysis because of magnetic saturation effects. All functional datasets were preprocessed using interslice time correction and resampled in a standardized 3‐D space [Talairach and Tournoux, 1988]. Motion time courses were obtained by estimating the values for translation (mm) and rotation (degrees) for each of the 396 consecutive volumes. Of 14 measured datasets, 4 second‐run datasets were discarded because of head movements larger than 0.8 mm occurring over several consecutive volumes, as obtained from the motion time courses. Functional data from individual subjects were depicted on standardized anatomical volume and on inflated and flattened anatomical representations, following procedures described elsewhere [Kriegeskorte and Goebel, 2001; Linden et al., 1999]. Group data were superimposed on an anatomical brain template (courtesy of the Montreal Neurological Institute [MNI]).

Functionally connected patterns of activity were estimated using spatial ICA. Formally, the observed data were modelled as:

(1)

where X is the n × v matrix of the observed time courses (n = number of scans, v = number of voxels), S is the m × v matrix whose rows S_i are to be filled with the (unknown) realizations of the spatial components (m ≤ n = number of components), and M is the n × m “mixing” matrix, whose columns contain the time courses of the m components, and is assumed to be of full rank. In this model, all the spatial components, with the possible exception of one, are assumed to be non‐gaussian [Hyvärinen, 1999]. Structured (non‐gaussian) artifacts in the data (e.g., head movements, machine and physiological artifacts) are not modelled explicitly, but instead are treated as independent sources and are thus expected to be represented in one or more of the components.

The problem of the ICA‐decomposition of fMRI time series can be formulated as the estimation of both the matrices of the right side of equation (1), under the constraint that the processes S_i are (in the ideal case) mutually statistically independent. No a priori assumption is made about the mixing matrix M, i.e., about the time courses. The amount of statistical dependence within a fixed number of spatial components can be quantified by means of their mutual information [Comon, 1994]. The ICA decomposition of X thus can be defined (up to a permutation of the components, a multiplicative constant and to the sign) as a linear transformation:

(2)

where the matrix W (the “unmixing” matrix) is determined such that the mutual information of the target components S_i is minimized. Matrix M can be computed as the pseudo‐inverse of W.

Different ICA algorithms use different strategies [see Hyvärinen, 1999 for review and Esposito et al., 2002 for an empirical comparison of the two ICA algorithms used most commonly in fMRI data analysis]. Here, the 4‐D functional datasets were decomposed using the cortex‐based sICA methodology [cbICA; Formisano et al., 2001, 2002a] that uses a fixed‐point ICA algorithm [FastICA, Hyvärinen, 1999] as implemented in http://www.cis.hut.fi/projects/ica/fastica/. The cortex‐based approach restricted the ICA to a subsample of the voxel time courses belonging to the cortical sheet, thus reducing the data by 65–70%. This approach was justified because we were interested primarily in cortical functional connectivity, without restricting the analysis to specific functionally specialized cortical regions. The FastICA algorithm minimizes the mutual information of the components using a robust approximation of the negentropy as a contrast function and a fast, iterative (non‐adaptive) algorithm for its maximization [for a detailed description of the FastICA algorithm, see Hyvärinen, 1999]. After sphering the matrix X and reducing the dimensionality of each dataset to 200 components using PCA, the hierarchical (deflation) mode of the FastICA algorithm was used and all the components were estimated one‐by‐one. The relatively high number of dimensions (200) was selected to preserve the original structure of the data (the reduced dataset included more than 99% of the original variance), as an excessive reduction of the dimensionality could negatively affect the ICA decomposition [McKeown and Sejnowski, 1998].

After the decomposition, voxel values of the ICA spatial maps were Z‐transformed and color‐coded according to absolute value and sign. For visualization, maps were thresholded by Z‐value (|Z| ≥ 2.2), and cluster size (>200 mm³), using a 3‐D six‐neighbor clustering algorithm [Pratt, 1991]. It should be noted that the Z‐values do not pertain to any significance statistic, because no comparison is made to a null distribution. Clusters of voxels within a component map that survived the thresholds were considered as clusters of functionally connected voxels. After component generation, the component maps were analyzed further in the space and time domains using custom software developed in MATLAB 6 (MathWorks, Natick, MA).

Post‐Hoc Analysis of Components of Interest and Reproducibility Across Subjects

From the component decomposition of each dataset, a subset of components of interest (COIs) was preselected in an automated fashion using only spatial information, as contained within two sets of volumes of interest (VOIs; see Creation of Volumes of Interest). Before application of VOI templates, component maps were sign‐corrected. For each component, the mean of the absolute Z‐values of voxels that matched coordinates of the VOIs was calculated (mean Z in Tables I and II). The absolute rather than the signed voxel values were used to prevent cancellation of signs when averaging voxel values. The components with the three highest absolute mean values were selected for further analysis (referred to as COIs). This criterion was based on consistent findings that component maps with interesting spatial patterns fell within the small range of highest mean voxel values. In addition, each component time course was mean‐corrected, linearly de‐trended, and cross‐correlated with the six motion time courses. Components whose time courses were highly correlated (r > 0.5) with the estimated motion time courses were discarded from further analysis. This second selection criterion was used because we found that in most cases a subsample of chosen COIs contained contributions from movement artifacts. This second criterion resulted in a further reduction of the number of COIs per VOI by one or two components. The remaining COIs were then used for further analysis.

Table I.

Detection characteristics of the components of interest for the first volume of interest set comprising sensory and motor cortices for the first sessions

VOI		Subject no.
		1	2	3	4	5	6	7
Left SMC	Mean Z	1.87	1.86	2.11	2.61a	—	1.66	4.71
	Mean Z supra	3.83	3.46	3.41	4.40	—	3.60	5.96
	Nvox in	9.65	2.62	7.36	11.17	—	7.13	18.77
	Rank	1	2	1	1	—	2	1
Right SMC	Mean Z	2.24	4.19	2.67	1.94a	—	2.23	4.65
	Mean Z supra	3.61	5.16	4.35	3.78	—	3.68	5.33
	Nvox in	12.12	18.48	10.98	8.77	—	10.83	16.50
	Rank	1	1	1	1	—	1	1
Left AC1	Mean Z	1.62	1.31a	2.64	1.16	1.14a	1.36	1.63
	Mean Z supra	4.03	2.99	3.85	3.97	3.50	3.20	3.42
	Nvox in	10.26	7.14	19.85	3.92	5.03	8.61	12.37
	Rank	1	1	1	2	2	2	1
Left AC2	Mean Z	1.39	—	—	—	—	—	—
	Mean Z supra	3.35	—	—	—	—	—	—
	Nvox in	7.48	—	—	—	—	—	—
	Rank	3	—	—	—	—	—	—
Right AC1	Mean Z	—	1.20a	1.54	1.47	0.74a	2.19	1.67
	Mean Z supra	—	2.88	3.47	3.96	2.71	4.03	3.58
	Nvox in	—	6.72	11.13	9.68	4.54	14.95	10.42
	Rank	—	1	1	2	3	1	1
Right AC2	Mean Z	0.88	—	—	—	—	—	—
	Mean Z supra	3.06	—	—	—	—	—	—
	Nvox in	3.45	—	—	—	—	—	—
	Rank	3	—	—	—	—	—	—
PVC	Mean Z	2.90	1.18	2.82	2.82	3.18	2.95	1.63
	Mean Z supra	4.29	3.36	4.46	5.25	4.71	4.85	4.00
	Nvox in	41.95	11.66	50.59	32.78	45.20	51.69	23.27
	Rank	1	1	1	1	1	1	1

Maps were sign‐corrected across sessions.

^aLeft and right sensory or motor VOI selected the same component, indicating that the component map represented bilateral connectivity patterns, except where indicated (^a). SMC, sensorimotor cortex; AC, auditory cortex; PVC, primary visual cortex; mean Z, mean |Z| values of the voxel values captured within the respective VOI template; mean Z _supra, mean |Z| values of voxel values within VOI template that exceed the Z‐threshold of 2.2; Nvox in, percent of suprathreshold voxels within template; Rank, ranking position within the selected subsample of COIs (n = 3) for each VOI template.

Table II.

Detection characteristics of the components of interest for the second volume of interest set comprising parietal regions for the first sessions

VOI		Subject no.
		1	2	3	4	5	6	7
Left IPCa	Mean Z	1.70b	2.66b	1.06b	1.60b	0.85b	1.66b	0.98b
	Mean Z supra	4.48	4.30	4.26	3.83	3.28	3.88	4.11
	Nvox in	12.23	17.74	7.07	9.32	5.57	13.01	5.59
	Rank	1	1	2	1	2	1	3
Right IPCa	Mean Z	1.60b	3.37b	1.50b	2.67b	0.94b	2.38b	1.52b
	Mean Z supra	4.10	4.72	4.87	4.48	2.26	4.79	5.45
	Nvox in	8.87	19.47	8.39	16.60	8.79	15.69	4.99
	Rank	2	1	2	1	3	1	2
pCC	Mean Z	1.92	2.33	2.03	1.32	1.65	1.70	1.69
	Mean Z supra	4.54	4.45	4.10	3.27	4.06	3.97	4.98
	Nvox in	26.57	28.07	24.11	16.80	20.36	23.83	23.92
	Rank	1	1	1	3	2	1	1
pCC/preC1	Mean Z	1.797	—	−1.254	−0.376	1.733	0.760	1.127
	Mean Z supra	4.716	—	−3.362	−0.705	3.965	2.713	3.985
	Nvox in	24.93	—	18.64	19.50	20.79	18.69	13.53
	Rank	2	—	3	2	1	2	2
pCC/preC2	Mean Z	—	—	—	2.33	0.67	—	−0.33
	Mean Z supra	—	—	—	4.11	2.49	—	0.70
	Nvox in	—	—	—	31.23	11.41	—	12.33
	Rank	—	—	—	1	3	—	3

^aLeft and right inferior parietal cortex (IPC) components also included clusters in dorsolateral prefrontal cortex and frontal eye fields in the same hemisphere.

^bLeft and right parietal VOI selected the same component, indicating that the component map represented bilateral connectivity patterns, except where indicated (^b). pCC, posterior cingulate cortex; preC, precuneus; mean Z, mean |Z| values of the voxel values captured within the respective VOI template; mean Z _supra mean |Z| values of voxel values within VOI template that exceed the Z‐threshold of 2.2; Nvox in, percent of suprathreshold voxels within template; Rank, ranking position within the selected subsample of COIs (n = 3) for each VOI template.

To analyze the contributions of different frequency bands to spontaneous fMRI activity, a power spectrum analysis of the COI time courses was carried out. COI time courses were high‐pass filtered (cut‐off = 0.01 Hz), and their power spectrum density was estimated using Welch's method [see Childers, 1987]. In particular, we estimated the contribution of the extremely low to low frequencies [0.01–0.1 Hz; Cordes et al., 2001] to the overall spectral power, using methods similar to those described in Thomas et al. [2002]. We quantified the contribution of low frequencies to the overall power as the ratio between the estimated area under the power spectral curve in the frequency band 0.01–0.1 Hz and the estimated total area. Contribution values range between 0 and 1, with higher values indicating higher contributions of the low frequency band to the overall power.

The spatial overlap of COIs across subjects was verified using intersubject consistency maps that were computed based on data from the first measurement of each subject (n = 7). In these maps, the voxel value indicates in what proportion of subjects a voxel pertained to the COI in question. For instance, a voxel value of 1 indicates that the Z‐value at that voxel exceeded the threshold of Z = 2.2 in all subjects. The maps were thresholded at a minimum of three subjects (map value >0.29) and were superimposed upon the MNI anatomy template.

Reproducibility Within Subjects

For subjects who had two valid measurements (n = 3; Subjects 1, 4, and 6) the COI reproducibility was assessed by verifying the spatial overlap between corresponding COIs obtained in different sessions (spatial correlations between sign‐corrected maps) and by evaluating their cross‐spectral density using Welch's method [see Childers, 1978]. The similarity of the replicated COIs was verified also based on two component‐descriptive parameters: (1) the degree of clustering of suprathreshold voxels (number of clustered voxels/number of suprathreshold voxels) within the component maps, which served as an index of spatial structure for each component; and (2) the one‐lag serial autocorrelation coefficient of the COI time course, which served as a measure of temporal structure [Formisano et al., 2002a]. Both measures ranged from 0 to 1. It has been shown that COIs tend to possess a sparse and spatially clustered distribution of high Z‐values and have an intermediate to high temporal structure, which is reflected in intermediate to high values of these measures [Formisano et al., 2002a; van de Ven et al., 2002].

Creation of Volumes of Interest

To preselect COIs based on standardized anatomical or functional information, we created two sets of VOIs. The first set comprised VOIs of auditory, visual, and sensorimotor regions, which are often the regions of interest in resting state functional connectivity analysis. For the auditory cortex VOI, a probabilistic mapping of Heschl's gyrus, the putative site of primary auditory cortex, was used [Rademacher et al., 2001]. Such maps depict the probability for any anatomical voxel to belong to left or right Heschl's gyrus with respect to an anatomically averaged template. In our study, the probability level of the maps was thresholded at a minimum of 20% to capture the high anatomical and functional variability of the auditory cortices (left CoM: x = −40, y = −20, z = 8, NoV = 4,910; right CoM: x = 45, y = −13, z = 10, NoV = 4,541). For visual cortex VOIs, the area around the calcarine fissure was chosen (CoM: 0, −79, 1, NoV = 10,576). For the sensorimotor cortex VOIs, regions were chosen using anatomical landmarks (pre‐ and postcentral gyri) and functional activity clusters from a study that used button presses to identify periods of auditory hallucinations [van de Ven et al., 2002] (left CoM: −37, −24, 43, NoV = 3,732; right CoM: 41, −22, 52, NoV = 5,159).

The second set of VOIs was derived from functional and anatomical information, and comprised cortical regions within the parietal lobe: bilateral intraparietal sulcus region (IPS) (left CoM: −30, −60, 38, NoV = 6,592; right CoM: 28, −54, 45, NoV = 7,089) and the posterior cingulate cortex/precuneus (pCC/ventral preC) (CoM: −1, −47, 24, NoV = 13,319). These regions were used for a post‐hoc COI selection to detect parietal resting state networks. The addition of these VOIs to the sensory and motor VOIs reflects our interest in parietal regions, which we investigated in a number of studies of visuospatial paradigms [e.g., Formisano et al., 2002b; Trojano et al., 2000].

RESULTS

Volumes of Interest of Sensory and Motor Cortex

For each dataset, some of the three selected COIs per VOI template were discarded because they reflected contributions of artifacts (criteria are described above). In most cases, the VOI‐based preselection using the VOIs of sensory and motor cortices (first VOI set) yielded one COI connectivity map of the bilateral primary and secondary auditory cortex (AC), one map of bilateral visual cortex (PVC), and one map of bilateral SMC (Table I). Selection of the same component by the left and right sensory or motor VOI indicated that the component contained bilateral connectivity patterns. These COIs ranked highest in the VOI‐based selection (see Table I). In addition, these components were largely free from motion artifacts.

In one subject, no left or right COI of the sensorimotor cortex passed the selection criteria. In another subject, the left and right SMC were represented separately by two different COIs. The functional connectivity clusters for the left and right auditory cortex were represented separately by two different COIs in two subjects. For the first session of Subject 1, two bilateral auditory cortex components were selected. One COI was more centered upon Heschl's gyrus in both hemispheres, whereas the other COI incorporated regions in the anterior and posterior superior temporal gyrus. In the second session of Subject 1, only one COI for the auditory cortex was found, which was not a spatial summation of the two COIs from the first session. For all subjects, a COI was found with functional connectivity clusters that included the calcarine fissure in both hemispheres. Figure 1 shows the COI maps of auditory, visual and sensorimotor regions of one representative subject (Subject 6). These connectivity clusters showed a marked consistency of spatial characteristics among the various decompositions, as is reflected by the intersubject consistency maps in Figure 2. Surprisingly, a functional connectivity cluster centered on the middle and lower parts of the central sulcus (CS) was identified by the SMC or the AC VOI in most cases (see Fig. 2), although we did not explicitly create a VOI for the entire extent of the bilateral central sulcus. The detection of this region of connectivity can be attributed to the fact that SMC and AC VOI‐voxels extended into the top or lower end of the CS clusters, respectively (see Fig. 2).

Figure 1.

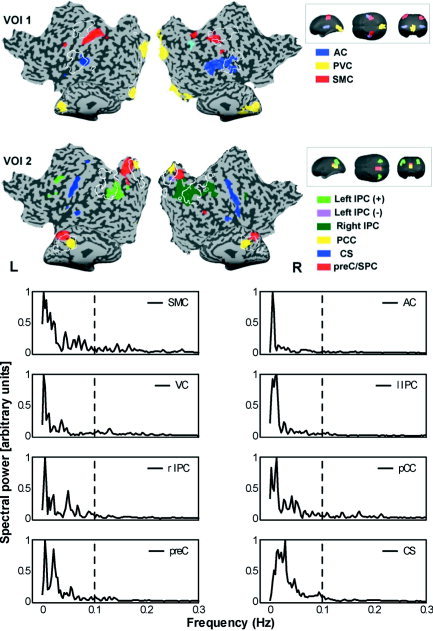
Upper panel: COIs obtained by using the first (VOI 1) and second (VOI 2) set of VOIs of Subject 6. Colors indicate the different COIs. White lines on flatmap indicate borders of VOI templates. Insets: VOI templates of first and second VOI set presented in glass brain format. Lower panel: Estimate of power spectral densities of the COI time courses (normalized according to maximum value of power), showing that highest powers are found within the low to very low frequency range (0.01–0.1 Hz). Broken line indicates 0.1 Hz. For explanation of abbreviations, see abbreviation list and text.

Figure 2.

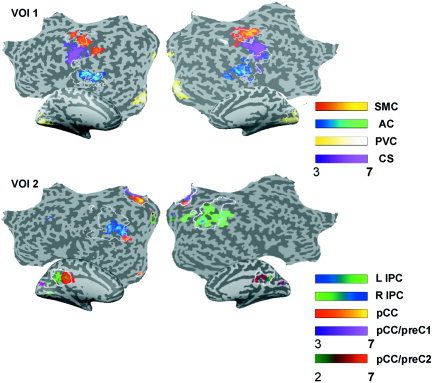
Intersubject consistency maps of first and second VOI set for the first session of all subjects. Maps are obtained by summing the suprathreshold voxels contained within the respective COIs across subjects, and divided by the total number of subjects. Map values range from 0–1, and are thresholded at >0.29. Maps are depicted on MNI template flatmaps. White lines on flatmap indicate borders of VOI templates.

Volumes of Interest of Parietal Areas

For the second VOI set, the pCC/ventral preC VOI selected one or two COIs comprising connectivity clusters in bilateral pCC/preC, and one COI connectivity map comprising preC and bilateral superior parietal lobule (SPL) in most of the decompositions (Fig. 1 and 2; Table II). The left and right IPS VOI selected one COI connectivity map comprising either the left or the right inferior parietal cortex (IPC) from most of the decompositions. The IPC connectivity maps consistently comprised small connectivity clusters in left or right dorsolateral prefrontal cortex (DLPFC) and frontal eye fields (FEF). In all cases, the COI for the IPC contained unilateral clusters, suggesting that these regions may not be connected functionally across hemispheres during rest.

Frequency Analysis of the Component of Interest Time Courses

The frequency plots for the COIs containing auditory, sensorimotor, and visual regions showed that the largest contributions to the frequency spectrum were within the extremely low range (0.01–0.05 Hz) of the component time course. Frequency plots for Subject 6 are presented in the lower part of Figure 1. For COIs selected by the second VOI set that comprised parietal regions, higher powers were observed for the higher frequencies. The contribution ratio of the spectral power in the frequency range of 0.01–0.1 Hz to the whole spectral range was estimated for the COIs of all first sessions. On average, all values exceeded the ratio of 0.4, which indicates that much of the spectral power is explained by the frequency powers of the low to very low range (Fig. 3).

Figure 3.

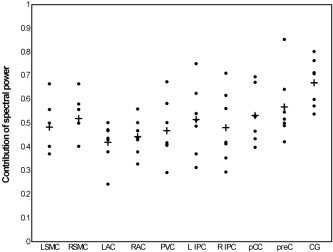
Dispersion plot of the contribution ratio of spectral power within the low to very low frequency range (0.01–0.1 Hz) for COIs for the sessions of all subjects (dots), and the average contribution for each COI (plus sign). L/R SMC, left/right sensorimotor cortex; L/R AC, left/right auditory cortex; L/R IPC, left/right inferior parietal cortex.

Reproducibility

In a post hoc investigation, we looked at the reproducibility of the COIs in spatial, temporal, and frequency domains within the same subject (n_subject = 3; Subjects 1, 4, and 6). COIs as identified by the sensory–motor and parietal VOI sets showed a high degree of spatial consistency across the two sessions of all three subjects (Table III). The upper part of Figure 4 depicts this consistency for Subject 1. The lower part of Figure 4 shows the consistency in frequency contributions of the COI time courses across the two sessions of the same subject in the form of cross‐spectrum densities. This overlap in spectral density was found for most reproduced COIs from the first and second session, which was reflected by the large contribution of extremely low frequencies to the COIs from the first VOI set (0.01–0.05 Hz), and low frequencies to the COIs from the second VOI set (0.05 Hz and higher; Table IV). The similarity of the first and second session COIs was also found in component‐descriptive parameters (degree of clustering of suprathreshold voxels and temporal structure of the COI time course), as is depicted in Figure 5. The pairs of COIs pertaining to similar anatomical regions can be found in close proximity in the plane defined by these component‐descriptive parameters. In addition, the component pairs can be found consistently in a specific quadrant (upper right) of the 2‐D plot, indicating that these components show a consistently high degree of spatial clustering of functionally connected voxels and that the time courses are highly structured.

Table III.

Intra‐subject spatial correlations

Subject no.	COI
	Bilateral AC	Bilateral SMC	PVC	Left IPC	Right IPC	pCC	preC	CS
1	0.45a	0.62	0.75	0.70	0.52	0.64	0.79	0.57
4	0.35	0.25a	0.67	0.54	0.62	0.26	0.80	0.48
6	0.26a	0.21a	0.69	0.75	0.83	0.79	0.71	0.66

Intra‐subject spatial correlations between the Z‐scored sign‐corrected spatial component of interest (COI) maps of Session 1 and 2 of Subjects 1, 4, and 6. All correlation values are highly significant (P < 0. 0001).

^aWhen in one of the sessions the left and right regions of interest were represented by two separate components, the sign‐corrected COIs were averaged into a single map. AC, auditory cortex; SMC, sensorimotor cortex; IPC, inferior parietal cortex; pCC, posterior cingulate cortex; preC, precuneus; CS, central sulcus.

Figure 4.

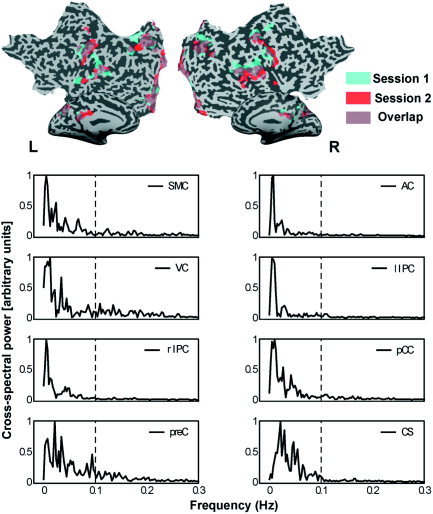
Upper panel: Spatiotemporal replication of COI functional connectivity maps of session 1 (blue) and 2 (red) of Subject 1. Overlapping regions are depicted in purple. For reference of the anatomical‐functional clusters, see Figures 1 and 2. Lower panel: Cross‐spectral densities for replicated COIs of Subject 1 are given for each of the paired COIs (normalized for maximum value). A high spectral density indicates high power for that frequency in both COI time courses.

Table IV.

Contribution ratio of spectral power within 0.01–0.1 Hz to the total spectral range of similar components of interest in the two sessions (S1 and S2) of Subjects 1, 4, and 6

VOI	Subject 1*		Subject 4		Subject 6		Mean
	S1	S2	S1	S2	S1	S2
Left SMC	0.40	0.36	0.50	0.25	0.40	0.61	0.42
Right SMC	0.40	0.36	0.50	0.25	0.40	0.49	0.40
Left AC	0.50	0.35	0.24	0.55	0.44	0.35	0.41
Right AC	0.50	0.35	0.56	0.55	0.44	0.59	0.50
PVC	0.29	0.38	0.58	0.32	0.67	0.75	0.50
Left IPC	0.62	0.37	0.49	0.57	0.54	0.45	0.51
Right IPC	0.35	0.51	0.29	0.49	0.71	0.38	0.46
pCC	0.40	0.45	0.67	0.39	0.53	0.49	0.49
pCC/preC	0.52	0.58	0.85	0.41	0.42	0.49	0.54
CG	0.76	0.79	0.71	0.59	0.80	0.83	0.75

^*Left/right auditory cortex (AC) components of interest (COIs) of Subject 1, session 1 (S1) is left/right AC1 in Table 1. SMC, sensorimotor cortex; PVC, primary visual cortex; IPC, inferior parietal cortex; pCC, posterior cingulate cortex; preC, precuneus; CG, central gyrus.

Figure 5.

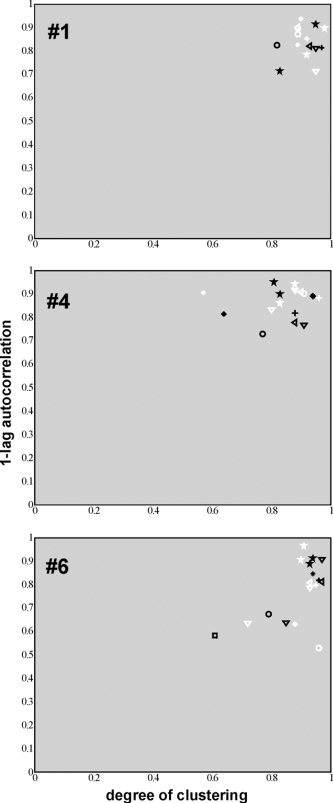
Scatter of the COIs of the first (white) and second (black) sessions according to a spatial (degree of clustering) and a temporal (absolute values of the one‐lag autocorrelation coefficient) measure. From top to bottom the plots are of Subject 1, 4, and 6. Asterisk, AC; plus sign, PVC; open circle, SMC; open square, CS; up triangle, preC; down triangle, pCC; left triangle, SPC; star, IPC/DLPFC.

DISCUSSION

We analyzed functional connectivity from resting state datasets with spatial cortex‐based independent component analysis. Using a VOI approach to automatically preselect a small number of components for further analysis, we found independent COIs for bilateral auditory, sensorimotor, and visual regions, as well as several parietal (preC, SPC, IPC) regions. Most of these components indicated a high degree of functional connectivity between homologous areas in the two hemispheres, presumably subserved by transcallosal connections. The left and right IPC regions, however, showed a consistent decoupling between hemispheres, whereas they were connected strongly to frontal regions (DLPFC/FEF) of the same hemisphere. Such a pattern has been reported in task‐related studies as well [Formisano and Goebel, 2003], suggesting that parietal homologous areas do not necessarily subserve homologous functions. Unexpectedly, for each subject ICA revealed a component map showing bilateral central sulcus connectivity stretching from motor cortices to inferior frontal gyri. Frequency‐power analysis of the COI time courses showed that extremely low frequencies (0.01–0.05 Hz) contributed largely to the frequency spectrum. Spatiotemporal decomposition and selection of the COIs proved to be highly consistent across as well as within subjects.

Our results are similar to previously reported functional connectivity maps of auditory, visual, and motor cortices in space [Biswal et al., 1997; Cordes et al., 2001; Lowe et al., 1998] and in time [Cordes et al., 2001; Xiong et al., 1999]. Our spatial ICA application yielded only one component for each region of interest in most cases, however, whereas Kiviniemi et al. [2003] reported multiple components for sensory and motor regions. This difference may reflect different samples (young patients vs. healthy adults) and measurement situations (anesthetized vs. awake) of the two studies. In addition, we used an automated component selection procedure that yielded only one, in some cases two COIs with the highest average absolute Z‐values, instead of selection by visual inspection of target areas. The spatial location and extent of our sICA‐derived connectivity maps of parietal areas show a high similarity to clusters of activity elicited by several visuospatial tasks, using both hypothesis‐ [e.g., Goebel et al., 1998; Trojano et al., 2000] and data‐driven analyses [Formisano and Goebel, 2003].

The contribution of low and very low frequencies to the COI time courses suggests that the COIs reliably represent the functional connectivity patterns in the time domain as well. Functional connectivity as measured by multiunit cell recording is associated often with frequencies in the γ range, and can show high coherence over short and long cortical distances [Fries et al., 2001; Leopold et al., 2003]. It has been demonstrated, however, that fluctuations with a frequency range similar to that observed in our COI time courses (<0.1 Hz) over a very large time scale (minutes) are a meaningful indicator of coherent fluctuations of higher frequencies (e.g., γ range) that occur over a very short time scale (milliseconds) [Leopold et al., 2003]. Functional connectivity maps, as measured by fMRI, thus might be good estimators of large‐scale functional connectivity at the neural level. Connectivity in BOLD signal maps, however, may also represent couplings in blood flow or capillary processes. The low frequencies reported in our study, as well as in other studies, have been linked to oscillations of cerebral blood flow regulation [Mitra et al., 1997], which have been found in frequency ranges as low as 0.04 Hz [Obrig et al., 2000]. Our current approach cannot convey any information about the direction of such connectivity patterns because the analyses are based only on zero‐lag covariation over time. In addition, fMRI functional connectivity is limited by a coarse temporal resolution (i.e., in the range of seconds), whereas at the same time subcortical activity (e.g., thalamic activity patterns) is explicitly neglected by the cortex‐based analysis. These constraints clearly prevent an interpretation in the context of possible biochemical or neurophysiological modulators of such connectivity patterns.

Spatial ICA does not rely on a predefined temporal model, and is therefore very suitable for functional connectivity analysis of resting state data, where a general model of ideal brain activity cannot be generated. Although several parameters of the dataset may vary within and between subjects (e.g., head movement, anatomical variation), VOI‐cbICA was able to reproduce functional connectivity maps of sensory, motor, and parietofrontal regions in most cases. Even more so, comparison of component‐descriptive parameters such as spatial layout of the functional clusters, frequency spectrum, and temporal structure of the COI time courses yields a high consistency between COIs obtained from different datasets. This is especially interesting in light of earlier studies where COIs related to acoustic stimulation [van de Ven et al., 2002], visual stimulation, and motor performance [Formisano et al., 2002a] were extracted from different tasks and measurements. The identified COIs showed a high degree of similarity in several component‐descriptive parameters across the various studies, as well.

CbICA is able to separate functionally connected networks from motion‐related artifacts and other BOLD‐signal patterns not related to neural activity. ICA has been applied as a noise reducer before [McKeown et al., 1998; McKeown and Sejnowski, 1998; Thomas et al., 2002], but was aimed mainly at separating noise‐related time courses from task activity related to block‐ or event‐related designs. In our study of resting state measurements, noise reduction was an important part of the analysis, because no prespecified hypothesis can be used to estimate and separate interesting BOLD signals from potentially noise‐related activity patterns [McKeown et al., 1998; Thomas et al., 2002].

Arfanakis et al. [2000] used ICA to identify and remove task‐related activity from functional datasets. The resulting data matrix contained only non‐task‐related activity that comprised the baseline conditions and noise components. Functional connectivity networks in sensory and motor regions were then identified with a seed voxel approach. The task‐related activity patterns, however, were identified based on a cross‐correlation between the stimulus protocol and the component time courses. Extracting independent components by relying on the stimulus protocol may ignore possible task‐dependent activity patterns that are not obviously captured by the shape of the protocol. Such a method may then leave traces of task‐dependent activity in the subvolume of the resting state dataset, resulting in task‐dependent connectivity. Our approach functions independently of time course information, whereas it emphasizes spatial information as a criterion for selection of COIs.

The finding of pCC/preC functional connectivity COIs is of special interest in light of recent findings on default states of brain activity in these and other regions. A decrease in BOLD signal in ventral anterior and posterior cingulate cortex during task performance in comparison to baseline activity has been reported on by Raichle et al. [2001]. This relationship was investigated by Greicius et al. [2003], who looked at activity in these regions during task execution and during resting state measurements. Not only did they find that these regions were connected functionally in the resting state, but that activity in these regions was inversely correlated with activity in prefrontal regions involved in working memory. This finding is supportive of a default brain state of activity that is disrupted when a task is carried out [Raichle et al., 2001]; however, the COI functional connectivity maps obtained in our study that comprised the pCC/preC did not contain clusters in the anterior cingulate cortex. This may suggest that the reported correlations between the regions do not describe a statistically dependent relation. This can be the case when a third region modulates the activity of the regions contained in the COI.

This study has several limitations. First, we chose to decompose each dataset using a relatively large number of independent components. An excessive reduction of the dimensionality may be particularly problematic for analysis of resting state measurements because the interesting sources are expected to be weak compared to other, artifactual sources [Green and Cordes, 2002]. Conversely, setting the number of components too high may result in functionally connected regions split into separate components. For example, in one case the bilateral auditory cortex was represented in two components, whereas the left and right IPC were each captured in a single component map in all cases. In most cases, however, the sensory and motor connectivity maps showed a bilateral pattern similar to connectivity patterns reported in other studies, indicating that our choice of component number did not play a major role in determining our results. Interestingly, in another resting state study using ICA in which a relatively small number of components was estimated, multiple connectivity maps for sensory and motor areas were found [Kiviniemi et al., 2003]. We conclude that further research on the optimum number of components for decomposition of fMRI data is needed. Second, we used an ICA algorithm that assumes that the time courses of cortical areas within one component are synchronous, which will result in the representation of areas with time courses that differ only in latency in separate components [Calhoun et al., 2003a]. This might be useful for studying, e.g., mental chronometry, when decompositions can be associated with different processing stages related to task performance [Formisano and Goebel, 2003]. Third, we did not assess subjects' compliance with the explicit instruction to keep their eyes open during the measurement, which was carried out in complete darkness. Assessment or control of eye movements during resting state measurements may become more important when psychiatric patients are involved, and can be done by using eye movement tracking devices that are scanner‐compatible.

Current models of functional and effective connectivity in the brain need to be supplemented by investigation of direct or indirect anatomical connections between functionally connected cortical areas. Recent developments in the field of diffusion tensor imaging (DTI) may allow for the estimation of trajectories of white matter fiber tracts in the brain. One recent study combined seed voxel‐based assessment of functional connectivity in the normal human resting brain with DTI, and reported high functional connectivity for spatially distinct areas that were connected through white matter tracts [Koch et al., 2002]. Correlations between the temporal patterns of spatially distant areas remained high, however, even when direct anatomical connections were lacking, showing that the relation between anatomical and functional connectivity is not straightforward.

A disrupted or otherwise altered pattern of communication within and between specialized brain areas or networks has been suggested to be involved in a number of neurological and psychiatric disorders. Such alterations may result in a default brain state that differs from the putative default state in healthy individuals. For instance, a reduced interhemispheric resting state connectivity based on BOLD measurements has been shown in multiple sclerosis patients [Lowe et al., 2002], whereas reduced functional and effective connectivity might be related to symptoms of schizophrenia [Friston, 1998; Hoffman and McGlashan, 1993]. Analysis of the connectivity patterns of the resting or default brain of these and other disorders is likely to provide useful insights into their underlying pathologies [Calhoun et al., 2003b]. Moreover, such analysis may supplement fMRI studies that use cognitive paradigms that typically comprise alternating periods of task and rest, which is used as baseline. The use of resting state brain activity as a baseline has been debated heavily [Gusnard and Raichle, 2001; Stark and Squire, 2001]. In this context, a better understanding of the patterns of resting state activity should lead to an improved interpretation of task‐ or stimulus‐related activation in fMRI studies.