Abstract
Multicenter studies can provide additional information over single center studies because of their increased statistical power. Because similar acquisition protocols are being used internationally for structural magnetic resonance imaging (MRI) studies of the human brain, volumetric MRI data studies seem suitable for this purpose. Possible systematic differences between sites should be avoided, however, particularly when subtle differences in tissue volume are being searched for, such as in neuropsychiatric diseases. In this calibration study, the brains of six healthy volunteers were (re)scanned with MR scanners from four different manufacturers at five different sites, using the local acquisition protocols. The images were segmented at a central reference site. The intraclass correlation coefficient (ICC) was determined for the whole brain, gray and white matter, cerebellum, and lateral and third ventricle volumes. When required, the processing algorithms were calibrated for each site. Calibration of the histogram analysis was needed for segmentation of total brain volume at one site and for gray and white matter volume at all sites. No (additional) calibration was needed for cerebellum and ventricle volumes. The ICCs were ≥0.96 for total brain, ≥0.92 for cerebellum, ≥0.96 for lateral ventricle, ≥0.21 for third ventricle, ≥0.84 for gray matter, and ≥0.78 for white matter volume. Calibration of segmentation procedures allows morphologic MRI data acquired at different research sites to be combined reliably in multicenter studies. Hum. Brain Mapping 22:312–320, 2004. © 2004 Wiley‐Liss, Inc.
Keywords: multicenter, brain, MRI, calibration, segmentation, reliability
INTRODUCTION
Investigation of complex psychiatric disorders may require large numbers of subjects to be included in studies. Because of these large numbers, such studies are often carried out at more than one research site. When such multicenter studies involve the measurement of brain volumes from magnetic resonance imaging (MRI) scans, one has to take into consideration that quantitative MRI brain measures are susceptible to the MR scanner properties and parameter settings during acquisition. Scanner upgrades and changes in acquisition protocols can influence subsequent brain volume measures, which may result in inaccuracies in measurements over time. In addition, when scans from different research sites are included, variability of MR scanners and acquisition protocols between sites must be taken into consideration.
Multicenter MR brain imaging data can be analyzed in several ways. First, multicenter MR brain imaging data can be analyzed using the brain volumes of interest as measured at each contributing site in a statistical analysis. A meta‐analysis is an example of such a study (e.g., Wright et al. [2000], who carried out a meta‐analysis on brain volumes in schizophrenia). Second, data analysis could be carried out by using images from all contributing sites and processing them (at a central site) according to one single established procedure to calculate the volumes of interest (e.g., Coffey et al. [2001] on brain aging in elderly human subjects). In the statistical procedure of the first and second approaches, a site variable can be introduced to detect and eventually control for systematic differences between the volumes of interest of different sites. A third approach would be to optimize the processing pipeline for comparability of the relevant brain volume measures between all contributing sites. Ideally, such a setup also involves optimizing MR acquisition for each site. Luft et al. [1996] and Tofts [1998] discussed several factors influencing volumetric results and provided guidelines for setting up multicenter MRI studies. We carried out such an optimization in a three‐center study in the Netherlands earlier [van Haren et al., 2003]. In many situations, however, tuning of the MRI acquisition protocols is not possible, e.g., when scans have already been acquired. In such cases, one is left with measuring the comparability and possibly optimizing the processing pipeline. Filippi et al. [1997, 1999] carried out such scan–rescan reproducibility tests for measuring multiple sclerosis (MS) lesions. Patwardhan et al. [2001] studied inter‐scanner variability of volumes of several anatomic structures, including gray and white matter of the cerebrum and cortical lobes, in the human brain. The scanned subjects did not overlap for most of the sites. Moreover, these studies only tested the comparability and did not investigate the possibility of optimizing the processing steps.
To utilize fully the information contained in MR images and maximally benefit from the combination of data in a multicenter study, we employed the third approach. It required a group of calibration subjects to be scanned at all participating research sites. By processing these calibration images and optimizing the comparability of their volumes of interest, the processing algorithms can be tuned for the multicenter study. To our knowledge, such an approach has not been carried out before. In this work, we report results of a reliability study in an international multicenter brain‐imaging project in patients with schizophrenia conducted at five international sites with MR scanners from four different manufacturers. All subjects participating in the study had been scanned already before the multicenter project started, so no scan acquisition protocol optimization was possible. For the optimization of the processing pipeline, six healthy control subjects were scanned at all research sites, using the same acquisition protocols as used for the subjects included in the multicenter study. The segmentation process was carried out at a central reference site, and contained some tunable parameters. From the segmented images, volumes of interest were calculated and compared between the different sites.
SUBJECTS AND METHODS
Study
The Schizophrenia Twin and Relatives (STAR) consortium investigates the relation between schizophrenia and brain morphology and their genetic background in twins and relatives. For this purpose, MRI brain scans were acquired at five research sites: University Medical Center Utrecht; Institute of Psychiatry London; Universitätskliniek Heidelberg; University of Jena; and University of Helsinki.
Subjects for Calibration
For the between‐site reliability test of Utrecht (U0), London, Heidelberg, and Jena, six healthy volunteers (c1–c6) were scanned at these sites in a time span of 8 months. For the within‐site reliability test of Utrecht, five of these subjects (c1–c5) were rescanned twice in Utrecht (U1 and U2), between 15 and 18 months after the first scan. In the same period, four (c1–c4) were scanned in Helsinki to test the comparability between this site and Utrecht (U1). The volunteers (two males, four females) were aged between 20–35 years. All volunteers signed written informed consent for participation in the calibration study.
MRI Acquisition
A summary of the scanners and acquisition protocols used at each site is given in Table I. MR images from Utrecht were obtained on two 1.5 T Philips Gyroscan NT scanners Release 5 (Best, Netherlands). For volumetric analysis a 3D T1‐weighted coronal spoiled gradient echo scan (3D‐FFE) (TE = 4.6 msec, TR = 30 msec, flip angle 30 degrees, 170 contiguous 1.2‐mm slices, in‐plane voxel size 1 × 1 mm2) of the whole head was acquired. In addition, a coronal dual‐contrast turbo (gradient) spin echo (DE‐TSE) scan (TE1 = 14 msec, TE2 = 80 msec, TR = 6,350 msec, 120 contiguous 1.6‐mm slices) of the whole head was acquired.
Table I.
Summary of the scanners and calibration scans at the five research sites
| Site | Code | Scan date(s) (m/d/y) | Scanner | Acquisition summary | TE (msec) | TR (msec) | Flip angle | Subjects | |
|---|---|---|---|---|---|---|---|---|---|
| Protocol/orientation/scan time (min) | Voxel dimensions (mm) (slices) | ||||||||
| Utrecht, reference | U0 | 07/10/2001–07/21/2001 | Philips NT 1.5T | 3D‐FFE/coronal/11 | 1×1×1.2 (180) | 4.6 | 30 | 30° | c1–c6 |
| Repeated 1 | U1 | 10/22/2002–01/16/2003 | c1–c5 | ||||||
| Repeated 2 | U2 | 10/29/2002–01/16/2003 | c1–c5 | ||||||
| London | L | 08/16/2001–11/10/2001 | GE Signa 1.5T | 3D‐SPGR/coronal/19 | 0.781×0.781×1.5 (124) | 5 | 35 | 35° | c1–c6 |
| Heidelberg | H | 03/15/2002 | Picker Edge 1.5T | 3D‐FLASH/sagittal/13 | 1×1×1.5 (128) | 3 | 30 | 30° | c1–c6 |
| Jena | J | 03/16/2002 | Philips ACS II 1.5T | 3D‐FFE/sagittal/11 | 1×1×1 (256) | 5 | 13 | 25° | c1–c6 |
| Helsinki | F | 01/18/2003 | Siemens Magnetom Impact 1.0 T | MPRAGE/sagittal/7 | 1×1×1.2 (128) | 4.4 | 11.4 | 12° | c1–c4 |
MR images from London were obtained on a 1.5 T General Electric Signa System scanner (Milwaukee, WI). For volumetric analysis a 3‐D T1‐weighted coronal spoiled gradient recalled echo (SPGR) scan (TE = 5 msec, TR = 35 msec, flip angle 35 degrees, 124 contiguous 1.5‐mm slices, in‐plane voxel size 0.781 × 0.781 mm2) of the whole head was acquired. In addition, a coronal dual‐contrast fast spin echo (DE‐FSE) scan (TE1 = 15 msec, TE2 = 100 msec, TR = 4,000 msec, 3‐mm slices, in‐plane voxel size 0.859 × 0.859 mm2) of the whole head was acquired.
MR images from Heidelberg were obtained on a 1.5 T Picker (Marconi) Edge scanner. For volumetric analysis a 3D T1‐weighted sagittal 3D‐FLASH scan (TE = 3 msec, TR = 30 msec, flip angle 30 degrees, 135 contiguous 1.5‐mm slices, in‐plane voxel size 1 × 1 mm2) of the whole head was acquired.
MR images from Jena were obtained on a 1.5 T Philips ACS II scanner (Best, The Netherlands). For volumetric analysis a 3D T1‐weighted sagittal 3D‐FFE scan (TE = 5 msec, TR = 13 msec, flip angle 25 degrees, 256 contiguous 1.0‐mm slices, in‐plane voxel size 1 × 1 mm2) of the whole head was acquired.
MR images from Helsinki were obtained on a 1.0 T Siemens Magnetom Impact scanner (Erlangen, Germany). For volumetric analysis a 3‐D T1‐weighted sagittal MPRAGE scan (TE = 4.4 msec, TR = 11.4 msec, flip angle 12 degrees, 128 contiguous 1.2‐mm slices, in‐plane voxel size 1 × 1 mm2) of the whole head was acquired.
Figure 1 depicts coronal slices from each of the five T1‐weighted scans at the same z‐coordinate for a single subject.
Figure 1.
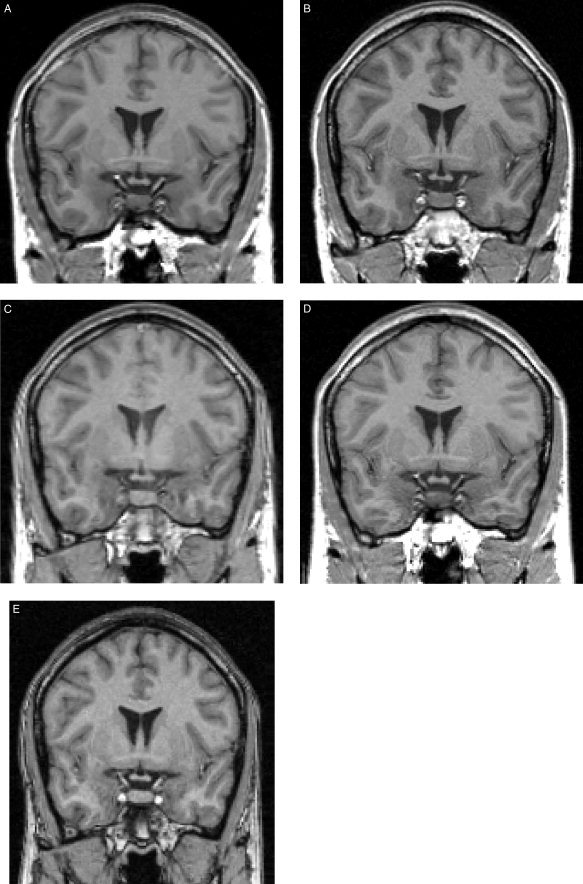
Sample images from each site. Resampled coronal slices at the same z‐coordinate are shown for a single subject. A: Utrecht. B: London. C: Heidelberg. D: Jena. E: Helsinki.
MRI Processing
The processing of the images as described below has been validated and described in detail for the Utrecht scans before. The reproducibility of the segmentation process was tested using the intraclass correlation coefficient [ICC; Bartko and Carpenter, 1976]; ICCs were 0.96 or higher for all structures [Hulshoff Pol et al., 2002; Schnack et al., 2001a, b]. For volumetric studies, ICC values higher than 0.7 were considered reasonable, higher than 0.8 good, and higher than 0.9 excellent.
Image processing of the brain scans from the healthy volunteers was done on the neuroimaging computer network of the Department of Psychiatry in Utrecht, which includes Hewlett Packard UNIX 9000 workstations, a computer server, and Pentium‐III PCs. The T1‐weighted image was first put into Talairach orientation (no scaling) [Talairach and Tournoux, 1988]. For the sagittal Heidelberg and Helsinki scans, a resampling to isotropic (1 × 1 × 1 mm3) voxels was included in this step. If a T2‐weighted image was available (Utrecht, London), an intracranial volume was automatically segmented from this image. After registration to the T1‐weighted image using a mutual information maximization algorithm [Maes et al., 1997], this segment served as a mask for further segmentation steps. If no T2‐weighted image was available, an intracranial mask was manually segmented directly on the T1‐weighted image. The intracranial volume was left out of the comparison for these sites; it was only used as a mask for further processing steps on the T1‐weighted image. The T1‐weighted images were corrected for scanner RF‐field nonuniformity [Sled et al., 1998]. This was a necessary step for segmenting total brain and separating gray and white matter on the total brain by means of intensity thresholds. Qualitative analysis revealed shape differences of the bias fields, showing the importance of nonuniformity correction, especially if volumetric analysis was extended to gray and white matter of parts of the brain (e.g., cortical lobes). Intensities of voxels inside the intracranial volume were divided by the so‐called gain field, which describes the variations in radio frequency (RF)‐field strength, calculated from the image. All further operations were done on the nonuniformity corrected T1‐weighted images. Total brain segmentations were done automatically, using mathematical morphology operations, based on thresholds obtained from the steepest slope of the gray matter peak in intensity histograms of the intracranial region (see Fig. 2), i.e., the cerebrospinal fluid (CSF)/gray matter separation threshold L tb = f tb × L ss, where L ss is the position of the steepest slope and f tb is a calibrated factor (0.73 for Utrecht scans) [see Schnack et al., 2001a]. Cerebellum and lateral and third ventricular segmentations were carried out semiautomatically based on histogram analyses followed by mathematical morphology operations on the T1‐weighted image. Anatomic knowledge‐based selection principles were used for these segmentations. All segments were checked visually and corrected manually if necessary. Separation of gray and white matter of the cerebrum was done by applying a single threshold to the voxels of the total brain in the T1‐weighted image. For each image, this threshold was obtained automatically from the intensity histogram of the T1‐weighted image (see Fig. 2). Tangential lines were drawn from the inflection points of the gray and white matter peaks (points A and B), and the crossing point of the two tangential lines was calculated. This was the characteristic point L cp of the histogram. The gray/white matter separation threshold was now, by our definition, related to the characteristic point L cp by: L gw = f gw × L cp, where f gw ∼ 1 to give a threshold close to the position of the minimum in the histogram, in which range the separation threshold is expected. It has been shown previously [Schnack et al., 2001a] that this scaling factor f gw has to be calibrated, because of the dependence of the shapes of the gray and white matter distributions on the acquisition parameters. It was calculated earlier for Utrecht scans based on a comparison in 80 scans where the gray/white separation had been determined manually twice by three raters (f gw = 0.960, for Utrecht). To obtain the cerebral white matter segmentation of the image, a selection of all voxels in the cerebrum with intensities L ≥ L gw was made. The gray matter segment was calculated from the difference between the cerebrum segment and cerebral white matter segment. Volumes of the segments were calculated by multiplying the number of voxels of the segments by the voxel volume.
Figure 2.
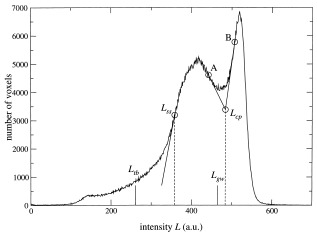
Intensity histogram of a T1‐weighted 3D‐FFE image made in Utrecht. Only voxels inside the intracranial volume were counted. The threshold L tb for segmentation of the total brain is calculated from the intensity L ss of the point on the gray matter peak where the histogram is steepest. The characteristic point L cp is the crossing point of the two tangential lines to the gray and white matter peaks in their respective steepest points (A and B). The threshold L gw for separating gray and white matter is calculated from this characteristic point.
Calibration and Statistical Analysis
All Utrecht images were processed according to the above description. The volumes from the scans made in Utrecht in July 2001 (U0) served as reference volumes for the between‐site validation of the scans from London, Heidelberg, and Jena. The second set of Utrecht images (U1) served as reference for the validation of the Helsinki scans and the within‐site (U1–U2) validation of the Utrecht scanners. The images from the other sites followed the same processing pipeline as that for the Utrecht scans, except that the threshold factors for total brain, f tb, and gray/white, f gw, could be optimized for each site. Comparability was measured by calculating the intraclass correlation coefficient [ICC; Bartko and Carpenter, 1976] between the volumes of a site and the reference volumes. For total brain segmentation, the default (Utrecht) value of f tb (0.73) was applied first. For each site, the ICC between the resulting brain volumes and the reference volumes was calculated. In case the ICC was low, a range of other values of f tb was inserted in the algorithm and total brain volumes and ICCs were calculated again. The value of f tb for which the ICC assumed its maximum value was used for the recalibrated version of the algorithm. After establishing this factor for each site and segmentation of the total brain, the cerebellum and lateral and third ventricles could be segmented. For the gray and white matter volumes, an optimization procedure comparable to the one for the total brain segmentation was carried out. A range of f gw values was applied to the segmentation algorithm. For each value of f gw the ICC between the resulting brain volumes and the reference volumes was calculated and an ICC versus f gw plot was made (see Fig. 3). The ICCs for both the gray and white matter volumes were optimized with respect to f gw. In case the two ICC curves did not assume their maxima for the same value of f gw, the value of f gw was chosen for which the sum of the ICCs was maximal. The value of f gw for which the ICC assumed its maximum value was used for the recalibrated version of the algorithm. This calibration was carried out on the whole set of subjects. To obtain an estimate of the ICC reliability, the Utrecht, London, Heidelberg, and Jena sets were split into all 20 different 3+3 subjects combinations. For each combination, the calibration procedure was carried out on the first set of three scans, leading to a calibration factor for that calibration set. This factor was then applied to the three remaining scans, the test set, and an ICC value was calculated to value the goodness of agreement between this calibration of the site with respect to the reference site. The means and standard deviations of the ICCs were calculated over the 20 different calibrations.
Figure 3.
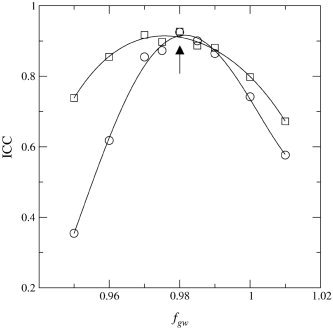
Plot of the ICC vs. calibration factor f gw for the London scans. Circles, white matter values; squares, gray matter values; lines, fourth‐degree polynomials fitted to the data; arrow, position of the combined maximum.
To probe the intrinsic tissue contrast differences between the sites before calibration, which were overcome by the calibration step, contrast‐to‐noise ratios were calculated from samples of gray and white matter in a chunk of the frontal lobe, and from ventricular CSF samples. Analyses of variance (ANOVAs) were carried out on the CSF/gray matter and gray/white matter contrast‐to‐noise ratios. After calibration, t‐tests were carried out to test for differences in volumes of interest between different sites.
RESULTS
ICCs for intracranial, total brain, cerebral gray and white matter, cerebellar, lateral and third ventricular volumes for the calibration subjects at the five research sites are given in Table II.
Table II.
Gray/white calibration factors and ICCs of volumes of interest between the different research sites
| Site (Code) | ICC | Cerebrum | ||||||
|---|---|---|---|---|---|---|---|---|
| Intracranium | Total brain | Cerebellum | Lateral ventricles | Third ventricle | GM ICC | WM ICC | f gw | |
| Utrecht, reference (U0) | — | — | — | — | — | — | — | 0.960 |
| London (L)a | 1.00 | 0.99 | 0.99 | 1.00 | 0.85 | 0.91 | 0.92 | 0.980 |
| Heidelberg (H)a | — | 0.96d | 0.92 | 0.96 | 0.21 | 0.74 | 0.78 | 1.026 |
| Jena (J)a | — | 0.97 | 0.95 | 0.99 | 0.81 | 0.93 | 0.95 | 0.970 |
| U0, L, H, J overall | — | 0.98 | 0.96 | 0.98 | 0.42 (0.84e) | 0.86 | 0.90 | — |
| Utrecht, repeated 2 (U2)b | 1.00 | 1.00 | 0.99 | 0.99 | 0.92 | 0.91 | 1.00 | — |
| Helsinki (F)c | — | 0.99 | 0.96 | 0.96 | 0.93 | 0.84 | 0.99 | 0.996 |
ICCs with respect to U0 (Subjects c1–c6).
ICCs with respect to U1 (Subjects c1–c5).
ICCs with respect to U1 (Subjects c1–c4).
After calibration (f lb = 0.89); without calibration (default f lb = 0.73) ICC = 0.80.
With the Heidelberg volumes excluded from the ICC calculation.
ICC, intraclass correlation; GM, gray matter; WM, white matter.
Within‐Site
The Utrecht scan–rescan ICCs were 0.99–1.00 for intracranium, total brain, cerebellum, lateral ventricles, and cerebral white matter. The ICC for gray matter was 0.91 and 0.92 for the third ventricle.
Between‐Site
The ICCs for total brain volume by applying the default Utrecht f tb factor were 0.97 or higher for scans from London, Jena, and Helsinki, so that for these sites there was no need to recalibrate the total brain procedure. For scans from Heidelberg, the default f tb yielded an overestimation of total brain volumes (107% on average) compared to the reference site, resulting in an ICC of 0.80. After calibration, the factor was set to f tb = 0.89 resulting in an ICC of 0.96. The mean total brain volumes are given in Table III.
Table III.
Mean volumes of interest of calibration subjects, for the different research sites after calibration
| Subjects and site | Code | Intra‐cranium | Total brain | Cerebellum | Lateral ventricles | Third ventricle | Gray and white matter (cerebrum) | |
|---|---|---|---|---|---|---|---|---|
| Subjects c1–c6 | ||||||||
| Utrecht, reference | U0 | 1,426 (146) | 1,279 (142) | 143.5 (19.5) | 10.17 (6.4) | 0.449 (0.22) | 656 (51) | 464 (83) |
| London, Maudsley | L | 1,428 (143) | 1,276 (127) | 145.4 (18.5) | 10.66 (6.3) | 0.537 (0.18) | 656 (43) | 462 (70) |
| Heidelberg | H | 1,263 (120) | 149.1 (19.5) | 11.90 (6.4) | 0.197 (0.16)b | 653 (47) | 447 (65) | |
| Jena | J | 1,257 (125) | 147.7 (17.6) | 10.32 (6.0) | 0.491 (0.13) | 647 (47) | 448 (69) | |
| Subjects c1–c5a | ||||||||
| Repeated 1 | U1 | 1,468 (143) | 1,312 (128) | 152.3 (19.3) | 10.96 (7.55) | 0.447 (0.173) | 665 (29) | 478 (84) |
| Repeated 2 | U2 | 1,470 (142) | 1,313 (122) | 151.0 (17.5) | 11.43 (6.97) | 0.465 (0.202) | 665 (21) | 482 (89) |
| Subjects c1–c4a | ||||||||
| Utrecht, repeated 1 | U1 | 1,319 (147) | 151.8 (22.2) | 10.42 (8.6) | 0.497 (0.151) | 665 (33) | 486 (94) | |
| Helsinki | F | 1,329 (138) | 153.3 (18.9) | 12.70 (8.4) | 0.531 (0.195) | 669 (34) | 493 (85) | |
Mean volumes (standard deviation) given as cc units.
Because not all subjects were scanned for U1, U2, F, mean volumes of subsets are calculated for comparison of these sites.
P < 0.05.
ICCs for cerebellum volume were 0.92 or higher and 0.96 or higher for lateral ventricles. The ICC for the third ventricle was 0.81 for Jena, 0.85 for London, 0.93 for Helsinki, and 0.21 for Heidelberg. From Table III, it can be seen that the third ventricle volume from Heidelberg was less than half the volume measured from the other scans.
The gray and white matter segmentation procedure needed to be calibrated for all non‐Utrecht sites. The resulting calibration factors f gw and the corresponding ICCs are given in Table II. The ICCs for all sites except Heidelberg were 0.84 or higher and 0.92 or higher, for gray and white matter respectively. The ICCs for Heidelberg were 0.74 for gray and 0.78 for white matter. These relatively low values, however, are not reflected in very deviant mean gray and white matter volumes (see Table III).
The gray/white calibrations on subsets of three subjects with tests on the remaining three subjects lead to the following mean (SD) ICCs: London, GM 0.83 (0.18), WM 0.76 (0.26); Heidelberg, GM 0.45 (0.34), WM 0.67 (0.29); Jena, GM 0.84 (0.21), WM 0.90 (0.12). The lower values for Heidelberg are in accordance with the relatively low ICC values from the full calibration.
The combined ICCs for Utrecht (U0), London, Heidelberg, and Jena were 0.84 or higher for all structures (for the third ventricle the volumes from Heidelberg were left out). Helsinki could not be included in this over‐all ICC measure because the data were obtained for a subgroup of the calibration subjects (c1–c4) and at a later time.
ANOVA on the CSF/gray matter contrast showed an overall significant site effect. Post hoc tests showed significant (P < 0.05) differences between all sites, except for between Utrecht and Jena, and between Jena and London.
ANOVA on the gray/white matter contrast showed an overall significant site effect. Post hoc tests showed significant (P < 0.05) differences between Heidelberg and Utrecht, Heidelberg and Jena, Jena and London, and Utrecht and London; The difference between London and Heidelberg reached trend level.
After calibration, t‐tests revealed no significant (P < 0.05) differences between all volumes of interest of all sites, except for the third ventricle from the Heidelberg scans, which differed significantly from the reference (t = 5.26, P = 0.045).
DISCUSSION
We carried out a study to investigate the reproducibility of including MRI brain scans from different scanners running different acquisition protocols in multicenter volumetric studies using histogram‐based segmentation algorithms. Six healthy volunteers were scanned at five research sites with scanners from four different manufacturers running different acquisition protocols. At the reference site, the calibration subjects were scanned a second and third time to test the scan–rescan reliability of this site. All scans were processed at the reference site and volumes of total brain, gray and white matter of the cerebrum, cerebellum, and lateral and third ventricles were calculated. These volumes were compared between the research sites. The results revealed good to excellent reproducibility of total brain, cerebellar, and lateral and third ventricular volume between the research sites and within the reference site. For one site, recalibration of the total brain procedure was necessary; the third ventricle volume of this site was not in good agreement with the reference site. Separation of gray and white matter of the cerebrum resulted in good to very good reproducibility of the volumes, but only after recalibration of the segmentation algorithm. Without this recalibration, comparability between sites was poor. The separation of gray and white matter is very sensitive to the underlying intensity distributions, which in turn are influenced by the parameters of the acquisition protocol, such as the voxel dimensions. The use of calibration of histogram‐based gray/white matter separation algorithms has been shown previously [Schnack et al., 2001a; van Haren et al., 2003]. In all tested combinations of acquisitions and segmentation algorithms, the volumetric data could be brought in good agreement by calibrating a linear scaling factor, such as that in the current study.
The volumes of most structures in this calibration study were found to be in good agreement with each other. It was also found, however, that the third ventricle volume of one site (Heidelberg) was not in agreement with the volumes of the reference site and the other sites. This was due probably to the relatively large voxel size of these scans and the fact that its longest dimension (1.5 mm) was in the direction in which the third ventricle's size is smallest (left/right). The third ventricle volumes of this site were systematically much lower than those of the other sites and including these data in the multicenter study would not increase the statistical power but rather decrease it. Indeed, volumetric error increased due to an increase in slice thickness and parallel image orientation in smaller, especially thinner and longer objects [Luft et al., 1996]. The calibration test revealed that data from this site should be left out for this structure.
It is notable that the ICCs for gray and white matter of this [Heidelberg] site were also relatively low. The current study is not suitable to answer the question of which scan parameters influence the segmentation process in which way, because the setup was to include scan protocols that had already been used to acquire the data, and the scan parameters could not be varied independently to monitor their effects. A plot showing a clear negative effect of voxel volume on gray matter volume ICC and third ventricle volume (Fig. 4) suggests that the “scan parameter” voxel size plays an important role in the segmentation goodness.
Figure 4.
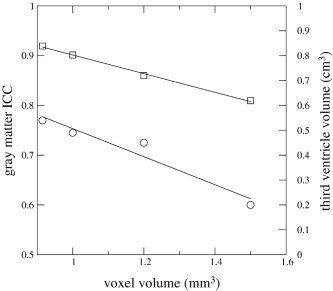
Plot of gray matter ICC (squares) and mean third ventricle volume (circles) vs. voxel size of the scans of the four sites London (0.915 mm3), Jena (1 mm3), Utrecht (1.2 mm3), and Heidelberg (1.5 mm3). Straight lines represent regression lines.
Although statistical analysis methods can also compensate for systematic differences between sites, the calibration of the MRI segmentation method for the different sites has several advantages, especially in the case of small data sets. First, unlike in the statistical analysis methods, calibration of the segmentation method does not introduce extra parameters in the analysis of the data. Moreover, it does not require all independent variables to be present at all sites. In contrast, after calibration of the MRI segmentation method inclusion of different populations, e.g., patients and controls, from multiple sites should be possible. Second, the proven comparability between the segmented images of different sites opens the way to carry out analyses other than volume measurements, such as shape analysis and voxel‐based morphometry. Of course, tests relating to these kinds of analyses then have to be carried out.
There are a number of qualifications to add to our conclusions. A repeated measurement within a site was only completed for the reference site and not for the other research sites, thus limiting our knowledge of reproducibility over time within these sites and with respect to the reference site. There is a large amount of work involved in a validation/calibration procedure such as the one carried out. A group of at least five healthy volunteers needs to be scanned at all participating sites. In the present study, one subject could not be scanned a second and third time at the reference site, and two subjects could not be scanned at one of the other sites, leaving only four subjects for the calibration of this site. The resulting lower volumetric variation between the remaining subjects limited the value of the ICC for this site.
The multicenter calibration study presented here is limited to post‐processing steps. The reproducibility of the processing pipeline itself was tested previously (ICC ≥ 0.95) by applying it to the same MRI data set twice in two independent studies [Hulshoff Pol et al., 2002]. In the present work, we found that application of the segmentation pipeline to T1‐weighted volume scans from different scanners running different acquisition protocols produced reproducible results, although for some structures recalibration was necessary. In the quest for reproducibility, Tofts [1998] suggested that high compatibility between sites of scan protocols contributes positively to the desired reproducibility. This was a factor that we could not control in this study; however, comparing ICC values of this international multicenter study to ones found in a Dutch three‐center study, in which we were able to control the MR scan protocols, revealed similar ICCs [van Haren et al., 2003]. Despite scan acquisition variation, most volumetric measurements thus turned out to be quite reliable across sites.
In conclusion, we have shown that multicenter MR brain imaging volumetric data can be tested on comparability and calibrated if necessary. For most anatomic structures measured, the volumes were in good agreement with each other, at all sites.
Acknowledgements
We thank R. Brans, I. Carati, X. Chitnis, M. Langen, and T. van Raalten for their assistance in the calibration study.
REFERENCES
- Bartko JJ, Carpenter WT (1976): On the methods and theory of reliability. J Nerv Ment Dis 163: 307–317. [DOI] [PubMed] [Google Scholar]
- Coffey CE, Ratcliff G, Saxton JA, Bryan RN, Fried LP, Lucke JF (2001): Cognitive correlates of human brain aging: a quantitative magnetic resonance imaging investigation. J Neuropsychiatry Clin Neurosci 13: 471–485. [DOI] [PubMed] [Google Scholar]
- Filippi M, Rocca MA, Gasperini C, Sormani MP, Bastianello S, Horsfield MA, Pozzilli C, Comi G (1999): Interscanner variation in brain MRI lesion load measurements in multiple sclerosis using conventional spin‐echo, rapid relaxation‐enhanced, and fast‐FLAIR sequences. Am J Neuroradiol 20: 133–137. [PubMed] [Google Scholar]
- Filippi M, van Waesberghe JH, Horsfield MA, Bressi S, Gasperini C, Yousry TA, Gawne‐Cain ML, Morrissey SP, Rocca MA, Barkhof F, Lycklama a Nijeholt GJ, Bastianello S, Miller DH (1997): Interscanner variation in brain MRI lesion load measurements in MS: implications for clinical trials. Neurology 49: 371–377. [DOI] [PubMed] [Google Scholar]
- Hulshoff Pol HE, Schnack HG, Bertens MGBC, van Haren NEM, Van der Tweel I, Staal WG, Baaré WFC, Kahn RS (2002): Volume changes in gray matter in patients with schizophrenia. Am J Psychiatry 159: 244–250. [DOI] [PubMed] [Google Scholar]
- Luft AR, Skalej M, Welte D, Kolb R, Klose U (1996): Reliability and exactness of MRI‐based volumetry: a phantom study. J Magn Reson Imaging 6: 700–704. [DOI] [PubMed] [Google Scholar]
- Maes F, Collignon A, Vandermeulen D, Marchal G, Suetens P (1997): Multi‐modality image registration by maximizing of mutual information: IEEE Trans Med Imaging 16: 187–198. [DOI] [PubMed] [Google Scholar]
- Patwardhan AJ, Eliez S, Warsofsky IS, Glover GH, White CD, Giedd JN, Bradley SP, Rojas DC, Reiss AL (2001): Effects of image orientation on the comparability of pediatric brain volumes using three‐dimensional MR data. J Comput Assist Tomogr 25: 452–457. [DOI] [PubMed] [Google Scholar]
- Schnack HG, Hulshoff Pol HE, Baaré WFC, Staal WG, Viergever MA, Kahn RS (2001a): Automated separation of gray and white matter from MR images of the human brain. Neuroimage 13: 230–237. [DOI] [PubMed] [Google Scholar]
- Schnack HG, Hulshoff Pol HE, Baaré WFC, Viergever MA, Kahn RS (2001b): Automatic segmentation of the ventricular system from MR images of the human brain. Neuroimage 14: 95–104. [DOI] [PubMed] [Google Scholar]
- Sled JG, Zijdenbos AP, Evans AC (1998): A nonparametric method for automatic correction of intensity nonuniformity in MRI data. IEEE Trans Med Imaging 17: 87–97. [DOI] [PubMed] [Google Scholar]
- Talairach J, Tournoux P (1988): Co‐planar stereotaxic atlas of the human brain. 3‐Dimensional proportional system: an approach to cerebral imaging. New York: Thieme. [Google Scholar]
- Tofts PS (1998): Standardisation and optimisation of magnetic resonance techniques for multicenter studies. J Neurol Neurosurg Psychiatry 64(Suppl): 37–43. [PubMed] [Google Scholar]
- van Haren NEM, Cahn W, Hulshoff Pol HE, Schnack HG, Caspers E, Lemstra A, Sitskoorn MM, Wiersma D, van den Bosch RJ, Dingemans PM, Schene AH, Kahn RS (2003): Brain volumes as predictor of outcome in recent‐onset schizophrenia: a multi‐center MRI study. Schizophr Res 64: 41–52. [DOI] [PubMed] [Google Scholar]
- Wright IC, Rabe‐Hesketh S, Woodruff PW, David AS, Murray RM, Bullmore ET (2000): Meta‐analysis of regional brain volumes in schizophrenia. Am J Psychiatry 157: 16–25. [DOI] [PubMed] [Google Scholar]


