Detection of functional connectivity using temporal correlations in MR images

Abstract

Functional connectivity among brain regions has been investigated via an analysis of correlations between regional signal fluctuations recorded in magnetic resonance (MR) images obtained in a steady state. In comparison with studies of functional connectivity that utilize task manipulations, the analysis of correlations in steady state data is less susceptible to confounds arising when functionally unrelated brain regions respond in similar ways to changes in task. A new approach to identifying interregional correlations in steady state data makes use of two independent data sets. Regions of interest (ROIs) are defined and hypotheses regarding their connectivity are generated in one data set. The connectivity hypotheses are then evaluated in the remaining (independent) data set by analyzing low frequency temporal correlations between regions. The roles of the two data sets are then reversed and the process repeated, perhaps multiple times. This method was illustrated by application to the language system. The existence of a functional connection between Broca's area and Wernicke's area was confirmed in healthy subjects at rest. An increase in this functional connection when the language system was actively engaged (when subjects were continuously listening to narrative text) was also confirmed. In a second iteration of analyses, a correlation between Broca's area and a region in left premotor cortex was found to be significant at rest and to increase during continuous listening. These findings suggest that the proposed methodology can reveal the presence and strength of functional connections in high‐level cognitive systems. Hum. Brain Mapping 15:247–262, 2002. © 2002 Wiley‐Liss, Inc.

INTRODUCTION

New functional magnetic resonance imaging (fMRI) protocols examining temporal correlations in steady state data have potential advantages over conventional fMRI protocols. In conventional fMRI studies, activated brain regions are identified by MR signal changes that occur in response to a specific stimulus or task or as a result of some other change in brain state. For example, block designs measure the differences in mean signal levels between two or more steady states, whereas event‐related paradigms measure the transient signal changes produced by isolated perturbations of a steady baseline. Within any such baseline state, however, the MR signal may exhibit temporal fluctuations that are not associated with features of any task or stimulus and which are not caused by instrumental variations or physiological effects originating outside the brain. These signal changes are treated as noise in conventional analysis techniques. The possibility exists, however, that such signal changes reflect alterations in blood flow and oxygenation that are coupled to neuronal activity. If so, the manner in which the variations in one region relate to those in other regions may provide insight into neuronal connectivity independent of any specific task. Thus, protocols examining temporal correlations in steady state data have the potential to reveal such connectivity. Given that a major aim of neuroimaging is to investigate functional brain networks, this possibility is of considerable interest. In addition, methods examining temporal correlations in steady state data are free from the limitations of more traditional functional imaging paradigms that arise from the need to design studies to examine one specific component of a cognitive system at a time.

Recently, the analysis of low frequency (<0.08 Hz) temporal fluctuations in MR signals measurable in the brain during resting state scans has generated a great deal of interest. The pattern of correlations between signal changes in a reference region and signal changes in other parts of the brain has repeatedly been found to reflect, to a remarkable degree, a set of plausible functional connections for the reference region. Such apparently functionally meaningful correlations were first seen between motor regions [Biswal et al., 1995; Cordes et al., 2000; Lowe et al., 1998; Xiong et al., 1999;], and have since been reported within the visual system [Biswal et al., 1995; Cordes et al., 2000; Lowe et al., 1998] and within other brain networks with known anatomical connectivity [e.g., Cordes et al., 2000; Lowe et al., 1998; Stein et al., 2000]. Examination of low frequency temporal correlations between brain regions under conditions other than resting state have revealed that some of the correlations change when subjects are performing different tasks [Lowe et al., 2000a], when they experience different emotions [Skudlarski et al., 2000b], and when they are subjected to different sensory conditions [Skudlarski and Gore, 1998]. These findings are consistent with the possibility that low frequency inter‐regional correlations occurring during a steady state reflect functional interactions between brain regions.

Although temporal correlations found in the resting state may reflect functional interactions between regions, other explanations for these correlations are also plausible. For example, they may arise from blood flow patterns that are independent of neural activity. Some of the strongest resting state correlations have been reported between homologous regions on opposite sides of the brain [Biswal et al., 1995; Lowe et al., 1998; Xiong et al., 1999]. The symmetry between the blood supply routes of homologous regions is likely to contribute to correlations in the hemodynamics of those regions. It is therefore particularly interesting when resting state correlations are reported between regions that are not contralateral homologues, but that are suspected to be functionally related, for example, between the amygdala and hippocampus [Lowe et al., 1998], or between primary motor cortex and supplementary motor area [Biswal et al., 1995; Xiong et al., 1999]. Even if the correlations reported between regions are due to neural activity, however, this shared pattern of activity may arise because the regions are influenced by the same structures, and not because they are interacting via direct (or indirect) anatomical connections.

If the correlations found between regions during resting state reflect functional interactions, they may be expected to change during the performance of different tasks or across different mental states in predictable ways. That is, correlations within a given functional system may increase when the system is recruited for a particular task or behavioral state, or when attention is shifted to or from the system. Conversely, the correlations may decrease when other brain systems are activated if the newly activated systems compete for attention or utilize the same regions in a manner that disrupts the interregional interactions of the original system. Changes in inter‐regional temporal correlations with changes in task or mental state have been reported [Lowe et al., 2000a; Skudlarski et al., 2000b]. The correlational structure in these studies, however, was not compared to resting state correlations and their relationship to correlational patterns found during resting state are not clear.

The present study examines low frequency temporal correlations across language regions of the brain both in a resting state and during a continuous listening task. The language system was chosen for this study primarily because Broca's area and Wernicke's area are good candidates for examining nonadjacent regions that are known to have strong ipsilateral connections. Blood flow artifacts are unlikely to induce greater correlations between these non‐homologous and nonadjacent regions than are typically found between spatially separated brain regions. If low frequency resting state correlations reflect the level of functional interactions between brain regions, however, we would expect these areas to be particularly correlated at rest. In addition, interactions between language regions of the brain are of general interest. For example, studies have implicated abnormalities of functional connectivity between language‐related brain areas in a range of language and reading disorders including dyslexia [Horwitz et al., 1998; Pugh et al., 2000] and certain forms of aphasia [e.g., Geschwind, 1974; Wernicke, 1874]. Therefore, this study may also provide some insight into the neural basis of language processing in healthy subjects that could ultimately be useful in understanding disordered language functions. Finally, language processing is a higher‐level cognitive function and it is of interest to know whether resting state correlational studies can reveal functional connectivity of such high level systems. If so, correlation analyses of resting state data would be a promising new approach to investigating the neurological basis of many complex psychological functions.

MATERIALS AND METHODS

A schematic diagram illustrating the general methodology is provided in Figure 1. Two independent sets of MR images are collected: one set of block design data and one set of steady state data (including both resting runs and listening runs). Analysis steps performed on the block design data are illustrated in the left‐hand column, and analysis steps performed on data from the steady state runs are shown in the right hand column. Each row represents a single iteration of analysis. Each iteration involves two steps. The first step (a) involves region identification and hypothesis generation in one data set. The second step (b) involved hypothesis testing in the remaining data set. Two iterations are performed in this study. The first iteration involves the identification of Broca's and Wernicke's areas and the evaluation of their connectivity. The second iteration involves the identification of a left premotor region of interest and the evaluation of its connectivity with Broca's area. These correspond to the first two rows of analyses illustrated in Figure 1. The process could be continued for further iterations as illustrated by the grey boxes in the third row. A detailed description of the methods employed is provided below.

Figure 1.

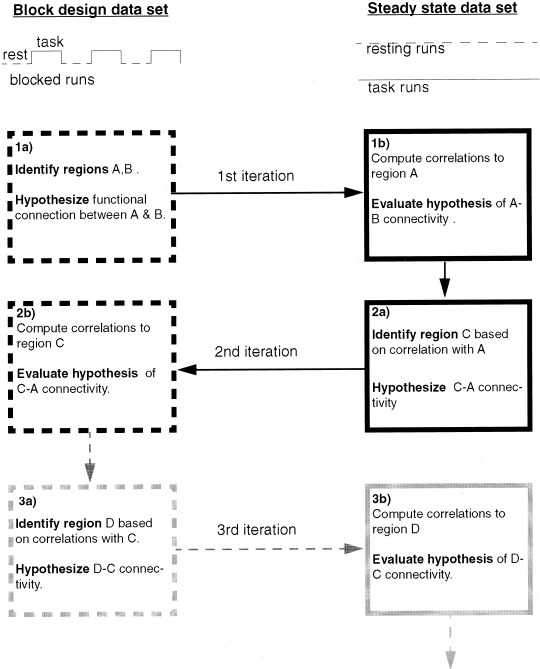
Diagram illustrating general methodology. In this study, Broca's and Wernicke's area are Regions A and B, respectively, and the left premotor region is C. See text for details.

Human subjects

Eleven healthy right‐handed volunteers (six men and five women, aged 23–49) who denied previous history of neurological disorders were scanned. All subjects gave informed consent in accordance with a protocol reviewed and approved by the Human Investigations Committee of the Yale University School of Medicine.

Data acquisition

Subjects wore headphones and lay in a supine position in the quadrature head coil of a GE 1.5T Signa LX scanner capable of performing single shot gradient echo‐planar imaging. Foam pillows and a band across the forehead were used to restrict head movements. Each scanning session began with the acquisition of 22 contiguous T1‐weighted sagittal localizing slices, using a repetition time (TR) of 505 msec, an echo time (TE) of 14 msec, a slice thickness of 5 mm, a field of view (FOV) of 24 cm by 24 cm, and an acquisition matrix of size 256 × 192. This was followed by the acquisition of nine contiguous 8 mm thick axial T1‐weighted images for anatomical identification (TR = 500, TE = 14, FOV = 20 cm × 20 cm, 256 × 192 acquisition matrix). The bottom slice was aligned 8 mm below the anterior‐posterior commissural line. Following the acquisition of anatomical reference images, seven functional imaging runs were acquired. Each functional run involved the acquisition of 340 images for each of the nine slices (prescribed in the same locations as the anatomical data). A T2*‐sensitive gradient‐recalled, single shot echo‐planar pulse sequence was used for acquisition of these functional images (TR = 1,000 msec, TE = 60 msec, flip angle = 60°, FOV = 20 cm × 20 cm, and a 64 × 64 acquisition matrix that resulted in a voxel resolution of 3.125 mm × 3.125 mm × 8 mm). The first 10 images taken in each scanning run were discarded to ensure the signal had achieved a steady state, and the remaining 330 images per slice were used for analysis.

Experimental paradigm

Of the seven functional imaging runs acquired for each subject, three employed a conventional block paradigm. These runs had 45‐sec periods of silence alternating with 45‐sec periods of continuous speech (from a recorded story). Three blocks of each were used, followed by a final silent period lasting 60 sec.1 These block design runs comprised one data set and analyses on the data from these runs are depicted in the left‐hand column of Figure 1. The second data set (analyses on this data are depicted in the right‐hand column of Fig. 1) was comprised of four steady state runs. In each subject, two of these runs were resting state, and two involved the presentation of continuous speech throughout the entire run. The seven functional runs were counterbalanced across subjects. All continuous speech was taken from an audio‐tape recording of the story “The Warden” [Trollope, 1855]. Before the scanning, subjects were instructed to stay alert, lie still and listen to the story whenever it was played. After the scanning, subjects were asked if they fell asleep during any of the runs. One male subject reported sleeping during several runs, so that subject was excluded from the analysis.

Data analyses

All data were motion‐corrected using the SPM algorithm (http://www.fil.ion.bpmf.ac.uk/spm/) without signal correction (to prevent disruption of correlational structure in the data). Pixels with a median value below 5% of the maximum median pixel value were set to zero, as well as any pixel that ever fell to zero or below (this removed those pixels outside the brain from the analysis). Data were then examined for ghosting and other obvious artifacts, and images that showed these artifacts were excluded. In addition, the translation and rotation motion estimates were examined and images that were associated with movement in any direction of greater than 1 mm or head rotation of greater than 1° were excluded from analysis. The specific analysis steps illustrated in Figure 1 are enumerated and described in detailed below.

Step 1a: defining Broca's area and Wernicke's area

Broca's and Wernicke's areas were defined based on a traditional activation analysis performed on data from the three block design runs. First, linear drift was removed from each run using the method described in Skudlarski et al. [1999], and the first three images of each block were discarded (to allow for the slow hemodynamic response). A pixel‐by‐pixel t‐test was then performed within each of the three runs, comparing each pixel's signal level during blocks acquired while listening to speech to its signal level during resting blocks. Results from the three runs were averaged to produce a t‐map for each subject. The individual t‐maps for each subject were used to identify the regions of interest (ROIs) for that subject in the following manner. First, a threshold of t = 2 was used as a cutoff for defining Broca's area, and a threshold of t = 3 was used as a cutoff for defining Wernicke's area (that had greater activation with a larger spatial extent).2 Second, each subject's t‐map was cluster‐filtered to remove activations involving less than three contiguous pixels. Third, Broca's area was defined to include all remaining activated pixels in Brodmann areas (BA) 44 and 45 (inferior frontal gyrus), as identified based on anatomical landmarks and Talairach coordinates. Finally, Wernicke's area was defined to include all remaining activated pixels in the superior part of BA 22, and adjacent portions of BA 39 (posterior aspects of superior temporal gyrus and portions of supramarginal gyrus), also identified based on anatomical landmarks and Talairach coordinates. These two ROIs were hypothesized to be functionally connected.

Step 1b: evaluating functional connectivity between Broca's and Wernicke's areas

The functional connection between Broca's area and Wernicke's area was evaluated by examining low frequency temporal correlations in the steady state data set. More specifically, correlation maps representing the magnitude of correlation between each pixel and Broca's area during the two steady state conditions (i.e., at rest and while listening to continuous speech) were produced, and ROI analysis was used to evaluate the significance of these correlations within Wernicke's area.

Correlations with the signal from Broca's area were computed for each of the steady state runs of each subject in the following manner. First, the data were low‐pass filtered using an eighth‐order Butterworth filter (forward and reverse filtered to prevent phase distortion) with a cutoff frequency of 0.08 Hz. This filtering was performed before the removal of images that showed motion, ghosting or other artifacts, as described above (but after motion correction). Low‐pass filtering was performed to maintain consistency with the literature on low frequency interregional steady state correlations [e.g., Biswal et al., 1995; Lowe et al., 1998, 2000a; Skudlarski et al., 2000b]. Second, the global timecourse of the data within the imaging run was found by averaging the timecourse across all non‐zero pixels. Third, the average timecourse of all pixels in the activation‐defined Broca's area of that subject was found. Finally, the partial correlation between the timecourse of each pixel and that of Broca's area was found, after removing the effect of the global timecourse.

For each subject, the correlations for each pixel were averaged across the two resting state scans to yield the net resting state correlation between that pixel and Broca's area. Similarly, for each subject, the correlations between each pixel and Broca's area were averaged across the two speech runs to yield a map of correlations with Broca's area found during continuous listening. These correlations were then transformed to an approximately normal distribution using Fisher's transformation [Hays, 1981]:

(1)

where r is the correlation at each pixel, computed as described above. This transformation yielded two approximately Gaussian distributions for each subject: one from the resting state runs, and one from the continuous speech runs. These approximately normal distributions were corrected to approximately standard normal distributions using the methods described in Lowe et al. [1998]. That is, for each approximately normal distribution, a least squares fit of a Gaussian to the distribution (restricted to the full‐width at half maximum) was performed. This fit had a χ² probability >0.05 in all cases. The free parameters were the mean, standard deviation, and area under the Gaussian. The z‐value for each pixel was then corrected by subtracting the mean of the Gaussian fit and dividing by the standard deviation of the Gaussian fit.

The z‐maps computed from resting data for each subject were then transformed to Talairach coordinates. A t‐test was performed on each pixel of these Talairach maps (using the data across all subjects) to produce a composite map of the statistical significance of resting state correlations with Broca's area. Similarly, the z‐maps of cross‐correlations during continuous listening were transformed to Talairach coordinates and combined across subjects to produce a composite map of correlations with Broca's area. These maps were cluster‐filtered to remove activations involving <10 contiguous pixels and are displayed in Figures 2 and 3 using a P = 0.01 cutoff (not Bonferroni corrected). Talairach slices that had data from all 10 subjects are shown.

Figure 2.

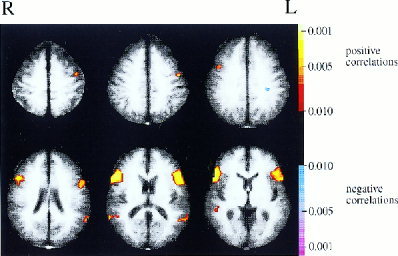
Composite map of resting state correlations with Broca's area (cutoff of P < 0.01, uncorrected).

Figure 3.

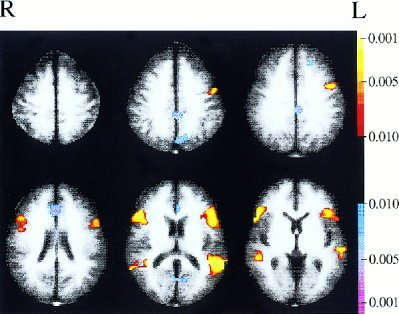
Composite map of correlations with Broca's area while subjects listened to continuous speech (cutoff of P < 0.01, uncorrected).

The correlations to Broca's area (these correlations were computed as described above) were evaluated within the Wernicke's ROIs that were defined for each subject in Step 1a. For each subject, the average z‐value across all pixels in Wernicke's area was computed for both the resting state and the continuous speech data. A t‐test comparing these values to zero was used to evaluate significance of the correlation between Broca's area and Wernicke's area across subjects. In addition, for each subject, the largest z‐values in the region were computed for the two conditions and used to evaluate the within‐subject significance of the Broca's‐Wernicke's correlation (after counting the number of pixels in Wernicke's region and adjusting for these multiple comparisons).

Step 2a: definition of premotor cortical region hypothesized to be functionally connected with Broca's area

Examination of the maps of correlations to Broca's area in the steady state data (Figs. 2, 3) revealed a left premotor region that appeared to be highly correlated with Broca's area. This area was hypothesized to be functionally connected to Broca's area. For each subject, the resting state map of correlations to Broca's area produced by the analysis described above was used to define the region of interest within left premotor cortex. A cutoff of P = 0.05 was used, and a cluster filter was applied to remove activations involving less than three contiguous pixels.3 All remaining positively correlated pixels falling in the left lateral dorsal portion of BA 6 (medial frontal gyrus) were selected. The region of interest was restricted to the dorsal portion of BA 6 to ensure a 15 mm distance from Broca's area and thus reduce the chances of picking up correlations arising simply from low spatial resolution.

Step 2b: evaluating functional connectivity between Broca's area and the premotor region

Because left premotor cortex was identified as a region of interest based on correlations to Broca's area in the steady state runs, only a post‐hoc ROI analysis would be possible if correlations to the left premotor region of interest were evaluated in the same data set. Post‐hoc analysis would involve a large correction for multiple comparisons and only a very strong correlation would pass such stringent standards. An alternate approach is to look for this correlation in an independent data set. By forming a hypothesis regarding the presence of a specific interregional correlation in one data set, and testing it in another, the need for multiple comparisons can be eliminated, and power can be increased. This was the approach adopted: the significance of steady state correlations between the left premotor ROI and Broca's area was evaluated in steady state portions of the block design runs (rather than in the steady state runs in which the correlation was first observed).

For each subject, correlations with the signal from the left premotor ROI were computed in steady state portions of the block‐design runs in the following manner. After motion correction, the data were low‐pass filtered using a cutoff frequency of 0.08 Hz and then motion and artifact related images were removed. The global timecourse of the data was found by averaging the timecourse across all non‐zero pixels, and the average timecourse of all pixels in the left premotor cortical region (defined as described above) was computed. Eighteen images were then discarded at the beginning of each block and a partial correlation removing effects arising from changes in the global timecourse was found between the timecourse of each pixel and that of the premotor ROI over the remaining images in that block. The partial correlations in resting blocks were averaged and the partial correlations in listening blocks were averaged. These average correlations were transformed to an approximately normal distribution using Fisher's transformation, and adjusted to an approximate z‐distribution following the same procedure described above.

The z‐maps for each subject were then transformed to Talairach coordinates and composite maps were created representing correlations with the left premotor cortical ROI in the two conditions. These maps were cluster‐filtered to remove activations involving less than ten contiguous pixels and are displayed in Figure 4. As fewer images were available to compute steady state correlations in the block‐design data set (compared to the number of images available in the steady state data set), the power was reduced in this analysis, and a lower cutoff is used in Figure 4 (P = 0.05 cutoff, not Bonferroni corrected). This reduced cutoff level is intended to reveal potentially interesting regions despite the reduced sensitivity of the analysis. The evaluation of statistical significance is not affected by the cutoff level of the composite images, which are simply intended to allow visualization of the results (significance is determined via ROI analysis). Those Talairach slices that had data from all 10 subjects are shown.

Figure 4.

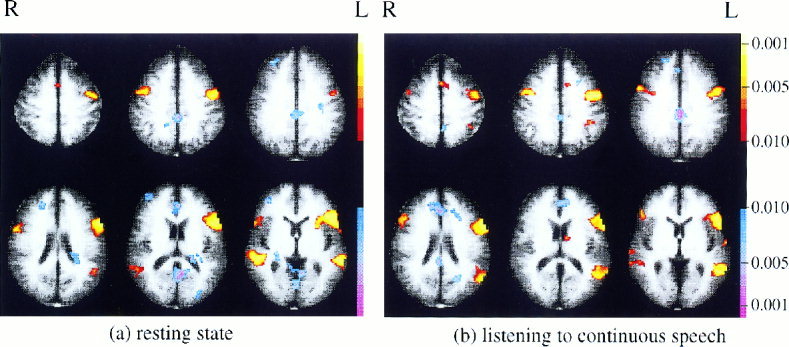
Correlations with the ROI in left premotor cortex evaluated during steady state portions of block design runs (cutoff of P < 0.05).

For each subject, the significance of the correlations with the left premotor ROI (computed as described above) were evaluated within Broca's area for that subject by identifying the pixel (in the correlation map) with the largest z‐value in Broca's area, and finding the significance of that z‐value after correcting for the number of pixels in the region. The average z‐value across all pixels in Broca's area was also computed for both the resting state and the continuous speech data. These average z‐values were used to evaluate across‐subject significance of the correlation between Broca's area and the left premotor ROI in the two conditions.

For verification purposes, maps of correlations to the left premotor ROI in the steady state runs were also computed (this is not shown in Fig. 1). The methods used were identical to those described in Step 1b, except premotor cortex, rather than Broca's area, was used as the reference region. The resulting correlation maps are shown in Figure 5 at a P = 0.05 cutoff.

Figure 5.

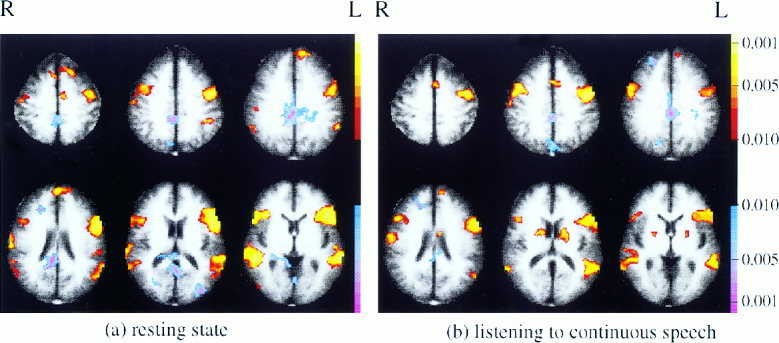
Correlations with the ROI in left premotor cortex evaluated during steady state runs (cutoff of P < 0.05).

Exploring the possibility of further iterations

Further analyses could be performed (although they were not illustrated in this study) by identifying new regions that appear to be correlated with Broca's area or the premotor ROI in one data set, and examining their correlations in the other data set. An example of such potential analyses is represented in Figure 1 by the grey boxes (Steps 3a and 3b).

One interesting question is whether it is possible to investigate the internal structure of a given brain network by finding regions more correlated with one ROI in the network than with other components of the network. For this reason, a map contrasting correlations to the premotor ROI with correlations to Broca's area in the continuous listening runs was created (this exploratory analysis is not shown in Fig. 1). Ten Talairach‐transformed correlation maps were created using the left premotor region as the reference region (defined as described in Step 2a) and employing an analysis similar to that described in Step 1b (i.e., the analyses were identical except that a different reference region was used). For each pixel, a t‐test was performed contrasting the value of that pixel in the 10 Talairach‐transformed premotor correlation maps with the value of that pixel in the 10 Talairach‐transformed Broca's correlation maps created as described in Step 1b. The resulting map of t‐values was cluster‐filtered to remove activations involving less than 10 contiguous pixels and thresholded at a P < 0.05 level (not Bonferroni corrected).

RESULTS

Step 1a: defining Broca's area and Wernicke's area

The conventional block design runs allowed identification of Wernicke's region and Broca's area in each subject. Although the terms Broca's area and Wernicke's region are generally used to refer to structures on the left side of the brain, all subjects showed some activation in our task in homologous regions of the right hemisphere as well. The bilateral activations may be due to the language task employed. It has been suggested that receptive language tasks are less lateralized than expressive language tasks [Boatman et al., 1998, 1999; Buchinger et al., 2000]. In a comparison of brain activity during four different language tasks, Lurito et al. [2000] found that passive listening to narrative text induced the least left hemisphere laterization. In addition, listening to recorded stories involves topic following that appears to induce right hemisphere activation [Caplan et al., 2000]. As functions such as topic following are arguably not basic language functions, the possibility that Broca's and Wernicke's ROIs should be restricted to include only left hemisphere activations was considered. Such a decision, however, requires the assumption that the subjects included in this study perform basic language processing using only the left hemisphere. There is insufficient data to support such an assumption, both because the role of the right hemisphere in language remains a matter of debate [e.g., Shaywitz et al., 1995] and because the performance of these particular subjects on more typically lateralized language tasks is unknown. Therefore, Broca's and Wernicke's ROIs were defined bilaterally for this study, and the terms will be used more loosely throughout this discussion to refer to these regions and their right hemisphere homologues.

Step 1b: evaluating functional connectivity between Broca's and Wernicke's areas

To evaluate the significance of correlations between Broca's and Wernicke's regions in the steady state conditions, a mean z‐statistic (representing the low frequency correlation with Broca's area) was computed across all pixels in the Wernicke's area of each subject. These mean z‐values are provided in columns 2 and 3 of Table I. T‐tests on these values revealed that the correlations during rest were significant at the p < 0.05 level (t(9) = 6.83, P = 7.6 × 10⁻⁵) and that the correlations during speech were also significant (t(9) = 5.69, P = 3.0 × 10⁻⁴). In addition, a paired t‐test revealed that the correlations during speech were significantly greater than the correlations at rest (t(9) = 2.82, P = 0.02). As a random effects analysis was used, these findings can be generalized beyond the specific group of subjects involved in the study. Within‐subject significance was also assessed by examining the maximum z‐value in the Wernicke's region of each subject (provided in columns 4 and 5 of Table I). At the P < 0.05 level, corrected for the number of pixels in the region (provided in column 6 of Table I), five subjects were found to have significant correlations in the resting task and six subjects were found to have significant correlations during the listening task.

Table I.

Mean and maximum z‐statistics in the Wernicke's region of each subject, representing correlations with Broca's area

Subject	Mean value		Maximum value		Number of pixels
	Resting state	Listening task	Resting state	Listening task
1	1.5717	4.0552	4.1021*	6.7606*	36
2	0.6633	1.2636	3.0175	3.2082	56
3	0.8980	3.2775	2.9388	5.9893*	93
4	0.3309	1.0454	2.8130	3.0005	75
5	1.5268	2.7510	3.6250*	5.4594*	65
6	1.7024	1.6320	3.4581*	3.5722*	51
7	0.5103	1.2895	2.9899	4.1698*	69
8	1.8814	3.2933	5.0054*	6.4739*	66
9	1.5373	1.2043	3.1883*	2.6863	32
10	1.1690	0.9097	3.2451	2.3791	89

^*Within‐subject significance (P < 0.05) for that condition.

The composite map of low frequency resting state correlations with Broca's area is shown in Figure 2. The largest correlations are clearly with pixels in or adjacent to Broca's area. Correlations with Wernicke's area are also present, although much weaker. The activations present in this correlation map cannot be considered statistically significant, because the threshold P‐value of 0.01 was not corrected for multiple comparisons (although subjects showed consistent correlations during resting state between Broca's and Wernicke's regions, the precise location of these areas varied across subjects, and this variability reduced significance in the composite map). As described above, however, region of interest (ROI) analysis of Wernicke's region did establish the significance of these correlations across subjects. Figure 2 also suggests that Broca's area may be correlated during rest with a region in left premotor cortex (BA 6).

The correlation between Broca's area and Wernicke's area present during resting state runs increased dramatically when subjects were listening to continuous speech, as shown in Figure 3 and established more rigorously in the ROI analysis (discussed above). Once again, the two regions most strongly correlated with Broca's area are Wernicke's region and premotor cortex.

Step 2a: definition of premotor cortical region hypothesized to be functionally connected with Broca's area

There remains the question of whether the correlation seen between Broca's area and left premotor cortex is significant. To investigate this, a left premotor ROI was defined for each subject based on correlations with the signal in Broca's area during the steady state resting runs.

Step 2b: evaluating functional connectivity between Broca's area and the premotor region

The significance of the Broca's‐premotor correlation cannot be rigorously assessed in the steady state data without a large correction for multiple comparisons, because left premotor cortex was not a defined region of interest before beginning analysis of the steady state data set. The significance of the correlation between Broca's area and premotor cortex, however, can be assessed more powerfully (i.e., without the need to correct for multiple comparisons) in an independent data set. Fortunately, an independent data set is available for this purpose and it includes both conditions of interest (i.e., rest and continuous speech): this data set is comprised of the three block design runs that were used for localizing Broca's and Wernicke's areas. Although data from block design runs is not generally used for examining steady state correlations within blocks, under appropriate conditions this may be possible [Skudlarski et al., 2000a]. Of course it will be necessary to throw out a large number of images in these runs to account for the slow hemodynamic changes between blocks. Using short imaging series (comprised of 15 images each), however, Skudlarski et al. [2000a] reported finding low frequency resting state correlations similar to those reported for longer imaging series. Therefore, it may be possible to evaluate correlations between the left premotor region of interest and Broca's area using short portions of steady state data extracted from the block‐design runs. This possibility was investigated.

The pattern of correlations with the left premotor region was computed for each of the two conditions (resting and listening) in the block design data set, and the significance of the correlation between the left premotor ROI and Broca's area was evaluated in the two conditions via ROI analysis. Table II documents the average and maximum z‐values (representing correlations with the left premotor ROI) found across pixels in the Broca's area of each of the 10 subjects. T‐tests on the average z‐values confirmed that Broca's area had a significant positive correlation with left premotor cortex both at rest (t(9) = 6.82, P = 7.7 × 10⁻⁵) and during continuous speech (t(9) = 13.24, P = 3.3 × 10⁻⁷). A paired t‐test comparing the two conditions was also performed. There was an increase in the correlation in the listening condition compared to the resting condition that was not significant at the P < 0.05 level, but was approaching significance (t(9) = 2.25, P = 0.051).

Table II.

Mean and maximum z‐statistics in the Broca's area of each subject, representing correlations with the left premotor ROI

Subject	Mean value		Maximum value		Number of pixels
	Resting state	Listening task	Resting state	Listening task
1	0.8322	1.0025	2.3020	3.0614	115
2	1.0036	1.3083	3.8661*	3.5967*	91
3	0.7360	0.8620	2.8849	2.9944	146
4	1.1694	1.3858	2.5905	3.6319*	74
5	2.0924	1.5032	4.0002*	2.8774	31
6	1.3448	1.9208	3.2445	4.4447*	65
7	0.9265	1.2467	3.1636	2.7894	52
8	1.3916	1.5471	4.7539*	2.7391	43
9	0.8885	1.8228	4.9362*	3.7339*	13
10	0.2222	1.2432	3.1760	3.6149*	62

Within‐subject significance (P < 0.05) for that condition.

The composite map of resting correlations with the left premotor ROI is shown in Figure 4a. The strongest positive correlations appear to be with right premotor cortex, Broca's area, and Wernicke's area. The strongest negative correlations appear to be with anterior cingulate and posterior cingulate.

The composite map of correlations with the left premotor ROI during the listening task is shown in Figure 4b. This is similar to the map of resting correlations, but does have several differences. Negative correlations with the posterior cingulate have decreased in the more ventral slices, and positive correlations appear in the left hemisphere near the supramarginal gyrus and caudate nucleus that were not present in the resting data. It is important to note that the activations and deactivations in these maps can not be considered statistically significant as the P‐value of 0.05 used was not corrected for multiple comparisons (rather, statistical significance was determined via ROI analysis).

An important issue to consider when examining correlations in steady state portions of block design data is how those correlations are influenced by hemodynamic changes at block boundaries. In this study, 18 sec worth of images at the start of each block were discarded (before analyzing each of the two conditions), but perhaps that was not sufficient to eliminate all correlations arising from the blocked structure of the data. To investigate this issue further, maps of correlations with the left premotor region of interest in the steady state runs were computed. Correlations with the premotor ROI in the steady state runs cannot be rigorously evaluated for significance (as such analysis would be post‐hoc), however, this does not preclude a qualitative examination of the correlations to the premotor ROI present in the steady state data set. These correlations can be compared to the those found in steady state portions of the block design data set to determine if the blocked structure of the data played a prominent role in the correlations shown in Figure 4.

The correlations with the left premotor ROI the two types of steady state runs are shown in Figure 5. These maps are strikingly similar to the maps of correlations to the left premotor ROI computed in steady state portions of the block design data (Fig. 4). Once again, in the resting condition, the strongest positive correlations are with right premotor cortex, Broca's area and Wernicke's area, and the strongest negative correlation is with posterior cingulate. There are also similarities in the changes in these correlations with condition. In particular, in the continuous listening condition, the negative correlation with the posterior cingulate disappears in the ventral slices and a positive correlation appears in the region of the caudate. There are some differences between the pattern of correlations to this premotor region seen in the steady state runs (Fig. 5) and those seen in steady state portions of the block design runs (Fig. 4). Given the low threshold used for these maps, however, the similarity in the patterns of correlations found in the two data sets for each condition are remarkable. This suggests that the correlations found in steady state portions of block design data were determined primarily by steady state correlations, and to a trivial degree (if at all) by block‐related hemodynamic effects.

Exploring the possibility of further iterations

The maps of correlations with the region in premotor cortex are suggestive of certain patterns of connectivity that could be investigated further. For example, an increase in correlation between the signals in the left premotor ROI and the left caudate nucleus is apparent during the listening task. This suggests that there may be a connection between these regions, and that this connectivity may play a role in speech perception. One possibility is that a correlation between premotor cortex and the caudate arises indirectly because these regions are mutually correlated with Broca's area. Examining the map of correlations with Broca's area found during the listening task at a variety of thresholds, however, did not reveal correlation with the caudate. Figure 6 presents a comparison between correlations with premotor cortex and correlations with Broca's area in the steady state listening data. The negative activation indicates that pixels in the vicinity of Broca's area have timecourses more correlated with the timecourse of Broca's area than with that of premotor cortex and, conversely, the positive activation in the vicinity of left premotor cortex indicates that those pixels were more correlated with left premotor cortex than with Broca's area. In addition, there is a positive activation seen in the left caudate. This indicates that the left caudate has a stronger correlation with left premotor cortex than with Broca's area, and suggests that the correlation between the premotor ROI and the caudate noted in Figure 4b, if significant, is probably not due to mutual correlations with Broca's area. The caudate may therefore be an interesting reference region for continuing correlational analyses.

Figure 6.

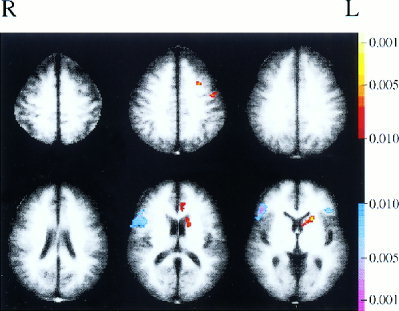
Difference map showing areas that are more correlated with the premotor ROI than with Broca's region in continuous listening runs (cutoff of P < 0.05).

DISCUSSION

A significant low frequency correlation was found between Broca's and Wernicke's ROIs in the resting data. As these regions are nonhomologous and nonadjacent, this correlation cannot be attributed to symmetry in the blood supply routes of these regions or to the low spatial resolution of functional MRI. Thus, the low frequency resting state correlation found between these functionally related brain areas supports the possibility that such correlations can reveal functional connections between brain regions that are components of high level cognitive systems. The pattern of correlations with Broca's area found during continuous speech qualitatively reproduced the pattern found in the resting state data set, suggesting that the correlations under the two different conditions (i.e., the rest and listening conditions) were reflecting connections within the same functional network. Additionally, the increase in the magnitude of correlation between areas long implicated in language processing (i.e., Wernicke's and Broca's) during the listening task supports the view that the magnitude of low frequency correlations in steady state data can reveal the degree of functional interaction between regions.

This study adds to a growing body of research suggesting that temporal correlations in resting (and other forms of steady state) functional imaging data can provide information regarding functional connections in the brain [e.g., Biswal et al., 1995, 1997a,b; Lowe et al., 1998, 2000a,b; Xiong et al., 1999]. This suggests a new approach to functional imaging that may have advantages over currently popular imaging protocols. Although conventional fMRI subtraction paradigms can investigate only those psychological functions that differ between the specific task performed and the control task used, data collected in steady state scans (such as resting scans) may be used to examine functional connectivity in many different psychological systems. More importantly, subtraction paradigms generally provide information regarding task‐related activation of individual regions, and correlational studies may have the potential to provide complementary information about the functional interactions between regions, and how those interactions change under different task conditions and mental states. Given that a major aim of neuroimaging is to identify networks of neural systems responsible for brain function, this possibility is of great interest.

There are a range of approaches to investigating functional connectivity. Previous studies of functional connectivity have examined correlations (or covariations) between regions across subjects [Clark et al., 1984; Horwitz et al., 1984, 1991; Metter et al., 1984; Moeller et al., 1987; Peterson et al., 1999], over time [Friston et al., 1993; Lowe et al., 2000b] or some combination of both [Buechel and Friston, 1997; Prohovnik et al., 1980]. These methods have great potential for investigating the neural bases of brain function. Interregional correlations, however, do not necessarily imply physical connectivity or even causal interactions between regions because confounding sources of correlations may be present. To address this limitation of correlational techniques, a range of studies have been developed that combine correlational analyses with known anatomical constraints [McIntosh and Gonzalez‐Lima, 1991; Paus, et al., 1996; Tamada et al., 1999]. An alternative to correlational studies, introduced by Paus et al. (1997), is to investigate causal interactions between brain regions directly by stimulating a brain area with transcranial magnetic stimulation and using positron emission tomography to measure the resulting changes in regional cerebral blood flow that occur across the brain. Although very promising, this approach has the drawbacks that it cannot at present reveal projections arising from subcortical structures, that it is invasive, that multiple cytoarchitectonic and functional areas are stimulated simultaneously, and that the stimulation is nonphysiologic. Finally, there are global variance‐based analyses that can be used to identify distributed networks of brain areas that behave in similar ways over time or across tasks, such as principle‐component analysis [Friston et al., 1993] and partial least squares [McIntosh et al., 1996]. These methods have great utility for investigating brain behavior at the systems level. They do not, however, provide estimates of the significance or strength of specific interregional functional connections.

When correlational studies of functional connectivity are undertaken, they should be designed to minimize sources of confounding correlations. In this respect, the examination of low frequency temporal correlations in steady state data has advantages over other correlational approaches to studying functional connectivity. For example, across‐subject correlational methodologies cannot distinguish whether correlations arise from temporal synchrony of regional activity within subjects, or from static differences in network activation across subjects. This is not an issue in studies that examine correlations within subjects over time. Even for studies examining within‐subject correlations, however, it is possible that correlations could arise between functionally unrelated brain regions responding to different aspects of the same stimuli. This problem is likely minimized (although not completely eliminated) in studies that examine correlations in steady state data because there are no onsets or offsets in the stimuli to drive correlations.

The examination of steady state temporal correlations within individual subjects may prove to have unique utility. One advantage to the use of within‐subject correlations rather than across‐subject correlations is that relationships between the correlations found and individual behavioral scores can be computed across the subject population. Such analyses may ultimately prove useful in elucidating brain‐behavior relationships. When examining correlations in resting data, there are the advantages that multiple systems can be investigated in a single data set, and that brain function can be studied without requiring subjects to perform tasks that may be difficult or impossible for certain patient populations.

In addition to providing support for the view that low frequency temporal correlations between brain areas in steady state data can reveal functional connectivity, this study proposes an iterative method for identifying and evaluating these interregional correlations. Two iterations were performed to illustrate the proposed methodology. These two iterations revealed patterns of functional connectivity in the language perception system. In the first iteration, the confirmation of a resting state correlation between Broca's and Wernicke's areas, and the confirmation of an increase in this correlation during the listening condition, were obtained. In the second iteration, a region in left premotor cortex was found to have a significant correlation with Broca's area at rest and during the listening task.

One possible explanation for the correlation found between Broca's area and the premotor region is that the premotor area plays a role in language perception. The role of motor processing in language perception has long been an intriguing issue [Liberman et al., 1967]. Previous studies have found activations in premotor cortex during tasks involving speech comprehension and have suggested that this region is involved in the semantic processing of linguistic material, particularly those aspects of semantic processing involving spatial imagery or relational analysis [Inui et al., 1998; Mellet et al., 1996; Nakai et al., 1999]. Alternately, a resting correlation between Broca's area and left premotor cortex could be interpreted to reflect a functional connection that is important for tasks other than language. For example, Broca's area has been implicated in motor imitation tasks (see Iacoboni et al., 1999; Nishitani and Hari, 2000). A connection between Broca's area and left premotor cortex could facilitate the involvement of Broca's area in such motor related tasks.

If the correlation between Broca's area and left premotor cortex reflects a functional connection that is important for language processing, it would be expected to increase during the listening task. If it reflects the importance of Broca's area in tasks other than language, however, it would be expected to diminish (or at least not to increase) during the passive listening task. Examination of correlations in steady state portions of the block design data set revealed that the correlation between Broca's area and the left premotor ROI did increase in the listening condition, although the change in correlation was not quite significant across condition (P = 0.051). Therefore, the findings from this study tentatively suggest that this left premotor region plays a role in language processing. Further investigation is warranted.

The analyses were not carried on for further iterations, although it would be possible to do so. There were many potentially interesting regions that could have been investigated. The left caudate nucleus was discussed as one particularly interesting candidate. This region appeared to be correlated with the left premotor ROI during the continuous listening task although it showed little or no correlation to Broca's area during the listening task.

The significance of the correlation between premotor cortex and the caudate nucleus during continuous listening could have been evaluated by continuing with further iterations of analyses. First the caudate would have to be defined for each subject based on that subjects' map of correlations with premotor cortex obtained from steady state continuous listening portions of the block‐design data set. These newly defined regions could then be used as the reference regions to create a new set of correlation maps using the continuous speech data from the steady state runs, and the correlation between the caudate and premotor cortex could then be evaluated based on these new correlation maps. This process would parallel that used in establishing significance of the premotor‐Broca's area correlations, except that the roles of the two data sets would be reversed. This time, the region would be defined based on correlations in the block‐design data set and then evaluated statistically based on correlations in the steady state data set.

Note that this type of analysis may be repeated multiple times, exchanging the roles of the two data sets each time. Therefore, via such an iterative procedure, it may be possible to track functional connectivity through a network of regions. A carefully designed protocol may allow multiple iterations and may thus be used to map out a complex cognitive network.

To map out multiple disjoint networks is more difficult for this method because to investigate a given network requires that two regions that are known to be involved in that network can be functionally localized (in the case of the example presented here, Broca's and Wernicke's regions were used as these “seed” regions and were localized using block‐design speech runs). It may be possible to investigate two networks in one study by including more than one set of block‐design runs (one for each network of interest) in the same scanning session. Limitations on the amount of data that can be collected in a scanning run, however, will severely limit the number of networks that can be investigated in a single study. Alternate approaches, such as the methods described by Worsley et al. [1998], should be considered for examining multiple networks at once, although the sensitivity of such methods may be a concern.

The proposed iterative method for examining functional connectivity provides increased sensitivity by avoiding the need to correct for many multiple comparisons. Results obtained using this method, however, must be interpreted with caution because correlations with predefined regions are not always independent. For example, a correlation between the caudate nucleus and Broca's area could arise in the steady state resting runs because the caudate is correlated at rest with left premotor, which was defined based on it's correlation with Broca's area in that data set. Additional strategies, however, such as partial correlation analysis or segmenting the data into multiple independent samples may address this potential limitation.

Finally, when interpreting data from any correlation‐based study of functional connectivity, it is important to remember that correlations between brain regions do not imply specific causal interactions (for example, a correlation between Regions A and B may arise because A influences B, because B influences A, because some third region, C, influences both A and B, or for many other reasons). To address such issues, methods designed to determine the direct, causal interactions between brain region (i.e., the effective connectivity) may be employed [Friston et al., 1997; McIntosh and Gonzalez‐Lima, 1991]. Such methods generally rely upon a model of the system of interest that incorporates information regarding which brain regions are involved in the system, and the possible anatomical connections between those brain regions. Methods that identify functional circuits, such as the one described in this study, can help in the development of such models. In addition, information regarding the functional connections between regions may be used directly in computing effective connectivity. For example, structural equation modeling [Gonzalez‐Lima and McIntosh, 1994; Grafton, et al., 1994; McIntosh and Gonzalez‐Lima, 1991, 1994] uses interregional correlation matrices to estimate effective connectivity within a brain circuit. Thus, to gain an understanding of causal relationships in brain circuitry, computational analyses that are designed to elucidate patterns of effective connectivity may be applied to functional connectivity data.

CONCLUSIONS

This study provides strong support for the hypothesis that functional connectivity between brain areas may be investigated by examining low frequency temporal correlations in steady state data. The biological basis of these low frequency correlations between functionally connected regions is a matter for further investigation. It has been suggested that they may be related to the low frequency oscillations in cerebral hemodynamics and metabolism that have been found in different species [Biswal et al., 1995; see discussion by Obrig et al., 2000]. It is also possible that they are related to variations in cognitive activities occurring during the so‐called “steady state” periods. Regardless of the underlying mechanism responsible for these correlations, they may provide a powerful way of examining brain circuitry.

This study confirms that such correlations can be found between highly neurally connected, nonadjacent, nonhomologous regions within a higher‐level brain system. In addition, a method has been proposed for tracking such correlations across functionally connected regions in a cognitive network. This method involves alternating between independent data sets, defining regions based on correlations in one data set and evaluating the significance of these correlations in the remaining data set. The results from the application of this method to a well‐studied system (the language perception system) are promising. Further studies using this approach and similar methodologies may potentially provide valuable insight into the nature of cognitive connectivity.