Spatial‐temporal structures of human alpha rhythms: Theory, microcurrent sources, multiscale measurements, and global binding of local networks

Abstract

A theoretical framework supporting experimental measures of dynamic properties of human EEG is proposed with emphasis on distinct alpha rhythms. Robust relationships between measured dynamics and cognitive or behavioral conditions are reviewed, and proposed physiological bases for EEG at cellular levels are considered. Classical EEG data are interpreted in the context of a conceptual framework that distinguishes between locally and globally dominated dynamic processes, as estimated with coherence or other measures of phase synchronization. Macroscopic (scalp) potentials generated by cortical current sources are described at three spatial scales, taking advantage of the columnar structure of neocortex. New EEG data demonstrate that both globally coherent and locally dominated behavior can occur within the alpha band, depending on narrow band frequency, spatial measurement scale, and brain state. Quasi‐stable alpha phase structures consistent with global standing waves are observed. At the same time, alpha and theta phase locking between cortical regions during mental calculations is demonstrated, consistent with neural network formation. The brain‐binding problem is considered in the context of EEG dynamic behavior that generally exhibits both of these local and global aspects. But specific experimental designs and data analysis methods may severely bias physiological interpretations in either local or global directions. Hum. Brain Mapping 13:125–164, 2001. © 2001 Wiley‐Liss, Inc.

1. INTRODUCTION

Spontaneous EEG was first recorded from a human scalp in the mid‐1920s by the psychiatrist [Hans Berger 1929]. These first human data were ubiquitous and robust alpha rhythms. Human alpha rhythms are defined as oscillations of electric potential in the 8–13 Hz range, normally recorded with larger amplitudes over posterior regions with eyes closed. Alpha rhythms and most other scalp EEG are believed to represent oscillations of postsynaptic potentials in neocortex [Klass and Daly, 1979; Nunez, 1981; Niedermeyer and Lopes da Silva, 1999]. However, the physiological bases for oscillatory EEG behavior, for example the underlying time constants responsible for specific frequency ranges, are poorly understood [Nunez, 1995, 2000a, 2000b; Steriade, 1999; Lopes da Silva, 1991, 1999].

Better understanding the complex dynamics of EEG will require a sophisticated grasp of interactions between several subfields of EEG. Of special importance are volume conduction, dynamic theory, the influence of neuromodulators on dynamic control parameters (e.g., time constants and feedback gains), distinction between robust and unusual spatial‐temporal EEG properties, and biases of specific experimental methods for revealing (or obscuring) dynamic behavior. This will require better communication among clinicians, experimental neuroscientists, and theoreticians. Misconceptions of EEG, especially of volume conduction and reference electrode effects, have been well documented. Such fallacies can influence both experimental design and physiological interpretations of data [Klass and Daly, 1979; Nunez, 1981, 1990, 1995; Gevins and Cutillo, 1986, 1995; Nunez et al., 1991, 1994, 1997, 1999; Silberstein et al., 1990; Silberstein, 1995a; Niedermeyer and Lopes da Silva, 1999].

In recent years more scientists with training in engineering or physics have published in the neuroscience literature, partly as a consequence of the relatively new fields of MEG, PET, and MRI. The resulting mathematical models have facilitated better understanding and experimental design. Still there is no substitute for experience with data. Genuine theory in any field, as opposed to isolated mathematics, requires close contact with data. Thus, EEG theoreticians must develop an intuitive feeling for experimental EEG in order to connect theory to experiment. While this may seem obvious, implementation of genuine theory in EEG has been slow to develop, partly because of its considerable interdisciplinary character [Nunez, 1995, 2000b].

The issues cited above provide motivation for this paper. We first review robust dynamic properties of EEG recorded from human cortex and scalp. Several theoretical issues concerning volume conduction, source dynamics, and their manifestations as EEG are discussed. Connections between synaptic current sources, dipole moment per unit volume at mesoscopic scales (between micro and macro), and scalp potential are outlined. High spatial resolution EEG is considered in the context of spatial filtering by the head volume conductor. The multiscale character of brain dynamics is emphasized, in which dynamic EEG properties may depend critically on both spatial and temporal measurement scales. We argue that conventional scalp EEG, high‐resolution scalp EEG and intracranial recordings with electrodes of different size provide overlapping but partly independent measures of brain function. We challenge the belief (perhaps widely held) that cortical recordings (ECoG) necessarily provide a “gold standard” for dynamic behavior of neocortex. ECoG typically provides very limited spatial sampling, is limited to a particular spatial scale determined partly by electrode size, and may be dominated by high spatial frequency dynamics. We suggest that different parts of the spatial spectrum may be of primary interest in different studies. In particular, cognition (and associated brain binding) may be strongly correlated with relatively low spatial frequency activity, involving the integrated activity of tens of millions of neurons.

This combined experimental/theoretical discussion provides background for new experimental data on human spontaneous EEG presented in Section 6, concerned with EEG amplitude, phase, and coherence while resting and performing mental calculations. Later papers are planned to address more detailed dynamic issues closely associated with local and global physiological theories as well as cognitive connections currently underway at the Brain Sciences Institute. Topics include high‐resolution estimates of spherical harmonic spectra, cortical resonance response to sine wave modulated light, and EEG dynamics during several drugs states. We mean for this (mostly) theoretical paper to provide guidelines for many later experimental EEG studies by other scientists as well as ourselves.

2. HUMAN SPONTANEOUS EEG

2.1 Alpha rhythms

Discussion of human spontaneous EEG begins appropriately with alpha rhythms for both historical and clinical reasons. Scalp alpha rhythms provide the appropriate starting point for clinical EEG exams [Kellaway 1979; Niedermeyer, 1999a]. Some initial clinical questions include: Does the patient show an occipital alpha rhythm? Are the spatial‐temporal characteristics appropriate for the patient's age? How does the patient react to eyes opening, hyperventilation, drowsiness, etc? For example, pathology is often associated with pronounced hemispheric asymmetry or low alpha frequencies. In most adults, alpha rhythms consist of frequencies in the 9–11 Hz range when recorded from the scalp with eyes closed. A resting alpha frequency lower than about 8 Hz in adults is abnormal in all but the very old.

Classical alpha rhythms may be recorded in roughly 95% of healthy adults with closed eyes [Nunez, 1981]. By “classical” we refer to the common clinical definition of near sinusoidal oscillations. (With the usual clinical definition, “nonalpha” EEG may exhibit substantial spectral spectral power in the alpha band, sometimes leading to confusion in studies of physiological bases for alpha.) Normal waking alpha rhythms usually have larger amplitudes over posterior regions, but are typically recorded over widespread scalp regions. Alpha amplitude in 75% of normal adults lies in the range 15 to 45 μV when recorded from the posterior bipolar electrodes P4–O2 (6.5 cm spacing); amplitudes recorded from frontal electrodes are lower [Kellaway, 1979]. A posterior rhythm of approximately 4 Hz develops in babies in the first 3 months after birth. It increases in amplitude with eye closure and is believed to be the precursor of alpha rhythm [Bickford, 1973; Niedermeyer, 1999b]. Posterior scalp alpha amplitudes in children older than about 3 years are substantially larger than adult amplitudes, perhaps partly because of volume conduction effects, e.g., incomplete skull closure. Maturation of the alpha rhythm is characterized by increased alpha frequency (between ages of about 3 and 10). A corresponding reduction in delta activity (0–4 Hz) is also common. Such delta reductions may continue through age 25 to 30 [Pilgreen, 1995; Niedermeyer, 1999a], a time when myelination of cortico‐cortical fibers is nearly complete [Yakovlev and Lecours, 1967; Courchesne, 1990].

Normal awake alpha rhythms may be “blocked” (substantially reduced in amplitude) by eye opening, drowsiness, and moderate to difficult mental tasks. EEG phenomena typically exhibit an inverse relationship between amplitude and frequency [Barlow, 1993]. Hyperventilation and some drugs often cause reductions of alpha frequencies together with increased amplitudes [Bickford, 1979]. This effect may occur with alcohol, for example [Shichijo et al., 1999]. Other drugs (e.g., barbiturates) are associated with increased amplitude of the small amount of beta activity often superimposed on scalp alpha rhythms [Niedermeyer and Lopes da Silva, 1999]. The physiological bases for inverse relations between amplitude and frequency and most other salient characteristics of EEG are unknown, although several physiologically based theories have been proposed to account for such properties.

2.2. Frontal alpha

The EEG literature sometimes treats alpha primarily as a occipital‐parietal rhythm. In extreme cases, a few “equivalent alpha dipoles” have been proposed. Yet in the classical studies by Jasper and Penfield [1949], alpha rhythms were recorded from nearly the entire upper cortical surface (including frontal and prefrontal areas) in a large population of patients awake prior to surgery [reviewed in Nunez, 1995]. The exceptions involved regions close to the central motor strip where beta activity (> 13 Hz) appeared to be dominant, at least by visual inspection (before spectral methods came to EEG). Furthermore, our own studies of healthy young subjects (and some not so young) in relaxed states show substantial frontal alpha [Nunez, 1995].

Some discrepancy of views about the spatial distribution of alpha can be explained as follows. First, EEG clinical populations are biased toward patients who are older, have neurological problems, or may be anxious during the recording. These factors tend to work against production of robust, widespread alpha. Second, the clinical definition of alpha is based on raw waveforms rather than spectra. With this view, “alpha rhythms” have quasi‐sinusoidal waveforms, i.e., distinct peak (or peaks) between 8 and 13 Hz in amplitude spectra. Often alpha is identified clinically by simply counting the number of zero crossings. While this definition of alpha is apparently appropriate clinically, it can provide misleading views of possible physiological bases. The reason is that raw EEG composed of broad frequency bands can appear very “nonalpha” to visual inspection, even though amplitude spectra show substantial contribution from the alpha frequency band. This potential misconception can be especially pronounced when the raw record contains substantial beta activity, which tends to attract the eye and increase the number of zero crossings, perhaps leading to overemphasis in qualitative descriptions. A third reason for differing views about spatial properties of alpha is that the human alpha band contains multiple rhythms that apparently interact to varying degrees in different brain states. Some alpha phenomena are widely distributed and some are more localized.

We demonstrate these ideas in Figure 1, which shows amplitude spectra for EEG recorded from four scalp locations of a normal (age 38) female subject. Potentials were recorded with respect to a (symmetric) averaged‐ears potential reference in the eyes closed, relaxed state. The scalp locations are left and right frontal (upper row) and left and right parietal (lower row). Spectral peaks in the alpha band are dominant at all scalp locations, with delta, theta, and beta activity also evident. Theta rhythm is most notable in frontal regions. The small amount of delta activity is believed to be brain generated, although it is difficult to separate from subtle, low amplitude, low frequency artifact (movement, EKG, and so on). These are normal alpha spectra for a healthy subject.

Figure 1.

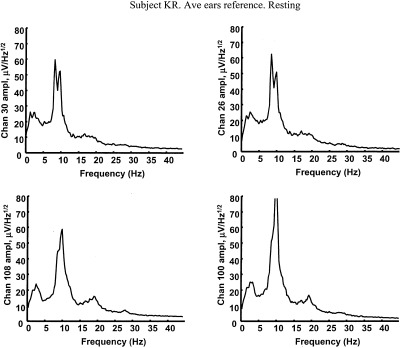
Amplitude spectra based on 5 min of resting EEG (0.2 Hz resolution) with eyes closed, referenced to the (symmetric) digitally averaged potential of the ears. The subject KR is a 38‐year‐old female engineering graduate student. The four locations correspond to left and right frontal and left and right posterior scalp (nose up), roughly sites F3, F4, P3, and P4.

When these raw scalp data are passed through high‐resolution algorithms (dura image or spline‐Laplacian), power in the alpha band is typically reduced relative to power in other bands. High‐resolution algorithms spatially filter potentials so that they only record activity from sources within a few centimeters of the electrode (both tangentially and in depth). They are “conservative” estimates in the sense that they mostly eliminate volume conduction effects, but they also remove genuine low spatial frequency source dynamics generated in cortex or subcortical regions, as shown in Section 3. Data presented in Section 6 suggest that alpha rhythms consist of spatially coherent global dynamic activity (partly removed by high‐resolution methods) plus local activity that remains after spatial filtering.

In scalp recordings, larger frontal alpha is often observed as subjects become more relaxed, e.g., while slowly counting breaths or with other relaxation techniques. Alpha rhythm of unusually large amplitude, occurring over the entire scalp and sometimes exhibiting frontal dominance, may be associated with mental retardation in children [Bickford, 1973] or some types of epilepsy [Kellaway, 1979]. Large amplitude frontal alpha rhythms may also be recorded in coma and anesthesia states [Nunez, 1981, 1995; Niedermeyer and Lopes da Silva, 1999]. In summary, frontal alpha rhythms of moderate amplitude are common in healthy relaxed subjects with closed eyes. Widespread alpha of large amplitude (often larger in frontal regions) may occur with trauma, disease or anesthesia. The physiological relationships between these disparate alpha phenomena are unknown. But, because they have similar frequencies, one may conjecture that they share some underlying physiology.

2.3. Synaptic action is imperfectly related to measured potentials

Cortical and scalp alpha potentials are believed generated through (millisecond scale) modulations of synaptic current sources at the surfaces of neocortical neurons [Lopes da Silva and Storm van Leeuwen, 1978; Nunez, 1981, 1995, 2000a, 2000b; Lopes da Silva, 1999]. Here we distinguish these millisecond “modulations” of synaptic current sources about background synaptic action from much longer time‐scale modulations associated with neurotransmitters (neuromodulators). For example, we might imagine the 40 Hz natural frequency of a local neural network (due to millisecond synaptic source modulations) to change as network parameters vary over relatively long time scales because of neurotransmitter action. A physical analog may help to distinguish modulation time scales. Sound waves in air are short time‐scale pressure modulations about background pressure, analogous to modulations of synaptic action in neocortex. But, sound properties (e.g., propagation speed) may be changed by external influences like long time scale modulations in air temperature, analogous to chemical modulations of neocortex.

The existence of such millisecond modulations does not, however, guarantee that corresponding scalp (or even cortical) surface potentials will be observed. Calling on our physical analog, the presence of sound waves does not guarantee that they will be recorded. Recordable surface potentials (cortex or scalp) require sufficient modulation depth of synaptic action, which can be measured as relatively large potential differences between deep and superficial cortex, e.g., several hundred microvolts [Lopes da Silva and Storm van Leeuwen, 1978; Petsche et al., 1984]. Recordable scalp potentials also require substantial source activity at low spatial frequencies, i.e., the sources must be “synchronously active” at scales of at least several centimeters [Cooper et al., 1965; Delucchi et al., 1975; Nunez, 1981; Ebersole, 1997].

In considering possible physiological bases for EEG, this imperfect connection between source modulations and measured potentials should be fully appreciated. In particular, many dynamic systems with finite spatial extent (e.g., with boundary conditions) and supporting signals that propagate with finite speed, exhibit global modulations of field variables. Physiologic‐based theory has suggested that global synaptic action modulations (synaptic action fields) can occur naturally in human neocortex in the general range of EEG frequencies [Nunez, 1974a, 1981, 1995]. Do such global modulations actually occur in human brains? If so, do they help to explain EEG origins? Do synaptic action fields (number densities of active excitatory and inhibitory synapses), which cause but are distinct from electric and magnetic fields, play a part in the processing of information, e.g., brain binding [Nunez, 2000a, 2000b]? While we cannot now provide definitive answers, these questions are central to the theory and experiments reported here and appear to have important implications for more general studies of brain function as well.

Many physical and biological processes can be represented by a field variable P(r, t), where r represents a vector location (in one, two, or three coordinates) in some medium, and t is time. The word “field” can be used to describe nearly any well‐behaved mathematical function of space and time; however, it is most useful when related to measurable variables. Surface potential differences (or macroscopic electric fields), which are measured as EEG, are believed generated by millisecond modulations of large‐scale synaptic action fields, which are not generally measured, but provide a convenient theoretical connection to neural sources. The synaptic action fields are defined simply in terms of the numbers of active excitatory or inhibitory synapses per unit volume of tissue, in a manner similar to definitions of physical macroscopic variables like mass density, temperature, or pressure. These synaptic action fields are purposely defined independently of brain function because of their direct connection to measured scalp potentials. The spatial‐temporal patterns of synaptic action fields developed in neocortex constitute one measure of its dynamic behavior. A dynamic theory may involve many such fields; but only some are directly accessible to experimental measure. The synaptic action fields proposed here involve concepts similar to early ideas about neural mass action [Lashley, 1931; Freeman, 1975; Freeman and Skarda, 1985].

We know of no convincing evidence that the small macroscopic electric fields in the EEG range substantially influence neural firing patterns. However, one can easily envision cell assemblies (e.g., neural networks) operating within a background environment of synaptic action fields [Nunez, 2000a, 2000b]. In this picture, neural networks may be defined in terms of strong preferential connections, strengthened by Hebbian mechanisms, and continuously reformed on millisecond time scales [Gevins and Cutillo, 1986, 1995; Silberstein, 1995b; Ingber, 1995a, 1995b; Nunez, 1995, 2000a; Jirsa and Haken, 1997; Haken, 1999; Edelman and Tononi, 2000]. However, such networks are likely to remain partly (functionally) connected to other tissue not part of the same network. This external tissue may be modeled in terms of synaptic action fields. The idea is analogous to the formation of social networks (neural networks), which are continuously influenced by the global culture (synaptic action fields) in which they are immersed.

2.4. Alpha coherence

Coherence structure of EEG provides clues about local versus global dynamic behavior [Livanov, 1977; Nunez, 1981; Thatcher et al., 1986; de Munck et al., 1992; Petsche and Etlinger, 1998; Nunez et al., 1997, 1999]. Coherence is a correlation coefficient (squared); it measures the phase consistency between pairs of signals in each frequency band. For example, the coherence between the voltages of any two nodes of a linear, isolated, and noise‐free electric circuit is equal to one at all source frequencies since all node voltage phases are fixed over time. By contrast, the coherence between voltages recorded in two noninteracting circuits is generally zero. Thus, coherence provides one important measure of functional interactions between oscillating systems. EEG coherence may yield information about network formation and brain binding.

EEG coherence is a somewhat different measure than EEG synchrony, which refers to sources oscillating roughly in phase with individual contributions to EEG added by superposition. Thus, desynchronization is often associated with amplitude reduction [Pfurtscheller, 1992; Pilgreen, 1995; Pfurtscheller and Lopes da Silva, 1999]. Sources that are synchronous (small phase differences) over substantial times will also tend to be coherent. But, the converse need not be true; e.g., coherent sources may remain approximately 180 degrees out of phase, so their individual contributions to EEG tend to cancel.

Measured EEG scalp coherence is typically moderate to large up to roughly 8–10 cm distances caused only by volume conduction effects [Nunez, 1981; Srinivasan et al., 1996, 1998; Srinivasan, 1999]. It was shown recently that the effects of volume conduction and reference electrode are largely removed using high‐resolution EEG. Resting alpha coherence, estimated with high‐resolution methods, is typically small at distances of a few centimeters or more, except in a narrow band near the peak alpha frequency [Nunez, 1995; Nunez and Pilgreen, 1991]. But, within a bandwidth of perhaps 2 Hz near the spectral peak, alpha often produces moderate to large coherence (e.g., 0.3–0.8) over large interelectrode distances, e.g., 10–25 cm [Nunez et al., 1997, 1999]. This implies that dynamic behavior of neocortical source activity (occupying several cm² of mainly local gyri) exhibits cross‐correlations (square root of coherence) in roughly the 0.5–0.9 range between many distant electrode sites. Thus, normal resting alpha has somewhat of a global character in addition to its local aspects.

Long‐range (e.g., 1 Hz band) alpha coherence may fall near zero during mental activity, even in subjects with minimal reduction in alpha amplitude [Nunez, 1995, 2000a; Nunez et al., 1999]. Upper and lower band alpha coherence can change in opposite directions. Furthermore, reductions in long‐range alpha coherence during mental activity can be concurrent with increases in short‐range coherence in both theta and alpha bands [Sarnthein et al., 1998; Nunez et al., 1999; Wingeier et al., 1999]. Other studies have shown that alpha band activity may increase in one region while decreasing in another in a motor task [Pfurtscheller and Neuper, 1992], i.e., blocking of the so‐called “mu rhythm” near motor cortex. These data are consistent with formation of cell assemblies (or networks) operating in theta and alpha bands, perhaps immersed in a global synaptic action field. The contrasting behavior of long‐ and short‐range coherence, the contrasting behavior of upper and lower band alpha coherence (typically with only 1–3 Hz frequency differences) and the complex amplitude, phase, and coherence behavior of local and global alpha phenomena call into question oversimplified interpretations of alpha origins. Thus, we challenge attempts to dismiss alpha by generic labeling like “pacemaker,” “idling,” or even “epiphenomenon,” labels that tend to explain away (e.g., with tautology) complex brain phenomena because they are poorly understood or don't fit preconceived notions about brain function.

Increases in coherence with maturation have been observed in a large population of children and young adults using reference recordings [Thatcher and Walker, 1985; Thatcher et al., 1986, 1987; Marosi et al., 1992]. However, it is difficult to distinguish the contributions of volume conduction from source coherence with conventional reference recordings [Nunez et al., 1997, 1999; Srinivasan et al., 1996, 1998]. To address this issue, Srinivasan [1999] studied alpha coherence in two groups: 23 normal young adults (age 18–23) and 20 normal children (age 6–11) using a 128‐channel system and high‐resolution algorithm. Larger posterior amplitudes were observed in children than adults with both raw potential and high‐resolution (spline‐Laplacian) estimates, consistent with the classical literature [Kellaway, 1979; Niedermeyer, 1999b]. By contrast, higher anterior‐posterior coherence (e.g., at 10–25 cm electrode separations) was observed in adults than children with both raw potential and high‐resolution estimates. The spline‐Laplacian eliminates most volume conduction (and all reference) effects. Because the higher coherence in adults occurred with (mostly) lower amplitudes, such high coherence is apparently not a volume conduction effect. Rather, it may result from increased cortico‐cortical fiber myelination. This work then supported several of the earlier conclusions about coherence maturation by Thatcher, Marosi and others.

Other studies of EEG coherence involved preparation for motor movements. Changes in EEG coherence between ipsilateral and contralateral sensorimotor regions during planning of finger movements were measured. During one such planning, upper alpha band (10–12 Hz) coherence decreased while gamma band (38–40 Hz) coherence increased in the same data [Andrew and Pfurtscheller, 1996]. Other studies by this group showed that alpha band activity consisted of a mixture of coherent activity (suggesting global mechanisms) with incoherent mu activity (suggesting local mechanisms), which were separately manipulated using motor tasks [Andrew and Pfurtscheller, 1996, 1997; Florian et al., 1998]. In some subjects, “local” and “global” alpha frequency peaks were matched within 1 Hz. In others, spectral peaks were separated by 2–3 Hz. A third kind of alpha rhythm has been recorded from temporal cortex, considered independent of occipital alpha in the sense that it is not blocked by eye opening [Niedermeyer, 1999a]. An apparently similar rhythm with reactivity to sound has also been reported in MEG studies [Hari and Salmelin, 1997; Hari, 1999]. These data may be interpreted in terms of specific local networks that can generate rhythms in the alpha and gamma bands.

We don't deny that rhythms in one cortical region are partly independent from rhythms in other regions; i.e., they exhibit local properties. However, we suggest that such local rhythms can occur simultaneously with global oscillations in the same frequency ranges, which in some states may facilitate and synchronize local rhythms [Nunez, 1989, 1995, 2000a, 2000b; Silberstein, 1995b]. Such top‐down interactions are well known in a variety of complex physical systems having spatial extent [Haken, 1983; Ma, 1985; Ingber, 1995; Nunez, 1995].

2.5. Alpha, theta, cognitive tasks and working memory

At least two prominent features of human scalp EEG show robust correlations with mental effort. First, broadband alpha amplitude often tends to decrease (desynchronization) with increases in mental effort [reviews by Pfurtscheller et al., 1996; Gevins et al., 1997]. Second, frontal theta band amplitude tends to increase as tasks require more focused attention [Gundel and Wilson, 1992; Gevins et al., 1997]. In addition to the amplitude changes, recent coherence studies have shown that mental tasks with working memory components can cause robust reductions in long‐range coherence in narrow (1 or 2 Hz) alpha bands, while theta coherence increases [Nunez, 1995; Petsche and Etlinger, 1998; Sarnthein et al., 1998; Nunez et al., 1999; Wingeier et al., 1999]. Large alpha coherence reductions can occur even with no appreciable reduction in alpha amplitude.

At least superficially, some of these data appear to support the common view of alpha rhythms as simple brain idling [Pfurtscheller et al., 1996]. However, the idling picture has recently been challenged from several disparate directions [Nunez, 1995, 2000a, 2000b; Klimesch, 1996; Basar et al., 1997; Silberstein, 1997; Petsche and Etlinger, 1998]. For example, upper and lower alpha band amplitude may change independently, depending on scalp location and task [Gevins et al., 1997; Petsche et al., 1997]. Some tasks cause lower alpha band amplitude to decrease while upper alpha band amplitude increases [Petsche and Etlinger, 1998; Klimesch et al., 1999]. It has been suggested that local reductions in alpha amplitudes occur in task‐relevant brain areas, whereas task‐irrelevant regions may be unchanged or even produce larger alpha amplitudes [Klimesch et al., 1999].

Increases in alpha amplitudes have been observed in short‐term memory tasks. In particular, higher memory demands were associated with increases in upper alpha band activity at frontal and temporal sites [Petsche and Etlinger, 1998; Klimesch et al., 1999]. Similar increases in amplitude of 13‐Hz steady state visual‐evoked potentials at frontal and occipital sites in a working memory task have been observed [Silberstein, 1997]. One interpretation of such increases in upper alpha band amplitude is reduced neural network activity (implying transition to larger scale synchronization) in regions not participating in the task, consistent with the idling hypothesis [Pfurtscheller and Lopes da Silva, 1999]. But another hypothesis is that increases in upper alpha and steady state‐evoked potential amplitudes in the upper alpha band (e.g., 13 Hz) indicate a specific memory processing function (and by implication, associated neural network) and not simple idling. Such hypothesis is consistent with findings of enhanced prefrontal upper alpha amplitude in a short‐term memory task known to activate the prefrontal cortex [Goldman‐Rakic, 1996].

Some data support the alpha idling idea, but other data refute it. However, all these data appear to fit naturally into a local‐global picture in which global modulations of synaptic action in multiple frequency bands (especially alpha) cooperate with local oscillatory dynamics to produce recordable EEG. This framework, which directly addresses the so‐called binding problem, is discussed in Section 2.6. Another common view, that alpha rhythm is caused by a thalamic pacemaker, has been severely challenged [Lopes da Silva et al., 1980, 1997; Nunez, 1981, 1995; Lopes da Silva, 1991, 1995, 1999; Basar et al., 1997; Steriade, 1999]. The recent data reviewed here and new data presented in Section 5 appear to render nonviable the idea of a simple thalamic alpha pacemaker. Rather, we suggest these data support the early (1964) description by EEG pioneer Grey Walter [quoted in Basar et al., 1997] based on extensive intracranial recordings: “We have managed to check the alpha band rhythm with intra cerebral electrodes in the occipital‐parietal cortex; in regions which are practically adjacent and almost congruent one finds a variety of alpha rhythms, some are blocked by opening and closing the eyes, some are not, some respond in some way to mental activity, some do not. What one can see on the scalp is a spatial average of a large number of components, and whether you see an alpha rhythm of a particular type or not depends on which component happens to be the most highly synchronized processes over the largest superficial area; there are complex rhythms in everybody.”

2.6. Phase synchrony and the binding problem

Reduction in alpha amplitude at the scalp is commonly referred to as desynchronization, implying that phase matching of cortical source activity over at least several cm² contributes more to large scalp amplitudes than the other obvious factor, source modulation depth (or amplitude of transcortical potential). This general view is supported by volume conductor theory and comparisons between EEG and simultaneous cortical recordings [reviews by Nunez, 1981, 1995]. We have discussed the importance of EEG coherence, but coherence and synchrony are not the same measure. Coherent activity need not be synchronous. However, as a general rule, synchronous source activity over long times (e.g., tens of seconds) and large distances (several cm or more) can generally be expected to produce substantially higher EEG coherence estimates than desynchronized sources.

Any study of synchrony or coherence in brains must consider spatial scale. High synchrony at one scale need not occur with high synchrony at a different scale [Nunez, 1995; Nunez and Silberstein, 2000]. Microsource synchrony in directions along cortical column axes will generally have a much different effect on scalp potential amplitude than mesoscopic synchrony between different columns as discussed in Section 3. Here, it is useful to distinguish short‐range synchrony (mm scale associated with intracranial microelectrodes), intermediate range synchrony (roughly the 1–3 cm scale), and long‐range synchrony (10–25 cm scale associated with scalp EEG). In animals, short‐range gamma synchrony [Singer and Gray, 1995] and long‐range synchrony over broad frequency bands at small scales [Bressler, 1995; Roelfsema et al., 1997] were measured in connection with various behavioral conditions.

In humans, increases in long‐range covariance (presumably related to synchrony at relatively low temporal frequencies, e.g., theta and alpha) has been associated with correct performance on working memory and other tasks using high spatial resolution scalp EEG [Gevins and Cutillo, 1995]. In another high‐resolution scalp EEG study, consistent reductions in long‐range alpha coherence together with increases in long‐range (e.g., frontal to frontal and frontal to central) theta coherence occurred during a mental calculation task with a memory component [Nunez et al., 1999]. Similar theta (4–7 Hz) coherence increases between prefrontal and posterior cortical association areas were reported during working memory retention using a digitally linked‐ears reference [Petsche and Etlinger, 1998; Sarnthein et al., 1998].

In MEG studies, binocular rivalry experiments (with dissimilar objects presented to the two eyes) have shown substantial increases in intrahemispheric and interhemispheric (driven) theta coherence during periods of perceptual dominance, i.e., conscious perception of a single object [Srinivasan et al., 1999; Edelman and Tononi, 2000]. Intracranial human recordings have associated long‐range gamma synchrony between hippocampus and frontal gyrus with performance of a visual discrimination task [Lachaux et al., 1999]. This later study estimated phase synchrony as a function of time by convoluting EEG time series with a Gabor wavelet, a synchrony measure more accurate than coherence when applied to the short time series obtained in these experiments.

While scalp coherence and covariance measures are not direct measures of source synchrony [Lachaux et al., 1999], robust increases in these estimates during task performance implies increases in large‐scale source synchrony. (It should be noted, however, that cross‐checking of physiological hypotheses with different data reduction measures is generally a good idea.) Furthermore, with many cognitive tasks, coherence (or perhaps just coherence based on standard FFT methods) may not be sensitive enough to measure subtle changes in phase synchrony, especially when such changes occur over short times [Andrew and Pfurtscheller, 1995; Schack and Krause, 1995]. The evidence for synchronous cortical source activity (direct or indirect) may be interpreted in terms of both “perceptual binding” at short range (e.g., within a single sensory area) and overall binding of cognitive functions involving sensory, motor, and memory systems at long range [Bressler, 1995; Silberstein, 1995a, 1995b; Singer, 1993; Singer and Gray, 1995; Gevins and Cutillo, 1995; Castelo‐Branco, 1998; Lachaux et al., 1999; Edelman and Tononi, 2000].

Increases in scalp amplitude in particular frequency bands are believed to occur largely as a result of increases in intermediate range synchrony between cortical columns (discussed in Sec. 3.4). Our experiments show that decreases in long‐range alpha coherence may occur simultaneously with increases in short‐range alpha coherence during a cognitive task. Also, upper alpha band coherence may increase while lower alpha band decreases. These data imply formation of local alpha and theta networks partly distinct from, but perhaps interacting with, global alpha rhythms. Generally, they challenge the ideas that cognitive events are exclusively associated with the gamma band, or that frequency bands associated with behavior are necessarily the same in different animal species and humans.

2.7. Possible physiological bases for alpha rhythms

A picture of multiple alpha rhythms similar to Grey Walter's description (Sec. 2.5) was also reported in dogs [Lopes da Silva and Storm van Leeuwen, 1978]. Some may interpret these multiple alpha rhythms as evidence for multiple isolated networks (generators) with different properties at different brain locations, e.g., the purely local interpretation. Perhaps this is the simplest explanation, but such application of Occam's razor should be used cautiously. Here we take a broader and more cautious view. We consider the isolated sources (or local) interpretation to be a special case of a more general picture consisting of local, regional, and global mechanisms, in which interactions between nonlocal sources may (or may not) be an essential aspect of the dynamics, depending partly on brain state. In particular, source oscillation frequencies may or may not be partly determined by mesoscopic (e.g., column) source interactions [van Rotterdam et al., 1982]. If such regional and global interactions turn out to be negligible for experiments conducted with electrodes of certain size and location (determining the spatial scale of measurement), for particular brain states or for certain animal species, then the isolated sources explanation is correct for these experimental conditions. If not, then regional or global influences should be considered.

We use the term “local theory” specifically to indicate networks in which fundamental time delays are independent of system size, as in simple electric circuits. Thus, the term “local” may include cortical or thalamic interactions with time delays caused mainly by rise and decay times of postsynaptic potentials [Wilson and Cowan, 1973; Freeman, 1975; 1992; van Rotterdam et al., 1982; Lopes da Silva, 1999]. The term “local” indicates that characteristic network frequencies can, in theory, be predicted from physiologic measurements in a small (local) tissue mass. We use the term “global theory” to indicate that characteristic (or resonant) frequencies depend on the entire neocortex/cortico‐cortical fiber system in which delays are caused by finite propagation speeds of action potentials [Nunez, 1974a, 1981], somewhat analogous to standing waves in closed transmission line networks and many other spatially extended systems [Nunez, 1995]. Thus, characteristic global frequencies depend on system size. Our use of the terms “local” and “global” is consistent with their use in various physical theories. By “regional” we mean intermediate networks in which both postsynaptic potential and axonal delays are in the same general range [Silberstein, 1995b]. Such networks might involve long‐range cortical‐cortical interactions, thalamocortical feedback, or both.

Several mathematical theories indicate that within the range of experimental error, both local and global delays can produce oscillations with frequencies in the range of human EEG frequencies. The theoretical models have also suggested several (partly overlapping) bases for other properties of EEG, including relations between: (1) Frequency and postsynaptic potential rise and decay times [Wilson and Cowan, 1973; Lopes da Silva et al., 1974; Freeman, 1975, 1992; van Rotterdam et al., 1982; Zhadin, 1984; Freeman and Skarda, 1985; Nunez, 1989; Robinson et al., 1997, 1998a, 1998b; Wright and Liley, 1996; Liley et al., 1999]; (2) Amplitude and frequency [Nunez, 1995, 2000a, 2000b; Lopes da Silva, 1999]; (3) Spatial frequency and temporal frequency, e.g., wave dispersion relations [Nunez, 1974b, 1981, 1995; van Rotterdam et al., 1982; Ingber, 1985; Robinson et al., 1997, 1998]; (4) Alpha maturation [Lopes da Silva et al., 1974; van Rotterdam et al., 1982; Nunez, 1995, 2000a]; (5) Frequency and brain size [Nunez et al., 1977; Nunez, 1981, 1995]; (6) Human and other mammalian EEG [Lopes da Silva and Storm van Leeuwen, 1978; Nunez, 1995, 2000a, 2000b; Wright and Liley, 1996]; (7) Frequency and phase or group velocity [Nunez, 1974b, 1995, 2000a, 2000b; Lopes da Silva and Storm van Leeuwen, 1978; Burkitt et al., 2000]; (8) Local versus global effects [Nunez, 1989, 1995, 2000a; Ingber, 1982, 1995; Jirsa and Haken, 1997; Robinson et al., 1997, 1998a, 1998b; Haken, 1999; Kelso et al., 1999]; (9) Frequency and neurotransmitter action [Lopes da Silva, 1995; Silberstein, 1995b; Wright and Liley, 1996; Liley et al., 1999]; (10) Brain state transitions [Nunez, 1995, 2000a, 2000b; Lopes da Silva, 1995; Silberstein 1995b; Jirsa and Haken, 1997; Kelso et al., 1999].

Of particular note in supporting global views is that unequivocal progressive phase shifts in anterior‐posterior and posterior‐anterior directions across the scalp have been observed in human alpha rhythm [Nunez, 1995] and steady state visually evoked potentials [Silberstein, 1995a; Burkitt et al., 2000]. The corresponding phase velocities closely match characteristic cortico‐cortical propagation speeds of 6–9 m/sec [Katznelson, 1981; Nunez, 1995]. These data plus studies showing reduced alpha coherence in children with incomplete myelination [Thatcher et al., 1986, 1987; Srinivasan, 1999], in split‐brain patients [Nunez, 1981] and in agenesis of corpus callosum [Nielsen et al., 1993; Koeda et al., 1995; Pilgreen, 1995] suggest an important role for cortico‐cortical fibers in EEG. In addition, the negative correlation between alpha frequency and head size (highly correlated with brain size) provided early evidence for global effects on EEG [Nunez et al., 1977].

Additional data on the likely role of cortico‐cortical fibers in EEG is provided by white matter tumors. These tumors cause the production of irregularly formed arrhythmic delta waveforms (0.5–2.5 Hz) at scalp locations in the general vicinity of the tumor [Gloor et al., 1968; Goldensohn, 1979a]. Delta activity is generally not observed if the tumor is confined only to gray matter. Delta activity may or may not occur with suppression of alpha rhythms. We are not suggesting that EEG current sources are located in white matter. Rather, it appears that white matter is involved in determining both EEG coherence and frequency of cortical source oscillations. It is generally believed that delta activity is generated by cortical tissue near the periphery of the tumor. White matter is composed of cortico‐cortical, thalamocortical and callosal fibers [Brattenberg and Schuz, 1991]. The relative importance of cortico‐cortical and thamocortical fiber destruction to the appearance of tumor‐related delta activity is not known. However, we note that in humans about 95–98% of the axons entering (or leaving) the underside of any large region of neocortex are cortico‐cortical fibers [Braitenberg, 1977, 1978]. Only a few percent are thalamocortical fibers.

The issue of relative importance of thalamocortical and cortico‐cortical fibers appears to be quite different in lower mammals. It has been estimated that only about 50% of the fibers entering (or leaving) the underside of rat neocortex are cortico‐cortical [Brattenberg, 1977, 1978; Katznelson, 1981; Nunez, 1995]. We suggest that delays in cortico‐cortical fiber propagation may play a global role in determining human EEG frequencies. These frequencies are called global because signal delays between pairs of cortical locations increase with separation distance up to τ ≅ 10–30 ms along the long myelinated cortico‐cortical fibers [Nunez, 1995]. A crude first guess for the lowest modes of such spatially extended system with this characteristic delay is ωτ ≈ 1, or ƒ ≈ 5–16 Hz [Nunez, 1981, 1995]. Much longer delays, implying frequencies in the delta range, may occur if some fibers are unmyelinated or only partly myelinated, as appears to be the case [Tomasch, 1954].

Another potential experimental connection to theory involves studies of closed head injury patients [Thatcher et al., 1998a, 1998b]. MRI, EEG, and neuropsychological measures were significantly correlated. Increased T2 relaxation times in cortical gray matter and white matter were correlated with a shift in relative EEG power to lower frequencies and reduced cognitive performance. Increased T2 times were also correlated with long‐range (28 cm) coherence increases and short‐range coherence decreases. Generally, these data are consistent with the idea that head injury somehow damages the ability of brains to form local cell assemblies within the global synaptic action field environment.

Physiologically based theory has predicted that interactions across spatial scales are likely, implying that local networks can strongly influence global dynamics (bottom up) and that the global system can strongly influence local networks (top down) [Ingber, 1982; 1995; Nunez, 1989, 1995]. The imagined dynamic system may be likened to multiple social networks immersed in a global culture, a system in which both bottom‐up and top‐down influences determine dynamic behavior [Nunez, 1995, 2000a, 2000b]. This picture also directly addresses the so‐called brain‐binding problem, as nonoverlapping social (or neural) networks can easily exhibit correlated behavior as a result of top‐down influences from the culture (or synaptic action fields produced by the neocortical/cortico‐cortical fiber system).

An area of recent dynamic interest in EEG is chaos. A number of reports of chaotic EEG signals have been reported. However, proper identification of low dimensional chaos requires comparison of EEG data with surrogate signals having the same power spectrum (but randomized phases) as the genuine data [Theiler et al., 1992], and only a few EEG studies have included this critical step. A comprehensive review of this literature and study of new scalp and intracranial (subdural) human alpha rhythm [Lopes da Silva et al., 1997] suggests very little evidence for chaotic alpha rhythms, except possibly in some exceptional short bursts recorded subdurally. These authors suggest that “most likely, alpha rhythms recorded with gross electrodes correspond to complex signals that result from mixing signals arising from different alpha source generators, in such a way that even if the underlying dynamics has chaotic components, the latter may be masked by dynamic noise.”

In connection with this picture of possible alpha origins, we note simulations of local chaos imbedded in noise [Ingber et al., 1996] or global deterministic (top‐down) influences [Ingber and Nunez, 1990; Nunez and Srinivasan, 1993; Srinivasan and Nunez, 1993] in physical systems. In these examples, local chaos was either masked or fully eliminated by top‐down influences. Spatially extended systems in which global boundary conditions strongly influence local properties appear to be of particular interest in this context [Nunez, 1995]. Examples include nonlinear physical systems where a symbiosis of temporal and spatial structure occurs, or as expressed in one study of a spatially extended complex system [Bishop et al., 1983]: “Spatial patterns inhibit the temporal chaos that occurs in the absence of spatial structure, but the competing tendencies of temporal versus spatial structure can lead to a rich intermittency in space and time … spatial coherence can be maintained even when the temporal behavior of individual (spatial) modes becomes chaotic.

The possible relevance of these complex nonlinear phenomena to brain dynamics is largely unknown. However, given the extreme complexity and interconnectedness of brains, it appears wise to consider them in attempts to find the physiological bases for EEG [Ingber, 1982, 1995; Freeman and Skarda, 1985; Nunez, 1995, 1999, 2000a, 2000b; Tononi et al., 1994; Friston et al., 1995; Tononi and Edelman, 1998; Haken, 1999; Kelso et al., 1999].

2.8. Changes of brain state and the “zoo” of EEG rhythms

A large variety of brain rhythms have been recorded from human scalp, depending on subject and brain state [Klass and Daly, 1979; Blume and Kalbara, 1995; Niedermeyer and Lopes da Silva, 1999]. Taking into account spectral methods and our modern understanding of spatial filtering by the head volume conductor [Nunez, 1981, 1995], classical cortical rhythms (ECoG) may be interpreted as follows:

• 1The awake, resting ECoG shows substantial waveform variations over the upper neocortex, with “pure” (near sinusoidal) alpha rhythm more usual in posterior regions and more complex rhythms more evident in central and frontal regions [Penfield and Jasper, 1954]. However, relatively pure alpha rhythm (defined by visual inspection before spectral analysis came to common use in EEG) has been recorded from almost the entire upper cortical surface. Regions of alpha production included frontal and prefrontal cortex, excepting only regions close to the central motor strip [Jasper and Penfield, 1949].
• 2Our studies of scalp alpha rhythms recorded in healthy, relaxed subjects show substantial power in raw (reference) potential, dura image and spline‐Laplacian data at widespread scalp locations, including frontal scalp [Nunez, 1995; Nunez et al., 1997, 1999]. Power in other frequency bands (especially beta rhythm) is much less evident on the scalp than on the cortex [Pfurtscheller and Cooper, 1975; Kellaway, 1979; Nunez, 1981], apparently because of the spatial filtering effects discussed in Sections 3.2 and 3.3.
• 3The data outlined above (1 and 2) suggest that cortical rhythms in the relaxed waking state typically consist of a mixture of alpha rhythms with substantial power at low spatial frequencies and other rhythms (delta, theta, other alpha, beta, and perhaps epileptic spikes) with spatial spectra more dominant at higher spatial frequencies. Earlier coherence studies of scalp data [Andrew and Pfurtscheller 1996, 1997; Florian et al., 1998] and our spherical harmonic analyses also suggest that alpha rhythms may cover a range of low and high spatial frequencies.
• 4We interpret this mixture of cortical rhythms recorded in awake patients (together with the scalp data) as evidence for combined local and global brain dynamic processes, resulting from functional segregation and integration, respectively [Nunez, 1989; 1995; Ingber, 1995]. We suggest that different brain states may reflect differences between more locally dominated and more globally dominated dynamics [Silberstein, 1995b; Petsche and Etlinger, 1998; Nunez, 2000a, 2000b]. Perhaps different states occur with different dynamic complexity, a measure that appears to be maximum for intermediate states between locally and globally dominated dynamics [Tononi et al., 1994; Frsiton et al., 1995; Tononi and Edelman, 1998; Edelman and Tononi, 2000]. This general description of state changes in terms of local versus global dominance appears compatible with other dynamic descriptions, e.g., phase transitions, bifurcations, and so on [Nunez, 1995; Jirsa and Haken, 1997; Kelso et al., 1999]. However, our proposed general conceptual framework is easily interpreted, robust, and readily connected to a variety of quantitative theories. For example, according to Penfield and Jasper's [1954] extensive studies of ECoG, “the normal electrographic differentation between cortical areas is obliterated with anesthesia.”

Based mostly on scalp data, this general description of transitions from a conscious to unconscious states with anesthesia appears also to apply, at least in part, to hypoxia, coma, some epilepsies, and (to a lesser extent) normal deep sleep. Thus, the general local versus global picture provides a theoretical entry point that should facilitate study of the complex world of brain dynamics in a more parsimonious manner well into the future [Nunez, 2000b].

A fully satisfactory theory of alpha rhythms must address the issue of how spatial‐temporal properties are changed by sensory input or brain state change, e.g., as a result of neuromodulatory influences [Pilgreen, 1995; Lopes da Silva, 1995; Silberstein, 1995b]. For example, the local/global theory of Nunez [Nunez, 1995, 2000a, 2000b], based partly on quasi‐linear standing waves of synaptic action, provides semiquantitative predictions of abrupt frequency reductions from alpha to delta ranges as a control parameter reaches a critical value. In this model, distinct global limit cycle modes of synaptic action modulation are predicted. Depending on modulation depth, spatial wavelength (roughly related to large‐scale synchrony) and locations of electrodes, these synaptic field modulations may or may not be recordable as EEG. Of course, such crude physiologic theory can provide only rough ideas that, at best, apply to a limited class of EEG phenomena.

A prolate spheroidal shell (roughly the shape of a rugby football) provides a simple example of physical standing waves [Morse and Feshbach, 1953], perhaps having some common ground with putative global synaptic modulation frequencies. A similar physical phenomenon is Schumann resonance in the spherical shell formed by the earth's surface and the bottom of the ionosphere [Jackson, 1975]. These are standing electromagnetic waves with multiple resonant frequencies determined by the velocity of light and the radius of the earth. The standing waves occur as a net result of interference of waves traveling away from hundreds of near simultaneous lightning strikes (epicenters in EEG terminology).

The prolate spheroidal shell of size and shape approximating one brain hemisphere and wave propagation speed roughly equal to the speeds of cortico‐cortical propagation provides a simple example of resonant frequencies in a closed system. The following preferred (or resonant) cortical synaptic modulation frequencies (fundamental and overtones in Hz) may be estimated as [9.1, 10.1], [15.7, 16.3, 18.1], [22.2, 22.6, 23.9, 26.0], [28.6, 29.0, 30.0, 31.7, 33.9], [35.1, 35.3, 36.2, 37.6, 39.4, 41.7] … and so on [Nunez, 1995, 2000a]. The square brackets identify frequencies associated with latitudinal spatial modes (l = 1, 4), with frequencies corresponding to longitudinal modes (m = 1, l) in each bracket. These numbers are based on a prolate spheroidal shell with small eccentricity (not strictly valid for genuine brains), but the physiologic parameters are not known with sufficient accuracy to make absolute frequency predictions closer than about a factor of two. In any case, the general range appears a reasonable match to EEG.

The main point is to demonstrate the general idea of multiple global resonant modes, with higher modes (e.g., beta and gamma) tending to be more closely spaced. These higher modes are less likely to be distinguished experimentally. One reason is that smearing of spectral peaks caused by brain nonstationary can be expected in any EEG data recorded over periods of minutes or more, as normally required to obtain significant statistical estimates. Another point is that only some of these spectral peaks can be expected to be observed in any particular experimental record, depending on the spatial distribution of external input, recording electrode pair, and so on [Katznelson, 1981; Nunez, 1995]. Most importantly, the frequencies above are based on simple physical model for linear and nondispersive waves. Serious EEG theory must be physiologically based, but may retain some of the general features of linear, nondispersive (physical) standing waves [Nunez, 1974a, 1995].

Is there any experimental evidence for such global modulations? The dip in spectral amplitude between alpha and beta in Figure 1 is roughly consistent with the gap between the l = 1 and 2 modes of standing waves in a spherical shell, a common but not universal feature of EEG spectra. On the other hand, this physical metaphor provides no explanation for delta and theta band activity, which could be caused by increases in a control parameter in a quasi‐linear version of physiologic theory, locally dominated processes, or fully nonlinear effects [Nunez, 2000a, 2000b]. In one study, ECoG was recorded from subdural occipital electrodes separated by 1.5 cm. A coherence spectrum was obtained with the patient in the eyes closed, resting state [Zaveri et al., 1999]. Peaks in the coherence spectrum were obtained at 8, 16, 22, 31, and 41 Hz, plus several smaller peaks at intermediate frequencies. These peaks may or may not be evidence for global modulations of synaptic action. The frequency ranges predicted by the metaphorical global model also bear a rough correspondence to the low (l = 1), medium (l = 2), and high (l = 3 or 4) frequency resonance curves obtained by driving the human visual system with sine wave modulated light [Regan, 1989; Silberstein, 1995a; Nunez, 1995]. Again, we are not proposing that neocortical dynamics is linear or otherwise “simple,” but rather that such global modulations could easily have a substantial influence on recorded potentials.

More recently, high resolution estimates of human scalp data have revealed complex, but quasi‐stable phase patterns, e.g., alternating regions, in phase and 180 degrees out of phase at the scale of several centimeters [Wingeier et al., 1999; Nunez, 2000b]. In Section 6, alpha data is examined in more detail to see if such phase structure can be plausibly interpreted as wave interference phenomena.

All theories attempting to model the vast complexity of neocortical physiology are, at best, crude oversimplifications of the genuine dynamics. We do not claim that the data cited above verify any particular model. Rather, we suggest that the general idea of substantial global contributions (including standing waves of synaptic action) to neocortical dynamics (in some brain states) is consistent with several disparate sets of EEG data and with plausible physiologically based theory. The main value of such models is to focus on specific experimental methods that may further illuminate EEG processes. For example, the studies cited above [Regan, 1989; Zaveri et al., 1999], potentially supporting the existence of global modes, were not designed for this purpose. Partly as a result, critical questions were not addressed. For example, do multiple ECoG coherence peaks with high statistical significance occur over large (e.g., 15–25 cm) interelectrode distances, either in alpha or anesthesia states? New studies can focus on such specific, model‐related issues.

3. RELATIONSHIP OF SYNAPTIC CURRENT SOURCES TO CORTICAL AND SCALP POTENTIALS

3.1. Dipole moment per unit volume at mesoscopic scales

To illuminate connections between synaptic current sources at small (microscopic) scales and macroscopic potentials at the scalp, a formalism making use of an intermediate (mesoscopic) scale is convenient. This approach takes advantage of the columnar structure of neocortex, believed to contain the dominant sources of scalp potentials recorded without time averaging. The description is readily generalized to synaptic action in subcortical tissue if needed. For macroscopic measurements, the “source strength” of a volume of tissue is defined by its electric dipole moment per unit volume [Nunez, 1981, 1990, 1995].

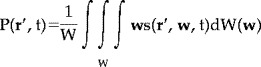(1)

Here dW(w) is the tissue volume element. s(r′, w, t) is the local volume source current (microamperes/mm³) near membrane surfaces inside a tissue volume with vector location r′. w is the vector location of sources within dW(w) as indicated in Figure 2. The current dipole moment per unit volume P(r′, t) in a conductive medium is fully analogous to charge polarization in a dielectric [Plonsey, 1969; Jackson, 1975; Nunez, 1981; Malmivuo and Plonsey, 1995]. Macroscopic tissue volumes satisfy the condition of electroneutrality at EEG frequencies. That is, current consists of movement of positive and negative ions in opposite directions, but the total charge in any mesoscopic tissue volume is essentially zero [Schwan and Kay, 1957; Plonsey, 1969]. This point has caused substantial confusion in the physiology literature [Nunez, 1981].

Figure 2.

Microcurrent (volume) sources at cell membranes s(r′, w, t) have units microamperes/mm³ and depend on vector location w within cortical column, located at r′, containing elemental volume elements dW(w). The sources are generally the result of synaptic and action potential activity and include (passive) return membrane currents. Microsources generate a dipole moment per unit volume P(r′, t) in each column (or more generally, voxel), depending on source magnitudes and distribution along the column axis. In this multiscale formalism, the intermediate scale dipole moment P(r′, t) can then be identified as the “meso‐source” of the differential scalp potential dV (r, r′, t). Total scalp potential V(r, t) is generally the result of the integrated contribution from all columns (or voxels), located at r′.

Cortical morphology is characterized by its columnar structure with pyramidal cell axons aligned normal to the local cortical surface. Physiology also supports the columnar picture, e.g., correlations between small electrode recordings taken normal to column axes are typically much higher than correlations between recordings at different cortical depths [Abeles, 1982; Petsche et al., 1984]. Because of this layered structure, it is often convenient to think of the volume elements dW(w) as cortical columns (height ≈ 2–5 mm), as shown in Figure 2.

For purposes of describing scalp potentials in terms of synaptic sources, the choice of basic cortical column diameter is somewhat arbitrary. Anything between the minicolumn (≈ 0.03 mm) and macrocolumn (≈ 1 mm) scales appears acceptable to describe scalp potentials [Nunez, 1990, 1995]. The dimensions of the basic column should be at least three or four times smaller than the closest distance to electrodes in order that the usual dipole approximation (avoiding quadrupoles, octupoles, and so on) is valid. The minicolumn scale is defined in terms of lateral spread of axons of inhibitory neurons [Szentagothai, 1978; Mountcastle, 1979; Eccles, 1984]. At this relatively small scale, simplifying assumptions about sources s(r′, w, t) within each column are more easily justified, e.g., that s(r′, w, t) is constant within each column in directions perpendicular to column axes.

The macrocolumn scale is defined by the (intracortical) spread of axon collaterals [Braintenberg, 1978; Mountcastle, 1979]. The macrocolumn is essentially a mesoscopic scale (between micro and macro, e.g., between synaptic sources and scalp potentials). While this language may be somewhat confusing, it is forced on us if the historical definition of macrocolumn is to be retained. Each macrocolumn contains about 10⁴ minicolumns, 10⁶ neurons, and 10¹⁰ synapses. The cortical surface consists of about 10⁴ macrocolumns [Nunez, 1995].

The sources s(r′, w, t) are generally positive and negative because of local inhibitory and excitatory synapses, respectively [Freeman, 1975; Lopes da Silva and Storm van Leeuwen, 1979]. In addition to these active sources, the s(r′, w, t) include passive membrane (return) current required for current conservation. Dipole moment per unit volume P(r′, t) has units of current density (microamperes/mm²). For the idealized case of sources of one sign confined to a superficial cortical layer and sources of opposite sign confined to a deep layer, P(r′, t) is the diffuse current density across the column [Nunez, 1981, 1990, 1995]. This corresponds roughly to superficial inhibitory synapses and deep excitatory synapses, for example. More generally, column source strength P(r′, t) is reduced as excitatory and inhibitory synapses overlap along column axes. Increased membrane capacity tends to confine the microsources s(r′, w, t) within each column [Nunez, 1981, 1995] to produce smaller effective pole separations, i.e., smaller meso‐source strengths P(r′, t). However, once this effect is fixed at the mesoscopic scale (column), capacitive effects at macroscopic scales may be neglected at EEG frequencies [Schwan and Kay, 1957; Plonsey, 1969; Nunez and Silberstein, 2000]. This provides still more motivation to adopt the multiscale formalism.

Human neocortical sources may be viewed as a large dipole sheet of perhaps 1,500 to 3,000 cm² over which the function P(r′, t) varies continuously with cortical location r′, measured in and out of cortical folds. In limiting cases, this dipole layer might consist of only a few discrete regions where P(r′, t) is large, e.g., focal sources. But, more generally, P(r′, t) is distributed over the entire folded surface. The question of whether P(r′, t) is distributed or localized in particular brain states has been the subject of controversy. It should be noted that averaging of evoked potentials (or PET or fMRI signatures) over trials can substantially alter the nature of this issue. Such time averaging strongly biases experimental measures toward (trial to trial) time stationary sources, e.g., sources confined to primary sensory cortex [Nunez, 1995; 2000b; Nunez and Silberstein, 2000].

Scalp potentials are believed to be generated by the summed activity of P(r′, t), mainly from upper regions of cortex. For convenience of description, we first consider columnar source regions confined to a smooth model cortex at fixed radial location in an idealized spherical head. Future extensions of this model to account for realistic folded cortex are considered in Section 3.7. In the idealized spherical model, the vector dipole moment per unit volume P(r′, t) has only a radial component (although this approximation is not required for most of this description). Any distribution of this scalar “dipole source strength” P(θ, ϕ) over the cortex may be expanded in a series of spherical harmonic functions.

(2)

Equation (2) is a generalized Fourier series where the basis functions are the (orthogonal) spherical harmonics Y_lm(θ, ϕ) replacing sine and/or cosine terms of common Fourier series [Morse and Feshbach, 1953; Jackson, 1975]. The angles (θ, ϕ) are essentially (latitude, longitude) on a spherical surface. The double sum in Eq (2) is over “spatial frequencies” in the (θ, ϕ) directions with indices (l, m).

The (generally unknown) functions p _lm(t) are determined by the dynamic properties of neocortical sources. These are known as order parameters in the field of complex systems theory or, more specifically, the field of synergetics [Haken, 1983, 1999]. The general idea of synergetics is that many disparate complex systems can be adequately approximated by a few such order parameters, thereby greatly simplifying quantitative descriptions. State changes in complex systems generally involve new order, i.e., new sets of order parameters [Friedrick et al., 1992; Fuchs et al., 1992; Kelso, 1995]. An example of such state change is the switch from out‐of‐phase to in‐phase finger tapping in response to an auditory stimulus [Kelso et al., 1999]. The measured MEG dynamics in this study was described as a competition between two spatial modes (the spherical harmonics used here or spatial functions determined by principal components analysis or other criteria). The time‐dependent coefficients of these modes, analogous to our p _lm(t) functions, were the order parameters. One order parameter dominated the pretransition state and oscillated with the stimulus frequency. A second order parameter, with twice the stimulus frequency, dominated the posttransition state. A theoretical model, based on a combination of local and global dynamics, was able to reproduce essential features of the observed MEG dynamics [Jirsa and Haken, 1997].

Regardless of the nature of the underlying neocortical dynamics, Eq (2) is general in the sense that it applies to localized sources, distributed sources, or anything in between. Furthermore, Eq (2) applies to linear or nonlinear dynamic processes, as discussed in [Haken, 1983; Nunez, 1995; Kelso et al., 1999]. The p _lm(t) are functions that weigh different parts of the spatial spectrum differently. Widespread synchronous sources are generally described accurately by a relatively small number of terms in Eq (2), i.e., the p _lm(t) tend to be small for large l and m. More focal sources require more terms in the sums, i.e., more contribution from higher spatial frequencies.

3.2. Spatial filtering of cortical source activity by the head volume conductor

EEG potentials are spatially low‐pass filtered between neocortex and scalp. The filtering is caused by the physical separation of cortical sources and sensors and by passive spread of currents by tissues in the head volume conductor, especially skull having an average electrical resistivity estimated to be roughly 80 times that of brain or scalp tissue [Rush and Driscoll, 1968, 1969; Nunez, 1981]. Potentials recorded with intracranial electrodes may also be spatially filtered by similar effects but typically to a much lesser degree. Rather, nonzero electrode size often determines the high spatial frequency cut‐off. By contrast, electrode size has minimal effect on scalp potentials, which have undergone severe spatial filtering by the volume conductor.

It is readily shown that the outer surface (scalp) potential generated by the source function P(θ, ϕ, t) may be expressed [Srinivasan et al., 1996, 1998].

(3)

Here, T _l is the spatial transfer function of the spherical volume conductor. It depends on the resistivities and radii of spherical surfaces, e.g., brain, CSF, skull, and scalp, independent of frequency in the EEG range. The scalp surface Laplacian, involving second spatial derivatives of V(θ, ϕ, t) with respect to θ and ϕ on a sphere of radius R may be expressed similarly to Eq (3), but with transfer function T _l replaced by l(l + 1)T _l, that is

(4)

Comparison of Eqs (3) and (4) shows that the time dependencies of scalp potential and Laplacian are both obtained by linear superposition of dynamic source behavior p _lm(t) but with different weighting coefficients reflecting different spatial filtering by the head volume conductor. This formalism involving linear superposition applies to both linear and nonlinear systems; however in nonlinear systems, the order parameters p _lm(t) will typically satisfy coupled (between different l, m) nonlinear differential equations. The weighting coefficients (transfer functions T _l) are independent of temporal frequency in the EEG range. The scalp potential and Laplacian transfer functions are plotted versus the spherical harmonic order l in Figure 3 for the case of radial dipoles at fixed depth. For /m/ small, latitudinal wave number or spatial frequency k on a spherical surface is approximately related to the l index and sphere radius R by

(5)

Here, spatial frequency is expressed in cycles/cm if the factor (2π) is included in the denominator or cm^‐1 if not included. For example, on a spherical cortex of 8 cm radius, l = 8 corresponds to a wave number k ≅ 1 cm^‐1 or a spatial wavelength of 2π cm. The longitudinal (ϕ) spatial frequency index /m/ in the orthogonal expansion Eq (2) is limited to latitudinal (θ) index l (so that the resulting eigenfunctions of the Laplacian operator are finite everywhere on the sphere). This feature of spherical harmonics allows concise expression of spatial filtering by the head volume conductor, i.e., in terms of only the l index. Figure 3 shows the extreme spatial filtering of (raw) unprocessed scalp potentials, which together with reference electrode distortions and sparse spatial sampling, accounts for the very poor spatial resolution of conventional EEG.

Figure 3.

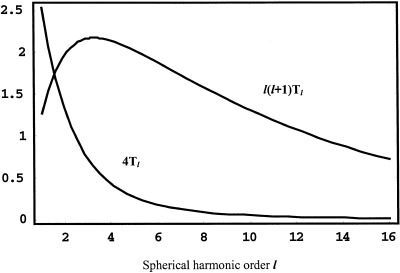
The spatial transfer functions 4T_l (potential) and l(l+1)T_l (Laplacian) for a four‐sphere volume conductor model of the head, defined by Eqs (3) and (4). Radial dipole source location is 7.8 cm. Radii of spherical shells are: brain (8.0), CSF (8.2), skull (8.7), and scalp (9.2). Conductivity ratios: brain/CSF (0.2), brain/skull (80.0) and brain/scalp (1.0).

3.3. Differences between EEG and ECoG waveforms and spectra

It has been long appreciated that scalp EEG and underlying ECoG (cortical) waveforms are often quite different [Penfield and Jasper, 1954; Goldensohn, 1979b]. For example, the ECoG may contain epileptic spikes not observed at the scalp [Ebersole, 1997]. Or, the ECoG may exhibit substantially more beta activity than the corresponding scalp EEG [Pfurtscheller and Cooper, 1975; Kellaway, 1979]. Differences in EEG waveforms (and temporal spectra) between cortex and scalp cannot be explained by passive volume conduction effects because tissue conductivities (and as a result, the transfer function T _l) are approximately independent of temporal frequency over the normal range of EEG frequencies [Schwan and Kay, 1957]. This was demonstrated explicitly by Cooper et al. [1965] who showed that the attenuation of potential between cortex and scalp due to implanted dipole sources is independent of source frequency in the EEG range.

Differences in temporal frequency spectra between cortex and scalp are plausibly explained as by‐products of spatial filtering by the volume conductor in dynamic brain states where cortical source dynamics tends to associate temporal and spatial frequencies [Nunez, 1981, 1995]. This association would not be expected in a brain medium conforming to the simple view, often expressed in the EEG literature, of isolated EEG generators. However, in nonlinear dynamic physical media with spatial extent (bearing some common ground with neocortex), a large variety of dynamic behavior is possible caused by interactions between current sources (Nunez 1995; Lopes da Silva, 1999]. One obvious example is provided by physical wave phenomena. In the case of physical waves, temporal frequency nearly always increases with spatial frequency. For electromagnetic waves in a vacuum or simple sound waves, temporal frequency is proportional to spatial frequency. With other waves (e.g., transmission line, water, plasma, quantum), the dispersion relation (the equation relating spatial and temporal frequency) is more complicated, but temporal frequency still tends to increase with spatial frequency. The temporal Fourier transform of scalp potential Eq (3) is given by

(6)

The Fourier transform of the Laplacian L(θ, ϕ, ω) follows similarly from Eq (4). Suppose (for what ever physiological reasons) neocortical dynamic behavior tends to associate higher temporal frequencies with higher spatial frequencies, say over the alpha, beta and gamma ranges as reported by Nunez [1974b] and Shaw [1991] for the resting alpha state in humans. This means that the Fourier transformed coefficients p _lm(ω) in Eq (6) with higher order (larger spatial frequencies l, m) tend to have more relative contributions at temporal frequencies ω in the higher alpha, beta, and gamma bands. But the effect of the volume conductor transfer function T _l is to filter out high spatial frequencies between cortex and scalp, associated by dynamic processes in neocortex to high temporal frequencies.

In strongly nonlinear systems with substantial interactions between different regions (as in neocortex), a large variety of relations between spatial and temporal frequency is possible. For example, such systems may exhibit turbulence (spatial‐temporal chaos) rather than quasi‐linear wave phenomena or only temporal chaos. Perhaps turbulent dynamic brain states correspond to generalized seizures, for example. Very little is known about the detailed spatial‐temporal characteristics of human EEG. A reasonable conjecture is that such relations are very complicated and change with brain state. However, independent studies of human scalp alpha rhythm have demonstrated robust relationships between spatial and temporal frequency for frequencies within the alpha band [Nunez, 1974b, 1981, 1995] and for frequencies larger than the alpha peak frequency, i.e., about 10–30 or 40 Hz [Shaw, 1991; review in Nunez, 1995]. These studies indicate that higher spatial frequencies tend to occur with higher temporal frequencies (at the scale of scalp recordings) in the normal resting “alpha state” of humans. We have recently reconfirmed this result by calculating spherical harmonic spectra at different temporal frequencies with 131‐channel recordings of spontaneous EEG.

To demonstrate that temporal filtering between cortex and scalp is an indirect result of spatial filtering by the volume conductor, an example waveform was constructed to represent simulated ECoG. In Figure 4, the upper waveform consists of 51 closely spaced frequency components with amplitudes inversely proportional to square root of frequency. Spikes occur in this record every few seconds when distinct waveforms are synchronous such that linear superposition produces very short periods with large amplitudes. This may or may not be similar to physiological mechanisms underlying genuine epileptic spikes, but this issue does not preclude our arguments here. The lower plot shows the corresponding simulated scalp potential (with scale change), obtained as follows: Assume that cortical dynamics satisfies the linear dispersion relation, i.e., spatial frequency is proportional to temporal frequency. Use the transfer function of the volume conductor model, shown in Figure 3, to spatially filter the simulated ECoG. The spike is much less evident in the simulated scalp record and might not be recognized as a spike in clinical EEG.

Figure 4.

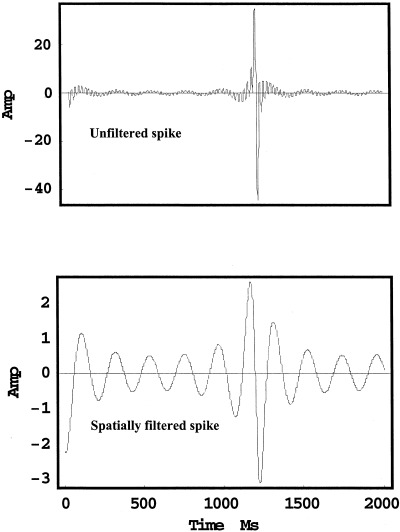
(Upper) A waveform composed of 51 unequally spaced frequency components (roughly 10–175 Hz) with pseudorandom phases simulating an epileptic spike recorded on the dura surface (ECoG). (Lower) The corresponding spatially filtered waveform simulating scalp potential. Obtained from the transfer function T _l and the assumption that temporal frequency is inversely proportional to spatial frequency (as in linear, nondispersive waves). Note scale change. There is no temporal filtering by the volume conductor (consistent with experimental evidence). Rather, the temporal filtering is a byproduct of spatial filtering.

Examples of temporal filtering of physical standing waves as a byproduct of spatial filtering are shown in [Nunez, 1995, Chap. 9]. While these examples probably represent, at best, vast oversimplifications of complex neocortical dynamic behavior, they provide a rough idea of why scalp EEG can look so different from the underlying ECoG with no passive temporal filtering by tissue. Similar analyses can be directed to the different measurement scales of intracortical recordings themselves, because of different size electrodes. The measured dynamics of EEG can be very sensitive to spatial scale.

3.4. Amplitude differences between EEG and ECoG

The linear scale of an EEG measurement refers to the cube root of the volume of tissue (or square root of cortical area) to which the measurement applies. Scalp measurements of raw EEG apply to weighted averages of neural activity at the scale of at least several cms (e.g., several tens of cm² of gyri surface). This has been studied with a simulation of radial dipole sources uniformly distributed over the upper (inner) sphere of concentric spheres models [Nunez et al., 1997]. In this idealized model, only about half the contribution to potentials measured by an electrode at the “north pole” were generated by sources within a surface distance of 3 cm from the electrode center. The other half contribution to scalp potential came from sources over the entire upper hemisphere (3–14 cm from the electrode center). The short explanation for this is that while sources close to an electrode make the largest individual contributions to potential, the number of distant sources is much larger if sources are widely distributed. A large number of weaker source contributions can be as large or larger than a small number of stronger contributions, an effect substantially enhanced by field spreading in the head volume conductor, especially skull.

A four concentric spheres model of the human head may also be used to estimate the ratio of dura to scalp potential [Nunez, 1981, 1995]. Estimates of this ratio for three different head models are plotted versus the area of synchronous gyri source activity in Figure 5. Although the details of these estimates depend on model assumptions as expected, the general idea that large regions of synchronous source activity are weakly attenuated between dura and scalp is correctly predicted by spherical models. Ratios of roughly 2–6 have been widely reported for widespread cortical activity [Penfield and Jasper, 1954; Abraham and Ajmone‐Marsan, 1958; Cooper et al., 1965; Goldensohn, 1979b; Nunez, 1981]. By contrast, the attenuation factor for focal cortical spikes can be 60 or more. We have found minimal quantitative information on the attenuation factor as a function of active cortical area; the only two experimental points providing both attenuation and corresponding cortical surface of which we are aware are the triangles in Figure 5. The arrow corresponds to the general clinical observation that a spike area of at least 6 cm² must be synchronously active in order to be observed on the scalp, or at least identified as a “spike” clinically [Cooper et al., 1965; Ebersole, 1997]. This point corresponds roughly to the steep upturn in the curves of Figure 5, providing addition confidence in the spherical head models.

Figure 5.

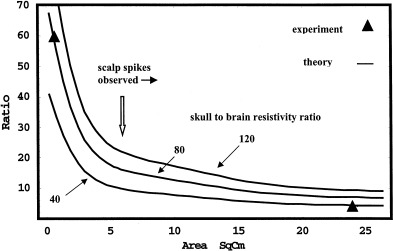
Theoretical estimates of the ratio of dura potential to scalp potential, expressed as a function of “synchronous area” of cortical sources. The three curves were generated by assuming cortical dipole layers of constant (mesoscopic) sources in the head model. The assumed skull‐to‐brain (or scalp) resistivity ratios are shown (40, 80, 120), bracketing the usual estimate of 80. The two triangles are experimental points [Abraham and Ajmone‐Marsan, 1958; Goldensohn, 1979b]. The large arrow near the steep upturn in the curves indicates the clinical observation that epileptic spikes must be synchronous over at least 6 cm² of cortex to be recognized on the scalp [Cooper et al., 1965; Ebersole, 1997].

Figure 5 has important implications for changes in intermediate range and long‐range phase synchrony of cortical sources on scalp potential amplitudes. Consider a hypothetical cortex where phase synchrony spreads over time, starting with a synchrony scale (square root of synchronous area) of less than 1 cm to more than 4 cm. From the exponential parts of curves in Figure 5, we expect large increases in amplitude between the 1–2 cm scales, but minimal amplitude changes at scales larger than about 4 cm. Thus, we might anticipate transitions between brain states for which long‐range coherence (in some frequency band) can either increase or decrease independent of scalp amplitude, an effect reported for a variety of mental tasks [Petsche and Etlinger, 1999]. On the other hand, we expect intermediate range (< 1 or 2 cm) synchrony changes to result in large scalp amplitude changes, as shown in simulations [Nunez, 1995].

3.5. Multiple spatial scales and the fractal‐like character of brain dynamics

There is still another way in which spatial filtering dictated by experimental choices can influence measured dynamics. Neocortical morphology exhibits a hierarchical structure, composed of neurons within microcolumns within cortico‐cortical columns within macrocolumns within lobes [Mountcastle, 1979; Eccles, 1984; review in Nunez, 1995]. Complex nonlinear physical systems often exhibit dynamic behavior that is very scale‐dependent, even in the absence of fixed multiscale physical structure to support the hierarchical dynamics [Wilson, 1979; Haken, 1983; Ma, 1985; Ingber, 1982, 1995]. Scale‐dependent neocortical dynamics has been often reported [Abeles, 1982; Petsche et al., 1984; Steriade, 1999]. The physical structure of neocortex together with its potential for highly nonlinear interactions strongly suggests scale‐dependent dynamics [Ingber, 1982, 1995; Nunez, 1981, 1995; Lopes da Silva et al., 1997].

This scale dependence is partly demonstrated in the simulations of Figures 4 and 5. EEG recorded from the scalp is a measure of very large‐scale dynamics. ECoG represents dynamics mainly at smaller scales. But, because all electrodes measure potentials averaged over their tip volumes, electrodes on the dura or inside cortex may also record quite different dynamics, depending on electrode size [Abeles, 1982; Petsche et al., 1984; review in Nunez, 1995]. To illustrate this, we extended the spatial filtering idea to the case of an electrode on the dura surface. The spatial transfer function is plotted versus the spherical harmonic index l in Figure 6; this is an extension of the volume conduction filtering shown in Figure 3. For the low spatial frequencies observed on the scalp [roughly l < 5), electrode size is of minimal importance. However, a dura electrode of diameter d is only able to record dynamic activity at spatial wavelengths longer than about 2d. On a sphere (brain) of 8 cm radius, l = 40 corresponds to a wavelength of 1.2 cm. As shown in Figure 6, an electrode of diameter d = 1.5 cm (lower curve) cannot “see” this activity at 1.2 cm or shorter wavelengths. The smaller electrode with diameter d = 1 cm is able to record activity near the 1.2 cm wavelength, but with only about half the sensitivity of a point electrode.

Figure 6.

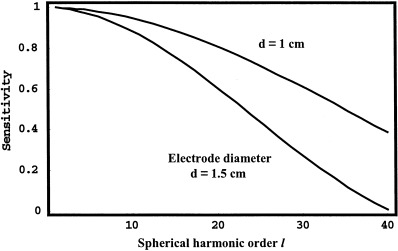
Theoretical dura electrode sensitivity is plotted as a function of spherical harmonic order l for two electrode diameters, d = 1 and 1.5 cm. Sensitivity (vertical axis) is normalized with respect to its value for a point electrode. Curves are obtained by averaging potentials generated by different spherical harmonic functions (of source distribution, as given by Eq [2]) over the surface area of the electrode.

Dura potential, scalp potential and scalp Laplacian waveforms all involve linear combinations of the source coefficients p _lm(t), as indicated in Eqs (3) and (4). However, the weighting of these source terms can be quite different for different experimental measures, including different references and different electrode sizes. For this reason, measured neocortical dynamics can be a sensitive function of experimental method. Different dynamics occurs at different spatial scales. We challenge the notion (sometimes implicit in EEG literature) that any particular scale (e.g., dura recordings with electrodes of a particular size) can be considered the gold standard to measure the dynamic behavior of neocortical function. Of course, if one is particularly interested in focal activity (e.g., in epilepsy surgery patients), dura potential distribution contains much more high‐spatial frequency content than scalp potential and will provide much more accurate localization of focal sources. However, other phenomena (e.g., cognition) may be more strongly correlated with large‐scale dynamics, e.g., the very large scales of scalp EEG. In this case, ECoG may be so dominated by small‐scale dynamics that the large‐scale is not observed, essentially “failing to see the forest for the trees.” This failure to observe large‐scale dynamics will generally be more pronounced for smaller intracranial electrodes, which can be expected to record mainly large amplitude local potentials [Abeles, 1982].

3.6. Multiscale coherence measures

Subdural human coherence measured with 2‐mm diameter electrodes typically falls to zero at all frequencies for electrode separations greater than about 2 cm [Bullock et al., 1995]. Such data may appear to conflict with large human alpha coherence estimates even with all reference and volume conduction effects removed [Nunez et al., 1997, 1999]. We suggest that such differences are easily explained by the large differences in spatial scales distinguishing extracranial and intracranial measurements. Dura image or spline‐Laplacian methods are believed to estimate coherence between synaptic action in pairs of cortical regions occupying perhaps 10–30 cm² of cortical surface, while standard potential‐based coherence estimates correspond to pairs of surface areas of perhaps 100 cm² [Nunez, 1995]. By contrast, intracranial coherence estimates typically apply to millimeter scales. Coherence between large neural populations may be large, while at the same time, coherence between specific subpopulations is close to zero. Again, picturing metaphorical human activity at the multiple scales of neighborhoods, cities, and nations helps to visualize such complex dynamic behavior.

3.7. Transformations between folded cortical surfaces and topologically equivalent spheres

In Sections 3.1 and 3.2, cortical source strength (dipole moment per unit volume) was expressed as a sum of spherical harmonic functions, most appropriate for sources in a spherical shell. A similar expansion may be applied to realistic cortical surfaces of individual subjects that have been mapped onto a sphere [Fischl et al., 1999]. Such transformations were allowed without need of surface cuts because the cortical surface of each hemisphere is topologically equivalent to a sphere (after closing the surface medially across subcortical structures). Application of these methods to models of dynamic processes will require further developments but appear feasible. In particular, dynamics might be described for two (spherical) cortical hemispheres by expansions similar to Eq (2). Spherical shells representing cortex would be coupled through a model of the corpus callosum. Sampling of this dynamics with EEG would occur on a much larger surface (scalp), obtained by appropriate transformation of the genuine head surface containing the two smaller cortical spheres.

4. HIGH‐RESOLUTION EEG

4.1. Spline‐Laplacian and dura imaging

A convenient definition of scalp spatial resolution is the minimum distance between cortical sources for which two sources can be distinguished from a single source [Wikswo and Roth, 1988; Nunez, 1995]. This distance is substantially larger than dipole localization accuracy, which normally refers to accuracy for a single implanted source. For example, 1 or 2 cm accuracy has typically been reported for implanted dipoles located with sophisticated EEG or MEG methods [Cohen et al., 1990; Leahy et al., 1999]. However, the number and nature of sources underlying EEG are nearly always unknown, and the spatial resolution obtained with the conventional 10/20 EEG methods is typically in the 6–10 cm range [Nunez et al., 1991, 1993, 1994]. This implies that one cannot distinguish spatial patterns at scales smaller than 6–10 cm with conventional EEG. Simply increasing the number of electrodes adds very little to accuracy in the absence of computer measures either to locate equivalent dipoles or, more generally, to improve spatial resolution by reducing reference and volume conduction effects. Because of the very modest increase in information yield and the extra time involved in electrode placement, clinical electroencephalographers have often resisted implementation of dense electrode arrays. However, when high‐resolution algorithms [Gevins and Cutillo, 1986, 1995; Nunez and Westdorp, 1991; Nunez et al., 1993, 1994; Nunez, 1995] are combined with high‐density electrode arrays, the amount of detailed information available in the EEG can be substantially increased. In special cases where EEG sources can be accurately characterized by a few isolated dipoles, combined high‐electrode density and sophisticated algorithms can provide accurate dipole localization [Mosher et al., 1993].

Two general approaches have been applied to improve EEG spatial resolution, the spline‐Laplacian and dura imaging. As shown in Figure 3, the transfer function of the analytic surface Laplacian provides a broader and often more satisfactory spatial frequency response than raw potential. Furthermore, the Laplacian is independent of head model (except for surface shape) and entirely free of reference effects [Hjorth, 1975; Nunez, 1981]. Simulation studies over the past 13 years have shown that spherical and three‐dimensional spline approximations to surface Laplacians obtained with 64 or more electrodes provide reasonably accurate and robust estimates of inner surface potential patterns at scales larger than about 2–4 cm. Positive dura potentials are closely related to negative scalp Laplacians (relative not absolute magnitudes). Such simulations have studied uncorrelated noise and (correlated) artifact generated outside the electrode array using spherical and more realistically shaped head models [Perrin et al., 1987, 1989; Nunez, 1988, 1990; Nunez et al., 1991; Law et al., 1993; Srinivasan et al., 1996, 1998; Babiloni et al., 1996].

The second approach, dura imaging, depends on a concentric spheres [Sidman, 1991; Cadusch et al., 1992, Silberstein, 1995a; Edlinger et al., 1998] or finite element models of the head [Le and Gevins, 1993; Gevins et al., 1991, 1994; Le et al., 1994]. Dura imaging methods have been presented with several labels (spatial deconvolution, software lens, deblurring, cortical imaging). But, such algorithms are all based the same principle. In a closed volume conductor, there is a unique relationship between outer surface potential and potential on an inner closed surface, provided that no current sources exist between the surfaces [Yamashita, 1982]. While the general inverse problem of locating brain sources from scalp potentials is fundamentally nonunique, the problem of calculating dura potential from scalp potential distribution is limited only by engineering issues, e.g., accuracy of the volume conductor model, density of spatial sampling, and noise.

The issues of head model error, sampling, and noise are partly addressed by most dura imaging algorithms (including the Melbourne version, Cadusch et al., 1992) by using an adjustable smoothing parameter. As the smoothing parameter is increased, less detail is accepted in spatial patterns. The rejected detail may not be reliable, depending on experimental circumstances. The New Orleans spline‐Laplacian [Nunez, 1988; Law et al., 1993; Srinivasan et al., 1996, 1998] has inherent spline‐based smoothing based on choosing the order of the spline to match (approximately) the volume conductor and electrode density [Perrin et al., 1987]. As a consequence of choosing a (conservative) third‐order spline in three spatial dimensions, high spatial frequencies are severely attenuated by the New Orleans spline‐Laplacian. When the Melbourne dura image smoothing parameter is set in the range 0–10^‐9, estimated dura potential patterns closely match those of the New Orleans spline‐Laplacian. These engineering details are very important, but unlike the circumstance of true inverse solutions like dipole localization, they do not provide fundamental limitations on accuracy. For this reason, progressively more accurate high‐resolution EEG methods to estimate dura potential can be expected as head models are improved. But, even with today's models, accurate dura imaging of somatosensory evoked potentials separately recorded from cortical surface has been achieved using dense scalp electrode arrays [Gevins et al., 1994; van Burik, 1999].

4.2. Simulations: head model

A four‐concentric spheres theoretical head model simulates scalp surface potentials caused by distributed cortical gyri sources. Simulated gyri rather than sulci sources were adopted here partly for convenience, but also because contributions to most EEG phenomena by distributed gyri sources are believed to be substantially larger than contributions by sulci sources [Nunez, 1981, 1995; Nunez and Silberstein, 2000].

An example source distribution is shown in Figure 7 (upper left). Filled spaces indicate positive sources, i.e., positive ends of dipoles or synaptic currents flowing out of local membranes near outer cortical surface. Empty spaces indicate negative sources. Magnitudes vary with location (not shown). The corresponding outer surface (scalp) potential was calculated at 131 locations and plotted using a standard MATLAB software routine [MathWorks, Inc., Natick, MA, upper right). These outer surface locations correspond to our experimental electrode positions projected to the surface of a best‐fit sphere. Solid lines indicate positive and dashed lines indicate negative isopotentials. The 131 surface potentials were submitted to the New Orleans spline‐Laplacian and Melbourne dura imaging algorithms. These algorithms provide independent estimates of inner surface (dura) potential at the 131 electrode locations.

Figure 7.

Simulation study using cortical source distributions at radial location 7.8 cm, each consisting of 3,602 randomly clumped dipole sources. Similar source patterns were used to construct parts 1–3 of Table I. For each source distribution, outer surface potentials were calculated at 131 locations corresponding to electrode positions of EEG experiments. Forward solutions were based on the four‐sphere model used in Figures 3, 4, 5, 6. Inner surface (dura) potentials were estimated with the New Orleans spline‐Laplacian (multiplied by negative sign, lower left) and Melbourne dura image algorithm with zero smoothing parameter (lower right). Point‐by‐point comparisons with actual inner surface potential at 131 dura locations were used to obtain correlation coefficients. Shell radii used by the three‐sphere dura imaging algorithm were 7.9, 8.45, and 9.2 cm, and conductivity ratios were brain/skull (80) and brain/scalp (1). Spline‐Laplacian estimates of dura potential are independent of head model, except for the assumption of a spherical scalp.

Contour plots of dura potential estimated with the spline‐Laplacian (lower left) and with the dura imaging algorithm (lower right) and are shown. The actual inner surface potential was also calculated directly from source distribution. By both visual inspection and the correlation coefficients listed under each figure, the two high‐resolution methods clearly yield far more accurate estimates of dura potential than raw scalp potential. Correlation coefficients between inner surface potential (dura potential calculated directly from the source distribution) and the inner surface potential estimated from sampled outer surface potential were obtained from point‐by‐point comparisons at 131 inner surface locations for 100 different source distributions (Table I, Group 1). These correlation coefficients also apply approximately to predicted cortical source distribution, provided it is assumed in advance that all sources are radial dipoles at fixed depth (thereby providing for unique solutions to the constrained inverse problem).

Table I.

Correlation coefficients for various dura measures using both simulated scalp potentials and EEG data

	Correlation Coefficient
1. Simulations: 100 Source distributions with perfect skull model, imperfect CSF
Spline‐Laplacian/Inner Surface	0.965 ± 0.010
Dura Image0/Inner Surface	0.957 ± 0.012
Spline‐Laplacian/Dura Image0	0.986 ± 0.006
2. Simulations: 100 Source distributions with skull resistivity variations (40 to 120)
Spline‐Laplacian/Inner Surface	0.963 ± 0.010
Dura Image0/Inner Surface	0.957 ± 0.014
Spline‐Laplacian/Dura Image0	0.983 ± 0.007
3. Simulations: 100 Source distributions with 15% noise added to surface potentials
Spline‐Laplacian/Inner Surface	0.736 ± 0.082
Dura Image0/Inner Surface	0.692 ± 0.087
Dura Image9/Inner Surface	0.835 ± 0.030
Spline‐Laplacian/Dura Image0	0.970 ± 0.006
4. EEG data: 600 time slices of alpha rhythm
Spline‐Laplacian/Dura Image0	0.950 ± 0.017
5. EEG data: Twenty 1‐sec epochs. Phase estimates with and without 15% noise added to raw data
Spline‐Laplacian clean/noise	0.950 ± 0.040
Dura Image0 clean/noise	0.952 ± 0.032
Dura Image9 clean/noise	0.978 ± 0.015

For each of Groups 1–3 in Table I, 100 different source distributions were generated. Each source distribution involved 3,602 radial dipoles of strength P(θ, ϕ) representing neocortical gyri source activity at roughly the macrocolumn scale (several mm). Forward solutions were calculated from the four‐sphere head model. In Group 1, dura image estimates based on a three‐sphere head model (no CSF layer) with brain to skull conductivity ratio equal to 80 were obtained from the 131 surface samples for each source distribution. A similar procedure yielded dura potential estimates by the spline‐Laplacian algorithm. Group 1 simulations assess the combined effects of limited spatial sampling and imperfect head model (CSF was included only in forward solutions). For practical purposes, these are essentially perfect fits and there is no obvious reason to choose one method over the other. Another comparison is between 64‐ and 131‐channel high‐resolution methods. With 64 channels, correlations between estimated and actual inner (dura) surface potentials were typically in the 0.80–0.85 range with zero noise [Nunez et al., 1993]. This range may be compared with the average correlation of 0.96, obtained with 131‐channel simulations, shown in Group 1 of Table I.

For Group 2 correlation coefficients, ratios of brain to skull conductivity were varied randomly (uniform distribution) over the range 40–120, bracketing the commonly cited ratio 80 [Rush and Driscoll, 1968, 1969; Nunez, 1981]. Raw simulated scalp potential was only moderately correlated with dura potential (r ≅ 0.6) even though no reference effects were included in this simulation. Other studies have shown that reference effects are typically substantial [Nunez, 1981; Nunez et al., 1991], so the advantage of the spline‐Laplacian is underestimated by this comparison. Both simulated spline‐Laplacian (r ≅ 0.96) and dura images (r ≅ 0.96), estimated only from scalp data, were strongly correlated with dura potential. Earlier simulations using finite element forward solutions indicated that accuracy is not substantially degraded by nonspherical surface geometry [Yan et al., 1991; Cao and Nunez, unpublished data].

Large variations in local skull resistance (caused by some combination of thickness and resistivity variation) can fool interpretation of data obtained with any EEG method. However, many EEG applications, especially those concerned with cognitive processing, are primarily concerned with robust changes in large‐scale (several cms) spatial‐temporal dynamics between brain states. For example, state changes corresponding to changes in amplitude, phase, coherence, or covariance patterns are of interest [Gevins and Cutillo, 1986, 1995; Rapplelsberger and Petsche, 1988; Silberstein et al., 1990; Gevins et al., 1991, 1994; Petsche et al., 1993, 1997; Silberstein, 1995a; Nunez et al., 1997, 1999; Sarnthein et al., 1998]. In such applications, moderate errors in dura potential distribution caused by head model errors (fixed over time) do not prevent meaningful and robust measures of brain state changes, even if the locations of such changes are inexact and dynamic details at scales smaller than 2 or 3 cm cannot be measured.

4.3. Simulations: noise

High‐resolution algorithms can be sensitive to noisy data [Le et al., 1994; Edlinger et al., 1998]. However, the importance of noise varies widely with EEG application. One issue is, of course, the signal‐to‐noise ratio of the raw data. Often this is known only very approximately and rarely published, except perhaps for hand‐waving statements about “artifact‐free” data. An equally important consideration involves the methods used to transform the raw data. In any study, the bottom‐line question is: Are the final results sensitive to the maximum noise level likely to have contaminated the raw data? Perhaps the most convincing test of this question involves purposeful addition of (separately recorded) artifact or other noise at a power level believed to be substantially larger that the genuine experimental noise [Silberstein, 1995a].

In Group 3 of Table I, the effects of adding 15% uncorrelated noise to forward solutions (fixed head model) are summarized. These simulated correlations provide a severe test since these dura potential estimates were all based on single time slices, and we avoid studies of single slices of genuine EEG data. With this level of noise, the accuracies of single slice high‐resolution EEG are substantially reduced. It should be appreciated, however, that the correlation coefficients obtained with this noisy, simulated 131‐channel data using high‐resolution EEG are somewhat larger than the equivalent correlations obtained from raw potentials (typically ≈ 0.6) with no noise and no distortions from the reference electrode. As expected with such noisy data, the smoothed version (parameter = 10^‐9) of the Melbourne dura imaging algorithm (average correlation = 0.835) performs better than either unsmoothed dura imaging (average correlation = 0.692) or spline‐Laplacian (average correlation = 0.736).

The alpha data described in Section 5 have amplitudes typically in the 30–40 microvolt range and are free of obvious artifact. EEG system noise is estimated to be less than a few microvolts. Thus, the signal‐to‐noise ratio was apparently very high. However, we know of no way to accurately estimate such low noise levels as many subtle biological artifacts can contribute over broad frequency bands. We did, however, check the self‐consistency of the two high‐ resolution methods. This check was obtained from 600 time slices of the raw (ear reference) EEG from two subjects without regard to amplitude. The data were transformed to average reference (for benefit of the dura imaging algorithm) and passed through Melbourne dura imaging and New Orleans spline‐Laplacian (reference independent) algorithms to estimate dura potential independently. A correlation coefficient comparing the two estimates was obtained for each of the 600 time slices. The average correlation coefficient was 0.950, showing the high self‐consistency of the two high‐resolution estimates (Group 4 of Table I) when applied to 131‐channel data. Such self‐consistency falls off sharply with sparser spatial sampling, e.g., correlation coefficients comparing the two high‐resolution methods for 64 channel EEG are typically in the 0.75–0.90 range.

Several of the analyses of Section 5 are based on Fourier transforms of 1‐sec EEG epochs with a 500 Hz/channel sampling rate. The real and imaginary parts of Fourier transforms were used to obtain amplitude, phase, and coherence estimates. With E% random noise in the raw data, the corresponding expected error level in the Fourier coefficients based on statistical fluctuation is E/√500%. This effect is demonstrated in Group 5 of Table I, obtained by estimating alpha rhythm phases at each electrode site (relative to phase at Cz) for each of 20 one‐second epochs. This process was repeated with uncorrelated noise (15% of RMS scalp potential magnitude) added to each measured scalp potential. The estimated phases with and without added noise were then compared for each epoch. Correlation coefficients were calculated for each of the 20 epochs. As shown in Table I (Group 5), the addition of this noise level to raw potentials (a level believed to be substantially higher than actual EEG noise) had minimal effect on phase estimates. In the experiments involving multiple time slices in Section 5, we have chosen zero smoothing parameter for dura imaging because this is the appropriate choice for data with low effective noise. These images closely match spline‐Laplacian estimates.

5. EXPERIMENTAL METHODS

5.1. Choice of experiments

Several experimental measures of EEG are presented here as part of a larger ongoing study. The motivation for presenting these particular data and analyses methods is to demonstrate: (1) high‐resolution EEG, (2) quantitative measures emphasizing both local and global dynamic behavior, (3) quasi‐stable global phase structure of alpha rhythm, (4) the fractal‐like sensitivity of EEG dynamic properties to measurement scale, and (5) upper alpha and theta phase locking during mental calculations. The cognitive task was chosen here mainly as a convenient means to manipulate EEG properties rather than to focus on specific cognitive functions. Our experimental measures address directly theoretical dynamic models, brain binding, and the functional significance of EEG. We show that different measures of EEG dynamics can substantially bias physiological interpretations toward either extreme local or extreme global physiological interpretations.

5.2. Recording spontaneous EEG

Spontaneous EEG was recorded from six healthy subjects with eyes closed. The resting state was alternated each minute with a mental calculation task (cognitive period, eyes also closed). Resting and cognitive periods were each repeated 4–6 times (depending on subject) to obtain a series of 1‐min alternating periods with 7–11 transitions between distinct brain states. In two subjects, EEG recordings were repeated after several days to test reproducibility. Three subjects (including the two repeaters) were chosen for detailed analyses based on data being nearly free of obvious artifact in all channels.

A commercial electrode cap with 131 embedded electrodes (diameter = 0.5 cm) was used to record EEG. Electrode placement and impedance checks required approximately 1 hour. Average center‐to‐center and edge‐to edge electrode spacing were 2.2 and 1.2 cm, respectively. Because of gel spreading beyond electrodes, the effective edge‐to‐edge separation was somewhat less than 1 cm. (Each data channel was tested individually to insure that no salt bridges between electrode pairs occurred.) Electrode positions are shown in Figure 8. Signals were band‐pass filtered with cutoffs at 0.5 and 80 Hz and subsequently digitized at 500 Hz. Data were recorded with respect to a right ear reference with amplifiers grounded to the nose. A separate channel recorded left ear potential with respect to the right ear. Prior to analyses, data were transformed to a symmetric reference equal to the instantaneous digital average potential of the two ears (mainly to provide data consistent with many other studies). Artifact rejection was by visual inspection of raw data. For the three subjects discussed here, very few data were excluded because of artifact.

Figure 8.

Electrode cap with 131 electrodes. The electrode positions were used in both simulations and EEG recordings. The cap was purchased from Electro‐Cap International, Inc.

Recording sessions started with a 5‐min period when subjects were asked to relax with eyes closed, using slow breath counting or other personal relaxation exercises. Each 1‐min mental calculation period was “seeded” with a two‐digit integer X, and involved summing the series X + (X + 1) + (X + 2) + (X + 3) + … to sums of several hundred. A break of 10 sec between each 1‐min period allowed subjects to make comfortable transitions between states, i.e., to get back into relaxed states after each “cognitive pressure” period. This mental task had several important technical features making it easy to implement with EEG: minimal artifact because of closed eyes and lack of motor components, ease of task lengthening to improve statistics, and robust changes of amplitude and coherence with brain state changes [Nunez, 1995; Nunez et al., 1997, 1999]. On the other hand, the task was not “clean” from a cognitive science viewpoint. That is, the task combined a short‐term memory component (holding both the last number and the partial sum of the series in short term memory) and an active component (adding the partial sum to the next largest integer). Obtaining fine distinctions between these mental processes is appropriate for separate studies, hopefully putting the methods and data reported here to good use. Here we were mainly concerned with the study of robust dynamical properties of human spontaneous EEG, which were easily and reliably manipulated with the simple mental task.

5.3. Data analyses

Standard (MATLAB release 11) fast Fourier analysis was applied to each data channel using a Hanning window, typically with 1‐sec epochs providing 1.0 Hz frequency resolution. Other studies involved 5‐sec epochs to obtain 0.2 Hz frequency resolution. Real and imaginary Fourier coefficients yielded magnitude, phase, and coherence estimates based on the average potential of the two ears or global average reference. In a few cases, phase estimates were based on the Hilbert transform (also MATLAB release 11) for comparative purposes. For dura imaging calculations, raw data were transformed to potentials referenced to the instantaneous average potential of all 131 electrode sites. With large electrode arrays, the average reference potential normally approximates the theoretical potential at infinity [Bertrand et al., 1986; Srinivasan, 1999]. As such, it is the appropriate reference for submission to the Melbourne dura imaging algorithm. But transformation to average reference had minimal effect on dura images in spot checks and no effect on spline‐Laplacian estimates, which are always reference free.

The average reference data were passed through the Melbourne dura imaging algorithm to obtain spatially filtered (high‐resolution) estimates of amplitude, phase, and coherence. Some Melbourne dura estimates were checked against the New Orleans spline‐Laplacian algorithm (using ear reference data), which also provided estimates of dura potential. No substantive differences between Melbourne dura image (with zero smoothing parameter) and New Orleans spline‐Laplacian estimates of dura potential were found in spot checks (see Table I).

Peak power plots, used to supplement information obtained from average amplitude spectra, were obtained as follows. Four to 6‐min records corresponding to estimates of resting scalp potential, resting dura potential, cognitive scalp potential, and cognitive dura potential were divided into 5‐sec epochs for each of the 131 channels. Fourier transforms then yielded estimates of amplitude (or power) versus frequency with 0.2 Hz resolution for each channel and for each epoch. The frequency component on the interval (3 ≤ ƒ ≤ 20 Hz) with maximum power for a particular channel and epoch was stored for plotting. The lower delta range (ƒ ≤ 2.8 Hz) was excluded from the peak power test because delta artifact and/or genuine brain dynamics can dominate the other frequency bands. Power at frequencies greater than 15 or 20 Hz was very low. We were not confident that we could reliably distinguish beta and gamma brain rhythms from artifact in the spontaneous EEG so results for these frequency ranges are not reported here. However, comprehensive studies of steady state visually evoked potentials in theta, alpha, beta, and gamma bands (narrow bands centered at the driving frequency) are planned in the future at the Brain Sciences Institute.

The method of peak power defines each five‐second epoch at each electrode site by a single frequency that best characterizes that epoch. Use of this procedure had several motivations. First, a better feeling for nonstationary EEG behavior was obtained than by using only average amplitude spectra. Second, it allowed spectral properties over the entire scalp to be viewed in a single graph. Most importantly, the dominant frequency components in low amplitude signals showed up nicely. This feature was more important for frontal regions, which often exhibit lower EEG amplitudes over most frequency bands.

Phase estimates were obtained at each electrode site for each 1‐sec epoch by transforming real and imaginary Fourier coefficients so that zero phase angle was obtained at Cz (site 88 in Fig. 1). Thus for each epoch, phase angle at each electrode site was measured with respect to phase at Cz. Without such transformation, “phase” would be physiologically meaningless, depending on the arbitrary separation times of records into epochs. Phase estimates are often sensitive to noise, especially near locations with low amplitude signals or when based on short time segments. To test this sensitivity, phase estimates presented here were spot‐checked by purposely adding 15% uncorrelated noise directly to raw EEG data and, in separate tests, by first passing the noise through a forward head model to simulate intracranial, biologic “noise,” which was spatially correlated only because of the head volume conductor. Thus, our conclusions about EEG phase estimates are based on the conservative proposition that genuine noise of this magnitude might have contaminated raw data. Delta, beta, and gamma frequency ranges typically have much lower signal to (artifact) noise ratios than theta and alpha bands. Delta or beta “phase” appeared to be less well‐defined in our data, apparently because of lack of phase stability, low signal‐to‐noise ratio, or some combination of these factors.

Coherence is a correlation coefficient (squared); it provides one important measure of dynamic relations between activity recorded at pairs of electrode sites. We defined phase based on records over a range of periods, between 1 sec and 1 min with FFT methods. In addition, a 1‐Hz band “instantaneous phase,” based on the Hilbert transform, was also used to check FFT‐based phase estimates. Tests for consistency of such phase estimates over time and frequency band provided supplementary information about accuracy and stability of neocortical phase structures.

Our coherence estimates are based on Fourier coefficients for 1‐sec epochs, averaged over 5‐ min periods. Such averages over 300 epochs provide high statistical confidence, but fail to provide information about variations in phase synchrony over time. Coherence issues relating to statistical significance, volume conduction, reference electrode, high‐resolution estimates, and interpretation at multiple spatial scales were studied in connection in an earlier project [Nunez, 1995; Nunez et al., 1997; 1999]. In the current study, each coherence estimate was associated with 5 min of data (resting or cognitive periods) for each of the 131 × 130/2 = 8,515 electrode pairs and each 1 Hz band. Many coherence changes were fully consistent with all (8–11) transitions between brain states, as demonstrated in an earlier study [Nunez et al., 1999].

6. EXPERIMENTAL RESULTS

6.1. Resting alpha topography

Scalp amplitude distributions of resting alpha rhythm at eight successive times are displayed in Figure 9. Individual plots are separated by about 50 ms and correspond to alternating positive and negative peaks in the average reference potential recorded by posterior‐midline electrode 130. Each plot was constructed by averaging over five adjacent time slices (about 10 ms with the 500 Hz sample rate) to minimize noise effects. This step was not critical for raw potentials since single time slices (2 ms averages) were very similar to the 10 ms averages. The short‐time averaging step was directed more to the Melbourne dura image plots shown in Figure 10. Dura spatial patterns show far more complexity than the corresponding raw scalp potentials as a result of filtering out the very low spatial frequencies associated with volume conduction. New Orleans spline‐Laplacian estimates yielded similar patterns as expected.

Figure 9.

Amplitude distributions of (average reference) resting alpha rhythm at 8 successive times separated by about 50 ms are shown. The times correspond to alternating positive and negative peaks in the potential recorded by posterior‐midline electrode 130. Each plot was constructed by averaging over five adjacent time slices with 2 ms separation between adjacent slices. Amplitudes were normalized with respect to the maximum positive and negative potentials (yellow and blue, respectively). Subject BMW.

Figure 10.

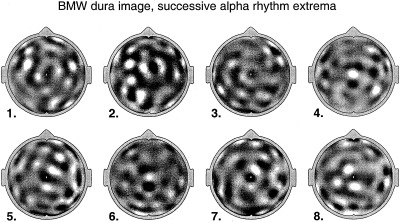
Estimates of dura potential for the same data shown in Figure 9, obtained by passing average reference data through the Melbourne dura imaging algorithm (with smoothing parameter set to zero). Normalized dura potentials are plotted, as in Figure 9. The New Orleans Spline‐Laplacian yields similar patterns of dura potential, e.g., correlation coefficients ≈ 0.95. Addition of uncorrelated 15% noise to the raw data had minimal effect. Subject BMW.

All magnitudes in Figures 9 and 10 were normalized with respect to potential extrema observed within the 0.4‐sec period to facilitate comparisons between scalp and dura estimates. This is an appropriate step because, in simulations, dura imaging and spline‐Laplacian algorithms accurately estimate relative but not absolute potential magnitudes. Two reasons for this are apparent: absolute scalp potentials depend strongly on skull conductivity and Laplacians (microvolts/cm²) do not even have electric potential units.

Subject BMW exhibited distinct spectral peaks in the alpha band, at 8.5 and 10.0 Hz. Figure 11 shows amplitude (upper row) and cosine phase plots (lower row) at 8.5 Hz for average reference potential (left column) and dura image (right column), obtained by Fourier transforms of 60 successive 1‐sec epochs (1 Hz resolution). Figure 12 shows amplitude and phase plots from the same data in Figure 11, but at the 10.0 Hz peak. The 10.0 Hz rhythm shows mainly anterior‐posterior variations in both amplitude and phase of the (low spatial frequency) potential plots. By contrast, the 8.5 Hz rhythm shows more right‐left variations in potential and phase. In other words, the coefficients p _lm(ω) in the spherical harmonic expansion, Eq (6) have substantially different weights at 8.5 versus 10.0 Hz. Dura images indicate much more detail at smaller spatial scales.

Figure 11.

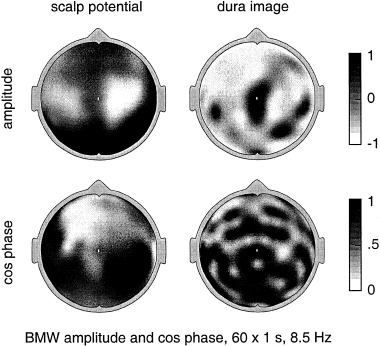
Magnitude (upper row) and cosine phase (lower row) at BMW's lower alpha peak (8.5 Hz) for the average reference potential (left column) and dura image estimate (right column). Plots were obtained by Fourier transforms of 60 successive 1‐sec epochs (1 Hz resolution). Dura image phase plot shows alternating regions at the scale of several centimeters that are 180 degrees out of phase, apparently similar to a wave interference pattern.

Figure 12.

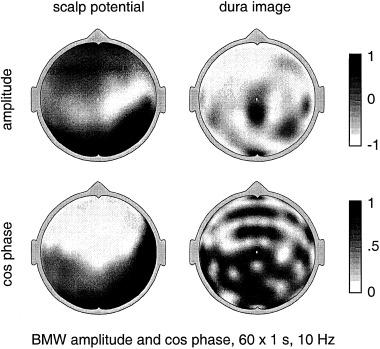
Amplitude (upper row) and phase (lower row) at BMW's upper alpha peak (10.0 Hz) for average reference potential (left column) and dura image estimate (right column). Plots were obtained by Fourier transforms of 60 successive 1‐sec epochs (1 Hz resolution). Produced from the same raw data used to produce Figure 11.

The plots in Figures 9, 10, 11, 12 demonstrate that alpha rhythms present quite different maps when viewed at different spatial and temporal scales. Each time slice of scalp potential exhibits a generally different spatial distribution, although anterior‐posterior phase reversal patterns tend to dominate, in a manner superficially similar to long‐standing waves in a drum surface. This behavior is indicated by Figure 9 and by earlier alpha studies using 64 electrodes [Nunez, 1995]. The corresponding dura image estimates in Figure 10 show that when low spatial frequency scalp potentials (caused by some combination of volume conduction and genuine source dynamics) are filtered out, the remaining spatial patterns are complex and quite variable over time. This complex dynamic behavior is even more apparent in a high‐resolution video that we constructed from 64 channel resting alpha [Cao et al., 1994, unpublished research].

Either averaging over time with Fourier transform methods (the examples in Figs. 11 and 12) or space averaging by the head volume conductor (all scalp potential plots) generally produces a greatly oversimplified and potentially misleading picture of the spatial‐temporal alpha source dynamics produced by neocortex. That is, the better the time and spatial resolutions, the more detail is observed in amplitude, phase, and coherence patterns.

Lower (8.5 Hz) and upper (10.0 Hz) alpha peaks generally have different spatial distributions over the scalp, as shown by earlier studies [Nunez, 1974b, 1981] and comparison of Figure 11 with Figure 12. Furthermore, these plots suggest that cross‐frequency dura amplitude estimates are more similar to each other than the corresponding cross‐frequency scalp amplitudes. To investigate this further, we computed cross‐frequency correlation coefficients for 300 successive 1‐sec epochs, for both log (scalp potential amplitude) and log (dura image amplitude). Correlation coefficients were obtained from 92 electrode‐by‐electrode comparisons, excluding the outer ring of 39 electrodes where estimates are less accurate. The average (over 300 epochs) cross‐frequency scalp potential correlation was 0.169, whereas the average cross‐frequency dura image potential correlation was 0.307.

At least one tentative explanation for BMW's data is consistent with several dynamic theories [overview in Nunez, 2000a, 2000b] and other data obtained here: The alpha process may consist of global modes (e.g., standing waves of relatively long wavelength) having generally distinct spatial distributions at different frequencies plus more localized alpha activity. Locations of large amplitude local sources may be less frequency dependent. By filtering out part of the global activity using the dura image algorithm, we were left with more locally dominated dynamics, as indicated by comparison of potential and dura plots in Figures 11 and 12. Comparison of cross‐frequency potentials and dura images was not studied in the other subjects because they did not produce clear double alpha peaks.

6.2. Spectral properties of resting alpha

The global effects of spatial filtering are illustrated by the peak power scalp (left) and dura (right) estimates for three subjects in Figure 13. The smaller electrode numbers on vertical axes near the upper parts of these plots correspond to more frontal scalp locations (see Fig. 8). Each peak power plot contains 60 (5‐sec epochs) × 131 (electrodes) = 7,860 points. The dominance of alpha band activity over the entire scalp is evident in all three subjects in the average reference potential plots. All three subjects show two or three distinct bands (vertical patches) of global alpha rhythm in the scalp potential plots. By contrast, the corresponding dura image plots show more sparsely patched alpha activity.

Figure 13.

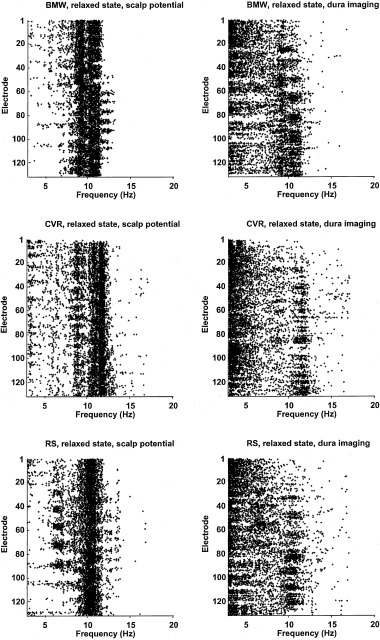
Peak power scalp potential (left column) and corresponding dura image (right column) estimates for the three subjects (BMW, CVR, and RS in rows 1–3, respectively). Smaller electrode numbers on vertical axes near the upper parts of plots correspond to more frontal scalp locations (see Fig. 8). For each 5‐sec epoch and each electrode site, the frequency component (0.2 Hz resolution) with the largest power (or amplitude) in the range 3.0 ≤ f ≤ 20.0 Hz was selected by the FFT. Other frequency components at each site are not plotted, even though they may be nearly as large as the peak components. The test was repeated with the same data first passed through the dura image algorithm (right column). Each plot contains 60 epochs × 131 electrodes = 7,860 points. The dominance of alpha band activity over the entire scalp is evident in all three subjects in the average reference potential plots but somewhat less evident in the dura image plots.

These and other data [Nunez, 1995, 2000a, 2000b; Andrew and Pfurtscheller, 1996, 1997; Nunez et al., 1997, 1999; Florian et al., 1998] suggest that the usual eyes closed resting EEG in humans has at least several distinct contributions: Long wavelength (low spatial frequency) activity near the alpha peak frequency that often exhibits moderate to high coherence over large scalp distances (e.g., 10–25 cm) and more localized, incoherent delta, theta, alpha, and (some) beta activity contributing mainly to dynamics at shorter spatial wavelengths.

These data may be interpreted naturally in the context of cortical source activity expressed in the spherical harmonic expansion Eq (2) for the idealized case of spherical scalp and cortical surfaces. Cortical “source strength,” i.e., dipole moment per unit volume P(θ, ϕ, t), at surface locations (θ, ϕ) is expressed as a sum over spherical harmonic functions (a sum over characteristic spatial functions or eigenfunctions) with progressively higher spatial frequencies. The coefficients in this expansion p _lm(t) are generally determined by the underlying dynamics.

Figure 3 shows the theoretical effects of spatial filtering by the volume conductor and high‐resolution estimates on such source activity. The data in Figures 10, 11, 12, 13 then illustrate the effects of filtering out the very lowest spatial frequencies (mainly the l = 0 and 1 modes of the spherical harmonics) with dura imaging. That is, measured EEG in an idealized spherical head may be generally expressed as a sum over the spherical harmonic functions, but with weighting coefficients p _lm(t) depending partly on spatial filtering. By mostly removing the lowest modes (e.g., l = 0, m = 0 and l = 1, m = ‐1, 0, 1) with dura imaging, we shifted the weighting away from the more global toward more local dynamics. Whereas measured globally dominated dynamics occurred mostly in the alpha band, more locally dominated dynamics also occurred in delta, theta, alpha, and beta bands.

6.3. Changes of peak power with brain state changes

Figure 14 shows peak power estimates obtained from average reference potentials (left) and dura image estimates (right) for the cognitive periods. Comparison with the corresponding resting plots in Figure 13 indicates that alpha blocking of scalp potential in subjects BMW and RS was minimal and occurred mainly in the lower alpha band. Alpha blocking was more evident in subject CVR but also occurred more in the lower alpha band.

Figure 14.

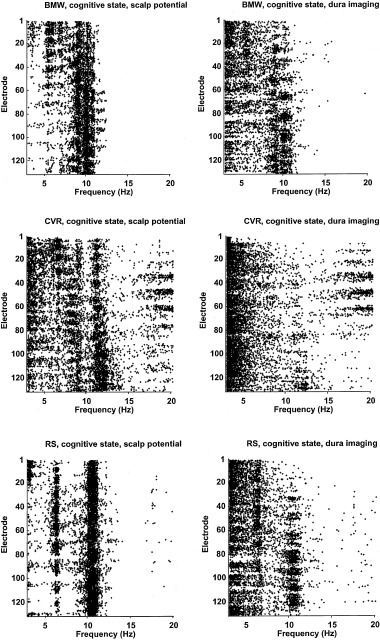
Peak power estimates obtained from average reference potentials (left) and dura image estimates (right) for the cognitive periods. Methods are identical to those used in Figure 13, except for some small changes in the number of total epochs.

Subject RS showed a robust theta rhythm at many frontal and central sites in the resting state. His theta was enhanced, and it became more narrow band and widespread during cognition. The other two subjects produced dominant theta mainly during cognitive periods. While theta activity was often evident in frontal regions, it was more widespread than implied by the usual description “frontal midline theta,” reported in several working memory studies [review by Gevins et al., 1997]. If theta were very localized, we would expect locally dense clusters of points in the peak power dura image plots. But, upper theta (5–6 Hz) was actually quite evident in the peak power potential plots, indicating dynamics at relatively low spatial frequencies. Of course, theta could have multiple origins, occur in both low and high spatial and temporal frequency bands, be sensitive to task details, or some combination of all these effects.

Subject RS showed some alpha blocking during cognition in the lower alpha band while his upper alpha band had increased peak power points in both potential and dura image plots. Subject BMW produced somewhat similar behavior. Subject CVR, female and physically smaller than the other two subjects, showed a substantial number of peak power points in the beta band, especially during the cognitive state. This could have been due to subtle muscle artifact, an indirect consequence of more alpha blocking, genuine cortical source activity in the beta band that was more evident because of a lower resistance (e.g., thinner) skull, or a combination of these factors. CVR's cognitive peak power plots (Fig. 14) indicate a number of sites with sparse points in the approximate range 13 ≤ ƒ ≤ 16 Hz, but a much higher density of peak power points in the range 17 ≤ ƒ ≤ 20 Hz. This suggests contribution from brain rather than muscle sources in the beta range, because muscle spectra are normally relatively flat over 13 ≤ ƒ ≤ 20 Hz, falling off slowly with increasing frequency. On the other hand, many of these channels were located near temporal muscles. Thus, our best guess is that these beta points reflect a combination of brain activity and subtle muscle artifact.

One should keep in mind that the peak power plots present a very conservative view of dominant frequencies of cortical source activity. That is, each plotted point in the theta or beta band means for that particular electrode site and 5‐sec epoch, a particular frequency was the single component (with 0.2 Hz resolution) with the largest power in the range 3 ≤ ƒ ≤ 20 Hz. Thus, absence of theta or beta points (especially in posterior regions) does not necessarily mean absence of substantial theta or beta activity. Generally, it means that whatever theta or beta power produced was dominated by larger alpha or high‐end (≥ 3 Hz) delta power.

6.4. Stability and accuracy of phase structure of resting alpha rhythm

Dura image phase plots (Figs. 11, 12) indicate many alternating regions out of phase. Regions of constant phase (zero phase lag) were typically separated by about 4–6 cm. In other words, regions 180 degrees out of phase were typically separated by about 2–3 cm., or roughly the spatial resolution of the high‐resolution methods. Many alpha phase structures based on dura imaging with epochs ranging from one second to one minute were studied. All dura phase structures obtained with zero smoothing parameter showed qualitatively similar complex structures at the same approximate scale of the EEG spatial resolution, suggesting even more complexity at scales too small to observe from the scalp. Dura image with nonzero smoothing parameters had levels of detail intermediate between those of raw scalp potential and dura image with zero smoothing parameter.

To test whether these phase structures genuinely represented cortical source dynamics, the accuracy and stability of dura phase estimates were studied as follows:

• 1Correlation coefficients comparing successive estimates of cosine phase (over the 131 electrode sites at all integer frequencies on 3 ≤ ƒ ≤ 40 Hz) were calculated for 5 min of resting alpha using 1‐sec epochs. Correlation coefficients, averaged over all 299 successive epoch pairs, are plotted versus frequency in the upper part of Figure 15. The correlation coefficients were all less than 0.2, reflecting large second‐to‐second dynamic changes in dura phase structure as expected. However, these correlation coefficients were substantially larger in the approximate range 6 ≤ ƒ ≤ 11 Hz, indicating much more stability of dura phase estimates in this frequency range.
• 2Phase stability at the peak alpha frequency was also studied by using different epoch lengths in 5‐min records of resting alpha. Correlation coefficients comparing successive epochs at individual alpha peaks 10 Hz (subject BMW) and 10 Hz (subject RS) are plotted versus epoch length in lower part of Figure 15. Correlation coefficients, averaged over all epoch pairs, increased monotonically with epoch length, ranging between about 0.1 for 1‐sec epochs to about 0.35–0.50 for 20‐sec epochs.
• 3Uncorrelated Gaussian noise with amplitude equal to 15% of the RMS amplitude of the raw data (averaged over all electrodes) was added directly to raw scalp potential measurements. The contaminated data (noise plus genuine EEG) were then passed to the dura image algorithm. All phase correlation coefficients in Figure 15 were recalculated with this purposeful addition of noise. No substantial differences were obtained, as suggested by Table I.
• 4Uncorrelated 1/ƒ noise with amplitude equal to 15% of the RMS amplitude of the raw data was passed through the forward solution of the four‐sphere head model to produce simulated, spatially correlated noise. This noise was then passed to the dura image and Fourier transform algorithms to produce phase estimates for successive epochs of varying lengths. The circles in the lowest plot of Figure 15 (random simulation) show epoch‐to‐epoch phase correlations as a function of epoch length resulting from this spatially correlated noise. All noise‐simulated correlation coefficients are close to zero as expected, thereby supporting the idea that the EEG dura phase correlations in Figure 15 genuinely represent brain dynamic processes.

Figure 15.

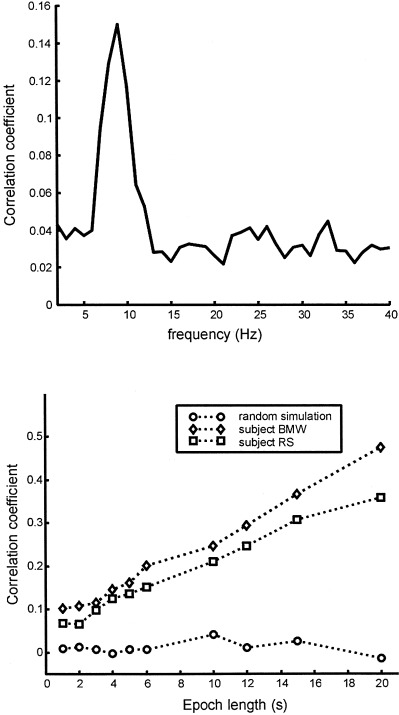
(Upper) Correlation coefficients comparing successive estimates of cosine dura image phase (over the 131 electrode sites) are plotted vs. integer frequencies. Phase plots were calculated for 5 min of resting alpha using 1‐sec epochs with phase at site 88 (Cz) defined as zero for each epoch. Correlation coefficients were averaged over all 299 successive epoch pairs. Subject BMW. (Lower) Dura cosine phase correlation coefficients comparing successive epochs at individual alpha peaks—10 Hz (subject BMW) and 10 Hz (subject RS) are plotted vs. FFT epoch length. Correlation coefficients, averaged over all epoch pairs, increase monotonically with epoch length, ranging between about 0.1 for 1‐sec epochs to about 0.4–0.5 for 20‐sec epochs (frequency resolution held fixed at 1 Hz). The lower plot (random simulation) was generated using 1/f noise passed through a head model (forward solution) to simulate spatially correlated scalp noise, which was then passed through the dura imaging and FFT algorithms to estimate dura phase.

These phase studies suggest that the phase structure of the alpha rhythm in these subjects may be described as quasi stable. This stability depends on both the temporal and spatial scales of phase estimates. That is, phase estimated with long epochs shows less epoch‐to‐epoch variation. Furthermore, phase estimated at large scales with reference potentials shows less epoch‐to‐epoch variation than (smaller‐scale) dura image phase. In other words, the closer we look, the more phase detail we observe. We conjecture that the observed phase structures may represent interference patterns of standing waves of synaptic action. Such synaptic action may be superimposed on and interact with neural networks that are embedded within the synaptic action fields [Nunez, 2000b].

6.4. Coherence of alpha and theta rhythms

Theta and upper alpha coherence patterns in subject RS are shown in Figure 16. Electrode pairs with dura coherence greater than 0.1 at the 99% confidence level [Bendat and Piersol, 1986] have connecting lines drawn. The columns represent 5 min of relaxed (left, RLX) and 5 min of cognitive (right, COG) state, respectively. During states of mental calculation, coherence at both 6.5 Hz and 10.0 Hz were generally higher in subject RS (averaged over 5‐min periods), whereas lower alpha band coherence was reduced (not shown). The coherence estimates between specific electrode pairs with lines draw in Figure 16 vary widely, e.g., for electrode pairs separated by 10 cm or more, coherence estimates (with lines drawn) varied from 0.33 to 0.65. The lower value was required to satisfy the criterion coherence > 0.1 at the 99% confidence level. Because coherence is a correlation coefficient squared, these data imply estimated dynamic correlations in the 0.57–0.81 range between remote cortical locations, providing justification for our characterization of alpha rhythm in terms of “more globally dominated dynamics.”

Figure 16.

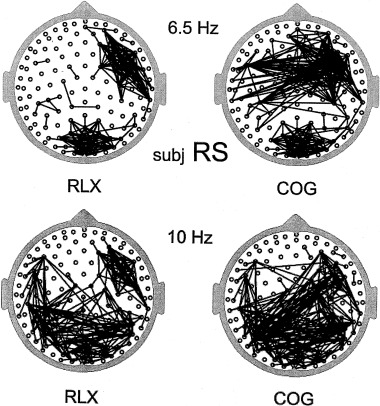
Dura image interelectrode coherence in the relaxed state for subject RS (RLX, left column, averaged over 5 min) and cognitive state (COG, right column, averaged over 5 min). All interelectrode coherences greater than 0.1 at the 99% confidence level are indicated by lines between the appropriate electrode pair, excluding nearest‐neighbor edge electrodes. Actual coherence estimates vary widely, e.g., from about 0.3 to 0.7 for electrode separations greater than 10 cm. Both upper 6.5 Hz theta coherence (upper row) and 10.0 Hz upper alpha coherence (lower row) generally increased during the cognitive task. However, lower alpha band coherence decreased during the cognitive task (not shown). Simulations confirmed that these patterns represent genuine source coherences rather than volume conduction or statistical artifact.

Another point is that the general behavior of coherence patterns varied substantially between the three subjects but was robust over different periods within the same subject. It should be further emphasized that dura coherence estimates are conservative in the sense that they may be artificially low because of the spatial filtering by the dura imaging algorithm. That is, the removal of erroneous high coherence caused by volume conduction by dura imaging may also remove genuine source coherence associated with very low spatial frequencies [Nunez et al., 1999]. Finally, coherence can very substantially over time even with our attempts to fix brain states over 1‐min periods. Such time variations in phase locking are described in Section 6.5.

The significance of these coherence estimates was first checked by passing random noise through the four shell head model to simulate scalp potentials generated by uncorrelated dura sources. These simulated scalp potentials were then passed through the dura imaging and Fourier transform algorithms to obtain dura coherence estimates. The resulting coherence plots based on the same 99% confidence level used for the EEG data were empty as expected, except for adjacent electrode positions on the outer ring. These erroneous coherence estimates resulted from inaccurate dura estimates at edge electrodes. Thus, all lines connecting adjacent electrodes in the outer ring were removed from the coherence plots for the genuine data in Figure 16. In a second test, the coherence pattern at 37 Hz was obtained for subject RS. Only five pairs of electrodes passed the 99% test and all were closer than 5 cm. This result shows that 37 Hz gamma activity was globally incoherent and that volume conduction did not substantially inflate dura coherence estimates, a finding consistent with earlier high‐resolution coherence studies [Nunez et al., 1997, 1999; Srinivasan et al., 1996, 1998; Srinivasan, 1999].

6.5. Theta phase synchronization during the cognitive task

Subjects BMW and RS displayed more coherent theta band activity at many frontal and frontal‐parietal electrode pairs during mental calculations than in the resting state. Several such electrode pairs were selected for more detailed phase analyses so that changes over shorter times could be observed. Phase estimates for each signal were obtained by Fourier transforms at the (observed) maximum coherent theta frequency. A Hanning window and overlapping 1‐sec epochs were used. The window was stepped by 0.1 sec to obtain successive phase estimates. A series of relative phase offsets between pairs of recording sites was calculated for signals over the entire (roughly) 10‐min recording. To visualize the phase offsets, phase distributions were computed in a series of 10‐sec sliding windows. When phase offset was near random over the immediate 10‐sec window, phase distributions were relatively uniform. But when phase offset was more consistent over multiple phase measurements within the 10‐sec window, phase distribution was peaked at this phase offset.

In Figure 17, the upper rows of each plot pair display 10‐sec phase distributions (represented as grayscale histograms) through successive 1‐min periods of constant state, alternating between resting and cognitive states, the latter indicated by shaded bars and the word “cog.” The subject is BMW and the electrode sites are 9–55 (upper plot pair) and 16–55 (lower plot pair), roughly phase locking of the frontal midline theta reported in other studies. In Figure 18, similar plots are presented for subject RS for electrode sites 45–54 (cross hemispheric frontal‐central) in the upper plot pair, and sites 9–55 (frontal‐central) in the lower plot pair. In these examples, phase offset distributions peak in roughly the 140–180 degree range.

Figure 17.

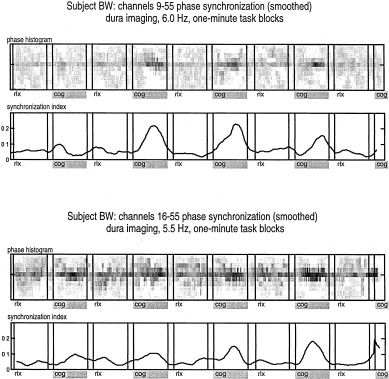
The upper rows of each plot pair display 10‐sec phase offset distributions (phase differences between electrode pairs) represented as gray‐scale histograms. Successive 1‐min periods of constant brain state are shown, alternating between resting and cognitive states. Cognitive periods are indicated by shaded bars and the word “cog.” The lower row of each plot pair is the synchronization index used by Tass et al. [1998]. Phase offsets peak at approximately 180 degrees. (Upper plot pair) Electrode sites 9–55 (Lower plot pair) sites 16–55 (essentially frontal midline theta). Subject BMW.

Figure 18.

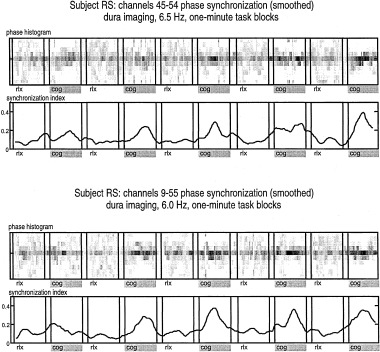
Plots similar to Figure 17 for subject RS. (Upper pair) Electrode sites 45–54 (cross‐hemispheric precentral) (Lower pair) sites 9–55. Phase offsets peak at approximately 140 degrees.

A synchronization index ρ, adopted by Tass and colleagues [1998], was used to quantify divergence of these distributions from uniformity. For each distribution, ρ = (S _max – S) / S _max, where S _max = ln N. Here N is the number of bins in the distribution. S is the entropy, defined in the context of information theory as

(7)

where q _i is the probability that a phase estimate falls within bin i.

The synchronization index ρ ranges from 0 to 1, where ρ = 0 indicates no synchronization, and ρ = 1 indicates perfect synchronization. Theta synchronization index (or phase offset consistency) increased with mental calculation in these electrode pairs, as shown in the lower row plots of each pair. The synchronization effect tended to increase as the 1‐min cognitive periods progressed. This was contrary to the habituation often observed in extended mental tasks. Perhaps this can be interpreted as facilitation of cell assembly formation by repetition of the mental task.

To check further the statistical significance of phase estimates, phase distribution and synchronization index were also calculated for a surrogate data set with amplitude retained and phase estimates presented in random order, independent of brain state. The residual synchronization was low (< 0.2), so no task effect was found in the surrogate data as expected. Finally, instantaneous phase was estimated with the Hilbert transform after band passing (1 Hz band) raw data, as described in Rosenblum et al. [1996]. Comparison of Hilbert transform and FFT methods revealed no substantial differences in several spot checks of phase estimates.

7. CONCLUSION

7.1. The proposed dynamic framework and coregistration with fMRI

A general working framework for experimental study of the large‐scale dynamics of EEG is suggested here, including proper interpretation of data recorded at different spatial and temporal scales. The framework is based on combined local, regional, and global mechanisms. We suggest that the relative importance of these contributions to EEG dynamics can vary substantially with animal species, brain state, frequency band, and measurement scale. This general framework has an important advantage over viewpoints that may prejudge the nature of EEG dynamics, thereby biasing experimental design. For example, dipole localization studies can only provide accurate pictures of underlying dynamics when applied to EEG phenomena that are genuinely generated by a few isolated sources. We recognize that the physiological bases for EEG are controversial and that several competing models have been widely published. But the general dynamic framework advocated here encompasses each of these models as special cases. As such it should be relatively noncontroversial.

The proposed conceptual framework also has implications for studies involving coregistration of EEG with fMRI. One popular approach is to constrain EEG inverse solutions (e.g., dipole localization) to regions where fMRI indicates relatively large hemodynamic signatures. This approach is partly supported by studies linking metabolic and hemodynamic activity with local neuronal synaptic and electrical events. But, EEG is a very selective measure of current source activity, often corresponding to small subsets of the total synaptic action in tissue volumes and largely independent of action potentials. Increases in neural firing rates can apparently occur with reduced large‐scale synchrony of current sources and, as a result, smaller scalp potentials. By contrast, hemodynamic and metabolic measures are believed to increase with neural firing rates. How closely do we expect these disparate measures of brain function to agree? In a recent paper [Nunez and Silberstein, 2000], we suggest that scalp EEG amplitudes and hemodynamic or metabolic activity can sometimes change in opposite directions for reasons having to do with the distinct spatial scales and selective frequency bands of cortical synchrony. Does coregistration of EEG with fMRI make sense? The answer may be a sensitive function of the specific experimental questions being asked.

7.2. Local versus global dynamics

Compelling evidence for alpha rhythm dynamics with substantial local character comes from studies of spatially selective reactivity to mental tasks [Petsche and Etlinger, 1998; Sarnthein et al., 1998; Klimesch et al., 1999], motor tasks [Pfurtscheller and Neuper, 1992; Pfurtscheller and Lopes da Silva, 1999], eye opening [Niedermeyer, 1999a], and auditory stimuli [Hari, 1999].

By contrast to the picture of independent alpha band activity generated in distinct cortical regions, global alpha activity is supported by moderate to high alpha coherence over large interelectrode distances (e.g., 10–25 cm) in resting states [Petsche et al., 1997; Nunez et al., 1997, 1999; Nunez, 2000a; Srinivasan et al., 1996, 1998, 1999; Srinivasan, 1999]. In addition, other studies have shown that local (mu) and globally coherent alpha band activity can be separately manipulated with a motor task [Andrew and Pfurtscheller, 1996, 1997; Florian et al., 1998].

Our experiments address the local versus global issue from several directions. The resting potential power plots in Figure 13 (left side) show two or three frequency bands of alpha activity occurring at all (or nearly all) electrode sites, covering all lobes. Spatially filtering these data with the dura image algorithm (right side) consistently reduced global contributions relative to local contributions. As a result, dura peak power plots were more patchy, indicating dominant alpha band activity in many cortical regions, but not in all. (Recall that peak power plots are very conservative, i.e., every point on the plots indicates dominant alpha activity over a 5‐sec epoch, but absence of a point does not mean absence of alpha.)

Comparison of the resting plots (Fig. 13) with the corresponding cognitive plots (Fig. 14) indicates that mental calculations may also change the relative contribution of global activity. Global coherence in the lower alpha band was reduced, whereas coherence in theta and upper alpha bands increased during cognitive periods. Comparison of the resting and cognitive dura image coherence plots in Figure 16 provides strong additional support for more globally or locally dominated dynamics, depending on brain state and narrow band frequency. The data also suggest a disconnection between upper and lower band alpha during mental calculations that is less evident in the resting state. (Many earlier broadband studies of alpha have lumped everything in the 8–13 Hz band into a single measure, thereby apparently missing important cognitive effects.) Our data fit the proposed conceptual framework and the established existence of global human brain states in which neocortical EEG looks very similar over its entire upper surface. Whereas alpha rhythms appear to involve a mixture of local and global activity, anesthetic, coma, and some epileptic phenomena appear to provide the best examples of globally dominated states.

The potential importance of global effects is also suggested by several theoretical considerations. Global effects may strongly influence (top‐down) local dynamics in a wide variety of complex physical systems [Haken, 1983; Bishop et al., 1983; Srinivasan and Nunez, 1993; Nunez and Srinivasan, 1993]. The dynamics of such systems, as measured at any particular location, is generally determined by the entire system. This is typical even in systems with only nearest neighbor interactions, often modeled with differential equations. Global effects may be even more important when nonlocal interactions (often modeled with integral equations) also occur [Morse and Feshbach, 1953; Haken, 1983; Ma, 1985]. Cortico‐cortical fibers provide such nonlocal interactions in human neocortex [Nunez, 1995; Ingber, 1995]. Physiological models, especially those including cortico‐cortical interactions, and many data suggest that EEG recorded at different locations can look quite different, but this can easily occur as a result of combined local and global influences [Nunez, 1995; Ingber, 1995; Silberstein et al., 1995a; Jirsa and Haken, 1997; Kelso et al., 1999].

7.3. Neocortical dynamics depends on spatial and temporal measurement scales

The “snapshot” amplitude plots in Figures 9 and 10 and the magnitude and phase plots in Figures 11 and 12 demonstrate that dynamic estimates of EEG depend strongly on both spatial and temporal measurement scales. Very large spatial scale dynamic measures were provided by raw scalp data, whereas dura image or spline‐Laplacian algorithms measured dynamics at smaller scales. Comparisons of one subject's magnitude and phase structures for potentials and dura images (for the same 1‐min data block) are shown in Figure 11 (8.5 Hz) and Figure 12 (10.0 Hz).

By adjusting the smoothing parameter in the dura imaging algorithm, we were also able to estimate spatial patterns at scales intermediate between scalp and (estimated) dura potential. Smoothed (magnitude and phase) dura estimates contained more detail than raw scalp potential estimates but less detail than unsmoothed dura or Laplacian estimates. In other words, the better the scalp spatial resolution, the more detail was observed in magnitude and phase plots. This result is inconsistent with alpha generation exclusively by a few isolated and stationary dipoles, as often proposed. Our data suggest that alpha dipoles (or localized alpha networks) may be partly but not fully isolated. Models consisting of a few dipoles or even a few tens of dipoles (e.g., less than the number of electrodes) are not sufficient to explain the dura phase structures or coherence patterns observed here. Rather, a plausible conjecture is that alpha dynamics exhibits a fractal‐like (or turbulence‐like) spatial structure at progressively smaller spatial scales, perhaps down to the minicolumn scale or smaller. The spatial structure appears to have substantial global as well as local properties.

Figure 15 shows that global phase structure also depends critically on both frequency and temporal scale. Different epoch lengths for magnitude or phase estimates provided dynamic measures at different time scales. Within the alpha band, progressively longer epochs yielded more stable global structures that masked short time fluctuations. By contrast, we did not find convincing evidence for stable global phase structure outside the band 6–11 Hz. We did find phase locking of upper band theta and upper band alpha frequencies between specific electrode sites (Figs. 16, 17, 18). Earlier studies of steady state visually evoked potentials [Silberstein, 1995a; Burkitt et al., 2000] at alpha band frequencies showed that cortical phase structures depend critically on 1 Hz changes in driving frequency [Nunez, 1995]. Related studies have demonstrated close connections between amplitude and phase of 13 Hz visually evoked potentials and a working memory task [Silberstein, 1997]. Also, steady state visually evoked magnetic field recordings (7 Hz) during binocular rivalry studies revealed substantial theta global coherence increases during periods of perceptual dominance [Srinivasan et al., 1999].

7.4. Relationships to other studies of brain function

We have proposed a conceptual framework that distinguishes between more locally and more globally dominated neocortical dynamic behavior. Such dynamic differences may occur in different brain states or in distinct frequency bands in fixed brain states. For example, fMRI measures brain function in the extreme (compared to EEG) low temporal frequency range. How much do we expect the dynamics measured in such widely separated frequency bands to agree [Nunez and Silberstein, 2000]? Our experiments and data analyses methods were chosen within a framework that attempts to avoid prejudging such issues. While these experiments barely scratched the surface of the very complex world of brain dynamic behavior, they illustrate several experimental connections to physiologically based dynamical theory. Our EEG work is ongoing and includes studies of spontaneous as well as driven activity. We are cautious about interpretations of measured dynamic behavior, partly because of the small number of subjects and limitations of our experimental measures. However, all data studied here fit naturally within the general, local/global conceptual framework and should help to guide studies of connections between EEG, quantitative dynamics, and cognitive processing in the near future. Our proposed framework is very much in agreement with the following description by Mountcastle [1979, p21] if we substitute “local network” with “system”—here meaning subsystem of the brain: “The brain is a complex of widely and reciprocally interconnected systems and the dynamic interplay of neural activity within and between these systems is the very essence of brain function.” The well‐know studies of event‐related potentials by Gevins and colleagues [Gevins and Cutillo, 1995, p332] support a similar view. Specifically, during cognitive processing, “many (cortical) areas probably are involved in a constellation of rapidly changing functional networks that provide the delicate balance between stimulus‐locked behavior and purely imaginary ideation.” Finally, the following view is expressed by Edelman and Tononi [2000, p131] in the context of a quantitative complexity measure associated with consciousness and brain binding: “High values of complexity correspond to an optimal synthesis of functional specialization and functional integration within a system. This is clearly the case for systems like the brain—different areas and different neurons do different things (they are differentiated) at the same time they interact to give rise to a unified conscious scene and to unify behaviors (they are integrated).” In this view, complexity (and by implication, cognition) tends to maximize between the extremes of isolated networks and global coherence. We find this a reasonable working hypothesis. It then follows that both local network dynamics and interactions between networks are important. But one of the central messages of this paper is that different experimental designs and methods of data analysis can bias EEG (or MEG or fMRI or PET) physiological interpretations in either extreme local or extreme global directions. By demonstrating this with both theory and EEG experiment, we have hopefully made a small step toward more thoughtful design of future experiments, e.g., in studies involving brain binding that reveal important long‐range coherence between regions as well as locally dominated dynamics. Such studies should further facilitate our understanding of connections between physiology, psychology, and dynamic theory.