Asymmetry of the brain surface from deformation field analysis

Abstract

The detection of asymmetry of exposed brain surfaces is examined, and a new method, deformation‐based asymmetry (DBA), is introduced. DBA is based on analysis of two high‐resolution magnetic resonance brain images, each with features representative of the subject group from which they were derived. Warping of individual brain images to their group representative image using octree spatial normalization provides sets of displacement vectors that are used in estimating deformation variance. For DBA group‐representative left and right hemisphere images are compared. Representative hemisphere images are warped to each other and asymmetry analyzed using standardized d‐values calculated as the ratio of displacement vector magnitude to the estimated component of variance in the direction of the displacement vector for each surface voxel. D‐values were calculated within hemispheres by dividing subjects into two equal groups and comparing left‐to‐left and right‐to‐right. D‐values from this ipsilateral hemisphere grouping were pooled. D‐values from contralateral hemispheres were compared with the pooled ipsilateral hemisphere data. The proportion of d‐values above a fixed level was used to test for difference between the two groups. High‐resolution magnetic resonance (MR) images from 20 young, right‐handed males were studied using DBA. No significant differences were seen between sub‐grouped ipsilateral d‐values (P > 0.10). Highly significant asymmetries (P < 0.0001) were found between hemispheres, and in each lobe. Common right frontal and left occipital petalias were seen. The DBA method can theoretically be applied to any two groups of globally similar structures where analysis of dissimilarity of regional features is sought. Hum. Brain Mapping 19:79–89, 2003. © 2003 Wiley‐Liss, Inc.

INTRODUCTION

Recent advances in the analysis of three‐dimensional (3‐D) MR images of the brain have led to several methods that automate the detection of anatomical differences between groups [Toga 1999]. Examples of these methods are voxel‐based morphometry (VBM) [Ashburner et al., 1998; Ashburner and Friston, 2000, 2001], deformation‐based morphometry (DBM) [Ashburner et al., 1998; Bookstein 1999; Wang et al., 2001], and tensor‐based morphometry (TBM) [Thompson, 1999; Thompson et al., 2001]. These brain morphometry methods are objective, highly automated, and free from user bias. VBM is simpler to implement and suitable to the capabilities of most research centers. While VBM can be prone to errors due to redundancy in positional and grey‐level information and group differences in registration accuracy [Bookstein 2001], it has been shown to be valid when used under appropriate conditions [Ashburner and Friston 2001]. Several large‐group studies of structural asymmetry in the human brain have been reported using VBM [Good et al., 2001 (N = 465); Watkins et al., 2001 (N = 142)]. In the large‐group studies classical right‐hander asymmetries were seen (frontal right‐greater‐than‐left and occipital left‐greater‐than‐right asymmetries). These regions of the cerebral cortex that extend slightly more in one hemisphere than in the opposite hemisphere are commonly called the right frontal and left occipital petalia.

Deformation‐based morphometry, introduced by Ashburner et al. [1998], was used to characterize differences in deformation fields that were attributed to gross anatomical difference in brain shape. This research group demonstrated how analysis of deformation fields could be used to study anatomical differences between small groups (N ≥ 20). Groups to be evaluated were aligned using nonlinear deformations [Ashburner and Friston, 1999] to a common brain template and differences in deformation fields analyzed using multivariate analysis of covariance and canonical variates analysis. Ashburner et al. [1998] found significant left‐to‐right brain asymmetries in several areas reported in the classic review of brain asymmetry by Geschwind and Galaburda [1987]. However, their DBM method failed to find two well‐known asymmetries, the right frontal and the left occipital petalia. This might be due to small group size coupled with low sensitivity of the DBM method. The low sensitivity for asymmetry might be due to their extensive spatial smoothing (8‐mm full‐width at half‐maximum Gaussian kernel). It appears that group size can resolve this problem, since subsequent large‐group studies using VBM reported these petalia [Good et al., 2001; Watkins et al., 2001].

An alternative method is introduced for assessment of brain asymmetry within small groups (N ∼20). It is based on fast 3‐D warping [Kochunov et al., 1999; 2000] and the concept of group‐representative brains [Kochunov et al., 2001; 2002]. The new method is a subset of DBM that focuses on asymmetry and is therefore called deformation‐based asymmetry (DBA). DBA deals directly with high‐resolution 3‐D brain images, and hemispheric asymmetry is evaluated using a derived statistical measure called a d‐value (Equation 3). In its present form DBA focuses on the exterior brain surface where asymmetries are readily seen, and it was designed to detect regional asymmetries in small groups. The goals of this investigation are twofold, first to introduce the theory of DBA and second to evaluate its capabilities in a small group of twenty right‐handed males.

MATERIALS AND METHODS

Theory

Discrete 3‐D deformation fields are used to warp one 3‐D brain image (source) to another (target), and this is being done with increasing accuracy [Collins et al., 1994; for review see Toga 1999; Kochunov et al., 2000]. The deformation fields described in this paper are 3‐D arrays of displacements vectors 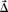(x,y,z) with components δx(x,y,z), δy(x,y,z), and δz(x,y,z), indexed by voxel location (x,y,z) in the target brain image. Each displacement vector points from a location in the target brain image (x,y,z) to an associated location (x + δx(x,y,z), y + δy(x,y,z), z + δz(x,y,z) in the source brain image. If the source brain image is accurately deformed to the target by a deformation field, then deformations are a measure of distance between corresponding locations in the two brains. To ensure that DBM analyses focus on regional rather than global differences in brain anatomy, a common preprocessing step is to remove (or at least consistently minimize) global differences in position, orientation, and size of brains [Ashburner and Friston, 2000; Kochunov et al., 2001].

The use of DBM to evaluate anatomical differences between 3‐D brain images can be time consuming and prone to errors in small regions where one‐to‐one correspondence fails [Ashburner and Friston, 2001]. A common solution to this problem is to restrict the deformations to larger scales when comparing such images [Ashburner and Friston, 2000]. This restriction can lead to failure to recover appropriate deformation values in small regions where one‐to‐one correspondence does not fail. The deformation field approach for DBA provides high‐speed high‐quality feature matching between 3‐D brain images that is not restricted to large‐scale processing. It is based on the octree spatial normalization (OSN) method [Kochunov et al., 1999–2002] that uses a multi‐scale approach where large scale increments in deformations are calculated first from analysis of large regions, and this proceeds down to the smallest scale increments and regions (2 × 2 × 2 voxels).

In DBA studies, a single high‐resolution representative image from one group is compared to a single high‐resolution representative image from a second group (i.e., from groups of left and right hemispheres). The deformation of one representative image to the other is analyzed to estimate spatial differences between the groups. The deformation fields created by warping each member of a group to its group representative image are used to estimate the variance for within‐group warping.

Group‐Representative Brain Images

A group‐representative image avoids outliers and retains common anatomical features of the group [Kochunov et al., 2002]. This is done while preserving the resolution and contrast of a single high‐resolution MR image. In DBA studies left (LH*) and right (RH*) hemisphere representative brain images are synthesized from groups of left and right hemisphere brain images (see Subjects and Methods ).

Deformation Variance

Figure 1 illustrates the processing used to make a representative brain position its voxels at the geometrical center for the group. The displacement vectors show the distribution of locations of group members about the corresponding representative brain location. The group's displacement vectors are used to estimate deformation variance for each representative brain voxel.

Figure 1.

Distribution of corresponding sites within a group of brains about the representative brain site. Displacement vectors point from the representative brain site to the sites within each brain in the group.

Since deformation variance may not be identical in all directions, it was estimated as the component of variance along the direction of interest, i.e., the direction of displacement between source and target brains. The first step was to calculate unit vectors [û_t−s(x,y,z)] directed from a locations in the target brain (t) to associated locations in the source brain (s), from the corresponding displacement vectors _t−s(x,y,z). The next step was to determine the displacement along the direction of interest for each brain (i) in the target group.

(1)

The directional variance was then calculated from the sum of squares of these directed components of deformation

(2)

The directional standard deviation [σ_d(x, y, z)] changes with position and is dependent on both source and test brains. It is an estimate of variance in the target brain group in the direction of displacement between target and source brains. The directional variance calculated in this manner accounts for anisotropy of displacement vectors in the target brain.

Standardized Deformation (D‐values)

The magnitude of the displacement vectors | (x,y,z)| provides an estimate of distance between x‐y‐z locations in the target brain and associated locations in the source brain. Dividing this magnitude by σ_d provides a standardized measurement of the deformation. The d‐value for each voxel of interest in the target brain model was calculated as

(3)

This study focuses on d‐values at exterior brain surfaces because these surfaces can be readily segmented, reducing confounds from segmentation errors. D‐values are used to test whether displacement vectors, from the target to the source representative brain, fall within the expected distribution of displacement within the target brain group (see Figure 1). The hypothesis is that the distribution of d‐values for ipsilateral and contralateral hemispheres are not different for regions of symmetry, and conversely that a failed test indicates asymmetry (see Appendix A).

SUBJECTS AND METHODS

Subjects

Twenty high‐resolution (1× 1× 1 mm³ voxels), T1‐weighted anatomical 3‐D MR brain images of right‐handed Caucasian males were selected from a large population study of healthy volunteers (ICBM project) [Mazziotta et al., 1995]. Images were acquired on an Eslcint Prestige 1.9T imaging system (Haifa, Israel) using a 3‐D T1 weighted spoiled gradient‐echo sequence (TR/TE = 24/6 msec, flip angle = 25 degrees, NEX = 1, with flow comp). Slice direction was sagittal (190 mm) with a rectangular field of view of 252 × 256 mm in the AP and SI directions. Subjects ranged in age from 21 to 34 with the average age of 27.6 ± 4.4 years.

Pre Processing

The brain was extracted using an automated skull stripping procedure (BET) [Smith, 2002] and FAST [Zhang et al., 2001] add‐ins for MEDx (Sensor Systems). The automated brain extraction tool—BET was used to perform gross deskulling. BET uses the CSF layer between pia and arachnoid matter to guide its processing. Next, WM/GM/CSF segmentation was performed using FAST. This step refined the outer GM border by removing the subarachnoid CSF structures. Also, because the pia matter layer is very thin membrane (∼0.3 mm), with a long T1 relaxation time, its contribution to the results of the analysis should be minimal. The extracted brain image was clipped at the level of brainstem. All brain images were globally spatially normalized to the Talairach template using the Convex Hull software [Lancaster et al., 1999] and resliced to an isometric spacing of 0.85 mm. Midline alignment was manually verified and corrected by two experienced neuroanatomists using interactive spatial normalization software [Lancaster et al., 1995]. Following this preprocessing, images for individual hemispheres (LH and RH) were created by segmenting the left and right hemispheres from each subject's 3‐D brain image using the inter‐hemispheric fissure as the dividing point. Individual hemispheres were filled with a constant value creating two classified regions, inside and outside brain. The exterior brain surfaces of LH and RH images were clearly defined by this preprocessing, and the surface asymmetry of these images was analyzed using DBA.

DBA Processing

The DBA processing stream creates left (LH*) and right (RH*) “representative brain images” for between‐hemisphere testing and mirrored versions for within‐hemisphere testing (Figure 2). The following DBA processing steps are used for the left and right hemisphere group images:

• 1An image is randomly selected from the group to calculate target quality scores (TQS) using the Fast method [Kochunov et al., 2001].
• 2The image with the best TQS is designated as the group target brain (TB). The TB is warped to every brain in the group using OSN. The geometrical centroid of deformations at each voxel location is calculated by averaging the deformation fields.
• 3The group representative brain is created by transforming each voxel in the TB into its corresponding average location within the group determined in step 2 [Kochunov et al., 2002].
• 4The group representative brain image is then warped to every image in the group using OSN. The spatial distribution of deformation vectors about the representative brain is stored for calculation of directional variance (Equation 2).

Figure 2.

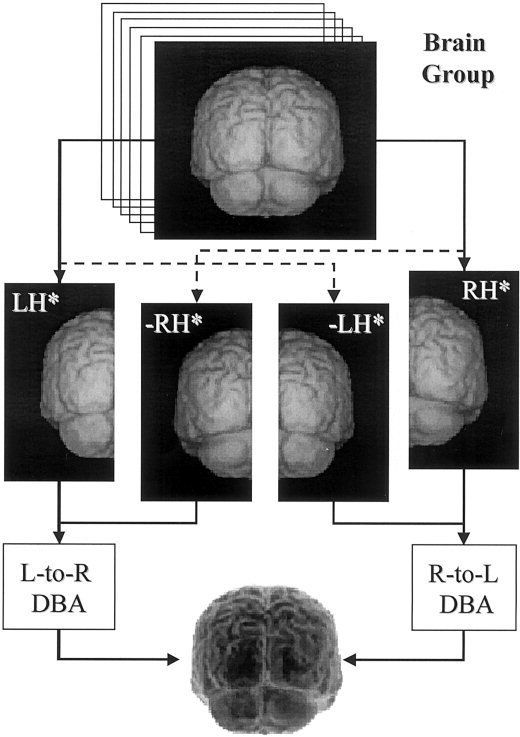
Schematic of the DBA processing stream. Left (LH*) and right (RH*) representative hemisphere models are formed from the brain group. Reflected right (–RH*) and left (–LH*) representative hemisphere models are created as mirror images of the LH* and RH*. The –RH* model is warped to the LH* models for left‐to‐right analyses and the –LH* model warped to the RH* model for right‐to‐left analyses. Results are reported on a representative brain formed by reassembling LH* and RH* (illustrated as a negative image here).

Following these steps, hemisphere representative images from each hemisphere are warped to each other to obtain deformation fields, and d‐values are calculated using the magnitude of displacement vectors and their directional standard deviation (Equation 3).

RESULTS

The brain surface asymmetry was studied by hemisphere and by lobe using the lobar definitions of the Talairach Daemon [Lancaster et al., 2000]. The analysis did not include cerebellum. Each hemisphere was analyzed to determine the proportion of surface voxels with d‐values > than 2.5. These proportions were used to formulate a Z‐score (Equation A.2) to test for significant differences of the proportions in ipsilateral and contralateral hemispheres, as an indication of hemispheric asymmetry.

Ipsilateral Hemispheres

The LH* and RH* groups were randomly subdivided into two left‐side (LH*₁, LH*₂) and two right side (RH*₁, RH*₂) groups of 10 images each. No significant differences were seen in p_i values for left and right hemispheres of frontal, parietal, and occipital lobes, though the temporal lobe and hemisphere differences were significant (Table I). To remove these differences as possible confounds in asymmetry testing left and right d‐values were pooled (Table II). The spatial distribution of the low proportion of surface voxels with d‐values ≥ 2.5 in the ipsilateral hemispheres is illustrated in Figure 3.

Table I.

Proportions for ipsilateral hemispheres

Lobe	Proportion (pi)		Z‐score
	Left	Right
Frontal	0.064	0.059	1.12 NS
Parietal	0.029	0.025	0.83 NS
Occipital	0.006	0.007	0.30 NS
Temporal	0.059	0.027	7.75*
Hemisphere	0.047	0.037	3.94*

^* P < 0.0001.

Table II.

Asymmetry test results

Lobe	N	Pc	Pi	Z‐score	Finding
Frontal	22,008	0.297	0.062	42.0*	R > L (19.9:1)
Parietal	10,193	0.206	0.027	36.6*	R > L (1.4:1)
Occipital	8,431	0.413	0.007	130*	L > R (6.1:1)
Temporal	13,799	0.328	0.044	45.7*	R > L (9.5:1)
Hemisphere	54,431	0.308	0.043	88.8*	R > L (2.5:1)

^* P < 0.0001.

Figure 3.

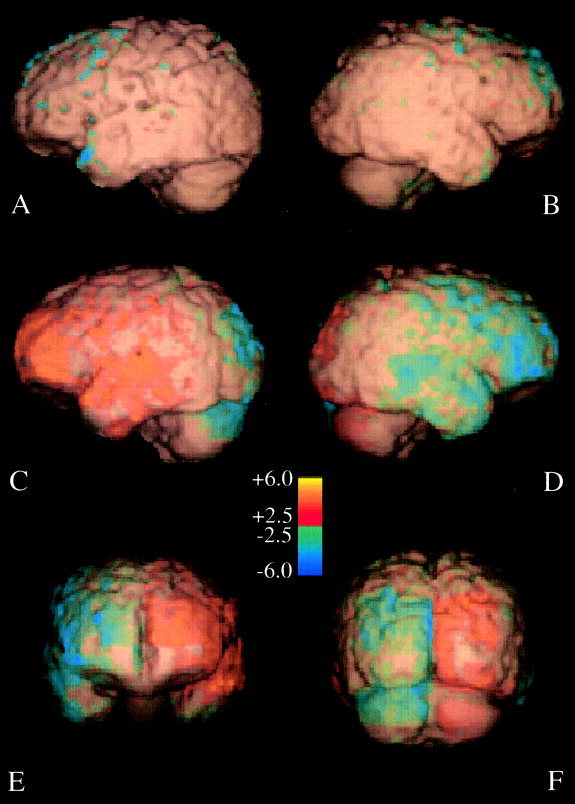
Surface rendering of a representative brain with d‐scores >2.5. The brain surface is color coded to indicate inward (blue) and outward (yellow) deformations needed to match the contralateral hemisphere. Left hemisphere colors are for Left‐to‐right analyses and right hemispheres are for Right‐to‐left analyses. (A, B) Within‐hemisphere asymmetry results with views of left and right sides. Between‐hemisphere asymmetry results with left (C), right (D), anterior (E), and posterior (F) views.

Contralateral Hemispheres: Direction of Warp

Differences in target brains for the left and right hemispheres can lead to differences in warping left‐to‐right vs. right‐to‐left. The denominator term in the d‐value is based on variance estimated in the target brain and this variance is likely different in the two hemisphere groups. Also, since representative brains are not identical, there are some differences in feature pairing that affect the magnitude of calculated deformations, i.e., the numerator in the d‐value equation. Analysis of p_c shows that there were statistically significant differences due to direction of warp in all but the parietal lobe (Table III). To remove these differences as possible confounds in asymmetry testing d‐values from left‐to‐right and right‐to‐left warping were pooled (Table II).

Table III.

Proportions for contralateral hemispheres

Lobe	Proportion (pc)		Z‐score
	L‐to‐R	R‐to‐L
Frontal	0.297	0.246	5.39*
Parietal	0.206	0.205	0.07 NS
Occipital	0.413	0.319	5.60*
Temporal	0.328	0.253	5.68*
Hemisphere	0.308	0.253	4.53*

^* P < 0.0001.

Asymmetry Testing

The proportion of d‐values exceeding the test level for contralateral hemispheres p_c was significantly larger that in ipsilateral hemispheres p_i (Table II). The value of P was largest in the occipital lobe (P = 0.37) and smallest in the parietal lobe (P = 0.21). While all regions tested in contralateral hemispheres were significantly different from those in ipsilateral hemispheres, the magnitude and sense of these differences varied by lobe. Well‐known cerebral asymmetries, the frontal (R > L) and occipital (L > R) petalias were found (Table II, right column) and are seen in Figure 2 C‐F, wherein inward deformations for one hemisphere correspond to outward deformations for the other. The magnitude of the temporal lobe R > L ratio (9.5:1) was intermediate, between the magnitudes of the frontal and occipital lobes. The smallest asymmetry was in the parietal lobe where the R > L ratio was only 1.4:1.

DISCUSSION

The hemisphere level comparison of fractional surface difference provides an omnibus test for DBA. This can be followed by regional analyses by dividing hemispheres into lobes following the Talairach Daemon scheme [Lancaster et al., 2000]. As can be seen in Tables I, II, III, the both proportions, p_i and p_c, vary regionally. The use of the ipsilateral group in null‐hypothesis testing adapts to these changes, whether they are methodological or anatomical in origin. The small lobe‐level proportions for ipsilateral hemisphere (1–6%) and large values for contralateral hemispheres (20–40%) indicate that the DBA method is both specific and sensitive when testing for the presence of asymmetry between paired lobes in small groups (n = 20).

The DBA analysis in 20 right‐handed subjects found statistically significant asymmetry in all tested lobes. The analysis performed by DBA relates primarily to petalias, outward or inward displacement of the brains exterior surface. The R > L asymmetry of the brain surface for the temporal lobe differs with some reports, however they analyzed other features such as length of the sylvian fissure or size of the planum tempori. The DBA study did not attempt to deal with these forms of asymmetry or for structures deeper within the brain.

While DBA was only applied regionally for lobes, similar analyses can be applied to smaller regions. For smaller regions (smaller n) the variance estimate of proportions (p_i and p_c) are larger (see Appendix, Equation A.2), reducing the sensitivity of the method. Also, if n is very small the assumption that the calculated Z‐value is normally distributed can fail. These issues can be moderated by lowering the reference d‐value, to raise p_i to the range of 0.1–0.2. This approach was not needed for the lobe level analyses, but might become an issue if gyral level or smaller regions are to be analyzed.

The high sensitivity of DBA surface based asymmetry testing is believed to come from its basic design, which is aimed at managing errors common to deformation field methods This design is summarized in the following sections.

Errors Due to Lack of Anatomical Homology

All DBM methods are based on an underlying assumption that deformation field analyses provide some estimate of the spatial distance between paired brain regions in two groups. However, pairing of corresponding regions is not possible for many anatomical features [Toga 1999]. This failed pairing (lack of feature homology) is clearly documented in many of the smaller sulci in the atlas of Ono et al. [1990]. Pairing success of corresponding left‐ and right‐sided regions is related to the size of the regions, with smaller regions having larger failure rates. Incorrect pairing is avoided in some DBM methods by using large‐extent Gaussian filtering to suppress contrast in smaller regions, effectively removing them from the analysis. However, this approach assumes that failed homology follows the same size trend across the entire brain, and this is not necessarily true [Ono et al., 1990].

The DBA method does not suppress small‐detail contrast, but rather uses high‐resolution representative brains for comparison, or representative brain hemispheres in the current study. DBA uses a 3‐D cross correlation function to quantitatively match similar features in source and target brains. Cross‐correlation analyses are performed in paired octants varying in size from 128³ down to 2³ mm³ [Kochunov et al., 2000]. Cross‐correlations are performed on three segmented and classified tissues (grey matter, white matter, and cerebral spinal fluid). This classified‐tissue cross‐correlation provides an optimal match of 3‐D shape in homologous tissues at each octant size. If homology fails a best‐match is found, therefore the method is not hampered by failed homology at larger sizes or at different brain locations. While no approach can guarantee complete paired matching of corresponding regions between two brains, the methods used in DBA (representative brains, classified tissues and cross‐correlation driven fitting) are believed to be superior to methods that remove finer details.

Errors in deformation estimates

A variety of errors have been reported for brain warping methods that use deformation fields [Toga 1999]. No method is absolutely accurate, so the key issue for asymmetry analyses is to understand how errors in deformation fields impact decisions in statistical testing. Deformation errors are expected to be larger for structures smaller than accommodated by the deformation model. For example, a global transformation model cannot accurately determine deformations for regional anatomical structures such as the lateral ventricle. However, several high‐dimensional warping methods provide low deformation errors when fitting such structures [Toga 1999], including OSN.

Based on the assumption that deformation errors will be larger for smaller structures, some DBM methods limit the detail in the brain images using large‐extent Gaussian filters [Ashburner et al., 1998]. This scheme, coupled with the use of only low‐order terms in the deformation model, avoids deformation errors in small regions by excluding them. The magnitude of deformations in intermediate‐size regions is altered when using this approach. DBA does not exclude high‐order terms in the deformation model or use large‐extent Gaussian filters. It supports small‐region analyses and assumes that deformation errors are partly due to random effects, which can be managed by group size, as is common practice for other statistical approaches.

Errors in variance estimates

The directional deformation variance in DBA is calculated using all members of a group. If there is a multiplicative bias in the calculation of the deformation it propagates into the deformation variance and is partly cancelled when forming d‐scores (Equation 3). Directional variance was designed to deal with cases where deformations are asymmetric. In preliminary testing directional variance was compared with a non‐directional average group variance, and both variance methods gave similar results in hemisphere and lobe analyses, with slightly different spatial distributions. This outcome was expected for many locations since the target brain voxel (i.e., in the representative brain) is positioned at the central location of the deformations. We chose to use the more theoretically sound directional variance for DBA.

Use of DBA with other structures

The DBA approach to asymmetry detection and analysis should be readily extendable to other brain regions where paired structures are present in both hemispheres. These include superficial features such as face, head, and ears; as well as deep structures such as the eyes, lateral ventricles, caudate, putamen, thalamus, and others. In fact, asymmetry need not be the basis of comparison, and whole brain differences between two groups can be evaluated by the methods outlined for DBA.

APPENDIX A.

The 3‐D probability density function (PDF) describing the distribution of vectors in a displacement vector field should generally be a function of both magnitude and orientation of the vectors. However, if vector magnitudes are independent of orientation, the PDF is greatly simplified, and can be expressed as a function of magnitude only. This was assumed to be the case for the PDF of d‐values (Equation 3) from the ipsilateral hemisphere test group. Histograms of d‐values calculated for ipsilateral and contralateral hemispheres show the general shape of corresponding PDFs (Figure A1). Several distribution functions (F, spherical T and Gaussian, χ², and γ) were evaluated to find an analytical model for these histograms, and the γ distribution provided the best fit. The general equation for the γ distribution is

(A.1)

where γ is the shape parameter, β is the scale parameter, μ is the location parameter, and Γ is the γ function (National Institutes of Health, online at http://www.nih.gov/div898/handbook/eda/section3/eda366b.htm).

Figure A1.

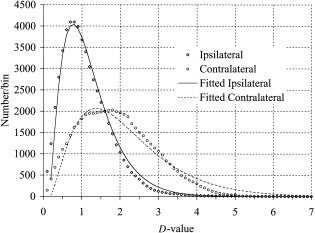
Ipsilateral and contralateral hemisphere data.

The γ model function (Equation A.1) was fit to d‐value histograms by varying β, γ, and μ using a least square error procedure. This was done using the Minerr function using Mathcad software (MathSoft, Cambridge, MA). The d‐value bin size used in fitting was 0.1, with a bin offset of 0.05 to center the data. The average RMS error between model and measured data was 2.0% of the peak value for ipsilateral and 5.4% for the contralateral. The fitted values of μ and γ values were similar for both distributions: (0.15, 2.37) for ipsilateral and (0.17, 2.56) for contralateral. The scale parameter (β) was significantly larger (0.77 vs. 0.44) for the contralateral data. Though the model equation did not fit as well to the contralateral histogram, its excellent fit to the ipsilateral data support the assumption that d‐values from this group are approximately distributed according to a γ distribution.

D‐values standardize the measurement of 3‐D deformation difference between two representative brain hemispheres. The shape parameter (β) in PDF(d) provides a semi‐quantitative indication of asymmetry. It is smaller when compared hemispheres are from the same side (ipsilateral) and larger when they are from the opposite side (contralateral). Anatomical asymmetry is expected to vary regionally, and this should be reflected as corresponding regional variability in the β parameter.

Whereas there are numerous options to test for statistical difference between d‐value distributions, we elected to use a method with an efficient processing scheme and that readily adapts to regional brain analyses. The method selected uses proportions from a population divided into two groups. The two groups are the proportion (p) with d‐values ≥ some reference d‐value and the remaining proportion (1‐p). A value of 2.5 was chosen for the reference d‐value. This led to an ipsilateral hemisphere proportion (p_i) of ∼0.04 and contralateral hemisphere proportion (p_c) of ∼0.28. The value of p_i ranged from ∼0.01 to ∼0.06 across the four lobes tested. For asymmetry testing p_i was compared with the contralateral hemisphere proportion (p_c) with a null hypothesis that p_c = p_i and the alternative of p_c ≠ p_i. The null hypothesis test was performed using a Z‐score derived from proportions estimated from two groups [Glantz, 1981; Zar, 1996]:

(A.2)

where n_c and n_i are the number of independent samples in each group. N values were estimated as the number of surface voxels divided by the number of voxels constituting an independent or uncorrelated group of voxels. We estimated this group size to be that of the smallest octant used in the OSN processing, i.e., 2³ = 8 voxels. Even with this conservative estimate the values of n ranged from ∼1000 for the occipital lobe to ∼6500 for each hemisphere. The use of equation A2 with normal Z‐tables is supported for cases where p · n and (1‐p) · n are greater than five (Zar), and this was the case for all regional analyses. AQ1: Please approve or provide running head