Estimation and detection of event‐related fMRI signals with temporally correlated noise: A statistically efficient and unbiased approach

Abstract

Recent developments in analysis methods for event‐related functional magnetic resonance imaging (fMRI) has enabled a wide range of novel experimental designs. As with selective averaging methods used in event‐related potential (ERP) research, these methods allow for the estimation of the average time‐locked response to particular event‐types, even when these events occur in rapid succession and in an arbitrary sequence. Here we present a flexible framework for obtaining efficient and unbiased estimates of event‐related hemodynamic responses, in the presence of realistic temporally correlated (nonwhite) noise. We further present statistical inference methods based upon the estimated responses, using restriction matrices to formulate temporal hypothesis tests about the shape of the evoked responses. The accuracy of the methods is assessed using synthetic noise, actual fMRI noise, and synthetic activation in actual noise. Actual false‐positive rates were compared to nominal false‐positive rates assuming white noise, as well as local and global noise estimates in the estimation procedure (assuming white noise resulted in inappropriate inference, while both global and local estimates corrected false‐positive rates). Furthermore, both local and global noise estimates were found to increase the statistical power of the hypothesis tests, as measured by the receiver operating characteristics (ROC). This approach thus enables appropriate univariate statistical inference with improved statistical power, without requiring a priori assumptions about the shape or timing of the event‐related hemodynamic response. Hum. Brain Mapping 11:249–260, 2000. © 2000 Wiley‐Liss, Inc.

INTRODUCTION

Event‐related analysis methods greatly extend the range of questions and hypotheses that can be addressed using fMRI. Importantly, event‐related methods can be applied to experiments where cognitive or perceptual events occur in a randomized order, thus eliminating potential confounding factors such as set or strategy effects [Buckner, 1996; Rosen et al., 1998]. Furthermore, the advent of rapid presentation event‐related analysis methods [Dale and Buckner, 1997; Clark et al., 1998; Burock et al., 1998; Dale, 1999] makes it possible to use identical experimental designs with fMRI, electroencephalography (EEG) and magnetoencephalography (MEG), thus facilitating the integration of different imaging modalities [Dale et al., 2000].

In order to estimate the event‐related fMRI responses, or to draw statistical inference from event‐related fMRI experiments, existing methods typically assume a particular form, or some limited set of basis functions, for the hemodynamic response [Cohen, 1997; Josephs et al., 1997; Zarahn et al., 1997b]. While the general linear model (GLM) framework used in these methods allows for the use of a complete, orthonormal basis set spanning the space of possible responses, most often only one component or a partial set is used. Imposing any assumed shape on the hemodynamic response necessarily produces biased estimates of the true response if the assumed responses do not span the space of all possible actual responses. Given that neuroimaging studies have only begun to probe the large space of possible behavioral, perceptual, cognitive, and pharmacological responses, it may be premature to presuppose that current models are universally valid over all brain locations and stimuli. Assuming a particular shape in the GLM leads to three potential problems for interpreting neuroimaging studies: 1) Statistical inference based on the estimated responses is inappropriate because the data does not meet the assumptions of the model, 2) interesting responses that are unlike typical sensory responses may not be detected, and 3) differences between the estimated hemodynamic responses elicited by different stimuli are difficult to interpret due to the biased nature of the estimated response timecourses.

Here we present a practical framework for obtaining statistically efficient, unbiased estimates of event‐related hemodynamic responses in the presence of temporally correlated noise. Our estimates are finite impulse response (FIR) estimates in that the hemodynamic response is assumed temporally finite. We further expand on the use of the F‐test for drawing statistical inference in event‐related fMRI [Friston et al., 1995b; Josephs et al., 1997]. Specifically, we use linear restriction matrices to incorporate various forms of knowledge about the response without biasing the underlying estimation. The linear restriction matrices are formally equivalent to the F contrast used in SPM99 and can be thought of as ‘multidimensional’ contrasts [Andrade et al., 1999]. These restriction matrices are different from traditionally used contrast vectors, which are a subset of restriction matrices, in that they are used to impose explicit temporal structure in the hypothesis test. The appropriateness and power of these estimation and inference procedures are assessed using both simulated and actual noise data.

Several studies have assessed the validity of the GLM in terms of its ability to produce experimental false‐positive rates equivalent to theoretical false‐positive rates [Zarahn et al., 1997a; Purdon and Weisskoff, 1998]. If the statistical hypothesis test is inappropriate, then it will incorrectly label too many (or too few) voxels as activations for a given significance level. Inference will, in general, be inappropriate when it does not account for the autocorrelations of the underlying noise. Worsley and Friston [1995] demonstrated a method that accounted for autocorrelations in fMRI signals; however, they concluded that estimating the true autocorrelations in fMRI noise was impractical and instead chose to filter all data with a known smoothing function. This approach, as stated in the above work, is not optimal in that it does not use the true autocorrelations of the noise. Zarahn et al. [1997a] found that including in the GLM an empirically determined smoothing function and model of intrinsic fMRI noise autocorrelation could bring false‐positive rates to expected theoretical levels. One potential problem with the method used in this study is that the empirically derived noise model was generated from runs not involved with the activation task and that the data was taken over multiple voxels, multiple experimental runs, and multiple subjects—a so‐called 'global' noise estimate. It has been shown that fMRI noise may not be wide‐sense stationary (WSS, a process having a constant mean and covariance structure over time) over these three dimensions, and thus it may be inappropriate to use a global noise model derived from a different dataset to draw inferences about activation in a particular voxel, run, and subject [Purdon and Weisskoff, 1998; Purdon et al., 1998]. One of the goals of the present study was to determine if a global noise estimate is appropriate or if a local noise estimate computed for the same voxel as the activation is needed to obtain correct false‐positive rates. Unlike previous studies, both the local and global noise estimates were obtained from the same data sets used to estimate the hemodynamic responses.

METHODS

MRI techniques

Noise data sets were collected from 8 healthy subjects (5 men, 3 women) using a 3‐T magnetic resonance imager (General Electric/Advanced NMR). For each subject, 16 slices were selected for the functional and anatomical echo‐planar acquisitions such that the entire brain was acquired. High‐resolution T1‐weighted inversion‐recovery echo‐planar image were acquired for anatomic alignment (TR = 22 sec, TI = 1,100 msec, 1. 5625 mm in‐plane resolution). An automated echo‐planar shim procedure was run to improve B_o magnetic field homogeneity [Reese et al., 1995]. T2*‐weighted functional images were acquired using an asymmetric spin echo sequence sensitive to BOLD contrast (TR = 2 sec, TE = 30 msec, α = 180°, 3.125 mm in plane resolution, 7 mm thickness). Functional images were acquired within runs of 128 samples for each subject. The room was dim, and subjects were not presented any external stimuli while being imaged. Four discarded samples were acquired prior to each functional run to achieve steady‐state magnetization.

Response estimation

The goal of this section is to present a procedure for calculating unbiased and statistically efficient estimates of the underlying hemodynamic responses associated with event‐related fMRI experiments. We assume that the BOLD fMRI signal corresponds to the output of a linear time‐invariant (LTI) system with a finite impulse response as suggested in several studies [Boynton et al., 1996; Dale and Buckner, 1997; Dale, 1999]. Therefore, the linear discrete‐time model for the fMRI signal is as follows

(1)

where y is the fMRI signal at a particular voxel, x _i is the binary stimulus sequence for the ith trial type, h _i is the hemodynamic response of the ith trial type, and w is a Gaussian noise sequence with arbitrary covariance matrix Λ_w. It should be noted that any other typical 'covariates' could be included in the model but are left out for simplicity. An equivalent familiar expression for (1) is

(2)

where y is the vector of all observed data, X is the convolution matrix for all trial types representing the experimental design, h is a vector of all hemodynamic responses to be estimated, and w is a Gaussian noise vector. If the covariance Λ_w is known, the maximum likelihood (ML) estimator of the hemodynamic response ĥ _ML could be computed according to

(3)

Note that this approach can also be used to estimate the hemodynamic response functions with higher temporal resolution than that of the measured fMRI signal, by jittering the timing of the events relative to the repetition time (TR) of the fMRI acquisition, as described in [Dale, 1999].

The ML estimate for a linear model with Gaussian errors is optimal in the sense that it has the smallest variance among all unbiased estimates of the response. This estimator is sometimes called the Aitken estimator (among other names) and is a special case of the generalized least‐squares estimator that one obtains when the data and model are whitened on the basis of the known autocorrelations among the errors. However, as discussed above, the noise covariance Λ_w is unknown and potentially varies across voxel, experimental run, and subject. Thus, (3) cannot be used directly until an estimate of the noise covariance is computed. Additionally, we wish to estimate the noise from the same task data and not use separate noise data sets that may not be representative of the noise in the particular voxel.

Estimation of the noise covariance within the same activation dataset

To estimate the noise covariance within the same activation data, first the ordinary least squares (OLS) estimate of the hemodynamic response is computed

(4)

The OLS estimator is an unbiased but inefficient estimate of the underlying hemodynamic response. Additionally, appropriate statistical inference cannot be drawn from (4) because the noise is nonwhite and unknown. Since ĥ _OLS is an unbiased estimator, the underlying noise structure is estimated from the residual error of the estimates given by e = Y − Xĥ _OLS. Note that the covariance structure of the residuals for a finite number of samples is not identical to the true covariance of the noise; however, it has been shown that statistically consistent covariance estimates can be derived from the residuals for various noise processes [Greene, 1993].

It is helpful (although not necessary) to have a parameterized model of the noise process in order to estimate the covariance matrix Λˆ _W from the residuals. The power spectral density of fMRI noise has been shown to contain a component that decays with frequency and a component that is relatively flat for all frequencies [Weisskoff et al., 1993; Friston et al., 1994; Boynton et al., 1996]. There is some debate whether the correlations in the noise are physiological in origin or induced by the measurement. For our purposes, we simply desire a robust description of the process with few parameters. We adopt a model for the noise similar to previously proposed models that assume that the noise can be modeled as the superposition of a white Gaussian noise process and a correlated component [Zarahn et al., 1997a; Purdon and Weiskoff, 1998]. Assuming that the noise process is wide‐sense stationary, our model covariance function (K _ww [n]) of the total noise process takes the form

(5)

We sought estimates of the parameters λ and ρ in order to form the estimated covariance matrix

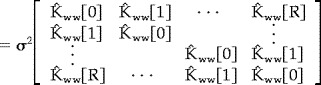It should noted that an estimate of σ² is not needed to form Λˆ _w because σ² is estimated from the residual errors of the fit. A simple linear estimate of λ and ρ can be formed from the sample covariance function by first normalizing it such that K̂ _ww [0] = 1. The model of the sample covariance function for lags greater than zero is then

(6)

which can be transformed to the 'linear' form

(7)

such that the OLS estimate of the transformed noise parameters is

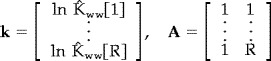(8)

Maximum likelihood or other estimation techniques can be used to estimate the parameters in Λˆ _w; however, solutions to their equations require iterative, nonlinear minimization routines that are ill suited to practical fMRI data processing. In testing these procedures we made two different classes of noise parameter estimates. The first was a spatially global noise estimate where the time courses from all voxels within a particular brain slice were used to estimate one set of parameters. The same global noise estimate was used to estimate the responses in all voxels for that slice. This method assumes that the noise process is spatially WSS across the slice. The second method was a spatially local estimate where a given voxel and its eight nearest neighbors contributed to the estimated noise parameters. For this method every location in the brain had a potentially different set of noise parameters. In both methods, activation and noise were estimated within the same datasets. Additionally, voxels outside of the brain did not contribute to the noise estimates.

It is of course possible that K̂_ww[n] could be negative for particular values of n, in which case the log transform in (7) is not defined. For the global noise estimates, no negative estimated autocorrelations where observed at lags less than 10 samples for all data sets. The local estimates were more variable, thus when the estimated correlations at lags greater than zero were sufficiently small, we assumed the noise was white. Specifically, when K̂_ww[0]/K̂_ww[1]>15, the noise process was considered to be white and no additional parameters were estimated. Lags up to 5 were used for local noise estimates, with voxels still having negatives autocorrelations considered to be white. It should be noted that noise estimates with the constraints above will be biased; however, we demonstrate that this bias is not significant using simulated and fMRI noise data sets.

Once Λˆ _w is estimated, the original data is used to compute the so‐called feasible generalized least squares (FGLS) estimate of the hemodynamic responses according to

(9)

The FGLS estimator has the same asymptotic properties as the ML estimator under very general conditions; specifically, it will be an asymptotically efficient estimate given that Λˆ _w is a consistent estimator of the noise. Depending on the mismatch between the assumed and actual autocorrelations (9) will have nearly the minimum variance. It is interesting to note that our FGLS estimator is the same as using an OLS estimator having first whitened the data and model with an estimate of the noise autocorrelations. A similar approach was first proposed by Bullmore et al. [1997] using a first‐order autoregressive noise model and later by Purdon and Weisskoff [1998] using an autoregressive moving average model, although neither method is directly applicable to event‐related response estimation.

Activation detection based on unbiased estimated responses

In order to generate activation maps, statistical inference must be drawn from the estimated hemodynamic responses. Because we did not assume an a priori functional shape but rather estimated the fMRI response directly, previously used statistical methods [Worsley and Friston, 1995] are not immediately applicable. Specifically, statistical inference from ĥ _FGLS is based on the generalized hypothesis test

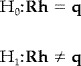(10)

where R is a restriction matrix and q is a deterministic vector typically equal to an appropriately sized column vector of zeros. R represents any linear transformation on the set of hemodynamic responses. It is important to note that h is the set of actual hemodynamic responses and not a vector of potentially unrelated covariates. The actual shape of h is important in defining the particular statistical test because its power is a function of the different knowledge incorporated into R. The F statistic is used to draw inference from (7), specifically

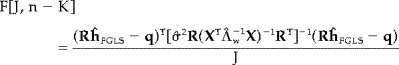(11)

where J is the number of rows in R, n and K are the number of rows and columns in X, respectively, and σˆ² is the standard error estimated from the whitened residual error e _* = Λ ${}_{\text{−1/2}}^{\text{w}}$(y − Xĥ _FGLS) where Λ${}_{\text{−1/2}}^{\text{w}}$ is computed from the Cholesky factorization of Λ${}_{\text{−1}}^{\text{w}}$ and can be considered the matrix representation of a causal whitening filter.

Although our FGLS estimator is unbiased, the statistic given by (11) may be biased in relation to the F distribution. This bias enters as a result of any discrepancy between the estimated and the true autocorrelation structures. We have addressed this potential bias in terms of false‐positive rates, using the above statistic, through simulated data. We show below that if any bias is incurred it is not substantial for both simulated and real fMRI noise.

We specifically tested these statistical techniques setting q = 0 and using three different R matrices, each imposing different restrictions in the hypothesis test:

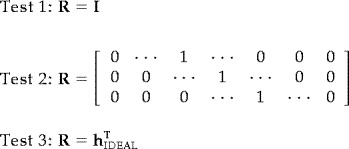Test 1 makes no assumptions about the specific waveform of the hemodynamic response. It is the most general and should be sensitive to any hemodynamic response form. The rationale of Test 2 is to draw inference based on the predicted range of possible latencies of the maximal hemodynamic response amplitudes. This test assumes that there is knowledge of when the peak values will occur, although it does not assume any particular shape. Test 3 assumes that the exact shape of the hemodynamic response is known and is akin to a matched filter. Because h ${}_{\text{T}}^{\text{IDEAL}}$ ĥ _FGLS is scalar for Test 3, the F‐statistic in equation 11 will reject whenever an analogously defined t‐statistic rejects for this case. The different tests, in addition to being more or less sensitive to the shape of the hemodynamic response, make different use of the statistical information in ĥ _FGLS. It is important to note that regardless of the restrictions imposed, statistical inference will be appropriate (theoretical false‐positive rates will equal nominal false‐positive rates); however, failure of the restrictions to meet the hypothesis test will result in decreased power to detect the actual hemodynamic responses.

To summarize the algorithm for estimating and detecting hemodynamic responses: 1) Compute ĥ _OLS (unbiased, but inefficient); 2) From residual error e = y − Xĥ _OLS, estimate Λˆ _w = Λ _w (λˆ,ρˆ) (global and local); 3) Compute ĥ _FGLS (asymptotically efficient); and 4) Compute F‐statistic for particular restrictions R.

ANALYSIS OF FALSE‐POSITIVE RATES

Methods

The goals of this experiment were (1) to determine the effect of nonwhite noise on the false‐positive error rate for three different hypothesis tests and (2) to contrast the performance between spatially global and local noise estimates. We examined both synthetic noise with known covariance structure and actual fMRI noise. The actual noise was collected as described in the MRI methods section above. The synthetic fMRI noise data sets were generated from a noise process (5) with model parameters λ= 0.75 and ρ = 0.88, values observed to be typical for a 2‐sec sampling interval experiment on our 3.0T scanner. The synthetic datasets consisted of 64 × 64 spatial points and 128 time points, consistent with the dimensions of the actual noise data collected. Each synthetic time course was generated independently and from the same process.

To test the estimation and inference procedures discussed above, we used a pseudo‐excitation sequence to generate synthetic activation data, from which we could estimate the hemodynamic response and corresponding residual error. The assumed excitation sequence consisted of a single event type, and the sequence of 60 events was randomized as described in [Dale, 1999] to optimize estimation efficiency. The mean stimulus onset asynchrony (SOA) was 4 sec.

We tested the error rate of our statistical test by first transforming the F‐statistic to a P ‐value (the smallest significance level (α) at which our test rejects the null hypothesis). For an appropriate hypothesis test, the distribution of the P ‐value given that the null hypothesis is true is uniform [0,1]. Noting this fact, we compared the actual false‐positive rate, Prob(P ‐value < α), of our tests to the nominal false‐positive rate (α) for 0. 0001 < α < 0.05 in steps of 0. 0001.

Results

The actual false‐positive rates are plotted against the nominal false‐positive rates for the synthetic noise data in Figure 1. Test 1 (no assumptions, Fig. 1A) and Test 3 (assumed shape, Fig. 1C) have similar error rates. The error rates for the two tests when the noise was not estimated (dashed lines) are significantly greater than the nominal rates as indicated by values above the shaded region. For all tests, including either a local or global estimate of the noise in the FGLS estimator and F statistic brought the actual false‐positive rates very close to nominal values, although for the synthetic noise with the same covariance structure the global estimate performed slightly better. The error rates of Test 2 (assumed peak values, Fig. 1B) are relatively unaffected by nonwhite noise, and in contrast to Tests 1 and 3, not including a noise estimate in Test 2 resulted in false‐positive rates below nominal level as indicated by values in the shaded region.

Figure 1.

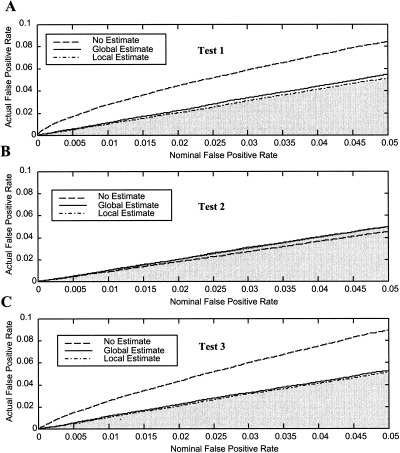
False‐positive rates for three tests and three noise estimates vs. the nominal significance level for synthetic noise data. A: Test 1 (no assumed form). B: Test 2 (assumed peak values). C: Test 3 (assumed hemodynamic shape). In all tests, not estimating the noise parameters produced false‐positive rates significantly different from nominal values, although Test 2 was least sensitive. Values above the shaded region are inappropriately high, while values in the shaded region are too low.

The Test 1 P ‐value histograms for the synthetic noise illustrate the actual P ‐value distributions (Fig. 2). An appropriate test should yield the uniform distribution. Not including noise estimates (Fig. 2A) resulted in greatly exaggerated P ‐values. The false‐positive rates deviate further from nominal values as the p‐value decreases. Figures 2B,C are relatively flat, indicating that the noise was appropriately estimated globally and locally, and that the test is valid.

Figure 2.

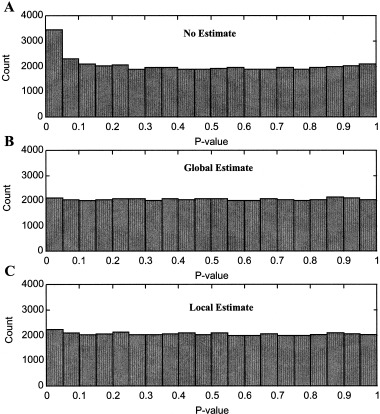
P‐value histograms for Test 1 (no assumptions) and three noise estimates. The histograms should be flat if inference is appropriate. A: No noise estimate. B: Global estimate. C: Local estimate. Not including noise estimates (A) produces more extreme p‐values than expected. B and C are relatively flat, indicating that the noise was appropriately estimated and that the test is valid.

The actual false‐positive rates are plotted against the nominal false‐positive rates for the actual fMRI noise data in Figure 3. The curves were computed from all 8 subjects, each with 16 slices of noise data encompassing the entire brain volume. Tests 1 and 3 (Fig. 3A,C) again exhibit similar false‐positive rates. Not accounting for the noise structure resulted in error rates significantly greater than nominal values at all significance levels. Additionally, the percentage deviation from the nominal values increases with decreasing significance level. In the worst case, for α = 0. 0001, the error rate of Test 1 with no noise estimate is approximately 200 times greater than the nominal rate. The local noise estimates for Test 1 and 3 brought the error rates closer to nominal values than the global estimate, although both are slightly elevated. Like with synthetic noise, Test 2 (Fig. 3B) is the least sensitive to nonwhite noise, and both global and local noise estimates bring false‐positive rates to the nominal rates.

Figure 3.

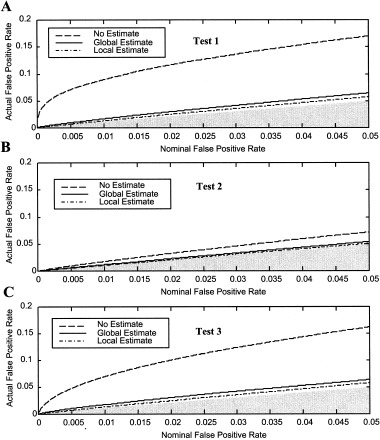
False‐positive rates for three tests and three noise estimates vs. the nominal significance level for actual noise data. A: Test 1 (no assumed form). B: Test 2 (assumed peak values). C: Test 3 (assumed hemodynamic shape). Similar to the synthetic data, not estimating the noise parameters produced false‐positive rates substantially greater than nominal values, although Test 2 was least sensitive. The false‐positive rates were slightly greater than nominal rates even when the noise was estimated. Values above the shaded region are inappropriately high, while values in the shaded region are too low.

EVALUATION OF STATISTICAL EFFICIENCY (POWER)

Methods

The goals of this experiment were 1) to determine the effect of nonwhite noise on the statistical power of three different hypothesis tests and 2) to contrast the performance between spatially global and local noise estimates. We added synthetic activation to the eight actual noise data sets. The activation was created by convolving the random interval stimulus sequence described in the previous section with an assumed ideal hemodynamic [Boynton et al., 1996; Dale and Buckner, 1997]. Thus, our simulated signal/activation corresponded to the output of a LTI system. Since fMRI responses are usually measured in percent signal change, we scaled our hemodynamic responses to a 1% signal change (a typical value for fMRI data) on a voxel by voxel basis. We randomly selected approximately half of the voxels within brain and added the synthetic activation only to these voxels. We estimated the receiver operating characteristics (ROC) of our tests by measuring the fraction of true‐positive and false‐positive test outcomes over all subjects and all brain slices [Xiong et al., 1996].

Results

Within‐test comparisons of the ROCs are shown as a function of the noise estimates in Figure 4. Test 1 (no assumptions, Fig. 4A) and Test 3 (assumed shape, Fig. 4C) show similar performance with regard to noise estimate. In Figure 4A, the no estimate (dashed line) ROC begins at false‐positive rate α = 0.02 because that was the smallest actual false‐positive rate measured given the smallest tested nominal α = 0. 0001. For all tests, estimating the noise locally (dash‐dot) yields the greatest statistical power for most significance levels. The performance of Test 2 (assumed peak values) is relatively insensitive to the particular noise estimate. For this test, the no estimate (dashed) ROC is slightly better than the global noise estimate (solid).

Figure 4.

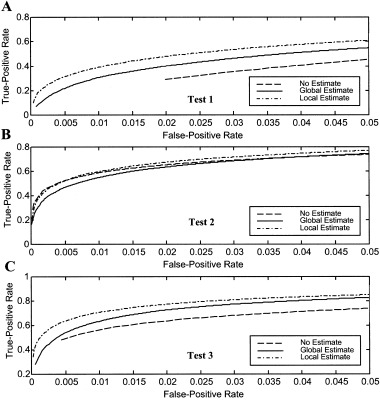
Within‐test comparisons of receiver‐operating‐characteristics (ROCs) as a function of noise estimate for actual fMRI noise data with synthetic activation A: Test 1 (no assumed form). B: Test 2 (assumed three peak values). C: Test 3 (assumed shape). For Tests 1 and 3, the local noise estimate performs best, followed by the global estimate. Test 2 performance is least sensitive to the noise estimate.

Within‐noise estimate comparisons of the ROCs are shown as a function of the hypothesis tests in Figure 5. When the noise is not estimated (Fig. 5A), Test 2 and 3 have very similar ROCs, and both significantly outperform Test 1 (125% greater true‐positive rate at positive rate α = 0.02). The global (Fig. 5B) and local (Fig. 5C) noise estimate ROCs are similar. Test 3 performs best for all false‐positive rates, followed by Test 2 and lastly Test 1, which exhibits the poorest performance.

Figure 5.

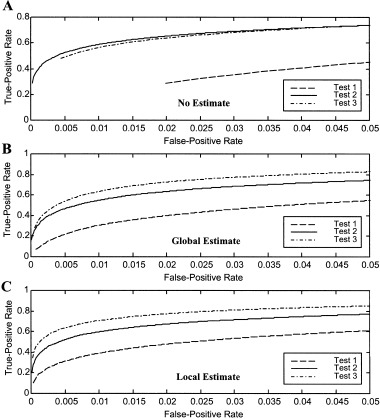
Within‐noise estimate comparisons of receiver‐operating‐characteristics (ROCs) as a function of test for actual fMRI noise data with synthetic activation A: No estimate. B: Global estimate. C: Local estimate. Test 1 (no assumptions) performs significantly poorer than the two test with assumptions for all noise estimates. Test 3 (assumed form) has the best performance for all noise estimates.

Figure 6 summarizes the ROCs for all tests and all noise estimates. Test 3 (triangles) with local (dash‐dot) noise estimates has the best overall performance for all false‐positive rates. For example, the true‐positive rate for this test at false‐positive rate α = 0.001 is 540% greater than that of Test 1 (circles) with a global (solid line) noise estimate.

Figure 6.

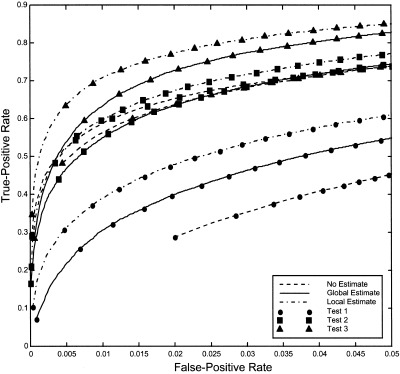
Comparison of ROCs for all tests and noise estimates. Test 3 with local noise estimates has the best overall performance for all false‐positive rates, with a 540% greater true‐positive rate than Test 1 with a global noise estimate, at the false‐positive rate α = 0.001.

DISCUSSION

We have demonstrated straightforward procedures for making efficient estimates of event‐related fMRI responses and drawing appropriate statistical inference from these estimates. The key features of this method are that it avoids heuristic smoothing of data, does not require any assumptions about the response shape to achieve adequate sensitivity, is theoretically asymptotically efficient, and does not require extra data collection to define noise and assumed response. Similar to previously analyzed block‐design statistical methods [Zarahn et al., 1997a; Purdon and Weiskoff, 1998], it was shown that not including the covariance structure of the noise in the statistical test resulted in actual false‐positive rates far exceeding assumed rates. The percentage deviation from the expected error rates increased with decreasing nominal P ‐values. In the worst case observed, false‐positive rates were 200 times greater than expected. Finally, estimation using the FGLS estimator resulted in more powerful statistical tests that were better able to detect fMRI activation as demonstrated by ROC analysis with synthetic activation in additive fMRI noise.

Both global and local noise estimates brought actual false‐positive rates close to the assumed false‐positive rates, although the local noise estimate performed slightly better than the global estimate. This result implies that the noise process in not spatially wide‐sense stationary (WSS); however, the departure from WSS is not so severe that the global estimate is wholly inappropriate. It has previously been suggested that using the across‐voxel global estimate of the noise may be inappropriate for correcting false‐positive rates [Zarahn et al., 1997a; Purdon et al., 1998]. The previous methods using global noise estimates differed from ours in that their 'global' estimate of the noise was across multiple slices and subjects while our 'global' estimate was only over a particular slice. There was little difference between false‐positive rates for our global and local estimates. Clearly, including some estimate of the noise is necessary in order to bring false‐positive rates closer to those assumed by the statistical test. As a practical consideration, the computation time of the statistics and estimates using the local noise estimate was several orders of magnitude greater than when using the global estimate. A compromise between the global and local noise estimates could be to compute a small subset of global estimates across the slice. Our results indicate (not shown) that the noise parameter ρ did not vary much over the slice and that a set of approximately four noise estimates with different noise parameters α would characterize the noise process over the entire brain well without significantly increasing computation time.

In this work we presented a practical method for estimating the parameters of an autoregressive moving average model thought to be representative of fMRI noise. Our noise estimation procedure is biased in that we had to avoid negative valued sample autocorrelations, although empirically this bias did not have a significant effect as demonstrated by its use on simulated and actual data. We chose this technique with the intent of avoiding iterative fitting procedures, which when applied on a voxel by voxel basis result in computational demands that most laboratories would find impractical. If computational demands are not an issue, then more robust iterative methods should be considered.

Although our tests with noise estimates for actual fMRI data had false‐positive rates close to the nominal values, the tests did not reach nominal values exactly. This result indicates that either the noise model is incorrect or that fMRI data includes a global signal that is not related to stimulus induced activation. It is likely that both of these explanations contribute to the slight departures from assumed false‐positive rates. The noise in the fMRI signal is the result of physiological processes (e.g., cardiac and respiratory), motion artifacts, as well as various forms of instrument measurement noise; and it is thus unlikely that our simple model explains the correlation structure exactly. Also, it has been demonstrated that the presence of a global signal in fMRI data could affect the actual specificity of the statistical tests [Zarahn et al., 1997a]. Additionally, the exact specification of the test did affect how well false‐positive rates were corrected; specifically, Test 2 (Fig. 3B), which tested the three latencies of maximal signal brought measured errors rates to nominal rates for all measured significance levels using both global and local noise estimates. This test would also be the test of choice if the noise were not estimated and independence was assumed because its false‐positive rate was least sensitive to the noise.

It should be stressed that the covariance structure of the residuals is not identical to the covariance structure of the underlying noise process. The design matrix induces model specific correlations in the residuals that are not present in the original noise process. It is therefore conceivable then that our method would lead to incorrect inference. To test this possibility, we used our method to estimate the noise parameters on the residuals of synthetic noise data and found that the false‐positive rates were appropriated controlled. This result suggests that the slight departure of the actual false‐positive rates from nominal rates when using real noise data is not due to fitting the residual errors but rather to incorrect model specification. It is, however, possible that our method would be less robust if different noise models or design matrices were used.

Since the noise covariance Λ _w is always unknown, modeling fMRI noise with a simple autoregressive moving average model may not be feasible in general. It is conceivable that different noise model structures may be necessary for different brain regions, subjects, and even MRI scanners or pulse sequences. In this situation, OLS may be the only estimator available, and the only strategy is to use an estimator of the asymptotic covariance matrix of ĥ _OLS which is known to have autocorrelated disturbances. This is similar to the approach taken by Worsley and Friston [1995], although their solution was to ‘smooth’ intrinsic autocorrelations rather than to estimate them directly. An alternative solution is to compute a non‐parametric estimate of the covariance of ĥ _OLS. If Λ _w were known, then the covariance of ĥ _OLS is given by

where S = X ^TΛ_wX. The problem can therefore be approached by estimating S rather than Λ _w directly. Estimating S in the case of autocorrelated noise is actually a more tractable problem, for which the estimate of S is given by

where N is the number of sample observations, e _i is the i ^th residual error of the OLS estimate, x _t is the t ^th column of the design matrix X, and Ŝ is the Newey‐West autocorrelation consistent covariance estimator of S [Newey and West, 1987]. The Newey‐West estimator will be consistent (and therefore asymptotically unbiased) so long as the correlations in the noise approach zero as observations become more separated in time. It must, however, be determined in advance the maximum lag L at which autocorrelations at lags longer than L are small enough to ignore. Use of consistent covariance estimates in models with unknown noise structure remains an avenue of future work.

In addition to measuring the false‐positive rates, we examined the sensitivity or power of our statistical tests. Although the FGLS estimator is not guaranteed to be efficient, it is clear that including the noise estimates for Tests 1 and 3 resulted in significantly increased sensitivity (Fig. 4A,C). In the best case, the true‐positive rate was increased by 67% for the local estimate of the noise relative to no estimate of the noise at the same significance level. This result implies that for a given imaging time, smaller signal changes will be detectable using the two‐step estimation method described here.

Throughout this work we state that our estimates are unbiased. This point is made in contrast to much of the literature on practical event‐related methods in which a partial set of basis functions are fit to the fMRI signal. Whenever a basis set is not complete and orthonormal over the time points of the hemodynamic response, the estimates of the signal will be biased [see Dale, 1999]. This subtlety is not often addressed when assessing the appropriateness of the statistical test. As the shape and latency of the hemodynamic response are known to vary considerably across the brain [Buckner et al., 1996; Schacter et al., 1997], statistical inference based on an assumed shape may be inappropriate. Note, however, that the statistical approach presented here can be easily extended to estimates constrained to lie within a specified subspace [Dale, 1999]. Specifically, if the columns of the matrix L form an orthonormal basis for the space of hemodynamic response vectors, then the (biased) maximum likelihood estimate of the of the hemodynamic response vector is given by

Although the validation studies presented here considered only experiments with one trial type, the methods described extend readily to any number of trial types. In most experiments it is desirable to make statistical comparisons between the different trial types. To this end, a restriction matrix can be formed that represents the difference operation between two trial types, or some linear function of the difference. Although our techniques were specifically designed for use with event‐related experiments, the procedures are general and can be extended for use with traditional block designs for appropriate and more efficient statistical inference.

CONCLUSIONS

We have described a general framework for obtaining efficient estimates of event‐related hemodynamic responses using fMRI and for drawing appropriate inferences from the estimated responses in the presence of temporally correlated noise. Analysis of simulated and actual noise data using these procedures gave the following results:

1) Not including an estimate of the noise in the statistical tests results in false‐positive rates far exceeding nominal values (200 times greater at worst) and less powerful statistical tests. Similar results were observed for synthetic and actual noise.

2) Including either global or local noise estimates into the statistical test brought false‐positive rates down to nominal values and led to increased efficiency (more powerful statistical tests), although the tests with local noise estimates performed slightly better. These results suggest that the FGLS estimator and statistical inference drawn from it are nearly appropriate.

3) The hypothesis test (Test 2), which restricted only the range of possible peak latencies of the hemodynamic response, was least sensitive to nonwhite noise in terms of the false‐positive rate. Additionally, it was nearly as powerful as the test incorporating exact a priori knowledge of the hemodynamic response waveform.

4) Hemodynamic responses can be detected without assuming any a prior response shape, although including assumptions about the specific form can increase the sensitivity of the test when the assumptions are correct. In general, the use of linear restrictions in the form of temporal hypothesis testing extends the flexibility of statistical procedures that can be tailored to the specific experiment and a priori knowledge without biasing estimation.