A simulator for evaluating methods for the detection of lesion‐deficit associations

Abstract

Although much has been learned about the functional organization of the human brain through lesion‐deficit analysis, the variety of statistical and image‐processing methods developed for this purpose precludes a closed‐form analysis of the statistical power of these systems. Therefore, we developed a lesion‐deficit simulator (LDS), which generates artificial subjects, each of which consists of a set of functional deficits, and a brain image with lesions; the deficits and lesions conform to predefined distributions. We used probability distributions to model the number, sizes, and spatial distribution of lesions, to model the structure–function associations, and to model registration error. We used the LDS to evaluate, as examples, the effects of the complexities and strengths of lesion‐deficit associations, and of registration error, on the power of lesion‐deficit analysis. We measured the numbers of recovered associations from these simulated data, as a function of the number of subjects analyzed, the strengths and number of associations in the statistical model, the number of structures associated with a particular function, and the prior probabilities of structures being abnormal. The number of subjects required to recover the simulated lesion‐deficit associations was found to have an inverse relationship to the strength of associations, and to the smallest probability in the structure‐function model. The number of structures associated with a particular function (i.e., the complexity of associations) had a much greater effect on the performance of the analysis method than did the total number of associations. We also found that registration error of 5 mm or less reduces the number of associations discovered by approximately 13% compared to perfect registration. The LDS provides a flexible framework for evaluating many aspects of lesion‐deficit analysis. Hum. Brain Mapping 10:61–73, 2000. © 2000 Wiley‐Liss, Inc.

INTRODUCTION

Identifying associations between the structure and function of the human brain is the goal of brain mapping. Traditionally, two approaches have been employed for this purpose. The first approach seeks associations among lesions in structures, or morphological abnormalities, and neurological or neuropsychological deficits. The second approach utilizes specifically designed activation experiments. Each of these approaches has its own merits and limitations. Independent of the approach used, a major limitation of structure–function studies is that they are typically based on data from relatively small numbers of subjects and, therefore, have low statistical power. The need to develop large databases for the purpose of meta‐analysis of data pooled from many studies has been recognized by the Human Brain Project [Huerta et al., 1993].

This paper is motivated by our previously reported work on the development of a Brain Image Database (BRAID) [Letovsky et al., 1998], which includes images and clinical data from over 700 subjects. BRAID is a large‐scale archive of normalized digital spatial and behavioral data with an analytical query mechanism. In this framework, we have implemented several methods to detect structure–function associations, one of which is the Fisher exact test of independence. In our previous work, we have reported associations between lesions in the visual cortex and visual deficits [Letovsky et al., 1998], and associations between basal‐ganglia lesions and subsequent development of attention deficit hyperactivity disorder (ADHD) [Herskovits et al., 1999]. However, evaluation of the registration and structure–function analysis methods has not been addressed.

Several researchers have studied systematically the problem of determining the minimum sample size needed to achieve a certain confidence level for statistical tests such as the chi‐square and Fisher exact tests of independence [Fu and Arnold, 1992; Larntz, 1978] and compared the relative power of different statistical tests [Harwell and Serlin, 1997; Lee and Shen, 1994; Oluyede, 1994; Tanizaki, 1997]. In addition, simulations have been performed to study the power of chi‐square analysis in sample spaces of much higher dimensionality, as one would expect to find in many epidemiological studies [Mannan and Nassar, 1995; Osius and Rojek, 1992; Tanizaki, 1997; Thomas and Conlon, 1992]. Although these and similar analyses of statistical methods that researchers may use to recover structure–function associations provide valuable information, closed‐form power analyses do not exist that can account for the simultaneous effects of image noise and registration error, in addition to the characteristics of the statistical methods being employed. The purpose of this study is to develop a unified framework for evaluating different methods used to detect lesion–deficit associations.

Given the impossibility of a general closed‐form solution for power analysis in this domain, we have designed a lesion–deficit simulator in which we can generate a large number of artificial subjects, construct a probabilistic model of lesion–deficit associations, model the error of a given registration method, and apply this nonlinear error to the image data, perform lesion–deficit analysis, and compare the generated associations with those detected by the analysis. The number of subjects required to recover the known associations reflects the statistical power of the particular combination of image‐processing and statistical methods being evaluated.

As a case study, we evaluated the Fisher exact test, which is one of the statistical methods currently available within BRAID for the detection of associations. We also evaluated the effects of registration error because of our nonlinear image‐registration algorithm on the power of lesion–deficit analysis within BRAID. Our objective is to use this simulator as a test bed for the subsequent development and evaluation of new methods for structure–function analysis, for determining the sample size required to detect a structure–function association of a given strength, and for quantifying the effects of new registration and other image‐processing methods on the power of lesion–deficit analysis.

The rest of the paper is organized as follows: Section 2 presents background information. Section 3 describes the method used for the evaluation of the analysis procedure including the various components of the Lesion‐Deficit Simulator (LDS). In Section 4, data generated by the simulator are used to evaluate the Fisher exact test, and experimental results are given. The paper concludes with a discussion in Section 5.

BACKGROUND

To perform lesion–deficit analysis within BRAID, we collect clinical data obtained via physical examination (e.g., development of visual problems), and image data obtained via magnetic‐resonance (MR) examination, and we then analyze these data to detect associations among brain structures and their functions. Once the data are incorporated into BRAID, we must ensure that the clinical and image data are comparable across subjects. In particular, for image data, brain lesions must be delineated, and image registration must be performed to map homologous anatomical regions to the same location in a stereotaxic space. Usually, lesions are identified manually, and the data are then registered to a common spatial standard, such as the Talairach anatomical atlas [Talairach and Tournoux, 1988]. In fact, BRAID contains several atlases: Talairach, Brodmann, CHS, Damasio, and an artificial atlas containing regions of interest to us. Here, we concentrate on Talairach atlas structures, although any other atlas could be used. Several groups have developed linear and nonlinear spatial transformations that bring an atlas and a subject's image data into register (i.e., spatial coincidence) [Bookstein, 1989; Collins et al., 1994; Miller et al., 1993; Talairach and Tournoux, 1988]. Because the accuracy of linear‐registration methods is limited, nonlinear transformation methods are generally preferable. Within BRAID, we use a nonlinear method based on a 3D elastically deformable model [Davatzikos, 1997; Davatzikos, 1998].

BRAID uses several methods to determine structure–function associations [Megalooikonomou et al., 1999], including the chi‐square test, Fisher exact test, and the Mann‐Whitney test. To demonstrate the use of the LDS, in this paper, we evaluate the Fisher exact test of independence. Within BRAID, this test is used in lesion–deficit analysis as follows: for each pair of structure–function variables, BRAID constructs a contingency table, and then computes the Fisher exact statistic to determine whether these variables are independent of each other. Because computing a statistic for each of many pairwise tests creates the multiple‐comparison problem, we apply the Bonferroni correction [Fisher and van Belle, 1993]. Because the Fisher exact test applies to categorical variables, we use thresholding to define a structure as normal or abnormal based on the lesioned fraction of that structure (i.e., the fraction of that structure's volume that overlaps with brain lesions). Evaluating other methods that can be used with continuous variables, such as the Student t‐test or the Mann‐Whitney test, presents no problem, because the abnormal fraction of structures can then be used directly.

METHODS

We designed the LDS to generate a large number of artificial subjects, each consisting of lesions and deficits that conform to predefined distributions, which could then be analyzed within BRAID to determine lesion–deficit associations. Comparing the results of this analysis to the known lesion–deficit associations in our simulation model would allow us to quantify the performance of our system as a function of the parameters of the simulation.

The Lesion‐Deficit Simulator (LDS)

The major components of the simulator are: generation of simulated lesions, modeling of registration error, and generation of simulated functional deficits.

To ensure that our simulator would generate a plausible dataset, we obtained simulation parameters from data collected as part of the Frontal Lobe Injury in Childhood (FLIC) [Gerring et al., 1998] study. This study was designed to discover predictors of psychiatric sequelae following severe closed‐head injury. These data were collected from 99 children (aged 4–19 years) with traumatic brain lesions. Previously, we reported the analysis of these data using BRAID, to determine whether there were associations among locations of lesions and subsequent development of ADHD [Herskovits et al., 1999].

Generation of Simulated Lesions

Because the data for the simulation parameters fit gaussian distributions with reasonable accuracy, we constructed gaussian distributions based on these data, although we could readily have used other functional forms had that been necessary. Thus, to construct the spatial distribution for brain lesions, we collected statistics from the sample dataset that describe the number of lesions per subject, their sizes, and their locations. Then, for each subject, we sampled these distributions, generating the number of lesions, and, for each lesion, its centroid and size. For simplicity in the generation of the synthetic lesions, we assumed spherical shape.

Number of lesions per subject.

We modeled the number of lesions for each subject in the simulated population with a gaussian distribution, in which negative numbers are excluded. The gaussian distribution used for the simulation, and the corresponding histogram collected from the FLIC dataset, are shown in Figure 2. The mean and standard deviation for the number of lesions per subject are 8.1 and 6.9, respectively.

Figure 2.

The gaussian distribution (a) and the FLIC data histogram (b) for the number of lesions per subject.

Sizes of lesions.

We modeled the volume of a lesion with a gaussian distribution, in which negative numbers are excluded. The gaussian distribution used for the simulation, and the corresponding histogram collected from the FLIC dataset, are shown in Figure 3. The mean and standard deviation for the volume of a lesion are 195.5 and 176.7 mm³, respectively.

Figure 3.

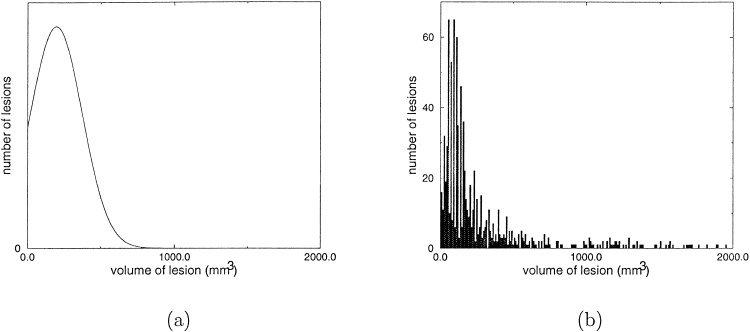
The gaussian distribution (a) and the FLIC data histogram (b) for lesion volumes.

Spatial distribution of lesions.

For each voxel of the brain image, we computed the probability that it would be the centroid of a lesion, by taking the following steps. First, we computed centroids for all lesions in the FLIC dataset, and we calculated the number of lesion centroids, c _l , that coincide with each point, l, of the brain in stereotaxic space (i.e., we formed the histogram of centroids for each of these points). Because the number of voxels is much larger than the number of lesions, most voxels did not coincide with any lesion centroids. This would incorrectly exclude most voxels from the set of possible lesion centroids. To remedy this problem, we performed smoothing, which effectively allows each lesion to influence the probability estimates in a neighborhound around it. The probability of observing a lesion at location l was calculated as follows: A spherical window of a certain radius was centered on l and the number of lesion centroids, c _l , that fall within that window was counted. Finally, the scalar probability field was normalized so that it forms a proper probability density function. The distribution of lesion centroids for the FLIC data obtained by smoothing with a sphere of radius 10, is presented in Figure 4 for several axial images of the Talairach atlas (where gray‐scale intensity represents probability density following smoothing). We chose the smoothing radius by visualization of the distributions for spheres of different radii and by examining the fraction of points in the brain with c _l = 0.

Figure 4.

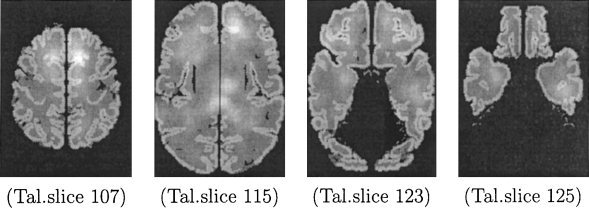
The distribution of lesion centroids (FLIC dataset), following smoothing, for four representative slices of the Talairach atlas.

Once we supplied the parameters for the LDS distributions with respect to the number, size, and location of lesions, the simulator generated the image dataset. A representative example of the lesions for a simulated subject is presented in Figure 5.

Figure 5.

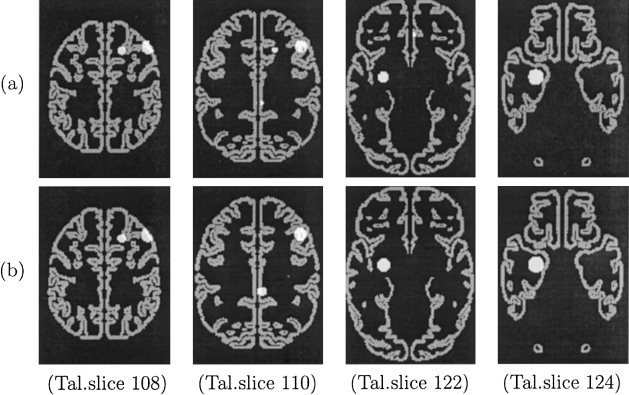
The artificial lesions of a simulated subject before (a) and after (b) taking into account registration error (slices 108, 110, 122, and 124 of the Talairach atlas are presented).

Modeling of Registration Error

As described in Section 2, image registration to a common standard is central to many systems for functional brain mapping. Within BRAID, the brain image data for all subjects are placed in the same coordinate system via an elastic‐registration method. Although this procedure is very accurate, it is imperfect (i.e., it does not necessarily map corresponding regions to exactly the same location in Talairach space). Misregistration introduces noise, in the form of false‐negative and false‐positive associations. We quantified this important source of error by assuming that it follows a 3D nonstationary gaussian distribution. To determine this distribution, we collected data from 19 subjects and measured the registration error on 20 distinct anatomical landmarks (see Table VI), then interpolated the error at all other points in the brain. Figure 5b shows an example of the displaced lesions in Figure 5a. A more detailed description of this procedure can be found in the Appendix.

Table VI.

The 20 landmarks selected for the registration error calculation (the registration error mean and standard deviation are also shown)

Landmark	Err. mean (mm)	Err. std (mm)
Anterior commissure	3.2	2.0
Posterior commissure	3.9	1.8
L & R anterior‐most voxel of head of caudate at AC level	4.8, 4.6	1.0, 1.2
L & R inferior‐most extent of central sulcus	7.0, 8.1	3.0, 3.6
L & R intersection of post‐central sulcus and Sylvian fissure	4.0, 4.4	2.0, 2.1
L & R caudothalamic notch	4.3, 3.2	3.0, 1.9
Anterior‐most corpus callosum (genu)	4.1	1.9
Torcular herophili (between occipital poles) at PC level	4.3	1.6
L & R gyrus rectus anterior pole at interpeduncular cistern level	4.0, 3.4	1.6, 1.1
L & R anteromedial aspect of Sylvian fissure	5.8, 6.8	2.3, 2.7
L & R superiormost point of precentral gyrus	10.0, 10.1	4.2, 3.3
L & R point of thalamus closest to splenium of corpus callosum	3.8, 4.4	1.2, 1.1

Generation of Synthetic Associations

The lesion–deficit association model quantifies the relationships among structures and functions. Because structure and function variables are categorical (i.e., normal/abnormal), we modeled these associations using Bayesian networks (BNs) [Pearl, 1988].

Briefly, a Bayesian network is a directed acyclic graph, in which nodes represent variables of interest, such as structures or functions, and edges represent associations among these variables. An example of a Bayesian network is shown in Figure 1. Each node has a conditional‐probability table that quantifies the strength of the associations among that node and its parents; in Figure 1, for example, function f ₁ depends only on structure s ₂. Given the prior probabilities for the root nodes and conditional probabilities for other nodes, we can derive all joint probabilities [Pearl, 1988] over these variables. Note that this nonparametric model is general enough to represent any set of multivariate lesion–deficit associations. Furthermore, although in this paper we use discrete structure and function variables, BNs based on multivariate gaussian distributions [Shachter and Kenley, 1989], and mixed discrete‐continuous distributions [Lauritzen and Wermuth, 1989], have been constructed.

Figure 1.

An example of a Bayesian network with six nodes (three structures and three functions) and four edges from structures to functions, and the conditional‐probability table for each node. Each node can be in either one of two states: A = Abnormal, N = Normal.

To use a discrete BN to model multivariate lesion–deficit associations, we specified the numbers of structure and function variables, the number and strengths of associations among these variables, and a function mapping the fraction of an atlas structure that is lesioned to the probability that this structure will function abnormally.

To examine the effect of the strength of the lesion–deficit associations on BRAID's ability to detect them, we considered three cases presented in Table I that correspond to strong, moderate, and weak associations. Thus, a strong association between a structure s _i and a function f _j is denoted by conditional probabilities p(f _j = A|s _i = N) = 0, p(f _j = A|s _i = A) = 1, p(f _j = N|s _i = N) = 1, and p(f _j = N|s _i = A) = 0, where A means abnormal and N normal. We similarly defined moderate and weak associations as shown in Table I. To simplify the generation of conditional‐probability tables, we used a noisy‐OR model [Pearl, 1986]. The noisy‐OR model is a boolean OR gate with a failure function associated with each input line—there is a leak probability q_i that line i will fail. When no failure occurs, each line's input is passed to a boolean OR gate. This overall structure induces a probability distribution that is easily computed; the probability of no failure occurring is denoted by p^nf: p^nf = 1 − ∑_iϵℳ︁ q_i, where ℳ︁ is the subset of lines with activated input. A boolean noisy‐OR model with leak probability 0.25 for a function associated with two structures (parents) is shown in Table II. For simplicity in this table we use a single leak probability instead of defining a leak probability for each parent. Note that our framework allows us to specify arbitrary conditional‐probability tables; we chose the noisy‐OR model because it requires relatively few parameters to generate a well‐characterized conditional‐probability table.

Table I.

The three cases of BNs considered

Case	Association	Conditional probabilities for functions
1	Strong	0/1
2	Moderate	0.25/0.75
3	Weak	0.49/0.51

Table II.

A noisy‐OR gate with leak probability 0.25 for a function associated with two structures (N = normal, A = abnormal)

Struct1	Struct2	p(function = N)
N	N	0.75
N	A	0.25
A	N	0.25
A	A	0.06

We calculated the prior probability of structure abnormality for each structure s_i, in each subject p_j, based on f ${}_{\text{s}{}_{\text{i}}\text{,p}{}_{\text{j}}}$: the fraction of the volume of s_i that overlapped with lesions for p_j. The conditional probability p(s_i|f ${}_{\text{s}{}_{\text{i}}\text{,p}{}_{\text{j}}}$) is expected to be a sigmoid function. One way to fit the sigmoid model is to compute p(s_i|f ${}_{\text{s}{}_{\text{i,}}\text{p}{}_{\text{j}}}$) for various function and structure variables in our dataset. This sigmoid function could differ for different structures. Computing this conditional probability from our dataset for the case in which the functional variable represents the absence or development of ADHD, and considering all of the Talairach structures and subjects from the FLIC study, demonstrated empirically that a step function with threshold fraction of 0.01 could be used in the simulations, instead of a sigmoid function (see Fig. 6). The threshold value 0.01 is also the mean of the optimal thresholds with respect to p‐value (i.e., the mean of the thresholds that gave the smallest Fisher‐exact p‐value for all 132 Talairach structures and the functional variable that corresponds to the development of ADHD. Thus, for the FLIC data, we labeled each structure for which at least 1% of its volume overlapped with lesions as abnormal for that subject; the remainder of the structures were labeled as normal. Averaging over all subjects, we could compute a prior probability of abnormality for each structural variable. The histogram in Fig. 7 shows, for each structure of the Talairach atlas that was considered, the percentage of simulated subjects with lesions in that structure for the simulated dataset. The first 66 structures are right‐sided and the remainder are the corresponding left‐sided structures. Observe that there are several clusters of lesions (see also Fig. 4 of the lesions' centroid distribution). The two peak points in the graph correspond to the right and left Talairach cortex structures, which are common sites for traumatic brain lesions.

Figure 6.

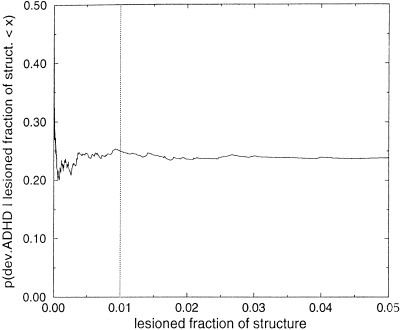
p (development of ADHD|lesioned fraction of structure < x) for all Talairach structures and subjects in the FLIC study. The vertical line is at the threshold fraction of 0.01 used in the simulations for labeling a structure as abnormal. The lesioned fraction of a structure is defined in Section 2.

Figure 7.

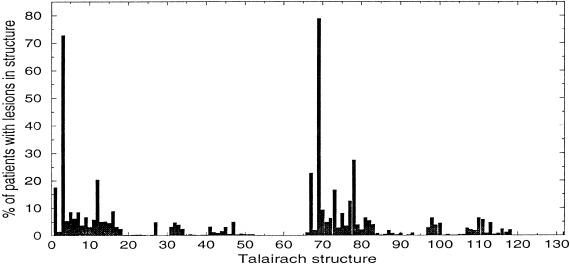
The percent of simulated subjects with lesions for each of the 132 Talairach structures.

For each simulated subject p^j and structure s _k , we sampled the prior‐probability distribution and generated a binary vector S ${}_{\text{K}}^{\text{j}}$ of dimension K (where S _j [k] = 1 means that structure s _k is abnormal for subject p^j ). By instantiating the states of all structure variables of the BN with S ${}_{\text{K}}^{\text{j}}$ for subject p_j, we could determine the conditional probability for each function variable by table lookup, and use this probability to generate stochastically the binary vector F ${}_{\text{M}}^{\text{j}}$ of dimension M for the function variables, where, F _j [i] = 0 if function f _i was abnormal for subject p^j. The binary vectors S ${}_{\text{K}}^{\text{j}}$ and F ${}_{\text{M}}^{\text{j}}$, for each subject p^j were then analyzed using the Fisher exact test of independence for each structure–function pair, as described earlier.

RESULTS AND DISCUSSION

In this section, we describe how we used the LDS framework to characterize the performance of the Fisher exact test of independence for lesion–deficit analysis. We studied its behavior as a function of the number of subjects needed to discover the simulated lesion–deficit associations represented by a BN, the strengths of associations, the number of associations, the degree of the BN (i.e., the number of structures related to a particular function), and the prior probabilities for structure abnormality. We also examined the effects of registration error. Recall that the input to the simulator includes the number of structure nodes, the number of function nodes and the number of edges (associations) among them. The parameters we chose for the stochastically generated BN were the following unless otherwise stated: 132 structure nodes (corresponding to the Talairach atlas structures), 20 function nodes, and 69 edges from structures to functions. This BN has sufficient complexity to demonstrate the use of the simulator, and can help us understand the performance of the Fisher exact test and the effects of misregistration. The maximum degree (i.e., the maximum number of incoming edges to a given function node), was fixed to four (for most of the experiments unless otherwise stated); thus, a function could be associated to at most four different structures. Because the performance of any method for detecting associations depends on the characteristics of the conditional‐probability tables, we examined the three cases of Table I to study this effect. The prior probability of abnormality for each structure was set to 0.5 to allow us to examine the behavior of the Fisher exact test for the optimal value of the prior probability (i.e., many examples of abnormal and normal structures would be available for analysis). To generate the conditional–probability table for those function variables that were related to more than one structure, we used a noisy‐OR model (see Table II for a noisy‐OR function that corresponds to the moderate case of Table I, i.e., when the leak probability is 0.25). For the results that follow, we report the total number of edges (i.e., associations) detected, as well as the number of simulated (i.e., true‐positive) edges found. The difference between these two numbers is the number of false‐positive associations that were identified.

Experiment 1: Determining the p‐Value Threshold

Table III quantifies the statement that the lower the threshold for the p‐value, the smaller the number of false positives and number of simulated edges detected (i.e., the more conservative the method). It presents the results for the case of moderate strength of associations (case 2 of Table I); however, similar results were observed for the cases of strong and weak associations. In the following experiments, we used the threshold 0.001 for the p‐value, because this is a good trade‐off between the number of simulated associations and the number of false positives detected.

Table III.

Percentage of simulated associations and false positives detected by the Fisher exact test for three values of the p‐value threshold and for moderate strength of lesion‐deficit associations

No. Subjects	% True pos.*	% False pos.*	% True pos.**	% False pos.**	% True pos.***	% False pos.***
500	84	35	72	4	55	0
1000	100	45	99	1	90	0
1500	100	35	100	4	97	0
2000	100	32	100	1	100	0

^* p ≤ 0.01, **p ≤ 0.001, ***p ≤ 0. 0001.

Experiment 2: Effect of Conditional Probabilities

In Figure 8a, we present the performance of the Fisher exact test (p ≤ 0.001) for the cases in which all structure–function conditional probabilities were set to strong (case 1), moderate (case 2), and weak (case 3) associations as described in Table I. The figures demonstrate the dramatic effects of the different conditional‐probability distributions on the power of lesion‐deficit analysis. Figure 8a demonstrates that, to discover 70% of the total number of simulated edges, we require approximately 180, 500, and 2000 subjects for the strong‐, moderate‐, and weak‐association cases, respectively. As expected, the more samples are required to detect weaker associations.

Figure 8.

Performance of the Fisher exact test (p ≤ 0.001) for (a) uniform (0.5) prior probabilities, and (b) data‐derived prior probabilities of structure abnormality, and for the three strengths of lesion‐deficit associations from Table I that correspond to strong (case 1), moderate (case 2), and weak (case 3) associations. The difference between the total number of associations detected, and the number of true associations detected is the number of false‐positive associations detected for each case. The horizontal line in (a) represents the total number of simulated edges (69), and in (b) represents the total number of simulated edges that can be detected (55).

Experiment 3: Effect of Number of Associations

For this experiment, we selected the moderate case (i.e., case 2) for the conditional‐probability tables, to investigate further the effect of the total number of associations on the statistical power of lesion–deficit analysis. Without loss of generality, we studied the case in which all function nodes have the same degree, which we call the degree of the BN. In Figure 9 we present the performance of the Fisher exact test for three BNs of degree 4. The networks have 20, 40, and 80 edges, respectively. These results demonstrate that the Fisher exact test performs similarly for BNs of the same degree that have different numbers of edges. The deterioration as the total number of edges increases is small. All edges are discovered after 900, 1300, and 1500 subjects for BNs with 20, 40, and 80 edges, respectively.

Figure 9.

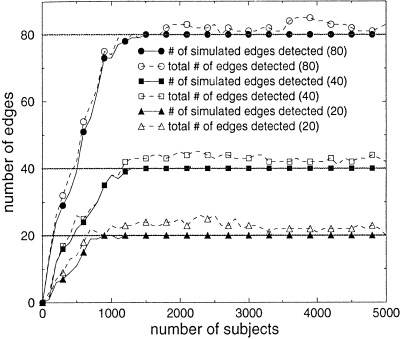
Performance of the Fisher exact test (p ≤ 0.001) for BNs with degree 4, and with 20, 40, and 80 edges.

Experiment 4: Effect of Degree of the BN

For this experiment, we again selected the moderate case for the conditional‐probability tables, to isolate the effect of the number of structures affecting a particular function, or the degree of the BN. Figure 10 shows the effect of increasing the degree of the BN while fixing the total number of edges. As expected, as the degree of the BN increases, more subjects are needed to detect the same number of associations. In particular, to discover 70% of the total number of simulated edges, we require approximately 500, 3700, and more than 8000 subjects for the cases of BNs that have degree 4, 6, and 8, respectively. As expected, the degree of the BN has a much greater effect on the performance of the Fisher exact test than does the total number of edges.

Figure 10.

Performance of the Fisher exact test (p ≤ 0.001) for BNs with 48 edges, and with degree 4, 6, and 8.

Because the parameters that most affect the performance are the conditional probabilities for the functions (i.e., strengths of associations) and the degree of the function nodes (i.e., number of structures related to a function), in Table IV we present the percent of the associations detected by the Fisher exact test, as a function of these parameters for 1000 and 5000 subjects. These results confirm the profound effect of the degree of the BN on the power of lesion–deficit analysis.

Table IV.

Percentage of simulated associations detected by the Fisher exact test (p ≤ 0.001) as a function of the conditional probabilities for the structure–function associations, and of the in‐degree of the function nodes

Cond. prob.	1000 subjects			5000 subjects
	Deg. 4	Deg. 6	Deg. 8	Deg. 4	Deg. 6	Deg. 8
0.0	100	100	17	100	100	58
0.1	100	48	15	100	100	44
0.2	94	25	15	100	94	42
0.3	79	19	15	100	83	42
0.4	63	17	15	100	71	38
0.5	52	17	15	100	63	35

Experiment 5: Using Priors From the Simulated Dataset

In the previous experiments, the prior probability of a given structure being abnormal was set to 0.5 for each structure variable, because our purpose was to evaluate the behavior of the Fisher exact test while manipulating the strengths and number of associations among the structure and function variables. For this experiment, we obtained the prior probabilities from the simulated dataset. The number of edges that could actually be discovered is 55 (80%), because there were 14 edges from structures that did not intersect any lesions. The prior probabilities for the structures are shown in the histogram in Figure 7. The smallest nonzero prior probability is 0. 0004, and only five out of the 132 Talairach structures have a prior probability of being abnormal that is above 0.2. Thus, in contrast to the experiments in which prior probabilities were uniform, most of the simulated cases in this experiment would not have abnormal structures.

Figure 8b demonstrates the performance of the Fisher exact test for the three cases of BN conditional probabilities (see Table I). Comparing this figure with Figure 8a, in which uniform prior probabilities were used, demonstrates that, as expected, more subjects are required to recover all associations when data‐derived prior probabilities are used in the LDS, when compared to the case in which uniform prior probabilities were used to simulate abnormal structures. Even when all structure‐function asociations are deterministic (case 1), the number of subjects required to recover all 55 associations is close to 5000. To discover 70% of the total number of simulated edges (i.e., 70% of 69 ≈48) would require approximately 2500, and more than 6000 subjects for the strong and moderate associations, respectively, instead of 180 and 500 in the case of uniform prior probabilities. As expected, the number of subjects needed is inversely proportional to the smallest prior probability. The detection of false‐positive associations is because of the existence of associations among neighboring structures. These associations are because of lesions that intersect more than one structure. Additional false positives can be observed in the case where there are associations among the function variables, such as hemiparesis and upper‐extremity weakness.

Experiment 6: Effect of Registration Error

Table V demonstrates the effect of registration error on the performance of the Fisher exact test, for two cases of conditional probabilities: strong (case 1) and moderate (case 2) strengths of lesion–deficit associations. As expected, registration error reduces the power of the Fisher exact test in detecting the associations, when compared with perfect registration. As shown in Table V, on average, our nonlinear registration method reduces the number of associations discovered by 13% for the same number of subjects.

Table V.

Percentage of detectable associations discovered by the Fisher exact test (p ≤ 0.001) with and without registration error, for strong (case 1) and moderate (case 2) lesion–deficit associations (a maximum of 80% of associations can be discovered)

No. subjects	Case 1		Case 2
	% with reg. err.	% without reg. err.	% with reg. err.	% without reg. err.
500	43	49	30	35
1000	54	60	35	38
1500	54	62	39	46
2000	57	68	39	46
3000	64	72	45	49
4000	65	75	48	58

CONCLUSIONS AND FUTURE WORK

Analyzing simulated data, we quantified the inverse relationship between the number of subjects required to detect all the associations, and the strength of these associations. In addition, we characterized the inverse relationship between the number of subjects required to detect all the associations and the smallest prior probability of structure abnormality. The number of subjects required to detect all and only those associations in the underlying model (i.e., the ground truth) may be in the thousands, even for strong lesion–deficit associations, particularly if the spatial distribution of lesions does not extend to all structures (i.e., some of the prior probabilities of structure abnormality are very small). These results underline the necessity of developing large image databases for the purpose of meta‐analysis of data pooled from several studies, so that more meaningful results can be obtained. The degree of associations (i.e., the number of structures related to a particular function, has much greater effect on the performance of statistical lesion‐deficit analysis than does the number of associations. This result implies that, for functions that are associated with many structures, identification of complex multivariate structure‐function associations will require very large sample sizes. We have also quantified the effects of misregistration on statistical power of lesion–deficit analysis. We found that our nonlinear‐registration algorithm, which has fairly high registration accuracy, results in 13% fewer associations being discovered for a given number of subjects. By using our simulator, we can take this reduction of power into account when calculating the sample size needed for a particular experiment.

In this paper, we limited our analysis to identical conditional‐probability tables, generated using a noisy‐OR gate, across function variables, and in some cases, equal in‐degree of function variables. This focus allowed us to isolate these characteristics, so that we could characterize their effects on required sample size. In fact, just as the LDS allows us to specify arbitrary prior‐probability distributions over structure variables, the LDS also allows us to specify any conditional‐probability distribution for each function variable given the states of its structure‐variable parents. The LDS also allows us to specify any number of associations among structure and function variables, including structure–structure associations (useful when one structure overlaps another) and function–function associations (useful when one function subsumes another). In summary, there is no joint distribution over discrete structure and function variables that we cannot model in our LDS.

Because of the flexibility and modular nature of our LDS, we can readily extend this work to evaluate other statistical, registration, and segmentation methods. For example, we could quantify the cost, in statistical power, of using a faster, but more error‐prone, segmentation or registration method. Similarly, we plan to use the LDS to compare multivariate Bayesian [i.e., Cooper and Herskovits, 1992; Herskovits, 1991], loglinear, and other statistical methods for lesion–deficit analysis, to the univariate statistical analysis described in this paper, ultimately with the aim of optimizing statistical power for the analysis of these complex datasets.

ACKNOWLEDGMENTS

This work was supported by the Human Brain Project, which is supported by the National Institute of Aging, the National Institute of Mental Health, NASA, and the National Cancer Institute. This work was also supported by an Engines for Innovation grant from Illustra, and the Informix Grants Program.

MODELING REGISTRATION ERROR

To model registration error, we first selected a number, N, of fiducial points (landmarks). The principal criterion for choosing these points was how reliably and accurately they could be identified on magnetic‐resonance images, and how representative they were of the performance of the registration algorithm; that is, the points should reflect areas of accurate (e.g., deep gray matter), as well as less accurate (e.g., cortex) registration. The landmarks were identified manually and their coordinates were calculated in spatially normalized images from M subjects as well as in the Talairach atlas itself. To reduce the variability of measurements obtained by different experts, we used the mean of two independent measurements for each landmark. The 20 landmarks we selected are shown in Table VI; similar landmarks have been used by other researchers [e.g., Evans et al., 1991].

Let E ${}_{\text{N}}^{\text{i}}$ , i:1, … , M be a vector of dimension N consisting of the Euclidean distance e_i,j, j:1, … , N between each landmark and the corresponding displaced landmark for subject i. We calculated the mean vector, μ, and the covariance matrix, ∑, from E ${}_{\text{N}}^{\text{i}}$. We used the Kolmogorov‐Smirnov and Shapiro‐Wilk tests of normality to verify the assumption that the displacement errors for the landmarks follow a gaussian distribution. Table VI also presents the mean value and standard deviation of the registration errors for the 20 landmarks. If ∑ is positive definite, a method that uses the Cholesky decomposition of ∑ and N univariate normal variates can be used to produce an N‐dimensional multivariate normal distribution [Tong, 1990], 𝒩_N (μ, ∑) for the displacement error.

Displacing a set of lesions for a given subject was then performed using a displacement produced from 𝒩_N (μ, ∑). Each lesion centroid was displaced using an inverse distance‐weighted markov‐random‐field equilibration from the displacements of the landmark points.