Abstract
Previous simulation studies have stressed the importance of the multimodal integration of electroencephalography (EEG) and magnetoencephalography (MEG) data in the estimation of cortical current density. In such studies, no systematic variations of the signal‐to‐noise ratio (SNR) and of the number of sensors were explicitly taken into account in the estimation process. We investigated effects of variable SNR and number of sensors on the accuracy of current density estimate by using multimodal EEG and MEG data. This was done by using as the dependent variable both the correlation coefficient (CC) and the relative error (RE) between imposed and estimated waveforms at the level of cortical region of interests (ROI). A realistic head and cortical surface model was used. Factors used in the simulations were: (1) the SNR of the simulated scalp data (with seven levels: infinite, 30, 20, 10, 5, 3, 1); (2) the particular inverse operator used to estimate the cortical source activity from the simulated scalp data (INVERSE, with two levels, including minimum norm and weighted minimum norm); and (3) the number of EEG or MEG sensors employed in the analysis (SENSORS, with three levels: 128, 61, 29 for EEG and 153, 61, or 38 in MEG). Analysis of variance demonstrated that all the considered factors significantly affect the CC and the RE indexes. Combined EEG–MEG data produced statistically significant lower RE and higher CC in source current density reconstructions compared to that estimated by the EEG and MEG data considered separately. These observations hold for the range of SNR values presented by the analyzed data. The superiority of current density estimation by multimodal integration of EEG and MEG was not due to differences in number of sensors between unimodal (EEG, MEG) and combined (EEG–MEG) inverse estimates. In fact, the current density estimate relative to the EEG–MEG multimodal integration involved 61 EEG plus 63 MEG sensors, whereas estimations carried out with the single modalities alone involved 128 sensors for EEG and 153 sensors for MEG. The results of the simulations also suggest that the use of simultaneous 29 EEG sensors during the MEG measurements carried out with full sensor arrangements (153 sensors) returned an accuracy of the cortical source estimate statistically similar to that obtained by combining 64 EEG and 153 MEG sensors. Hum. Brain Mapp. 22:54–64, 2004. © 2004 Wiley‐Liss, Inc.
Keywords: linear inverse source estimate, EEG, MEG, multimodal integration, realistic head model
INTRODUCTION
There is a great interest in estimation and localization of cortical neural sources from high resolution EEG and MEG recordings [Dale et al., 2000; David et al., 2002; Fuchs et al., 1998; Huizenga et al., 2002; Mizoguchi et al., 2002; Schimpf et al., 2002; Yoshinaga et al., 2002; Zijlmans et al., 2002]. In fact, both recording techniques have shown a very good temporal resolution (msec scale) and a moderate spatial resolution (in the order of 2–3 cm), making it possible to follow the complex temporal dynamics of brain phenomena [Nunez, 1995]. Furthermore, the wide availability of magnetic resonance imaging (MRI) of subjects' heads have made possible the use of realistic models for the head and for the cortical surface in procedures involving the estimation of cortical current activity. It has been demonstrated that by electroencephalography (EEG) or magnetoencephalography (MEG) data the use of realistic head models increases the accuracy of the cortical current reconstruction.
Point‐like models of cortical sources (such as the current dipole) have been largely used in the analysis of primary evoked potentials/fields, epileptic spikes, and in the analysis of more complex cognitive experiments [Ahlfors et al., 1999; Otsubo et al., 2001; Stenbacka et al., 2002; Torquati et al., 2002]. Such point‐like source models could be insufficient to represent spatially extended cortical activations that can be generated from the cerebral engagement in particular motor or cognitive tasks [Anourova et al., 2001; Okada and Salenius, 1998]. Over the last few years, several studies have investigated the simultaneous use of EEG and MEG data for the estimation of the cortical sources in the human brain by using distributed source models [Babiloni et al., 2001; Liu, 2000; Liu et al., 2002]. In the distributed source approach, thousands of equivalent current dipoles covering the cortical surface modeled have been used, their strengths estimated by using linear and non‐linear inverse procedures [Baillet and Garnero, 1997; Baillet et al., 1999; Dale and Sereno, 1993; Phillips et al., 1997; Uutela et al., 1999]. The solution space (i.e., the set of all possible combinations of the cortical dipole strengths) is generally reduced by using geometric constraints. For example, dipoles can be disposed along the reconstruction of cortical surface with a direction perpendicular to the local surface. An additional constraint involves forcing the dipoles to explain the recorded data with a minimum or a low amount of energy (minimum‐norm solutions) [Hämäläinen and Ilmoniemi, 1984]. It is worth pointing out, however, that the minimum‐norm solution fails to reproduce the cortical source distribution if the true generators are focal. In the context of the linear inverse source estimate approach, the advantage of combining EEG and MEG data has been suggested based on simulation studies [Babiloni et al., 2001; Liu, 2000; Liu et al., 2002] using the concepts of point spread function (PSF) and resolution kernels [Dale et al., 2000; Grave de Peralta and Gonzalez Andino, 1998]. Such studies have pointed out how the multimodal integration of EEG and MEG increases the accuracy of cortical current estimates by using distributed source models. These studies, however, did not explicitly address how a variable signal‐to‐noise ratio (SNR) could change the efficacy of current estimation. In fact, such simulations were generated by using noise‐free data [Babiloni et al., 2001] or data with an SNR equal to 10 [Liu, 2000; Liu et al., 2002]. In contrast, it is well known that EEG or MEG recordings have shown SNR values ranging between 10 and 20 only during particular highly synchronized and spatially focused events like epileptic spike seizures or evoked potential/field from the primary sensory cortical areas. Indeed, values of SNR ranging from 5, 3, or even 1 normally occur during the recording of single EEG/MEG trials related to other motor or cognitive activities [Regan, 1989]. There therefore remains the problem of whether multimodal integration of EEG and MEG is beneficial also in the condition of variable SNR of the recorded EEG/MEG data.
Another point of interest that has been addressed in part by previous simulations focuses on testing accuracy of distributed source estimates from multimodal integration of EEG and MEG data in the presence of high‐resolution acquisition devices. In fact, there is currently a wide selection of high‐resolution EEG systems with 64 or 128 electric sensors and there exists an extended availability of MEG devices with more than hundreds of measurement sites. Previous simulations have addressed the issue of multimodal integration of EEG/MEG data from 30 and 61 sites of measurements of electric and magnetic modalities [Liu, 2000; Liu et al., 2002] or from 128 electric sensors linked to up to 43 MEG sensors [Babiloni et al., 2001]. The issue, however, relating to the practical use of multimodal EEG–MEG integration by using devices with more than 100 EEG and MEG measurement sites, for a variety of SNRs of acquired data, remains unexplored. In addition, because during MEG recordings additional EEG sensors can be placed, needing only extra time for the subject's preparation, it could be of interest to quantify the benefits (if any) of the multimodal integration of data from a full recording MEG with 29, 61, or 128 EEG sensors.
We investigated the accuracy of the cortical current reconstruction from EEG and MEG simulated signals, gathered from up to 128 electric and 153 magnetic sensors by using realistic head and distributed source modeling. Simulations were carried out under different SNRs of generated data. For the realistic cortical reconstruction of the head model used, we considered five regions of interest (ROI) in which the simulated cortical waveforms were generated. The dependent variables used for the statistical analysis were the relative error (RE) and the correlation coefficient (CC) values between estimated and generated waveforms at the cortical level in each ROI analyzed. Factors used in the statistical analysis were the level of the noise superimposed on the scalp recorded data and the number of EEG and MEG sensors used for the multi‐ and unimodal estimation of cortical current density.
The specific questions underlying the present experimental design are: (1) whether the estimation of cortical current density is more accurate with multimodal integration of EEG and MEG data compared to a single modality alone (either EEG or MEG) when using the same total number of sensors; (2) whether an “optimal” number of EEG and MEG sensors exist for the multimodal estimations of the cortical current density; and (3) the SNR influence on simulated electromagnetic data for estimation of cortical current density with respect to the unimodal (i.e., EEG or MEG) and multimodal (EEG–MEG) inverse techniques.
MATERIALS AND METHODS
Combined Electric and Magnetic Forward Solution
The forward solution specifying the potential scalp field due to an arbitrary dipole source configuration can be computed on the basis of the solution x of the following linear system
| (1) |
where E is the electric lead field matrix obtained by the boundary element technique for the realistic magnetic resonance (MR)‐constructed head model, B is the magnetic lead field matrix obtained for the same head model, x is the array of the unknown cortical dipole strengths, v is the array of the recorded potential values, and m is the array of magnetic values. The lead field matrix E and the array v must be referenced consistently. To scale EEG and MEG, the rows of the lead field matrix E and B were first normalized by the rows norm [Baillet et al., 1999; Phillips et al., 1997]. This scaling was equally applied on the electrical and magnetic measurement arrays, v and m. After row normalization the linear system can be restated as:
| (2) |
where A is the matrix composed by the normalized electric and magnetic lead fields, n is the noise vector and b is the normalized measurement array of EEG and MEG data (v and m, respectively). Among the several equivalent solutions for the underdetermined system in equation (2), the current density solution vector ξ was chosen by solving the following variational problem for the sources x [Grave de Peralta and Gonzalez Andino, 1998]:
| (3) |
where M, N are the matrices associated to the metrics of the data and of the source space, respectively, λ is the regularization parameter and (x)M represents the M norm of the vector x. The solution of the variational problem depends on adequacy of the data and source space metrics. Using the hypothesis of M and N positive definite, the solution of equation (3) is given by computing the linear inverse operator G according to the following expressions:
| (4) |
An optimal regularization of this linear system was obtained by the L‐curve approach [Hansen, 1992]. This curve, which plots the residual norm versus the solution norm at different λ values, was used to choose the optimal amount of regularization in the solution of the linear inverse problem. Computation of the L‐curves and optimal λ correction values was carried out with the original Hansen's routines [Hansen, 1994]. The metric M, characterizing the idea of closeness in the data space, can be particularized by taking into account the sensor noise level, by using either the Mahalanobis distance [Grave de Peralta and Gonzalez Andino, 1998] or the identity matrix [Hämäläinen and Ilmoniemi, 1984].
Electrical Source Constraints
In the following, we describe two characterizations of the inverse source metric N used in literature and also in this study for the solution of the linear inverse problem. The first one involves the so‐called minimum norm source metric [Hämäläinen and Ilmoniemi, 1984], in which no a priori information on the sources is available. In this case the inverse of the source metric is represented by the following equation:
| (5) |
where I is the identity matrix and N −1 the inverse of the source metric matrix. Another characterization of the source metric N takes into account all the cortical voxels on the basis of their electrical “closeness” to the EEG sensors to remove their inverse dependence on the sensor‐to‐dipole distance (column norm normalization) [Pascual‐Marqui, 1995]. In this case, the inverse of the resulting source metric N is:
| (6) |
in which (N −1)ii is the ith element of the inverse of the diagonal matrix N, and all the other matrix elements N ij are set to 0. The L2 norm of the ith column of the lead field matrix A is denoted by (A .i). In the following, the inverse operators characterized by the choice of the source metric described by equations (5) and (6) will be referred as minimum norm (MN) and column‐normalized minimum norm (MNC), respectively.
Realistic Head and Source Models
Sixty‐four T1‐weighted sagittal MR images were acquired (30‐msec repetition time [TR], 5‐msec echo time [TE], and 3‐mm slice thickness without gap) from a subject's head. These images were processed with contouring and triangulation algorithms for construction of a model reproducing the scalp, skull, and dura mater surfaces with about 1,000 triangles for each surface. Source model was built with the following procedure: (1) the cortex compartment was segmented from MRI and triangulated obtaining a fine mesh with about 100,000 triangles; (2) a coarser mesh was obtained by resampling the one described above down to about 3,000 triangles, taking care that the general features of the neocortical envelope were well preserved especially in correspondence of pre‐ and postcentral gyri and frontal mesial area; and (3) an orthogonal unitary equivalent current dipole was placed in each node of the triangulated surface, with direction parallel to the vector sum of the normals to the surrounding triangles. The average distance between dipole sources in the cortical tessellated surfaces was equal to 3.6 mm.
Regions of Interest
Cortical regions of interest (ROIs) were represented by the supplementary motor area (SMA), as well as the right and left primary sensory‐motor areas (S1‐M1). The boundaries of these ROI were traced based on the following anatomic landmarks: (1) the precentral and central (omega zone) sulci, delimitating the precentral gyrus for the M1‐ROI; (2) the central (omega zone) and postcentral sulci, delimitating the postcentral gyrus for the S1‐ROI; and (3) the sulcus anterior to the vertical anterior commissure line, the medial precentral sulcus, and the cingulate sulcus, delimitating the medial frontal gyrus for the SMA‐ROI. The M1‐ and S1‐ROI were located anteriorly and posteriorly to the central sulcus, respectively. The M1‐ROI did not extend anteriorly up to the precentral sulcus, but might have included a minor part of the ventral premotor area lying in the lateral precentral gyrus (border region between Brodmann area [BA] 4 and 6). Finally, the SMA‐ROI was coincident with the BA 6 but did not comprise the cingulate motor areas located in the upper bank of the cingulate sulcus.
Sensor Configurations
Three scalp electrode arrays for the simulation of EEG data were considered. The first involved 128 electrodes regularly disposed on the scalp surface, whereas the others had 61 and 29 electrodes resulting from a uniform and regular downsampling of the full electrode configuration. This subsampling aimed to simulate both standard (29) as well as high‐resolution EEG recordings, in agreement with the standard of the extension of the International 10/20 system [Sharbrough et al., 1991]. Three sensor configurations were chosen for the MEG data. The first one comprised 153 sensors regularly disposed along the helmet surface whereas the second and third involved 63 and 38 sensors, respectively. All MEG sensors were simulated as magnetometers.. These last two configurations were obtained by a uniform subsampling of the 153 helmet sensor spatial distribution. MEG sensor positions were chosen to minimize distances between their scalp projection and the position of EEG sensors. Figure 1 shows the different sensor arrays used in simulation on the realistic head model for the EEG (upper row) as well as for the MEG (lower row) data.
Figure 1.
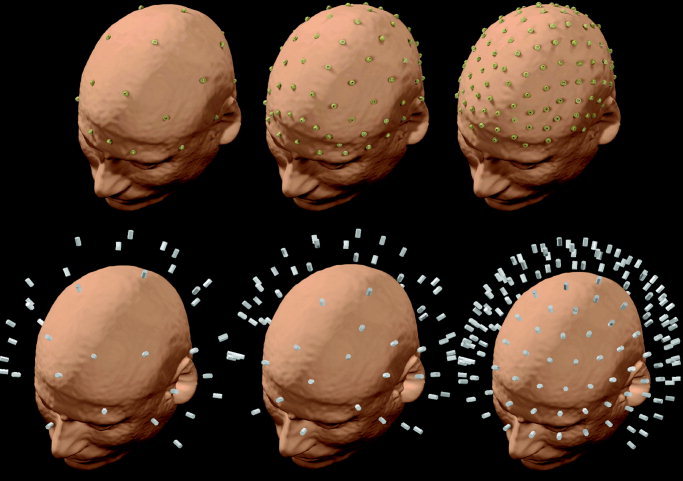
Different sensor arrays employed in this simulation study and their position with respect to the realistic scalp reconstruction. Top: Three different sensor arrays using 29, 61, and 128 electric measurement sites. Bottom: Three different sensor arrays using 38, 63, and 153 magnetic measurement sites. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com]
Source Reference Waveforms
Five source waveforms estimated from a high‐resolution movement‐related potential (MRP) recording (128 electrodes) were used as reference for the simulation. The EEG was recorded in a healthy subject who executed a set of un‐aimed, self‐paced, brisk movements of the right middle finger. The original MRP data were sampled at 300 Hz, from 3 sec before to 2 sec after the electromyograph (EMG) onset (1,500 data points). To reduce the dimension of the dataset, it was downsampled to 128 data points after proper low‐pass, finite impulse response, zero phase filtering. The collapsed source waveforms were estimated by means of the minimum norm inverse operator [Dale and Sereno, 1993; Hämäläinen and Ilmoniemi, 1984], with the head volume conductor, cortical models, and ROIs described above (thus the same used for the simulations).
Instead of cortical generated waveforms, another series of simulations employed binary levels of activation (0 and 1) in all the possible combination for the ROIs analyzed. Because the results obtained in such simulations are identical to those presented here for the generated waveforms, however, we present below only the waveform‐related set of results.
Experimental Design
The experimental design, the steps of which are also represented in Figure 2, was constructed as follows:
Figure 2.
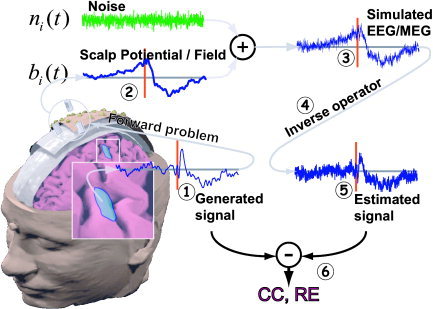
Different steps involved in this simulation study. 1: The simulated cortical source reference waveforms. 2: Simulated EEG and MEG signals obtained by propagation via the realistic volume conductor to the simulated sensor arrays. 3: Addition of white noise at different SNRs to the simulated sensor waveforms. 4: Application of different inverse operators to simulated EEG/MEG datasets. 5: Estimates of current source density for each ROI, obtained as the average of current estimates of each dipoles belonging to such ROI. 6: Evaluation of reconstructed cortical activity by computing CC and RE at the ROI level between the generated and estimated activities. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com]
-
1
The same source reference current density waveform was attributed to each dipole belonging to a particular selected ROI
-
2
Different source reference waveforms were attributed to the different ROIs selected for this study
-
3
Each cortical dipole that did not belong to a particular ROI received a randomly generated noise current density waveform. Such random waveforms have a power intensity equal to the 5% of those presented by the waveforms attributed to the ROIs
-
4
The signals in the simulated sensor arrays were calculated using a realistically shaped volume conductor model. In this calculation, locations and orientations of sources were constrained to the cortical mantle. The amplitudes of the sources varied in time as described in steps 1–3 above. Such arrays had variable number sensors thus producing separate EEG and MEG data sets (point 2 of Fig. 2)
-
5
White noise was added to these EEG/MEG datasets, to reach different levels of SNRs (infinite, 30, 20, 10, 5, 3, 1). These values were chosen to simulate the typical range of SNR commonly encountered in evoked, motor‐ and cognitive‐related EEG/MEG recordings, respectively (point 3 of Fig. 2)
-
6
The inverse operators described above were applied to these EEG/MEG datasets and the cortical activity was estimated for all 3,000 cortical dipoles used in simulations. Two types of weights for the inverse operators have been used: the minimum norm estimate (MN, equation [4]) and the column normalized minimum norm estimate (MNC, equation [5]) (point 4 of Fig. 2)
-
7
The estimated current source density waveform for each ROI was obtained by calculating the average of the current estimates of each dipole belonging to the respective ROI (point 5 of Fig. 2)
-
8The accuracy of the estimated cortical current strength array (Es) with respect to the generated one (Gs) in the different experimental conditions was evaluated by computing two indexes, to be used in the following simulations as dependent variables. The first one was the correlation coefficient (CC) between the generated and the estimated average source waveforms, according to the following formula:
where • stands for the usual inner products between the Gs and the Es vectors. The second one was the relative error (RE) computed according to the following formula: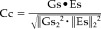
(7)
where (x)2 is the standard L2 norm of a vector x.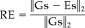
(8)
For each level of SNR adopted, 32 occurrences of white noise data were considered on the simulated EEG and MEG waveforms, resulting in 32 values of CC and RE variables for each level of the independent variables considered. Such computations were carried out to increase reliability of the statistical results obtained. The average values of CC and RE were then used in the successive statistical analysis.
Influence of Sensor Number on the Cortical Current Estimated Solutions
A principal source of variance for the present results could be the different number of sensors used in the EEG, the MEG, and the combined EEG–MEG conditions. Accuracy of the linear inverse source solutions could have been affected by the total amount of spatial samples (EEG plus MEG) rather than by the combination of EEG and MEG data per se. We thus compared source estimate obtained by the integration of the whole EEG data set (128 electrodes) versus the full MEG one (153 sensors) and the combined EEG–MEG data with a similar number of total electric and magnetic sensors (61 and 63, respectively). To extend results obtained in a previous study [Liu et al., 2002], the same analysis was carried out on estimations computed from EEG data sampled with 61 electrodes, MEG data sampled with 63 sensors, and combined EEG and MEG data sampled with 29 and 38 sensors, respectively. Another set of simulations was intentionally carried out using the full MEG sensor array (153 measurement points) coupled in turn with 29, 61 and 128 EEG sensors. Performance indexes assessing quality of current strengths of the estimated source were then applied.
Statistical Analysis
The obtained results were subjected to separate analysis of variance (ANOVA), in a full within design. The main factors of the ANOVA were the SNR, the type of inverse operator used denoted as INVERSE, and the number of sensors employed in the inverse procedure (SENSORS). Table I reports the independent variables used and their relative levels of variations employed for statistical analysis. The correction of Greenhouse‐Gasser for violation of the spherical hypothesis in all employed ANOVAs was used. The post‐hoc analysis was carried out with the Scheffe's test at the P = 0.05 statistical significance level.
Table I.
Independent variables used for the statistical analysis of the estimated current densities, and their relative levels of variation
| Variable | Description | Levels |
|---|---|---|
| SNR | SNR generated at EEG sensors | ∞, 30, 20, 10, 5, 3, 1 |
| INVERSE | Type of inverse operator, described by equations (4–10) | MN, MNC |
| SENSORS | Number of simulated sensors | 29, 61, 128 for EEG and 153, 63, 38 for MEG |
SNR, signal‐to‐noise ratio; EEG, electroencephalogram; MN, minimum norm; MNC, column‐normalized minimum norm; MEG, magnetoencephalogram.
RESULTS
The analysis of the simulation results was carried out for each ROI separately. All ANOVAs carried out included the main factors SNR, SENSORS, and INVERSE. The five ANOVAs carried out (one for each ROI analyzed) returned a coherent and similar pattern of results. In the following, without lack of generality, we present data for only one representative ROI.
Comparisons of Current Density Estimations Using 128 EEG Sensors, 153 MEG Sensors, or Combined 61 EEG and 63 MEG Sensors
For both CC and RE indexes, the three‐way ANOVA returned statistically significant values of all main factors analyzed and their interactions with at least P < 0.001. In particular, the main factors SENSORS (F[2,62] = 507.4, P < 0.0001), INVERSE (F[1,31] = 186, P < 0.0001), and SNR (F[6,186] = 122, P < 0.001) significantly decrease the data variance of CC index. The RE data decrease significantly the variance for the factors SENSORS (F[2,62] = 6,274, P < 0.0001), INVERSE (F[1,31] = 93.8, P < 0.0001), and SNR (F[6,186] = 197.8, P < 0.001). Interactions between factors SENSORS and INVERSE were highly significant as indicated by the values of F(2,62) = 31,5 and F(2,62) = 2,450 obtained for the CC and RE indexes, respectively. In addition, interactions between the factors INVERSE and SNR were significant for both CC (F[6,186] = 14.7, P < 0.0001) and RE (F[6,186] = 30.7, P < 0,001) indexes. Finally, also the triple interaction between all the factors (SENSORS × INVERSE × SNR) was significant with F(12,372) = 28.96 for the CC index and F(12,372)= 29.1 for the RE index.
One observes that the EEG–MEG‐based inverse operator obtained with 61 EEG and 63 MEG sensors returned statistically significant improved current density estimations (as stated by both CC and RE indexes) with respect to those estimated using 128 EEG or 153 MEG sensors. In fact, all comparisons carried out with Scheffe's test returned a statistical significance level of at least P < 0.0001. This has occurred for all the SNRs considered in the simulations.
Figure 3 shows spatial distributions of estimated current density strengths obtained by unimodal inverse operators (based on 128 EEG sensors or 153 MEG sensors) as well as the multimodal one (with 61 EEG and 63 MEG sensors). In particular, three instantaneous activated cortical areas were shown on the realistic head model (Fig. 3A); the other realistic heads show the estimates of the cortical current density carried out using 128 EEG channels (Fig. 3B); 153 MEG sensors (Fig. 3C), and 63 MEG and 61 EEG sensors (Fig. 3D). All cortical areas were activated with the same unitary strength, whereas the other cortical dipoles were set to a random value between −0.05 and 0.05. The reconstruction carried out with the multimodal EEG–MEG inverse operator recovered the current density activation in all three active cortical areas (namely, the SMA and the left and right M1). The estimation of the right S1/M1 cortical activity with 63 MEG and 61 EEG sensors, however, was carried out using half‐strength values (light blue) with respect to those used for the left S1/M1 (purple).
Figure 3.
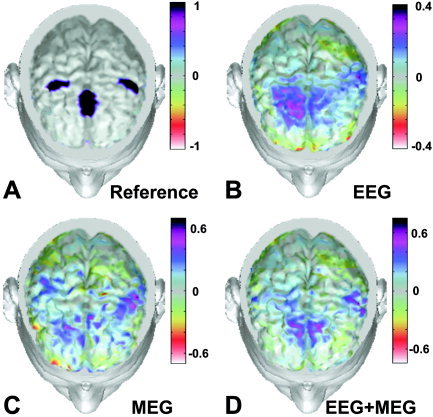
Spatial distributions of estimated current density strengths obtained by pure unimodal inverse operators (based on 128 EEG or 153 MEG sensors) and multimodal one (with 61 EEG and 63 MEG sensors). In particular, the map in A shows three instantaneous activated cortical areas. The rest of the figure shows reconstruction of the cortical current density carried out using data from 128 EEG channels (B), 153 MEG sensors (C), and combined 63 MEG and 61 EEG sensors (D). Percent color scale is normalized with reference to the maximum amplitude calculated for each map. Maximum negativity (−100%) is coded in red and maximum positivity (+100%) is coded in black. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com]
Figure 4 presents the average data of the RE index for the main factors analyzed (SENSORS, INVERSE, SNR) in the left S1‐ROI. The cortical current density estimate carried out with 153 MEG sensors showed a statistically significant lower value of RE index compared to those carried out with 128 EEG sensors (Scheffe's test, P < 0.001) for SNR values ranging from infinite to 3. Post‐hoc tests carried out with Scheffe's test reported no statistically significant differences between the MN and MNC inverse operators in the EEG and MEG cases for a wide range of SNRs (from infinite to values of 3). For the EEG–MEG case, the MN inverse operator returned statistically significant lower values of RE compared to that with the MNC inverse operator for the range of SNRs values obtained.
Figure 4.
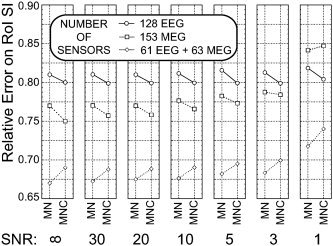
Each section of figure corresponds to a particular SNR value employed in simulations. Vertical axis reports the average of the relative error (RE) index computed after the current density estimation; horizontal axis reports the different inverse operators used for estimation of current density. Each data point is an average value of the RE index computed at a particular SNR and with a particular sensor configuration during the simulations. Circles, data from 128 EEG sensors; squares, data from 153 MEG sensors; diamonds, data from 61 EEG plus 63 MEG sensors. Data are relative to the S1‐ROI. Significant reductions of RE were noted for estimations carried out with multimodal integration of EEG and MEG compared to other unimodal estimation methods (EEG and MEG) for any SNR used. Such reduction was independent of the number of sensors, similar in all the three cases.
Comparisons of Current Density Estimations Using 61 EEG Sensors, 63 MEG Sensors, or Combined 29 EEG and 38 MEG Sensors
In this case, for both CC and RE indexes, the three‐way ANOVA returned statistically significant values of all main factors analyzed and their interactions with a statistical significance of at least P < 0.001. One observes that the EEG–MEG‐based inverse operator obtained with 29 EEG and 38 MEG sensors returned statistically significant (P < 0.0001, Scheffe's test) lower RE values and higher CC values with respect to those estimated using unimodal inverse operators. This result holds for the entire range of SNRs analyzed. In addition, it was observed that the current density estimation carried out with 61 EEG sensors returned statistically significant lower RE and higher CC values compared to those obtained using 63 MEG sensors, for a wide range of the SNRs used (from infinite to 3).
Figure 5 presents the average data of the RE index in the SMA‐ROI for the main factors SENSORS, INVERSE, and SNR using the EEG data sampled with 61 sensors (circles), the MEG data sampled with 63 sensors (squares) and the combined EEG and MEG data with 29 and 38 sensors (diamonds), respectively.
Figure 5.
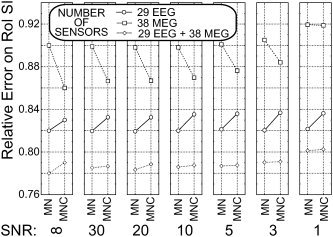
Average data for RE in the SMA‐ROI at the different levels of main factors considered (ELECTRODES, INVERSE, and SNR). Simulations were carried out using EEG data sampled with 61 sensors (circles), MEG data sampled with 63 sensors (squares), and combined EEG and MEG data with 29 and 38 sensors (diamonds), respectively. Same conventions as those used for Figure 4.
Comparisons of Current Density Estimations Using 153 MEG Sensors Combined With 29, 61, and 128 EEG Sensors
In this set of simulations, we analyzed accuracy of the current density reconstruction obtained using multimodal integration of 153 MEG sensors with 29, or 61, or 128 EEG data. The results were once again compatible in all ROIs analyzed, and we describe the results for the ROI representing the S1 area. The three‐way ANOVAs carried out on both CC and RE indexes returned a statistically significant decrease of data variance for all main factors considered and their interactions (at P < 0.001). For both CC and RE indexes, the three‐way ANOVA returned statistically significant values of all main factors analyzed and their interactions with at least P < 0.001. In particular, the main factors SENSORS (F[2,62] = 52.4, P < 0.0001), INVERSE (F[1,31] = 22.6, P < 0.0001), and SNR (F[6,186] = 9.89, P < 0.001) significantly decrease the data variance of the CC index. The RE data significantly decreased the variance for the factors SENSORS (F[2,62] = 60.98, P < 0.0001), INVERSE (F[1,31] = 290.9, P < 0.0001), and SNR (F[6,186] = 628.5, P < 0.0001). Interactions between factors SENSORS and INVERSE were highly significant as indicated by the values of F(2,62) = 21.7 and F(2,62) = 22.9 obtained for the CC and RE indexes, respectively. The interactions between the factors INVERSE and SNR were significant for both CC (F[6,186] = 54.7, P < 0.0001) and RE (F[6,186] = 466.3, P < 0.001) indexes. Finally, the triple interaction between all the factors (SENSORS × INVERSE × SNR) was also significant with F(12,372) = 290.9 for the CC index and F(12,372) = 5.83 for the RE index.
Figure 6 shows the mean values of RE indexes for current density estimations carried out with 153 MEG sensors and 29, 61, and 128 EEG sensors. It is possible to appreciate the similarity in values of the RE index obtained for 153 MEG and 29 EEG sensors compared to all the other multimodal combinations employed. Post‐hoc Scheffe's tests suggested that the values for the RE and CC indexes obtained with 153 MEG and 29 EEG sensors were statistically similar to those returned with 153 MEG and 61 or 128 EEG sensors, for a wide range of SNRs investigated (from infinite to value of 3). When the SNR of data moved from 3 to 1, however, current density estimations carried out with many EEG and MEG sensors (i.e., 128 EEG sensors and 153 MEG sensors) returned statistically significant lower reconstruction errors (at P < 0.001) compared to other alternative multimodal current reconstruction used (i.e., with 153 MEG sensors and 29 or 61 EEG sensors). The multimodal integration of 153 MEG sensors and 29 EEG sensors returned values of RE lower than those obtained by single modalities alone (EEG and MEG; see Fig. 4 and 5) for a large set of SNR values.
Figure 6.
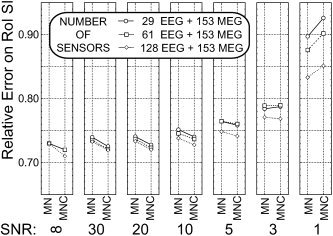
Average data for RE in the S1‐ROI at the different levels of main factors considered (ELECTRODES, INVERSE, and SNR). Simulations were carried out using combined MEG and EEG data sampled with 153 MEG sensors and 29 EEG sensors (circles), 153 MEG sensors and 61 EEG sensors (squares), and 153 MEG sensors and 128 EEG sensors (diamonds), respectively. Same conventions used for Figure 4.
DISCUSSION
Generalities on Simulations Carried Out
This study addressed the question as to whether multimodal integration of high‐resolution EEG and MEG data improves estimation of cortical current density. These results were reported at the ROI level instead of the level of each one of the 3,000 cortical dipoles used as a source model. An ROI‐dependent result such as the one used in our study was chosen due to our interest in the reported efficacy of the estimation process at this still acceptable spatial scale resolution. Although it is possible to obtain current density estimation at higher spatial scales (in the order of several square millimeters), the inherent difficulties of the electromagnetic inverse problem would suggest rather a lower level of spatial resolution, the results of which we discuss conservatively. Accordingly, the obtained estimates of current density were computed at the level of the ROI employed, by computing the average of each single dipole moment belonging to the ROI. The use of indexes furnished indications about the capability of the linear inversion system to return correct information about the shape (CC index) and the absolute values (RE index) of the generated waveforms. Previous simulation studies on estimation of cortical current densities with multimodal integration of EEG and MEG modalities have taken into account indexes such as the resolution kernel and the point spread function (PSF) [Babiloni et al., 2001; Liu, 2000; Liu et al., 2002]. Such indexes could not be taken into account, however, when the SNR of the data is systematically varied, as in this study; therefore, we adopted the CC and RE indexes instead of PSF or resolution kernel indicators.
The generated waveforms have been chosen to mimic cortical current estimates during preparation and execution of simple unilateral finger movements in humans. Such estimates were obtained using high‐resolution EEG data from MRPs recorded in a subject with 128 sensors, and the same realistic head and cortical models used for simulations. It may be argued that the reference current density waveforms used contained a contribution of the noise already present on the MRP recordings and back‐projected by the inverse operator from the scalp to the cortex. This consideration doesn't affect the results obtained, because reference waveforms are here used as a “gold standard” for the inverse procedures tested. The simulations proposed used realistic SNR values in connection with EEG and MEG recordings from humans.. In fact, such SNR values moved from 20 or 10 as similarly observed in some epileptic spike seizures or evoked potentials/fields to the values of SNR from 5, 3 or even 1 occurring during the recording of single EEG/MEG trials related to motor or cognitive activities. The estimation of current density from 29, 61, and 128 EEG sensors was carried out due to the large availability of high‐resolution EEG systems using 64 and 128 sensors.
Simulation Results
The results offered by the present simulation study have demonstrated the general efficacy of inverse operators used in recovery of cortical activity at the level of ROIs. In fact, a good recovery of generated waveforms was obtained for all SNR levels and number of electrodes/sensors employed. As expected, there was a relevant effect of noise levels on estimation of current density; however, the higher the spatial sampling of the EEG and MEG distributions, the higher the obtained quality of the current reconstruction for any level of SNR. Using multimodal integration of 64 EEG and MEG sensors, we obtained current density estimate 20% more accurate than that using only 128 EEG or 153 MEG sensors. This error percentage, obtained for each ROI analyzed, can produce severe misinterpretation of data when current density over the whole cortex was estimated. The multimodal integration carried out with 29 EEG and 38 MEG sensors still returned current density estimates about 10% more accurate than those carried out with only 61 EEG or 63 MEG sensors. The absolute quality of estimated current density in the multimodal case is lower than in the case in which hundreds of EEG and MEG sensors have been used (Fig. 4). Furthermore, simulation results suggest that during high‐resolution MEG recordings (153 sensors), the addition of 29 EEG sensors improves current density estimation in the same way as with the addition of 64 or even 128 EEG sensors.
We also noted that for all experimental conditions employed there was a substantial equivalence of accuracy in current density estimation produced by inverse operators with and without column norm normalization (MN and MNC). The presented simulations, however, were carried out by constraining the neural sources to the modeled cortical mantle. In general, column norm normalization has been introduced mainly for linear inverse systems dealing with a tomographic model of the brain, in which the cerebral source space for the solution was coincident with the whole‐head model [Grave de Peralta and Gonzalez Andino, 1998; Pascual‐Marqui, 1995]. It can be hypothesized that the relative subtle differences in depth of modeled sources in sulci and gyri of the generated cortical surface with respect to the sensor positions could be responsible for such results.
Additional simulation results suggested that current density estimation carried out by unimodal MEG data (153 sensors) returned lower error in amplitude and waveform shape estimation in each ROI analyzed (as described by low RE and high CC indexes) compared to those carried out with unimodal EEG data (128 sensors) over a large set of SNR values. This particular result was reversed when subsampling with roughly 63 sensor points was carried out for EEG and MEG. The estimates obtained with unimodal 61 EEG sensors, however, were superior to those obtained by 63 MEG sensors for the whole set of SNR values employed. This result is in line with that reported in previous publications for the same number of EEG and MEG sensors and for an SNR level equal to 10 [Liu, 2000; Liu et al., 2002]. These last results, although statistically significant, are relative to modest absolute values of the differences. In this case, their statistical significance means that the findings are not due to chance alone, but low absolute values of estimation errors suggest a negligible practical implication of such results.
Simulations carried out demonstrated clearly that current density estimations carried out using 153 MEG and 29 EEG sensors have the same statistical accuracy as those employing 153 MEG and 61 or 128 EEG sensors. This result is compatible with a previous simulation study that showed that the use of few EEG channels was useful to increase the accuracy of current density estimate when 61 MEG measurement points (each one with two orthogonal planar gradiometers) were used [Liu et al., 2002]. We obtained the same conclusions for a larger set of MEG measurement points (153) and for a wider SNR range. The present simulation results were obtained using same SNR levels for both EEG and MEG recordings during the multimodal integration, in line with previous work [Liu et al., 2002]. It is possible to imagine, however, a situation in which multimodal integration has to be carried out in the presence of different SNRs for EEG and MEG data. This could happen when a significantly different number of trials were used for acquisition of MEG and EEG data. In this case, only the figure of merit relative to the unimodal EEG or MEG current density estimation will remain valid. Of course, it is always possible to reduce off‐line the number of EEG/MEG trials used for the average to obtain a common SNR level in both modalities.
CONCLUSIONS
There is a rather large consensus about the need and utility of multimodal integration of magnetic and neuroelectric data. Results reported previously [Babiloni et al., 2001; Liu, 2000; Liu et al., 2002] and in the present work suggest that it is possible to obtain real improvement in spatial details of the estimated distributed neural sources by carrying out multimodal integration of EEG and MEG data. Based on simulations carried out, we are able to answer the questions raised earlier. First, the use of multimodal EEG and MEG data returns improved current density estimations compared to those provided by unimodal data (EEG or MEG). This result was obtained throughout the SNR range employed and for all sensor numbers considered. Second, there is a significant SNR influence on estimation of cortical current density; however, this influence is similar for separate EEG, MEG, and combined EEG–MEG estimation techniques. Third, the use of few EEG sensors (29 sensors) together with full MEG recordings (153 sensors) returns current density estimations equivalent to those obtained using larger EEG sensor arrays (61 and 128) in conjunction with the 153 MEG sensors.
This last point of interest given the relatively shorter time needed to set 29 electrodes under the MEG system compared to that needed to set‐up 64 (let alone 128) electrodes. Taken together, our results could return quite accurate estimations of cortical current densities using realistic models for the head and cortical surfaces. This clearly makes such techniques appealing for the study of complex brain functions that are characterized by high spatial and temporal variability.
REFERENCES
- Ahlfors SP, Simpson GV, Dale AM, Belliveau JW, Liu AK, Korvenoja A, Virtanen J, Huotilainen M, Tootell RB, Aronen HJ, Ilmoniemi RJ (1999): Spatiotemporal activity of a cortical network for processing visual motion revealed by MEG and fMRI. J Neurophysiol 82: 2545–2555. [DOI] [PubMed] [Google Scholar]
- Anourova I, Nikouline VV, Ilmoniemi RJ, Hotta J, Aronen HJ, Carlson S (2001): Evidence for dissociation of spatial and nonspatial auditory information processing. Neuroimage 14: 1268–1277. [DOI] [PubMed] [Google Scholar]
- Babiloni F, Carducci F, Cincotti F, Del Gratta C, Pizzella V, Romani GL, Rossini PM, Tecchio F, Babiloni C (2001): Linear inverse source estimate of combined EEG and MEG data related to voluntary movements. Hum Brain Mapp 14: 197–210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baillet S, Garnero L (1997): A Bayesian framework to introducing anatomo‐functional priors in the EEG/MEG inverse problem., IEEE Trans Biomed Eng 44: 374–385. [DOI] [PubMed] [Google Scholar]
- Baillet S, Garnero L, Marin G, Hugonin P (1999): Combined MEG and EEG source imaging by minimization of mutual information. IEEE Trans Biomed Eng 46: 522–534. [DOI] [PubMed] [Google Scholar]
- Dale A, Liu A, Fischl B, Buckner R, Belliveau JW, Lewine J, Halgren E (2000): Dynamic statistical parametric mapping: combining fMRI and MEG for high‐resolution imaging of cortical activity. Neuron 26: 55–67. [DOI] [PubMed] [Google Scholar]
- Dale AM, Sereno M (1993): Improved localization of cortical activity by combining EEG and MEG with MRI cortical surface reconstruction: a linear approach. J Cogn Neurosci 5: 162–176. [DOI] [PubMed] [Google Scholar]
- David O, Garnero L, Cosmelli D, Varela FJ (2002): Estimation of neural dynamics from MEG/EEG cortical current density maps: application to the reconstruction of large‐scale cortical synchrony. IEEE Trans Biomed Eng 49: 975–987. [DOI] [PubMed] [Google Scholar]
- Fuchs M, Wagner M, Wischmann HA, Kohler T, Theissen A, Drenckhahn R, Buchner H (1998): Improving source reconstruction by combining bioelectrical and biomagnetic data. Electroencephalogr Clin Neurophysiol 107: 69–80. [DOI] [PubMed] [Google Scholar]
- Grave de Peralta R, Gonzalez Andino S (1998): Distributed source models: standard solutions and new developments In: Uhl C, editor. Analysis of neurophysiological brain functioning. New York: Springer Verlag; p 176–201. [Google Scholar]
- Hämäläinen M, Ilmoniemi R (1984): Interpreting measured magnetic field of the brain: Estimates of the current distributions. Technical report TKK‐F‐A559. Helsinki: Helsinki University of Technology. [Google Scholar]
- Hansen PC (1992): Analysis of discrete ill‐posed problems by means of the L‐curve. SIAM Rev 34: 561–580. [Google Scholar]
- Hansen PC (1994): Regularization tools: a Matlab package for analysis and solution of discrete ill‐posed problems. Numerical Algorithms 6: 1–35. [Google Scholar]
- Huizenga HM, de Munck JC, Waldorp LJ, Grasman RP (2002): Spatiotemporal EEG/MEG source analysis based on a parametric noise covariance model. IEEE Trans Biomed Eng 49: 533–539. [DOI] [PubMed] [Google Scholar]
- Liu AK (2000): Spatiotemporal brain imaging. PhD dissertation. Cambridge, MA: Massachusetts Institute of Technology.
- Liu AK, Belliveau JW, Dale AM (2002): Monte Carlo simulation studies of EEG and MEG localization accuracy. Hum Brain Mapp 16: 47–62. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mizoguchi C, Kobayakawa T, Saito S, Ogawa H (2002): Gustatory evoked cortical activity in humans studied by simultaneous EEG and MEG recording. Chem Senses 27: 629–634. [DOI] [PubMed] [Google Scholar]
- Nunez PL (1995): Neocortical dynamics and human EEG rhythms. New York: Oxford University Press. [Google Scholar]
- Okada YC, Salenius S (1998): Roles of attention, memory, and motor preparation in modulating human brain activity in a spatial working memory task. Cereb Cortex 8: 80–96. [DOI] [PubMed] [Google Scholar]
- Otsubo H, Ochi A, Elliott I, Chuang SH, Rutka JT, Jay V, Aung M, Sobel DF, Snead OC (2001): MEG predicts epileptic zone in lesional extrahippocampal epilepsy: 12 pediatric surgery cases. Epilepsia 42: 1523–1530. [DOI] [PubMed] [Google Scholar]
- Pascual‐Marqui RD (1995): Reply to comments by Hämäläinen, Ilmoniemi and Nunez. ISBET Newsletter 6: 16–28. [Google Scholar]
- Phillips JW, Leahy R, Mosher JC (1997): Imaging neural activity using MEG and EEG. IEEE Eng Med Biol Mag 16: 34–41. [DOI] [PubMed] [Google Scholar]
- Regan D (1989): Human brain electrophysiology. evoked potentials and evoked magnetic fields in science and medicine. New York: Elsevier Press. [Google Scholar]
- Schimpf PH, Ramon C, Haueisen J (2002): Dipole models for the EEG and MEG. IEEE Trans Biomed Eng 49: 409–418. [DOI] [PubMed] [Google Scholar]
- Sharbrough F, Chatrian GE, Lesser RP, Luders H, Nuwer M, Picton TW (1991): American electroencephalographic society guidelines for standard electrode position nomenclature. J Clin Neurophysiol 8: 200–202. [PubMed] [Google Scholar]
- Stenbacka L, Vanni S, Uutela K, Hari R (2002): Comparison of minimum current estimate and dipole modeling in the analysis of simulated activity in the human visual cortices. Neuroimage 16: 936–943. [DOI] [PubMed] [Google Scholar]
- Torquati K, Pizzella V, Della Penna S, Franciotti R, Babiloni C, Rossini PM, Romani GL (2002): Comparison between SI and SII responses as a function of stimulus intensity. Neuroreport 13: 813–819. [DOI] [PubMed] [Google Scholar]
- Uutela K, Hämäläinen M, Somersalo E (1999): Visualization of magnetoencephalographic data using minimum current estimates. Neuroimage 10: 173–180. [DOI] [PubMed] [Google Scholar]
- Yoshinaga H, Nakahori T, Ohtsuka Y, Oka E, Kitamura Y, Kiriyama H, Kinugasa K, Miyamoto K, Hoshida T (2002): Benefit of simultaneous recording of EEG and MEG in dipole localization. Epilepsia 43: 924–928. [DOI] [PubMed] [Google Scholar]
- Zijlmans M, Huiskamp GM, Leijten FS, Van Der Meij WM, Wieneke G, Van Huffelen AC (2002): Modality‐specific spike identification in simultaneous magnetoencephalography/electroencephalography: a methodological approach. J Clin Neurophysiol 19: 183–191. [DOI] [PubMed] [Google Scholar]


