Abstract.
We evaluated whether using synthetic mammograms for training data augmentation may reduce the effects of overfitting and increase the performance of a deep learning algorithm for breast mass detection. Synthetic mammograms were generated using in silico procedural analytic breast and breast mass modeling algorithms followed by simulated x-ray projections of the breast models into mammographic images. In silico breast phantoms containing masses were modeled across the four BI-RADS breast density categories, and the masses were modeled with different sizes, shapes, and margins. A Monte Carlo-based x-ray transport simulation code, MC-GPU, was used to project the three-dimensional phantoms into realistic synthetic mammograms. 2000 mammograms with 2522 masses were generated to augment a real data set during training. From the Curated Breast Imaging Subset of the Digital Database for Screening Mammography (CBIS-DDSM) data set, we used 1111 mammograms (1198 masses) for training, 120 mammograms (120 masses) for validation, and 361 mammograms (378 masses) for testing. We used faster R-CNN for our deep learning network with pretraining from ImageNet using the Resnet-101 architecture. We compared the detection performance when the network was trained using different percentages of the real CBIS-DDSM training set (100%, 50%, and 25%), and when these subsets of the training set were augmented with 250, 500, 1000, and 2000 synthetic mammograms. Free-response receiver operating characteristic (FROC) analysis was performed to compare performance with and without the synthetic mammograms. We generally observed an improved test FROC curve when training with the synthetic images compared to training without them, and the amount of improvement depended on the number of real and synthetic images used in training. Our study shows that enlarging the training data with synthetic samples can increase the performance of deep learning systems.
Keywords: computer-aided detection, deep learning, breast mass detection, mammography, synthetic mammogram images, in silico imaging
1. Introduction
Deep convolution neural networks have shown groundbreaking performance in medical image analysis compared to traditional machine learning techniques. These neural networks generally consist of many parameters that are determined from the training data set. Several studies in the literature have investigated the effect of training dataset size on the performance of machine learning systems.1–10 In general, as the number of training cases increases, overfitting tends to decrease and the performance on the targeted population tends to improve, with a diminishing rate of improvement after the training set size gets large enough.
Unlike other computer vision tasks where the data set for training a deep learning neural network contains a large number of labeled samples, annotated data sets are much more limited in the medical imaging domain. In order to increase the training data set size, and thus increase the variability of the images that the networks are trained on, several alternative strategies have been utilized, including data augmentation using transformations such as flip, rotation, and jittering within an image, seamless insertion of lesions into other locations with or without transformations,11,12 and transfer learning, where the network weights are initialized with a pretrained model from a different task and/or data set such as natural image classification for which large labeled data sets are available.
Another method for increasing the training data set is to generate synthetic data. Recently, generative adversarial networks (GANs),13 where a neural network is trained to generate random image samples from a desired distribution by attempting to deceive another network that aims at distinguishing between real and generated images, have shown promise in generating synthetic images.14 Specifically in medical imaging, there have been efforts in liver lesion classification15 and lymph node segmentation16 that use GANs for data augmentation.
Another method, which we have used in this study, is to use procedurally generated images using biology-inspired object models and physics-based image generation. The synthetic mammogram images used in this study are produced by the methods described by Badano et al.17 in the virtual clinical trials for regulatory evaluation (VICTRE) study, which investigated the possibility of performing an in silico clinical trial, specifically for comparing performance of digital mammography and digital breast tomosynthesis for breast cancer detection.
In this study, we show that the performance of a deep learning neural network for breast mass detection algorithm in mammography can be increased by training the system using procedurally generated synthetic images. We also study the dependence of any improvement on the number and relative proportion of real and synthetic images and demonstrate that adding larger and larger sets of synthetic training images does not necessarily result in progressively increasing performance.
2. Materials and Methods
2.1. Data Set
The data sets used in this study contained real images from the Curated Breast Imaging Subset of the Digital Database for Screening Mammography (CBIS-DDSM) data set, and synthetic images, generated using the pipeline in the VICTRE study.17
2.1.1. CBIS-DDSM images
The CBIS-DDSM data set,18 available through the Cancer Imaging Archive (TCIA), is an updated and standardized version of the public Digital Database for Screening Mammography19 (DDSM) data set that was made available in 1997.18 It was curated with the help of a trained mammographer who removed images in which the lesion was not clearly seen, or which contained personal information. In the conversion process from DDSM to CBIS, the images were decompressed, pixel values were converted to standardized optical density values, remapped to 16-bit grayscale and saved as DICOM. CBIS-DDSM provides mass outlines obtained by applying a level set algorithm to the original contours provided in the DDSM data set.
We used all the images containing masses in the CBIS-DDSM data set, which is prepartitioned into 1231 mammograms (1318 masses) for training, and 361 mammograms (378 masses) for testing. We further partitioned the training data set into 1111 mammograms (1198 masses) for training of the mass detection algorithm, and 120 mammograms (120 masses) for validation and hyperparameter selection.
2.1.2. Synthetic images
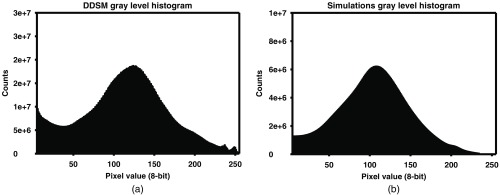
A total of 2000 synthetic mammogram images, consisting of 1000 CC view and 1000 MLO view images, containing 2522 masses were generated and used during the training of the network. A validation set of 30 synthetic images with 15 CC and 15 MLO view images, containing a total of 35 masses, and a test set of 202 synthetic mammogram images, consisting of 101 CC view and 101 MLO view images (254 masses) was generated for testing the algorithms’ performance on synthetic images. The synthetic training, validation, and test sets were separated sequentially. The first 2000 synthetically generated images (1000 CC and 1000 MLO) were assigned to the training data set, the next 30 (15 CC and 15 MLO) assigned to the validation set, and the last 202 mammograms (101 CC and 101 MLO) assigned to the test sets. The CC and MLO views were not paired for the synthetic images. Histograms of the mass sizes in terms of largest diameter, gray levels, and the contrast-to-noise ratio (CNR) of the masses for both the DDSM and the synthetic images training sets are shown in Figs. 1–3, respectively. As shown in Fig. 1, the mass sizes in the CBIS-DDSM data set and the synthetic data set did not completely overlap; in particular, the synthetic data set has a larger fraction of masses less than 10 mm in diameter. However, we preferred to use the distribution shown in Fig. 1(b) to generate synthetic masses because it better reflects the true mass size distribution reported by Welch et al.20 and having smaller masses in the training data set may help network training because smaller masses are frequently missed by computer-aided detection (CAD) systems. The gray levels and CNR histograms, shown in Figs. 2 and 3, respectively, are generally consistent between the DDSM and the synthetic data sets.
Fig. 1.
Histogram of the mass sizes in the (a) DDSM and (b) synthetic images training sets.
Fig. 2.
Histogram of the gray levels for the masses in the (a) DDSM and (b) synthetic images training sets.
Fig. 3.
Histogram of the CNR for the masses in the (a) DDSM and (b) synthetic images training sets.
2.2. Synthetic Mammogram Generation
Synthetic mammogram images were generated using the methods described by Badano et al.17 We briefly describe these methods here. First, virtual three-dimensional (3-D) anthropomorphic phantoms were produced using a procedural analytic model in which major anatomical structures (including fat and glandular tissues, ductal tree, vasculature, and ligaments) are stochastically generated within a predefined breast volume. The anthropomorphic phantoms were generated across the four BI-RADS breast density categories (dense, heterogeneous, scattered, and fatty). The percentage of images were 10%, 40%, 40%, and 10%, respectively, of the total number of synthetic images generated for each view, CC and MLO, for the dense, heterogeneous, scattered, and fatty categories.
Finite-element analysis, using the open-source program FEBio, was used to compress the breast in both cranial-caudal (CC) and medial-lateral-oblique (MLO) orientations to simulate the breast compression process used in standard screening mammography. The MLO view phantoms were generated by rotating the breast 45 deg before performing the breast compression. Figure 4 shows examples of a breast model and the compression process.
Fig. 4.
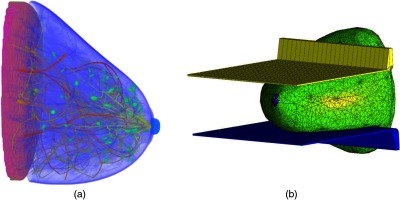
Example of (a) a synthetic breast model and (b) the compression process.
The masses were modeled with realistic sizes, shapes, and margins following previous work.21 Both spiculated and nonspiculated masses were modeled, and the diameter ranged from 0.5 to 3 cm, using information from Ref. 20 for determining the distribution of the mass sizes. Each mammogram contained one or two lesions, with every lesion being equally likely to be spiculated or nonspiculated. The masses were inserted in physiologically likely locations, specifically at ends of the ductal trees.
A Monte Carlo-based x-ray transport simulation code, MC-GPU, was used to project the 3-D phantoms, voxelized at resolution, into realistic-looking synthetic mammograms. The full-field digital mammography (FFDM) acquisition was modeled after a Siemens Mammomat Inspiration digital breast imaging system, with an amorphous-selenium direct conversion detector with a pixel size of and a 5:1 ratio, 31-line pairs/mm antiscatter grid. As the breast phantoms used in this study do not have an accurate representation of the pectoral muscle, the regions where the pectoral muscles would generally be found were masked using the average intensity value of the mammogram. Additional information regarding the generation of the synthetic mammogram images can be found in literature.17 The code for generating the synthetic mammograms for the CC views is available publicly in a Github repository: https://github.com/DIDSR/VICTRE. Figure 5 shows examples of the generated synthetic mammograms.
Fig. 5.
Examples of generated synthetic mammogram images with masses. (a) An image from a CC view. (b) An image from an MLO view, with the pectoral muscle region masked. Note that the two images are not from the same breast model.
2.3. CBIS-DDSM Images Preprocessing
The images from the CBIS-DDSM data set were preprocessed for use with our network initialized which was initialized with weights from the ILSVRC2012 ImageNet22 training data set. As the images from the DDSM data sets are 12-bit with varying pixel sizes (42, 43.5, and ), the images were converted into 8-bit images (range 0 to 255) using a linear conversion, and the images were downscaled by a factor of 2 using a average filter so that the image resolution is similar to the synthetic images.
2.4. Breast Mass Detection Algorithm
We used a Python implementation of faster R-CNN23 for our deep learning network,24 using the Tensorflow backend. The network was initialized with pretrained weights from the ILSVRC2012 ImageNet22 training data set and uses the Resnet-101 architecture for the detection of breast masses. Data augmentation was performed by adding horizontally and vertically flipped training images to the training data set. A stochastic gradient descent optimizer with momentum with a learning rate of 0.001 was used to minimize the loss function.
For each batch in our training, one mammographic image was presented into our network, as it was shown in the literature that this improved training time.17 Both the region proposal network and the region classifier were trained using 256 regions that are randomly sampled from the total number of extracted regions as proposed by the network. The intersection over union (IoU) threshold for foreground objects in the region proposal network was set to 0.7 during nonmaximum suppression (NMS). During inference using the network, 300 regions are extracted per image, and 0.1 is used for the IoU threshold for NMS. Additional details of the faster-RCNN can be found in the literature.23,24
The networks were trained for 50,000 iterations, and detection results on the validation data set for every 10,000 iterations were measured. Training took on a Nvidia Tesla V100 GPU, taking around 3 s per iteration. The stopping criteria for the network training were determined using the performance on the validation data set based on highest sensitivity at two false positives (FPs) per image. The weights at the iteration that provided the highest sensitivity at two FPs per image (FPs/image) on the validation set were saved as the trained network, which was then applied to the test set.
2.5. Evaluation
We compared the detection performance of the faster R-CNN when the network was trained using only the DDSM training images, and when the network was augmented with 250, 500, 1000, and 2000 synthetic mammograms. Free-response receiver operating characteristic (FROC) analysis was performed to compare test performance with and without the synthetic mammograms. To characterize overfitting, we also plotted the resubstitution FROC curves, which were obtained by feeding the training images into the trained network. We statistically evaluated the network performance by studying the sensitivity at two FPs per image. The 95% confidence intervals at this FP rate were estimated using a normal approximation to the binomial distribution. JAFROC25 analysis was used to determine the statistical significance between the FROC curves, and McNemar’s test26 was used to determine statistical significance of the sensitivity at the two FPs/image operating point, with a -value less than 0.0042 (0.05/12) considered significant after Bonferoni correction for multiple hypotheses, comparing the addition of the synthetic images and the subsets of the DDSM data set. The operating point of two FPs/image was chosen based on our experience, that this may be a tolerable number of FPs/image for radiologists.
3. Results
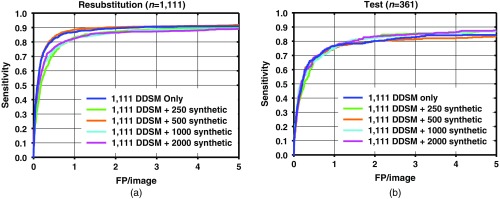
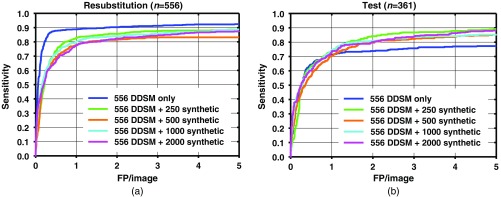
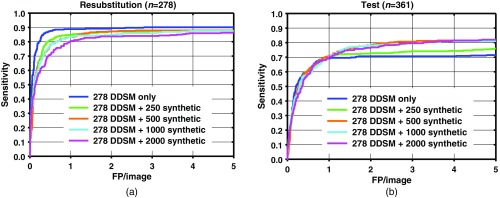
The resubstitution for the DDSM training images, and test FROC curves for the detection performance on the training and test data sets for different number of additional synthetic images are shown in Figs. 6–8. As the number of synthetic images used for training increases, the resubstitution performance on the DDSM training set slightly decreases in general, which demonstrates that overfitting is reduced, which may be leading to the higher test performance.
Fig. 6.
FROC curves for mass detection from the network trained with 1111 DDSM images only, and DDSM images plus 250, 500, 1000, and 2000 synthetic mammogram images on (a) resubstitution using DDSM training set and (b) the DDSM test set.
Fig. 7.
FROC curves for mass detection from the network trained with half (556) of the DDSM images only, and DDSM images plus 250, 500, 1000, and 2000 synthetic mammogram images on (a) resubstitution using DDSM training set and (b) the DDSM test set.
Fig. 8.
FROC curves for mass detection from the network trained with quarter (278) of the DDSM images only, and DDSM images plus 250, 500, 1000, and 2000 synthetic mammogram images on (a) resubstitution using DDSM training set and (b) the DDSM test set.
Table 1 shows the test sensitivity at two FPs/image for training with and without the synthetic images. A statistically significant improvement in the sensitivity was achieved when 1000 and 2000 synthetic images were added, compared to not using synthetic images. When 250 and 500 synthetic images were added, only one condition (, full DDSM) did not achieve statistical significance. JAFROC analysis did not show a statistically significant difference between the FROC curves.
Table 1.
Sensitivity at two FPs/image on the DDSM test set with and without synthetic training images.
| Number of additional synthetic training images, | Sensitivity on DDSM test images () | ||
|---|---|---|---|
| Full DDSM () training | Half DDSM () training | Quarter DDSM () training | |
| 0 | |||
| 250 | * | * | * |
| 500 | * | * | |
| 1000 | * | * | * |
| 2000 | * | * | * |
Improvement with adding synthetic training images is statistically significant compared to no synthetic images for training () ().
A comparison among test results from Figs. 6–8 indicates that when a smaller number of DDSM images are present in the training, there is a larger change in the performance from the addition of synthetic images. When the full DDSM data set was used as part of the training, the change in performance is small, compared to when half or quarter of the DDSM data set is used.
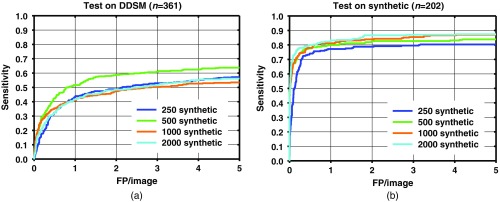
Figure 9 shows the FROC curves when only the synthetic images, without the DDSM images, were used to train the faster R-CNN. As the number of synthetic images in the training set increased, the performance on the synthetic image test set increased, as expected. On the other hand, the performance on the DDSM test set increased when using 500 synthetic images compared to 250, but the performance decreased as more synthetic trainers were added. Table 2 shows the test sensitivity on DDSM test set at two FPs/image for training with only the synthetic images.
Fig. 9.
FROC curves for mass detection on (a) DDSM test set and (b) synthetic mammogram test set from the network trained with 250, 500, 1000, and 2000 synthetic mammogram images using networks with the highest sensitivity at two FPs/image on the validation sets.
Table 2.
Sensitivity at two FPs/image on the DDSM test set training with only synthetic images.
| Number of synthetic images | Sensitivity on DDSM test images |
|---|---|
| 250 | |
| 500 | |
| 1000 | |
| 2000 |
4. Discussion
The results show that the performances of faster R-CNN algorithms increase when synthetic images are added to the training set. The sensitivity between with and without synthetic images is generally similar at low number of FPs/image. The increase in performance generally starts to show past one FPs/image. The increase in sensitivity at two FPs/image is when using the full DDSM data set, while it is larger when using a smaller number of real images as shown in Figs. 7 and 8. It is possible that for the full DDSM data set, there are sufficient training data such that adding additional synthetic data does not change the performance much. On the other hand, when we use half and quarter of the DDSM data set for training, the increase in sensitivity is more prominent. This indicates that the synthetic images are more useful for improving performance when the number of real samples for training is low. However, we also note that the performance does not continuously increase as the number of synthetic training cases increases. This may be due to the difference in the distribution of the image properties between the real and synthetic images. We are further studying the effects of training machine learning algorithms with differences in the distributions to characterize this peak in performance that we have observed in this study.
While the results are not shown in this study, as it was not a focus of this paper, we did not see a change in performance when a transfer learning approach (where the algorithms initialized with ImageNet weights, then were trained on the synthetic images first, then fine-tuned with the real images) was applied. On the other hand, we observe that the synthetic images do hold some useful information regarding detecting masses in the real images, as the algorithms trained only on the synthetic images were able to detect some masses in the real images, albeit with low performance.
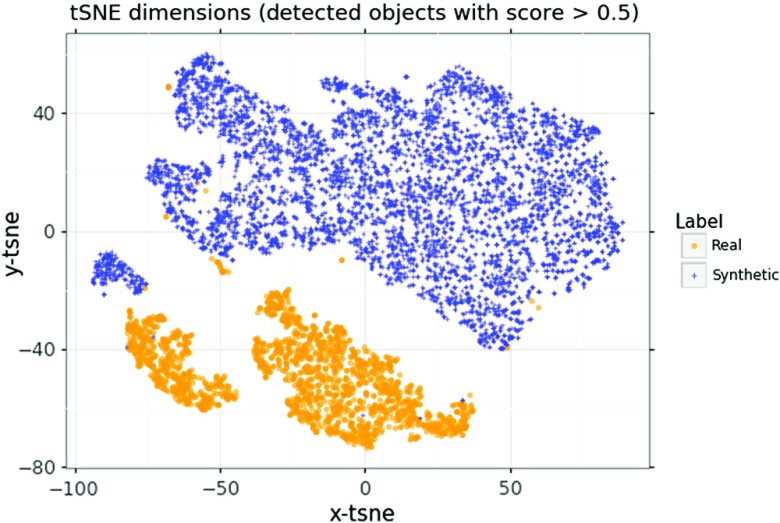
In order to see if there is a latent difference in the distributions between the real and synthetic images, a -distributed stochastic neighbor embedding27 (tSNE) analysis on the training data set with all of the DDSM images, and 1000 synthetic images, was performed, using two components for 1000 iterations. The tSNE was performed on the region proposal outputs from the faster R-CNN, and only on objects that had a score above 0.5, as shown in Fig. 10.
Fig. 10.
A tSNE representation of the region proposals from real and synthetic images, using the features from the network trained with full DDSM data set and 2000 synthetic images.
We observe from the tSNE representation that there is a separation between the mass candidates from the real and synthetic images. This indicates that there are differences in the mass candidates from the two image types, and that a CNN would likely be able to distinguish between the real and synthetic images. Using synthetic images that better represent the real images may have increased the detection performance more than the current synthetic images used in this work. However, this work also shows that while the synthetic images do not completely match the real images, as would be expected because our in silico model does not completely match clinical reality, an improvement in performance was observed, and the improvement was found to depend on the number of real and synthetic images.
There are limitations to the study. The procedure used for generating the synthetic images did not simulate the physics of the CBIS-DDSM data set acquisition. The synthetic images were modeled based on the Siemens FFDM, while the CBIS-DDSM data set is digitized screen film. Matching the two acquisitions may improve the results. In addition, only four distinct breast types were simulated. There is a lack of diversity within each type, including the size and shape of the breast. Generation of additional breast sizes, densities, and characteristics may result in a more diverse synthetic data set and may improve the training results. Due to computational and data set size limitations, only one network was trained for each combination of real/synthetic images shown in Table 1. Training with different sets but the same number of real/synthetic images may provide useful information about training variability.
Despite these limitations, our results showed that using biology-inspired object models and physics-based image generation is a viable way for data augmentation for deep learning in medical images. We were able to generate realistic synthetic images with similar gray level and CNR characteristics compared to real images. These synthetic images were found to improve the performance of the faster RCNN for detection of masses in breast mammography. Increasing the number of synthetic images in training showed diminishing performance improvement compared to without using the synthetic images. This may be due to the network learning the characteristics of the masses of the synthetic cases as the number of these cases increases at the expense of learning from the smaller percentage of real cases. The resubstitution performance slightly decreased, while the test performance increased, showing that the overfitting of the network decreased, and the generalizability of the network increased. In general, the networks trained with synthetic images achieved higher maximum sensitivity compared to not using synthetic images, which may indicate that the synthetic images improve the region proposal portions of the network.
Future directions include identifying the categories of missed masses and increasing the number of synthetic masses in those categories, better aligning the simulation methods with the physics of acquisition of the real data set and increasing the diversity of both the normal breast anatomy and masses in the synthetic data set. We would also like to compare the reduction of overfitting using data augmentation via synthetic images against different regularization methods to see how they behave together.
5. Conclusion
Using the synthetic mammograms to enlarge the training data set shows promise in improving the performance of deep learning systems mass detection on mammograms. Our study showed that augmenting the training data with synthetic mammograms increased the performance of deep learning systems for mass detection on mammograms.
Acknowledgments
This work was supported by CDRH Critical Path funding and in part by an appointment to the Research Participation Program at the Center for Devices and Radiological Health administered by the Oak Ridge Institute for Science and Education through an interagency agreement between the U.S. Department of Energy and the U.S. Food and Drug Administration. We would like to acknowledge Thomas Petrick for his help in running the experiments.
Biographies
Kenny H. Cha is a staff fellow in the Division of Imaging, Diagnostics, and Software Reliability within the U.S. Food and Drug Administration, Center for Devices and Radiological Health. He received his BSE, MSE, and PhD degrees in biomedical engineering from the University of Michigan. His research interests include artificial intelligence, machine learning, and deep learning for medical data, computer-aided diagnosis, and radiomics.
Nicholas Petrick is a deputy director for the Division of Imaging, Diagnostics, and Software Reliability within the U.S. Food and Drug Administration, Center for Devices and Radiological Health and is an FDA senior biomedical research scientist. He received his BS degree from Rochester Institute of Technology in electrical engineering and his MS and PhD degrees from the University of Michigan in electrical engineering systems. His research interests include imaging biomarkers, computer-aided diagnosis, image processing, and medical imaging physics.
Aria Pezeshk received his BS degree from Michigan Technological University, Houghton, Michigan, USA, and his PhD from Pennsylvania State University, University Park, Pennsylvania, USA, both in electrical engineering. From 2011 to 2012, he was an R&D engineer with the Portland Technology Development group at Intel. He is currently a research scientist with the Division of Imaging, Diagnostics, and Software Reliability within the U.S. Food and Drug Administration. His research interests include deep learning, machine learning, computer vision, and medical imaging.
Christian G. Graff is a visiting scientist in the Division of Imaging, Diagnostics, and Software Reliability at the U.S. Food and Drug Administration. His research is currently focused on developing methods for assessing the performance of radiological imaging devices and related machine learning algorithms. He received his BASc degree in electrical engineering from the University of British Columbia and his PhD in applied mathematics from the University of Arizona.
Diksha Sharma is a staff fellow in the Division of Imaging, Diagnostics, and Software Reliability at the U.S. Food and Drug Administration. She received her BE in electronics and communications engineering from the Rajasthan Technical University, India, and her MS degree in computer engineering from George Washington University, Washington, DC, USA. Her research interests include modeling x-ray imaging detectors using Monte Carlo methods and high-performance computing applications.
Andreu Badal is a staff fellow in the Division of Imaging, Diagnostics, and Software Reliability at the U.S. Food and Drug Administration. He received his BSc degree in physics from the University of Barcelona and his PhD at the Universitat Politecnica de Catalunya in Barcelona, Spain. He is an expert in the use of Monte Carlo radiation transport simulations methods in medical applications and was the developer of the first GPU-accelerated Monte Carlo code for the simulation of x-ray imaging devices.
Berkman Sahiner received his BS and MS degrees in electrical engineering from Middle East Technical University and his PhD in electrical engineering from the University of Michigan. He has been involved in medical imaging for over 25 years, first as a faculty member at the University of Michigan Radiology Department for over 15 years, and since 2009, as a senior biomedical research scientist with the Division of Imaging, Diagnostics and Software Reliability at the U.S. Food and Drug Administration. His research interests include computer-aided diagnosis, machine learning, image analysis, breast imaging, image perception, and performance assessment methodologies.
Disclosures
The authors declare no conflicts of interest.
References
- 1.Fukunaga K., Hayes R. R., “Effects of sample size in classifier design,” IEEE Trans. Pattern Anal. Mach. Intell. 11(8), 873–885 (1989). 10.1109/34.31448 [DOI] [Google Scholar]
- 2.Wagner R. F., et al. , “Finite-sample effects and resampling plans: applications to linear classifiers in computer-aided diagnosis,” Proc. SPIE 3034, 467–478 (1997). 10.1117/12.274133 [DOI] [Google Scholar]
- 3.Chan H. P., et al. , “Classifier design for computer-aided diagnosis: effects of finite sample size on the mean performance of classical and neural network classifiers,” Med. Phys. 26(12), 2654–2668 (1999). 10.1118/1.598805 [DOI] [PubMed] [Google Scholar]
- 4.Sahiner B., et al. , “Feature selection and classifier performance in computer-aided diagnosis: the effect of finite sample size,” Med. Phys. 27(7), 1509–1522 (2000). 10.1118/1.599017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Kupinski M. A., et al. , “Ideal observer approximation using Bayesian classification neural networks,” IEEE Trans. Med. Imaging 20(9), 886–899 (2001). 10.1109/42.952727 [DOI] [PubMed] [Google Scholar]
- 6.Azizi S., et al. , “Transfer learning from RF to B-mode temporal enhanced ultrasound features for prostate cancer detection,” Int. J. Comput. Assist. Radiol. Surg. 12(7), 1111–1121 (2017). 10.1007/s11548-017-1573-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Cho J., et al. , “How much data is needed to train a medical image deep learning system to achieve necessary high accuracy?,” arXiv:1511.06348 (2015).
- 8.Sun C., et al. , “Revisiting unreasonable effectiveness of data in deep learning era,” in IEEE Int. Conf. Comput. Vision (ICCV), pp. 843–852 (2017). [Google Scholar]
- 9.Gulshan V., et al. , “Development and validation of a deep learning algorithm for detection of diabetic retinopathy in retinal fundus photographs,” J. Am. Med. Assoc. 316(22), 2402–2410 (2016). 10.1001/jama.2016.17216 [DOI] [PubMed] [Google Scholar]
- 10.Mohamed A. A., et al. , “A deep learning method for classifying mammographic breast density categories,” Med. Phys. 45(1), 314–321 (2018). 10.1002/mp.12683 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Pezeshk A., et al. , “Seamless insertion of pulmonary nodules in chest CT images,” IEEE Trans. Biomed. Eng. 62(12), 2812–2827 (2015). 10.1109/TBME.2015.2445054 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Pezeshk A., et al. , “Seamless lesion insertion for data augmentation in CAD training,” IEEE Trans. Med. Imaging 36(4), 1005–1015 (2017). 10.1109/TMI.2016.2640180 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Goodfellow I., et al. , “Generative adversarial nets,” in Adv. Neural Inf. Process. Syst., pp. 2672–2680 (2014). [Google Scholar]
- 14.Antoniou A., Storkey A., Edwards H., “Data augmentation generative adversarial networks,” arXiv:1711.04340 (2017).
- 15.Frid-Adar M., et al. , “GAN-based synthetic medical image augmentation for increased CNN performance in liver lesion classification,” Neurocomputing 321, 321–331 (2018). 10.1016/j.neucom.2018.09.013 [DOI] [Google Scholar]
- 16.Tang Y., et al. , “CT-realistic data augmentation using generative adversarial network for robust lymph node segmentation,” Proc. SPIE 10950, 109503V (2019). 10.1117/12.2512004 [DOI] [Google Scholar]
- 17.Badano A., et al. , “Evaluation of digital breast tomosynthesis as replacement of full-field digital mammography using an in silico imaging trial,” JAMA Network Open 1(7), e185474 (2018). 10.1001/jamanetworkopen.2018.5474 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Lee R. S., et al. , “A curated mammography data set for use in computer-aided detection and diagnosis research,” Sci. Data 4, 170177 (2017). 10.1038/sdata.2017.177 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Heath M., et al. , “The Digital Database for Screening Mammography,” in Digital Mammography; IWDM 2000, Yaffe M. J., Ed., pp. 457–460, Medical Physics Publishing, Toronto, Canada: (2001). [Google Scholar]
- 20.Welch H. G., et al. , “Breast-cancer tumor size, overdiagnosis, and mammography screening effectiveness,” N Engl. J. Med. 375(15), 1438–1447 (2016). 10.1056/NEJMoa1600249 [DOI] [PubMed] [Google Scholar]
- 21.de Sisternes L., et al. , “A computational model to generate simulated three-dimensional breast masses,” Med. Phys. 42(2), 1098–1118 (2015). 10.1118/1.4905232 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Deng J., et al. , “ImageNet: a large-scale hierarchical image database,” in Proc. IEEE Conf. Comput. Vision and Pattern Recognit., pp. 248–255 (2009). [Google Scholar]
- 23.Ren S., et al. , “Faster r-CNN: towards real-time object detection with region proposal networks,” in Adv. Neural Inf. Process. Syst., pp. 91–99 (2015). [DOI] [PubMed] [Google Scholar]
- 24.Chen X., Gupta A., “An implementation of faster RCNN with study for region sampling,” arXiv:1702.02138 (2017).
- 25.Chakraborty D. P., “Recent advances in observer performance methodology: jackknife free-response ROC (JAFROC),” Radiat. Protect. Dosim. 114(1–3), 26–31 (2005). 10.1093/rpd/nch512 [DOI] [PubMed] [Google Scholar]
- 26.McNemar Q., “Note on the sampling error of the difference between correlated proportions or percentages,” Psychometrika 12(2), 153–157 (1947). 10.1007/BF02295996 [DOI] [PubMed] [Google Scholar]
- 27.van der Maaten L., Hinton G., “Visualizing data using t-SNE,” J. Mach. Learn. Res. 9(November), 2579–2605 (2008). [Google Scholar]