The Relationship Between Lifetime Out-of-pocket Medical Expenditures, Dementia, and Socioeconomic Status in the U.S.

Abstract

Dementia is one of the most expensive medical conditions. The costs are borne by families, by private insurance and by society via public programs such as Medicaid in the U.S.. There is extensive research on the relationship between dementia and annual medical spending. This paper, instead, estimates cumulative lifetime medical expenditures that can be attributed to the onset of dementia using a nationally representative longitudinal survey from the U.S., the Health and Retirement Study. The lifetime expenditures are estimated by summing any out-of-pocket medical spending reported in the panel from age 65 to death. Censored cases are imputed using a non-parametric matching algorithm called splicing. For example, survivors to the most recent wave are matched to similar individuals from older cohorts who are observed at the relevant ages all the way through death. We find that those who live with dementia for at least half a year pay, on average, $38,540 more out of pocket from age 65 to death when controlling for length of life, demographics, lifetime earnings and comorbidities. The costs of dementia are almost exclusively due to spending on nursing homes. Spending on drugs, doctor visits or hospitals, is not significantly related to dementia. The lifetime costs of dementia are significantly larger for white and rich individuals, perhaps because they use higher quality nursing homes and because they have more financial resources to spend down before becoming eligible for Medicaid support.

1. Introduction

Dementia is the loss of cognitive functioning such as thinking, remembering and reasoning, and of the ability to perform the activities of daily life. Alzheimer’s disease and vascular dementias (e.g. due to a stroke) are the most common forms of dementia. Dementia affects a large number of older adults. In 2010, about 4.2 million U.S. adults (or about 14.7% of the 70+ years old) and more than 36 million around the world lived with dementia (Hurd, et al., 2013; Prince et al., 2013). Because age is a strong risk factor, and life expectancies are increasing, the prevalence of dementia may continue to grow.

Dementia is also a very costly condition, primarily because affected individuals need nursing care. The care can be provided in formal settings, such as in nursing homes, or it can be informally supplied by family members, friends or others in the community. Parts of these costs are paid by families, private insurance or by public programs, such as Medicaid in the U.S. There is extensive research on the relationship between dementia and annual medical expenditures. The total economic impact of dementia was estimated at $200 billion per year in the United States (Hurd et al., 2013) and $600 billion worldwide, or about 1% of global GDP (Wimo et al., 2013), making dementia the most expensive medical condition. The distribution of the costs was also found uneven across regions. Even though only about 40% of people with dementia live in high income countries, these countries are responsible for almost 90% of the total costs (Wimo et al., 2017). Less attention has been paid in the literature to whether and to what extent the costs of dementia vary by socio-economic status (SES) within countries.

From the perspective of society, these overall annual costs are important to know, but from the perspective of a family or individual, lifetime (as opposed to annual) costs are more relevant, because individuals need to be prepared to cover all of these cumulative costs. Similarly, insurance companies that supply long-term care (LTC) insurance are also interested in the lifetime risk of dementia, which is an important factor in optimally pricing their financial products.

In Hudomiet, et al. (2018a), we estimated the lifetime risk of dementia in the U.S. using data from the Health and Retirement Study (HRS). We found that 41% of Americans who died after the age of 65 lived with dementia for at least half a year. We build on that work to estimate how the lifetime risk of dementia affects lifetime out-of-pocket (OOP) medical expenditures from age 65 to death, holding other variables constant; and we estimate how these costs vary by SES. To simplify language, we will sometimes refer to lifetime OOP medical expenditures as “lifetime costs.”

We use the HRS, which has several unique features for studying dementia-related outcomes: 1) It is a large, nationally representative, longitudinal dataset with a wide range of information about health status, cognitive abilities, SES, demographics, and other variables. 2) It has good coverage of the population with dementia, because it follows individuals into nursing homes; and proxy interviews are available for cognitively impaired sample members. 3) It collects EXIT interviews after the death of sample members, including questions about end-of-life medical expenditures that are known to be disproportionally higher than spending at younger ages. And 4) a subset of HRS members were administered a clinical assessment for dementia within the Aging, Demographics and Memory Study (ADAMS), which we use to calibrate the cognitive variables that are available in the entire HRS.

To estimate lifetime expenditures we add up any OOP medical expenditures of individuals between age 65 and death. However, the HRS is still not long enough to fully observe all individuals’ complete lifetimes. We thus chose a baseline cohort aged 74-79 in the 1998 wave, followed them from 1998 to 2014, and accumulated all their reported OOP health care spending. Their medical spending between age 65 and the baseline age of 74-79 is therefore missing, which is a left-censoring problem. Moreover, about a fifth of the final sample survive to the 2014 wave (or leave the panel), which is a right-censoring problem. We impute spending by these censored cases using a nonparametric matching algorithm called “splicing” that is based on a methodology developed in our earlier research (Hurd, et al., 2017). Right-censored individuals are matched to people with similar characteristics in older HRS cohorts, who are observed at the relevant ages all the way to death. For example, if a person was 85 years old (and alive) in 2014, we matched him or her to someone who was 85 years old in 1998, and who was similar in other dimensions, such as gender, lifetime earnings, marital status, dementia probabilities, OOP medical expenditures and nursing home residence. Then we borrowed the values from this donor person to fill up the missing values of the recipient. Left censoring was imputed with a similar methodology, but in this case we used younger HRS cohorts as donors. By choosing late enough baseline ages of 74-79, most of our sample are observed to die within the HRS, and do not need right splicing. To preserve the correlations among explanatory variables our method borrows all donor variables together, including left- and right-hand side variables of regressions, and therefore the relationships among the regression variables are not (necessarily) affected by occasional mismatches between donors and recipients. This method has the advantage over parametric methods that it captures better the extreme upper tail of spending. We carried out extensive robustness checks of this methodology and found it very reliable.

We found that the mean lifetime OOP spending from age 65 to death is $61 thousand in 2014 dollars, assuming a 0% discount rate. Those who live with dementia for at least six months pay, on average, $38.5 thousand more out of pocket (about 60% of the mean OOP) when controlling for length of life, demographics, lifetime earnings and comorbidities. When we looked at medical expenditure subcategories, we found that spending on nursing homes is statistically significantly higher for those with dementia, while none of the other spending categories were related to dementia after the other control variables were included in the regressions. These results were expected, and they may suggest that the control variables adequately adjusted for the differences between those who live with dementia and the rest of the population. We also found that the cost of dementia is significantly lower for blacks, Hispanics, and low SES individuals (measured by education or lifetime earnings), while we found weaker and not statistically significant differences by gender. Even though high SES individuals living with dementia spend significantly more on nursing homes than low SES individuals, we found little difference in lifetime nursing home usage between these groups. This suggests that Medicaid, which only provides financial support for nursing home care for poor families, significantly reduces inequalities in the population that lives with dementia in the U.S.

2. Background on the costs of dementia

The loss of cognitive functioning and of the ability to perform the activities of daily life require that those suffering from dementia be provided with help. Dementia is expensive primarily because of the high costs of providing that care, and, indeed dementia has been found to be among the costliest medical conditions in many countries. (Allegri et al., 2008; Connolly et al., 2014; Hurd et al., 2013; Leicht et al., 2011; Lowin, et al. 2001; Vossius, et al., 2014; Wang et al., 2010; Wimo, et al., 2013; Wimo, et al., 2017; Zhaorui, 2013). Help can be provided either via formal and informal care arrangements. Informal care is typically provided at home by family members, such as spouses or children. Formal care can be provided in institutional settings (i.e. in nursing homes), or in the community. The cost of this formal care is borne by individuals and their families, unless they bought private insurance coverage or qualify for public assistance. Countries show a large variation in the type and amount of public support they provide for long-term care (OECD, 2011). In some countries, such as Norway, nursing home stays are covered by the social care system. Other countries, such as Germany, set up a dedicated, but still mandatory, insurance system for LTC. Yet others, like the U.S. and the U.K. rely on means-tested public programs to cover LTC. In the U.S., Medicaid only covers the costs of nursing home stays of eligible households, which means that the households have low wealth and income net of health care expenses. The wealth and income thresholds for eligibility vary from state to state.

Independently of the particular funding patterns, however, the overall annual costs of dementia are very high in most developed countries.

From the perspective of families or individuals, the cumulative lifetime costs of dementia would be the most relevant for financial planning purposes. Due to data limitations, most of the literature has used cross-sectional methods to estimate the costs of dementia and ignored the lifetime aspect, as pointed out by Deb, et al. (2017).

A few studies have looked at dynamic effects of dementia. Skira (2015) found that providing informal care for older parents has a strong adverse effect on future employability and wages of women. Yang et al. (2012) used administrative data to estimate the lifetime cost of dementia to Medicare and Medicaid. Jutkowitz et al. (2017) calibrated a microsimulation model to estimate the lifetime costs of dementia, and Kelley et al. (2015) estimated the relationship between dementia, and costs in the last five years of people’s lives. Our approach has much in common with the study by Kelley et al. (2015), but we consider a longer time window (from age 65 until death) and we improve on the estimation of the lifetime risk of dementia.

3. Methods

3.1. The Health and Retirement Study

The HRS is a nationally representative biennial longitudinal survey of the 51+ year-old American population. It collects a wide range of information about participants, including demographics, labor force status, income, wealth and health (Sonnega et al., 2014). The HRS is unusually detailed about health and cognitive ability (Crimmins et al., 2011) compared with other population representative surveys. It started in 1992, and new cohorts of 51-56 year-old individuals are added every six years. Several unique features of the HRS help in the study of dementia-related outcomes with high accuracy. First, individuals are followed into nursing homes, which is important, since many cognitively impaired individuals live in nursing homes (Magaziner et al., 2000; Yaffe et al., 2002). In contrast with the HRS, most household surveys are community based. Second, if a study member is unable or unwilling to participate in a survey wave, HRS surveys a proxy respondent (typically a spouse or a child). Around half of the demented sample members answer through proxies (Hurd et al. 2013). Third, the HRS collects EXIT interviews from proxy informants to learn about end-of-life events of deceased individuals. This is important, because prior research found that medical expenditures are exceptionally high in the last year of life (French et al., 2017; Kelley et al., 2013). Fourth, because the HRS core lacks a direct measure of dementia status, 856 HRS respondents of age 70+ underwent a detailed in-home clinical assessment for dementia as part of ADAMS in 2001-2003. The duration of the assessment was 3-4 hours, and it concluded in a final diagnosis of 1) demented; 2) cognitively impaired but not demented; or 3) normal cognitive function (Heeringa et al., 2007). The ADAMS subsample can be used to calibrate the cognitive measures that are available in the entire HRS (Hurd et al., 2013).

We use nine waves of the HRS from 1998 to 2014.¹ Our baseline sample includes 74-79-year-old individuals from the 1998 HRS (N = 2,853). Even though the HRS started in 1992, we ignored the early waves due to differences in the way medical expenditures were reported. About 75% of the baseline sample (N = 2,145) died by the latest 2014 HRS wave and provide a valid EXIT interview. The rest of the sample are right-censored and need imputations (see below). The baseline sample also misses medical spending between age 65 and the baseline age, which is a left-censoring problem and needs imputation as well. Some individuals died between the age of 65 and the baseline age, and therefore are missing from our baseline sample, which is an early mortality problem. The next section explains how we imputed these cases. The sample used in these models include all 65+ year old participants from the 1998-2014 waves of the HRS (N = 21,455).

In Hudomiet et al. (2018a) we estimated the lifetime risk of dementia. In that paper we took all HRS participants who died after age 65 between the 1998 and the 2014 survey waves (N = 9,479). Then we used a longitudinal econometric model to estimate the probabilities of dementia six month prior to these individuals’ deaths. The model made use of the ADAMS subsample with clinical dementia diagnosis as well as longitudinal measures of cognitive ability, functional limitations, and health, from the HRS. Because individuals cannot recover from dementia, the probability of dementia six months prior to death is equivalent to the probability of living with dementia for at least half a year. The average was 41%, and we found large variation by gender, race, education, and lifetime earnings. High SES individuals were significantly less likely to die with dementia, even though these individuals lived to greater ages where the risk of dementia was higher.

In the current paper we use the estimated dementia probabilities six months before death reported in Hudomiet et al. (2018a) to study how the lifetime risk of dementia predicts lifetime medical expenditures. Hudomiet et al. (2018a) also produced wave-by-wave dementia probabilities for the entire 65+ year-old sample (including survivors), which are used in our splicing (imputation) models below.

We use a version of the HRS that has been produced by RAND as a service to the research community. These data files are available to the public on registration with HRS. The RAND HRS Data file is an easy to use longitudinal data set based on the most commonly used HRS variables. It was developed at RAND with funding from the National Institute on Aging and the Social Security Administration (SSA). We use the RAND HRS variables whenever available. We obtained the detailed components of the RAND Medical Expenditure Imputations from the RAND HRS Detailed Imputations File.² We use the following medical expenditure categories:

1. Drugs

2. Doctor and dental visits, and outpatient surgery

3. Nursing home stays

4. Hospital stays

5. Other medical spending

The HRS typically asks about medical spending since the previous HRS interview with two exceptions: 1) New sample members are asked about spending in the last two years; and 2) Drug spending is queried with reference to the last month. Any missing medical expenditure values were imputed by RAND as discussed in RAND HRS (2016).

In the 1998 and 2000 waves, those who reported to have both nursing home and hospital spending (N = 642), were only asked about the sum of their values. The more detailed spending categories are available since the 2002 wave. Because nursing home spending is strongly related to dementia, we kept the disaggregated categories and imputed the fraction of nursing home spending within the reported sum in the 1998-2000 waves. We used a regression-based imputation on the complete 2002-2014 observations with positive reported spending on both nursing homes and hospitals. We multiplied the predicted values of this regression with the HRS reported total spending in 1998 and 2000 to approximate spending on nursing homes; and the rest was allocated to hospital spending. The output of the regression model is in Appendix Table B1. The total spending on nursing homes and hospitals was found to be the strongest predictor, and the model had a reasonably high R-squared value of 0.24.

To approximate drug spending between survey waves, we multiplied drug spending in the last months (reported in the HRS) by the number of months between the two HRS surveys.

Because we wanted to measure medical expenditures after age 65, reports in the first HRS interview after age 65 were prorated. For example, if the last HRS interview was 27 months ago, but the individual turned 65 only 8 months ago, we multiplied the reported medical spending by 8/27.

We used two measures of SES. The first was individuals’ highest level of education (less than high school, high school, some college, college or more). Second, we estimated individuals’ primary insurance amount (PIA). The PIA is the Social Security benefit a person would receive if he elected to begin receiving the benefits at the normal retirement age. In the U.S. the PIA is a rank-ordered measure of lifetime Social Security earnings, and therefore we refer to it as a lifetime earnings index. We use a household-level PIA measure, defined as the larger of the husband’s or the wife’s PIA. Hudomiet et al. (2018a) discuss the details of deriving this measure using HRS data.

3.2. Estimating lifetime out-of-pocket medical expenditures

We adjusted OOP expenditures to 2014 dollars using the CPI, and added up all spending from 1998 to the latest available wave, 2014, or earlier if the person attrited from the sample. Our preferred estimate does not discount expenditures, effectively assuming a real interest rate of zero, but we also provide estimates using alternative discount rates from 1% to 3%, in which case all spending is discounted back to age 65. We prefer a discount rate of zero because the discounted value is the amount of real wealth necessary at age 65 to finance the future flow of spending when the real opportunity cost of funds is zero. The real interest rate is now close to zero (Laubach and Williams, 2015). We do, however, implicitly discount by mortality because we add up costs until an individual’s death.

We correct for left and right censoring and early mortality. We used a non-parametric matching algorithm, called splicing (Hurd et al., 2017). Figure 1 and Table A3 in the appendix provide an overview The end of individuals’ lives is not observed in the HRS for those who survive to the latest wave as well as those who die but do not provide EXIT interviews. For all these right-censored cases we matched pairs from the 1998-2004 HRS waves who were most similar to the recipients in their latest available waves (2014 or earlier) in the following dimensions: age, gender, education, lifetime earnings (PIA), nursing home residence, marital status, wave-by-wave dementia probabilities (estimated by Hudomiet et al, 2018a³), ever had a stroke, and total OOP medical expenditures. Including too few variables in the splicing model may lead to biases; but including too many may make it impossible to find valid pairs for everyone. We selected these variables because prior research indicated they are strong predictors of both medical expenditures and dementia. In certain dimensions we required perfect matches, in other dimensions we minimized a distance between the pairs (Appendix A).

Figure 1. Overview of the splicing methodology to define a sample of lifetimes from age 65 to death in the HRS.

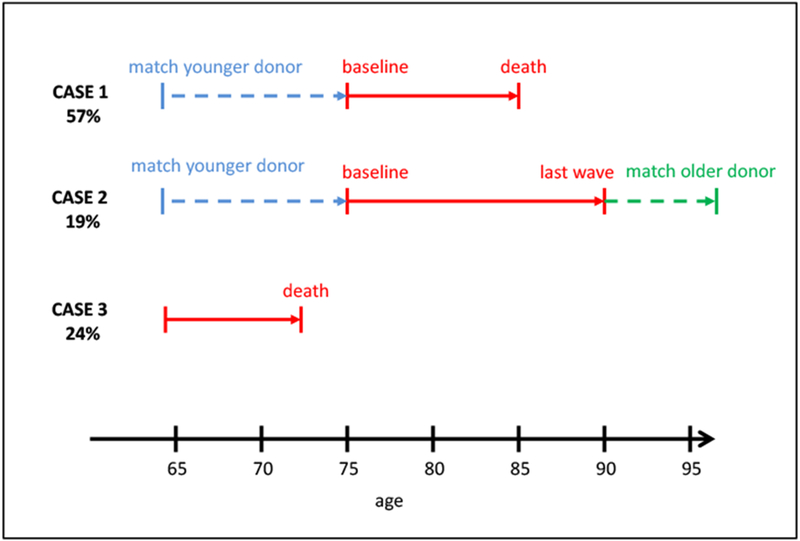
Notes: Case 1 represents cases who are observed in the HRS from the baseline age of 74-79 until death. Case 2 represents cases that are not observed to die in the HRS sample and people with missing Exit interviews. Case 3 represents the “Early Mortality” sample, who did not survive to be eligible for the baseline sample.

Spending between age 65 and the baseline age of 74-79 is missing. We used an analogue procedure to right censoring. We chose pairs from the 1998-2004 HRS who were 65 years old, survived to the baseline age of the baseline sample, and were similar in the same dimensions as for right splicing.

Appendix A provides further details of the splicing procedure, and it discusses some of the sensitivity analyses and quality checks we performed. Overall, we found that the dementia probabilities are very similar between donors and recipients, but medical expenditures are somewhat less similar between donors and recipients: the correlations are only about 0.6-0.7. The reason was that OOP has a more dispersed and less persistent distribution. Nevertheless, the cross-wave correlations were similar across donor-donor, donor-recipient and recipient-recipient waves, and the donor-recipient differences were fairly small in the bottom 90% of the distribution.

We also experimented with alternative versions of this splicing methodology: using extended or reduced sets of variables in the splicing model and using different baseline ages. We found that all of the main results of the paper were robust to these changes, including the distributions of lifetime medical expenditures and the regression coefficients.

The next step was to deal with mortality prior to the baseline age. A sample of those who died after age 65, but before becoming eligible for our baseline sample (i.e., before turning 74-79 years old), needed to be added to our baseline sample. For each baseline age we used the HRS to estimate the number of people who would be dead by that age. For example, we first estimated the number of people who would be dead by age 74; then we did the same for baseline age 75, and so on. Then we randomly drew the appropriate number of individuals (without replacement) from the 2004-2010 HRS sample (Appendix A).

Appendix Table A3 shows the survival and non-response patterns in our final sample. Only about 19% of the sample needed right splicing, the rest was observed until death. Table A4 in the appendix shows how much of the total lifetime OOP spending comes from the baseline, right spliced, left spliced, and early mortality samples. The majority of spending comes from the baseline sample.

In addition to lifetime OOP medical spending, we created three additional lifetime measures: Years alive since age 65, years single after age 65, and the number of nights spent in nursing homes using the same donor pairs as above. We assumed that changes in marital status (typically from married to widowed) happened at the midpoints between the neighboring HRS interviews.

3.3. Estimating the contribution of dementia to lifetime OOP spending for health care services

To find the effect of dementia on lifetime expenditures we estimated OLS regressions using length of life, comorbidities, lifetime earnings, and demographic covariates as controls. These variables are important to include in the regressions because they simultaneously predict medical expenditures and dementia. It is, however, not evident whether this set is enough to adjust for all relevant differences between the demented and cognitively normal populations. To get a sense of the validity of our empirical models, we estimated regression models on different medical expenditure subcategories. We expected dementia to have a large effect on nursing home spending, and a smaller or no effect on any other medical spending categories, since dementia is not currently treatable.

It is worth noting that even though we use dementia probabilities as opposed to dementia status on the right-hand side of our regressions, the estimated coefficients are consistent in a statistical sense. Our methodology is essentially a two-sample two-stage least squares model. In stage 1 the HRS cognitive scores are used as instruments to predict dementia status in the ADAMS sample. In stage 2, the predicted values of stage 1 are used to predict expenditures in the entire HRS sample (Hurd et al., 2013). The main assumption of this model is that the HRS cognitive scores from stage 1 have no direct effects on medical expenditures, which is reasonable.

Under the assumptions of the model our approach produces consistent estimates, but the standard errors need to be adjusted to take into account the fact that dementia probabilities are estimated rather than known. We used a bootstrap procedure, analogous to Hudomiet et al. (2018a). This procedure, however, does not adjust for splicing, which was not feasible using the bootstrap. Ignoring splicing may introduce some bias in our standard error estimates, but our investigations on synthetic data suggested that the bias is negligible, probably because splicing borrowed all left- and right-hand side variables in the regressions from the donor sample simultaneously.

All of our estimates are weighted by the HRS survey weights from the last core HRS interviews.

4. Results

4.1. Descriptive statistics

Table 1 shows descriptive statistics of the variables in our final sample. As expected, a little over half of the sample is female; almost 90% are white; 9% are black; and about 5% have Hispanic origin (irrespectively of race). About two thirds have a high school education or less, and the average sample member lived an additional 18.6 years after age 65. This latter number is similar to SSA cohort life tables. For the 1930 birth cohort SSA predicted a 16.1 years life expectancy of 65-year old men and 19.2 years for women.⁴ Our corresponding numbers are slightly higher: 16.8 years for men and 20.1 years for women. As for comorbidities, the most frequent conditions between age 65 and death were arthritis (76%), high blood pressure (71%) and heart problems (63%). The prevalence of the other comorbidities was lower, but non-negligible, ranging from 27% (diabetes) to 40% (cancer). About 60% of the sample spend at least one night in a nursing home. However, many of these stays are short, and only 31% spend more than 100 nights in total between age 65 and death. The average unconditional number of nights in nursing homes is 280. Similar numbers were reported by Hurd et al. (2017).

Table 1.

Descriptive statistics of the main variables in the analytic sample

	mean	sd
Female	0.541	0.498
White	0.888	0.315
Black	0.091	0.287
Other race	0.021	0.143
Hispanic	0.052	0.222
Less than highschool	0.350	0.477
High school	0.326	0.469
Some college	0.178	0.383
College	0.146	0.353
Years alive	18.56	8.70
Ever single	0.664	0.472
Years single	8.60	9.26
Lifetime earnings index (primary insurance amount)	15,659	5,582
Dementia probability six months prior to death	0.431	0.407
Total lifetime OOP, not discounted	60,810	84,596
Total lifetime OOP, 1% discount rate	52,189	70,173
Total lifetime OOP, 2% discount rate	45,198	59,086
Total lifetime OOP, 3% discount rate	39,481	50,463
Lifetime drug spending, not discounted	23,595	33,841
Lifetime nursing home spending, not discounted	17,539	60,304
Lifetime doctor spending, not discounted	11,004	13,665
Lifetime hospital spending, not discounted	5,341	19,071
Lifetime other medical spending, not discounted	3,331	17,657
Spent at least one night in a nursing home	0.601	0.490
Spent at least 100 nights in nursing homes	0.304	0.460
Total nights spent in nursing homes	280.3	614.2
Ever arthritis	0.759	0.428
Ever hypertension	0.713	0.452
Ever heart condition	0.632	0.482
Ever cancer	0.396	0.489
Ever stroke	0.343	0.475
Ever lung disease	0.287	0.452
Ever psychiatric problems	0.275	0.446
Ever diabetes	0.268	0.443
Number of children (own and spouse)	3.17	2.34

Notes: N = 3,766. Expenditures are in 2014 dollars. The discounted versions discount to age 65. Weighted by the sample weight in the last HRS interview.

Table 2 shows detailed distributions of the three most important measures: length of life, probabilities of dementia six months prior to death, and total lifetime OOP medical expenditures using four alternative discount rates. Table 3 shows the distribution of lifetime medical expenditures on different subcategories using our preferred 0% discount rate.

Table 2.

Distribution of years survived, probabilities of dementia, and lifetime OOP medical expenditures

N=3,766	Years alive after age 65	Dementia probability	Lifetime OOP expenditures with assumed discount rate…
		6 months before death	0%	1%	2%	3%
mean	18.56	0.431	60,810	52,189	45,198	39,481
sd	8.70	0.407	84,596	70,173	59,086	50,463
10 th pct	5.79	0.001	4,864	4,572	4,282	4,097
20th pct	10.83	0.010	11,789	10,737	9,817	9,042
30th pct	14.42	0.048	18,874	17,218	15,833	14,486
40th pct	16.75	0.130	27,100	24,300	21,901	19,789
Median	19.00	0.291	36,612	32,497	29,009	25,903
60th pct	21.33	0.529	47,412	41,650	36,801	32,894
70th pct	23.67	0.817	63,069	54,947	48,481	42,487
80th pct	26.25	0.980	86,287	75,994	66,070	57,229
90th pct	29.67	1.000	135,000	114,649	97,543	85,720

Notes: Sample members are followed from age 65 to death. Expenditures are in 2014 dollars. The discounted versions discount to age 65. Weighted by the sample weight in the last HRS interview.

Table 3.

Distribution of lifetime OOP medical expenditures by spending categories

	Total	Drugs	Nursing home	Doctor	Hospital	Other
mean	60,810	23,595	17,539	11,004	5,341	3,331
sd	84,596	33,841	60,304	13,665	19,071	17,657
10th pct	4,864	1,417	0	457	0	0
20th pct	11,789	4,272	0	1,664	0	0
30th pct	18,874	7,241	0	3,169	0	0
40th pct	27,100	10,977	0	4,852	172	0
50th pct	36,612	14,913	0	6,962	633	122
60th pct	47,412	19,667	0	9,359	1,334	428
70th pct	63,069	26,211	1,101	12,385	2,774	999
80th pct	86,287	35,193	9,092	16,940	5,575	2,287
90th pct	135,000	50,949	46,601	26,260	12,586	5,857

Notes: N = 3,766. Sample members are followed from age 65 to death. Expenditures are in 2014 dollars. 0% discount rate used. Weighted by the sample weight in the last HRS interview.

The mean of total lifetime medical expenditures (after age 65) is high and the distribution is strongly right-skewed: the median is $37 thousand, and the mean is $61 thousand when a 0% discount rate is used. The corresponding numbers for a 3% discount rate are $26 thousand and $39 thousand. Drug expenditures have the highest mean ($24 thousand), and the distribution is relatively symmetric (the median is $15 thousand). The second highest mean is for spending on nursing homes, but it has a very skewed distribution. The mean is $18 thousand, the median is $0, and the 90^th percentile is $47 thousand. Expenditures on doctor visits (including dental care and outpatient surgery) constitute the third most expensive category, and their distribution is relatively symmetric: the mean is $11 thousand, and the median is $7 thousand. Hospital and other medical spending have lower means, and almost zero medians.

Total years alive (after age 65) has a symmetric distribution: the median (19 years) is only a few months above the mean (18.6 years).

The probabilities of dementia six months prior to death are bimodal with many zeros and ones. This means that the HRS variables (in stage 1 of our procedure) strongly predict dementia status, and so they can successfully discriminate demented and cognitively normal individuals. The mean probability of dementia is 43% in this sample which is slightly higher than the 41% reported in Hudomiet et al. (2018a), which was based on a different sample: all individuals who were observed to die after age 65 in any HRS waves since 1998.

4.2. The effect of dementia on lifetime out-of-pocket medical expenditures

Figure 2 shows the means of lifetime expenditure subcategories by whether the probability of dementia six months before death is above or below 50%. The means are systematically higher in the likely dementia group (p_d≥50%), but the differences are typically not very large. The only exception is the mean of nursing home spending which is more than 6 times higher in the likely dementia group compared to the rest of the sample ($34,668 vs. $5,646). These descriptive results conform to expectations. Dementia has a strong positive correlation with nursing home spending; and weaker positive correlations with other medical spending categories, perhaps partly due to confounding comorbidities and survival patterns, which are controlled in the regressions below.

Figure 2. Mean medical expenditures by spending categories and dementia probabilities six months before death.

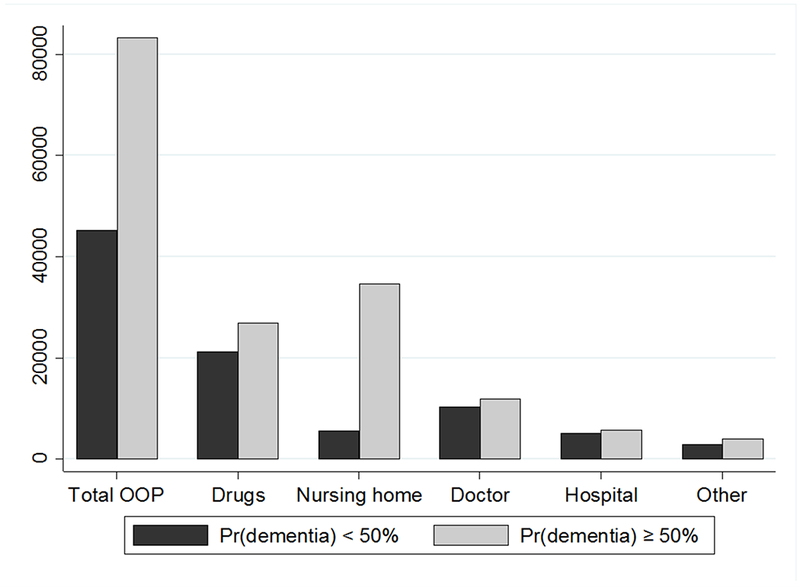
Notes: N = 3,766. Sample members are followed from age 65 to death. Expenditures are in 2014 dollars. 0% discount rate used. Weighted by the sample weight in the last HRS interview.

Table 4 and 5 show the main results of this paper: OLS regressions of lifetime expenditures on the probability of dementia six months prior to death, length of life, demographics, lifetime earnings and comorbidities (Table 4), and regressions in which the dementia probability is interacted with gender, race and SES (Table 5).

Table 4.

OLS regressions of lifetime OOP medical expenditures by spending categories

	Total [1]	Drugs [2]	Nursing h. [3]	Doctor [4]	Hospital [5]	Other [6]
Dementia probability six months prior to death	38,540*** [5,617]	−154 [1,765]	37,729*** [4,372]	−995 [731]	1,527 [1,094]	432 [1,246]
Years alive	1,726*** [222]	918*** [75]	137 [173]	588*** [34]	−33 [70]	115*** [38]
Less than high school	−6,804** [3,371]	−126 [1,127]	−4,212 [2,640]	−1,217** [519]	118 [832]	−1,368** [551]
High school	ref.	ref.	ref.	ref.	ref.	ref.
Some college	12,781*** [4,429]	6,037*** [2,174]	1,100 [2,827]	3,270*** [687]	825 [966]	1,550 [1,380]
College or more	22,891*** [5,124]	3,969** [1,742]	10,983*** [4,141]	5,904*** [890]	801 [1,120]	1,234 [1,103]
Female	10,381*** [3,342]	4,368*** [1,308]	5,363** [2,504]	653 [522]	−933 [754]	931 [811]
Ever single	6,467* [3,386]	670 [1,391]	3,301 [2,446]	453 [623]	366 [967]	1,677** [789]
Years single	273 [255]	−96 [105]	484** [200]	−78* [40]	11 [47]	−49 [53]
Black	−11,599*** [4,201]	−2,841* [1,560]	−9,712*** [3,070]	−1,080* [557]	999 [1,273]	1,036 [952]
Other race	−682 [9,031]	−1,311 [3,355]	2,560 [7,145]	−1,654* [939]	928 [1,988]	−1,205** [557]
Hispanic	−14,539*** [4,121]	−4,533** [1,769]	−6,281** [2,798]	−2,690*** [655]	−772 [1,548]	−263 [514]
Lifetime earnings quintiles
Lowest quintile	ref.	ref.	ref.	ref.	ref.	ref.
2nd quintile	7,196* [3,789]	3,399** [1,356]	54 [2,835]	2,145*** [693]	680 [1,170]	918 [816]
3rd quintile	7,263** [3,517]	2,681** [1,313]	4,022 [2,594]	276 [605]	−115 [1,245]	399 [752]
4th quintile	23,876*** [4,941]	8,844*** [1,949]	10,542*** [3,500]	1,633** [709]	994 [1,568]	1,864 [1,454]
Highest quintile	24,485*** [5,567]	7,643*** [2,133]	11,640*** [4,306]	3,863*** [979]	676 [1,396]	663 [1,057]
Ever hypertension	1,635 [3,109]	3,203*** [1,090]	−909 [2,191]	−535 [539]	570 [790]	−694 [1,018]
Ever diabetes	7,742** [3,297]	5,518*** [1,689]	889 [2,281]	788 [494]	435 [763]	112 [569]
Ever cancer	1,113 [2,683]	−87 [1,043]	517 [1,958]	742 [476]	−95 [717]	35 [665]
Ever lung disease	2,428 [3,194]	1,385 [1,245]	−90 [2,376]	85 [493]	359 [816]	689 [716]
Ever heart condition	3,401 [3,063]	3,604*** [1,191]	−1,522 [2,198]	197 [484]	−123 [790]	1,246 [760]
Ever stroke	1,189 [3,353]	2,681** [1,290]	−2,956 [2,462]	789 [548]	16 [637]	660 [1,004]
Ever psychiatric problems	6,899** [3,472]	1,118 [1,376]	5,127* [2,701]	560 [545]	−29 [697]	123 [563]
Ever arthritis	1,232 [3,311]	1,128 [1,485]	1,229 [2,017]	131 [538]	−188 [1,096]	−1,069 [1,195]
No children	ref.	ref.	ref.	ref.	ref.	ref.
1 child	2,706 [7,956]	1,326 [2,698]	4,173 [6,767]	−1,285 [933]	−1,026 [1,737]	−482 [1,011]
2 children	−2,994 [5,530]	2,264 [1,804]	−5,444 [4,519]	93 [868]	−415 [1,705]	508 [1,346]
3-6 children	−12,126** [4,894]	−198 [1,594]	−11,035*** [4,108]	−114 [813]	125 [1,697]	−903 [802]
7+ children	−14,459*** [5,081]	−584 [1,764]	−13,837*** [4,112]	478 [935]	−1,211 [1,671]	695 [1,293]
Constant	−15,166* [7,825]	−9,595*** [2,428]	−7,214 [6,220]	−2,275* [1,164]	4,582 [2,851]	−665 [1,177]

Notes: N = 3,766. Bootstrapped standard errors in brackets.

^***p<0.01

^**p<0.05

^*p<0.1.

Sample members are followed from age 65 to death. Expenditures are in 2014 dollars. 0% discount rate used. Weighted by the sample weight in the last HRS interview.

Table 5.

OLS regressions of lifetime OOP medical expenditures, models with interactions

	Total ODP spending, alternative specifications
	[1]	[2]	[3]	[4]
Dementia probability six months prior to death (Pd)	37,054*** [8,989]	11,659 [8,438]	19,737** [9,333]	21,877* [11,659]
Pd X High school dropout	−19,453* [9,932]			−15,255 [9,862]
Pd X Some college	1,169 [13,022]			−28 [13,138]
Pd X College	31,582** [15,987]			29,370* [16,219]
Pd X Female	11,985 [8,459]	12,646 [8,240]	12,061 [8,261]	12,956 [8,431]
Pd X Black	−23,052** [9,856]		−23,781** [9,542]	−17,847* [9,920]
Pd X Other race	2,750 [22,043]		3,902 [22,321]	7,222 [21,846]
Pd X Hispanic	−26,410** [10,623]		−29,963*** [9,901]	−21,917** [10,574]
Pd X LT earnings 2nd quintile		7,4 96 [10,389]	3,297 [10,457]	2,825 [10,588]
Pd X LT earnings 3rd quintile		23,737*** [9,081]	18,648** [9,486]	16,506* [9,456]
Pd X LT earnings 4th quintile		31,365** [13,629]	25,186* [13,734]	21,240 [14,077]
Pd X LT earnings 5th quintile		49,470*** [16,266]	42,890*** [16,315]	34,745** [16,442]
Control variables	YES	YES	YES	YES

Notes: N = 3,766. Bootstrapped standard errors in brackets.

^***p<0.01

^**p<0.05

^*p<0.1.

Sample members are followed from age 65 to death. Expenditures are in 2014 dollars. 0% discount rate used. Weighted by the sample weight in the last HRS interview. The control variables are the same as in Table 4. The full output is in Appendix Table B2.

Dementia has a large and statistically significant effect on total lifetime medical expenditures. Living with dementia for at least half a year increases total spending by $38.5 thousand. As for the control variables, those who live longer face higher lifetime medical expenditures as do the highly educated, females, whites, singles and those with higher lifetime earnings. These results suggest that health spending is a normal good, because richer individuals spend more on it. Comorbidities are less strongly related to total OOP medical expenditures than is dementia.

Dementia only affects spending on nursing homes among the subcategories we investigated (Table 4). Those who live with dementia for at least six months should expect to pay $38 thousand more on nursing homes on average. Dementia has a weak positive, but not significant effect on hospital spending, a weak negative, but not significant effect on doctor visits, and the effects on the other subcategories are practically zero. These results are in line with our expectations. The control variables tend to predict nursing home and drug spending the most; and the coefficients are similar across these two columns. One exception is that the length of life has a substantially stronger effect on drug spending compared to nursing home spending, likely because many seniors use drugs on a daily basis, while nursing home spending is episodic.

The interaction models in Table 5 show that the effect of dementia on total OOP medical expenditures varies by socioeconomic status, although the interaction coefficients are not always statistically significant, likely due to the relatively small sample size and correlations between the predictor variables.

The lifetime cost of dementia is substantially higher for those with more lifetime earnings (column 2). For example, those in the highest wealth quintile spent about $50 thousand more than those in the lowest wealth quintile. The magnitude of these interaction effects is reduced when interactions of the dementia probability with race and education are added to the model (column 4). The lifetime cost of dementia is considerably lower for blacks, and these interactions are always statistically significant at 10% level (often even at 5%). The lifetime costs of dementia are significantly higher for the highly educated. According to the point estimate they are higher for females (by about $12 thousand), but this interaction term is not statistically significant in any of the specifications. Having three or more children reduces lifetime spending by $11-$14 thousand which is consistent with the notion that the availability of informal caregivers reduces nursing home use.

High SES individuals with dementia may spend more on nursing homes for several reasons: 1) they may be more likely to enter nursing homes, possibly because they have more limited access to informal care by their children; 2) they may be less likely to receive financial support, for example, from Medicaid; or 3) they may use higher quality and more expensive nursing homes. In Table 6, we estimated OLS regressions of lifetime nights spent in nursing homes, independent of the associated costs. The first three columns show regressions without interactions between the dementia probability and SES, and the second three include the interactions. Overall, even though dementia is a very strong predictor of nursing home use, SES (education or lifetime earnings) and their interactions with dementia are close to zero and they are almost never statistically significant. We conclude that there is relatively little variation in lifetime nursing home use by SES; and the spending differences by SES likely reflect differences in eligibility for Medicaid support and/or differences in nursing home quality. Unfortunately, the HRS has very little information about the quality of nursing homes, so we could not disentangle these two explanations.

Table 6.

OLS regressions of lifetime nursing homes use

	No interactions			With interactions
	Any NH	NH>100	Total NH	Any NH	NH>100	Total NH
	[1]	[2]	[3]	[4]	[5]	[6]
Dementia probability six months prior to death (Pd)	0.267*** [0.031]	0.423*** [0.030]	557.2*** [42.2]	0.263*** [0.065]	0.386*** [0.060]	378.7*** [84.1]
Pd X Female				−0.063 [0.044]	0.084** [0.042]	318.1*** [61.5]
Pd X Black				−0.016 [0.067]	−0.096 [0.062]	−184.0** [85.4]
Pd X Other race				0.228* [0.123]	0.018 [0.134]	126.7 [229.0]
Pd X Hispanic				−0.070 [0.090]	−0.126 [0.079]	−171.7 [114.1]
Pd X LT earnings 2nd quintile				0.013 [0.063]	−0.026 [0.062]	61.0 [90.0]
Pd X LT earnings 3rd quintile				0.051 [0.065]	0.010 [0.061]	−12.6 [88.0]
Pd X LT earnings 4th quintile				0.128* [0.067]	0.060 [0.067]	−18.5 [92.7]
Pd X LT earnings 5th quintile				0.025 [0.073]	−0.043 [0.071]	19.8 [109.7]
LT high school	−0.023 [0.021]	−0.020 [0.021]	−2.1 [27.9]	−0.023 [0.021]	−0.018 [0.021]	3.8 [27.5]
High school	ref.	ref.	ref.	ref.	ref.	ref.
Some college	−0.000 [0.024]	−0.016 [0.024]	14.8 [30.3]	0.002 [0.024]	−0.013 [0.024]	17.5 [30.2]
College or more	0.017 [0.027]	−0.016 [0.027]	1.0 [33.9]	0.021 [0.027]	−0.015 [0.027]	−3.2 [32.3]
Female	0.058*** [0.022]	0.076*** [0.023]	73.0*** [28.3]	0.085*** [0.031]	0.040 [0.028]	−60.3* [31.6]
Black	−0.036 [0.027]	−0.049* [0.027]	−54.3 [36.3]	−0.024 [0.047]	0.003 [0.038]	47.6 [42.4]
Other race	−0.087 [0.054]	−0.038 [0.048]	30.0 [76.4]	−0.191** [0.078]	−0.046 [0.059]	−25.5 [90.0]
Hispanic	−0.099*** [0.036]	−0.102*** [0.033]	−79.5* [44.2]	−0.066 [0.055]	−0.045 [0.040]	−0.6 [42.2]
Lifetime (LT) earnings quintiles
Lowest quintile	ref.	ref.	ref.	ref.	ref.	ref.
2nd quintile	−0.033 [0.024]	0.040* [0.023]	31.3 [29.4]	−0.038 [0.042]	0.050 [0.034]	0.8 [31.1]
3rd quintile	−0.017 [0.024]	0.012 [0.023]	−9.1 [27.7]	−0.039 [0.043]	0.007 [0.033]	−6.7 [29.5]
4th quintile	−0.004 [0.026]	0.034 [0.024]	29.7 [29.3]	−0.055 [0.044]	0.008 [0.033]	32.3 [30.1]
Highest quintile	−0.024 [0.028]	0.006 [0.027]	41.6 [35.5]	−0.034 [0.047]	0.021 [0.035]	26.5 [35.1]
Control variables	YES	YES	YES	YES	YES	YES

Notes: N = 3,766. Bootstrapped standard errors in brackets.

^***p<0.01

^**p<0.05

^*p<0.1.

Sample members are followed from age 65 to death. Weighted by the sample weight in the last HRS interview. “Any NH” indicates at least one night spent in a nursing home from age 65 to death; “NH>100” indicates more than 100 nights; and “Total NH” measures the cumulative number of nights in nursing homes. The control variables are the same as in Table 4. The full output is in Appendix Table B3.

5. Conclusion and discussion

Dementia affects a large number of older persons. It has significant financial impact on individuals, insurance companies and public programs, mostly due to the high use and costs of formal and informal nursing care. As the lifetime risk of dementia is high, individuals may need to better prepare for this risk. Currently only about 10%-15% of older Americans are covered by long-term care insurance (Brown et al., 2012; Coe et al., 2015), leaving the majority of the population exposed to a large uninsured risk.

Cognitive decline and dementia can affect people for an extended period of time between the onset of the disease and death, and individuals need to be prepared to cover all cumulative lifetime costs. The majority of the health economic literature, however, estimated annual, as opposed to lifetime, medical expenditures. This is partly due to limitations of many available datasets, and partly because government programs, such as Medicare and Medicaid, are more interested in annual expenditures, which directly relates to their annual budgets.

We estimated the lifetime OOP costs of dementia and how it varied by socioeconomic status, using a large, nationally representative longitudinal survey from the U.S. In general, high SES individuals tend to have significantly better health outcomes than the rest of the population (Adler and Newman 2002). However, it was not obvious how SES is related to the lifetime risk and the lifetime costs of dementia. High SES individuals may be less likely to live with dementia at any given age, but they survive to greater ages where the risk of dementia is substantially higher. Thus, the lifetime risk of dementia may increase or decrease with SES. Moreover, high SES individuals may not be eligible for Medicaid, which is a primary funder of nursing home care in the U.S. In our prior research Hudomiet et al. (2018a) found that the lifetime risk of dementia significantly declined with measures of SES. In this paper we also analyzed how the lifetime cost of dementia varies by SES.

We first estimated lifetime medical expenditures by summing any expenditures reported in the panel survey from age 65 to death. Left- and right-censored observations were imputed using a non-parametric matching method we developed. We then regressed lifetime expenditures on dementia probabilities, controlling for length of life, demographics, lifetime earnings and comorbidities. To estimate heterogeneity in the lifetime costs of dementia, we sometimes included interaction terms of the dementia probability with gender, race, and SES.

We found that those who live with dementia for at least six months pay, on average, $38.5 thousand more out of pocket from age 65 to death in 2014 dollars under a 0% discount rate. We can compare this number to a naive estimate of the lifetime costs of dementia. We estimate that by multiplying the average annual costs of dementia with the average number of years individuals live after the first diagnosis of dementia. Hurd et al. (2013) found that dementia increased annual OOP medical expenditures per person by about $6,000 (in 2010 dollars). Other papers estimated median survival times after the diagnosis of Alzheimer’s disease, the most common form of dementia (Helzner et al, 2008; Larson et al., 2004; Mayeda et al., 2015; Rait et al., 2010). Depending on the methods and the samples used, patients were found to live, on average, about 3-6 years after diagnosis. Thus, the naive estimate of the lifetime costs of dementia is about $18,000-$36,000. However, this naive method ignores any correlation between mortality and the cost of dementia even though there are good reasons to expect a correlation because there are many variables that are common predictors of both. For example, the age of onset of dementia likely affects both the annual costs of dementia and the length of time individuals live with the disease. Our method is to directly model the cumulative medical expenditures observed in a long panel dataset and their association with dementia onset. The correlation between mortality and the costs of dementia is preserved.

Dementia strongly increases spending on nursing homes, while the relationship between dementia and the other spending categories is not statistically significant. The cost of dementia is significantly lower for blacks, and poorer individuals (assessed by a measure of lifetime earnings), possibly because of differences in Medicaid eligibility and nursing home quality between these groups. This was suggested by our finding that the total nights individuals spend in nursing homes from age 65 to death did not significantly vary by SES, even though the total costs did.

Kelley et al. (2015) found that dementia increased OOP medical spending in the last five years of life by about $27 thousand, which is about 70% of our estimated $38.5 thousand. It is not surprising that our estimates are larger, because we followed individuals for a longer time from age 65 to death, on average for about 19 years. In a very different microsimulation framework Jutkowitch et al. (2017) found the lifetime OOP cost of dementia to be $25 thousand, even lower than that reported in Kelley et al. (2015). The microsimulation framework allowed the authors to run interesting policy experiments. However, that framework is likely less accurate for estimating the lifetime cost of dementia compared to data driven models such as those used by Kelley et al. (2015) or by us.

The lifetime cost of dementia is high. As life expectancies are increasing, we may expect further increases in the prevalence and total costs of dementia over time.⁵ Moreover, as younger cohorts are less likely to be married and they have fewer children, access to informal care may decline over time, which may force individuals to rely more on expensive formal arrangements. These points all suggest that the burden of dementia for individuals and families may increase in the future, unless medical research finds a cure (or manages to delay onset), and/or the government finds new ways to help people cope with the large and growing costs of dementia.

This paper has limitations. First, the HRS is currently not long enough to observe the entire life spans of all individuals from age 65 to death. We developed a non-parametric methodology to deal with this censoring problem, but this method relies on assumptions. Section A.5. in the appendix discusses direct tests of the splicing procedure. We took the sample of individuals in our baseline sample who died between 1998 and 2014. The lifetime medical expenditures are fully observed in this sample. Then we artificially censored their data in 2006, and we used our splicing procedure to find donors and impute the deleted data. We then compared the spliced trajectories to the observed ones, and we found that the model performed well: the distributions of the main variables as well as their associations (correlations, regression coefficients) were very similar in the observed and the spliced data.

Second, our procedure assumed that the different birth cohorts provide valid imputation data to each other. If medical expenditures, dementia, or other important related variables change across cohorts, our imputation procedure may be biased. However, our splicing algorithm matches donors and recipients on the actual values of the variables, and appropriate donors may be available even if the population means of some variables are trending.

Third, even though our bootstrap methodology for standard errors appropriately dealt with the fact that dementia status was not directly observed in the HRS, our procedure ignored the problem of splicing, which cannot be accounted for with the bootstrap. Our investigations on synthetic data suggested that the biases in the standard errors are negligible, but we cannot know for sure. Fourth, we only focused on OOP medical expenditures, and we ignored other medical costs, such as informal care, and costs covered by private insurance and Medicaid. Lifetime costs are most relevant for individuals, and that is why we primarily focused on OOP spending. But we believe it would be an interesting extension of our procedure to include other costs, especially the cost of informal care. Fifth, we carried out our analysis on individuals, rather than households, because the non-parametric splicing methodology would have been very complicated in a household framework. Household level lifetime costs would also be an interesting extension. Sixth, we used U.S. data and therefore our results are primarily relevant for the U.S. Cross-country comparisons reveal large heterogeneity across countries in the total costs of dementia as well as how different parties pay for it (Wimo et al., 2013).

Appendix A: Details on the splicing methodology

A.1. Details on right splicing

For the right-censored cases we matched pairs from the 1998-2004 HRS waves who were most similar to the recipients in their latest available waves (2014 or earlier) in the following dimensions: age, gender, education, lifetime earnings (PIA), nursing home residence, marital status, wave-by-wave dementia probabilities, ever having a stroke, and total OOP medical expenditures. In certain dimensions we required perfect matches, in other dimensions we minimized a distance between the pairs. In particular, we required perfect matches in gender, education (high school or less vs. some college or more), PIA tertiles, nursing home residence, ever had a stroke, and marital status (single vs. not); we allowed for a maximum of one year difference in age; and we minimized a distance measure defined as the sum of squared age-adjusted⁶ percentile difference in dementia probabilities and OOP costs: $D_{jk}={({\pi }_j^{dem}-{\pi }_k^{dem})}^2+{({\pi }_j^{oop}-{\pi }_k^{oop})}^2$, where D_jk is the distance between observations j and k, ${\pi }_j^{\mathit{dem}}$ is the age-adjusted percentile ranking (between 0 and 100) of observations j in dementia probabilities, and ${\pi }_j^{\mathit{oop}}$ is the percentile ranking (between 0 and 100) of observations j in total household OOP health expenditures. In some cases (N=118) the procedure failed, because no pair was available with a perfect match in the required dimensions; or the squared difference was too large (defined as D_jk distance larger than 100). In such cases we started requiring less perfect matching: in round 2 we ignored the levels of education and the marital status of the pairs. In round 3 (N=48), we also ignored nursing home residency and stroke. In round 4 (N=17) we also ignored gender, and we allowed for 2-year differences in age. In round 4 we managed to find valid donors to all recipients, but for a single person the distance measure was still a bit high (D_jk = 109).

42 chosen donors also survived to 2014, so we repeated the matching procedure for them (double-splicing). All of these donor individuals were observed to die in the HRS, so we did not need to use more right splicing.

A.2. Details on early mortality

A sample of those who died after age 65, but before becoming eligible for our baseline sample (i.e., before turning 74-79 years old), needed to be added to our baseline sample. For each baseline age we used the HRS to estimate the number of people who would be dead by that age. For example, we first estimated the number of people who would be dead by age 74; then we did the same for baseline age 75, and so on. Then we randomly drew the appropriate number of individuals (without replacement) from the 2004-2010 HRS sample among those who actually died before reaching the eligibility ages.

Table A1 shows twelve subsamples of the HRS we used for these calculations. Subsample 1 (in column 1) includes individuals who were 65 in 1998. Subsample 2 includes 65-year-olds in the 2000 wave. Both subsamples 1 & 2 can be used to estimate the fraction of individuals who die before age 79, since these individuals would turn 79 before the latest HRS wave. Similarly, the other subsamples were used to estimate the fraction of the sample who die before ages 78, 77, …, 74.

Table A1.

Subsamples used to estimate the size of the early mortality sample,

	Potential ages (if survive to waves 11-12)
Waves	s1	s2	s3	s4	s5	s6	s7	s8	s9	s10	s11	s12
1998	65
2000	67	65	66		65
2002	69	67	68	66	67	65	66		65
2004	71	69	70	68	69	67	68	66	67	65	66
2006	73	71	72	70	71	69	70	68	69	67	68	66
2008	75	73	74	72	73	71	72	70	71	69	70	68
2010	77	75	76	74	75	73	74	72	73	71	72	70
2012	79	77	78	76	77	75	76	74	75	73	74	72
2014		79		78		77		76		75		74

Table A2 shows how we calculated the size of the early mortality sample. Column [p] is the probability that a 65-year-old person would die before becoming eligible for our sample based on the HRS. Column [L] shows the baseline sample (74-79-year olds in 1998) by age in 1998. The estimated size of the original 65-year-old sample (including survivors to the baseline age as well as the dead) is L / (1 − p). Then the size of the early mortality sample is D ≡ L × p / (1 − p), shown in column [D]. The last column shows the available candidates in the HRS which always exceed the values in [D], and so we can draw individuals from the candidate sample without replacement.

Table A2.

Estimated size of the early mortality sample

	Fraction of 65-year-olds who die by target age	HRS alive sample size in 1998	Estimated size of early mortality sample	Available candidates in the HRS
Target age	[p]	[L]	[D]
74	0.180	566	124	246
75	0.200	490	122	277
76	0.200	478	119	264
77	0.270	485	179	362
78	0.279	437	169	350
79	0.335	397	200	441

A.3. Results

Table A3 shows the survival and non-response patterns in our final sample. Only about 19% of the sample needed right splicing. 16% survived to 2014 (13% with a valid 2014 interview, 3% without one), and 3% died, but exit interviews were not provided. The rest of the sample were observed to their deaths. 76% of the sample correspond to members of the baseline cohort, and 24% to the early mortality sample. Table A2 shows how much of the total lifetime OOP spending comes from the baseline, right spliced, left spliced, and early mortality samples. The majority of spending comes from the baseline sample.

Table A3.

Survival and non-response patterns between 1998 and 2014 in the final sample

	N	%
In baseline sample, died by the 2014 wave, provided exit interviews	2,145	56.96
Died between age 65 and baseline eligibility	913	24.24
Alive in 2014, valid 2014 interview	485	12.88
Alive in 2014, no interview in 2014	115	3.05
Died before 2014, exit interview missing	108	2.87
Total	3,766	100.00

Notes: The baseline sample includes 74-79 years old individuals in the 1998 HRS wave.

Table A4.

Distribution of lifetime OOP medical expenditures in the different interview types

	N	Mean	Median
Total lifetime OOP	3,766	60,810	36,612
Baseline, if positive	2,853	42,667	21,915
Right spliced, if positive	708	43,941	15,275
Left spliced, if positive	2,853	17,714	11,019
Early mortality, if positive	913	27,582	13,266
Baseline	3,766	33,322	13,134
Right spliced	3,766	7,613	0
Left spliced	3,766	13,834	7,290
Early mortality	3,766	6,041	0
Core interviews	3,766	45,866	27,591
Exit interviews	3,766	14,943	2,668

A.4. Diagnostics

The six panels of appendix Figures A1 and A2 and Tables A5-A14 show diagnostics of the quality of the donor-recipient pairs for left and right censoring. They show the distribution of the donor-recipient differences in dementia probabilities and total medical expenditures, as well as means and correlations in these variables over time. The dementia probabilities are very similar between donors and recipients: the correlations are above 0.95; the cross-wave correlations are very similar between donor-donor, donor-recipient, and recipient-recipient reports, and the differences are closely clustered around zero. Medical expenditures are somewhat less similar between donors and recipients: the correlations are only about 0.6-0.7. The reason was that OOP has a more dispersed and less persistent distribution. Nevertheless, the cross-wave correlations were similar across donor-donor, donor-recipient and recipient-recipient waves, and the donor-recipient differences were fairly small in the bottom 90% of the distribution.⁷

Figure A1.

Difference between the recipients’ and the spliced donors’ dementia probabilities

Figure A2.

Difference between the recipients’ and the spliced donors’ OOP medical expenditures

Table A5.

Difference between the recipients’ and the spliced donors’ dementia probabilities

	N	Mean	Sd	Min	1st pct	10th pct	Median	90th pct	99th pct	Max
Left splicing	2,853	0.004	0.083	−0.571	−0.286	−0.025	0.000	0.031	0.376	0.665
First right splicing	708	0.005	0.091	−0.499	−0.294	−0.076	0.004	0.079	0.307	0.506
Second right splicing	42	0.015	0.080	−0.244	−0.244	−0.073	0.023	0.083	0.275	0.275

Table A6.

Difference between the recipients’ and the spliced donors’ OOP medical expenditures

	N	Mean	Sd	Min	1st pct	10th pct	Median	90th pct	99th pct	Max
Left splicing	2,853	531	8,729	−84,781	−6,606	−444	0	696	20,594	157,464
First right splicing	708	134	22,125	−157,230	−78,385	−2,166	36	1,879	67,745	258,021
Second right splicing	42	−15,205	89,593	−569,670	−569,670	−2,968	492	2,734	23,204	23,204

Table A7.

Dementia probabilities in the last two left spliced donor and the first two recipient waves

	N	mean	sd
[1a] Wave before splicing	2,447	0.050	0.136
[2a] Spliced donor wave	2,447	0.081	0.182
[2b] Spliced recipient wave	2,447	0.085	0.193
[3b] Wave after splicing	2,447	0.127	0.240

Table A8.

Dementia probabilities in the last two recipient and first two right spliced donor waves

	N	mean	sd
[1a] Wave before splicing	430	0.274	0.321
[2a] Spliced recipient wave	430	0.353	0.354
[2b] Spliced donor wave	430	0.345	0.355
[3b] Wave after splicing	430	0.467	0.358

Table A9.

OOP medical expenditures in the last two left spliced donor and the first two recipient waves

	N	mean	sd
[1a] Wave before splicing	2,447	3,592	11,088
[2a] Spliced donor wave	2,447	3,226	6,685
[2b] Spliced recipient wave	2,447	3,564	9,553
[3b] Wave after splicing	2,447	4,464	13,345

Table A10.

OOP medical expenditures in the last two recipient and first two right spliced donor waves

	N	mean	sd
[1a] Wave before splicing	430	5,817	22,184
[2a] Spliced recipient wave	430	7,684	24,995
[2b] Spliced donor wave	430	8,006	23,924
[3b] Wave after splicing	430	11,330	26,976

Table A11.

Correlations between donor-recipient dementia probabilities, left spliced cases

N = 2,447	[1a]	[2a]	[2b]	[3b]
[1a] Wave before splicing	1.000
[2a] Spliced donor wave	0.699	1.000
[2b] Spliced recipient wave	0.618	0.917	1.000
[3b] Wave after splicing	0.456	0.674	0.733	1.000

Table A12.

Correlations between donor-recipient dementia probabilities, right spliced cases

N = 430	[1a]	[2a]	[2b]	[3b]
[1a] Wave before splicing	1.000
[2a] Spliced recipient wave	0.832	1.000
[2b] Spliced donor wave	0.802	0.973	1.000
[3b] Wave after splicing	0.607	0.735	0.753	1.000

Table A13.

Correlations between donor-recipient OOP medical expenditures, left spliced cases

N = 2,447	[1a]	[2a]	[2b]	[3b]
[1a] Wave before splicing	1.000
[2a] Spliced donor wave	0.446	1.000
[2b] Spliced recipient wave	0.197	0.581	1.000
[3b] Wave after splicing	0.077	0.251	0.274	1.000

Table A14.

Correlations between donor-recipient OOP medical expenditures, right spliced cases

N = 430	[1a]	[2a]	[2b]	[3b]
[1a] Wave before splicing	1.000
[2a] Spliced recipient wave	0.192	1.000
[2b] Spliced donor wave	0.171	0.619	1.000
[3b] Wave after splicing	0.100	0.326	0.317	1.000

A.5. A direct test of the splicing procedure

We implemented a direct test of the procedure by applying it to a subsample of the HRS data, in which we observed the lifetime measures. We took the sample of individuals in our baseline sample who died between 1998 and 2014 and provided EXIT interviews (N=2,145). The lifetime medical expenditures (and other lifetime measures) are fully observed in this sample. Then we artificially censored their data in 2006, that is, we deleted any available information after the 2006 wave of HRS. Then we used the same splicing procedure to find donors for the censored cases, and we compared the spliced and the observed data. We want to note that this test provides an upper bound of the problems with splicing, since in this sample, due to the shorter time window, we have far more censored cases than in our original sample.

Table A15 shows the distributions of the main variables (lifetime medical expenditures, years survived, dementia probabilities) in the observed and the spliced data. The first four columns include all 2,145 individuals. Columns 5-8 focus on the censored cases, and we dropped from the sample anyone who died before 2006 and provided a valid EXIT interview. The means and the medians of the variables are fairly close to each other. The largest discrepancy is in drug spending, which is slightly (about 7.5%) higher in the spliced data.

Table A15.

Testing the splicing model: Comparing observed vs. artificially censored data, distributions

	All observations, N=2,145				Censored observations, N=1,035
	Mean		Median		Mean		Median
	Observed data	Spliced	Observed data	Spliced	Observed data	Spliced	Observed data	Spliced
Total lifetime OOP	41,795	42,789	19,814	20,355	56,243	58,302	32,675	34,073
Lifetime nursing home spending	14,246	14,937	0	0	20,270	21,701	0	0
Lifetime hospital spending	3,965	3,880	22	57	4,376	4,200	283	367
Lifetime doctor spending	5,569	5,478	2,328	2368	7,953	7,765	4,254	4,384
Lifetime drug spending	14,983	16,095	7,279	7840	19,181	21,485	11,515	13,145
Lifetime other medical spending	3,033	2,400	0	0	4,463	3,151	65	0
Years alive	7.95	7.93	7.92	7.83	11.90	11.85	11.83	11.83
Dementia probability six months prior to death	0.464	0.456	0.352	0.341	0.552	0.536	0.609	0.528

We also investigated the association between lifetime expenditures and dementia. Table A16 shows correlations and regression coefficients based on observed and spliced data. We considered both simple regressions with no control variables, and multivariate models with all the explanatory variables from Table 4. Though we now see some differences between the two data sources, the coefficients based on observed and spliced data are similar, and there is no obvious pattern in the differences.

Table A16.

Testing the splicing model: Comparing observed vs. artificially censored data, relationships

	All observations, N=2,145		Censored observations, N=1,035
	Observed data	Spliced	Observed data	Spliced
Total lifetime OOP and dementia
Correlation	0.182	0.209	0.153	0.198
Regression coefficient, no controls	30,613	33,391	31,108	36,843
Regression coefficient, all controls	30,254	28,000	39,330	35,061
Lifetime nursing home spending and dementia
Correlation	0.243	0.239	0.249	0.237
Regression coefficient, no controls	28,170	26,579	35,740	31,612
Regression coefficient, all controls	30,935	26,803	40,651	33,186

Finally, we also compared subsamples in which it was harder to find good donors. Table A17 splits the sample based on whether the distance measure between donors and recipients (defined as the sum of squared age-adjusted percentile difference in dementia probabilities and OOP costs) is above or below 100. In the sample with larger distance (i.e. worse donors), medical expenditures are considerably higher, but the spliced and the observed data are still close to one another.

Table A17.

Testing the splicing model: Comparing observed vs. artificially censored data, by the distance between donors and recipients

	Small distance, N = 899		Large distance, N = 136
	Observed data	Spliced	Observed data	Spliced
Total lifetime OOP	53,351	55,104	75,361	79,446
Lifetime nursing home spending	18,514	19,988	31,874	33,023
Lifetime hospital spending	4,482	4,161	3,677	4,452
Lifetime doctor spending	7,694	7,339	9,669	10,580
Lifetime drug spending	18,460	20,665	23,943	26,907
Lifetime other medical spending	4,200	2,950	6,197	4,484
Years alive	11.92	11.83	11.79	11.98
Dementia probability six months prior to death	0.540	0.518	0.632	0.657

Appendix B: Additional Tables

Table B1.

Imputation model of the fraction of nursing home spending

	coef.	s.e.
Female	0.024*	[0.013]
Black	−0.022	[0.019]
Other race	0.021	[0.048]
Hispanic	−0.044	[0.031]
Age (in years)	0.035***	[0.013]
Age squared over 100	−0.017**	[0.008]
Less than HS	−0.005	[0.014]
High school	ref.	ref.
Some college	0.015	[0.017]
College	0.009	[0.018]
Married	ref.	ref.
Divorced	0.049**	[0.022]
Widowed	0.068***	[0.014]
Never married	0.071**	[0.035]
Exit interview	0.003	[0.012]
log total spending (S)	−0.295***	[0.059]
S squared	0.047***	[0.008]
S cube	−0.002***	[0.000]
Constant	−0.983*	[0.554]
R-squared	0.237
N	4248
Distribution of the predicted fraction in wave 4&5
Mean	0.631
Sd	0.209
N	642

Notes:

^***p<0.01

^**p<0.05

^*p<0.1.

The table shows a regression of the fraction of nursing home spending in the last two years to total spending on nursing homes and hospitals, using 2002-2014 HRS data on age 65+ core and exit interviews.

Table B2.

OLS regressions of lifetime OOP medical expenditures, models with interactions, full output

	Total OOP spending, alternative specifications
	[1]	[2]	[3]	[4]
Dementia probability six months prior to death (Pd)	37,054*** [8,989]	11,659 [8,438]	19,737** [9,333]	21,877* [11,659]
Pd X High school dropout	−19,453* [9,932]			−15,255 [9,862]
Pd X Some college	1,169 [13,022]			−28 [13,138]
Pd X College	31,582** [15,987]			29,370* [16,219]
Pd X Female	11,985 [8,459]	12,646 [8,240]	12,061 [8,261]	12,956 [8,431]
Pd X Black	−23,052** [9,856]		−23,781** [9,542]	−17,847* [9,920]
Pd X Other race	2,750 [22,043]		3,902 [22,321]	7,222 [21,846]
Pd X Hispanic	−26,410** [10,623]		−29,963*** [9,901]	−21,917** [10,574]
Pd X LT earnings 2nd quintile		7,496 [10,389]	3,297 [10,457]	2,825 [10,588]
Pd X LT earnings 3rd quintile		23,737*** [9,081]	18,648** [9,486]	16,506* [9,456]
Pd X LT earnings 4th quintile		31,365** [13,629]	25,186* [13,734]	21,240 [14,077]
Pd X LT earnings 5th quintile		49,470*** [16,266]	42,890*** [16,315]	34,745** [16,442]
Years alive	1,743*** [217]	1,666*** [224]	1,676*** [224]	1,682*** [222]
Less than high school	2,604 [3,704]	−6,277* [3,343]	−5,919* [3,359]	876 [3,635]
High school	ref.	ref.	ref.	ref.
Some college	12,689** [5,215]	13,150*** [4,355]	13,249*** [4,364]	13,239** [5,190]
College or more	11,526** [5,744]	23,663*** [5,115]	23,742*** [5,124]	12,915** [5,739]
Female	4,657 [3,775]	4,843 [3,806]	4,920 [3,793]	4,162 [3,789]
Ever single	6,914** [3,388]	5,683* [3,355]	5,535* [3,358]	5,995* [3,374]
Years single	273 [256]	317 [257]	336 [258]	327 [257]
Black	2,136 [5,450]	−10,503** [4,090]	1,791 [5,477]	−200 [5,458]
Other race	−483 [10,080]	1,816 [8,866]	−842 [10,114]	−1,226 [10,009]
Hispanic	−1,652 [5,550]	−14,207*** [4,102]	−541 [5,507]	−3,595 [5,533]
Lifetime (LT) earnings quintiles
Lowest quintile	ref.	ref.	ref.	ref.
2nd quintile	6,107 [3,795]	3,753 [4,650]	5,042 [4,685]	5,025 [4,714]
3rd quintile	6,587* [3,509]	−3,338 [4,333]	−1,395 [4,439]	−578 [4,420]
4th quintile	23,478*** [4,886]	10,256* [6,215]	12,591** [6,262]	14,450** [6,246]
Highest quintile	24,125*** [5,572]	3,715 [5,910]	6,348 [5,911]	9,875* [5,849]
Ever hypertension	2,025 [3,117]	2,107 [3,124]	2,035 [3,128]	2,115 [3,120]
Ever diabetes	7,407** [3,269]	7,402** [3,254]	7,346** [3,264]	7,167** [3,272]
Ever cancer	762 [2,657]	942 [2,665]	1,013 [2,667]	662 [2,653]
Ever lung disease	2,431 [3,301]	2,842 [3,263]	2,855 [3,272]	2,584 [3,288]
Ever heart condition	3,306 [3,011]	3,628 [3,053]	3,482 [3,049]	3,487 [3,020]
Ever stroke	1,894 [3,378]	1,853 [3,422]	2,112 [3,417]	2,187 [3,403]
Ever psychiatric problems	6,985** [3,390]	6,905** [3,354]	6,848** [3,352]	7,003** [3,352]
Ever arthritis	1,297 [3,382]	1,062 [3,380]	1,174 [3,389]	1,263 [3,385]
No children	ref.	ref.	ref.	ref.
1 child	3,377 [8,010]	2,936 [8,020]	3,178 [8,022]	3,475 [7,980]
2 children	−2,107 [5,552]	−2,847 [5,581]	−2,621 [5,590]	−2,100 [5,539]
3-6 children	−11,201** [4,821]	−11,461** [4,845]	−11,133** [4,858]	−10,852** [4,825]
7+ children	−12,889** [5,187]	−13,614*** [5,223]	−12,849** [5,247]	−12,647** [5,193]
Constant	−15,928** [7,563]	−3,459 [7,722]	−7,230 [7,953]	−8,558 [7,746]
N	3,766	3,766	3,766	3,766

Notes: Bootstrapped standard errors in brackets.

^***p<0.01

^**p<0.05

^*p<0.1.

Sample members are followed from age 65 to death. Expenditures are in 2014 dollars. 0% discount rate used. Weighted by the sample weight in the last HRS interview.

Table B3.

OLS regressions of lifetime nursing homes use, full output

	No interactions			With interactions
	Any NH	NH>100	Total NH	Any NH	NH>100	Total NH
	[1]	[2]	[3]	[4]	[5]	[6]
Dementia probability six months prior to death (Pd)	0.267*** [0.031]	0.423*** [0.030]	557.2*** [42.2]	0.263*** [0.065]	0.386*** [0.060]	378.7*** [84.1]
Pd X Female				−0.063 [0.044]	0.084** [0.042]	318.1*** [61.5]
Pd X Black				−0.016 [0.067]	−0.096 [0.062]	−184.0** [85.4]
Pd X Other race				0.228* [0.123]	0.018 [0.134]	126.7 [229.0]
Pd X Hispanic				−0.070 [0.090]	−0.126 [0.079]	−171.7 [114.1]
Pd X LT earnings 2nd quintile				0.013 [0.063]	−0.026 [0.062]	61.0 [90.0]
Pd X LT earnings 3rd quintile				0.051 [0.065]	0.010 [0.061]	−12.6 [88.0]
Pd X LT earnings 4th quintile				0.128* [0.067]	0.060 [0.067]	−18.5 [92.7]
Pd X LT earnings 5th quintile				0.025 [0.073]	−0.043 [0.071]	19.8 [109.7]
Years alive	0.009*** [0.001]	0.001 [0.001]	2.6 [1.9]	0.008*** [0.001]	0.002 [0.001]	3.5** [1.8]
Less than high school	−0.023 [0.021]	−0.020 [0.021]	−2.1 [27.9]	−0.023 [0.021]	−0.018 [0.021]	3.8 [27.5]
High school	ref.	ref.	ref.	ref.	ref.	ref.
Some college	−0.000 [0.024]	−0.016 [0.024]	14.8 [30.3]	0.002 [0.024]	−0.013 [0.024]	17.5 [30.2]
College or more	0.017 [0.027]	−0.016 [0.027]	1.0 [33.9]	0.021 [0.027]	−0.015 [0.027]	−3.2 [32.3]
Female	0.058*** [0.022]	0.076*** [0.023]	73.0*** [28.3]	0.085*** [0.031]	0.040 [0.028]	−60.3* [31.6]
Ever single	0.079*** [0.024]	0.096*** [0.021]	83.1*** [25.9]	0.073*** [0.024]	0.099*** [0.021]	97.4*** [24.9]
Years single	0.000 [0.001]	0.002* [0.001]	4.6** [1.9]	0.001 [0.001]	0.002* [0.001]	3.5* [1.9]
Black	−0.036 [0.027]	−0.049* [0.027]	−54.3 [36.3]	−0.024 [0.047]	0.003 [0.038]	47.6 [42.4]
Other race	−0.087 [0.054]	−0.038 [0.048]	30.0 [76.4]	−0.191** [0.078]	−0.046 [0.059]	−25.5 [90.0]
Hispanic	−0.099*** [0.036]	−0.102*** [0.033]	−79.5* [44.2]	−0.066 [0.055]	−0.045 [0.040]	−0.6 [42.2]
Lifetime (LT) earnings quintiles
Lowest quintile	ref.	ref.	ref.	ref.	ref.	ref.
2nd quintile	−0.033 [0.024]	0.040* [0.023]	31.3 [29.4]	−0.038 [0.042]	0.050 [0.034]	0.8 [31.1]
3rd quintile	−0.017 [0.024]	0.012 [0.023]	−9.1 [27.7]	−0.039 [0.043]	0.007 [0.033]	−6.7 [29.5]
4th quintile	−0.004 [0.026]	0.034 [0.024]	29.7 [29.3]	−0.055 [0.044]	0.008 [0.033]	32.3 [30.1]
Highest quintile	−0.024 [0.028]	0.006 [0.027]	41.6 [35.5]	−0.034 [0.047]	0.021 [0.035]	26.5 [35.1]
Ever hypertension	−0.009 [0.019]	−0.017 [0.018]	−19.9 [22.4]	−0.011 [0.018]	−0.016 [0.017]	−13.2 [21.8]
Ever diabetes	0.035* [0.020]	0.037* [0.019]	7.9 [22.4]	0.036* [0.020]	0.037** [0.019]	10.5 [22.1]
Ever cancer	−0.005 [0.017]	−0.018 [0.016]	−48.7*** [17.7]	−0.005 [0.017]	−0.018 [0.015]	−47.9*** [17.1]
Ever lung disease	−0.006 [0.019]	−0.001 [0.017]	26.1 [21.5]	−0.007 [0.019]	0.001 [0.017]	32.4 [21.9]
Ever heart condition	0.031* [0.017]	0.015 [0.016]	−42.3** [21.3]	0.031* [0.017]	0.015 [0.016]	−44.5** [21.2]
Ever stroke	0.084*** [0.018]	0.033* [0.019]	7.3 [23.9]	0.084*** [0.018]	0.035* [0.019]	14.4 [23.9]
Ever psychiatric problems	0.048** [0.020]	0.046** [0.020]	93.3*** [27.9]	0.049*** [0.019]	0.047** [0.020]	91.5*** [27.7]
Ever arthritis	0.014 [0.019]	−0.011 [0.018]	17.5 [20.6]	0.015 [0.019]	−0.011 [0.017]	14.5 [19.7]
No children	ref.	ref.	ref.	ref.	ref.	ref.
1 child	0.021 [0.033]	−0.031 [0.033]	−46.3 [47.1]	0.024 [0.033]	−0.028 [0.034]	−46.0 [49.0]
2 children	−0.028 [0.031]	−0.077*** [0.030]	−113.1*** [41.1]	−0.025 [0.030]	−0.076*** [0.029]	−114.2*** [42.7]
3-6 children	−0.034 [0.029]	−0.075*** [0.028]	−128.7*** [38.7]	−0.030 [0.028]	−0.072*** [0.027]	−126.5*** [40.2]
7+ children	−0.119*** [0.039]	−0.120*** [0.035]	−181.5*** [45.4]	−0.115*** [0.039]	−0.114*** [0.035]	−172.2*** [47.0]
Constant	0.226*** [0.048]	0.026 [0.048]	−35.8 [64.7]	0.232*** [0.058]	0.032 [0.054]	11.1 [63.1]
N	3,766	3,766	3,766	3,766	3,766	3,766

Notes: Bootstrapped standard errors in brackets.

^***p<0.01

^**p<0.05

^*p<0.1.

Sample members are followed from age 65 to death. Weighted by the sample weight in the last HRS interview. “Any NH” indicates at least one night spent in a nursing home from age 65 to death; “NH>100” indicates more than 100 nights; and “Total NH” measures the cumulative number of nights in nursing homes.