A laser-plasma accelerator driven by two-color relativistic femtosecond laser pulses

Driving a laser-plasma accelerator by two-color laser pulses, e.g., 800 and 400 nm, leads to a considerable electron energy boost.

Abstract

A typical laser-plasma accelerator (LPA) is driven by a single, ultrarelativistic laser pulse from terawatt- or petawatt-class lasers. Recently, there has been some theoretical work on the use of copropagating two-color laser pulses (CTLP) for LPA research. Here, we demonstrate the first LPA driven by CTLP where we observed substantial electron energy enhancements. Those results have been further confirmed in a practical application, where the electrons are used in a bremsstrahlung-based positron generation configuration, which led to a considerable boost in the positron energy as well. Numerical simulations suggest that the trailing second harmonic relativistic laser pulse is capable of sustaining the acceleration structure for much longer distances after the preceding fundamental pulse is depleted in the plasma. Therefore, our work confirms the merits of driving LPAs by two-color pulses and paves the way toward a downsizing of LPAs, making their potential applications in science and technology extremely attractive and affordable.

INTRODUCTION

In recent years, schemes of copropagating two-color laser pulses (CTLP) have been extensively used to study and control microscopic dynamics of electrons on the femtosecond or attosecond time scales (1−11). For instance, by virtue of the synthesized laser field, manipulation of energy and angular distribution of the emitted electrons enabled investigations of the above-threshold (1, 2) and the dissociative ionization (3, 4) of atoms, dichroism in ionization (5), and the orientation of molecules (6). Furthermore, the two-color laser fields have also been applied to generate and control the above-threshold photoemission from nanotips (7), terahertz emission from air plasmas (8, 9), and high-order harmonic attosecond pulses from gases (10) and solid targets (11). It is, therefore, clear that the application of two-color laser pulses in laser-matter interactions is receiving considerable attention.

Recently, the concept of a laser wakefield acceleration (LWFA) (12) driven by CTLP has been proposed via particle-in-cell (PIC) simulation studies, which can be briefly summarized as follows: In 2014, Yu et al. (13) proposed using CTLP for generating low-emittance electron beams. Such a method relies on exciting a large plasma wake wave by a relativistic midinfrared laser pulse while triggering the electron injection via the ionization of some inner-shell Kr ions (14, 15) using a properly delayed second harmonic (SH; 2ω) intense laser pulse. In 2015, Zeng et al. (16) proposed overlapping two relativistic laser pulses at the fundamental (FL; 1ω) and third harmonic (3ω) inside a plasma; the coherent interference of the two laser pulses can trigger an ionization injection of electrons only within a very short distance (because of the plasma dispersion), leading to the possibility of generating polychromatic narrow energy spread electron bunches. In 2018, Pathak et al. (17) proposed using the CTLP in an all-optical dual-stage LWFA to enhance the electron bunch energy, where the leading FL laser pulse acts as an injector, whereas the subsequent SH laser pulse acts as an accelerator or booster. In this scheme, electrons can potentially gain threefold higher energy as compared with the energy gain from a standard LWFA driven by an 800-nm wavelength laser pulse with equivalent power. Those theoretical studies suggest that using the CTLP with well-defined relative phases and timing can precisely control the injection of electrons into the plasma wake wave leading to boost the electron beam quality, which eventually translates to generation of ultrabright electron beams that are essential, for instance, to drive a desktop x-ray free-electron laser. Thus, the CTLP scheme appears to provide two types of benefits: One is to enhance ionization injection for an early trapping and higher energy acceleration of the electrons (13–16), and the other is to use the SH pulse as a second stage of acceleration beyond that from the FL pulse (17, 18). To date, there has been no experimental research on this two-color LWFA scheme to verify the conditions under which different benefits may occur. We present here the first experimental demonstration of a laser-plasma electron acceleration scheme using CTLP at the FL (800 nm) and SH (400 nm) wavelengths. By spatially and temporally overlapping two-color ultrashort relativistic laser pulses having a combined power of 67 TW in an underdense 4-mm-long plasma, we observed a substantial enhancement in electron acceleration as compared with that obtained from a standard LWFA driven by a single 800-nm laser pulse at a full power of~70 TW in the same plasma medium and at the same plasma density. Furthermore, the results were further confirmed by conducting additional experiments on ultrarelativistic positron beam generation based on the CTLP electron beams where we observed a marked enhancement in the positron beam energy as well. Two-dimensional (2D) PIC simulations were conducted to deliver insights in explaining the results.

RESULTS

Implementation of the two-color LWFA scheme

The experiments were conducted using the “Pulsar” Ti:sapphire laser (wavelength λ₁ = 800 nm) at Shanghai Jiao Tong University. Figure 1 schematically shows the setup; laser pulses with energy of 2.1 J and duration of 30 fs are split into a driver beam (E₁ = 1.9 J) and another beam (E₂ = 0.2 J) by a 25-mm-diameter dielectric mirror, which is placed in the laser beam path after the compressor. The driver pulse is focused down to a spot size $w_{0({\mathrm{\omega }}_1)}$ = 25 μm using F/20 optic to an intensity of 6.5 × 10¹⁸ W/cm² [$a_{0({\mathrm{\omega }}_1)}$ = 1.74], which can excite a plasma wakefield that self-traps and accelerates background electrons from the underdense plasma (n_e = 4 × 10¹⁸ to 8 × 10¹⁸ cm⁻³) in a laser-ionized helium or a mixed helium-nitrogen (99.5% He +0.5% N₂) gas flow from a 4-mm-long slit-shaped wave-free nozzle (see Fig. 1A) (19). The 200-mJ laser pulse passes a 300-μm-thick β-barium borate (BBO) crystal to generate an SH laser pulse (central wavelength λ₂ ≈ 400 nm) with ~65% efficiency (see Materials and Methods). After passing a variable delay stage (τ₁), the SH pulse is collinearly focused tightly, to a spot size of $w_{0({\mathrm{\omega }}_2)}$ = 2.5 μm, onto the gas jet by a short focal length off-axis parabola to a peak intensity of 2.8 × 10¹⁹ W/cm² [$a_{0({\mathrm{\omega }}_2)}$ = 1.81, where ω₂ = 2ω₁]. The remaining FL pulse after the BBO crystal is extracted through a dichroic beam splitter (DBS) and is used for online probing the plasma via interferometry (see Fig. 1B) (20) and for synchronization, i.e., determination of the zero relative time (T₀ ~ 0 fs) between the two-color laser pulses via shadowgraphy (21) (see Materials and Methods) with the assistance of another variable delay stage (τ₂). A forward optical imaging system is moved in and out of the laser axis regularly (every 5 laser shots, with roughly 1 shot/min), used to monitor and correct the two focal spots and to ensure the coaxial overlapping of the two laser beams (see Fig. 1C). Another top-view imaging system collects the scattered laser-plasma light to discern the propagation and overlapping of the two laser beams. By means of those imaging systems and the shadowgrams, we managed to monitor and control the overlapping of the two laser beams in space and time.

Fig. 1. Schematic of the experimental setup for a laser-plasma electron accelerator using the CTLP scheme.

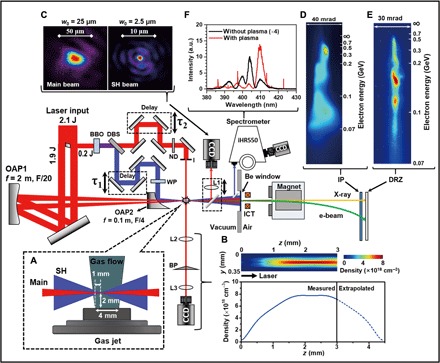
The 4-inch, 2.1-J, 800-nm, and 30-fs p-polarized laser pulses are split into two laser beams: 1.9-J FL infrared (800 nm) beam and 100-mJ SH ultraviolet (400 nm) beam. The former is focused onto 4-mm-long slit-shaped gas jet using an (F/20) off-axis parabolic mirror (OAP1) [see (A)]. The SH 1-inch laser pulses are generated in a BBO crystal and filtered by a DBS. After a variable time delay of τ₁, they are focused collinearly with the 1.9-J FL beam onto the gas jet by using a short focal length (F/4) optic with a small hole (OAP2). The polarization of the SH beam is controlled via half- or quarter-wave plates (WP) (see text). The remnant FL laser beam after the BBO serves as an ultrafast probe laser beam (~30-fs pulse duration). After a proper time delay of τ₂, the probe laser is used for a precise temporal-overlapping of the two ultrashort laser pulses via plasma shadowgraphy (see Materials and Methods and the Supplementary Materials). (B) The probe laser beam was also used for measuring the electron density profile via interferometry. (C) The two laser foci are monitored at lower intensities via a movable forward optical imaging system, which helps in simultaneously monitoring the spatial overlapping of the two laser beams just before shooting the CTLP lasers at high energy. These monitoring and optimization of the two laser spots and their spatial overlapping are repeated every five laser shots (roughly 1 shot/min) during the whole experimental campaigns. The accelerated electron beams exit the vacuum chamber through a thin Be window, propagate through an integrating current transformer (ICT) for measuring the charge, and then enter a 1-T permanent magnet spectrometer. (D) The electron energy spectra are recorded on an Al foil–shielded image plate (IP). (E) The electron spectra are also simultaneously recorded by a fluorescent (DRZ) screen coupled with an ICCD. (F) After the interaction, a portion of the scattered SH spectra is collected by an imaging optical spectrometer. a.u., arbitrary units.

The accelerated electron beams exit the vacuum chamber through a 300-μm-thick beryllium window into air and are detected by a calibrated integrating current transformer (ICT) (22) for monitoring the beam charge. Then, they are dispersed by a 16-cm-long, 1-T dipole magnet and simultaneously recorded on an absolutely calibrated image plate (IP) (23) and a Gd₂O₂S:Tb x-ray fluorescent (DRZ) screen, which is coupled with an intensified charge-coupled device (ICCD) to get the energy spectra, as shown in Fig. 1 (D and E). After interaction, the forward transmitted SH light is deflected by an off-axis glass plate onto an imaging spectrometer. Figure 1F shows the transmitted SH laser spectra in vacuum (black line) without plasma (gas jet off) and after interaction (red line) with the plasma, respectively. The vacuum SH laser spectrum has a main peak located around 404 nm, consistent with the numerical calculation (see Materials and Methods). As the LWFA is now driven by two copropagating femtosecond relativistic laser pulses, the frequency of the SH pulse is locally decreased by the wake wave excited by the leading FL pulse via the photon deceleration (24), indicating an energy loss from the SH pulse into the wake wave. In addition, the increase in the SH pulse spectral intensity (by a factor of 4) indicates a well-guidance of the SH pulse in the wake of the main FL beam. Here, note that the spectrum in Fig. 1F shows no features from laser-plasma parametric instabilities such as the forward Raman scattering, wave-wave interaction, and the Brillouin scattering. Generally, Raman instability is important for the self-modulated LWFA regime that uses long laser pulses. Although the stimulated Raman side scattering of an ultrashort (35 fs) high-power laser pulse has been observed in experiments, it is symptomatic of an unmatched interaction with a laser pulse longer than the relativistic plasma wavelength (relatively high plasma density) and occurs at the beginning of the interaction (25). In the experiments reported here, the laser had a pulse length of 30 fs, which is shorter than the plasma wavelength corresponding to the highest plasma density (8 × 10¹⁸ cm⁻³) in our experiments. Furthermore, the SH pulse plays an important role in a later stage of the acceleration process, as shown below in simulations. Similarly, the wave-wave and Brillouin instabilities are not playing an important role in our case because of the ultrashort nature of the laser pulses (plasma ions, which are essential for the Brillouin instability, are irresponsive on such an ultrafast time scale) and the relatively low plasma density, especially inside the wakefield cavity where the pulses are located (18).

Enhanced laser-plasma acceleration using two-color laser pulses

The experiments were carried out in two campaigns in 2017 and 2018. The first one was focused on self-trapping with wakefield wavebreaking injection in a helium gas jet, while in the second campaign, the focus was on ionization injection using a mixed gas target. This arrangement turned out to be very useful since the two different sets of experimental conditions allow one to examine the experimental data for possibly different physical mechanisms (18) in action when two laser pulses are used together to drive an LWFA. In the first campaign, a helium gas jet was used as the plasma source, and an IP was used to record the electron beam energy spectra. To save time from lengthy data retrieval procedures and to improve statistics over jittering of the spatial overlap of the two laser pulses, we accumulated five shots for each electron spectra read on the IP. Typical results (at timing overlap of the FL and SH) are shown in Fig. 2 (A to E). Using the 800-nm laser pulse alone with the full available energy of 2.1 J (P = 70 TW, τ = 30 fs, and $w_{0({\mathrm{\omega }}_1)}$ = 25 μm), we obtained an electron beam energy spectrum having two monoenergetic peaks at ~150 MeV ± 3% and ~75 MeV ± 1.5% at a plasma density of 8 × 10¹⁸ cm⁻³, as shown in Fig. 2A and in black in Fig. 2E (spectrum integrated over the transverse direction). On the other hand, by using the CTLP scheme with the SH laser beam having a linear polarization (p and s polarization states) and a time delay between the two laser beams of ≈0 fs at the same plasma density, the cutoff energy (maximum energy) of the electron beams has been markedly boosted [see Fig. 2 (B and C)]. The cutoff energy here is defined as the electron energy where the charge of the electron beam is below 0.02 pC/MeV.

Fig. 2. Electron energy spectra from the LWFA in a helium gas jet for four different cases and the effect of the time delay between the CTLP on the electron beam energy and charge.

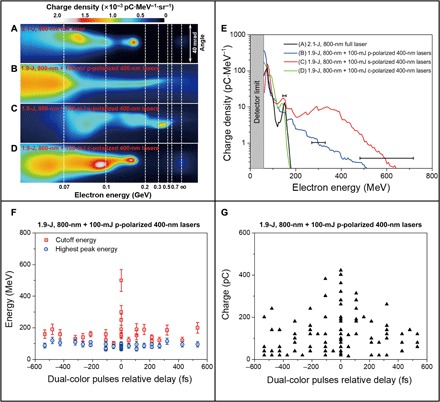
Each spectrum is obtained with an accumulation of data on the IPs from five laser shots (A) using the full FL (800 nm) laser pulse (E = 2.1 J) and (B to D) using the CTLP scheme with the clipped FL (800 nm, 1.9 J) and the SH (400 nm, 100 mJ) laser pulses of various polarizations for the SH pulse at a relative time delay of T₀ ≈ 0 fs. The plasma density, inferred from the interferometry, is n_e = 8 × 10¹⁸ cm⁻³. The signals shown at the ∞ direction are x-rays emitted spontaneously by the electrons as a result of their transverse betatron oscillations in the ion channel. (E) Vertically integrated electron spectra in logarithmic scale for the shots in (A) to (D). The horizontal error bars correspond to the resolution [estimated according to a method given in (29)] of the spectrometer, which are ±4.5, ±9, and ±19% at 150, 300, and 600 MeV, respectively. (F) Cutoff energies (red squares) and highest monoenergetic peak energy (blue circles) as a function of the time delay τ₁ between the two laser pulses, measured using the IPs. (G) Total electron beam charge as a function of τ₁, measured using the ICT. Each data point in (G) represents the result from a single laser shot. The data in (F) and (G) are obtained for the p-polarized SH laser pulses case. Positive time delays indicate that the SH pulse leads the FL pulse.

When the SH laser pulses are having parallel (p-) polarization (the same polarization as the FL pulses), the electron energy got a substantial boost (higher than twice), generating a bunch with a broad energy spectrum with a cutoff energy at ≈510 MeV ± 17%, as shown in Fig. 2B and in blue in Fig. 2E. Such a high-energy electron bunch is collimated with a full width at half maximum (FWHM) angular divergence of ~5 mrad. For the vertically (s-) polarized SH pulses (Fig. 2C and the red curve in Fig. 2E), the CTLP scheme leads to a further energy enhancement generating a quasi-monoenergetic (QME) bunch with a peak at ~340 MeV ± 10% and higher cutoff energy of up to ≈640 MeV ± 19% and an FWHM energy spread of 36%. Figure 2D shows the electron energy spectrum for the case when the polarization of the SH laser pulses was set to circular (c-). In this case, there was no clear enhancement of the electron energy. However, the total yield (charge) of the electron beam appeared to be higher than the case with the full FL pulses, as shown in green in Fig. 2E.

The time delay between the FL and the SH pulses τ₁ (being positive when the SH leads the FL), which can be controlled by a motorized optical delay stage, plays an important role in the observed boost of the electron acceleration. The minimum time step was around one laser pulse duration (~30 fs). Figure 2F shows the cutoff energy (red squares) and the highest monoenergetic peak energy (blue circles) in the electron energy spectra for various time delays between the two laser pulses of the CTLP scheme for p-polarized SH. Each data point is the result obtained from one IP, which accumulated five successive shots taken at the same polarization and time delay. The highest energy peaks only fluctuate at around 100 MeV over the whole range of timings, meaning that most of the electrons in the beam were self-trapped and accelerated in the plasma wake driven by the FL pulse. According to the statistical calculation for all the highest energy peaks at different delays, the ratio of the SD (σ = 15 MeV) to the mean value ($\overline{E}$ = 87 MeV) is 17%, which is much higher than the electron energy resolution at 100 MeV (±3%). Thus, this ratio can be considered as the percentage error in energy measurements for the current experiment, and the error bars in Fig. 2F are marked accordingly. Some enhancements appear in the electrons’ cutoff energy when the SH pulse leads the FL pulse, indicating that the SH pulse might have driven its own small wake wave and preaccelerated some electrons to enhance their subsequent injection by the FL pulse. However, when the CTLP overlapped sufficiently near the T₀ = 0 fs, a marked boost in the cutoff energy of the electron beam appears (as shown in Fig. 2F), a clear evidence of the beneficial effect of the CTLP scheme.

A similar time delay scan for the electron beam charge also shows enhancements around the T₀ = 0 fs, as shown in Fig. 2G. Since the beam charge measured from the IP only refers to those electrons with energies above 60 MeV and some of the electrons were lost during the propagation toward the magnet due to pointing instability as well, we used a calibrated ICT placed before the magnet (see Fig. 1 and fig. S1) to monitor the total beam charge with the whole range of energies in a single shot. Despite the substantial spread of the measured beam charges at one time delay, one can still see from Fig. 2G that as τ₁ is reduced from +533 to 0 fs, the maximum charge of the accelerated electron beam went up to ~420 pC from its initial value of ~120 pC. Similarly, the maximum charge measured drops down to ~140 pC at the timing of −426 fs. When the SH pulse lags the FL pulse by ≈107 fs, the maximum charge remains relatively high at ~380 pC. The considerable charge enhancement appearing between the timings of 0 and − 107 fs coincide with a distance of 32 μm, which is larger than two times but smaller than three times the plasma wavelength (for n_e = 8 × 10¹⁸ cm⁻³), ${\mathrm{\lambda }}_{\mathrm{p}}(\mathrm{\mu }\mathrm{m})=3.3 \times {10}^{10}/\sqrt{n_{\mathrm{e}}({\text{cm}}^{‐3})}=12 \mathrm{\mu }\mathrm{m}$, driven by the FL pulse. It suggests that the SH pulse has affected the injection-acceleration of electrons in the first and second plasma waves driven by the FL pulse. The underlying physics for the electron acceleration by using the CTLP scheme will be discussed below.

In the second experimental campaign, we first adapted the self-truncated ionization injection (STII) to maximize the electron beam energy and quality using the full FL laser pulse alone, as previously reported (26–28). This was simply done by shooting the main 800-nm laser pulses at the gas jet of mixed helium (99.5%) and nitrogen (0.5%) gases at a relatively low electron density. Meanwhile, a florescent DRZ screen imaged into an ICCD was added to the diagnostic system (behind the existing IP) to simultaneously record single-shot spectra of the accelerated electrons. Figure 3 shows six typical single-shot electron spectra obtained from 2.1-J (70 TW) laser pulses and a plasma density of 4 × 10¹⁸ cm⁻³. We can see that well-collimated (with average FWHM angular divergence of ~3 mrad) QME electron beams are produced with some energy fluctuations due to the fluctuations in the shot-to-shot laser power. However, it is shown that the energies of the electrons are enhanced by a factor of 2 or more as compared with the electron beams generated from the helium gas jet using the 800-nm pulses with the same laser power, at the plasma density of 8 × 10¹⁸ cm⁻³ (see Fig. 2A). The peak and cutoff energies could reach 300 and 350 MeV ± 5%, respectively, as shown in shots #3 and #5 (Fig. 3). Two vertically separated electron bunches are sometimes generated from a single laser shot, as shown in shots #3 to #6 (Fig. 3). This could be a result of multiple injections of two electron bunches at different times during the propagation.

Fig. 3. Typical electron energy spectra (left column) recorded on the fluorescent DRZ screen and the vertically integrated spectra in linear scale (right column) from 2.1-J, 800-nm full laser pulses.

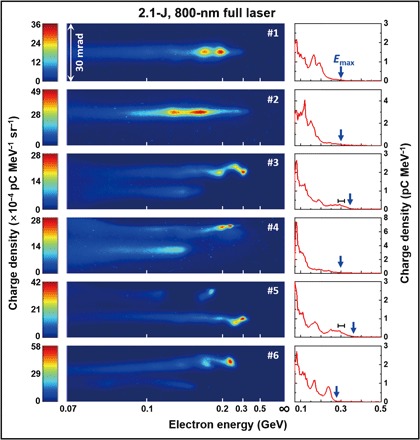
The plasma medium is composed of mixed gases of 99.5% He and 0.5% N₂, and the plasma density is n_e = 4 × 10¹⁸ cm⁻³. The blue arrows indicate the cutoff energy E_max in the integrated spectra. The horizontal error bars in the right column correspond to the resolution of the spectrometer, which is ±5% at 300 MeV, applicable to each spectrum in this figure.

On the other hand, by using the CTLP scheme with a zero time delay in the same plasma medium (99.5% He +0.5% N₂) at the same plasma density (4 × 10¹⁸ cm⁻³), a further enhancement has been achieved in the electron beam acceleration. Figure 4A presents three typical electron energy spectra obtained from the CTLP scheme (1.9-J FL + 100-mJ p-polarized SH pulses). The left column shows images of the electron spectra recorded on the DRZ screen; to recognize the cutoff high-energy tails, we separated the vertically integrated spectra into two ranges of energy: 50 to 200 MeV (middle column) and 200 to 700 MeV (right column). It is seen that the cutoff energies of the electron beams in this case are boosted up to a maximum of 550 MeV ± 9% (shots #1 and #3) by using the CTLP. When the state of the SH laser pulses was changed into s-polarization, we observed additional boosts on the cutoff energies, as shown in Fig. 4B, where three typical shots are presented and a cutoff energy of ~ 600 MeV ± 10% is recorded on shot #5. In contrast to the CTLP results from the helium plasma (see Fig. 2D), when c-polarized SH laser pulse is used, Fig. 4C shows enhancement of the electron acceleration as well. The cutoff energies in this case are around 500 MeV ± 8% in all the three shots in Fig. 4C. We have therefore demonstrated a clear and additional enhancement by 50 to 250 MeV in the cutoff electron beam energy using the CTLP scheme in the plasma of He-N₂ gas mixture as compared with the energies achieved from the STII using full-power single laser pulses.

Fig. 4. Electron energy spectra from the two-color LWFA in a helium-nitrogen gas jet.

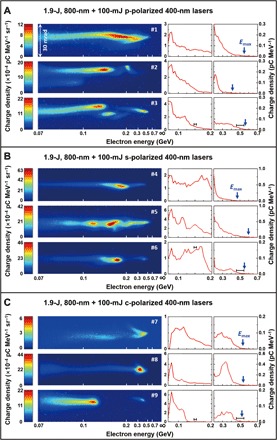
Typical electron energy spectra (left column) recorded on the fluorescent DRZ screen and the vertically integrated spectra in linear scale (middle column, electron spectra in the range of 50 to 200 MeV; right column, electron spectra in the range of 200 to 700 MeV) from the two-color LWFA (CTLP) scheme using (A) 1.9-J, 800-nm laser and 100-mJ p-polarized 400-nm laser; (B) 1.9-J, 800-nm laser and 100-mJ s-polarized 400-nm laser; and (C) 1.9-J, 800-nm laser and 100-mJ c-polarized 400-nm laser. The plasma medium is formed from the gas mixture of 99.5% He and 0.5% N₂, and the electron density is n_e = 4 × 10¹⁸ cm⁻³. The blue arrows indicate the cutoff energy E_max in the integrated spectra. The horizontal error bars (applicable to each spectrum in this figure) in the middle and right columns correspond to the resolution of the spectrometer, which are ±2.5 and ±8% at 150 and 500 MeV, respectively.

Applicability of two-color LWFA to generation of positron beams

To further confirm the enhancement in the electron acceleration from the CTLP-LWFA scheme and to explore its effectiveness, we adapted a standard setup (shown schematically in Fig. 5A and as a photograph in fig. S1) for positron beam generation through the bremsstrahlung radiation from the electron beams in 5-mm-thick Pb block (29). Previous research (29, 30) has shown that the yield and cutoff energy of the positrons can be enhanced by using a primary electron beam of higher energy and charge. For the positron beam generation, we used LWFA electron beams from the 99.5% He +0.5% N₂ plasma using the 2.1-J, 800-nm full laser pulses case and the CTLP scheme case (i.e., similar electron beams whose spectra are shown in Figs. 3 and 4B, respectively). The electrons impacted a lead slab (placed outside the vacuum chamber along the laser beam axis at a distance of 57.5 cm from the gas jet) with the size of 5.0 cm by 5.0 cm by 0.5 cm. The positrons, γ-rays, and secondary electrons escaping from the rear side of the Pb target are separated and spectrally resolved by a magnetic spectrometer, which comprised a pinhole entrance with a diameter of ~1 cm through 20 cm of plastic (Teflon, polytetrafluoroethylene) followed by 10 cm of lead (Fig. 5A). This plastic-lead wall is necessary to shield the positron detection from the strong radiation background generated during the primary electron beam impact onto the Pb block. After this collimator, the same permanent dipole magnet (B = 1 T, length of 16 cm) as in Fig. 1 was installed to spectrally resolve the secondary electrons and positrons, which were recorded by another calibrated IP (23) located 2 cm after the magnet. Such an arrangement allows resolving positron energies in the 40- to 400-MeV range.

Fig. 5. Experimental setup for the generation of positron beams based on the LWFA and energy spectra of electron-positron pair beams as recorded by the IPs for 5 mm of a Pb bremsstrahlung target.

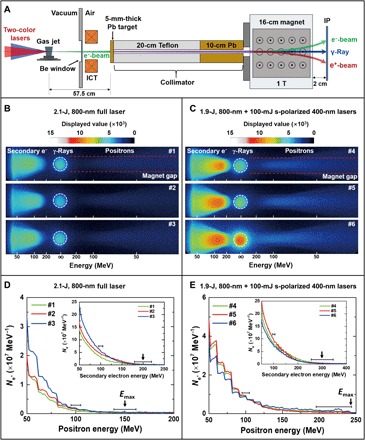
(A) Schematic of the experimental setup. The incident electron beams into the Pb target are produced from an LWFA driven by (B) full 2.1-J, 800-nm laser pulses alone and (C) two-color (CTLP) scheme where the SH pulses are in s-polarized state, respectively. The white dashed circles depict the bremsstrahlung γ-rays, whereas the red dashed lines depict the projection of the magnet gap. Because of the clear presence and collimation of the γ-rays, it is easy to distinguish and resolve the secondary electron beam spectra and the positron beam spectra. (D and E) Vertically integrated positron beam spectra in linear scale from (B) and (C) for two cases. The insets in (D) and (E) show the secondary electron beam spectra in linear scale. The horizontal error bars correspond to the resolution of the spectrometer, which are ±7, ±10, ±11, and ±15% at 150, 200, 220, and 300 MeV, respectively.

Figure 5 (B to E) shows the energy spectra of the positrons and secondary electrons resulting from an accumulation of 15 consecutive shots (i.e., 15 accumulated shots for each of the spectra from #1 to #6). Data recorded by the IP in the same range of displayed value are shown in Fig. 5 (B and C) for the two cases where the incident LWFA electron beams are accelerated by using the full 2.1-J, 800-nm single laser pulses (#1 to #3; Fig. 5B) and from the CTLP scheme (#4 to #6; Fig. 5C), respectively. The right sides (with respect to the γ-rays) in the images show the energy spectra of the positrons, whereas the left side shows the spectra of the secondary electrons.

It is clear that the yields of the positrons and secondary electrons are considerably boosted using the electron beams from the CTLP scheme. Vertically integrated spectra from the data (Fig. 5 D and E) indicate that the cutoff energies E_max of the positrons and secondary electrons have both increased by 1.5 times. In the case of using only the 2.1-J, 800-nm full laser pulse, the cutoff positron energy reached ≈150 MeV ± 7%, and the average yield of positrons is 3.4 × 10⁷ per shot. By using the CTLP scheme, the cutoff energy and average yield of the positrons are enhanced to ≈250 MeV ± 15% and 7.4 × 10⁷ per shot, respectively. The enhancements in the cutoff energy and average yield of the secondary electrons are also seen in Fig. 5C and are plotted in the inset of Fig. 5E, where the cutoff energy has increased from 200 MeV ± 10% (inset of Fig. 5D) up to 300 MeV ± 15% and the average yield rose from 2.5 × 10⁸ per shot to 4.5 × 10⁸ per shot.

DISCUSSION

To gain insight on the physical mechanisms involved in our LWFA experiments, we conducted a series of PIC simulations using the code OSIRIS (31) (see Materials and Methods) for the single laser pulse 2.1-J, 800-nm LWFA case and the CTLP scheme case, both in a helium plasma. First, the 2D simulation results obtained for the single laser pulse case are summarized in fig. S2, where panels (A) to (E) plot the laser fields and the corresponding electron density distribution in the x-z simulation plane at various stages of the acceleration process and panels (F) to (J) show the corresponding electron distribution in phase-space and energy spectra. Since the trailing bubbles evolve faster than the front ones, self-injection of electrons occurred primarily in the second wake bubble (32) after a propagation distance of ~1.22 mm, where the laser pulse is self-focused and the normalized vector potential a₀ reached ~4. After 1.28 mm of propagation, few electrons inside the second bubble (see fig. S2A) are accelerated to an energy of ~100 MeV (see fig. S2F). However, the acceleration of these electrons is quickly terminated at ~1.35 mm of propagation with a cutoff energy of 100 MeV because of the deformation of the second bubble and beam loading (33). Meanwhile, injection of the first electron bunch into the first wake bubble that contains the laser pulse started when a₀ reached a maximum value of ~6, as shown in fig. S2 (B and G), where the second bubble has almost disappeared. As the laser pulse propagates further in the plasma, the first-injected electron bunch in the first bubble has continually accelerated to higher energies, and the trapping into the first bubble of a second bunch started at ~1.9 mm and terminated at ~2 mm (see fig. S2C). As can be seen in the figure, a leading part of the first bunch already entered the deceleration phase, leading to the generation of a QME peak at around 300 MeV (see fig. S2H), and the second bunch could not catch up with the first bunch because of a weak accelerating field. As the depletion of laser pulse in the plasma continues rapidly, the first electron bunch gradually replaced the laser pulse as a driver, and the acceleration is transformed into a particle-driven wakefield acceleration (34). As shown in fig. S2D, the laser pulse has almost depleted, and the first bubble has greatly elongated. The second bunch is further accelerated up to ≈200 MeV by the wakefield, which is dominated by the first bunch with a cutoff energy of 375 MeV (see fig. S2I). After a propagating length of ≈3.1 mm, the whole accelerating structure has been washed away (see fig. S2E), and a final electron beam with the cutoff energy of 320 MeV (see fig. S2J) is emitted to the vacuum, while most electrons at the QME peaks have <200-MeV energy, which makes a reasonable agreement with the experimental results in Fig. 2A. The occurrence of two trapped bunches in the same bubble shown in the simulation could also explain the observation of multiple vertically separated electron signatures in some energy spectra in Figs. 2A and 3.

On the other hand, Fig. 6 shows the 2D-PIC simulation result for the laser wakefield accelerator driven by two-color laser pulses, where a combination of p-polarized FL and s-polarized SH laser pulses have been simulated. The combined laser fields (E_x, FL and E_y, SH pulses) and the electron density distribution in the x-z simulation plane at various acceleration stages are shown in Fig. 6 (A to E), and the corresponding electron phase-space and energy spectra are shown in Fig. 6 (F to J). First, the guidance of the SH laser pulse inside the wake bubble created by the main FL pulse is seen over the entire 4-mm length of interaction. At the early stage of interaction in this case, there seems to be no advantage for the CTLP scheme; the first electron bunch was self-injected into the second bubble and accelerated to nearly 100 MeV as shown in Fig. 6 (A and F).

Fig. 6. 2D-PIC simulation results for an LWFA using the two-color (CTLP) scheme with p-polarized 1.9-J, 800-nm FL pulse and s-polarized 100-mJ, 400-nm SH pulse.

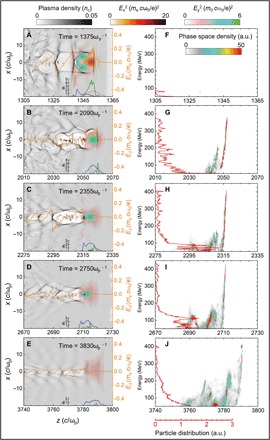
(A to E) Snapshots of the laser E-fields (E_x for the FL pulse; E_y for the SH pulse) and electron density distribution in the x-z plane at different times. (F to J) Energy-space distribution of the accelerated electrons with energies ≥50 MeV at respective times. a.u., arbitrary units. The red dashed plot in (A) is the initial laser normalized vector potential (a₀) distribution of FL pulse. The green and blue plots in (A) to (E) are the evolution of a₀ for the FL and SH pulses, respectively. The orange lines in (A) to (E) show the evolution of the on-axis longitudinal electric field (E_z) at different times. The red solid lines in (F) to (J) represent energy spectra of the electrons at respective times, showing a cutoff energy around 450 MeV at 2.7 mm; then, it drops to 420 MeV after 3.8 mm of propagation.

Then, the two bunches in the second bubble gradually dissipated in the plasma because of the extinction of the wake bubble structure; at the same time, self-injection and acceleration of electrons into the first bubble appeared when the 1.9-J, 800-nm FL pulse was self-focused to its maximum value. After that, several electron bunches are trapped and accelerated in the first bubble (Fig. 6B), and the cutoff electron energy could reach 375 MeV at this stage (Fig. 6G). As the depletion of the 1.9-J, 800-nm FL pulse continues rapidly, the SH pulse takes over as a booster for an additional acceleration of the electrons, which partially overtook the SH pulse’s tail. As can be seen in Fig. 6C, the leading electron bunch, which has a much smaller geometrical size [as compared with that produced using the single-pulse case (see fig. S2D)], started entering the fields of the SH pulse and then was accelerated directly by those fields (see Fig. 6D) up to the cutoff energy of 450 MeV (see Fig. 6I). Therefore, the trailing SH pulse allows the acceleration process to persist and continue for a longer distance of >1 mm as compared with the acceleration by a single full FL laser pulse, leading to the electron energy boost. Such an energy gain for the electrons and the long interaction distances of the SH laser beam are consistent with the fact that, theoretically, the laser pump depletion length in an underdense plasma (12, 35) [given by $L_{\text{pd}}=({\mathrm{\omega }}^2/{\mathrm{\omega }}_{\mathrm{p}}^2){\mathrm{\lambda }}_{\mathrm{p}}(a_0/3\mathrm{\pi })$; $a_0^2>>1]$ for the shorter wavelength SH (400 nm) laser beam is fourfold longer than the depletion length for the longer wavelength FL (800 nm) beam for the same plasma density. The same scaling also applies for the acceleration distance or the dephasing length [given by, $L_{\mathrm{d}}=({\mathrm{\omega }}^2/{\mathrm{\omega }}_{\mathrm{p}}^2){\mathrm{\lambda }}_{\mathrm{p}}(2a_0^2/\mathrm{\pi })$; $a_0^2>>1]$ (12, 35). Last, close to the end of the simulation (see Fig. 6E), an electron beam having a cutoff energy of 420 MeV is generated (see Fig. 6J). Because of the limits of the 2D-PIC simulation, the cutoff energy of the final electron beam generated appears lower than those of the experiment. However, the main physical mechanism for the LWFA using the CTLP scheme of combined and enhanced wakefield acceleration from the two-color laser pulses has been reasonably elucidated, in good agreement with the 3D simulations (17).

In addition, more simulations have been conducted for the CTLP scheme for the cases of p- and c-polarized SH laser beams. In those simulations, the SH beam again could propagate distances much longer than the main FL beam, being guided within the wake bubble and eventually boosting the energy of the accelerated electrons. For linearly polarized laser beams, the electric field is enhanced by $\sqrt{2}$ than circularly polarized laser beam of the same intensity. Ionization injection is therefore enhanced when linearly polarized light is used, qualitatively explaining the polarization dependences observed in the experiments using pure helium gas (Fig. 2). When mixed gases are used, the reduced ionization potential of nitrogen gas allows enhanced ionization injection even when circularly polarized SH was used, leading to the observed mild dependence on polarization in the second campaign of experiments using mixed gas jet targets.

In conclusion, we experimentally demonstrated a two-color laser-plasma electron accelerator based on a relativistically intense CTLP scheme in pure helium and in a mixture of helium and nitrogen gas targets. Such a scheme yields considerably higher electron energies and charges as compared with the results from an LWFA driven by a single FL pulse of equivalent power. The enhancement in the electron energy spectrum has been further confirmed experimentally in a bremsstrahlung-based positron beam generation, which then led to a substantial boost in the positron beam energy spectrum as well. 2D-PIC simulations support the experimental results quite reasonably. In addition to an enhanced ionization injection from the intense SH pulse, the well-guidance of the SH pulse inside the wake wave leads to the persistence of the acceleration process for a distance longer than possible in the single FL laser beam case, in agreement with some of the theoretical research. In the future, more studies on the CTLP scheme may potentially lead to energy enhancements for a larger population of electrons, namely, those at the monoenergetic peaks. It is also important to exploit the CTLP scheme for achieving very hard synchrotron (betatron) x-rays from laser-plasma accelerators using laser systems of modest power; this is expected because the critical energy (ħω_c) of the betatron x-ray photons scales quadratically with the electron beam’s relativistic factor γ. Thus, the CTLP scheme has the potential in reducing the laser power requirements for the generation of higher-energy electron beams from laser-plasma accelerators and paves the way toward their use in practical applications such as compact sources of hard x-rays, secondary radiation, and particles.

MATERIALS AND METHODS

Simulation of SH generation process in a BBO crystal

A 3D (x, t, z) calculation of the coupled-wave equations describing the process of the SH generation (SHG) was conducted using the split-step Fourier method (36). The transverse diffraction and longitudinal dispersion effects were considered in the calculation. The incident FL wave was assumed to be a Fourier transform–limited pulse with a duration of τ₀ = 30 fs. With a beam aperture of 25 mm in flat-top shape, this incident pulse at 800 nm had an average intensity of 1.36 × 10¹² W/cm². All the widths refer to the FWHM. The SHG crystal adopted a 0.3-mm-thick type I β-BBO crystal (cut at θ = 29.2°) with an effective nonlinear coefficient of 1.93 pm/V. By setting the FL spectrum to the experimentally measured one (see fig. S3A), the calculation gave the theoretical SH spectrum plotted as the blue line in fig. S3B, which shows a spectral range (390 to 420 nm), matching the experimental spectrum well (Fig. 1F). Figure S3C depicts the intensity profile of the SH (blue line) and FL (solid red line) pulses output from the SHG crystal, as well as the incident FL pulse (dashed red line). This result shows that the generated SH pulse had a walk-off from the FL wave, which was attributed to their different group velocities. Such a temporal walk-off was bound to lead to the increase of SH pulse energy level off, as indicated by fig. S3D, at the range of 130 mJ, corresponding to an SHG efficiency of 65%.

Synchronization of FL and SH laser pulses

We used a method based on side-view shadowgram (21) obtained from the 800-nm probe beam to determine the relative time zero T₀ between the FL and SH pulses at low energy. As shown in Fig. 1, we used two optical delay stages (τ₁ and τ₂) to change the delay of the SH and probe beams with respect to the main FL beam, respectively. Because the optical path of main FL beam was fixed, we adjusted the delay stage τ₂, at first, to capture the shadowgraph of the main plasma filament by the probe beam and to determine the FL pulse front in the shadowgram. Then, we fixed the delay stage τ₂ and adjusted τ₁ to capture the shadowgraph of the narrow SH laser-plasma filament and to see the waist of the SH pulse in the shadowgraph. Last, the zero time was determined when the laser fronts of the two pulses coincided on the side-view shadowgraph, as shown in fig. S4. To get a clear shadowgram (e.g., fig. S4), the energy of the main FL and SH laser pulses was set to 120 and 8 mJ, respectively, and a nitrogen gas jet at high pressure was used. In fig. S4, the FL and the SH pulses were intentionally misaligned in the vertical direction for the purpose of visualization.

PIC simulation

The 2D-PIC simulations were conducted using the code OSIRIS (31). In the simulations, the plasma medium was helium with a trapezoidal profile extended from z = 0 to 5 mm (1-mm linear entrance and exit ramps and a 3-mm plateau). The electron density of the plateau was 8 × 10¹⁸ cm⁻³ in all simulations, where the critical density for 800 nm laser was 1.745 × 10²¹ cm⁻³. The simulation box size was 100c/ω_p × 100c/ω_p, which moved with the speed of light c and was divided into 2400 × 700 cells along the z and x directions, respectively, with 16 particles per cell. For the single FL pulse simulation (see fig. S2) case, the laser beam at the FL frequency ω₁ = 7.854ω_p was initialized in vacuum and focused at 1200c/ω_p with the following parameters: $a_{0({\mathrm{\omega }}_1)}$ = 1.83, pulse duration ${\mathrm{\tau }}_{\mathrm{L}({\mathrm{\omega }}_1)}$ = 9ω_p⁻¹, spot size $w_{0({\mathrm{\omega }}_1)}$ = 25c/ω_p, and p-polarization. For the two-color (CTLP) scheme simulation (see Fig. 6), only $a_{0({\mathrm{\omega }}_1)}$ was changed to 1.74 for the main FL beam, and the SH beam with frequency of ω₂ = 2ω₁ was initialized in the simulation box at a distance of 5c/ω_p behind the main FL beam and focused at 1200c/ω_p with the following parameters: $a_{0({\mathrm{\omega }}_2)}$ = 1.8, pulse duration ${\mathrm{\tau }}_{\mathrm{L}({\mathrm{\omega }}_2)}$ = 9ω_p⁻¹, spot size $w_{0({\mathrm{\omega }}_2)}$ = 2.5c/ω_p, and s-polarization. Here, “ω_p” was a reference plasma frequency determined by either reference plasma density “n₀” or ω_p in the simulation setup. If we set the laser frequency ω₀ = A in the simulation, it means that ω₀ = A × ω_p; then, we have (ω₀/ω_p)² = A² = n_c/n₀, c/ω_p = λ_p/2π = (A/2π)λ₀, and 1/ω_p = T_p/2π = (A/2π)T₀. In the simulation, space and time were normalized to laser units, respectively. Thus, if A = 7.854, then we have c/ω_p = 1 μm. In the simulation, the neutral gas was defined as helium, and the ionization was modeled in a code based on the Ammosov-Delone-Krainov tunnel ionization model (37). We specified the maximum number of ionization levels of helium to be 2, and the ionization rate for each ionization level was defined and given in (38).

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/5/11/eaav7940/DC1

Fig. S1. A top-view photograph of the experimental setup used for the generation of positron beams based on the LWFA.

Fig. S2. 2D-PIC simulation results for an LWFA driven by full 2.1-J, 800-nm, and 30-fs laser pulse with p-polarization.

Fig. S3. Simulation of the SHG process.

Fig. S4. Side-view plasma shadowgraph for the relative time zero (T₀ ~ 0 fs) between the main FL and SH pulses. A 30-fs probe laser beam (800 nm) was used as a back lighter.