Experimentally quantifying the feasible torque space of the human shoulder

Abstract

Daily tasks rely on our ability to generate multi-dimensional shoulder torques. When function is limited, strength assessments are used to identify impairments and guide treatment. However, these assessments are often one-dimensional and limited in their sensitivity to diagnose shoulder pathology. To address these limitations, we have proposed novel metrics to quantify shoulder torque capacity in all directions. To quantify the feasible torque space of the shoulder, we measured maximal volitional shoulder torques in 32 unique directions and fit an ellipsoid model to these data. This ellipsoid model was used to quantify overall strength magnitude, strength balance, and the directions in which participants were strongest and weakest. We used these metrics to characterize three-dimensional shoulder strength in healthy adults and demonstrated their repeatability across days. Finally, using musculoskeletal simulations, we showed that our proposed metrics can distinguish between changes in muscle strength associated with aging or rotator cuff tears and quantified the influence of altered experimental conditions on this diagnostic capacity. Our results demonstrate that the proposed metrics can robustly quantify the feasible torque space of the shoulder and may provide a clinically useful description of the functional capacity of the shoulder in health and disease.

Introduction

Every day we use our arms and hands to complete a variety of tasks. From brushing our teeth to serving a volleyball, these tasks rely on our ability to generate three-dimensional (3D) shoulder joint torques [Hall et al., 2011, Santago et al., 2017, Vidt et al., 2016]. We transition between tasks in part by adjusting the magnitude and direction of torque about the shoulder to meet task-specific mechanical demands. Injury or pathology can impair muscle strength and coordination, disrupting torque production and often resulting in pain or dysfunction [Kelly et al., 2005, Steenbrink et al., 2010].

Many rehabilitation paradigms aim to identify and resolve the factors contributing to functional impairments by evaluating shoulder torque capacity (i.e. strength). Though normative shoulder strength has been established in particular planes of motion [Hughes et al., 1999, Van Harlinger et al., 2015, Westrick et al., 2013], overall torque capacity remains poorly understood. Strength in all directions can be quantified by the feasible torque space – the set of achievable torques about the shoulder defining the bounds within which we function [Valero-Cuevas, 2009]. Feasible sets have been used to describe human neuromuscular capacity, including the center-of-mass acceleration during standing balance [Kuo and Zajac, 1993] and isometric endpoint force generation [Gruben et al., 2003, Hernandez et al., 2015, Kutch and Valero-Cuevas, 2011], but have not been used to describe in vivo shoulder torque capacity. We propose that quantifying the feasible torque space of the shoulder may lead to a better understanding of the strength required for daily tasks and how this strength is altered by age, injury, or pathology.

There are many clinical assessments of shoulder strength; strength can be measured isometrically or dynamically, in functional planes or in postures targeting particular muscles [Greenfield et al., 1990, Hislop et al., 2013, Kendall et al., 2005, Leggin et al., 1996]. In each case, torque or force production is quantified by a dynamometer or graded using a 0 to 5 scale while participants produce maximal effort or resist motion in a direction that is cued by the assessor [Kendall et al., 2005]. Because torque direction is not typically quantified, clinical assessments are limited in their ability to quantify strength in the many degrees of freedom required for daily tasks. This limits the sensitivity of current tests for detecting pathology or explaining differences in performance [Hegedus et al., 2012, Kim et al., 2009]. To address these limitations, we propose that metrics describing the 3D feasible torque space of the shoulder are needed to improve diagnostic sensitivity and inform rehabilitation.

Our goal was to develop metrics capable of assessing the influence of muscle strength and coordination on shoulder torque production in all directions. We measured maximal volitional torques in 32 unique directions and used these data to model torque capacity about the shoulder. This model was parameterized by an ellipsoid that characterized the maximum feasible torque space. The parameters of this ellipsoid were used to quantify overall shoulder strength, the balance of strength about the joint, and the directions in which participants were strongest and weakest. We used these metrics to characterize the feasible torque space of 16 healthy adults, evaluated the repeatability of the metrics describing this space across days, and simulated the sensitivity of these metrics to changes in muscle strength that are commonly associated with aging and rotator cuff tears. Finally, we simulated how variation in participant effort or a reduction in the number of directions collected would impact the certainty with which we could detect strength differences associated with aging and rotator cuff tears. We anticipated that the proposed metrics would be robust and provide a clinically useful description of the functional capacity of the shoulder in health and disease.

Methods

Participants

Sixteen healthy volunteers (8 men, 8 women) from 21 to 36 years old (mean ± standard deviation: 27.3 ± 4.7 years) participated in this experiment. All participants were right hand dominant and reported no history of right shoulder pain or injury that required medical care. A brief clinical screening was performed to ensure participants had full, symmetric, and pain-free shoulder and cervical spine active range of motion. All participants completed the experiment without pain.

To assess test-retest repeatability, nine participants (5 men, 4 women, 27.9 ± 5.0 years) repeated the protocol on a second day (2 to 87 days after initial session). Participants reported no injury or change in activity level between sessions. This study was approved by Northwestern University’s Institutional Review Board and all participants provided written informed consent prior to completing the experiment.

Experimental setup and protocol

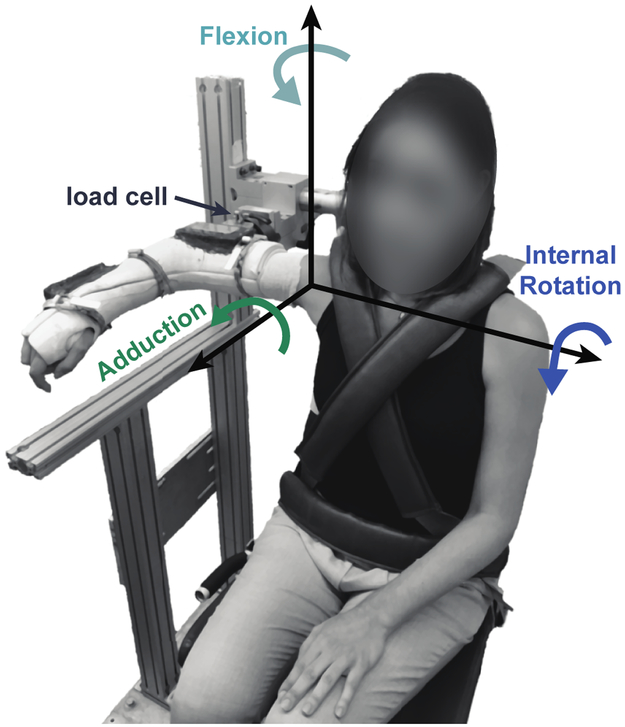
Participants generated isometric shoulder torques while seated with their right arm casted and attached to a six degree-of-freedom load cell (45E15A4, 630N80 load rating, JR3, Woodland, CA, USA). Data were collected in a single posture, with the arm abducted 90 degrees in neutral external/internal rotation with the elbow flexed 90 degrees (Figure 1). Forces and torques were measured at the attachment point of the cast to the load cell. Resting forces and torques from the weight of the arm were subtracted, and the remaining data were transformed to a local glenohumeral coordinate system [Wu and Cavanagh, 1995].

Figure 1: Experimental set-up.

Participants were seated with their right arm casted, abducted 90 degrees, and attached to a 6 degree-of-freedom load cell. Real-time visual feedback of 3D isometric shoulder torques were provided on a computer screen in front of the participant to assist with task completion.

To establish the feasible torque space, each participant maximized their isometric shoulder torque in 32 distinct directions. This number was a compromise between the many possible directions for exploring the feasible torque space and avoiding participant fatigue. First, participants maximized their shoulder torque in 26 uniformly distributed directions. Aided by real-time 3D torque visual feedback, participants maintained their maximum shoulder torque for at least one second in each target direction. Participants were allowed multiple attempts and unlimited time to accomplish this task. To minimize the influence of fatigue, the 3D target directions were grouped into three blocks and randomized within blocks. In the first block, target directions had only one non-zero component. In the second block, target directions had two non-zero components. In the third block, targets had three non-zero components. For example, a target in the first block may require participants to maximize their torque in abduction while keeping torque in all other directions close to zero. A target in the third block may require participants to maximize their combined torque in abduction, internal rotation, and flexion together. Practice trials were standardized to familiarize all participants to the visual feedback and task. In addition to the 26 uniformly distributed directions, participants also maximized their torque along each direction of our measurement coordinate frame (Figure 1). In these six trials, participants were not required to precisely control torque direction and often generated out of plane torques.

Metrics describing the feasible torque space of the shoulder

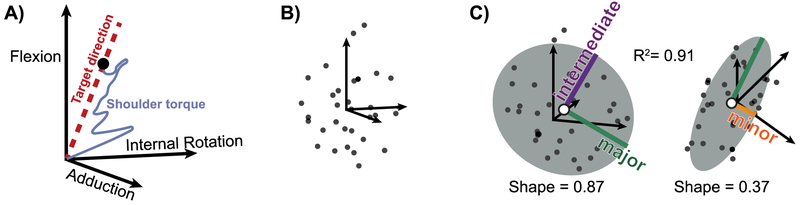
Torque data were processed to quantify overall shoulder strength, the balance of strength about the joint, and the directions in which participants were strongest and weakest. Data were smoothed using a 1-second moving average filter and the maximum torque in each direction was identified (Figure 2A). Together, these data represented a set of maximal feasible shoulder torques for each participant (Figure 2B). Each data set was fit with an ellipsoid using least squares [Turner et al., 1999]. We calculated R² as a measure of how well an ellipsoid model fit each participant’s data (Figure 2C). Each ellipsoid was defined by nine parameters. From these parameters, we computed the principal axes and 3D center location for each ellipsoid and used these values to compute descriptive metrics of the feasible torque space [Petrov, 2015].

Figure 2: Data processing to characterize the feasible torque space.

A) Raw 3D torque data were smoothed with a 1-second moving average filter and the maximum torque along each target direction was found (black dot). A single trial is plotted, with a target direction (red dotted line) corresponding to torque in flexion combined with adduction. B) Each participant maximized their torque in 32 unique directions. Here, the maximum torque in all directions are plotted for a single participant. C) An ellipsoid model (grey) was fit to each participant’s feasible torque set (black dots) using least squares. We computed the R² as a measure of goodness of fit. The major (green), intermediate (purple), and minor (orange) principal axes and center of the ellipsoid (white dot) are shown. Ellipsoid shape was computed in each plane as the ratio of the intermediate to major ellipsoid axes and the ratio of the minor to major ellipsoid axes.

Strength is typically quantified as the magnitude of force or torque generated in a particular direction. To quantify strength in all directions, we computed the Euclidian norm of the vector containing the radii along each ellipsoid principal axis, which produces units that are consistent with strength magnitude as opposed to alternative metrics of ellipsoid size, such as volume (Figure 2C, Eq. 1).

$$\text{Strength Magnitude}=\sqrt{{({\text{radius}}_{\text{jmajor}})}^2+{({\text{radius}}_{\text{jintermediate}})}^2+{({\text{radius}}_{\text{jminor}})}^2}$$ (1)

In addition to strength magnitude, strength balance in opposing directions is also used to assess injury risk and diagnose shoulder pathology [Byram et al., 2010, Kim et al., 2009]. Strength balance is typically assessed as a ratio of strength in two antagonistic directions, a measure not easily generalized for more than two directions. To expand this concept, we used the 3D location of the ellipsoid center to quantify the balance of strength between antagonist directions across the full feasible torque space (Figure 2C). An ellipsoid centered at the origin would indicate that strength is balanced along each axis (i.e. flexion strength equal to extension strength). In contrast, if the shoulder was stronger in flexion than in extension this imbalance would be quantified as a shift in the ellipsoid center toward flexion. To compare across participants, strength balance in each axis was normalized by overall strength magnitude.

Finally, the directions in which strength is altered also informs clinical decision-making. For example, external rotation and abduction weakness may suggest rotator cuff pathology [Hegedus et al., 2012]. Therefore, we were interested in determining participants’ strongest and weakest directions across the entire feasible torque space. We quantified participants’ strongest and weakest directions as unit vectors defining the major and minor principal axes of their strength ellipsoids (Figure 2C). In addition, we used the magnitude of these axes to characterize the shape of each participant’s ellipsoid. Specifically, we computed shape as the ratio of the intermediate to major ellipsoid axes and the ratio of the minor to major ellipsoid axes [Gomi and Osu, 1998, Krutky et al., 2013, Perreault et al., 2001],

We performed statistical analyses to evaluate overall shoulder strength, the balance of strength about the joint, and the directions in which participants were strongest and weakest in healthy adults. We tested the null hypothesis that each strength metric was equal to zero using one-sample t-tests. To determine if the metrics were different between men and women, we used two-tailed, two-sample t-tests. We used a significance level of α= 0.01 to account for multiple comparisons.

Test-retest repeatability of the feasible torque space metrics

We quantified the test-retest repeatability of our approach by calculating the intraclass correlation and cross-correlation coefficients for each metric across two sessions. The intraclass correlation coefficients (ICC) compared the variance across participants to the variance across sessions using the ICC(1,1) calculations proposed by Shrout and Fleiss [Shrout and Fleiss, 1979]. While ICCs are widely used as a measure of repeatability, they do not account for the mean value across samples and are known to be sensitive to sample homogeneity [Atkinson and Nevill, 1998]. Therefore, to account for these characteristics of our data, we also computed the cross-correlation coefficient for each metric, which does not have the same limitations [Stoica and Moses, 2005].

Sensitivity to simulated changes in shoulder function

Part of our motivation for quantifying the feasible torque space of the shoulder was to improve the sensitivity of strength assessments to changes in shoulder function. We used musculoskeletal simulations of aging and rotator cuff tears to evaluate how these conditions might influence our proposed metrics. We used an established upper extremity model developed in OpenSim as our baseline condition [Delp et al., 2007, Saul et al., 2015]. Similar to previous studies at 90 degrees of shoulder abduction, we reduced the anterior deltoid flexion moment arm in the baseline model to match measurements made in this posture [Hu et al., 2011, Kuechle et al., 1997]. This change helped match our baseline simulation to our experimental data but did not influence our conclusions regarding the sensitivity of our metrics to simulated changes in shoulder function. Aging was simulated by scaling the force generating capacity of each muscle by its ratio of muscle volume in older adults to younger adults [Holzbaur et al., 2007, Vidt et al., 2012]. The force generating capacity of 8 of the 11 included muscles was reduced by 10% or more (24 ± 13%, range 10-48%). In contrast, the biceps brachii, teres major, and latissimus dorsi muscle volumes did not differ with age and therefore their force generating capacity remained relatively intact. Finally, we simulated full-thickness rotator cuff tears of the supraspinatus alone (RCT 1), supraspinatus and infraspinatus (RCT 2), and supraspinatus with infraspinatus and subscapularis (RCT 3) by setting the force generating capacity of the involved muscles in the older adult model to zero [Vidt et al., 2018].

To compare the feasible torque space of the shoulder across conditions, we computed each model’s maximum shoulder torque in the same 32 directions used experimentally. We found the maximum feasible torque in each direction using an optimization algorithm developed previously [McKay et al., 2007, Sohn et al., 2013]. We computed feasible torque metrics from these simulated data as was done for the experimental data. Our ability to detect changes in shoulder function with each metric independently was determined by a z-score comparing each simulated condition to the baseline model. We used the standard deviation of our male participants (n=8) to estimate population variability because the models were developed using anatomical data from men. Assuming a normal distribution, we computed the probability associated with each z-score. We then used the Mahalanobis distance to evaluate differences between our simulated conditions using all metrics combined. The Mahalanobis distance is a statistical measure of the distance between two n-dimensional vectors [Mahalanobis, 1936]. In our analysis, the vectors being compared each contained the feasible torque space metrics for a musculoskeletal model. The Mahalanobis distance is analogous to an n-dimensional z-score in which the variance used to compute the z-score is replaced by an n-dimensional covariance matrix. Because there is no variability associated with the musculoskeletal models, we computed the covariance matrix of our experimental data (n=8 male participants) to estimate population variability. To compare between models, we computed the Mahalanobis distance from the feasible torque space metrics of each model and our estimated population variability. Assuming a multivariate normal distribution, we found the probability associated with each distance as a measure of certainty that both models were from the same population [Elfadaly et al., 2016].

Sensitivity to number of torque directions and variation in participant effort

Our ability to detect strength differences between the baseline, older adult, and rotator cuff tear models is dependent on the variability of the population. Our ability to quantify this population variability will be affected by experimental factors, such as the number of torque directions collected and variation participant effort. Therefore, we tested the impact of these experimental factors on our estimate of population covariance, and hence the Mahalanobis distance between models. To assess the influence of the amount of data, we randomly sampled X points from the full set of collected torques for each participant. Points were sampled without replacement while reducing X from 32 (full data set) to 9 (minimum needed to fit an ellipsoid). We resampled each participant’s data 1000 times at each value of X and computed the feasible torque metrics for each new data set. Next, we simulated variation in effort by scaling each participant’s experimentally measured torques by a random gain. The random gain was selected from a normal distribution with a mean of 1 and a standard deviation that varied from 0 to 0.2, resulting in a simulated torque standard deviation ranging from 0% to 20%. We chose an upper limit of 0.2 because this was twice the average standard deviation of torque magnitude across sessions from our repeatability study. Again, we repeated this 1000 times at each level of torque variation (0 to 0.2) for each participant and computed the feasible torque metrics for each simulated data set. At each number of data points or level of torque variation we computed the average covariance matrix of the feasible torque metrics for the eight male participants across the 1000 repetitions. Using these estimates of population variability, we computed the Mahalanobis distance and associated probability between each of our simulated conditions at each number of torque directions and level of torque variation. We compared the probability for detecting strength differences across conditions to examine the robustness of our metrics to these potential experimental variations.

Results

The feasible torque data were characterized well (R²=0.86 ± 0.11; mean ± standard deviation) by subject-specific ellipsoids (Figure 2C). Therefore, we were confident that our computed metrics were representative of the underlying feasible torque space for each participant. Results are reported as the mean ± standard deviation unless otherwise noted.

The shoulder feasible torque space in healthy adults

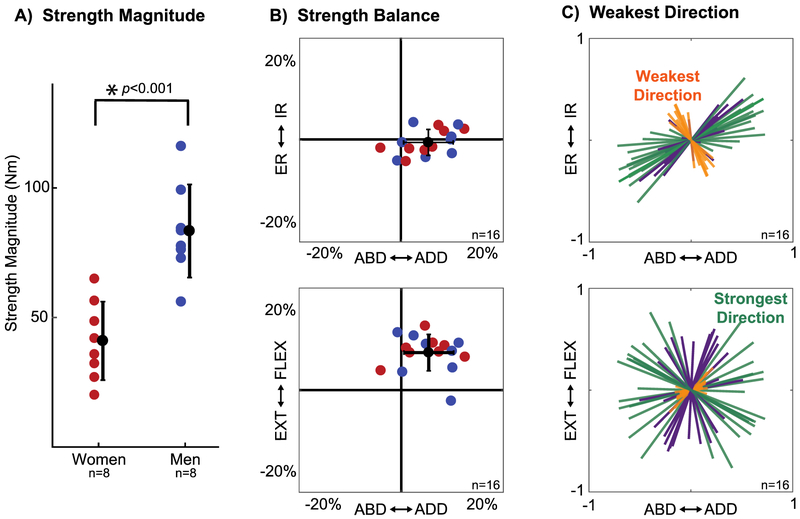
Strength varied across participants and was greater in men than in women (Figure 3A, Table 1). Strength was balanced in internal and external rotation (−0.7 ± 3.2%; p=0.37, t₁₅=−0.92), but imbalanced in the remaining axes (Figure 3B). This imbalance was small, but consistent, with participants 6.7 ± 6.1% stronger in adduction than abduction (p<0.001, t₁₅=4.43) and 9.2 ± 4.5% stronger in flexion than extension (p<0.001, t₁₅=8.20). We found no difference in strength balance between men and women (Table 1).

Figure 3: Characterization of the feasible torque space of the shoulder in healthy, young adults.

A) Overall strength magnitude for men (blue) and women (red). B) Strength balance (3D location of the ellipsoid center) shown from two perspectives for each participant (n=16). C) The orientation of the major (green), intermediate (purple), and minor (orange) principal axes of each participant’s ellipsoids plotted from two perspectives. The ellipsoid’s minor axis corresponds to participants’ weakest direction and the ellipsoid’s major axis corresponds to participants’ strongest direction. The mean and standard deviation of these metrics across participants are presented in Table 1. ABD: Abduction, ADD: Adduction, ER: External rotation, IR: Internal rotation, EXT: Extension, FLEX: Flexion.

Table 1.

The mean ± standard deviation of each metric reported for all participants (n=16) and for men and women separately (n=8). Seven metrics characterized the feasible torque space of the shoulder for each participant: strength magnitude; strength balance in abduction/adduction, external/internal rotation, and extension/flexion; and the abduction/adduction, external/internal rotation, and extension/flexion coordinates of a unit vector aligned to each participant’s weakest direction. Differences between men and women are represented by the p-values and t-statistics for each metric.

	Strength Magnitude (Nm)	Strength Balance			Weakest Direction
		ABD / ADD (%)	ER / IR (%)	EXT / FLEX (%)	ABD / ADD (unitless)	ER / IR (unitless)	EXT / FLEX (unitless)
All(n=16)	62.2 ± 27.1	6.7 ± 6.1	−0.7 ± 3.2	9.2 ± 4.5	0.45 ± 0.13	−0.83 ± 0. 12	0.16 ± 0.22
Women (n=8)	41.0 ± 15.2	6.0 ± 6.4	−0.8 ± 3.1	10.0 ± 3.1	0.38 ± 0.12	−0.89 ± 0.05	0.15 ± 0.15
Men (n=8)	83.4 ± 18.0	7.5 ± 6.1	−0.7 ± 3.5	8.4 ± 5.6	0.53 ± 0.09	−0.77 ± 0.14	0.18 ± 0.28
p-value	<0.001	0.623	0.955	0.491	0.014	0.039	0.831
t-statistic (t14)	−5.10	−0.50	−0.05	0.71	−2.81	−2.28	−0.22

ABD: Abduction, ADD: Adduction, ER: External rotation, IR: Internal rotation, EXT: Extension, FLEX: Flexion

Participants were not equally strong in all directions. Shape in the intermediate-major axis plane was 0.74 ± 0.15 across participants (p<0.001, t₁₅=−6.98), whereas shape in the minor-major axis plane was 0.37 ± 0.11 (p<0.001, t₁₅=−21.96). This contrast in shape between planes demonstrated that the strength ellipsoids were primarily flattened along the minor axis of each ellipsoid. This axis corresponded to participants’ weakest direction, which was highly consistent across our population (Figure 3C). All participants were weakest when combining internal rotation with abduction or external rotation with adduction. The weakest direction was aligned closer to the external/internal rotation axis in women than men, but this difference was not significant (Table 1). In contrast, we did not find a consistent strongest direction across participants, but rather a plane in which participants tended to be strongest. Feasible torques within this plane were close in magnitude, with the shape in this plane being closer to one (Figure 3C). Due to the lack of a clear and consistent strongest direction, we chose to use participants’ weakest direction as our sole metric of feasible torque space orientation. Therefore, for the remainder of our results, seven metrics were used to quantify the feasible torque space of the shoulder: overall strength magnitude; strength balance in abduction/adduction, external/internal rotation, and extension/flexion; and the abduction/adduction, external/internal rotation, and extension/flexion coordinates of a unit vector aligned to each participant’s weakest direction.

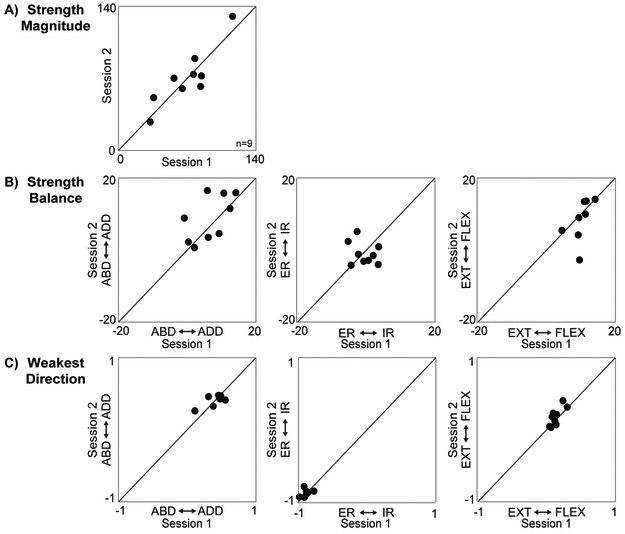
Test-retest repeatability

Strength magnitude was highly repeatable across sessions (Table 2, Figure 4A). While the cross-correlation was high for nearly all remaining metrics, the ICC(1,1) was low to moderate (0.40-0.69) for these same data (Table 2, Figure 4B-C). Lastly, we found very poor repeatability for the external/internal rotation component of strength balance (Table 2, Figure 4B); however, this was not surprising given that we found no significant internal/external rotation strength imbalance in healthy adults (Figure 3B).

Table 2.

Cross-correlation coefficients and intraclass correlation coefficients (ICC) for each metric, computed across two sessions (n=9).

	Strength Magnitude	Strength Balance			Weakest Direction
		ABD / ADD	ER / IR	EXT / FLEX	ABD / ADD	ER / IR	EXT / FLEX
Cross-Correlation Coefficient	0.99	0.86	−0.20	0.91	0.98	1.00	0.94
ICC(1,1)	0.89	0.57	−0.23	0.57	0.65	0.40	0.69

ABD: Abduction, ADD: Adduction, ER: External rotation, IR: Internal rotation, EXT: Extension, FLEX: Flexion

Figure 4: Test-rest repeatability.

Nine participants repeated the experimental protocol to determine how consistent the feasible torque space metrics were across sessions. We computed each participant’s overall strength magnitude, strength balance, and weakest direction from the torque data collected in each session. The metrics computed from session 2 are plotted vs. session 1 for each participant. The corresponding intraclass and cross correlation coefficients quantifying the repeatability of these data across sessions are presented in Table 2.

Feasible torque metrics are sensitive to simulated changes in shoulder function

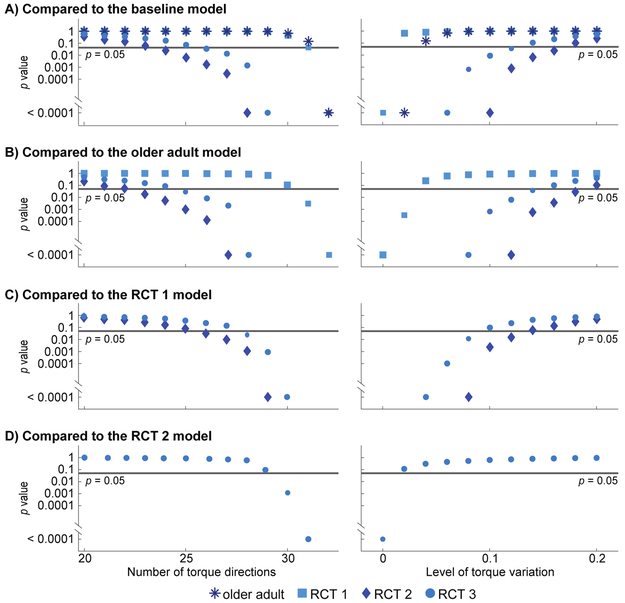
Using the feasible torque space metrics – strength magnitude, strength balance, and weakest direction - we were able to distinguish between musculoskeletal simulations of healthy individuals, older adults, and those with rotator cuff tears. While the models were fairly difficult to distinguish by each metric independently (Table 3), they became easy to discriminate when the metrics were combined and compared using the Mahalanobis distance (Table 4). Both the number of torque directions and simulated variation in the measured torque magnitude affected our certainty in distinguishing between conditions (Figure 5). The impact of these experimental factors varied across comparisons. For example, we could detect a strength difference between the RCT 2 model (tear of supraspinatus and infraspinatus) and older adult model using as few as 23 torque directions (Figure 5B). This difference could also be detected when simulated variations in torque magnitude had a standard deviation of up to 18% of the maximal torque. In contrast, it was more difficult to distinguish the RCT 1 model from the older adult model because an isolated supraspinatus tear caused a more subtle change in strength. We needed at least 31 torque directions to detect a strength difference between the RCT 1 model and older adult model (Figure 5B). In addition, simulated variations in torque magnitude with a standard deviation greater than 2% would obscure this difference. In spite of this sensitivity to experimental factors, these results show important clinical promise, as isolated supraspinatus tears cannot be reliably detected using current one-dimensional strength assessments [Hegedus et al., 2012, Kim et al., 2009]. Across all conditions, these results demonstrated that strength magnitude, balance, and weakest direction together were more sensitive to detecting different patterns of shoulder weakness than any single metric alone.

Table 3.

Z-scores and associated p-values comparing each simulated condition (aging and rotator cuff tears) to the baseline healthy model.

	Strength Magnitude	Strength Balance			Weakest Direction
		ABD / ADD	ER / IR	EXT / FLEX	ABD / ADD	ER / IR	EXT / FLEX
Older Adult	−1.04 (p=0.299)	0.14 (p=0.886)	−0.93 (p=0.351)	−0.93 (p=0.351)	0.12 (p=0.901)	0.02 (p=0.988)	−0.04 (p=0.968)
RCT 1	−1.32 (p=0.187)	0.81 (p=0.416)	0.45 (p=0.653)	−0.99 (p=0.323)	−0.43 (p=0.669)	−0.17 (p=0.864)	−0.09 (p=0.928)
RCT 2	−1.63 (p=0.103)	2.27 (p=0.023)	3.91 (p<0.0001)	−0.45 (p=0.650)	−2.00 (p=0.046)	−0.62 (p=0.533)	−0.41 (p=0.685)
RCT 3	−1.95 (p=0.052)	1.98 (p=0.048)	1.51 (p=0.132)	−1.13 (p=0.259)	−2.45 (p=0.014)	−0.76 (p=0.448)	−0.79 (p=0.428)

RCT 1: simulated full-thickness tear of the supraspinatus

RCT 2: simulated full-thickness tear of the supraspinatus and infraspinatus

RCT 3: simulated full-thickness tear of the supraspinatus, infraspinatus, and subscapularis

ABD: Abduction, ADD: Adduction, ER: External rotation, IR: Internal rotation, EXT: Extension, FLEX: Flexion

Table 4.

Multidimensional comparison between models using all seven metrics of the feasible torque space. The Mahalanobis distance and associated p-value for comparisons between all models are reported. In addition to comparing all simulated conditions to the baseline model (column 1), simulated conditions are also compared to each other (older adult vs. RCT 1, etc.).

	Baseline	Older Adult	RCT 1	RCT 2
Older Adult	55.3 (p<0.0001)
RCT 1	10.9 (p<0.0001)	44.7 (p<0.0001)
RCT 2	148.0 (p<0.0001)	203.3 (p<0.0001)	158.6 (p<0.0001)
RCT 3	130.1 (p<0.0001)	185.4 (p<0.0001)	140.8 (p<0.0001)	18.1 (p<0.0001)

RCT 1: simulated full-thickness tear of the supraspinatus

RCT 2: simulated full-thickness tear of the supraspinatus and infraspinatus

RCT 3: simulated full-thickness tear of the supraspinatus, infraspinatus, and subscapularis

Figure 5: The certainty with which strength differences between models could be distinguished was impacted by experimental factors.

The p-value associated with each Mahalanobis distance is plotted on a logarithmic scale for each model compared to the baseline (A), older adult (B), RCT 1 (C), and RCT 2 (D) models. The horizontal line indicates p=0.05 and symbols denote the model being compared to. Although we assessed as few as 9 torque directions, here we show the results only down to 20 directions (left column) as any fewer were unable to distinguish between models. The results corresponding to the original data set (full torque set with no torque variation) are presented in Table 4. RCT 1: simulated full-thickness supraspinatus rotator cuff tear; RCT 2: simulated full-thickness supraspinatus and infraspinatus rotator cuff tear; RCT 3: simulated full-thickness supraspinatus, infraspinatus, and subscapularis rotator cuff tear.

Discussion

This study provides the first description of the in vivo feasible torque space for the human shoulder. Our use of 3D torque visual feedback, multi-dimensional target directions, and a model to describe strength in all directions make these methods unique. By fitting subject-specific ellipsoids to maximal shoulder torques, we found that strength magnitude, strength balance, and a participant’s weakest direction could reliably describe the feasible torque space of the shoulder in healthy adults. We also demonstrated the potential utility of these metrics by determining their ability to distinguish between musculoskeletal simulations of healthy individuals, older adults, and those with rotator cuff tears.

Our quantification of the feasible torque space is consistent with reported measures of shoulder strength in healthy adults. As expected, overall strength varied across participants. Though it is difficult to compare our measure directly to literature values, the standard deviation of strength in our experiments (27.1Nm) closely matched results from prior studies (external rotation: 28.4Nm, abduction: 21.6Nm) [Kim et al., 2009]. We also found a difference in strength magnitude between men and women (Table 1, Figure 3A) that is consistent with prior studies [Riemann et al., 2010, Roy et al., 2009, Van Harlinger et al., 2015, Westrick et al., 2013]. For strength balance, we found a significant bias into flexion and adduction with relatively equal internal and external rotation strength in healthy adults (Table 1, Figure 3B). This is similar to prior studies that showed healthy adults are stronger in horizontal adduction than abduction (flexion vs. extension in our study) [Van Harlinger et al., 2015] and stronger in adduction than abduction [Hughes et al., 1999]. Symmetric isometric internal and external rotation strength has also been reported [Cools et al., 2016, Riemann et al., 2010], although this may differ in overhead athletes [Codine et al., 1997]. Finally, while previous studies found that internal/external rotation is the weakest axis when compared to adduction/abduction and flexion/extension [Van Harlinger et al., 2015], we found no studies that examined this over all directions. We extended these results to show that internal rotation with abduction or external rotation with adduction is the shoulder’s weakest direction when the full feasible torque space is considered (Table 1, Figure 3C). This is not surprising given that these actions are opposite to the natural coupling of muscle moment arms in the shoulder [Ackland et al., 2008, Ackland and Pandy, 2011, Ruckstuhl et al., 2009].

All but one of the feasible torque space metrics were consistent across days. Because strength magnitude varied across participants, and was repeatable across days, it has shown the greatest potential for describing individual differences within a healthy population. In contrast, strength balance and weakest direction were consistent across participants (Figure 3B-C), with low to moderate ICCs but high cross-correlation coefficients (Table 2). A low ICC in spite of a high cross-correlation coefficient can be explained by the size of within-subject variability relative to between-subject variability. Because strength balance and weakest direction were homogeneous across participants, even very low within-subject variability resulted in low ICC values for these metrics [Atkinson and Nevill, 1998]. In contrast, the cross-correlation coefficient takes into account a similar mean value across all participants and therefore was much higher despite low between-subject variability (Figure 4). These results suggest that strength balance and weakest direction may not distinguish between healthy adults, but instead may provide consistent markers of healthy shoulder strength from which to identify shoulder pathology.

While the diagnostic utility of our metrics has yet to be tested in vivo, our musculoskeletal simulations demonstrate promising initial results to support this potential. Given a fairly homogeneous population description, we found that our proposed metrics were quite sensitive to simulated changes in shoulder function (Table 4). Most notably, using the strength magnitude, strength balance, and weakest direction metrics together, we were able to distinguish between models of an isolated supraspinatus tear and an older adult with an intact rotator cuff (p<0.0001), which is not possible using current one-dimensional shoulder strength assessments [Hegedus et al., 2012, Kim et al., 2009]. Our modeling results showed that a full characterization of the feasible torque space resulted in greater discriminatory power than any single metric alone. In the future, this performance might be further improved by generating a more consistent set of normative data that accounts for age, sex, activity level, and other relevant factors to reduce inter-subject variability. In addition, these results suggest that it will be feasible to identify those with pathology using a classification algorithm. Together, these findings motivate experimental studies to further explore these metrics in older adults and those with pathology.

To improve the clinical feasibility of our proposed metrics, a few limitations must be addressed. First, the large number of measurements used to characterize the feasible torque space may restrict the clinical feasibility of this approach. In our current simulations, we needed 23 to 32 torque directions depending on the compared populations to detect differences in strength. Thus, this approach may be more feasible to distinguish between certain populations than others. In the future, it may be possible to reduce this number further by identifying the most critical directions for estimating the feasible torque space rather than taking a random sample. These optimal torque directions may identify a reduced set of directions to implement clinically, and may even allow for repeated measures that are often required in clinical populations [Abizanda et al., 2012]. Another limitation was that this study was restricted to a single posture. It will be important to determine how the feasible torque space varies throughout the range of motion to identify which postures are most sensitive to changes in shoulder function.

In conclusion, we developed, implemented, and assessed novel metrics to quantify the feasible torque space of the human shoulder. We presented normative data for the overall strength, strength balance, and weakest direction in healthy adults, and showed that these metrics are repeatable across days. Finally, our musculoskeletal simulations provided initial support for the diagnostic utility of these metrics, their robustness to the number of collected data points or small variations in participant effort, and their potential to improve our understanding of shoulder strength in healthy individuals, older adults, and those with pathology.

Biography

Emma Baillargeon is a Ph.D. candidate in the Department of Biomedical Engineering at Northwestern University. She is in a dual-degree program at Northwestern University, earning her Doctor of Physical Therapy degree in 2016. Prior to this, she received her B.S. and M.S. degrees in Bioengineering from the University of Pittsburgh. Her current research interests are in understanding how age impacts muscle coordination of the shoulder and the role of altered neuromuscular control in the onset and progression of orthopaedic pathologies.

Daniel Ludvig is a Research Assistant Professor at Northwestern University and Research Scientist at the Shirley Ryan AbilityLab. He completed his M.Eng. and Ph.D. degrees in Biomedical Engineering at McGill University. He then pursued a Postdoctoral Fellowship at the Rehabilitation Institute of Chicago and Northwestern University followed by a Research Fellowship at the University of Montreal. His research interest is in quantifying the role neuromechanics play in movement and postural control, and how alterations in these neuromechanics can lead to injury and disease.

M. Hongchul Sohn is currently a Postdoctoral Fellow at Northwestern University. He completed his B.S. degree in Mechanical and Aerospace Engineering from Seoul National University and earned his Ph.D. in Mechanical Engineering from Georgia Institute of Technology. His current research interests are in understanding the sensorimotor mechanisms underlying learning and generation of human movement, and how they are altered after neuromuscular injury and disease.

Constantine Nicolozakes is a dual M.D./Ph.D. student in the Department of Biomedical Engineering at Northwestern University. He received his B.S. in Biomedical Engineering from The Ohio State University in 2015. His current research interests are in quantifying the active neuromuscular control of shoulder stability and understanding how alterations in shoulder instability can be targeted with rehabilitative treatment.

Amee Seitz is an Associate Professor and Principal Investigator of the Musculoskeletal Biomotion Research Laboratory in the Department of Physical Therapy and Human Movement Sciences at Northwestern University. She completed her B.S. in Physical Therapy at Ohio University and M.S. in Orthopaedic Physical Therapy and Clinical Doctor of Physical Therapy degree from the MGH Institute of Health Professions. She earned a Ph.D. in Rehabilitation & Movement Science from Virginia Commonwealth University and completed a Postdoctoral Fellowship focused on Neuromuscular Control at the University of Kentucky. The focus of her research is to better understand the underlying mechanisms of musculoskeletal shoulder injuries, diagnosis, and treatment.

Eric Perreault is Professor and Chair of Biomedical Engineering at Northwestern University, with joint appointments in the Department of Physical Medicine and Rehabilitation, and at the Shirley Ryan AbilityLab. He received his B.Eng. and M.Eng. degrees in Electrical Engineering from McGill University and his Ph.D. in Biomedical Engineering from Case Western Reserve University. Eric’s research focuses on understanding the neural and biomechanical factors involved in the control of multi-joint movement and posture and how these factors are modified following neuromotor pathologies such as stroke and spinal cord injury. The goal is to provide a scientific basis for understanding normal and pathological motor control that can be used to guide rehabilitative strategies for individuals with motor deficits.