Dual-Domain Convolutional Neural Networks for Improving Structural Information in 3T MRI

Abstract

We propose a novel dual-domain convolutional neural network framework to improve structural information of routine 3T images. We introduce a parameter-efficient butterfly network that involves two complementary domains: a spatial domain and a frequency domain. The butterfly network allows the interaction of these two domains in learning the complex mapping from 3T to 7T images. We verified the efficacy of the dual-domain strategy and butterfly network using 3T and 7T image pairs. Experimental results demonstrate that the proposed framework generates synthetic 7T-like images and achieves performance superior to state-of-the-art methods.

1. Introduction

Magnetic resonance imaging (MRI) scanners use strong magnetic fields to generate soft-tissue images and are widely used for medical diagnosis and disease monitoring. It is often desirable to acquire images with fine voxel resolution for greater anatomical details, but this often results in lower signal-to-noise ratio (SNR) and longer scan times. To improve the resolution of magnetic resonance(MR) images while retaining sufficient SNR [12], efforts have been dedicated in the past three decades to enhance the magnetic field strength of MRI scanners.

The world’s first commercial MRI scanner was manufactured using a permanent magnet with low field strength in 1980 [20]. In 1982, the first MRI scanner operating at 1.5T with superconducting magnet was introduced. By 1985, 1.5T MRI scanners have become standard in clinical practices and remained so even to 2010. 3T MRI emerged in the early 2000s has been becoming more common in clinical settings. In 2017, the first 7T MRI scanner was approved for clinical use by the United States Food and Drug Administration (FDA)¹.

Fig. 1 shows a visual comparison of 3T and 7T MR images obtained from the same subject. Compared with 3T MRI, 7T MRI typically affords greater anatomical details, which can benefit disease diagnosis [28]. However, 7T MRI scanners are significantly more expensive and are hence less common in hospitals and clinical institutions. Todate, there are less than 100 7T MRI scanners worldwide [6]. In contrast, there are more than 20,000 3T MRI scanners conducting more than 60 million examinations annually.

Figure 1:

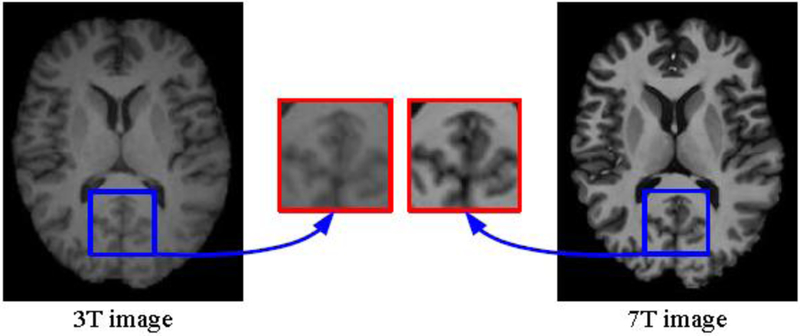
Compared axial views of 3T and 7T images acquired from the same subject.

In this paper, we propose a method for synthesizing high-resolution (HR) 7T-like images from low-resolution (LR) 3T images. Note that this is not a simple 25 super-resolution problem because the appearance and contrast of 7T images can be different from 3T images. We demonstrate that the reconstruction of 7T-like images from 3T MRI can be improved by concurrently considering the spatial and frequency domains in a convolutional neural network (CNN) framework.

2. Related work

To acquire high-quality synthetic images, quite a few machine learning methods have been proposed in recent years. Yang et al. [30] proposed a single image super-resolution method using coupled dictionaries trained from paired LR and HR image patches. Zhang et al. [34] presented a hierarchical patch-based sparse representation method for computed tomography (CT) resolution enhancement. Bhavsar et al. [4] introduced a group-sparse representation method for resolution enhancement of CT lung images. Rueda et al. [23] proposed a sparsity-based super-resolution method using coupled LR and HR dictionaries for brain MR images. Roy et al. [22] presented an example-based super-resolution framework to synthesize high-quality MR images from multi-contrast atlases. By joint modeling of complementary image priors on the gradients, self-similarity and sparsity, Zhang et al. [32] proposed a structure-modulated sparse representation method for image super-resolution. Bahrami et al. [3] presented a hierarchical sparse representation method based on multi-level canonical correlation analysis (M-CCA) for the reconstruction of 7T-like MR images from 3T MR images. To enhance the resolution of neonatal images, Zhang et al. [33] proposed a neonatal image super-resolution method with the guidance of longitudinal data of an identical subject. Subsequently, they [35] proposed a residual structured sparse representation method for neonatal image super-resolution using longitudinal data across subjects. However, restricted by hand-crafted features, these model-based methods cannot be automatically adapted to handling complex image synthesis problems. Besides, they also require tricky parameter tuning and time-consuming calculations for testing.

Recently, deep learning achieves impressive results and attracts great attention in the community of artificial intelligence. Dong et al. [5] introduced a deep learning approach for resolution enhancement. Mao et al. [18] presented a deep convolutional encoder-decoder network with symmetric skip connections for the improvement of training convergence and local optimal solutions. Bahrami et al. [2] developed a CNN-based approach that takes into account the appearance and anatomical features (CAAF) to predict 7T images from 3T images. By integrating adversarial loss and content loss as perceptual loss, Ledig et al.[16] proposed a generative adversarial network to generate super-resolved photo-realistic images. Tai et al. [26] proposed a deep recursive residual network via residual learning in a global and local sense. McDonagh et al. [19] proposed a context-sensitive upsampling method using a residual CNN model to produce sharp HR images. By generating more data for model training, Krizhevsky et al. [13, 14] proved that data augmentation can benefit the generalization ability of deep learning models for image classification. By introducing data augmentation, Li et al. [17] proposed a fully convolutional network based on deformable image registration for hippocampus segmentation. Touloupou et al. [27] employed data augmentation to estimate the marginal likelihood for the selection between competing statistical models. However, these data-driven methods are still unsatisfactory due to their limited modeling capabilities, even without consideration of specific attributes of MRI.

In this paper, we propose a dual-domain convolutional neural network (DDCNN) framework to solve the above-mentioned problems. DDCNN synthesizes 7T-like images from 3T MRI with two parallel and interactive multi-layer streams based on spatial and frequency domains. Our contribution is threefold:1) We propose a novel dual-domain convolutional neural network framework to learn complex mappings from 3T to 7T modalities; 2) We introduce both two complementary domains and parameter-efficient butterfly modules to assist deep learning; and 3) We implement numerical experiments to verify the efficacy of the proposed framework for improving structural information in 3T MRI.Comparisons with existing methods indicate that synthesized 7T-like images with higher quality can be obtained with DDCNN.

In our previously published conference paper [31], we proposed a dual-domain cascaded regression (DDCR) method for synthesizing 7T-like images from routine 3T images. As linear regression has limited ability to model complex mappings between 3T and 7T modalities, in this paper, we generalize DDCR to DDCNN using convolutional neural networks due to their high non-linear modeling ability. This paper serves three purposes. The first purpose is to further verify the efficacy of the dual-domain strategy and butterfly modules for deep learning. The second purpose is to provide additional method details,examples, results, discussion, and insights that are not presented in our conference publication [31]. The third purpose is to introduce a modification for the fusion of feature maps and domain transform, which uses fast Fourier transform(FFT), instead of discrete cosine transform (DCT), because FFT has wide applications. In experiments, we found the performance of DDCNN in this paper was often better than that of DDCR in our conference paper [31].

The remainder of this paper is organized as follows. Section 3 elaborates the proposed method. Section 4 presents experimental results and analysis. Section 5 provides discussions. Section 6 concludes the paper.

3. Method

In this section, given an input 3T image, we present a DDCNN model to directly learn a mapping function for improving its structural information and reconstructing its corresponding 7T-like image. We will elaborate the network architecture, image preprocessing and implementation details of the proposed model below.

3.1. Network Architecture

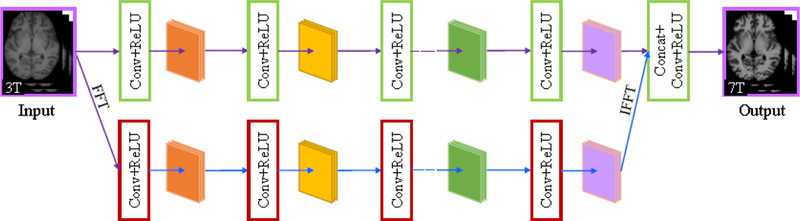
Fig. 2 illustrates the architecture of DDCNN. DDCNN uses five types of operations: forward fast Fourier transform (FFT), inverse fast Fourier transform(IFFT), convolution (Conv), concatenation (Concat), and rectified linear unit (ReLU) as the activation function. FFT and IFFT are used for signal conversion between spatial and frequency domains. Compared with the spatial domain, the frequency domain describes distribution features of signals from another aspect.By exploiting complementary information between spatial and frequency domains, we introduce the dual-domain strategy and butterfly modules to achieve high-quality synthesized images.

Figure 2:

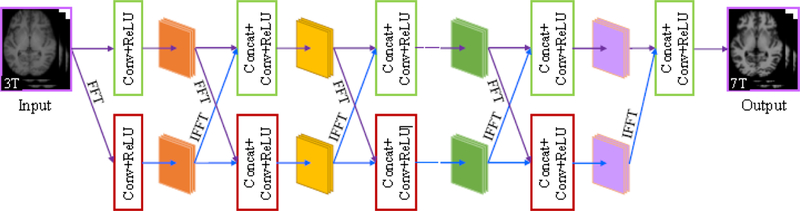
Network architecture of DDCNN.

As shown in Fig. 2, the proposed model consists of two parallel and interactive multi-layer network streams. These two streams complement each other on respective spatial and frequency domains, which help model the complex mappings between 3T and 7T images. To prevent the signal leakage in the network implementation, we employ complex-to-complex Fourier transforms for the interconversion between spatial and frequency domains. For data compatibility in the spatial domain, we take an input 3T block as the real part and its corresponding zero matrix as the imaginary part of complex-valued network input.On the other hand, we extract the magnitude component of complex-valued network output in the spatial domain as the synthesized 7T-like block.

With the 3T block of size H ×W × c as the input, DDCNN with depth L consists of three types of layers: input feature extraction layer, middle feature mapping layer, and output feature reconstruction layer. Fig. 3 shows the respective architectures of these layers. In each layer, both real and imaginary parts of complex-valued features are separately treated by the same operations, i.e., Conv+ReLU or Concat+Conv+ReLU. To verify the efficacy of the dual-domain strategy and butterfly modules, all layers are assumed to have the same number 2n_f of convolution filters on respective spatial and frequency domains.In the following, we will give a detailed illustration of these three layers. For simplicity, we only describe Concat, Conv and ReLU operations on real parts of complex-valued feature maps below.

Figure 3:

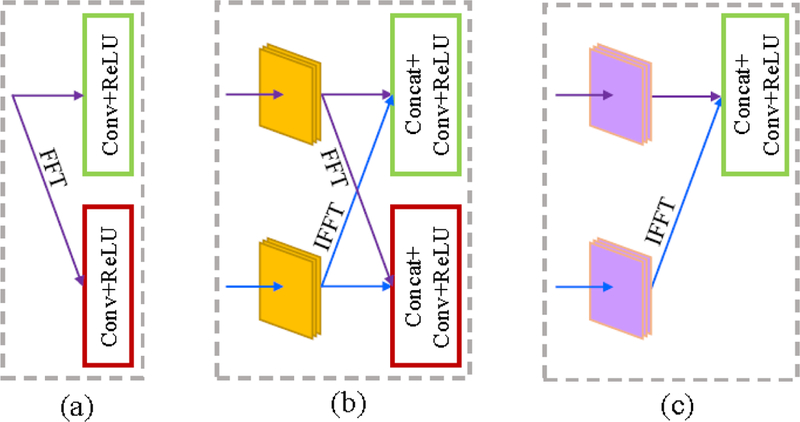
The respective architectures of three layers. From left to right: (a) the input feature extraction layer, (b) one butterfly module in the middle feature mapping layer, and (c) the output feature reconstruction layer.

(a). The input feature extraction layer:

This input layer consists of FFT and two Conv+ReLU operations on respective spatial and frequency domains,which is used to extract the feature maps from the original 3T images in two diffierent complementary domains. In this layer, FFT is used to convert the input 3T image block from the spatial domain to the frequency domain. n_f convolution filters of size k₁ × k₁ × c are applied to produce n_f feature maps and then ReLU is used for nonlinear mapping and training acceleration in the spatial domain. Similarly, another nf convolution filters of size k₁ × k₁ × c and ReLU are applied successively in the frequency domain.

(b). The middle feature mapping layer:

As shown in Fig. 2 and Fig. 3(b), this middle layer consists of L – 2 butterfly modules. Each butterfly module is composed of FFT, IFFT and two Concat+Conv+ReLU operations on respective spatial and frequency domains. Specifically, FFT is used to convert the output feature maps of the previous module (or layer) from the spatial domain to the frequency domain. On the other hand, IFFT is used to convert the output feature maps of the previous module (or layer) from the frequency domain to the spatial domain. For butterfly module L – 2l ∈{2,⋯, L–1}, in the spatial domain, after concatenating two groups of output feature maps from the previous module (or layer), n_f convolution filters of size k_l × k_l × 2n_f and ReLU are applied sequentially to generate n_f feature maps. Similarly, Concat, Conv and ReLU are applied sequentially to produce new feature maps in the frequency domain.

3.2. Image Preprocessing

A set of 3T and 7T image pairs are registered to the Montreal Neurological Institute (MNI) standard space [8] using FLIRT [9, 10] to remove pose diffierences. Specifically, all 7T images are linearly registered to the MNI standard space with an individual template [8]. Each 3T image is then rigidly aligned to its corresponding 7T image. After registration, bias correction [25] and skull stripping [24] are performed.

To reduce adverse impact of signal variation across different scanners and sites, we first normalize all MR images and then use histogram matching to make them similar in the intensity range. Specifically, first, an input 3T image and all pairs of aligned 3T and 7T training images are normalized to the Range [0,1] using $z=(z-z_{\text{min}})/(z_{\text{max}}-z_{\text{min}})$. Here z is the voxel value, z_min is the minimum value, and z_max is the maximum value of an image. Then all normalized 3T training images are matched to the normalized input 3T image by three-dimensional (3D) histogram matching, ensuring that all matched 3T training images have similar contrast ranges. Correspondingly, by 3D histogram matching, all normalized 7T training images are matched to the corresponding 7T training image, whose 3T training image is closest to the input 3T image.Thus, these matched 7T training images also have similar intensity and contrast ranges.

As the training data is small in this study, we use several data augmentation techniques [13, 14, 7], such as crop, flip and rotation, to enlarge the dataset for avoiding the over-fitting problem. We first crop the brains from the original training images. Then we use horizontal flip, vertical flip, 90-degree left rotation and 90-degree right rotation for data augmentation. Fig. 4 shows axial views of augmented training samples from one randomly selected subject. Data augmentation provides abundant variability of training dataset and makes it possible to train the proposed model without overfitting.

Figure 4:

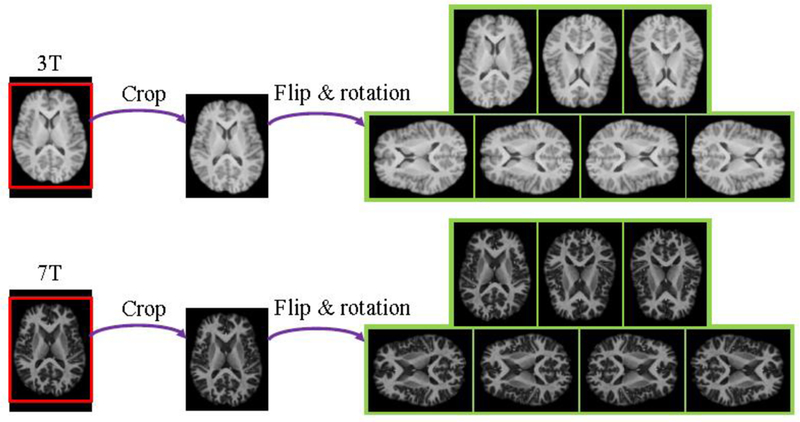
Visual comparison of axial views of augmented training samples from one subject.

3.3. Network Implementation Details

For an input 3T image X, DDCNN aims to learn a mapping function $\mathcal{F}(\mathbf{\text{X}};\Theta )$ for the prediction of the latent real 7T image Y. To learn the model parameters Θ, the loss function is enforced by minimizing the averaged mean squared error (MSE) between the synthesized 7T-like blocks and the groun-truth 7T blocks as follows:

$$\ell \left(\mathrm{\Theta }\right)=\frac{1}{2N}\sum _{i=1}^N{\Vert {\mathbf{\text{y}}}_i-\mathcal{F}({\mathbf{\text{x}}}_i;\mathrm{\Theta })\Vert }_F^2,$$ (1)

where ${\left\{\left({\mathbf{\text{x}}}_i,{\mathbf{\text{y}}}_i\right)\right\}}_{i=1}^N$ denotes N pairs of 3T and 7T training blocks, and ${\Vert \cdot \Vert }_F$ represents the Frobenius norm.

In our model, each 3T or 7T training block consists of several consecutive two-dimensional (2D) slices, which are extracted from corresponding 3D 3T or 7T training images. Once the model is properly trained, it is applied to an input 3T test image block by block and then the results are assembled to construct the whole synthesized 7T-like image. Due to the limitations of memory capacity and small data sets, it is not feasible to directly train a full 3D model in this study. As several consecutive 2D slices contain rich contextual information, the full 3D modeling is not necessary for this task.

We adopt an adaptive moment estimation (Adam) solver [11] with parameters β₁ = 0.9, β₂ = 0.999 and eps =1e – 08 for optimization. The learning rate starts at lr = 0.0001and then is decayed by a factor of 0.1 every 50 epochs. To reconstruct high-quality 7T-like images, we employ the cross-validation [1] for model selection by checking whether the model has been overfitted. The best trained model is applied to test images for synthesizing 7T-like images.

4. Experiments and Results

4.1. Dataset

Approved by the local institutional review board (IRB), 15 subjects were recruited for MR data acquisition in a large study of brain MRI measurement.They consist of 5 healthy subjects, 8 patients with epilepsy and 2 patients with mild cognitive impairment (MCI). The 3T and 7T brain images of all subjects were acquired with Siemens Magnetom Trio 3T and 7T MRI scanners,respectively. Specifically, for 3T MRI, T1 images of 224 coronal slices were obtained with the 3D magnetization-prepared rapid gradient-echo (MP-RAGE) sequence. The imaging parameters of 3D MP-RAGE sequence were as follows: repetition time (TR) = 1900 ms, echo time (TE) = 2.16 ms, inversion time (TI) = 900 ms, ip angle (FA) = 9°, and voxel size =1×1×1 mm³ For 7T MRI, T1 images of 191 sagittal slices were also obtained with the 3D MP2-RAGE sequence. The imaging parameters of 3D MP2-RAGE sequence were as follows:TR = 6000 ms, TE = 2.95 ms,TI = 800/2700 ms, FA = 4°, and voxel size = 0.65×0.65×0.65 mm³ All 3T images were resampled to the same spatial resolution of corresponding 7T images. As the gradient echo pulse sequences were used for image acquisition, there is only little distortion between the acquired 3T and 7T MR images, which ensures the imaging consistency across magnetic fields.

4.2. Experimental Setup

Extensive experiments were conducted to demonstrate the effectiveness of the proposed method. In all experiments, we adopted the leave-one-out cross-validation (LOOCV) for the evaluation. In each fold of LOOCV, one 3T image was chosen for testing, whereas the remaining paired 3T and 7T images were divided into 10 image pairs for training and 4 image pairs for validation. The real 7T image paired with the testing 3T image was treated as the ground-truth image. For avoiding overfitting in the cross-validation, the training and validation images were used to select the best model from different network architectures and training parameters. In network configuration, the network depth L = 4, the batch size b = 6, the input channel number c = 9, filter number n_f = 48, the convolution kernel size k₁ = 5 in the input feature extraction layer, k₂ = 3in the middle feature mapping layer, and k_L = 1 in the output feature reconstruction layer. The proposed models were implemented in Python with PyTorch and took approximately 2 days to train on an NVIDIA Titan Xp (i.e.graphics processing unit abbreviated as GPU).

For parameter settings, we manually tuned the parameters from the first layer to the last one, ensuring DDCNN close to its best performance. We also analyzed the robustness of DDCNN by changing a parameter while keeping all other parameters at their current values. As a function of the parameter value, the peak signal-to-noise ratio (PSNR) values were calculated between synthesized images and ground-truth images. For a randomly selected subject,

Fig.5 shows PSNR values by DDCNN against the changes of key parameters: c, n_f, L, k₁, k₂ and k_L. Given training data and optimization algorithms, PSNR first increases faster and then hardly increases as c or n_f grows, whereas PSNR decreases as k_L increases. With the increase of other parameters (i.e, L, k₁, k₂), PSNR basically increases first and then decreases. Further explanation of these parameters can be seen in the Discussion section.

Figure 5:

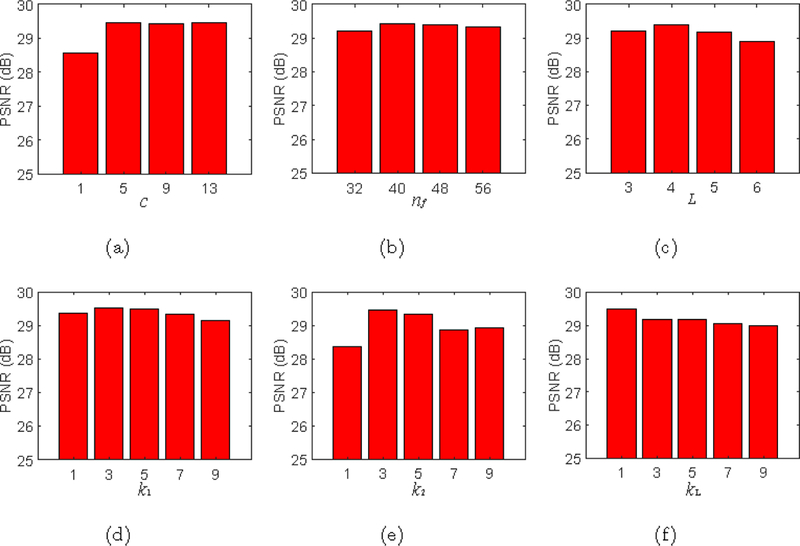
PSNR values given by DDCNN w.r.t. its key parameters.

4.3. Experimental comparison

Several relevant methods, such as histogram matching (HMAT) and CAAF[2], were used as baseline methods for comparison both qualitatively and quantitatively. We adopted Structural SIMilarity (SSIM) index [29] for quantitative mage quality assessment. All synthesized images achieved by baseline methods and our method were compared with the ground-truth images in term of SSIM.

Fig. 6 shows the box-plots of SSIM values of 15 synthesized 7T-like images obtained by different methods. As can be observed, DDCNN generally achieves higher SSIM than the other baseline methods. For further evaluation, the two sample t-tests [15, 33] was used to evaluate whether or not DDCNN outperforms the competing methods in SSIM. Table 1 gives $\mathcal{P}$ values of two-sample t-tests of SSIM results between DDCNN and the competing methods. The $\mathcal{P}$ values marked with an asteroid imply that DDCNN achieves significantly larger SSIM means than the competing methods.

Figure 6:

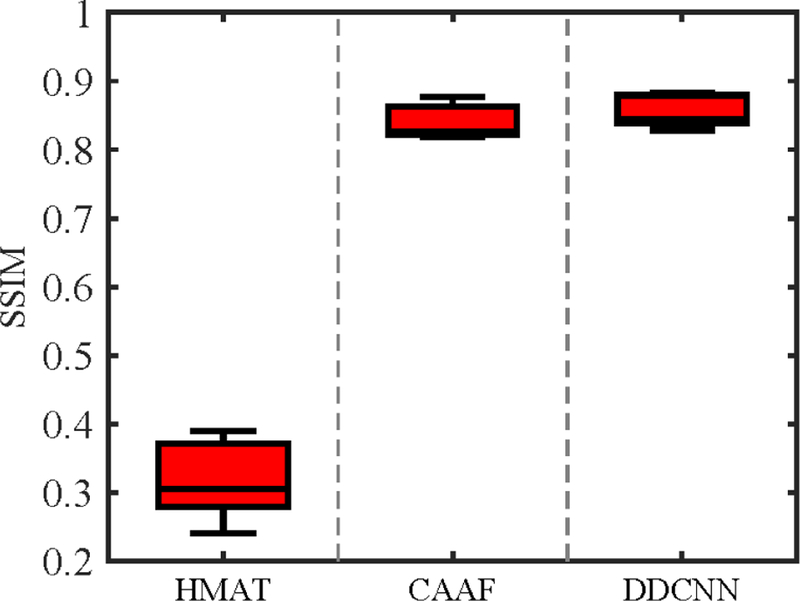
Box-plots for SSIM values. The middle line of each box is the median, the edges markthe 25th and 75th percentiles, and the whiskers extend to the minimum and the maximum. For all methods, the respective medians of SSIM values are as follows: (a) HMAT (SSIM=0.3050),(b) CAAF (SSIM=0.8258), and (c) DDCNN (SSIM=0.8438).

Table 1:

$\mathcal{P}$ values of two-sample t-tests of SSIM results between DDCNN and the competing methods. The asterisks indicate $\mathcal{P}$ values less than the threshold α_t = 0.05 chosen for statistical significance.

Index	HMAT	CAAF	SDCNN	PDCNN
SSIM	<0.0001*	0.0856	0.0097*	0.0176*

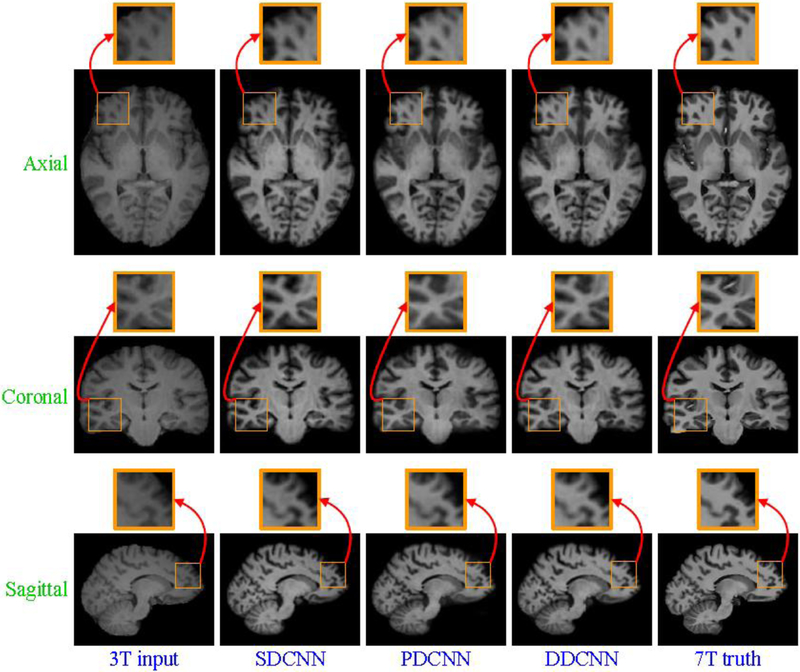
Besides quantitative evaluation w.r.t. SSIM, Fig. 7 and Fig. 8 separately show axial, sagittal and coronal views of synthesized 7T-like images for two randomly selected subjects, indicating that DDCNN achieves better visual effect and less distortion than the competing methods, i.e., HMAT and CAAF [2].

Figure 7:

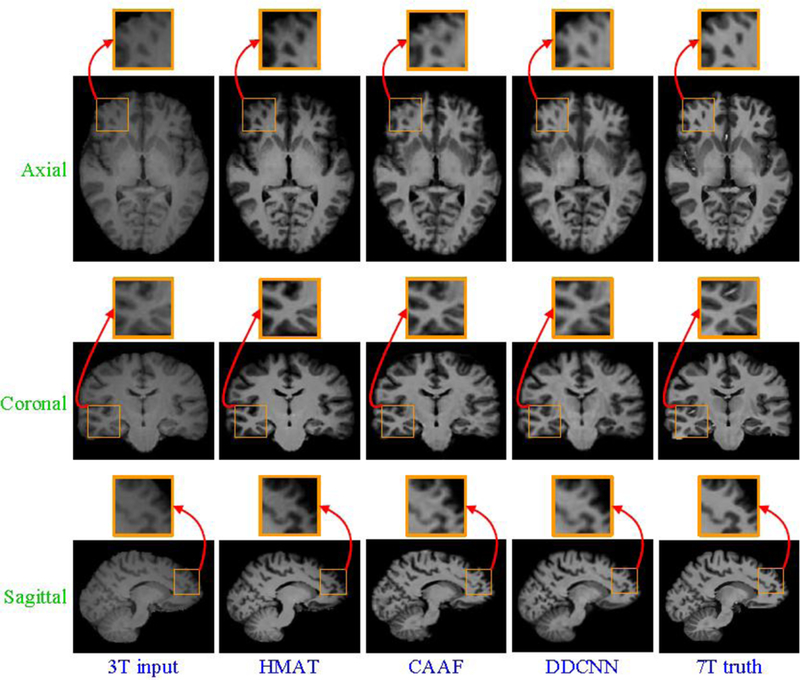
Visual comparison of axial, sagittal and coronal views of synthesized 7T-like images with close-up views of specific regions for one subject. For all methods, SSIM values are as follows: (a) 3T input, (b) HMAT (SSIM=0.3025), (c) CAAF (SSIM=0.8590), (d) DDCNN (SSIM=0.8792), and (e) 7T truth.

Figure 8:

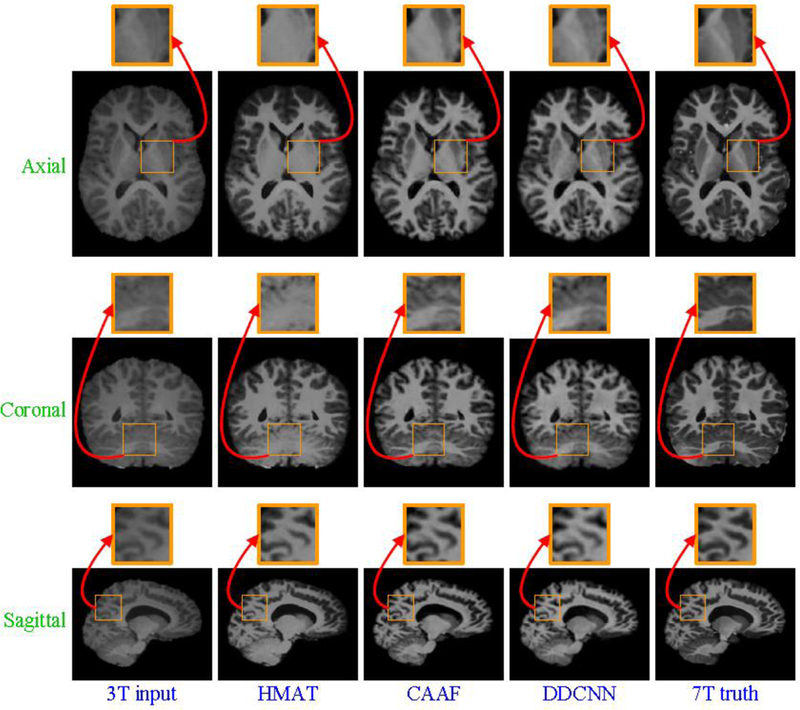
Visual comparison of axial, sagittal and coronal views of synthesized 7T-like images with close-up views of specific regions for another subject. For all methods, SSIM values are as follows: (a) 3T input, (b) HMAT (SSIM=0.3948), (c) CAAF (SSIM=0.8261), (d) DDCNN (SSIM=0.8359), and (e) 7T truth.

4.4. Ablation study

For further elaboration on the benefit of the dual-domain strategy for deep learning, we also compared DDCNN with single spatial-domain convolutional neural network (SDCNN) constructed by choosing the same parameters in the spatial domain. Fig. 9 shows the network architecture of SDCNN.

Figure 9:

Network architecture of SDCNN.

To evaluate the superiority of butterfly modules, we introduced a parallel-domain convolutional neural network (PDCNN) as a competing method. PDCNN was constructed by replacing the butterfly modules (see Fig. 10(a)) with the parallel modules (see Fig. 10(b)) and keeping the others invariant to DDCNN.Fig. 11 shows the network architecture of PDCNN.

Figure 10:

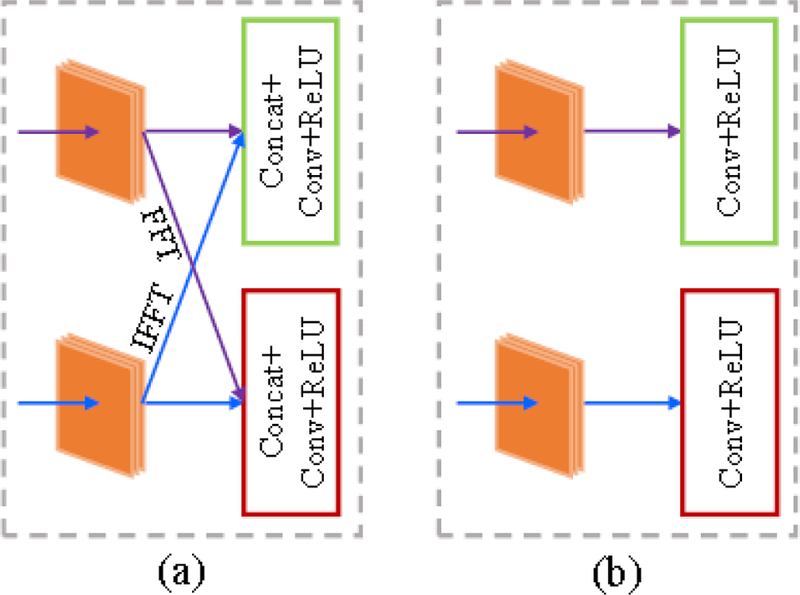
Structural comparison of the butterfly module and the parallel module. From left to right: (a) butterfly module, and (b) parallel module.

Figure 11:

Network architecture of PDCNN.

To verify the necessity of two domains and butterfly modules, we separately synthesized 7T-like images from the same set of 3T images with SDCNN, PDCNN and DDCNN. Fig. 12 shows the box-plots of SSIM values of 15 synthesized 7T-like images by these different methods. From Fig. 12, DDCNN achieves much higher SSIM than SDCNN and PDCNN. Table 1 indicates that DDCNN achieves significantly larger SSIM means than SDCNN and PDCNN, judging based on two-sample t-tests.

Figure 12:

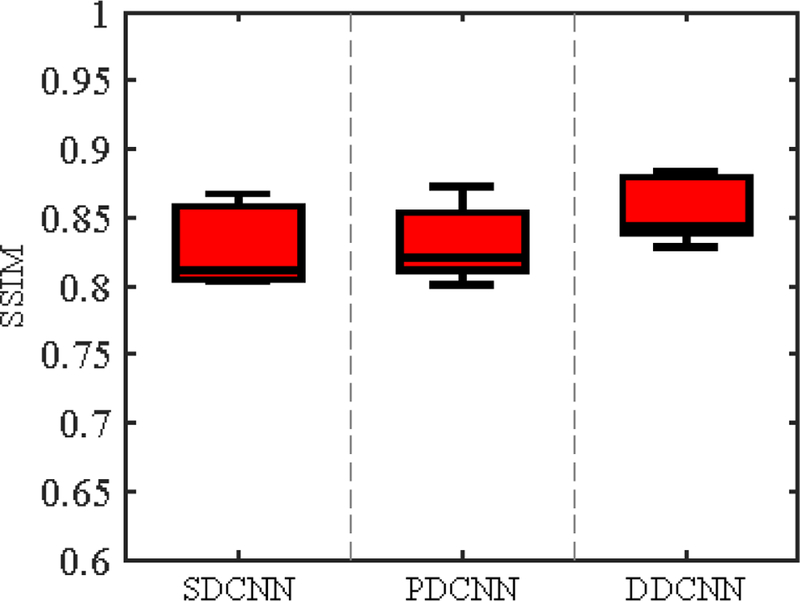
Box-plots for SSIM values. For all methods, the respective medians of SSIM values are as follows: (a) SDCNN (SSIM=0.8113), (b) PDCNN (SSIM=0.8206), and (c) DDCNN (SSIM=0.8438)

Besides the quantitative evaluation w.r.t. SSIM, Fig. 13 and Fig. 14 separately show axial, sagittal and coronal views of synthesized images for two randomly selected subjects, indicating that DDCNN has better visual results than SDCNN and PDCNN. Compared with SDCNN and PDCNN with parallel modules, DDCNN with butterfly modules makes great contributions to performance improvement of image synthesis. This indicates the necessity and superiority of the dual-domain strategy and butterfly modules.

Figure 13:

Visual comparison of axial, sagittal and coronal views of synthesized 7T-like images with close-up views of specific regions for one subject. For all methods, SSIM values are as follows: (a) 3T input, (b) SDCNN (SSIM=0.8584), (c) PDCNN (SSIM=0.8531), (d) DDCNN (SSIM=0.8792), and (e) 7T truth.

Figure 14:

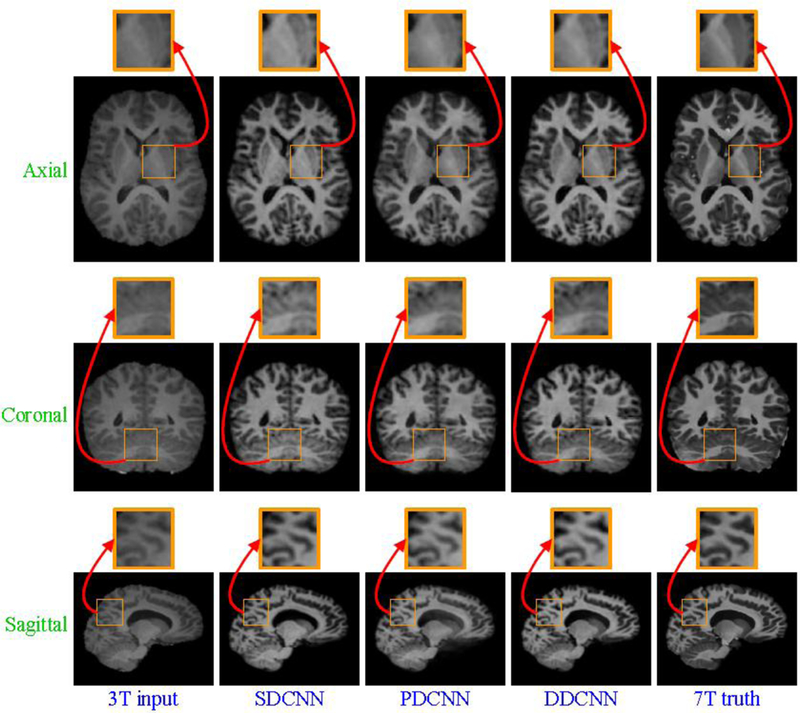
Visual comparison of axial, sagittal and coronal views of synthesized 7T-like images with close-up views of specific regions for another subject. For all methods, SSIM values are as follows: (a) 3T input, (b) SDCNN (SSIM=0.8134), (c) PDCNN (SSIM=0.8073), (d) DDCNN (SSIM=0.8359), and (e) 7T truth.

4.5. Brain tissue segmentation

We further evaluated the inuence of the 15 synthesized 7T-like MR images on the post-processing procedures, such as brain tissue segmentation. We adopted a two-dimensional (2D) U-Net [21] with default parameters for brain tissue segmentation. The brain tissues were separated into gray matter (GM),white matter (WM), and cerebrospinal uid (CSF). The hand-segmented results of 7T brain images were used as the ground truth. We compared the segmentation results of the original 3T images, and the synthesized 7T-like images by the competing HMAT, CAAF [2], SDCNN, PDCNN, and our DDCNN.

The segmentation results of synthesized images by U-Net [21] were evaluated using Dice similarity coefficient (DSC). Fig. 15 shows the box plots of DSC metrics for three brain tissues (i.e., GM, WM and CSF). Fig. 16 provides the visual comparison of segmentation results for one randomly selected subject.From Figs. 15 and 16, the segmentation results of synthesized images obtained by DDCNN are closer to the ground truth than those obtained by the competing methods, indicating that DDCNN improves the accuracy of brain MRI measurement.

Figure 15:

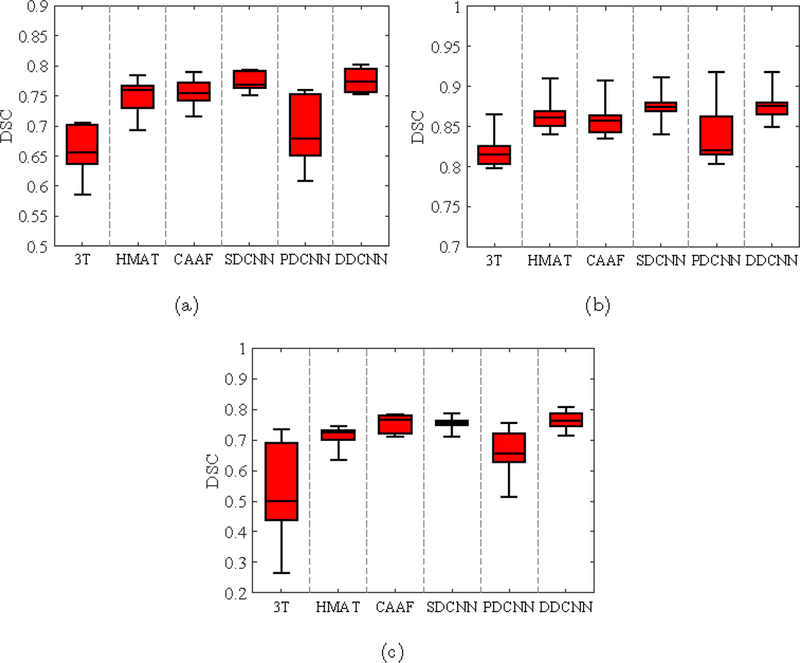
Box-plots of DSC values for segmentation of (a) GM, (b) WM, and (c) CSF from the reconstructed brain images by the competing methods and our DDCNN.

Figure 16:

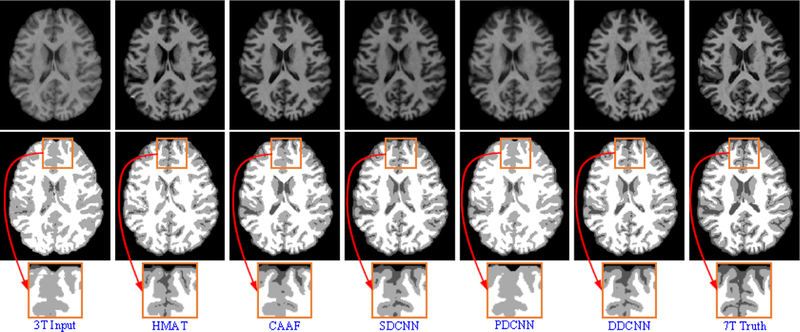
Brain tissue segmentation results of reconstructed images by the competing methods and our DDCNN. From top to bottom, reconstructed images, segmentation results and close-up views.

5. Discussion

We construct a dual-domain convolutional neural network model by introducing two complementary domains and parameter-efficient butterfly modules.To verify its superiority, this model is used to learn an end-to-end mapping between pairs of 3T and 7T training images for image synthesis. The mapping is represented as a trained model that takes the 3T image as the input and outputs the synthetic 7T-like image. Fig. 5 shows the robustness behavior of the proposed method in PSNR. Referring to Fig. 5, the depth and width of network model do not obey the rule of “Bigger is better”, but depend on training data and optimization algorithms. Kernel size of convolutional layer also fails to comply with this rule. In fact, the performance of DDCNN depends on its network architecture, the optimization algorithm, hyperparameter selection, the number of model parameters, and the amount of training data. As can be found from Fig. 12 to Fig. 14, PDCNN achieves higher SSIM values than SDCNN, but lower than DDCNN. From Fig. 6 to Fig. 8, DDCNN with simple architecture outperforms the state-of-the-art methods (e.g., CAAF [2]) both qualitatively and quantitatively. It is suggested that the synthesized images obtained by DDCNN are more like real 7T images and thus validate the effectiveness of the dual-domain strategy and buttefly modules.

In the experimental verification, we evaluated the proposed method on the 3T and 7T images at the spatial resolution of range about 0.5 ~ 1 mm³, whereas test images of other spatial resolution will be used for the assessment in our future work. The proposed method works well and can synthesize the high-quality 7T-like images from the input 3T images. In this paper, we assume that pairs of 3T and 7T training images are well aligned using FLIRT [9, 10] in image preprocessing. However, the registration error between 3T and 7T training images, especially at tissue boundaries, may affect the quality of synthesized images, which is beyond the scope of this paper due to another challenging issue of cross-modality image registration. Moreover, as we only focus on improving structural information of 3T MRI in this paper, the evaluation on functional information and disease diagnosis of synthesized images is left as our future work due to the lack of enough data.

6. Conclusions

In this paper, we have proposed a novel image synthesis method based on dual-domain convolutional neural networks. By introducing two complementary domains and parameter-efficient butterfly modules, two interactive streams of DDCNN on respective spatial and frequency domains benefit each other in learning complex mappings between 3T and 7T training images. With the well-trained model, the proposed method can synthesize high-quality 7T-like images from input 3T images. The experimental results suggest that the proposed method generally achieves better results than the state-of-the-art methods both qualitatively and quantitatively. The benefit of the dual-domain strategy and butterfly modules is also corroborated by the convincing results. To evaluate image synthesis comprehensively, we will research on functional information and disease diagnosis of synthesized images in the future.