Using Deep Siamese Neural Networks for Detection of Brain Asymmetries Associated with Alzheimer’s Disease and Mild Cognitive Impairment

Abstract

In recent studies, neuroanatomical volume and shape asymmetries have been seen during the course of Alzheimer’s Disease (AD) and could potentially be used as preclinical imaging biomarkers for the prediction of Mild Cognitive Impairment (MCI) and AD dementia. In this study, a deep learning framework utilizing Siamese neural networks trained on paired lateral inter-hemispheric regions is used to harness the discriminative power of whole-brain volumetric asymmetry. The method uses the MRICloud pipeline to yield low-dimensional volumetric features of pre-defined atlas brain structures, and a novel non-linear kernel trick to normalize these features to reduce batch effects across datasets and populations. By working with the low-dimensional features, Siamese networks were shown to yield comparable performance to studies that utilize whole-brain MR images, with the advantage of reduced complexity and computational time, while preserving the biological information density. Experimental results also show that Siamese networks perform better in certain metrics by explicitly encoding the asymmetry in brain volumes, compared to traditional prediction methods that do not use the asymmetry, on the ADNI and BIOCARD datasets.

1. Introduction

Alzheimer’s Disease (AD) is a neurodegenerative disorder that is usually associated with a progressive and irreversible degradation of episodic memory and other domains of cognitive function in elderly populations. The global prevalence of AD was 26.6 million in 2006 and it is forecast to affect 1 out of 85 people worldwide by 2050 [1]. Early diagnosis of AD is crucial for improving the efficacy of potential treatments. The clinical trajectory of AD begins with a long preclinical stage and progresses to mild cognitive impairment (MCI) [2]. Individuals with MCI are at highly increased likelihood of developing AD dementia. The use of imaging biomarkers has been recommended for aiding diagnosis of individuals along the AD spectrum [3, 4]. Magnetic Resonance Imaging (MRI) can measure brain atrophy which is correlated with pathophysiological neuronal injury associated with AD [5, 6]. As a result, MRI analyses have attracted significant interest for developing imaging biomarkers to aid in diagnosis and prediction. Several MRI biomarkers have been proposed for identifying individuals in the early stages of AD. For example, studies found that MCI subjects have significantly greater atrophy rates compared to normal controls in the hippocampus, the entorhinal cortex, and the amygdala [7, 8, 9].

In addition to volumetric measures, morphometric patterns are another important potential feature for the diagnosis or prediction of individuals along the AD spectrum. Some MRI studies have indicated that the cortical atrophy rate is faster in the left hemisphere than the right [10,11]. For subcortical regions, volumetric asymmetry of the hippocampus has been observed in AD dementia patients [12, 13]. Shape asymmetry of subcortical structures was seen to predict the conversion from MCI to AD dementia more accurately than volumetric asymmetry in sub-cortical structures [14]. Furthermore, a recent longitudinal genetics study has shown that there is a significant association between the shape asymmetries in the amygdala, hippocampus, putamen, and AD-candidate single nucleotide polymorphisms (SNPs) in the genes TNKS and DLG2 [15]. PET imaging studies have also found asymmetric metabolic features in subjects along the AD spectrum [16,17,18], and have reported a positive correlation between the asymmetric spatial distribution of amyloid-β deposition and asymmetric hypometabolism in AD dementia subjects [19]. Histopathological data has further demonstrated asymmetry in AD [20]. These studies suggest that the lateralization of pathology and neurodegeneration associated to brain asymmetry in selected regions may be a potential biomarker of AD.

There have been several recent studies that apply machine learning techniques to the task of discriminating between subjects with MCI or AD dementia and normal controls using neuroimaging. These algorithms can be classified between feature-based (utilizing anatomical or functional derived regions) and whole-brain. Feature-based methods have the advantage of greatly reducing the dimensionality of the classification task, by expertly extracting important features or regions-of-interest (ROIs) from structural MRI (sMRI). They, however, run the risk of losing important information present in the images that is not adequately represented by the extracted features. On the other hand, whole-brain methods use the entirety of the available data, at the cost of computational speed and a more complex feature search space that does not have the benefit of historical regional definitions, and are prone to learning covariates present in the sMRI. Support Vector Machines (SVMs) are a popular technique that use separating hyperplanes on the feature space for subject classification based on features extracted from sMRI. These perform dimensionality reduction on raw sMRI by extracting specific features that characterize the ontological features of the disease, such as tissue densities [21], sampled local image patches [22, 23], components from Independent Component Analysis (ICA) [24] or Principal Component Analysis (PCA) [25], LDA [26], and voxel-wise ROIs from sMRI images [27, 28]. Others have explored the use of alternate classifiers, such as Gaussian Process classification [29] and semi-supervised methods like low density separation [30]. Further studies have also looked at fusing multiple modalities of imaging with sMRI to improve discrimination [31, 32, 33,34].

More recently, deep learning methods have rapidly emerged as a popular approach to discover multiple levels of representation across many medical imaging domains for downstream clinical applications. Some have utilized deep learning architectures to perform classification using the raw 3D sMRI using either pre-trained sparse autoencoders with convolutional neural networks (CNNs) [35], or trained 3D CNNs from scratch [36, 37]. Finally, others have also explored training CNNs on features extracted from 3D sMRI by using techniques such as sparse regression [38].

Methods that specifically utilize the shape asymmetry of the brain were also explored, such as shapeDNA, where brain structures were encoded by the eigenfunctions of the Laplace-Beltrami operator calculated on the surfaces of the subcortical structures [39]. The shape asymmetries in these structures were measured by the Mahalanobis metric of the reweighted eigenvalues [40, 41]. This study also revealed preclinical changes in the shape asymmetry of subcortical brain structures (the hippocampus and amygdala) which provide better accuracy for the prediction of the convention of AD compared to volumetric asymmetry [14].

Although these studies report that anatomical shape asymmetries of subcortical structures provide better accuracy for detection of AD than anatomical volumetric asymmetries, whole-brain anatomical volumetric asymmetries can still serve as potential features for distinguishing between normal controls and those with MCI or AD dementia. Asymmetry in the shapes of certain paired structures implies that their surrounding regions might also have different shapes or volumes. In this study, Siamese networks were trained to encode a proposed alternative descriptor of whole-brain volumetric asymmetry for building classification models for MCI/AD diagnosis at both scan time and using the latest diagnosis.

The proposed method has several advantages. Firstly, reducing high-dimensional MRI data into low-dimensional features greatly reduces the modeling complexity and computational time required for analysis, while preserving the biological information density. Secondly, Siamese networks explicitly capture the asymmetry between left and right hemisphere volumes for those with MCI or AD dementia and learn to ignore the asymmetries present in control subjects, resulting in higher specificity and balanced accuracy for prediction compared to methods that do not use volumetric asymmetry. Thirdly, the proposed non-linear kernel trick self-normalizes within a subject’s volumetric features and is more robust to variance in subjects across different datasets and populations. Finally, instead of working in the image voxel domain where deep networks require very large datasets to guarantee convergence and generalization, Siamese networks search for decision boundaries in a low-dimensional feature space, which has better guarantees for optimization while having comparable prediction performance.

2. Materials and methods

2.1. Dataset and preprocessing

Subjects and scans in this study were selected from the ADNI1, ADNI GO, ADNI 2, and BIOCARD databases [42,43]. In total, 3566 1.5T T1 scans across 819 subjects were selected from the ADNI database; and 744 1.5T T1 scans across 324 subjects were selected from the BIOCARD database. Data used in the preparation of this article were obtained from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) database (adni.loni.usc.edu). The ADNI was launched in 2003 as a public-private partnership, led by Principal Investigator Michael W. Weiner, MD. The primary goal of ADNI has been to test whether serial magnetic resonance imaging (MRI), positron emission tomography (PET), other biological markers, and clinical and neuropsychological assessment can be combined to measure the progression of mild cognitive impairment (MCI) and early Alzheimer’s disease (AD).

All MRIs were processed and parcellated by MRICloud [44], which is an automated segmentation pipeline that utilizes Large Diffeomorphic Deformation Metric Mapping (LDDMM) [45] to map each scan onto multiple atlases and then utilizes the Multi-Atlas Likelihood Fusion (MALF) algorithm [46, 47] to fuse the parcellation labels of atlases for each scan. A set of 26 adults atlases, age range 50–82 years-old, 20 of them cognitively normal and 6 subjects with AD, with variable patterns of brain atrophy (the so-called Adult50_90yrs_283labels_26atlases_M2_252_V9B) was used, in which 283 brain structures are defined with a multi-level hierarchical ontology [48,49]. In the pipeline, the raw images were automatically preprocessed (skull-stripped, orientation adjusted, intensity matched, and inhomogeneity corrected), prior to the LDDMM and MALF fusion step. Figure 1 illustrates the MRICloud workflow from images to volume features. Several past researches in our group have been extensively investigating and testing MRICloud pipeline, in terms of performance compared with human evaluators, stability to technical and biological effects, and test-retest reproducibility, such as [50] and [51]. In [50], it illustrates that there is no significant difference between the performance of MRICloud Tl-segmentation pipeline for 1.5T and 3T scans either in normal subjects or in those with atrophy (Alzheimer’s disease). Furthermore, the reliability of MRICloud pipeline for Basal Ganglia segmentations in ADHD and Autism subjects rivals or outperforms other two state-of-the-art algorithm, Freesurfer and FSL [51].

Figure 1:

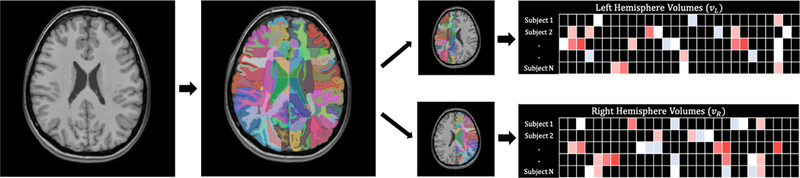
This is an illustration for the MRICloud segmentation pipeline and volumetric feature extraction. Left panel is original MRI; the middle panel is the overlay with MRICloud segmentation labels and they are split by hemispheres; the right panel is an illustration for the volume size per structure per subject.

The data from the automated segmentation underwent a quality control step. Data considered “low quality” was excluded; we opted by not performing any human correction on the segmentation as our aim is to report the results of an automated process, including its strengths and caveats. The sample size before and after quality control is described in Table 1. The two most common issues were the following:

Table 1:

Number of subjects and scans from the ADNI and BIOCARD datasets before and after Segmentation Quality Control Elimination.

Dataset	Before Segmentation Quality Control		After Segmentation Quality Control
	# Subjects	# Scans	# Subjects	# Scans
BIOCARD	324	744	289	601
ADNI	819	3566	716	2703

1. Failure in the very first step of linear transformation to MNI space, either because of particularities in the original orientation (for instance, too much translation in the z-axis), and/or because the images included too much of body (for instance, when the field of view extended too inferiorly in the z-axis, sampling shoulders).

2. Very enlarged spaces between skull and brain and/or changes in intensity in the diploe, affecting the cortical segmentation. Note that this is a common issue for all automatic segmentation tools. Indeed, this may create a bias (age- and atrophy-related) in the cohort. However, the bias would be in the opposite direction (the more atrophic subjects were excluded), therefore reducing the “false-positive” chances.

The associated diagnosis of each scan for each subject was split into three categories, based on the primary diagnoses used in these studies: AD dementia, MCI, and Normal Controls (NC), according to the ADNI and BIOCARD diagnosis protocols [42, 43]. Each scan had two different time-point labels: one labelled by the diagnosis at scan time or nearest scan time, the other labelled by the diagnosis from the latest diagnosis for each subject. The latest diagnosis can be different from the diagnosis at the last scan time. For example, if a normal subject converted to MCI after their latest scan time, the diagnosis at scan time for all their scans was labelled as normal, but the latest diagnosis was labelled as MCI for all their scans. In this study, models aimed at group discrimination were trained separately on (1) diagnosis at scan time and (2) latest diagnosis. For using the diagnosis-at-scan-time labels, the goal is to train the models to classify subjects based on their scans and the current clinical diagnosis. For using the latest diagnosis, the goal is to train the models to predict the subject diagnosis in subsequent years by measuring the anatomical symmetry changes seen in MRI before clinical onset.

Table 2 illustrates the demographics of the ADNI and BIOCARD datasets for each group (AD, MCI, NC) used in this study after segmentation quality control elimination. It should be noted that the characteristics of the subjects at enrolment differed for the two studies. For ADNI, subjects were NC, MCI or AD dementia at enrolment and the mean age of the samples was 75.19 years. For BIOCARD, all subjects were NC at enrolment, with a mean age of 57.26 years. Additionally, the follow-up times differed considerably. For the scans included in these analyses, the average follow-up time for ADNI was 2.02 years, whereas for BIOCARD the average follow-up time was 2.61 years. The average time between the latest scan and the latest clinical diagnosis was 11.12 years for BIOCARD, and for ADNI the latest diagnosis is the same as the diagnosis at the latest scan time in the study.

Table 2:

Demographic data for subjects and scans from the ADNI and BIOCARD datasets after Segmentation Quality Control Elimination. Age values and MMSE scores are displayed as mean (standard deviation).

Dataset	Diagnosis Type	Scan Distribution			Gender Ratio (M/F)			Age Mean (SD)			MMSE Mean (SD)
		Normal	MCI	AD	Normal	MCI	AD	Normal	MCI	AD	Normal	MCI	AD
BIOCARD	Diagnosis at scan time	578	17	6	191/387	13/5	4/2	58.93 (9..93)	62.24 (9.10)	62.78 (8.48)	29.65 (0.70)	29.12 (0.70)	27.00 (1.55)
	Latest Diagnosis	437	89	75	133/304	36/53	38/37	57.11 (8.97)	63.64 (10.42)	65.01 (10.42)	29.69 (0.65)	29.44 (0.89)	29.37 (1.06)
ADNI	Diagnosis at scan time	839	1129	735	420/419	692/437	362/373	76.75 (6.67)	76.18 (6.71)	76.74 (6.89)	29.12 (1.12)	26.85 (2.56)	22.23 (4.42)
	Latest Diagnosis	829	837	1037	434/395	478/359	562/475	76.99 (6.72)	75.84 (6.78)	76.57 (6.72)	29.10 (1.14)	27.24 (2.51)	23.30 (4.28)

2.2. Siamese networks

In this task, we trained a Siamese network to seek an encoding for asymmetric volumetric features that can be utilized to distinguish between groups of subjects categorized as NC, MCI or AD dementia. Siamese networks have previously been conventionally utilized in metric representative learning on paired images (such as faces [52, 53]) to distinguish whether paired images contain similar subjects.

Instead of directly learning asymmetry-encoding features on the 3D MRI domain, we trained Siamese nets on a set of selected volumetric features. The Siamese nets were trained to learn a metric that represents the volumetric asymmetry between normal controls and symptomatic subjects, i.e. MCI and AD dementia. We built two Siamese nets to predict (1), clinical diagnosis (normal v.s. symptomatic AD) at scan time and (2), latest diagnosis (normal v.s. symptomatic AD) for each subject beyond scan time. All MCI and AD dementia subjects were labelled as symptomatic.

The purpose of using the latest diagnosis labels for subjects is to build a separate preclinical prediction model that is better suited to predict subject conversion between normal and MCI or AD dementia. For example, even if the subject was classified in one category during their scan times, the Siamese network only focuses on classifying them based on the latest diagnosis labels, which may be made at a different time from when the last scan was taken.

Among the predefined 283 structures with volumetric features from the atlases in the MRICloud pipeline, we excluded extra cerebral structures (e.g., background, cranium) and those that are not represented bilaterally (e.g., subdural space, III ventricle) were not considered because they are either pathologically irrelevant or not abled to be presented as paired structures used in Siamese network. A subset of the paired (left and right hemispheric) ROIs was selected as training input features to build the Siamese network in Figure 2. A total of 274 features (137 pairs) of the whole brain ROIs were selected, including cortical structures, sub-cortical structures, white matter, gray matter, cerebrospinal fluid, Midbrain, Medulla and Cerebellum. A detailed list of ROI labels is provided in the supplementary material.

Figure 2:

Siamese Net Architecture, L_ker, R_ker are the left and right hemispheric kernel features which are sequentially passed into the same n-layer network (n = 6) to be separately encoded into their corresponding asymmetry-encoding features, f_L, f_R. The final error updates that are calculated for the weights of this neural network using backpropagation depend on the final contrastive loss term, which involves both the left and right feature terms. Each layer is fully-connected and feed-forward with L₂-regularization on the weights and biases and followed by the ReLU non-linear activation function. $\mathcal{L}\left(\parallel f_L-f_R{\parallel }_2\right)$ is the contrastive loss function as defined in Eq. (2).

The non-linear kernel trick in Eq. (1) was applied to the paired volumetric features, (v_L, v_R), to normalize them (with respect to each other). This scheme is more invariant to covariates that may be present in normalization schemes that normalize across subjects.

$$R_{ker}=\tanh \left(\frac{v_R}{v_L+ϵ}-1\right);L_{ker}=\tanh \left(\frac{v_L}{v_R+ϵ}-1\right)$$ (1)

where ϵ = 10⁻⁶.

The motivation behind the kernel trick lies in the fact that each structure has a different scale in volume, ranging from about 10⁴ mm³ for the frontal lateral ventricle to about 600 mm³ for the fornix. The absolute difference between the paired left and right hemisphere volumes varies dramatically and depends on the scaling of each feature. A 100 mm³ volumetric asymmetry, for example, may be critical for the fornix but would not amount to much, relatively, for the lateral ventricles. By applying the kernel trick, each paired feature is centered and normalized relative to their ratios. The hyperbolic tangent function ensures that the kernel encodes the ratio of paired volumes linearly when the ratio is around 1, and non-linearly compresses them when the ratio is larger than 2, which may happen for structures with small volumes due to mis-segmentation or being missed completely by the automatic segmentation pipeline.

All kernel features lie between [−1,1] and are centered at 0. Compared to other normalization methods used in deep learning architectures, such as batch normalization [54], this non-linear normalization kernel both accelerated the training of the deep network and depended only on individual subject information. Also, by not normalizing over the whole data batch the procedure is potentially more robust against population variation.

The Siamese network architecture is depicted in Figure 2. Initially, the left and right hemispheric kernel features, L_ker, R_ker were sequentially passed into the same n-layer neural network (n = 6), in order to be separately encoded into their corresponding asymmetry-encoding features, f_L, f_R. Each layer is fully-connected and feed-forward with L₂-regularization on the weights and biases, followed by the ReLU non-linear activation function. Following this, the network was trained to optimize its parameters by optimizing the L₂-difference between asymmetry encoding features f_L, f_R, using the contrastive loss function as defined in (Eq.2)

$$\mathcal{L}\left(\parallel f_L-f_R{\parallel }_2\right)={(1-y)}^2\parallel f_L-f_R{\parallel }_2+y^2\max (0,\lambda -\parallel f_L-f_R{\parallel }_2)$$ (2)

where y ∈ {0,1} are diagnosis labels for {normal, symptomatic (MCI/AD dementia)} subject scans; and the margin parameter, λ =1, controls the degree of separation to enforce between asymmetry-encoding features. By training the Siamese network to minimize the contrastive loss, the model learns to embed the left and right features in the asymmetry-encoding space so that the L₂-difference is minimized between the asymmetry encoding features if the subject is a control. On the other hand, the L₂-difference is maximized up to the margin λ if the subject is symptomatic. By minimizing the contrastive loss, the Siamese network learns an embedding where -

• Normal - the paired asymmetric encoding features f_L, f_R are very similar to each other

• Symptomatic - the paired asymmetric encoding features f_L, f_R are very dissimilar to each other.

At testing time, in order to make a prediction using the Siamese Net, the testing left and right features are passed through the trained network, and the L₂ difference $\parallel f_L-f_R\parallel$ are thresholded at λ/2, such that testing samples with L₂ norm less than λ/2 are predicted as belonging to the controls, whereas testing samples with L₂ norm higher than λ/2 are predicted as belonging to the diseased group.”

We used the ADAM optimization algorithm with a fixed learning rate of 1e-4 to train a 6-layer fully-connected neural network with 1024 nodes per layer, with L₂ regularization imposed on the weights and biases [55]. The final asymmetry-encoding features were also 1024-dimensional, in order to sufficiently capture high-dimensional, non-linear relationships between the asymmetry across the left and right hemispheric volumes. After tuning on the learning rate, the number of layers, the number of nodes per layer, and the parameters of the ADAM optimizer, we found that the parameters reported above performed best on classification accuracy on a held-out testing set with 5-fold cross-validation at the scan level.

2.3. Benchmarking methods

The performance of the Siamese network was compared to Linear Discriminant Analysis (LDA), Quadratic Discriminant Analysis (QDA), Random Forests (RF) and fully-connected feedforward neural networks in Table 3–11. These methods were trained using the 274-dimensional features as inputs, with no distinction being made for the asymmetry information present in the features. We include further analysis performed using a 3D convolutional neural network previously shown to have good performance in the task of discriminating patients with AD from normal controls, using the sMRI scans in ADNI dataset. We use the 3D VGG-Net architecture with a learning rate of 1e-5, the ADAM optimizer, and a batch size of 12 trained over 50 epochs for the task of discriminating symptomatic AD vs. normal controls. The metrics used for comparison are described below.

Table 3:

Comparison of performance between methods applied on the ADNI dataset with diagnostic labels from scan time. Values are displayed as mean (standard deviation).

ADNI (Diagnosis at Scan Time)
Methods	Performance Metrics
	SEN	SPEC	BACC	F1
LDA	0.7543 (0.0388)	0.3890 (0.0581)	0.5719 (0.0319)	0.7426 (0.0258)
QDA	0.9986 (0.0034)	0.0031 (0.0050)	0.5011 (0.0030)	0.8160 (0.0240)
RF	0.8696 (0.0863)	0.1983 (0.1262)	0.5340 (0.0298)	0.7770 (0.0357)
Neural Net	0.9487 (0.0133)	0.8572 (0.0244)	0.9036 (0.0119)	0.9431 (0.0073)
Siamese Net	0.8992 (0.0160)	0.9523 (0.0219)	0.9272 (0.0114)	0.9372 (0.0090)
3D CNN	0.6759 (0.0821)	0.4778 (0.1000)	0.5768 (0.098)	0.6213 (0.121)

Table 11:

Comparison of performance between methods applied on the ADNI dataset with latest diagnostic labels where for each patient, scans at initial time points constitute the training dataset, and scans at later time points constitute the validation dataset. Values are displayed as mean (standard deviation).

ADNI (Latest Diagnosis, First-Last Split)
Methods	Performance Metrics
	SEN	SPEC	BACC	F1
LDA	0.6881 (0.0110)	0.4009 (0.0210)	0.5445 (0.0341)	0.7012 (0.0200)
QDA	0.9866 (0.0240)	0.0002 (0.0080)	0.4934 (0.0194)	0.7988 (0.0653)
RF	0.7881 (0.0983)	0.2134 (0.0787)	0.5007 (0.0210)	0.7328 (0.0431)
Neural Net	0.9322 (0.0880)	0.8957 (0.0748)	0.9193 (0.0781)	0.9341 (0.0743)
Siamese Net	0.9130 (0.0211)	0.9430 (0.0011)	0.9280 (0.0412)	0.9330 (0.0112)
3D CNN	0.7319 (0.2110)	0.5453 (0.1878)	0.6134 (0.1039)	0.6679 (0.1050)

$$\begin{gathered} \text{Sensitivity}\text{(SEN)}=\frac{\text{TP}}{\text{TP}+\text{FN}} \\ \text{Specificity}\text{(SPEC)}=\frac{\text{TN}}{\text{TN}+\text{FP}} \\ \text{Positive}\text{Predictive}\text{Value}\text{(PPV)=}\frac{\text{TP}}{\text{TP}+\text{FP}} \\ \text{Balanced}\text{Accuracy}\text{(BACC)=}\frac{\text{SEN}+\text{SPEC}}{2} \\ \text{F1}\text{Score}\text{(F1)}=\frac{2}{{\text{SEN}}^{-1}{+\text{PPV}}^{\text{-1}}} \end{gathered}$$

Here, TP, FP, TN, and FN denote the count of True Positives, False Positives, True Negatives, and False Negatives in the validation set predictions, respectively. Due to the unbalanced number of samples in each class (normal vs. symptomatic), Balanced Accuracy (BACC) is a better metric for measuring performance than raw accuracy [56]. Based on parameter tuning trials, we found that Random Forests with 100 trees, a max-depth of 10, and using the Gini index for node-splitting performed the best. We consider feed-forward neural networks of the same shape as the Siamese Network, but trained on the 274-dimensional features directly to perform binary classification between normal and MCI/AD using Binary Cross-Entropy Loss, with a learning rate of 1e-5. The ADAM Optimizer was used to optimize parameters, and the learning rate and optimization parameters were treated as hyperparameters and independently tuned for the lowest validation loss on a held out dataset.

4. Discussion

The MRICloud brain segmentation pipeline provides a high-throughput neuroinformatics workflow [44]: (1) it reduces the dimensionality of MRI features on the order of 10⁶ image voxels to the order of 1000 atlas-defined structural volumetric features, and (2) it also preserves the biological information density contained in these MRIs. Due to the low dimensionality of the selected feature space in our study, the 274 volumetric features are therefore searchable. We also show that the Siamese network can accurately cluster these low-dimensional volumetric features by explicitly learning the asymmetry encoding, which can be seen in Figure 3, where we plot the first 3 tSNE dimensions for both of these feature spaces [57]. These results imply that the low-dimensional volumetric features preserve the biological information density present in the original MR images that may be associated to MCI and AD dementia. Compared to other deep learning methods, such as CNNs [35, 36, 37, 38], according to Table 4 and Table 8, the Siamese network provides comparable prediction balanced accuracies (BACC), 0.9436 for the ADNI dataset and 0.9220 for the combined BIOCARD and ADNI datasets. Furthermore, in Table 11, the Siamese network outperforms the 3D CNN we built and trained on the ADNI dataset. These suggest that MRICloud’s high-throughput informatics allows us to greatly reduce the modeling complexity and computational time for training deep networks, by starting ML in the reduced feature space. Using volumetric data makes the Siamese network more robust to other CNN approaches that work on the full high dimensional MR image space of order 10⁶ voxels directly, as these approaches require very large training datasets to guarantee their convergence and generalization.

Figure 3:

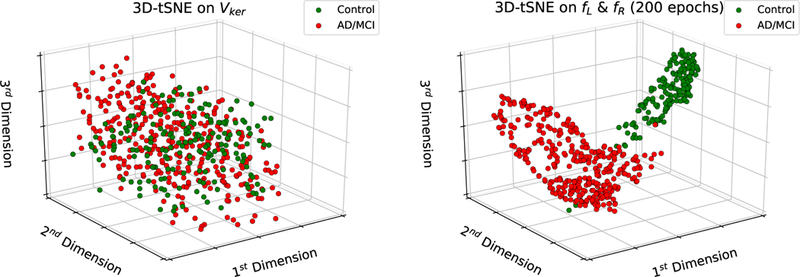
Visualization of the top 3 tSNE dimensions; the left panel shows a plot of the top 3 tSNE dimensions trained on the input features to the Siamese network V_ker, which are the concatenated L_ker and R_ker features; the right panel shows the top 3 tSNE dimensions trained on the asymmetry-encoding feature outputs from the Siamese network; these plots show that the Siamese network learns features that separate subjects into two potentially discriminative clusters in the tSNE domain after 200 epochs.

Table 4:

Comparison of performance between methods applied on the ADNI dataset with latest diagnostic labels. Values are displayed as mean (standard deviation).

ADNI (Latest Diagnosis)
Methods	Performance Metrics
	SEN	SPEC	BACC	F1
LDA	0.7558 (0.0393)	0.4102 (0.0673)	0.5831 (0.0366)	0.7488 (0.0304)
QDA	0.9980 (0.0030)	0.0030 (0.0050)	0.5012 (0.0030)	0.8184 (0.0220)
RF	0.8781 (0.0899)	0.1993 (0.1123)	0.5387 (0.0112)	0.7993 (0.0214)
Neural Net	0.9680 (0.0084)	0.8860 (0.0266)	0.9264 (0.0146)	0.9584 (0.0083)
Siamese Net	0.9244 (0.0403)	0.9615 (0.0199)	0.9436 (0.0259)	0.9512 (0.0270)
3D CNN	0.7781 (0.1210)	0.5601 (0.109)	0.6691 (0.0981)	0.6883 (0.1980)

Table 8:

Comparison of performance between methods applied on the combined ADNI and BIOCARD datasets with latest diagnostic labels. Values are displayed as mean (standard deviation).

ADNI and BIOCARD (Latest Diagnosis)
Methods	Performance Metrics
	SEN	SPEC	BACC	F1
LDA	0.7002 (0.0412)	0.3342 (0.0441)	0.5172 (0.0196)	0.7345 (0.0314)
QDA	0.9994 (0.0021)	0.0011 (0.0020)	0.5002 (0.0023)	0.8130 (0.0030)
RF	0.8132 (0.0453)	0.1654 (0.0109)	0.4893 (0.0031)	0.7866 (0.0034)
Neural Net	0.9296 (0.0099)	0.8840 (0.0205)	0.9067 (0.0104)	0.9284 (0.0092)
Siamese Net	0.8839 (0.0277)	0.9584 (0.0.015)	0.9220 (0.0120)	0.9259 (0.0144)

Considering the ADNI dataset, according to Table 3 and Table 4, the Siamese network has the best SPEC and BACC score for both diagnosis at scan time and the latest diagnosis with an acceptably comparable SEN, in comparison to the other benchmarking methods (LDA, QDA, RF, and Neural Net). Of course, diagnostic performance is a trade-off between sensitivity and specificity, therefore, we prefer the BACC. These results show that the Siamese network working on volumetric asymmetric features can be used to aid classifying symptomatic cases along the AD spectrum, according to Table 4, as the Siamese network has better BACC (0.9436) in detecting the latest diagnosis. We also report the QDA algorithm having very high SEN values in Table 3 – 8. This is due to the algorithm classifying almost every scan as symptomatic, which we believe is due to the larger number of symptomatic scans versus the number of control scans.

We also trained the Siamese network on the combined BIOCARD and ADNI datasets and the results reported in Table 7 and Table 8 show that the Siamese network continues to have higher SPEC and BACC for both categories of diagnosis labels, even though the values decrease compared to only using the ADNI dataset in Table 3 and Table 4. However, compared to other classifiers such as LDA and random forests, the drop in BACC is much less for the Siamese network, implying that the deep network is robust to minimizing batch effects across the two datasets. This consistency is likely from the self-normalized kernel features.

Table 7:

Comparison of performance between methods applied on the combined ADNI and BIOCARD datasets with diagnostic labels from scan time. Values are displayed as mean (standard deviation).

ADNI and BIOCARD (Diagnosis at Scan Time)
Methods	Performance Metrics
	SEN	SPEC	BACC	F1
LDA	0.6943 (0.0311)	0.3265 (0.0434)	0.5104 (0.0218)	0.7101 (0.0322)
QDA	0.9934 (0.0031)	0.0016 (0.0030)	0.4975 (0.0020)	0.8010 (0.0210)
RF	0.8011 (0.0658)	0.1123 (0.1010)	0.4567 (0.0110)	0.7494 (0.0321)
Neural Net	0.9276 (0.0174)	0.8932 (0.0213)	0.9096 (0.0142)	0.9244 (0.0135)
Siamese Net	0.8588 (0.0161)	0.9616 (0.0118)	0.9103 (0.0090)	0.9096 (0.0080)

Discriminating MCI from normal controls is more clinically relevant. Hence, we also trained all models to distinguish MCI cases from normal controls at the latest diagnosis basis on the ADNI dataset and the combined BIOCARD and ADNI datasets. The result is reported in Table 9 and Table 10. Table 9 illustrates that the Siamese network still has better SPEC (0.9887) and BACC score (0.9278) for just using ADNI dataset, compared to the other benchmarking methods. Furthermore, even for the combined BIOCARD and ADNI datasets, Table 10 indicates that Siamese has better SPEC (0.9760) and BACC (0.8980). These results imply that the Siamese network could have clinical potential to assist classifying MCI cases from normal controls.

Table 9:

Comparison of performance between methods applied on the ADNI dataset with latest diagnostic labels for the task of discrimination between MCI and Controls. Values are displayed as mean (standard deviation).

ADNI (Latest Diagnosis, MCI vs Controls)
Methods	Performance Metrics
	SEN	SPEC	BACC	F1
LDA	0.7506 (0.0210)	0.7411 (0.0450)	0.7515 (0.0219)	0.7501 (0.0318)
QDA	0.6301 (0.0420)	0.7500 (0.0501)	0.6860 (0.0310)	0.6610 (0.0464)
RF	0.6301 (0.1023)	0.7442 (0.0981)	0.6901 (0.0101)	0.6600 (0.0340)
Neural Net	0.9010 (0.0912)	0.9403 (0.0524)	0.9205 (0.0817)	0.9201 (0.0819)
Siamese Net	0.8662 (0.0239)	0.9887 (0.0451)	0.9278 (0.0812)	0.9231 (0.0431)

Table 10:

Comparison of performance between methods applied on the combined ADNI and BIOCARD datasets with latest diagnostic labels for the task of discrimination between MCI and Controls. Values are displayed as mean (standard deviation).

ADNI and BIOCARD (Latest Diagnosis, MCI vs Controls)
Methods	Performance Metrics
	SEN	SPEC	BACC	F1
LDA	0.6490 (0.0360)	0.7691 (0.0291)	0.7362 (0.0280)	0.7092 (0.0189)
QDA	0.6356 (0.0286)	0.1995 (0.0417)	0.5894 (0.0172)	0.3232 (0.0522)
RF	0.6355 (0.0290)	0.1992 (0.0411)	0.5892 (0.0182)	0.3222 (0.0529)
Neural Net	0.8968 (0.0140)	0.8680 (0.0269)	0.8948 (0.0126)	0.8812 (0.0153)
Siamese Net	0.8201 (0.0601)	0.9760 (0.0143)	0.8980 (0.0295)	0.8901 (0.0410)

We also propose the use of the Siamese network for downstream use in a clinical setting, where earlier scans from patients are used to train and fine-tune the algorithm for clustering of scans at later time points. In this setting, cross-validation is done by splitting the ADNI dataset such that earlier scans of patients belong to the training dataset, and later scans belong to the validation dataset. It is ensured that no scans from a patient can be present in the validation dataset if a later scan exists in the training dataset. This setting is more clinically practical, because early scans of subjects could always be used to train models to classifying the future diagnosis. For this proposed application of the Siamese network, Table 11 still shows that the Siamese network has better SPEC (0.9430) and BACC (0.9280) in classifying scans at later time points in the comparison to the other benchmarks methods, including a 3D VGG-Net.

We report our results for diagnosis using Siamese networks for the BIOCARD dataset in Table 5 and Table 6, despite not having significantly better results compared to our baseline methods. We believe that this performance can partly be explained by the unbalanced nature of the BIOCARD dataset, since the subjects were all cognitively normal at baseline. The performance for labels with the latest diagnosis has better performance comparatively. However, the BIOCARD dataset in isolation may not have enough training samples to train a neural network robustly, since the majority of the subjects followed so far are still categorized as controls, with approximately one quarter having progressed to MCI and very few having progressed to AD dementia. Additionally, the ADNI dataset contains large numbers of individuals who were MCI or AD dementia at baseline, thus providing more information regarding scans from subjects with these diagnoses for the training samples. Another factor for the decreased performance could be the overall younger age for subjects in the BIOCARD study compared to the ADNI study; the mean age of the BIOCARD subjects at baseline is approximately 56 years whereas the mean age of the ADNI subjects at baseline is approximately 76 years. Significant asymmetric changes may not manifest in symptomatic subjects at this age for the Siamese network to detect.

Table 5:

Comparison of performance between methods applied on the BIOCARD dataset with diagnostic labels from scan time. Values are displayed as mean (standard deviation).

BIOCARD (Diagnosis at Scan Time)
Methods	Performance Metrics
	SEN	SPEC	BACC	F1
LDA	0.4440 (0.2700)	0.9477 (0.0199)	0.6961 (0.1339)	0.3044 (0.1697)
QDA	1.0 (0.0)	0.0 (0.0)	0.5 (0.0)	0.0 (0.0)
RF	0.0 (0.0)	0.9996 (0.0010)	0.5 (0.0)	0.0 (0.0)
Neural Net	0.2904 (0.2422)	0.9915 (0.0083)	0.6424 (0.1223)	0.3660 (0.2681)
Siamese Net	0.1800 (0.2200)	0.9972 (0.0053)	0.5883 (0.1096)	0.2275 (0.2120)

Table 6:

Comparison of performance between methods applied on the BIOCARD dataset with latest diagnostic labels. Values are displayed as mean (standard deviation).

BIOCARD (Latest Diagnosis)
Methods	Performance Metrics
	SEN	SPEC	BACC	F1
LDA	0.5799 (0.0820)	0.7367 (0.0515)	0.6581 (0.0488)	0.5052 (0.0700)
QDA	1.0 (0.0)	0.0 (0.0)	0.5 (0.0)	0.0 (0.0)
RF	0.0 (0.0)	0.9994 (0.0010)	0.5 (0.0)	0.0 (0.0)
Neural Net	0.6008 (0.0996)	0.9279 (0.0281)	0.7640 (0.0494)	0.6636 (0.0722)
Siamese Net	0.4356 (0.0294)	0.9808 (0.0174)	0.7080 (0.0403)	0.5811 (0.0747)

Important research has led to a better understanding of the input-output behavior of a deep learning network, in order to improve interpretability [58]. Current algorithms calculate the importance of the input features to the prediction of the network by looking at the integrated gradients of the prediction made by the network with respect to the input features. This is because gradients with large positive values convey which input features, upon being changed, would contribute most to the prediction changing from one class to the other ([58], [59]). We use integrated gradients with the Siamese network to calculate the relative importance of each paired volume to the prediction of a subject’s group, with results in Table 12.

Table 12:

Top 5 volumes selected from feature importance analysis for the Siamese network using integrated gradients; a higher value for the average integrated gradient over 100 trials of feature importance corresponds to a more important feature for prediction. The top 5 features are fimbria, lateral ventricle Inferior (LV Inferior), subcallosal anterior cingulate white matter (Subgenual WM ACC), lateral ventricle occipital (LV occipital, and superior parietal gyrus (SPG))

Volume	Average Integrated Gradient	Std. Deviation
Fimbria	0.0380	0.0113
LV Inferior	0.0202	0.0061
Subgenual WM ACC	0.0191	0.0083
LV Occipital	0.0165	0.0055
SPG	0.0127	0.0032

Although shape asymmetry has been reported to have more accurate predictions for the convention of MCI to AD dementia compared to volumetric asymmetries [14, 41], whole-brain volumetric asymmetry can still be used to assist detecting symptomatic cases along the AD spectrum via the proposed Siamese network. One possible reason might be that whole brain volumetric asymmetry potentially encodes shape asymmetry as well, as the asymmetric shapes of certain paired anatomical structures imply that their surrounding anatomical regions might also have different shapes or volumes.

Looking at the feature importance analysis in Table 12, the Siamese network considers the Fimbria to have the most importance for classifying subjects. The Fimbria is a very thin fiber bundle that covers the temporal region of the hippocampus. On the one hand, Fimbria is part of a circuit of core importance in AD; on the other hand, Fimbria is a hard-to-define structure, more prone to movement and sampling artifacts. Further analysis of the Fimbria segmentation revealed a number of scans / sides where the structure was not identified (“zero volume”, in Table 13). The asymmetry in these numbers likely drove the importance of the Fimbria in the models. From the biological point of view, this finding may be attributed to both shape and volumetric asymmetry, in the Fimbria itself or connected regions (e.g., hippocampus), even though these “connected structures” were not directly selected by the Siamese network. However, the lack of ground truth (e.g., macroscopic tissue evaluation or clear land-mark) impedes us to segregate biological from technical/artifactual effects, as it is usually the case for most of imaging methods. Nevertheless, this does not invalidate the point that a few structures (including Fimbria) were important features in the model, independently of the biological causality.

Table 13:

The number of zero volumes for the Fimbria across scans

Dataset	Controls		MCI/AD
	Left Volumes	Right Volumes	Left Volumes	Right Volumes
BIOCARD	65	14	44	10
ADNI	356	91	1271	681

5. Conclusions

In this study, Siamese networks were shown to be successfully applied to the discrimination of controls vs symptomatic cases of AD using the proposed kernel-normalized whole-brain anatomical volumetric asymmetry-encoding features. The proposed Siamese framework explicitly encoded the differences of anatomical volumetric asymmetry between normal vs symptomatic AD cases and was seen to have better Balanced Accuracy and Specificity in the combined ADNI and BIOCARD datasets, as opposed to other discrimination methods working on the volumetric features, such as LDA, QDA, Random Forests and Neural Networks. Furthermore, compared to CNNs that are directly applied on MR image voxels of order O(10⁶), the proposed Siamese framework has comparable prediction balanced accuracies for the ADNI dataset, with the advantage of having reduced modeling complexity and computational time for training, due to the low dimensionality of the volumetric asymmetry feature space. In future work, we plan to apply the proposed Siamese framework to different asymmetric features, such as shapes, voxel intensities, and cortical thickness, to seek other promising biomarkers associated with AD. In addition, more works need to be investigated to verify the connection between biomarkers in MRIs and clinical diagnosis associated with AD pathological features.