Erythrocyte plasma membrane potential: past and current methods for its measurement

Abstract

The plasma membrane functions both as a natural insulator and a diffusion barrier to the movement of ions. A wide variety of proteins transport and pump ions to generate concentration gradients that result in voltage differences, while ion channels allow ions to move across the membrane down those gradients. Plasma membrane potential is the difference in voltage between the inside and the outside of a biological cell, and it ranges from ~− 3 to ~− 90 mV. Most of the most significant discoveries in this field have been made in excitable cells, such as nerve and muscle cells. Nevertheless, special attention has been paid to some events controlled by changes in membrane potential in non-excitable cells. The origins of several blood disorders, for instance, are related to disturbances at the level of plasma membrane in erythrocytes, the structurally simplest red blood cells. The high simplicity of erythrocytes, in particular, made them perfect candidates for the electrophysiological studies that laid the foundations for understanding the generation, maintenance, and roles of membrane potential. This article summarizes the methodologies that have been used during the past decades to determine Δψ in red blood cells, from seminal microelectrodes, through the use of nuclear magnetic resonance or lipophilic radioactive ions to quantify intra and extracellular ions, to continuously renewed fluorescent potentiometric dyes. We have attempted to highlight the advantages and disadvantages of each methodology, as well as to provide a description of the technical aspects involved.

Introduction

The plasma membrane is the biophysical barrier that defines the external boundaries of biological cells. The charge difference between both sides of the membrane is mainly given by three factors: (a) the intrinsic selective permeability of the membrane to ions and charged molecules that are both in the cytoplasm and the extracellular space, (b) embedded charged molecules in the plasma membrane (both in the inner and outer leaflet of the bilayer), and (c) osmotic equilibrium (Glynn 1957; Gordon 1959; Lefevre 1964; Teorell 1952).

The ionic composition of the cytosol is usually very different from that of the extracellular milieu. In most cells, cytosolic K⁺ concentration is tens of times greater than that of Na⁺, while the opposite occurs in the extracellular space (Hodgkin 1951; Koechlin 1955; Steinbach 1952).

Transmembrane potential (Ψ) is a physical property given by the differences in electric potential between two sites separated by a membrane. In biological membranes, ionic pumps and channels originate ionic currents that separate the electric charges, generating voltage gradients through the membrane (Stein and Lieb 1986). While hyperpolarization is the change in a cell's Ψ that makes it more negative, the opposite is a less negative Ψ known as depolarization (Fig. 1). Ψ has two basic functions in the cell. First, it provides the energy to operate a variety of molecular devices embedded in the plasma membrane. Second, and not restricted only to electrically excitable cells such as neurons and muscle cells, it is used for transmitting signals between different regions of a cell. The opening or closing of ion channels at one point in the membrane generates a local change in the resting Ψ, triggering the electric signal, a common feature of cells from different kingdoms (Catterall et al. 2017; Choi et al. 2016; Prindle et al. 2015).

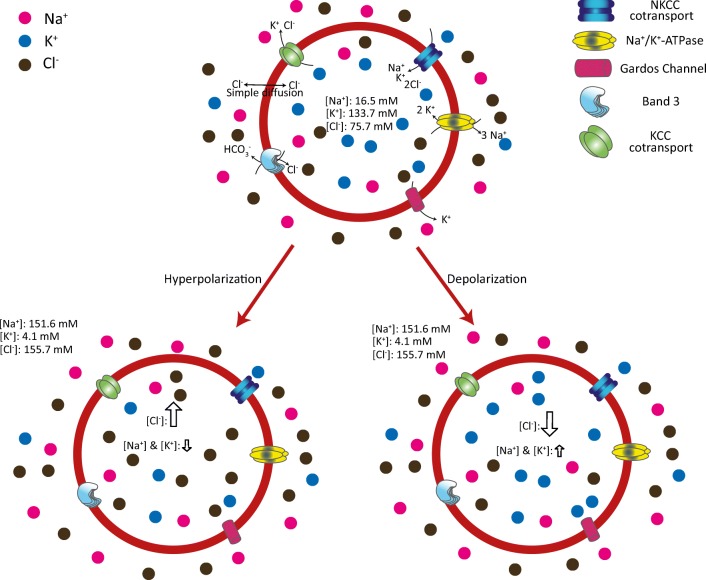
Fig. 1.

Schematic description of RBC plasma membrane potential variation. The low cation permeability in the RBC plasma membrane prevents osmotic swelling and lysis. K⁺ and Na⁺ transport is mainly driven by Na⁺/K⁺-ATPase, and their respective intra and extracellular concentrations are very marked. Conversely, chloride anions (Cl⁻) are highly permeable with differences in intra and extracellular concentration which are not so marked. During hyperpolarization, there is a prominent increase in intracellular negative charges (Cl⁻), with a less evident increase in positive charges. The opposite is observed in depolarized RBCs, where intracellular Cl⁻ anions decrease considerably, while intracellular cations increase slightly. The dynamically orchestrated variation of cytosolic ion concentration depends on the turning on-off of several pumps and membrane transporters like Na⁺/K⁺-ATPase, Band 3, NKCC, and KCC. Some voltage-dependent anion channels also participate in plasma membrane potential variation. The ion concentrations in RBCs are from (Barbosa et al. 2015)

Plasma membrane potential variation (ΔΨ) has been linked to a long list of cellular processes, with nervous impulse transmission and muscle contraction being the best described. In the context of non-excitable cells, resting Ψ is an important regulator of several cellular properties, including migration, proliferation, and shape. A well-described link has been established between cell cycle progression and plasma membrane potential and its unbalance is a key factor in the development of several pathologic processes with cancer development being the most studied. In this context, it has been proposed that cancer cells possess depolarized Ψ (Blackiston et al. 2009; Campetelli et al. 2012; Cone 1971; Cortese et al. 2014; Levin 2007; Patel and Brackenbury 2015; Sundelacruz et al. 2009; Yang and Brackenbury 2013). The proliferation of some tumor cells is dependent on voltage-gated potassium channels. For instance, the KCNK9 K⁺ channel has been found to have increased expression in colorectal tumor (Kim et al. 2004) while the EAG K⁺ channel was expressed in 100% of cervical cancer biopsies analyzed in a screening (Farias et al. 2004). However, not only K⁺ channels has been involved in cancer development, since the Cl⁻ efflux channel ClC-3 has been associated with uncontrolled cell division in glioma cells (Habela et al. 2008) and Na⁺ and H⁺ channels potentiated breast cancer metastasis and fibroblast tumorigenicity, respectively (Fraser et al. 2005; Perona and Serrano 1988).

Erythrocytes are anucleated cells that display a biconcave discoidal shape in their mature form and lack all intracellular organelles. Because no endomembranous systems are present, they are considered classic model systems for studying how ions and other in-solution compounds go through the plasma membrane (Freedman 2001). Around 150–300 voltage-dependent non-selective ion channels have been described in RBCs. These channels open or close depending on the membrane surface charge, and thus unbalance ion concentrations (Bennekou et al. 2003; Levinson and Sather 2001; Nilius and Droogmans 2001).

Mammalian red blood cells (RBC) are responsible for transporting the oxygen required by the cells from the lungs to the tissues and CO₂ in the opposite direction (Cole 2004; Knight and Holgate 2003). For successful gas exchange, erythrocytes must fulfill some general conditions: (1) to have functional hemoglobin; (2) to regulate intracellular pH, ATP production, and redox status; and (3) to be highly deformable and resistant to osmotic and mechanical stress, etc. While some pathologies related to oxygen binding or release by hemoglobin may have its origin at membrane-centered regulation of pH, ATP production, and/or redox status, the defective cytoskeleton-membrane interactions result in the alteration of rheological parameters (Amaiden et al. 2012; Rodriguez-Garcia et al. 2015; Smith et al. 2018). Clearly, the RBC plasma membrane plays a central role in regulating metabolic and structural functions in these cells (for more details, see An and Mohandas (2008)). In this sense, the assembly-disassembly of proteins that constitute the sub-membranous cytoskeleton in eukaryotic cells is regulated by biophysical factors such as Ψ, pH gradients, and the lipid composition of the inner leaflet of the plasma membrane. So, the availability of an easy to use, accurate, and reproducible technique to measure Ψ becomes indispensable and great efforts have been made to develop techniques that would allow determination of its value in an accurate and reproducible manner.

In this short review, we will summarize both older and more recent methodologies, with an emphasis on their advantages and disadvantages considering the context where ΔΨ must be determined.

First approaches to finding out plasma membrane potential in RBCs: an overview

The earliest studies aimed at measuring ΔΨ in RBCs assumed that it could be calculated by substituting the chloride concentration ratio in the Nernst equation for equilibrium ΔΨ (Eq. 1) where ΔΨ is the potential (V), R is the gas constant (J mol⁻¹ K⁻¹), T is the absolute temperature (°K), z is the ion valence, and F is the Faraday constant (C mol⁻¹). At least two conditions were necessary for this assumption to be correct: (1) a passive bidirectional chloride flux and (2) the activity coefficients for chloride ions being equal in the two phases (Warburg 1922). The assumption is invalidated by any direct pumping of the ion or coupling of its transport to any other ions that are not in equilibrium, and binding to any components of the system introduces an error in the calculated ΔΨ.

$$\mathrm{∆\Psi }=\frac{\mathrm{R}\times \mathrm{T}}{z\times \mathrm{F}}{log}_e\left(\frac{{\left(a_{{\mathit{Cl}}^{-}}\right)}_{\mathit{\text{in}}}}{{\left(a_{{\mathit{Cl}}^{-}}\right)}_{\mathit{\text{out}}}}\right)$$ 1

Given the high membrane permeability for chloride ions in red cells (Tosteson 1959), condition 1 is fulfilled. Trouble arises when it comes to condition 2, however. The interior of the cell contains a 34% solution of anionic hemoglobin against only 7% of extracellular proteins, introducing the Donnan effect (Freedman and Hoffman 1979; Lassen and Sten-Knudsen 1968), which results in conditions where the activity coefficients for water and solutes could not have the same value on both sides of the cell membrane. This impossibility to estimate ΔΨ solely from chloride distribution led to the development of a more direct method of measurement, which was feasible thanks to improvements in microelectrode technology.

Microelectrodes

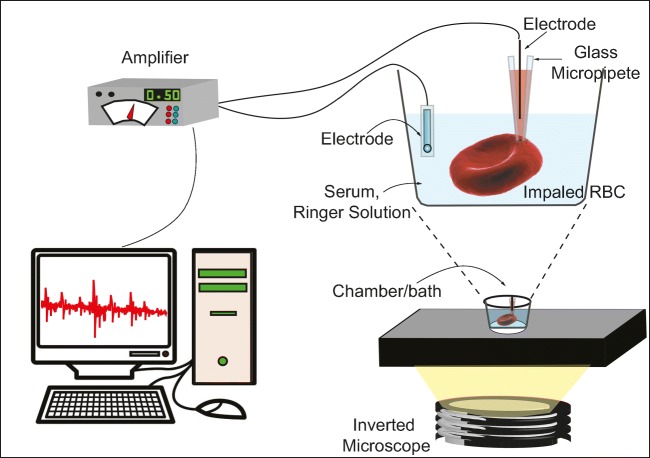
Microelectrodes were used early on to determine ΔΨ in RBCs in a direct and apparently accurate manner. Because RBCs are smaller than other common mammalian cells, Lassen and Sten-Knudsen swapped traditional micropipettes for a device they developed themselves, which consisted of ultra-thin micropipettes mounted on a piezoelectric holder, which when driven electrically, rapidly advanced the microelectrode over a small distance. To measure ΔΨ, RBC were diluted to very low hematocrit with isotonic solution and mounted into a micro-well or cavity slide. Then, the microelectrode (made of glass and filled with 3 M KCl) was slowly submerged in the solution, and with the aid of a microscope, erythrocytes were impaled. A slight deformation of the cell was taken to indicate that it had been penetrated. The microelectrode was connected to the input of a preamplifier capable of neutralizing capacitances, thus allowing for the improvement of temporal resolution from sec to msec (Fig. 2) and the values obtained promediated − 5.1 ± 2× 7 mV. This methodology was believed to be more accurate since the data obtained came from one direct measurement in an individual cell and not from cell populations (Lassen and Sten-Knudsen 1968). However, it required highly skilled operators, given that successful impalements were scarce and glass effect-related echinocytosis appeared soon after loading the blood into the cavity slide. Jay and Burton (1969) were able to improve on the technique and obtained less variable values of ΔΨ (− 8.0 ± 0.2 mV) in human erythrocytes. They followed almost the same protocols as Lassen et al., but they re-suspended the erythrocytes in a modified Ringer solution instead of serum. The improvement was attributed to the fact that the ionic composition of the ringer solution was less complex than that of the serum.

Fig. 2.

Direct plasma membrane potential determination in RBC by using microelectrodes. The RBC were suspended in isotonic solutions like serum or Ringer solution at low hematocrit. Then, single cells were placed in a microchamber on a microscope and with the aid of a piezoelectric micromanipulator, cells were impaled with the micropipette carrying the microelectrode. Both the intracytoplamatic and the external electrodes were connected to an amplifier and the potential was measured

This remained the technique of choice for some time, in part due to the novelty of a microelectrode being able to measure ΔΨ in a single RBC, but above all, because of its directness. Nevertheless, it has been set aside in favor of simpler techniques where, for instance, impalement-related ion leakage is prevented.

Distribution of ions

Another way to determine ΔΨ in RBCs is by measuring the distribution of the dominant permeable ion in a steady state cell. In the case of RBCs, the dominant ion is Cl⁻ (Hodgkin 1951) and ΔΨ at equilibrium is determined by the distribution of the ion’s activity at equilibrium. The ratio of intracellular to extracellular Cl⁻ activities is known as the Donnan ratio, K:

$$K=\frac{{\left(a_{{\mathit{Cl}}^{-}}\right)}_{\mathit{\text{in}}}}{{\left(a_{{\mathit{Cl}}^{-}}\right)}_{\mathit{\text{out}}}}$$ 2

Then, ΔΨ can be known from K through the Nernst equation

$$\mathrm{∆\Psi }=\frac{\mathrm{R}\mathrm{T}}{z\mathrm{F}}{log}_{e}K$$ 3

To measure Cl⁻ distribution, Gedde et al. (Gedde and Huestis 1997) used 0.1 μCi of Na³⁶Cl. After 5 min of incubation to reach equilibrium, the cells were centrifuged and the disintegrations per minute (dpm) were quantified both in the pellet and the supernatant, using a ³⁶Cl⁻ quench curve and a scintillator counter. With dpm data and using the Nernst equation, the authors determined ΔΨ.

To determine α_Cl⁻_, it is necessary to consider Cl⁻ milli equivalents, the exact volume where these milli equivalents are found, and the extracellular water that forms part of the pellet, among other things. These considerations, which are usually measured or sometimes assumed, can introduce errors that make the values obtained for ΔΨ somewhat unrealistic.

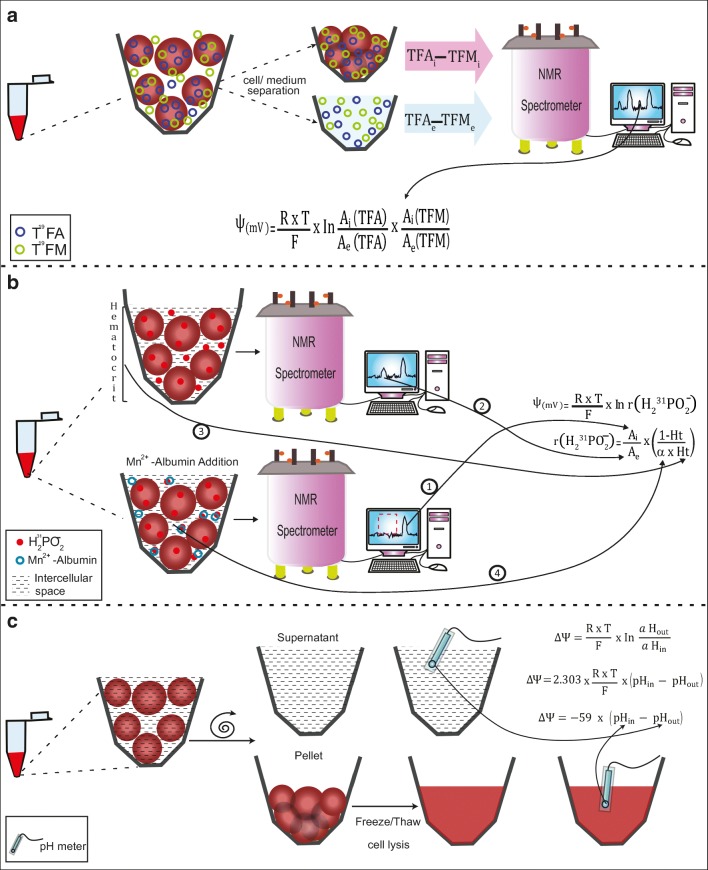
If detection is performed by nuclear magnetic resonance (NMR) instead, the resonance of intracellular ³⁵Cl⁻ in human RBCs overlaps the spectra of extracellular ³⁵Cl⁻ because the former binds hemoglobin, rendering the technique ineffective (Brauer et al. 1985). In a bid to tackle this problem, Wittenkeller et al. (1992) used the potentially more advantageous fluorinated anion probe trifluoroacetate (TFA) as a marker for Cl⁻ flux, and neutral trifluoroacetamide (TFM) to measure variations in the cellular volume. There are several advantages to these fluorinated probes: the higher sensitivity of ¹⁹F detection with its related improvement in time resolution, the extremely low metabolic activity of TFA, and the parallel measurement of the distribution of a neutral analog, TFM, which provides an independent means of determining the ratio of intra/extracellular volume that can be, in its turn, directly used to convert the TFA intensity measurements into concentration ratios. All of this allows for the direct and rapid estimation of ΔΨ from the NMR measurement alone (Fig. 3a).

Fig. 3.

Determination of Δψ by quantifying the ion distribution. Because of the impossibility of measuring intracellular and extracellular ³⁵Cl⁻, different methodologies are used to measure Cl⁻ changes by NMR spectrometry. a Trifluoroacetate (TFA) and trifluoroacetamide (TFM) are used as Cl⁻ and volume markers, respectively. RBCs are incubated with TFA and TFM. Then, the cells are centrifuged and the supernatant is separated. Both the cell pellet and the supernatant are subjected to NMR spectroscopy, and the abundance of intra and extracellular TFA and TFM obtained is then used to calculate intra and extracellular TFA/TFM activities. These activities are then used in the Nernst derived equation. b The hypophosphite ion is also used as a Ψ probe. Low hematocrit RBC suspensions are incubated with H₂³¹PO⁻₂ and then subjected to NMR spectroscopy. In the NMR spectrum, two ³¹P peaks are detected, corresponding to the intracellular and extracellular hypophosphite (① and ②). The addition of Mn⁺²-albumin to the solution eliminates the high-frequency resonance peak, corresponding to the extracellular hypophosphite population. Ht is the hematocrit (③) and α is the fraction of the total cellular volume accessible to the intracellular solute (④). These parameters make reference to the volume where the two hypophosphite ion populations are distributed, so A can be assumed as concentration. c The distribution of H⁺ is also used to determine Δψ. The pH of the extracellular medium is measured. Basically, the RBC suspension is centrifuged and the supernatant is extracted, and pH is measured at room temperature. The RBCs are then lysed by freeze/thaw cycles and pH is measured, also at room temperature. Finally, the pH values are introduced into the equation, and Δψ is determined

Wittenkeller et al., then, detected ¹⁹F⁻ by NMR and differentiated the intra and extracellular ¹⁹F⁻ peaks. With the obtained spectra, and using the following equation, they calculated the ΔΨ:

$$\mathrm{∆\Psi }=\frac{\mathrm{R}\mathrm{T}}{\mathrm{F}}{log}_e\left(\frac{{\mathrm{A}}_{\mathrm{i}}\left(\mathrm{TFA}\right)}{{\mathrm{A}}_{\mathrm{e}}\left(\mathrm{TFA}\right)}\frac{{\mathrm{A}}_{\mathrm{e}}\left(\mathrm{TFM}\right)}{{\mathrm{A}}_{\mathrm{i}}\left(\mathrm{TFM}\right)}\right)$$ 4

where A_i corresponds to the peak areas for the intracellular resonances and A_e to peak extracellular resonances of TFA and TFM, respectively.

A similar method was used by Kirk et al. (1988). They measured ³¹P by NMR, using the hypophosphite ion. Hypophosphorous acid has a single pKa of 1.1, so it exists as a hypophosphite ion at pH values close to physiological ones. In a red cell suspension, the ion crosses the cell membrane via the anion exchange protein and equilibrates rapidly. In the NMR spectrum, two ³¹P peaks are detected, corresponding to intracellular and extracellular hypophosphite. The addition of Mn⁺²-albumin to the solution eliminates the high-frequency resonance peak, which was therefore identified as corresponding to the extracellular hypophosphite population, while intracellular hypophosphite is not affected by extracellular Mn²⁺ and appears as a broader lower frequency resonance (Fig. 3b). In this case, the ΔΨ is calculated using the equation:

$$\mathrm{∆\Psi }=\frac{\mathrm{R}\mathrm{T}}{\mathrm{F}}{log}_{e}r\left({\mathrm{H}}_2\mathrm{P}{\mathrm{O}}_2^{-}\right)$$ 5

$$r\left({\mathrm{H}}_2\mathrm{P}{\mathrm{O}}_2^{-}\right)=\frac{{\mathrm{A}}_{\mathrm{i}}}{{\mathrm{A}}_{\mathrm{e}}}\left(\frac{1-{\mathrm{H}}_{\mathrm{t}}}{\mathrm{\alpha }{\mathrm{H}}_{\mathrm{t}}}\right)$$ 6

where r(H₂PO₂⁻) is the concentration distribution ratio for the hypophosphite ion, and A_i and A_e correspond to the peak areas for the intracellular and extracellular resonances of the hypophosphite ion, respectively. Ht is the hematocrit and α is the fraction of the total cellular volume accessible to the intracellular solute. The inclusion of H_t and α makes reference to the volume where the two hypophosphite ion populations are distributed, so A can be assumed as concentration.

More recently, the effect of pH and cell volume on the chemical shift of water NMR spectra in a protein solution was studied (Larkin et al. 2007). These authors determined cell volume, ΔΨ, and intracellular pH in erythrocytes suspended at near physiological pH values. The ΔΨ was calculated using the relative areas of the intracellular and extracellular resonances of dimethyl methylphosphonate (DMMP) which are used to determine intra and extra cellular volume, respectively, and hypo-phosphorous acid (HPA) in a modified Nernst equation,

$$\mathrm{∆\Psi }=\frac{\mathrm{R}\mathrm{T}}{\mathrm{No}\mathrm{F}}{log}_e\left(\frac{{\mathrm{HPA}}_{\mathrm{i}}/\mathrm{DMM}{\mathrm{P}}_{\mathrm{i}}}{{\mathrm{HPA}}_{\mathrm{s}}/\mathrm{DMM}{\mathrm{P}}_{\mathrm{s}}}\right)$$ 7

where N_o is the Avagadro’s number, HPA_i and DMMP_i are the integrals of the intracellular resonances, and HPA_s and DMMP_s are the integrals of the extracellular resonances. The HPA/DMMP ratio stands for hypophosphite ion activity.

NMR seems to be an efficient technique to measure the distribution of Cl⁻, although indirectly. It allows the intracellular and extracellular populations to be correctly differentiated from each other without the need to separate them. As can be seen, it is also necessary to know the volumes in which the compounds are, since Δψ cannot be calculated without referring to concentrations. In the case of ¹⁹F and ³¹P, trifluoroacetamide and the DMMP intra and extracellular resonance values are used, respectively, to know the volumes inside and outside the cell in order to calculate ion activity. However, the method used by Kirk and colleagues (Kirk et al. 1988) used the value of the hematocrit to refer to hypophosphite concentration values. This means that an imprecise value may be obtained for r(H₂PO₂), since the error for measuring hematocrit can be higher, and this error would be transferred to the value calculated for Δψ.

The distribution of H⁺ is also often used to determine Δψ. Here, the pH of the medium where the erythrocyte is located is measured, i.e., it is centrifuged, the supernatant is extracted, and the pH is measured at room temperature. RBCs are then lysed through freeze/thaw cycles and the pH is measured again, also at room temperature (Fig. 3c). This way of measuring the pH of RBC lysates is more accurate because it has a standard variation of 0.02 units of pH (Gedde and Huestis 1997), whereas if the cells are lysed with detergent, there is a deviation of 0.35 pH units in the values obtained (Semplicini et al. 1989). By introducing the Nernst equation, the following equation can be worked out (Gedde and Huestis 1997):

$$\begin{array}{c}\Delta \mathrm{\Psi }=\frac{\mathrm{R}\mathrm{T}}{\mathrm{F}}{log}_e\frac{a{H}_{\mathit{\text{out}}}^{+}}{a{H}_{\mathit{\text{in}}}^{+}}\\ \Delta \mathrm{\Psi }=2.303\frac{\mathrm{R}\mathrm{T}}{\mathrm{F}}\left({\mathrm{pH}}_{\text{in}}-{\mathrm{pH}}_{\text{out}}\right)\\ \Delta \mathrm{\Psi }=-59\left({\mathrm{pH}}_{\text{in}}-{\mathrm{pH}}_{\text{out}}\right)\end{array}$$ 8

where αH⁺ is the proton activity.

This method differs widely from those described before, where the integrity of the cell and its environment are maintained as under physiological conditions (Gedde and Huestis 1997; London and Gabel 1989). Furthermore, as more than one equation is required to calculate Δψ, the variations observed by different labs can be attributed to errors introduced during the obtaining of the parameters involved (αH⁺_in, αH⁺_out, pH_in, etc). Nonetheless, several ions and equations to calculate Δψ are involved, and the values obtained by the different labs are quite similar, which means this method could easily be one of the most accurate and reproducible to get real Δψ values in erythrocytes.

Radioactive lipophilic ions

The triphenylmethylphosphonium cation (TPMP⁺) is a hydrophobic ion which quickly equilibrates through the plasma membrane when co-incubated with its hydrophilic counter ion, tetraphenylborate (TBP⁻). This equilibrium distribution depends on the value for the resting Ψ in a variety of systems. Because of this property, TPMP⁺ was used to follow the dynamic changes in Ψ in erythrocytes and other cells (Cheng et al. 1980).

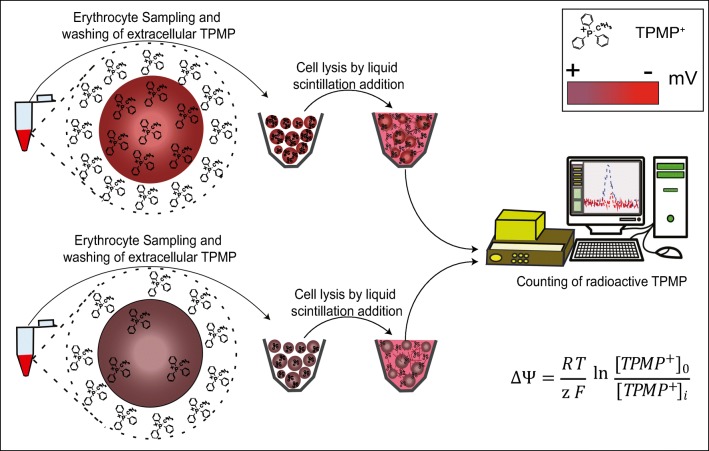
Methodologically, the technique is simple. One volume of RBC (10% hematocrit) is incubated with nine volumes of a buffer containing 10 μM H³-TPMP⁺ (100 mCi/mmol) and 2 μM TPB⁻ a 37 °C. After a very short incubation (40 s), a representative aliquot of cells was placed in scintillation vials, the cells were lysed and the radioactivity measured by liquid scintillation counting (Fig. 4) The extracellular [H³]-TPMP⁺ that remained trapped in the cell pellets was determined in separate control experiments using [H³]-inulin.

Fig. 4.

Determination of ΔΨ with radioactive lipophilic ions. The triphenylmethylphosphonium cation (TPMP⁺) is a hydrophobic ion which quickly equilibrates through the plasma membrane. This equilibrium distribution depends on the resting Ψ in a variety of systems. Two RBC suspensions (hyperpolarized and depolarized cells, see color code ΔΨ in mV) are incubated with a buffer containing 10 μM H³-TPMP⁺ a 37 °C. After incubation, an aliquot of cells is placed in scintillation vials, the cells are lysed and the radioactivity measured by liquid scintillation counting. The data obtained are filled into the equation to determine ΔΨ

To determine Δψ, the transmembrane TPMP⁺ gradient was introduced into the Nernst equation

$$\mathrm{∆\Psi }=\frac{RT}{zF}{log}_e\frac{{\left[{\mathit{\text{TPMP}}}^{+}\right]}_0}{{\left[{\mathit{\text{TPMP}}}^{+}\right]}_i}$$ 9

where [TPMP⁺]_o and [TPMP⁺]_i are the extracellular and intracellular concentrations of the hydrophobic cation, respectively.

Given the fast distribution of TPMP⁺ across the plasma membrane, this method would seem optimal to measure dynamic changes in Δψ in living cells. However, the fact that it involves radioactive material and that other techniques have emerged (such as fluorescent dyes) mean that its implementation has declined.

Voltage-sensitive dyes

Voltage-sensitive dyes (VSDs), or potentiometric probes, provide the physical basis for the optical measurement of ΔΨ. They are molecular voltmeters that insert into and intercalate among the phospholipids that compose either leaflet of the bilayer. VSDs sense a representative portion of the membrane’s electric field and alter their absorption and/or emission of light in response to changes in that field (Cohen and Salzberg 1978; Salzberg et al. 1973). Potentiometric probes can be classified according to its response velocity. Rapid response probes (RRP) change their electronic structure and, consequently, their fluorescence properties, in response to changes in the surrounding electric field. Its optical response is fast enough to detect potential transient changes (msec) in excitable cells. However, the magnitude of their potential dependent fluorescence change is often small, showing a fluorescence change of 2 to 10% per 100 mV (Bullen and Saggau 1999; Knisley et al. 2000).

Conversely, slow response probes (SRP) exhibit potential dependent changes in their transmembrane distribution that are accompanied by a fluorescence shift. The extent of their optical responses is much greater than that of RRP (around 1% fluorescence change per mV). SRP, which include anionic oxonoles, cationic carbocyanins, and rhodamines, are suitable for detecting changes in the average membrane potentials of non-excitable cells caused by respiratory activity, permeability of ion channels, drug binding, etc (Klapperstuck et al. 2009; Zhang and Zhu 2015).

Generally, signals from fluorescent dyes must be calibrated with respect to an independent measure of ΔΨ, such as the pH gradient. VSDs are usually diluted in organic solvents such as ethanol or DMSO, so users must be careful to avoid a final solvent concentration higher than 0.5% when using these probes in in vivo experiments. At lower concentrations, these solvents do not change the Ψ in RBCs (Hoffman and Laris 1974; Moersdorf et al. 2013) and no other alterations are observed.

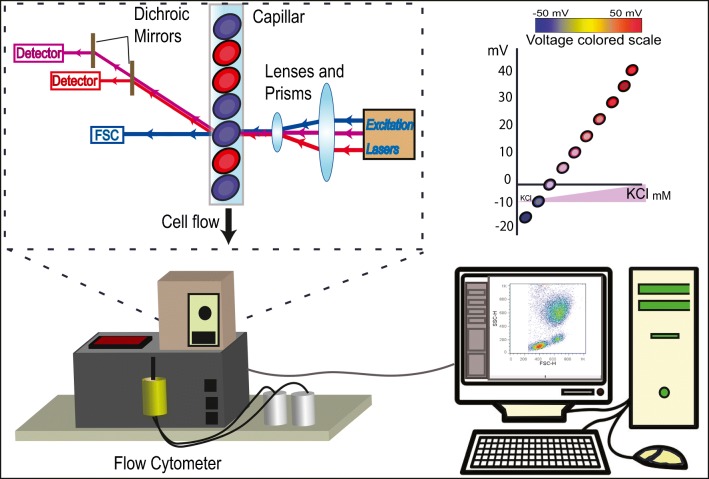
Typically, experiments are performed using 0.2% hematocrit. For calibration curves, RBCs are placed in KCl solutions of different concentrations and a VSD is added. After the time required to stabilize the dye, the K⁺ ionophore valinomycin is added to the samples at a concentration of 1 μM. The fluorescence intensities of the dye are measured spectrofluorimetrically before and after valinomycin addition (Fig. 5).

Fig. 5.

Determination of ΔΨ with potentiometric fluorescent dyes. Voltage-sensitive dyes (VSDs), like DiBAC₄(3), CC6 or DiS-C3 are molecular voltmeters that intercalate into the phospholipids that compose either leaflet of the bilayer. VSDs sense the membrane's electric field. Basically, cells are incubated with the selected VSD and after a wash, their fluorescence is determined by flow cytometry or other related techniques (spectrofluorometry, etc). Signals from fluorescent dyes must be calibrated with respect to an independent measure of membrane potential, and calibration curves using valynomicin are a general rule for this kind of technique.

Hoffman and Laris (1974) and Zavodnik et al. (1997) used the VSD 3,3′-dipropyl-2,2′-thiadicarbocyanine iodide (DiS-C₃). Carbocyanines are cationic dyes that accumulate on hyperpolarized membranes and are translocated into the lipid bilayer (Cabrini and Verkman 1986). These two teams obtained different ΔΨ values, but this difference was attributed to a slight variation in the concentration of the VSD used.

Hoffman et al. used another carbocyanine, 3,3′-dihexyl-2,2´-oxacarbocyanine (CC6 or DiS-C₆). However, this VSD increased the permeability of Na⁺ and K⁺ ions through the membrane of RBCs and also displayed non-specific binding to other compounds, all of which makes it inadvisable for Ψ measurements. These drawbacks were overcome by using DiS-C₃, which had higher sensitivity/specificity to changes in Ψ.

On the other hand, Moersdorf et al. (2013) and Zhang and Zhu (2015) used bis-(1,3-dibutylbarbituric acid) trimethine oxonol (DiBAC₄(3)) (also known as bis oxonol). This anionic dye enters depolarized cells and binds to intracellular proteins or membranes and exhibits enhanced fluorescence and red spectral shifts (Epps et al. 1994). When the cell becomes depolarized, more dye accumulates and more fluorescence is detected. Conversely, under hyperpolarization, the dye leaves the cell and the fluorescent signal decreases. In these experiments, Moersdorf et al. (2013) quantified the dye bound to the cells. They incubated RBCs with 250 nM of DiBAC₄(3) for 30 min in darkness; then, RBCs were washed and the supernatant was replaced by buffer. As for other potentiometric methods, the calibration curve was performed using several KCl concentrations in the buffer and the ionophore Valynomicin, but fluorescence in the RBCs was determined by flow cytometry.

Interestingly, the values for ΔΨ obtained by the different labs with different dyes are quite disparate, even for groups using very similar methodologies. One explanation for this variation could be a difference in the concentrations of dye used, as described by Hoffman (Hoffman and Laris 1974), who correlates dye concentration with the values of ΔΨ obtained. Unification of criteria into one general protocol would therefore solve this issue.

Summary

As shown by this review, there are quite a few different methodologies to determine ΔΨ in RBCs. Microelectrodes have been largely preferred since they allow researchers to obtain information in a direct manner about ΔΨ in individual cells, while other techniques rely on indirect measurements and the values they provide generally correspond to media population values. However, many authors argue against the use of microelectrodes, since the 0.25-μm impalement process entails local ionic leakage that could result in Δψ values of uncertain accuracy (Cheng et al. 1980). Another issue is that the relatively small size of erythrocytes makes them hard to impale. Still, this obstacle could be partially overcome through use of latest optical and mechanical technologies.

Conversely, the Δψ data obtained with methods other than microelectrodes represent values that come from cell population measurements, as it is the case of the ion distribution method, which is usually implemented on the basis of its supposedly greater reproducibility (see Table 1). Regardless, it should be kept in mind that this method can only determine Cl⁻ distribution (measured directly as the quantification of [³⁶Cl⁻] or indirectly with trifluoroacetate), or H⁺ distribution, or the distribution of any other single ionic pair. This use of only one ionic pair proves insufficient when using the Nernst equation, which can result in altered Δψ values. Another disadvantage is the fact that the equilibration rate of the ion whose distribution is measured can be so slow that it is inadequate to measure dynamic changes in Δψ.

Table 1.

Plasma membrane potential values obtained with the discussed methods. advantages and disadvantages of each method

Method	ΔΨ (mV)	References	Advantages	Disadvantages
Microelectrodes	− 5.1 ± 2.7	Lassen and Sten-Knudsen (1968)	-Direct measurement - Single cell measurement	-High complexity. -Time consuming -Expensive -Single cell measurement -Ion leakage upon cell impalement
	− 8 ± 0.21	Jay and Burton (1969)
Potentiometric dyes	− 5 to − 8	Hoffman and Laris (1974)	-Low complexity -Low cost -Can be used at the single cell and/or population level	-Indirect measurement -Poorly standardized protocols. -Vehicle derived artifacts
	− 9	Hoffman and Laris (1974)
	− 13.8 ± 5.6	Moersdorf et al. (2013)
	− 10.1 ± 1.8	Zavodnik et al. (1997)
Distribution of ions	− 10	Gedde and Huestis (1997)	-Highly reproducible -Reasonable accuracy -Low-medium complexity -Low cost	-Indirect measurement -Cell population measurements -Involves the determination of several parameters that can introduce errors when used in Nernst equation
	− 9.4 ± 0 5	Wittenkeller et al. (1992)
	− 10	Kirk et al. (1988)
	− 8.4	London and Gabel (1989)
	− 9.8	Larkin et al. (2007)
	− 9	Hoffman and Laris (1974)
Lipophilic ions	− 8.4 ± 1.3	Cheng et al. (1980)	-Low-medium complexity -Low cost -Advisable for measuring dynamic changes in Ψ	-Involves the determination of several parameters that can introduce errors when used in Nernst equation -Involves radioactive material -Only for cell population measurements

On the other hand, lipophylic ions seem to be very attractive molecules to study dynamic changes in ψ, given their fast distribution between both sides of the plasma membrane, which allows for an almost instantaneous follow-up of the potential changes. However, the potentially dangerous isotopic labeling needed for these molecules has made the scientific community lose interest in their use, and opt for safer alternatives.

For methodologies involving voltage sensitive dyes (VSDs), the ψ values obtained by different authors are diverse, as observed in Table 1. This could be explained by the fact that these methodologies are still relatively poorly defined, since several VSDs are used at different concentration. Nowadays, the use of these dyes is preferred for several reasons, including their use at very low concentrations, general innocuousness (i.e., safety), in their simple way of use and the constant advance in optical detection methods that make the determinations more sensitive and reproducible. The development of flow cytometry, which enables population study at the single cell level, is a clear example of these advances. The combination of these dyes with flow cytometry leads to more accurate, more easily repeated determinations, and therefore to standardizations which are difficult to achieve with the other methodologies described before.

Authors’ contribution

M.M.B and A.N.C performed the literature search and analysis and drafted the work, C.H.C and A.N.C critically revised the work. This article is an initiative of A.N.C who supervised the work.

Compliance with ethical standards

Conflict of interest

The authors declare that they have no conflict of interest.