Appropriate implementation and rigorous reporting of randomization procedures is vital in factorial trials for ensuring the efficiency and validity of the results.
Keywords: Multiphase optimization strategy, Randomization, Factorial trials, CONSORT, SPIRIT
Abstract
The multiphase optimization strategy (MOST) is an increasingly popular framework to prepare, optimize, and evaluate multicomponent behavioral health interventions. Within this framework, it is common to use a factorial trial to assemble an optimized multicomponent intervention by simultaneously testing several intervention components. With the possibility of a large number of conditions (unique combinations of components) and a goal to balance conditions on both sample size (for statistical efficiency) and baseline covariates (for internal validity), such trials face additional randomization challenges compared to the standard two-arm trial. The purpose of the current paper is to compare and contrast potential randomization methods for factorial trials in the context of MOST and to provide guidance for the reporting of those methods. We describe the principles, advantages, and disadvantages of several randomization methods in the context of factorial trials. We then provide examples to examine current practice in the MOST-related literature and provide recommendations for reporting of randomization. We identify two key randomization decisions for MOST-related factorial trials: (i) whether to randomize to components or conditions and (ii) whether to use restricted randomization techniques, such as stratification, permuted blocks, and minimization. We also provide a checklist to assist researchers in ensuring complete reporting of randomization methods used. As more investigators use factorial trials within the MOST framework for assembling optimized multicomponent behavioral interventions, appropriate implementation and rigorous reporting of randomization procedures will be essential for ensuring the efficiency and validity of the results.
Implications
Practice: When determining the clinical value of published results of factorial trials in the multiphase optimization strategy (MOST) framework, practitioners should critically assess the randomization methods, given the increased complexity of factorial trials over standard two-arm parallel randomized trials.
Policy: Journals and authors should ensure factorial trials in the MOST framework follow the appropriate reporting guidelines.
Research: Given the complexity of factorial designs, researchers using factorial trials in the MOST framework should be diligent in performing valid and defensible randomization procedures, and in comprehensively reporting on the details of the randomization.
INTRODUCTION
The multiphase optimization strategy (MOST) is an increasingly popular framework for developing, testing, and implementing multicomponent behavioral health interventions. Pioneered by Collins et al. [1, 2], MOST is an engineering-inspired framework. MOST consists of three phases: preparation, optimization, and evaluation [3]. First, candidate components of an intervention are identified using theory (preparation). Next, the intervention is optimized by simultaneously evaluating the components to determine whether to include each component and, if so, which level (e.g., high or low) of the component to include (optimization). Finally, the optimized treatment package is evaluated using a traditional randomized controlled trial (RCT) design (evaluation). These three phases can then be repeated as needed (by the original investigative team or others) in order to continue evaluating intervention components and testing the newly optimized intervention.
The study design used in the optimization phase is typically, though not necessarily, a factorial or fractional factorial trial and is used to evaluate the effect of k discrete intervention components on the outcome of interest. In its most basic form where each component has two levels, a full factorial design would be a 2k factorial with 2k conditions, namely 2k unique combinations of components. In contrast, a fractional factorial trial would use select combinations of k components resulting in fewer than 2k conditions.
Many behavioral intervention factorial trials conducted in the context of MOST include four or more components with 16 or more conditions. For example, in the Charge study currently being implemented by our team (clinicaltrials.gov: Charge: A Text Messaging-based Weight Loss Intervention. [https://ClinicalTrials.gov/show/NCT03254940; last accessed December 6 2018]), we are testing five text message components to examine their impact on weight change over 6 months using a full factorial design. With such a large number of conditions, randomization can seem more challenging than for a two-arm parallel trial. Given that proper randomization is essential to protect the internal validity of a trial, it is important for researchers to understand the advantages and disadvantages of available randomization procedures when selecting an appropriate method to implement when conducting a factorial trial. Briefly, such methods include a choice of randomizing to each condition [4–6], randomizing to components separately [7] or randomizing to components sequentially [8, 9]. Then, for the chosen approach, there is the possibility of using a restricted randomization procedure such as permuted block randomization [5], minimization [10], or stratification [4–6].
The purpose of the current paper is to examine a range of randomization methods and procedures for factorial designs in the context of MOST for optimizing multicomponent behavioral health interventions, and to provide guidance for the reporting of the randomization methods used. We first give an overview of factorial trials and describe the advantages and disadvantages of a range of randomization procedures for such designs. We then provide guidance for the reporting of the methods. Our goal is to assist researchers conducting factorial trials in the optimization phase of MOST to implement valid and defensible randomization procedures to generate the best evidence about the intervention components.
BACKGROUND: FACTORIAL TRIALS
Several articles have been written providing information on factorial trials, specifically in the context of MOST [11–13]. Briefly, a factorial or fractional factorial trial can be used to efficiently and simultaneously test the main effects and interactions of several intervention components on the outcome of interest. For example, in the five-factor text messaging intervention for weight loss currently being conducted by our team—the Charge study, the design of which motivated the current paper—the corresponding full factorial trial is a 2 × 2 × 2 × 2 × 2 factorial trial with 25 = 32 conditions (unique combinations of components; Table 1), since each of the five components has two levels. The main effect of one intervention component compares all conditions where this component is “on” to all those where this component is “off”, averaging over all other components. The definitions of “on” and “off” depend on the component. Importantly, they do not necessarily indicate presence or absence of a component but could instead represent intensity or levels of a component. For example, in the Charge study, the main effect of the frequency of text messaging component is average weight loss across all conditions where frequency is set to “daily” (on) minus the average weight loss across all conditions where frequency is set to “weekly” (off). In theory, components tested in the MOST framework may have more than two levels. However, to our knowledge, no factorial MOST-related study has tested such components, likely because of the large increase in sample size and additional resources needed. (All else being equal, adding one three-level component to a factorial design increases the number of conditions by 50% and the required sample size by at least 50% [3].) Therefore, we focus on designs with two-level components.
Table 1.
| Components of a text messaging intervention for weight loss
| Experimental condition | Texting Frequency | Motivational messaging | Reminders | Feedback type | Comparison unit |
|---|---|---|---|---|---|
| 1 | Weekly | Self-generated | One | Summary score | Self |
| 2 | Weekly | Self-generated | One | Summary score | Group |
| 3 | Weekly | Self-generated | One | Individual goal | Self |
| 4 | Weekly | Self-generated | One | Specific goal | Group |
| 5 | Weekly | Self-generated | Multiple | Summary score | Self |
| 6 | Weekly | Self-generated | Multiple | Summary score | Group |
| 7 | Weekly | Self-generated | Multiple | Individual goal | Self |
| 8 | Weekly | Self-generated | Multiple | Individual goal | Group |
| 9 | Weekly | Expert-generated | One | Summary score | Self |
| 10 | Weekly | Expert-generated | One | Summary score | Group |
| 11 | Weekly | Expert-generated | One | Individual goal | Self |
| 12 | Weekly | Expert-generated | One | Individual goal | Group |
| 13 | Weekly | Expert-generated | Multiple | Summary score | Self |
| 14 | Weekly | Expert-generated | Multiple | Summary score | Group |
| 15 | Weekly | Expert-generated | Multiple | Individual goal | Self |
| 16 | Weekly | Expert-generated | Multiple | Individual goal | Group |
| 17 | Daily | Self-generated | One | Summary score | Self |
| 18 | Daily | Self-generated | One | Summary score | Group |
| 19 | Daily | Self-generated | One | Individual goal | Self |
| 20 | Daily | Self-generated | One | Individual goal | Group |
| 21 | Daily | Self-generated | Multiple | Summary score | Self |
| 22 | Daily | Self-generated | Multiple | Summary score | Group |
| 23 | Daily | Self-generated | Multiple | Individual goal | Self |
| 24 | Daily | Self-generated | Multiple | Individual goal | Group |
| 25 | Daily | Expert-generated | One | Summary score | Self |
| 26 | Daily | Expert-generated | One | Summary score | Group |
| 27 | Daily | Expert-generated | One | Individual goal | Self |
| 28 | Daily | Expert-generated | One | Individual goal | Group |
| 29 | Daily | Expert-generated | Multiple | Summary score | Self |
| 30 | Daily | Expert-generated | Multiple | Summary score | Group |
| 31 | Daily | Expert-generated | Multiple | Individual goal | Self |
| 32 | Daily | Expert-generated | Multiple | Individual goal | Group |
See the Charge study description for more information. (clinicaltrials.gov: Charge: A Text Messaging-based Weight Loss Intervention. [https://ClinicalTrials.gov/show/NCT03254940; last accessed December 6 2018]).
Fractional factorial designs are also commonly used in the optimization phase of MOST. In the Charge study example given above, we could have tested the components using 25–1 = 16 conditions, rather than 32 conditions. An advantage of fractional factorial designs is that with fewer conditions, they may be easier to implement logistically and thus likely (though not necessarily) less costly. For an automated text messaging intervention like the Charge intervention, the logistics of more combinations of components may not be burdensome. But if the intervention involves delivering physical items to participants or meeting with participants in person, the administrative logistics and added cost of implementing 32 or more combinations of intervention components could be burdensome. For example, Piper et al. [14] describe the implementation of a MOST-related optimization fractional factorial trial. The authors wished to simultaneously test the effect on abstinence from smoking of six components of an intervention designed to help smokers quit. A full factorial design would consist of 26 = 64 unique combinations of components (conditions). Citing their desire to make the research “more logistically manageable” (since some components required in-person counseling or provision of nicotine gum), the study team implemented a ½-fraction fractional factorial trial with 26–1 = 32 conditions (i.e., ½ as many conditions as the full factorial design).
A primary disadvantage of fractional factorial designs is that effects are combined in bundles of two or more and cannot be disentangled. For example, a main effect may be combined, or “aliased,” with a higher-order interaction (see Collins et al. [11] for a more detailed discussion of aliasing, which is beyond the scope of the current paper). However, when planning a fractional factorial design, researchers will know a priori which effects are aliased and can strategically alias effects of scientific interest with effects that are expected to be minimal (e.g., main effects aliased with five-way interactions).
A major advantage of the factorial design or fractional factorial design is the ability to test multiple intervention components efficiently, particularly when the data are analyzed using effect coding [15], in which components are coded as 1 and –1 for “on” and “off” rather than the 1 and 0 dummy coding that is commonly implemented as the default coding in major statistical software. Such efficiency gains result from the fact that the effects of the components on the outcome are uncorrelated with each other when all conditions have equal sample size. As a consequence, the power of a factorial trial is based not on the sample size per condition, but on the number of individuals per level (“on” or “off”) of a factor (i.e., intervention component). As Collins et al. point out, this allows a researcher to test many components efficiently, saving on sample size [11]. As the number of components the researcher wishes to test increases, the efficiency (in terms of sample size) of the factorial design is even more advantageous. Suppose that the total number of participants needed for a factorial trial is N. Using more traditional design methods, testing k components using a series of two-arm parallel RCTs would require a total of k*N participants to compare each component against a control arm in separate experiments, and a multi-arm RCT would require (k + 1)*(N/2) participants to test all k components against a single control arm in a (k + 1)-arm trial [11]. For example, in the Charge study, we originally planned to recruit 448 participants in a full factorial design. To have the same statistical power to test the components against control in separate experiments would require 5*448 = 2,240 participants, and to test all components against control in a six-arm RCT would require 6*224 = 1,344 (three times as many) participants. This efficiency of the factorial trial makes it an ideal design when optimizing a behavioral intervention. Importantly, it aligns with one of the fundamental principles underlying MOST—the resource management principle—which states that investigators using MOST “must strive to make the best and most efficient use of available resources when obtaining scientific information” [3].
POTENTIAL RANDOMIZATION METHODS IN FACTORIAL TRIALS
In this section, we discuss a range of methods for randomization in factorial trials. Given that, under effect coding, statistical efficiency is reduced when there is sample size imbalance (i.e., unequal sample size) across conditions, effective and balanced randomization is especially important in factorial trials. Additionally, because of the number of components and conditions, implementation of randomization can also be more challenging than in a standard two-arm RCT. To facilitate an understanding of these challenges, we identify and discuss two key choices to be made regarding randomization in factorial trials.
Randomization to components or to conditions
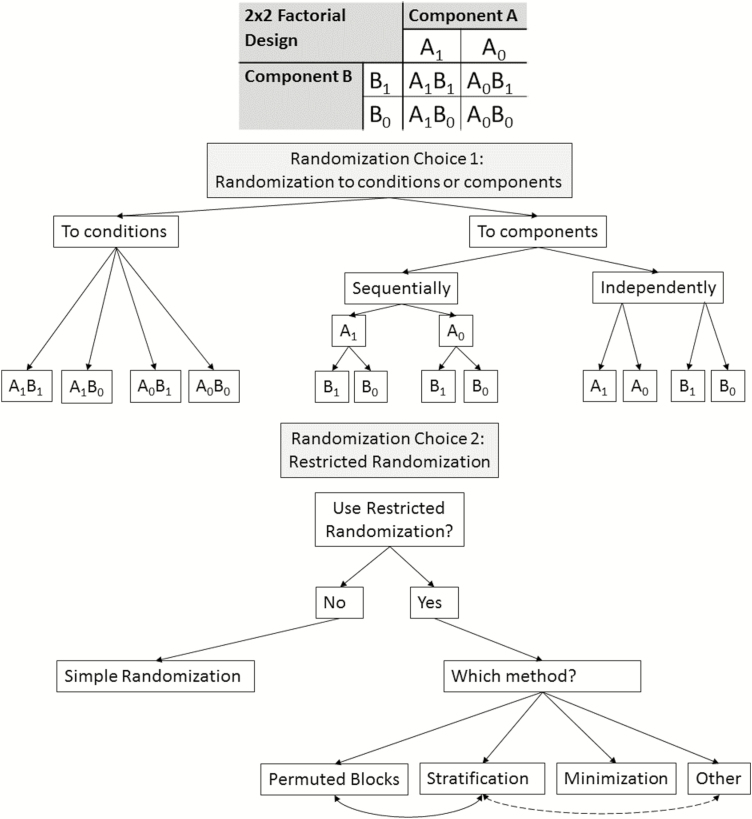
The first choice to make regarding randomization in a factorial trial is whether to randomize to components or conditions. Additionally, if randomizing to components, such randomization can be performed sequentially or independently. Figure 1 displays the resulting three randomization approaches in the case of a 2 × 2 factorial design. Importantly, randomizing to levels of components may not be feasible in fractional factorial designs, as one could end up with participants randomized to combinations of components (i.e., conditions) not contained within the fraction of conditions. To our knowledge, randomizing to components sequentially has not yet been used in practice in factorial trials in the context of MOST, and it is unclear from the reporting of some trials whether randomizing to components independently has been used in the context of MOST. An example of randomizing to components sequentially comes from a 2 × 2 × 2 factorial trial of three binary treatments conducted outside of the MOST framework [8, 9]. In this case, the researchers ordered the treatments and randomized to one of the two levels of the first treatment, then randomized to one of the two levels of the second treatment within the two randomization groups created in the previous stage, followed by randomization to the third treatment within the four randomization groups created in the previous stage. An example of randomizing to components independently is found in another 2 × 2 × 2 factorial trial outside of the MOST framework [7]. The Charge study is randomizing to conditions, and several other factorial trials conducted in the MOST framework have also randomized to conditions (e.g., [5, 16]).
Fig. 1.
| Schematic diagram of randomization approaches for factorial trials, using a simple 2 × 2 factorial design as an example. Note: Permuted block randomization should theoretically be possible when randomizing to components (either sequentially or independently), but we are unaware of its use in this setting in practice.
Randomization to conditions is most straightforward, as it involves a single-stage randomization procedure assigning participants to combinations of components rather than requiring separate randomization procedures for each component, whether it be sequential or independent randomization. If each participant is randomized to all conditions/components as soon as they are enrolled in the trial, the difference between randomization to conditions and randomization to components may simply be whether the computer used for randomization runs k independent randomizations simultaneously or runs one randomization across the 2k conditions. Using appropriate restricted randomization procedures (see next section), all three types of randomization should arrive at approximately balanced sample sizes across conditions. Randomization to components sequentially may be necessary to use in designs where each individual is randomized at different points during the trial, which is the case in certain experimental designs—such as the sequential multiple assignment randomized trial (SMART)—that are used in the optimization of adaptive interventions [2].
Restricted randomization
The second choice to make regarding randomization in a factorial trial is whether to use a form of restricted randomization, and if so, which method(s) to use. Restricted randomization methods include permuted blocks, stratification, and minimization, all of which can also be used in the two-arm parallel RCT design (see Table 2 for a summary of these methods) and could be adopted for each of the three randomization approaches described above. While permuted block randomization is an attempt to balance sample size across randomization groups, stratification seeks to balance select covariates across randomization groups. The goal of minimization is to balance on both sample size and covariates, and is particularly popular when recruitment into a trial occurs over time. In contrast to restricted randomization, simple randomization may be compared to a coin flip or roll of a m-sided die, where m is the number of randomization groups (e.g., conditions). Simple randomization is rarely used in practice when designing factorial trials because of the relatively high probability of imbalance in sample size across randomization groups, especially when there are more than two randomization groups, as in factorial trials [17].
Table 2.
| Description of restricted randomization methods
| Method | Purpose |
|---|---|
| Permuted block | Ensure balance in sample size across randomization groups |
| Stratification | Ensure balance on stratification factors across randomization groups |
| Minimization | Balance several variables at once (including continuous variables, potentially), as well as sample size, across randomization groups |
These approaches can be applied to both randomization to components and randomization to conditions (e.g., see Fig. 1). In both cases, the ultimate goal is to balance across conditions.
Given that the main goal of many types of restricted randomization is to achieve sample size balance across randomization groups, it is a valuable design procedure for ensuring efficient analyses of factorial trials with binary components [12, 15]. This is because when balance has been achieved and effect coding is appropriately used in data analysis, “tests for main effects and interactions are uncorrelated” which is not the case if the sample sizes per condition are unequal, although these tests are nearly uncorrelated when sample sizes are unequal, unless the inequality is severe [12]. Sample size imbalance across conditions will almost certainly be minimal if a restricted randomization procedure has been correctly implemented.
Permuted block randomization
Permuted block randomization is a method of restricted randomization that is commonly used in factorial trials (as well as in two-arm RCTs) [5, 14, 18–21]. Its main goal is to balance sample size across randomization groups. In permuted block randomization, blocks of size M are created where the size of the block must be equal to, or a multiple of, the number of randomization groups. For example, when randomizing to 32 conditions in a 25 factorial trial, the block size would be 32 or a multiple of 32. Each block will be a list of the 32 conditions (or a multiple of the 32 conditions) where the list is a random ordering of all 32 randomization groups so that each condition appears only once (or the exact same number of times, in the case of multiples). In our 25 factorial trial, the Charge study investigators are using permuted block randomization with a block size of 32. When a participant is enrolled, he or she is randomized to the next condition listed in the permuted block currently being used by the study team. Once all allocations in a block have been used, a new list from the next permuted block is used. In this whole process, those allocating the intervention are blinded to the permuted blocks. Huffman et al. [20] used blocks of size 16, for their 23 (8 conditions) factorial trial. Blocks may vary in size within the same trial. For example, McMahon et al. [21], in their 2 × 2 factorial trial, used permuted blocks of size 16–24, depending on “enrollment wave and community center.” In practice, varying the block size becomes less feasible as the number of factors (components) increases. Randomly varying the size of blocks has been proposed as a way to reduce the selection bias that could arise if it was possible to predict the next intervention assignment. This is true especially as the number of components and block size increases. This highlights the importance of reporting about blinding and implementation of randomization, as we discuss under Reporting Guidelines below. Permuted block randomization is commonly used in factorial trials that randomize to conditions, but we are not aware that it has been used by factorial trials randomizing to components.
An additional goal of block randomization is to achieve balance on calendar time [22], which is particularly important if the type of recruited participants may change over time (e.g., healthier participants recruited initially). Given the large number of conditions that are commonly considered in factorial trials of behavioral interventions in the MOST framework, such a consideration is especially important.
Stratification
An additional restriction method that is sometimes combined with block randomization or used on its own is stratification, which could be applied both when randomizing to components separately or randomizing to conditions. While the main goal of permuted block randomization is sample size balance across conditions, the goal of stratification is balance on important covariates across conditions, namely those that are associated with (i.e., predictive of) the outcome of interest. Potential advantages of stratification include making the randomization groups more comparable in terms of the stratification variables, increased ability to detect real effects (i.e., power), and protection against false positive results (i.e., type I error), among others [23]. However, in many factorial trials, it is only feasible to stratify on a very limited number of categorical variables, especially if permuted block randomization is used in conjunction with stratification. For example, in the 25 Charge study with a target sample size of 448 participants, given that a block size of at least 32 would be needed, there would be 14 blocks of size 32 in the case of no stratification. Stratification on a single binary covariate would result in two strata each with seven blocks of size 32, although in practice the number of blocks may not be equal depending on the expected number of participants in each stratum. Since the Charge study is stratifying on gender (male/female), and if we expect approximately 35% males and 65% females, we should end up with approximately nine full blocks of women and five full blocks of men. With additional strata, the target sample may have to be increased to be a multiple of p*s, where p is the block size and s is the number of strata, in order to avoid incomplete blocks and to attain balance by condition. With more than one stratification variable, it can be even more complex as the number of levels of each variable must be multiplied to determine the number of blocks. For example, if the study stratifies by 10 primary care clinics from which participants are recruited and gender (male/female), then each clinic will have two separate permuted blocks, leading to 20 distinct permuted blocks in the trial. With a block size of 32, this leads to a sample size of 640, assuming all randomization groups (i.e., conditions) are the same size. Since this is larger than the target sample size of 448 participants, this leads to a higher probability of imbalance on sample size across conditions. An additional complexity associated with an increased number of stratification factors is that if, for example, clinics are of varying size or the speed of recruitment differs between clinics, the final allocation could result in incomplete blocks.
As noted above, stratification may be used in conjunction with permuted blocks. Both the Charge study and the Piper et al. [14] study described previously use permuted blocks and stratification. In the case of an unfilled block, as can happen when the total sample size attained is not a multiple of the block size, the maximum imbalance on sample size per condition is j, where j is the number of strata. For example, if researchers are stratifying on gender (male/female), as in the Charge study, the maximum imbalance at any stage of enrollment would be for half of the conditions to have two more participants than the other half of the conditions. This occurs when the current permuted blocks for randomizing males and females are both half filled.
There has been debate in the literature on when and whether to use stratification in trials. When it is used, the general recommendation is that it is better to have as few strata as possible and to choose the covariates hypothesized to have the largest impact on the trial outcome [17, 23].
Minimization
Minimization is another restricted randomization approach to assign participants to components or conditions [24, 25]. It uses an algorithm to determine which condition to assign each participant to, based on the characteristics of the participants who have already been assigned. For example, minimization could be used in the Charge study to balance the conditions on sample size, gender and obesity status (body mass index ≥ 30). Consider a situation in which a man who is obese is eligible and signs up for the study. In this situation, minimization will consider the percentage of males and people who are obese in all randomization groups, and assign the participant to the group which reduces the imbalance across groups on these variables. A variety of minimization algorithms is available, and weighting can be applied if some variables are considered more (or less) important than others to balance randomization arms on [26].
An advantage of this method is that it can assist in balancing the interventions on several covariates at once, although in practice the balance will be less satisfactory the more variables which are included in the algorithm. This method also aims to balance sample size across conditions. To our knowledge, minimization has not yet been used in MOST optimization factorial trials. Outside of the MOST framework, De Placido et al. [10] report that they used minimization based on two binary variables in a 2 × 2 factorial trial, in which sample size across conditions was fairly well balanced. Another group of researchers also use minimization in their 2 × 2 × 2 factorial trial “to ensure comparability between women with respect to three prognostic factors” [7]. Of note, in this trial, the researchers randomized women to intervention components separately. In practice, unless a researcher has many baseline covariates they wish to balance on, permuted block randomization with stratification should be an acceptable method for most factorial studies, given the relative simplicity of implementation.
Concerns have been raised concerning selection bias when using minimization [27], given its deterministic allocation of participants to randomization groups, although selection bias is also a potential concern when using permuted blocks [28, 29]. On the other hand, some argue that minimization should be used more often than it currently is used in trials of any design, because of its performance in achieving balanced randomization groups and its ability to incorporate more baseline covariates than stratification [26]. Minimization remains a viable option for assigning participants to components or conditions in factorial trials.
If non-restricted randomization (i.e., simple randomization) is chosen, the sample size per condition could be greatly imbalanced, leading to violation of the assumption of uncorrelated main effects as well as loss of statistical efficiency. In addition, errors in how the randomization and intervention assignment is carried out (either computer or human errors) could create severe bias and threaten validity of the trial results, much more so than in a two-arm RCT.
RANDOMIZATION PROCEDURES: CASE STUDIES
In this section, we will discuss some examples of factorial trial articles in the MOST optimization literature with differing level of detail on randomization. We comment on the completeness of their reporting of randomization, using the Consolidated Standards of Reporting Trials (CONSORT) statement (for reporting of results) or Standard Protocol Items: Recommendations for Interventional Trials (SPIRIT) statement (for reporting of protocols) as guidelines [30, 31].
We examined articles based on the four items related to randomization in the CONSORT 2010 statement on the reporting of randomized trials [32]. These four items (8a, 8b, 9, and 10) are elaborated upon in Table 3. They are also found in the 2001 CONSORT statement [33], which predates the development of MOST [1]. They correspond directly to those (16a, 16b, and 16c) outlined in the SPIRIT guidelines (first published in 2013) for the reporting of a protocol of a trial [34]. These items cover details such as the type of randomization (e.g., restricted or not; CONSORT item 8b, SPIRIT item 16a), method used to generate (e.g., computer-generated), implement, and conceal the randomization allocation sequence (CONSORT items 8a and 9; SPIRIT items 16a and 16b), and who was or will be responsible for generating the allocation sequence, enrolling participants, and assigning them to interventions (CONSORT item 10, SPIRIT item 16c).
Table 3.
| Consolidated Standards of Reporting Trials (CONSORT) and Standard Protocol Items: Recommendations for Intervention Trials (SPIRIT) items related to randomization
| Statement | Item number | Checklist item |
|---|---|---|
| CONSORT | 8a | Method used to generate the random allocation sequence |
| 8b | Type of randomization; details of any restriction | |
| 9 | Mechanism used to implement the random allocation sequence, describing any steps to conceal the sequence until interventions were assigned | |
| 10 | Who generated the random allocation sequence, who enrolled participants, and who assigned participants to interventions | |
| SPIRIT | 16a | Method of generating the allocation sequence, and list of any factors for stratification. To reduce predictability of a random sequence, details of any planned restriction should be provided in a separate document that is unavailable to those who enroll participants or assign interventions |
| 16b | Mechanism of implementing the allocation sequence, describing any steps to conceal the sequence until interventions are assigned | |
| 16c | Who will generate the allocation sequence, who will enroll participants, and who will assign participants to interventions |
In the (25) factorial trial main results paper authored by Schlam et al. [19], it is reported that randomization schemes were computer-generated (CONSORT 8a), that randomization was stratified by gender and clinic, and that permuted block randomization with a block size of 32 was used (CONSORT 8b). The authors also describe how they concealed the allocation sequence (CONSORT 9), and who assigned participants to intervention (CONSORT 10). All of this description was accomplished in one paragraph, showing that it can be possible in only a small amount of space in an article to fulfill the CONSORT reporting recommendations. This paper appears in a journal (Addiction) in which instructions indicate that authors should adhere to the CONSORT guidelines for reporting trial results.
However, in an informal review of the current MOST-related trials literature, we found several recent papers (all of which were published after the publication of the SPIRIT and CONSORT guidelines) with incomplete reporting of randomization methods [16, 35–37], based on the SPIRIT and CONSORT guidelines. One journal where some of these were published states that it requires the CONSORT or SPIRIT guidelines be adhered to when publishing randomized trial results or protocols (even requiring a SPIRIT of CONSORT flow chart and checklist provided as supplementary material to that manuscript). Another journal currently only requests rather than requires that authors adhere to the SPIRIT or CONSORT statement. Journals should play a role in promoting more comprehensive reporting on randomization procedures by requiring authors to submit a CONSORT (or SPIRIT) checklist with their manuscripts, and emphasizing to editors and reviewers the importance of examining the checklist for accuracy and completeness. Another consideration when examining the completeness of reporting of randomization procedures is the fact that extensive study design information, of which randomization is one part, should be included in the article, all within the space requirements of the journal. Nevertheless, as indicated in the example given above from Schlam et al. [19] example given above, complete reporting can be accomplished in one short paragraph.
REPORTING GUIDELINES
Given the possibility of bias and threats to internal validity if randomization is performed incorrectly in a factorial trial, we recommend that authors of MOST optimization factorial trials adhere to the CONSORT 2010 statement on the reporting of randomization in two-arm parallel trials [32] when publishing a description of main results, or equivalently the 2013 SPIRIT guidelines on reporting of trial protocols when publishing their protocols [34]. More specifically, details of any restricted randomization procedures should be reported on and authors should state if none were used. When permuted block randomization is used, the block size should be reported; and when stratification is used to balance the design on covariates, the number and levels of these stratification factors should be specified (e.g., gender: male and female). If both permuted block randomization and stratification is used, and there is more than one stratification variable (e.g., gender and clinic), the authors should report on whether they were completely crossed in determining the number of blocks. Authors should also report how the allocation sequence was generated and who generated it, how the sequence was implemented and concealed, and who assigned participants to interventions. All such detail should be placed in a prominent paragraph within the methods section of the paper.
Importantly, in addition to the CONSORT (equivalently SPIRIT) items, we recommend that authors of MOST optimization factorial trials also state whether participants were separately randomized to components or were randomized to conditions, and the rationale for this choice. In outcomes papers, researchers would ideally provide additional details about actual implementation, including whether there were any unforeseen challenges in the randomization, such as computer or human errors in randomizing and assigning participants. In addition, authors should report the sample sizes in each condition, so that readers can determine the extent of imbalance on condition sample sizes. These recommendations are summarized in checklist form in Table 4.
Table 4.
| Randomization reporting checklist for factorial trials
| Item number | Checklist item |
|---|---|
| 1 | Randomization unit: components or conditions and rationale for this choice |
| 1b | If components: randomization conducted sequentially or independently and rationale for this choice |
| 2 | Method used or planned to be used to generate the random allocation sequence |
| 3 | Type of randomization; details of any restriction |
| 4 | Mechanism used or planned to be used to implement the random allocation sequence, describing any steps to conceal the sequence until interventions were assigned |
| 5 | Who generated or will generate the random allocation sequence, who enrolled or will enroll participants, and who assigned or will assign participants to interventions |
| 6 | (Protocola and results papers) Additional details about actual implementation, such as unforeseen challenges. |
| 7 | (Protocola and results papers) Final sample sizes in each condition |
CONCLUSION
In this paper, we have focused on randomization procedures for multicomponent behavioral factorial trials in the MOST framework. We have described advantages and disadvantages of potential types of randomization, summarized current practice, and provided recommendations for reporting. We have highlighted the important decision to make regarding randomizing to components or conditions. Since randomizing to components may not be feasible in fractional factorial designs, and given that randomizing to conditions is more straightforward, randomizing to conditions may be preferred, regardless of the restricted randomization procedure used. Because of the implications of sample size imbalance in factorial trials, simple randomization should rarely, if ever, be used. Instead, some type of restricted randomization, such as permuted blocks, should be used to ensure approximate balance in sample size across conditions.
Our discussion of potential randomization methods was not exhaustive; instead, we focused on all methods that have been used to date and some others that could be used in MOST optimization factorial trials. There are several other restricted randomization methods which could in theory be applied to factorial trials (e.g., Efron’s biased coin, Wei’s urn, etc.), but are beyond the scope of this paper given their infrequent use. The reader is referred to a reference such as Rosenberger and Lachin [17] for more information on such alternative methods.
The application of MOST to the development of multicomponent behavioral interventions is only about a decade old. The optimization of behavioral interventions using factorial trials has its own unique challenges in design, implementation, and analysis. In the designing of a factorial trial, special care should be given to choosing whether to randomize to components or conditions, and what types of restricted randomization approaches to use. Such choices will have implications for the implementation and analysis of the trial. Rigorous reporting of randomization methods in protocol and results publications will help readers understand what randomization procedures are being used and how they are carried out, so that they can judge the appropriateness of the methods used, whether internal validity was or is likely to be achieved, and the implications for analysis. As more investigators use factorial trials in the MOST framework for optimizing multicomponent behavioral interventions, appropriate implementation and rigorous reporting of randomization procedures will be essential for ensuring the efficiency and validity of the results.
ACKNOWLEDGMENTS
The authors wish to acknowledge and thank the rest of the Charge study team, including Eric Finkelstein, Kathryn Pollack, Erica Levine, Jamiyla Bolton, Melissa Kay, and Christina Hopkins. This work was supported by NIH grant 1R01DK109696-01A1. The funders had no role in decision to publish or preparation of the manuscript. The authors also wish to thank two anonymous reviewers for their comments which helped improve the final version of the manuscript.
Compliance with Ethical Standards
Conflicts of Interest: G. G. Bennett is currently on the scientific advisory board of Nutrisystem and has equity in Interactive Health. D. M. Steinberg is a consultant with Omada Health. Remaining authors declare that they have no conflicts of interest.
Ethical Approval: This article does not contain any studies with human participants performed by any of the authors.
Informed Consent: This study does not involve human participants and informed consent was therefore not required.
Welfare of Animals: This article does not contain any studies with animals performed by any of the authors.
References
- 1. Collins LM, Murphy SA, Nair VN, Strecher VJ. A strategy for optimizing and evaluating behavioral interventions. Ann Behav Med. 2005;30(1):65–73. [DOI] [PubMed] [Google Scholar]
- 2. Collins LM, Murphy SA, Strecher V. The multiphase optimization strategy (MOST) and the sequential multiple assignment randomized trial (SMART): new methods for more potent eHealth interventions. Am J Prev Med. 2007;32(Suppl. 5):S112–S118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Collins LM. Optimization of Behavioral, Biobehavioral, and Biomedical Interventions: The Multiphase Optimization Strategy (MOST). New York, NY: Springer; 2018. [Google Scholar]
- 4. Apfel CC, Korttila K, Abdalla M, et al. ; IMPACT Investigators. A factorial trial of six interventions for the prevention of postoperative nausea and vomiting. N Engl J Med. 2004;350(24):2441–2451. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Pellegrini CA, Hoffman SA, Collins LM, Spring B. Optimization of remotely delivered intensive lifestyle treatment for obesity using the Multiphase Optimization Strategy: Opt-IN study protocol. Contemp Clin Trials. 2014;38(2):251–259. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Pellegrini CA, Hoffman SA, Collins LM, Spring B. Corrigendum to “Optimization of remotely delivered intensive lifestyle treatment for obesity using the Multiphase Optimization Strategy: Opt-IN study protocol” [Contemp. Clin. Trials 38 (2014) 251-259]. Contemp Clin Trials. 2015;45(Pt B):468–469. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. The CAESAR Study Collaborative Group. Caesarean section surgical techniques: a randomised factorial trial (CAESAR). BJOG. 2010;117(11):1366–1376. [DOI] [PubMed] [Google Scholar]
- 8. Manson JE, Gaziano JM, Spelsberg A, et al. A secondary prevention trial of antioxidant vitamins and cardiovascular disease in women. Rationale, design, and methods. The WACS Research Group. Ann Epidemiol. 1995;5(4):261–269. [DOI] [PubMed] [Google Scholar]
- 9. Cook NR, Albert CM, Gaziano JM, et al. A randomized factorial trial of vitamins C and E and beta carotene in the secondary prevention of cardiovascular events in women: results from the Women’s Antioxidant Cardiovascular Study. Arch Intern Med. 2007;167(15):1610–1618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. De Placido S, De Laurentiis M, De Lena M, et al. ; GOCSI Cooperative Group. A randomised factorial trial of sequential doxorubicin and CMF vs CMF and chemotherapy alone vs chemotherapy followed by goserelin plus tamoxifen as adjuvant treatment of node-positive breast cancer. Br J Cancer. 2005;92(3):467–474. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Collins LM, Dziak JJ, Li R. Design of experiments with multiple independent variables: a resource management perspective on complete and reduced factorial designs. Psychol Methods. 2009;14(3):202–224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Collins LM, Dziak JJ, Kugler KC, Trail JB. Factorial experiments: efficient tools for evaluation of intervention components. Am J Prev Med. 2014;47(4):498–504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Baker TB, Smith SS, Bolt DM, et al. Implementing clinical research using factorial designs: a primer. Behav Ther. 2017;48(4):567–580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Piper ME, Fiore MC, Smith SS, et al. Identifying effective intervention components for smoking cessation: a factorial screening experiment. Addiction. 2016;111(1):129–141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Kugler KC, Trail JB, Dziak JJ, Collins LM.. Effect Coding Versus Dummy Coding in Analysis of Data From Factorial Experiments. The Methodology Center, State College, PA: The Pennsylvania State University; 2012. [Google Scholar]
- 16. Gwadz MV, Collins LM, Cleland CM, et al. Using the multiphase optimization strategy (MOST) to optimize an HIV care continuum intervention for vulnerable populations: a study protocol. BMC Public Health. 2017;17(1):383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Rosenberger WF, Lachin JM.. Randomization in Clinical Trials: Theory and Practice. Hoboken, NJ: John Wiley & Sons, Inc; 2016. [Google Scholar]
- 18. Cook JW, Collins LM, Fiore MC, et al. Comparative effectiveness of motivation phase intervention components for use with smokers unwilling to quit: a factorial screening experiment. Addiction. 2016;111(1):117–128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Schlam TR, Fiore MC, Smith SS, et al. Comparative effectiveness of intervention components for producing long-term abstinence from smoking: a factorial screening experiment. Addiction. 2016;111(1):142–155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Huffman JC, Albanese AM, Campbell KA, et al. The positive emotions after acute coronary events behavioral health intervention: design, rationale, and preliminary feasibility of a factorial design study. Clin Trials. 2017;14(2):128–139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. McMahon SK, Lewis B, Oakes JM, Wyman JF, Guan W, Rothman AJ. Assessing the effects of interpersonal and intrapersonal behavior change strategies on physical activity in older adults: a factorial experiment. Ann Behav Med. 2017;51(3):376–390. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Matts JP, Lachin JM. Properties of permuted-block randomization in clinical trials. Control Clin Trials. 1988;9(4):327–344. [DOI] [PubMed] [Google Scholar]
- 23. Kernan WN, Viscoli CM, Makuch RW, Brass LM, Horwitz RI. Stratified randomization for clinical trials. J Clin Epidemiol. 1999;52(1):19–26. [DOI] [PubMed] [Google Scholar]
- 24. Taves DR. Minimization: a new method of assigning patients to treatment and control groups. Clin Pharmacol Ther. 1974;15(5):443–453. [DOI] [PubMed] [Google Scholar]
- 25. Pocock SJ, Simon R. Sequential treatment assignment with balancing for prognostic factors in the controlled clinical trial. Biometrics. 1975;31(1):103–115. [PubMed] [Google Scholar]
- 26. Scott NW, McPherson GC, Ramsay CR, Campbell MK. The method of minimization for allocation to clinical trials. A review. Control Clin Trials. 2002;23(6):662–674. [DOI] [PubMed] [Google Scholar]
- 27. Berger VW. Minimization, by its nature, precludes allocation concealment, and invites selection bias. Contemp Clin Trials. 2010;31(5):406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Taves DR. Minimization does not by its nature preclude allocation concealment and invite selection bias, as Berger claims. Contemp Clin Trials. 2011;32(3):323. [DOI] [PubMed] [Google Scholar]
- 29. McEntegart D. Letter to the editor in response to Berger. Contemporary Clin Trial. 2010;31:507. [DOI] [PubMed] [Google Scholar]
- 30. Schulz KF, Altman DG, Moher D; CONSORT Group CONSORT 2010 statement: updated guidelines for reporting parallel group randomised trials. BMC Med. 2010;8:18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Chan AW, Tetzlaff JM, Altman DG, et al. SPIRIT 2013 statement: defining standard protocol items for clinical trials. Ann Intern Med. 2013;158(3):200–207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Moher D, Hopewell S, Schulz KF, et al. ; Consolidated Standards of Reporting Trials Group. CONSORT 2010 explanation and elaboration: updated guidelines for reporting parallel group randomised trials. J Clin Epidemiol. 2010;63(8):e1–37. [DOI] [PubMed] [Google Scholar]
- 33. Moher D, Schulz KF, Altman DG; CONSORT The CONSORT statement: revised recommendations for improving the quality of reports of parallel group randomized trials. BMC Med Res Methodol. 2001;1:2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Chan A-W, Tetzlaff JM, Gøtzsche PC, et al. SPIRIT 2013 explanation and elaboration: guidance for protocols of clinical trials. Br Med J. 2013;346:e7586. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Buman MP, Epstein DR, Gutierrez M, et al. BeWell24: development and process evaluation of a smartphone “app” to improve sleep, sedentary, and active behaviors in US Veterans with increased metabolic risk. Transl Behav Med. 2016;6(3):438–448. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Brophy-Herb HE, Horodynski M, Contreras D, et al. Effectiveness of differing levels of support for family meals on obesity prevention among head start preschoolers: the simply dinner study. BMC Public Health. 2017;17(1):184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Fraser D, Kobinsky K, Smith SS, Kramer J, Theobald WE, Baker TB. Five population-based interventions for smoking cessation: a MOST trial. Transl Behav Med. 2014;4(4):382–390. [DOI] [PMC free article] [PubMed] [Google Scholar]