Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2019 Oct 24;123(46):9912–9921. doi: 10.1021/acs.jpcb.9b07916

Dielectric Decrement for Aqueous NaCl Solutions: Effect of Ionic Charge Scaling in Nonpolarizable Water Force Fields

Sayan Seal 1, Katharina Doblhoff-Dier 1, Jörg Meyer 1,*
PMCID: PMC6875873  PMID: 31647235

Abstract

graphic file with name jp9b07916_0005.jpg

We investigate the dielectric constant and the dielectric decrement of aqueous NaCl solutions by means of molecular dynamic simulations. We thereby compare the performance of four different force fields and focus on disentangling the origin of the dielectric decrement and the influence of scaled ionic charges, as often used in nonpolarizable force fields to account for the missing dynamic polarizability in the shielding of electrostatic ion interactions. Three of the force fields showed excessive contact ion pair formation, which correlates with a reduced dielectric decrement. In spite of the fact that the scaling of charges only weakly influenced the average polarization of water molecules around an ion, the rescaling of ionic charges did influence the dielectric decrement, and a close-to-linear relation of the slope of the dielectric constant as a function of concentration with the ionic charge was found.

1. Introduction

Electrolytic solutions and the solid–electrolyte interface are of importance in biological systems as well as for various chemical applications, such as batteries, and in the electrochemical industry. The computational modeling of electrolytes and solid–electrolyte interfaces is, however, challenging due to the large amount of atoms and molecules that need to be simulated. Implicit solvation models augmented by (modified) Poisson–Boltzmann models to account for nonzero ionic strength provide a computationally cheap workaround.1,2 These continuum models alleviate the need for thermodynamic sampling of the electrolyte degrees of freedom. On the downside, these models commonly require a parametrization, and the fitted parameters are often not transferable (e.g., between neutral solutes and charged solutes3 or between molecules and surfaces4,5). Even when using available experimental data as “parameters” (e.g., the concentration- and temperature-dependent dielectric constant of the electrolyte), implicit solvation models systematically fail at high ion concentrations when the atomistic nature of the solvent becomes important.6 Force-field-based molecular dynamics calculations on the other hand provide a comparatively cheap option to access the solvent degrees of freedom explicitly. It is, however, nontrivial to devise force fields that correctly describe important properties such as the solubility, density-over-temperature curves at different ionic concentrations, and activity coefficients.7−9

Most available and commonly used electrolyte force fields combine nonpolarizable water models with Lennard-Jones and Coulomb interactions for the ion–ion and water–ion interactions. In recent years, it has, however, been realized that this approach generally leads to an incorrect prediction of diffusivity constants—a fact that Kann and Skinner10 have remedied by rescaling the ionic charges. This rescaling of charges was originally proposed by Leontyev and Stuchebrukhov.11 It is based on the idea of phenomenologically including the effect of an electronic dielectric continuum contribution to the polarizability in classical molecular dynamics.12 Leontyev and Stuchebrukhov have coined this the molecular dynamics electronic continuum (MDEC) model,11,12 which has also been referred to as the electronic continuum correction (EEC) method.13 It has been widely used with good results,9,14 for example, for the structure of concentrated ionic solutions,13 electronic conductivity,15 as well as solvation and ion pairing.16 The rescaled charges should account for the missing static polarizability of the water in the force field but could cause other undesired effects: for example, when ions sample regions in space that have a polarizability different from that of water or when ion association becomes important at high concentrations.10 Addressing the latter concern, Benavides et al.17 showed that while the scaling of ion charges has a considerable effect on the free energy of the solid, the melting temperature can still be captured correctly by scaled ion force fields. In the present paper, we want to investigate the influence of the ion scaling approach on the dielectric decrement, that is, the reduction of the dielectric constant of water with increasing ion concentration.

The fact that solvated ions can influence the dielectric constant of the solvent was already recognized in the early 20th century18 and was rigorously studied experimentally by Hasted et al.19 for a large number of salts and wide concentration ranges. For NaCl, they found a linear dielectric decrement at low concentrations that levels off at concentrations above 2 M. A tentative explanation of this effect, which is actually still in line with today’s commonly accepted explanation, was already put forward by Blüh18 in 1924. The basic idea is that, in the vicinity of an ion, the water dipoles will rather align along the field created by the ion than react to an external field. As a result of this, the water molecules in the so-formed solvation shell will not contribute to the dielectric response18,20 or contribute to a lesser extent21 than “free” water molecules, thus lowering the dielectric constant. This effect can be expected to be linear with concentration as long as the concentrations are low. At higher concentrations, volume exclusion effects,22,23 as well as effects of overlapping hydration shells,24 ion–ion correlations (dressed ions),25,26 ion–ion correlations beyond the mean field,23,27 ion pair formation,28 and ion polarizabilities29 may become important. Alternatively (or additionally), the dielectric decrement may also be caused by an ion-induced breakdown of dipole–dipole correlation, as put forward by Rinne et al.30 Such a breakdown in dipole–dipole correlation would reduce the Kirkwood g factor31 and thus reduce the dielectric constant.

Although most force fields suffer from an incorrect representation of the dielectric constant at zero ionic strength, the effect of the dielectric decrement can be captured astonishingly well on the force field level (see, e.g., refs (30, 32−37)). Remarkable accuracy, even at high concentrations, can be obtained with force fields optimized toward the correct representation of the dielectric constant.38

In spite of a plethora of force-field-based studies on the dielectric decrement, there are only a few comparative studies, and several questions remain.

  • 1.

    How far is the observed dielectric decrement influenced by the force field used?

  • 2.

    Will the decrement diminish if the ionic charges are rescaled?

  • 3.

    Are our observations more in line with an effect of dielectric saturation close to the ions, or may the decrement indeed be influenced more strongly by the breakdown of water correlation as suggested by Rinne et al.?30

To answer these questions, we simulate the dielectric constant at different concentrations of NaCl between 0 and 5 M using 4 different force fields, two of them with ionic charges equal to qion = ±1.0e and two with scaled ionic charges of qion = ±0.85e.

The paper is organized as follows. In Section 2, we describe the computational methods, including the different FF parameters, the details regarding the computational setup, the procedure to calculate the dielectric constant, and the analysis of the MD data. Then, we present our results for the dielectric constant at different temperatures and ionic concentrations, discuss ion-pairing effects, and analyze the influence of rescaled ionic charges in Section 3, which is followed by the conclusions in Section 4.

2. Methods

2.1. Force Fields

All force fields that are used in this work describe interactions among and between (rigid) water molecules and the sodium and chloride ions based on Coulomb

2.1. 1

where ϵ0 is the vacuum permittivity, and 12-6 is Lennard-Jones (LJ)

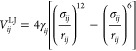2.1. 2

(pair) potentials. Here, the indices i and j refer to H and O atoms as well as Na+ and Cl– ions, and rij is the distance between the pair (i, j). The atomic and ionic charges qi for the Coulomb interaction and the well depth γij and distance parameters σij appearing in the LJ potential are tabulated in full detail in the Supporting Information for the four different force fields employed in this study. Here, we only summarize the essential distinguishing features.

  • CC (qion = ±1e): This force field is based on ion parameters determined by Smith and Dang by fitting to energies of small clusters.39 Since we combine the ionic parameters with SPC/E40 as a water force field, as proposed by Chowdhuri and Chandra,33 we refer to this force field as “CC”. Deviating from what has been proposed by these authors, we use geometric combination rules for the LJ potential parameters in this work.

  • MP (qion = ±1e): We also include a force field that relies on the ion parameters from Mao and Pappu41 (MP). These parameters are based purely on crystal lattice properties and are hence independent of the water force field. We combine it with TIP4P/200542 in the present work.

  • MP-S (qion = ±0.85e): Kann and Skinner10 proposed to rescale the ionic charges appearing in the MP force field to account for the lack of static polarizability in TIP4P/2005.42 This scaled MP force field (termed MP-S in the following) is thus equivalent to MP, except for the fact that the ion charges are scaled by a factor 0.85.

  • BPCEAV (qion = ±0.85e): This recent force field by Benavides et al.17 (our acronym results from the first letter of the authors’ last names) is also based on TIP4P/200542 and employs ionic charges scaled by 0.85. BPCEAV differs from MP-S because it has been fitted more carefully to properties of the ionic solution.

2.2. Molecular Dynamics Simulations

All molecular dynamics (MD) simulations were performed using the Lammps code.43 Cubic boxes with box length L = 25.5 Å (i.e., with volume V = L3) were used. The number of water molecules was adjusted to match the experimental values for the density of NaCl solutions at different molarities at 300 K. We studied a large range of ionic concentrations c ∈ 0.0, 0.1, 0.2, 0.5, 1.0, 1.5, 2.0, 2.5, 3.0, 4.0, and 5.0 M. At zero ionic strength (c = 0 M), the box contained NH2O = 556 water molecules corresponding to a density ρH2O = 0.99 g/cm3.

The initial structures for the simulations were generated using Packmol.(44) The resulting water boxes were equilibrated in a 300 ps run, using a Berendsen45 thermostat with a target temperature of 300 K (unless stated otherwise) and a damping time of 100 fs. The integration time step was set to 1 fs. To obtain results for the dielectric constant, simulations were run for 12 ns with a time step of 1 fs using a Nosé–Hoover46,47 thermostat with a damping time of 100 fs. During both equilibration and thermodynamic sampling, the long-range part of the Coulomb potential was treated via the Ewald summation technique48 for CC, while for MP, MPS, and BPCEAV the particle–particle mesh solver49 was used. The LJ potential was cut off at 12.5 Å for CC and at 10 Å for MP, MPS, and BPCEAV in both parts of the simulations. The typical runtime of an entire simulation (both equilibration and thermodynamic sampling together) for any concentration was 13 hours, parallelizing 16 physical cores of two eight-core Xeon E5-2630 CPUs residing in the same compute node and using the standard spatial decomposition implemented in Lammps.43

2.3. Dielectric Constant

In a pure dipolar solvent, the dielectric constant can be obtained from the linear response theory50 according to

2.3. 3

where kB is the Boltzmann constant, T is the temperature, and M denotes the sum over all dipole moments pi in the simulation cell. Here and in the following, ⟨·⟩ denotes time averages.

In the presence of ions, the situation becomes more complicated. The only measurable quantity then becomes the frequency-dependent dielectric susceptibility, χ(ω), and dynamic cross-terms in the solution dielectric function ϵ(ω) as well as purely ionic terms would have to be taken into account in calculating the dielectric susceptibility.30,51 Capturing these effects at the low-frequency limit is, however, computationally extremely challenging.30 The influence of kinetic cross-terms33,52 and ion contributions30,35 on the dielectric susceptibility can be expected to be small as long as ion paring, which can significantly enhance the low-frequency dielectric susceptibility, is negligible.35 As discussed in more detail in Section 3.4, the ion-pairing times observed for the force field discussed in this paper are such that an influence on the dielectric response cannot be ruled out for certain without calculating the dielectric response. However, rather than aiming at a full reproduction of the dielectric spectrum, in the present contribution, we are specifically interested in the effect of different force fields on the dielectric decrement and, especially, to what extent the scaling of ionic charges influences dielectric decrement. We therefore do not aim at a full, computationally challenging, simulation of the dielectric susceptibility. Instead, we follow the commonly adopted approach36,38 to limit our simulations to computing the static solution dielectric constant ϵ as defined in eq 3 (i.e., neglecting dynamic cross-terms to ϵ and ion contributions to χ).

In computing eq 3, we take advantage of the fact that ⟨M⟩ = 0. (Note that this is only true if atoms constituting a single water molecule are taken from adjacent periodic cells using a minimum distance convention.) Test calculations showed that taking the statistical average of ⟨M⟩ into account does not significantly influence our result, proving that ⟨M⟩ is well converged to zero for the simulation times used.

Generally, the convergence of time-averaged quantities (like ϵ as defined by eq 3) is judged based on plots of the cumulative average, which should stabilize if the sampling time is long enough. From such plots, it is, however, difficult to estimate error bars for the averaged quantity. To obtain statistical error bars for our estimates of ϵ, we therefore make use of a reblocking analysis.53 This allows us to estimate a value for the correlation-corrected standard deviation σ of the observable. To this end, we first compute estimators of the standard error for different block lengths M = 1, 2, 4, 8, ... of the observable x = ⟨x⟩

2.3. 4

where

2.3. 5

and NM is the number of blocks of length M contained in the time series xk with k ∈ [1, NM·M]. The value of σM will increase as long as serial correlation is still present and will stabilize at the correlation-corrected value σ as soon as M is large enough. For very large M, the estimate of σM becomes noisy. Making use of the python module pyblock,54 we automatically choose the ideal value of M for estimating σ as suggested by Lee et al.55

To extract the excess polarization α, which defines the dielectric decrement at low concentrations, as well as the dielectric constant in the very high concentration (i.e., molten salt) limit ϵms = ϵ(c → ∞ M), we fit our data for ϵ(c) to an analytic model proposed by Gavish and Promislow.24

2.3. 6

ϵw = ϵ(c = 0 M) is the dielectric constant of pure water (which we calculate separately and is thus not fit parameter). The function L is given by

2.3. 7

For low concentrations, eq 6 reduces to the linear equation as proposed by Hasted et al.19

2.3. 8

2.4. Ion Pairing

To quantify the pairing between Na+ and Cl– ions, we calculate the coordination number

2.4. 9

where

2.4. 10

is the radial distribution function (RDF) for the ion pair (Na+, Cl–), NNa+ (NCl–) are the total numbers of Na+ (Cl–) ions, and 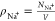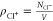Inline graphic (Inline graphic) are the corresponding number densities. The ion pair distances |ri – rj| are calculated according to the minimum image convention. We also compute a qualitative measure for the (Na+, Cl–) ion pair formation times tijasc. These are defined as the continuous time span during which an ion i and a counterion j are at distances below 4 Å under the prerequisite that the ion pair i, j approaches distances smaller than 3.2 Å at least once during this period. The 4 Å cutoff distance is chosen at distances slightly larger than the first minimum in the Na+, Cl– RDF. This mainly constrains the definition of an ion pair to the first solvation shell while still allowing ions to fluctuate to distances somewhat out of the first shell. This reduces the number of times in which an ion briefly breaks the pair, just to form it again shortly thereafter. The additional constraint of reaching distances smaller than 3.2 Å is implemented to avoid counting ions fluctuating in and out of this range from within the second solvation shell without actually pairing. This definition allows one to give an estimate for the time of tij during which one particular ion pair i, j is in continuous close contact. If ion i is replaced by an ion ĩ, tijasc stops and a new tij̃ starts. Furthermore, ions i and j can pair multiple times during one simulation run, and ion j can be paired simultaneously with two counterions i and ĩ. While we believe this descriptor to be relevant in the context of enhanced low-frequency dielectric response (see Section 3.4), it should be kept in mind that the estimates for the mean ion association time will depend on the chosen cutoff distance and that the resulting pairing time distribution will be different from the average time during which an ion j is closely surrounded by at least one counterion i.

With this definition, we calculate the ion pair formation time distribution as

2.4. 11

where Nij is the number of times that ion i forms an ion pair with ion j.

2.5. Water Dipole Alignment

The alignment of water molecules surrounding the Na+ and Cl– ions is characterized by

2.5. 12

where X ∈ {Na+, Cl–}. This average dipole alignment PXr is based on the projection of the individual water dipole moments pj onto the radial unit vector 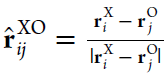Inline graphic, which connects the ion i and the oxygen atom of the water molecule j. |pH2O| is the (static) magnitude of the dipole moment of a single water molecule, which differs for the different force fields.

3. Results and Discussion

3.1. Validation of Computational Setup

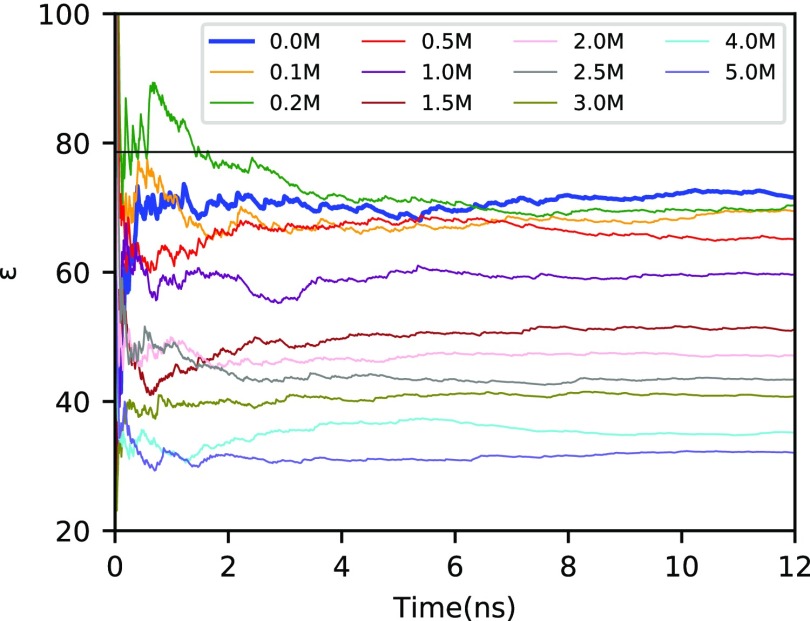
We start our discussion by validating the convergence of ϵ with respect to the simulated time interval of the MD simulations, which is shown in Figure 1 for the CC force field as a representative example. When using eq 3 to evaluate the dielectric constant, relatively long simulations times are required to obtain satisfactory convergence.57 In our case, simulation times of 12 ns give satisfactory convergence. Other methods to compute ϵ may converge faster (see ref (58) for a recent comparison) but were deemed unnecessary here since 12 ns of simulation time for systems of the size considered here is nowadays easily accessible for force-field-based MD calculations. In addition to the visual convergence check, we computed estimates for the standard deviations of the mean, σ, from a blocking analysis. We checked the reliability of these estimates by computing error bars to σ (error of the error). Independent of the force field, the corresponding relative errors do not considerably exceed 10%, thus providing confidence in our computational setup used to obtain σ.

Figure 1.

Figure 1

Open in a new tab

Dielectric constant (ϵ) as obtained with the CC force field at 300 K for various ionic concentrations c (colored lines). The result for pure water (ϵ(c = 0 M) = ϵw) is highlighted by the thick blue line, and the corresponding experimental value56 (black horizontal line) is shown for comparison.

Focusing on the minimum (c = 0 M, i.e., pure SPC/E water) and maximum (c = 5 M) concentrations, we have also checked the dependence of the calculated dielectric constants on system size by increasing the size of the cubic simulation boxes to box length L = 50.0 Å. The results shown in Table 1 are identical within the statistical uncertainty. Consequently, the smaller box (L = 25.5 Å) is large enough to avoid errors for ϵ that are caused by finite size effects.

Table 1. Dielectric Constant ϵ as Obtained with the CC Force Field for Cubic Simulation Boxes with Different Box Lengths L for Different Concentrations c. c = 0 M Corresponds to Pure SPC/E Water.

ϵ L = 25.5 Å L = 50.0 Å
c = 0 M 71.5 ± 1.9 71.5 ± 1.7
c = 5 M 32.0 ± 0.8 31.1 ± 0.8
Open in a new tab

Our result for the dielectric constant of the CC force field at zero ionic strength (resulting in pure SPC/E water) ϵwCC = ϵSPC/ E = 71.5 ± 1.9 is in good agreement with literature results.59 The same holds true for MP, MP-S, and BPCEAV, all of which result in pure TIP4P/2005. For these cases, we find ϵw = 59.3 ± 1.3, in agreement with Abascal and Vega.42 We emphasize here the known fact that SPC/E as well as TIP4P/2005 strongly underestimates ϵ, when compared with experimental results (ϵw = 78.3).56 This should be kept in mind during the following analysis of the dielectric decrement.

3.2. Temperature Dependence of Dielectric Constants

Before we turn to our results for the dielectric decrement obtained with the different force fields, we briefly discuss whether its temperature dependence is relevant in the context of our MD simulations. Experimental data is available for temperatures ranging from 278 to 308 K and concentrations between 0 and 5 M.60 The factor T–1 in the second term of eq 3 leads to a “trivial” temperature dependence of our MD results for the dielectric constants. The fluctuations of the total dipole moment M may, however, also show a temperature dependence, which is in principle included in our MD simulations by the use of a thermostat. If this “nontrivial” temperature dependence of ϵ is significant, then the dielectric decrement should be considered at different temperatures.

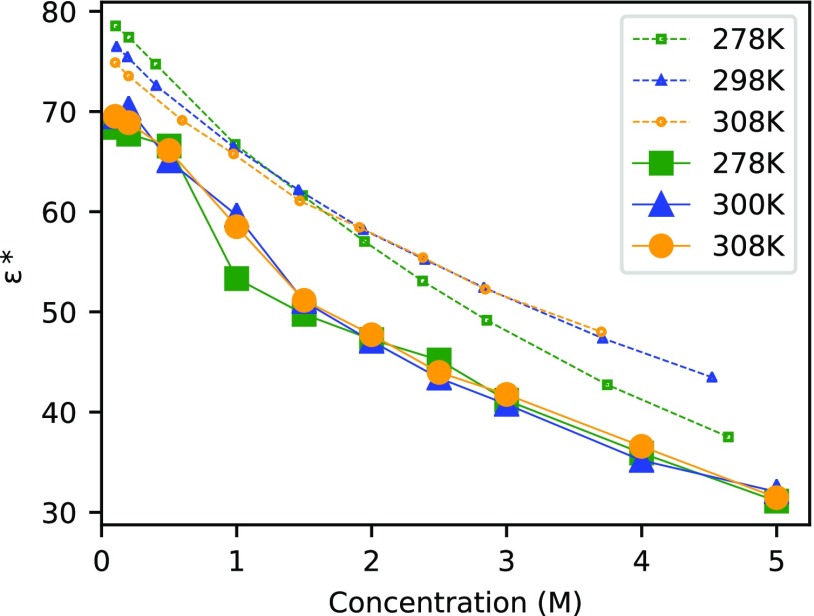
For a given data set of concentration-dependent dielectric constants, the aforementioned trivial temperature dependence can be eliminated by defining the temperature rescaled quantity

3.2. 13

for a given reference temperature T*. We have plotted ϵ* in Figure 2 for T* = 300 K as a function of concentration for 278, 300, and 308 K, again using the CC force field as a representative example. (The same trends are obtained for the other force fields as well.) Considering the error bars in our calculations (see Section 3.1), we find the three solid lines corresponding to our MD data to overlap. Within the temperature range considered here, our MD simulations do not show any temperature dependence of the dipole fluctuations, and the temperature dependence of the dielectric decrement is uniquely governed by the trivial temperature dependence included in eq 13. We have also applied eq 13 to the experimental data from Buchner et al.60 that is available for ϵ(c) at 278, 298, and 308 K and plotted the results in Figure 2 (dashed lines). A significant nontrivial temperature dependence is only observed experimentally for T < 300 K and c > 2 M, whereas the data for ε*(c) almost overlaps at 298 and 308 K. This latter observation agrees with the predictions from the MD simulations at those temperatures.

Figure 2.

Figure 2

Open in a new tab

Concentration-dependent rescaled dielectric constant ϵ*(c; T) as defined by eq 13 for NaCl solutions as obtained from our MD simulations with the CC force field (solid lines) and experiments60 (dashed lines) each at three different temperatures. The lines connecting the data points are only to guide the eye.

Since the MD simulations did not show any nontrivial temperature dependence, we focus our analysis on the data obtained from MD simulations at 300 K.

3.3. Dielectric Decrement

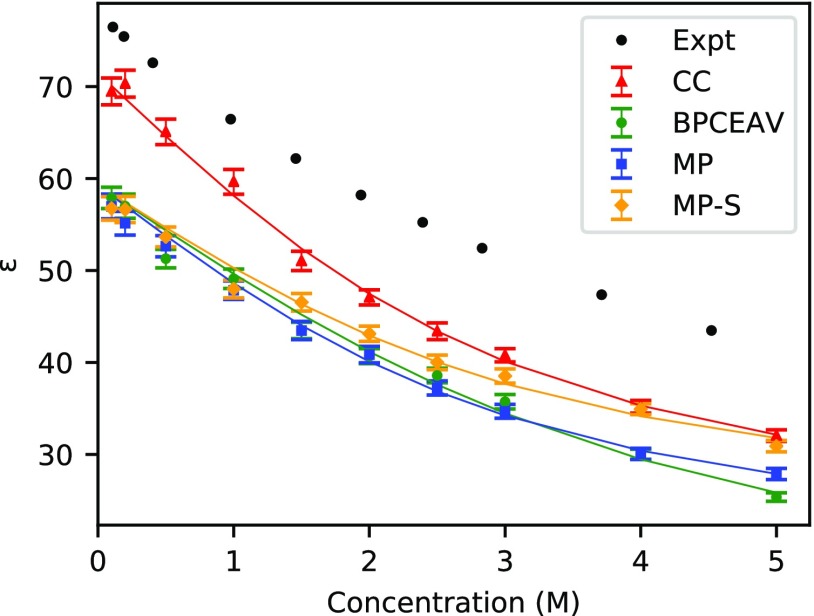
As already indicated by the results presented before (Sections 3.1 and 3.2), our MD simulations predict a continuous decrease of the dielectric constant with increasing concentration. This is true not only for the CC force field discussed above but also for the other force fields. A comparison of the resulting ϵ(c) is plotted in Figure 3. For CC, MP, and MP-S, the dielectric decrement is approximately linear only below a 2 M concentration and strongly levels off thereafter. For BPCEAV, the deviation from linearity appears to be weaker and more in line with the experiment. To put this onto a more quantitative basis, we fit the data obtained for the four force fields by eq 6. The fit parameters are compiled in Table 2.

Figure 3.

Figure 3

Open in a new tab

Dielectric constant ϵ at 300 K as a function of salt concentration as obtained from the MD simulations with the CC, BPCEAV, MP, and MPS force fields (colored symbols) in comparison to the experimental data from60 (black symbols). The indicated errors ϵ obtained from the MD simulations have been obtained as described in the text. The solid lines (of same colors) are the result of fitting eq 6 to the corresponding data. The fit parameters are compiled in Table 2.

Table 2. Parameters α and ϵms Obtained by Fitting Equation 6 to ϵ(c) from the MD Simulations with the Different Force Fields (See 2.1) and the Experimental Data from Buchner et al.60,a.

  α (M–1) ϵms ϵw ϵw – ϵms
CC 13.9 ± 0.4 18.9 ± 1.3 71.5 ± 1.9 52.6
BPCEAV 9.9 ± 0.5 9.1 ± 3.3 59.3 ± 1.3 50.2
MP 11.1 ± 0.4 17.4 ± 1.4 59.3 ± 1.3 41.9
MPS 9.3 ± 0.5 21.8 ± 2.1 59.3 ±1.3 37.5
expt. 11.7 ± 0.3 28.8 ± 2.1 78.3 ± 1.3 49.5
Open in a new tab
a

ϵw = ϵ(c = 0 M) is obtained directly from the simulations for pure water or the experimental value,56 respectively, and used to calculate the relative decrement ϵw – ϵms.

At low concentrations, the dielectric decrement is proportional to α (see eq 8). Although the error bars on the fit parameters obtained from the correlation matrix of the fit are relatively large, we can clearly distinguish two groups of force fields: CC and MP giving a value above 10 M–1, and MP-S and BPCEAV giving a value below 10 M–1. We will come back to this with a more detailed analysis in Section 3.5.

We now turn to the high concentration limit. Comparing ϵms directly with the experiment is complicated due the fact that SPC/E and TIP4P/2005 predict incorrect dielectric constants for pure water at room temperature. We therefore focus on the difference ϵw – ϵms. Clearly, this difference, which we may consider as the maximally achievable dielectric decrement, is more in line with the experiment for BPCEAV and CC than it is for MP and MP-S. Furthermore, although ϵw – ϵms is similar for CC and the experiment, the shape of these two data sets differs strongly. While CC shows a stronger fall-off at low concentrations (indicated by a large value of α), it stabilizes much more strongly at high concentrations, while for the gradient of ϵ(5 M), BPCEAV is in much better agreement with the experiment. We attribute this overstabilization of the dielectric decrement at high concentrations for CC, MP, and MP-S to excessive ion pairing observed for these force fields, as discussed next.

3.4. Ion-Pairing Effects

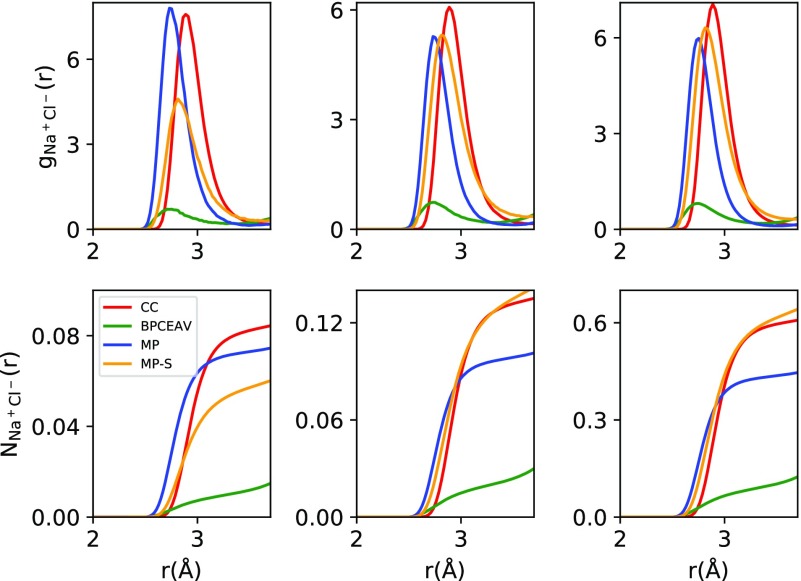
In Figure 4 and Table 3, we have quantified the (Na+, Cl–) ion pairing as described by the different force fields. BPCEAV shows the smallest values for the RDF gNa+Cl–(r) and the corresponding coordination number NNa+Cl–(r) at the small Na+–Cl– distances (r < 4Å) considered here. This can be rationalized by the distance and well-depth parameters of the Lennard-Jones potentials, which are significantly different for BPCEAV compared with the other force fields (see the Supporting Information). At larger distances, where the Coulomb interactions dominate, these differences are washed out. On the other hand, CC, MP, and MP-S show much stronger ion pairing, which may (partially) be responsible for the reduced dielectric decrement at high molarities. The question remains whether this is realistic or a shortcoming of the force fields used. Compared to ion association constants determined from conductometric measurements, our results clearly indicate too high probability of ion pairing. Fuoss61 found an ion association constant of Ka = 0.82 for NaCl. Estimating the activity coefficients entering the equilibrium equation from a Davies expression, this would give ion association of below 1‰ at 0.5 M concentration, much lower than what we observe. The strong ion association observed at 4 M would also suggest these ion pairs might be visible in X-ray diffraction measurements. No ion–ion contacts were, however, detected in X-ray diffraction measurements in 5 M solutions of NaCl.62 At first glance, the strong formation of contact ion pairs in CC, MP, and MP-S thus seems to be a shortcoming of these force fields. It may even indicate an incorrect solubility of NaCl in CC, MP, and MP-S. For the case of CC, a strongly reduced solubility compared with the experiment has actually been shown by Moučka et al.7 (where CC is called SDGM). Reassuringly, however, although we observe a relatively high probability to form (Na+, Cl–) pairs, no excessively sharp peaks that could suggest formation of a solid phase were observed in the Na+Na+ and Na+Cl– radial distribution functions even at high molarities.

Figure 4.

Figure 4

Open in a new tab

Radial distribution functions gNa+Cl–(r) (top row) and corresponding coordination numbers NNa+Cl–(r) (bottom row) calculated at c = 0.5 M (left column), 1.0 M (middle column), and 4.0 M (right column) using the four different force fields.

Table 3. Value of the Coordination Number NNa+Cl–(r = 3.4Å) Compared to the Probability of Ion Association Calculated Using a Value of Ka = 0.82 Determined by Fuoss61 from Conductometric Measurements (Ion activities Were Estimated Using a Davies Expression)a.

  0.5 M 1.0 M 4 M
CC 0.074 0.12 0.586
BPCEAV 0.009 0.020 0.095
MP 0.069 0.111 0.519
MP-S 0.050 0.122 0.559
Expt.61 <0.001    
MD30   ∼0.15  
Open in a new tab
a

Finally, we also compare with the probability of contact ion pair formation obtained in molecular dynamics (MD) simulations by Rinne et al.30

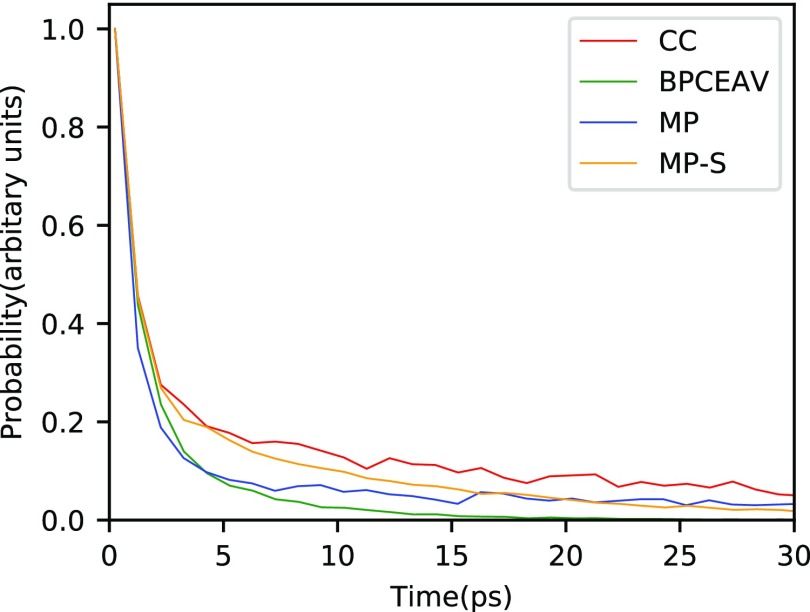
To investigate this further, we compute ion association times from our MD simulations as described in Section 2.4. Figure 5 shows a histogram of these ion association times for the different force fields in a 3 M solution. The average pairing times for CC, BPCEAV, MP, and MP-S are 20, 3, 24, and 8 ps, respectively. This is on the same order of magnitude as the average pairing times observed by Rinne et al.30 (12 ps) and still shorter than the decay times of 70 ps extracted by Sega et al.35 from the dielectric response for the GROMOS force field.

Figure 5.

Figure 5

Open in a new tab

Histogram of contact ion pair formation times for a 3 M solution. Note that all of the probability density functions pNa+Cl–pair(t) are scaled to give a value of 1 at the shortest association times evaluated to allow for easier comparison of the different force fields.

As shown by Sega et al.,35 long-lived ion pairs can significantly enhance the low-frequency dielectric response χ(ω → 0). On the other hand, Rinne et al.30 found that pair formation times on the order of 12 ps do not spuriously enhance the low-frequency dielectric response. These authors also obtained reasonable agreement of their simulated dielectric response with experimental results, that is, χ(ω → 0) decreased with increasing molarity, as expected.

Even in the case that the ion association times in our simulations (especially for CC and MP) and the probability to form such an ion pair were sufficient to enhance the low-frequency dielectric response, χ, this would not show up in our calculations of ϵ. ϵ, as defined in eq 3, does not include ion-pairing effects, since the ion–ion and ion–water cross-terms are not considered. Since the effective field of the ion pair is reduced compared with that of an ion, ion pairing can therefore be expected to reduce the slope of ϵ(c) compared with a case without ion pairing. Our analysis hence suggests that the reduced slope of the dielectric constant as a function of concentration c observed for CC, MP, and MP-S at high concentrations, which is not in line with experimental results, may be due to the formation of spurious contact ion pairs.

3.5. Influence of Scaled Ionic Charges

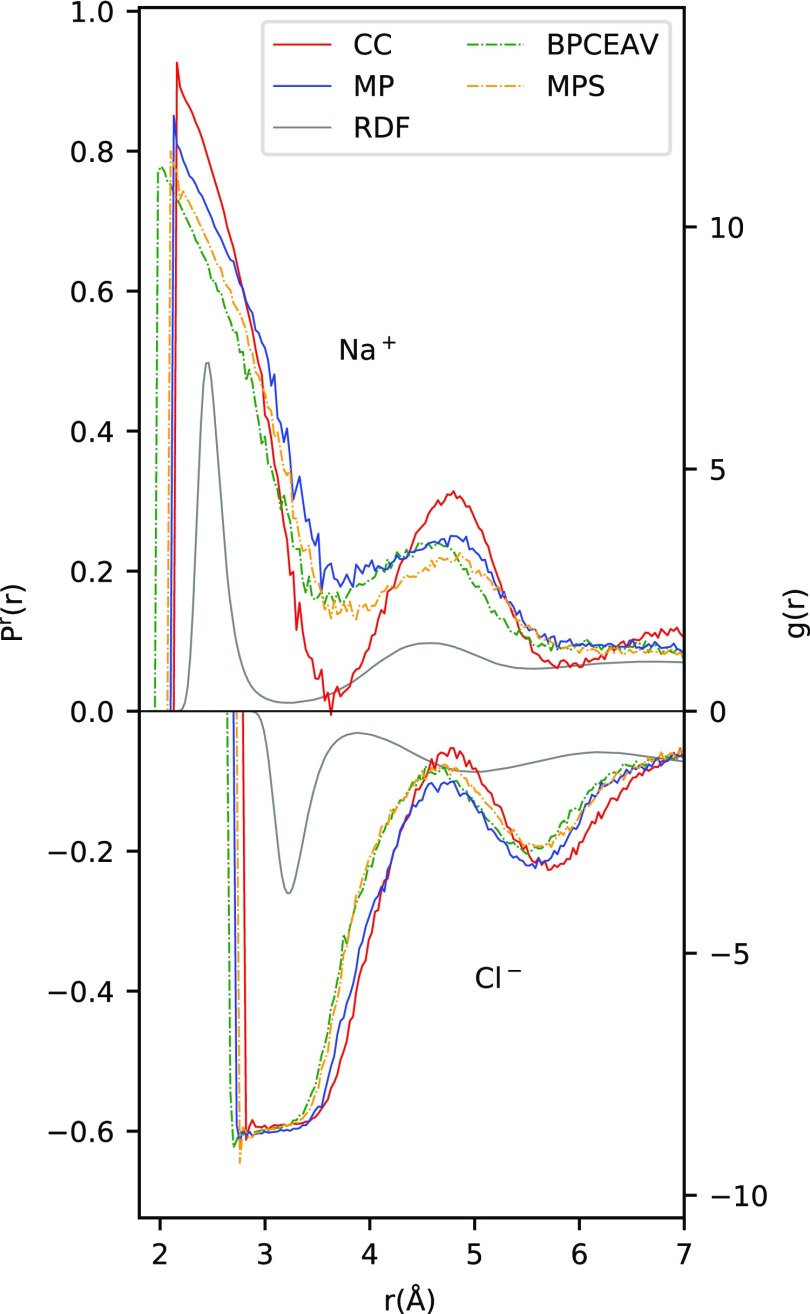
As mentioned above, MP-S and BPCEAV result in a smaller ionic excess than CC and MP. It is immediately striking that the magnitude of α seems to correlate with the ionic charge used in the force field. On average, αMP–S, BPCEAV is smaller than αCC,MP by a factor of 0.77. Comparing only αMP–S and αMP, we find a factor 0.84. Considering the error bars in α, this compares reasonably well with the difference in ionic charges in the two groups of force fields (qion = ±0.85e for MP-S and BPCEAV and qion = ±1e for CC and MP). To investigate this further, we plot the average alignment of the water dipoles PNa+r(r) and PCl–(r) (around the Na+ and Cl– ions; see eq 12) in Figure 6.

Figure 6.

Figure 6

Open in a new tab

Average alignment of dipole vectors Pr(r) around Na+ (top) and Cl– (bottom) ions. To allow a judgment on how likely it is to find a dipole at distance r, we also plot the ion-oxygen RDF for the CC force field (gray line). The RDFs for the other force fields are similar. Note that the results for Pr(r) naturally become noisy at distances where the ion-oxygen RDF becomes small. All results are taken from 0.1 M solutions to avoid ion–ion interactions.

Naively, one would expect single water dipoles to align more strongly in the field of more strongly charged ions and Pr(r) to decrease as qion/r2, corresponding to the electric field caused by the respective ion. This effect is, indeed, apparent in Figure 6 for the sodium ion at small distances below ∼4 Å: Here, we observe a strong polarization near the ions that decreases rapidly as r increases. Furthermore, for r < 3 Å, the average polarization is clearly lower for MP-S and BPCEAV (both having charges scaled by 0.85) than for CC and MP (with charges qion = ±1e). As we go to larger distances around 4.8 Å, the average polarization increases again. This is likely caused by water–water interactions rather than direct water–ion interactions, which would also explain why there is no trend visible any more with the magnitude of qion in the different force fields. Interestingly, the second peak in the mean polarization does not correspond to the second solvation shell as indicated by the second maximum in the RDF but is shifted toward the tail of the second RDF peak.

For the chlorine ion, the situation becomes somewhat more complicated. At small distances below ∼3.6 Å, the average polarization is constant and does not increase above ∼0.6, independent of the force field used. A maximum value of 0.6 in average polarization around an anion may not come as a surprise, since this corresponds to the average polarization that we would expect if all water molecules point one H atom toward the Cl– ion. That this value does not decrease up to r ≈ 3.6Å likely indicates a saturation effect. This is indeed supported by the fact that the plateau region stops earlier for MP-S and BPCEAV (scaled charges) than for CC and MP and that the average polarization continues to lie lower for MP-S and BPCEAV than for CC and MP up to r ≈ 4.3Å. As for Na+, we observe a second maximum in the average polarization at even larger distances (r ≈ 5.7Å), which again corresponds to the (late) tail of the second solvation shell. We show in the Supporting Information that this analysis (qualitatively) does not change when PCl–r(r) is calculated based on the distance to the closest hydrogen atom of the surrounding water molecules.

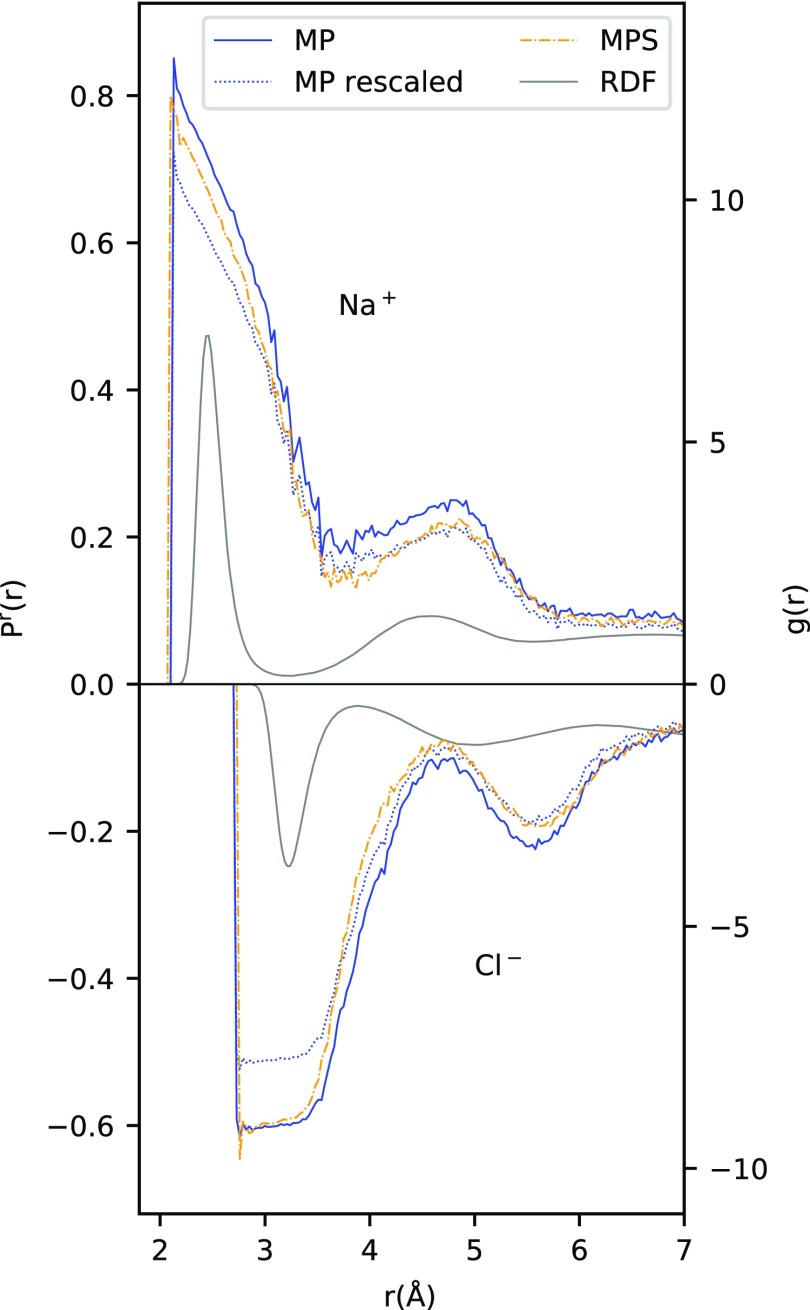
To analyze this in even more detail, we will now concentrate on a comparison of the results for MP and MP-S only. Since these two force fields differ only in the size of the ionic charges, their comparison allows us to directly extract the effect of the scaled charges without any influence of other force field parameters. From simple electrostatics, we would expect the average polarization to scale linearly with the charge qion of the ion. We therefore present in Figure 7 the results not only for Pr; MP and Pr; MP–S but also for Pr; MP rescaled = 0.85·Pr; MP, which we might expect to lie on top of Pr; MP–S if the electrostatic ion–water dipole interaction is the only effect influencing Pr. Indeed, at large distances, we observe a much better correlation between Pr; MP rescaled and Pr; MP–S than between Pr; MP and Pr; MP–S, suggesting that the pure electrostatic argument of qion acting on the water dipoles holds. At smaller distances, however, deviations between the average polarization Pr; MP rescaled and Pr; MP–S become apparent. For Cl–, we have already attributed this to saturation effects becoming important at r < 3.6 Å, that is, within the first solvation shell. The observed deviations for Na+ at r < 3.0 Å, that is, again within the first solvation shell, indicate that saturation effects also become important for the Na+ ion. This beginning saturation at r < 3.0 Å also explains why we do not observe a qualitative 1/r2 behavior of Pr(r) at small distances.

Figure 7.

Figure 7

Open in a new tab

Same as Figure 6 for MP and MP-S, but also Pr; MP rescaled = 0.85·Pr; MP for comparison.

This information should now be put together with the observations made for α, that is, that αMP–S ≈ 0.85 αMP. Let us first consider the case of Cl– in which Pr(r) within the first solvation shell is saturated independent of the force field and the ionic charge qion used. Invoking the commonly accepted view of the dielectric decrement being caused on a single particle level by each independent water molecule orienting preferentially along the ionic field direction, the constant Pr would rather suggest a dielectric decrement that is independent of qion for the cases studied here. This is, however, not the case as seen by the change in α when changing qion in MP and MP-S. Our observation, which can (to a lesser extent) also be extended to the Na+ ions, thus seems to back the idea put forward by Rinne et al.:30 that the dielectric decrement is caused by an ion-induced breakdown of water–water interactions, which would show up to a much lesser extent in Pr. Since the saturation effect in PNa+r is weaker than in PCl–, it would be interesting to split the dielectric decrement into a part stemming from the anions and one from the cations. This is, however, not easily achievable for neutral cells.

4. Conclusions

We have presented a comparative study of the performance of four different force fields for the description of the dielectric decrement observed at high ionic concentrations. Our focus was thereby not only to analyze the origin of the dielectric decrement in the different force fields but also to investigate the influence of the scaling of ionic charges on the dielectric decrement.

For three of the force fields studied, we found strong contact ion pair formation at high concentrations. For a 3 M solution, lifetimes between 8 and 24 ps were found. The strong contact ion pair formation in these force fields correlates with a reduced dielectric decrement at high concentrations, which is not in line with the experiment. We therefore argue that this strong ion pair formation is a result of an inaccurate description of interactions in those force fields.

The influence of scaling of ionic charges was investigated at low concentrations. Our analysis of the dielectric decrement suggests a close to 1:1 relation between the ionic charge and the initial slope of the dielectric constant as a function of concentration. While this may be expected, it seems to be at odds with the average polarization Pr(r) of water molecules around an ion. Within the first solvation shell, where polarization effects are the strongest, we found a negligible influence of the ion charge on Pr(r) around Cl–. Around Na+, the polarization did depend on the ion charge, but the scaling was not linear. Only at larger distances, a linear scaling of Pr(r) with the ion charge was found. If the ionic decrement were thus a pure saturation effect, we would not expect the dielectric decrement to scale linearly with ionic charge. This observation strengthens the argument put forward by Rinne et al.,30 who suggested that the dielectric decrement may be caused by an ion-induced disturbance of the water–water correlations, which causes a reduction of the Kirkwood g factor and hence of the dielectric constant, rather than by a saturation effect in the water alignment.

Acknowledgments

J.M. gratefully acknowledges financial support from The Netherlands Organisation for Scientific Research (NWO) under Vidi Grant no. 723.014.009.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpcb.9b07916.

  • Force field parameters: well-depth parameters of Lennard-Jones potentials, distance parameters of Lennard-Jones potentials, charges of hydrogen and oxygen atoms as well as sodium and chloride ions used in the different force field parameter sets; average dipole vector alignment around the Cl– ion (PDF)

Author Contributions

† S.S. and K.D.-D. contributed equally to this work.

The authors declare no competing financial interest.

Supplementary Material

jp9b07916_si_001.pdf (225.4KB, pdf)

References

  1. Mathew K.; Sundararaman R.; Letchworth-Weaver K.; Arias T. A.; Hennig R. G. Implicit Solvation Model for Density-Functional Study of Nanocrystal Surfaces and Reaction Pathways. J. Chem. Phys. 2014, 140, 084106 10.1063/1.4865107. [DOI] [PubMed] [Google Scholar]
  2. Fisicaro G.; Genovese L.; Andreussi O.; Marzari N.; Goedecker S. A Generalized Poisson and Poisson-Boltzmann Solver for Electrostatic Environments. J. Chem. Phys. 2016, 144, 014103 10.1063/1.4939125. [DOI] [PubMed] [Google Scholar]
  3. Dupont C.; Andreussi O.; Marzari N. Self-Consistent Continuum Solvation (SCCS): The Case of Charged Systems. J. Chem. Phys. 2013, 139, 214110 10.1063/1.4832475. [DOI] [PubMed] [Google Scholar]
  4. Sundararaman R.; Letchworth-Weaver K.; Schwarz K. A. Improving Accuracy of Electrochemical Capacitance and Solvation Energetics in First-Principles Calculations. J. Chem. Phys. 2018, 148, 144105 10.1063/1.5024219. [DOI] [PubMed] [Google Scholar]
  5. Hörmann N. G.; Andreussi O.; Marzari N. Grand Canonical Simulations of Electrochemical Interfaces in Implicit Solvation Models. J. Chem. Phys. 2019, 150, 041730 10.1063/1.5054580. [DOI] [PubMed] [Google Scholar]
  6. Valiskó M.; Boda D. The Effect of Concentration- and Temperature-Dependent Dielectric Constant on the Activity Coefficient of NaCl Electrolyte Solutions. J. Chem. Phys. 2014, 140, 234508 10.1063/1.4883742. [DOI] [PubMed] [Google Scholar]
  7. Moučka F.; Nezbeda I.; Smith W. R. Molecular Force Fields for Aqueous Electrolytes: SPC/E-Compatible Charged LJ Sphere Models and Their Limitations. J. Chem. Phys. 2013, 138, 154102 10.1063/1.4801322. [DOI] [PubMed] [Google Scholar]
  8. Nezbeda I.; Moučka F.; Smith W. R. Recent Progress in Molecular Simulation of Aqueous Electrolytes: Force Fields, Chemical Potentials and Solubility. Mol. Phys. 2016, 114, 1665–1690. 10.1080/00268976.2016.1165296. [DOI] [Google Scholar]
  9. Smith W. R.; Nezbeda I.; Kolafa J.; Moučka F. Recent Progress in the Molecular Simulation of Thermodynamic Properties of Aqueous Electrolyte Solutions. Fluid Phase Equilib. 2018, 466, 19–30. 10.1016/j.fluid.2018.03.006. [DOI] [Google Scholar]
  10. Kann Z. R.; Skinner J. L. A Scaled-Ionic-Charge Simulation Model That Reproduces Enhanced and Suppressed Water Diffusion in Aqueous Salt Solutions. J. Chem. Phys. 2014, 141, 104507 10.1063/1.4894500. [DOI] [PubMed] [Google Scholar]
  11. Leontyev I. V.; Stuchebrukhov A. A. Electronic Continuum Model for Molecular Dynamics Simulations. J. Chem. Phys. 2009, 130, 085102 10.1063/1.3060164. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Leontyev I.; Stuchebrukhov A. Accounting for Electronic Polarization in Non-Polarizable Force Fields. Phys. Chem. Chem. Phys. 2011, 13, 2613–2626. 10.1039/c0cp01971b. [DOI] [PubMed] [Google Scholar]
  13. Mason P. E.; Wernersson E.; Jungwirth P. Accurate Description of Aqueous Carbonate Ions: An Effective Polarization Model Verified by Neutron Scattering. J. Phys. Chem. B 2012, 116, 8145–8153. 10.1021/jp3008267. [DOI] [PubMed] [Google Scholar]
  14. Li P.; Merz K. M. Metal Ion Modeling Using Classical Mechanics. Chem. Rev. 2017, 117, 1564–1686. 10.1021/acs.chemrev.6b00440. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Wendler K.; Dommert F.; Zhao Y. Y.; Berger R.; Holm C.; Site L. D. Ionic Liquids Studied across Different Scales: A Computational Perspective. Faraday Discuss. 2011, 154, 111–132. 10.1039/C1FD00051A. [DOI] [PubMed] [Google Scholar]
  16. Pegado L.; Marsalek O.; Jungwirth P.; Wernersson E. Solvation and Ion-Pairing Properties of the Aqueous Sulfate Anion: Explicit versus Effective Electronic Polarization. Phys. Chem. Chem. Phys. 2012, 14, 10248–10257. 10.1039/c2cp40711f. [DOI] [PubMed] [Google Scholar]
  17. Benavides A. L.; Portillo M. A.; Chamorro V. C.; Espinosa J. R.; Abascal J. L. F.; Vega C. A Potential Model for Sodium Chloride Solutions Based on the TIP4P/2005 Water Model. J. Chem. Phys. 2017, 147, 104501 10.1063/1.5001190. [DOI] [PubMed] [Google Scholar]
  18. Blüh O. Die Dielektrizitätskonstanten von Elektrolytlösungen. Z. Phys. 1924, 25, 220–229. 10.1007/BF01327524. [DOI] [Google Scholar]
  19. Hasted J. B.; Ritson D. M.; Collie C. H. Dielectric Properties of Aqueous Ionic Solutions. Parts I and II. J. Chem. Phys. 1948, 16, 1–21. 10.1063/1.1746645. [DOI] [Google Scholar]
  20. Haggis G. H.; Hasted J. B.; Buchanan T. J. The Dielectric Properties of Water in Solutions. J. Chem. Phys. 1952, 20, 1452–1465. 10.1063/1.1700780. [DOI] [Google Scholar]
  21. Glueckauf E. Bulk Dielectric Constant of Aqueous Electrolyte Solutions. Trans. Faraday Soc. 1964, 60, 1637–1645. 10.1039/tf9646001637. [DOI] [Google Scholar]
  22. Liszi J.; Felinger A.; Kristóf E. H. Static Relative Permittivity of Electrolyte Solutions. Electrochim. Acta 1988, 33, 1191–1194. 10.1016/0013-4686(88)80148-8. [DOI] [Google Scholar]
  23. Adar R. M.; Markovich T.; Levy A.; Orland H.; Andelman D. Dielectric Constant of Ionic Solutions: Combined Effects of Correlations and Excluded Volume. J. Chem. Phys. 2018, 149, 054504 10.1063/1.5042235. [DOI] [PubMed] [Google Scholar]
  24. Gavish N.; Promislow K. Dependence of the Dielectric Constant of Electrolyte Solutions on Ionic Concentration: A Microfield Approach. Phys. Rev. E 2016, 94, 012611 10.1103/PhysRevE.94.012611. [DOI] [PubMed] [Google Scholar]
  25. Persson R. A. X. On the Dielectric Decrement of Electrolyte Solutions: A Dressed-Ion Theory Analysis. Phys. Chem. Chem. Phys. 2017, 19, 1982–1987. 10.1039/C6CP07515K. [DOI] [PubMed] [Google Scholar]
  26. Kjellander R. Focus Article: Oscillatory and Long-Range Monotonic Exponential Decays of Electrostatic Interactions in Ionic Liquids and Other Electrolytes: The Significance of Dielectric Permittivity and Renormalized Charges. J. Chem. Phys. 2018, 148, 193701 10.1063/1.5010024. [DOI] [PubMed] [Google Scholar]
  27. Levy A.; Andelman D.; Orland H. Dielectric Constant of Ionic Solutions: A Field-Theory Approach. Phys. Rev. Lett. 2012, 108, 227801 10.1103/PhysRevLett.108.227801. [DOI] [PubMed] [Google Scholar]
  28. Adar R. M.; Markovich T.; Andelman D. Bjerrum Pairs in Ionic Solutions: A Poisson-Boltzmann Approach. J. Chem. Phys. 2017, 146, 194904 10.1063/1.4982885. [DOI] [PubMed] [Google Scholar]
  29. Démery V.; Dean D. S.; Podgornik R. Electrostatic Interactions Mediated by Polarizable Counterions: Weak and Strong Coupling Limits. J. Chem. Phys. 2012, 137, 174903 10.1063/1.4763986. [DOI] [PubMed] [Google Scholar]
  30. Rinne K. F.; Gekle S.; Netz R. R. Dissecting Ion-Specific Dielectric Spectra of Sodium-Halide Solutions into Solvation Water and Ionic Contributions. J. Chem. Phys. 2014, 141, 214502 10.1063/1.4901927. [DOI] [PubMed] [Google Scholar]
  31. Kirkwood J. G. The Dielectric Polarization of Polar Liquids. J. Chem. Phys. 1939, 7, 911–919. 10.1063/1.1750343. [DOI] [Google Scholar]
  32. Anderson J.; Ullo J.; Yip S. Molecular Dynamics Simulation of the Concentration-Dependent Dielectric Constants of Aqueous Nacl Solutions. Chem. Phys. Lett. 1988, 152, 447–452. 10.1016/0009-2614(88)80439-1. [DOI] [Google Scholar]
  33. Chowdhuri S.; Chandra A. Molecular Dynamics Simulations of Aqueous NaCl and KCl Solutions: Effects of Ion Concentration on the Single-Particle, Pair, and Collective Dynamical Properties of Ions and Water Molecules. J. Chem. Phys. 2001, 115, 3732–3741. 10.1063/1.1387447. [DOI] [Google Scholar]
  34. Sala J.; Guàrdia E.; Martí J. Effects of Concentration on Structure, Dielectric, and Dynamic Properties of Aqueous NaCl Solutions Using a Polarizable Model. J. Chem. Phys. 2010, 132, 214505 10.1063/1.3429253. [DOI] [PubMed] [Google Scholar]
  35. Sega M.; Kantorovich S. S.; Holm C.; Arnold A. Communication: Kinetic and Pairing Contributions in the Dielectric Spectra of Electrolyte Solutions. J. Chem. Phys. 2014, 140, 211101 10.1063/1.4880237. [DOI] [PubMed] [Google Scholar]
  36. Pache D.; Schmid R. Molecular Dynamics Investigation of the Dielectric Decrement of Ion Solutions. ChemElectroChem 2018, 5, 1444–1450. 10.1002/celc.201800158. [DOI] [Google Scholar]
  37. Zasetsky A. Y.; Svishchev I. M. Dielectric Response of Concentrated NaCl Aqueous Solutions: Molecular Dynamics Simulations. J. Chem. Phys. 2001, 115, 1448–1454. 10.1063/1.1381055. [DOI] [Google Scholar]
  38. Fuentes-Azcatl R.; Barbosa M. C. Sodium Chloride, NaCl/ϵ: New Force Field. J. Phys. Chem. B 2016, 120, 2460–2470. 10.1021/acs.jpcb.5b12584. [DOI] [PubMed] [Google Scholar]
  39. Smith D. E.; Dang L. X. Computer Simulations of NaCl Association in Polarizable Water. J. Chem. Phys. 1994, 100, 3757–3766. 10.1063/1.466363. [DOI] [Google Scholar]
  40. Berendsen H. J. C.; Grigera J. R.; Straatsma T. P. The Missing Term in Effective Pair Potentials. J. Phys. Chem. A 1987, 91, 6269–6271. 10.1021/j100308a038. [DOI] [Google Scholar]
  41. Mao A. H.; Pappu R. V. Crystal Lattice Properties Fully Determine Short-Range Interaction Parameters for Alkali and Halide Ions. J. Chem. Phys. 2012, 137, 064104 10.1063/1.4742068. [DOI] [PubMed] [Google Scholar]
  42. Abascal J. L. F.; Vega C. A General Purpose Model for the Condensed Phases of Water: TIP4P/2005. J. Chem. Phys. 2005, 123, 234505 10.1063/1.2121687. [DOI] [PubMed] [Google Scholar]
  43. Plimpton S.Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. 10.1006/jcph.1995.1039. [DOI] [Google Scholar]
  44. Martínez L.; Andrade R.; Birgin E. G.; Martínez J. M.. PACKMOL: A Package for Building Initial Configurations for Molecular Dynamics Simulations. J. Comput. Chem. 2009, 30, 2157–2164. 10.1002/jcc.21224. [DOI] [PubMed] [Google Scholar]
  45. Berendsen H. J. C.; Postma J. P. M.; van Gunsteren W. F.; DiNola A.; Haak J. R. Molecular Dynamics with Coupling to an External Bath. J. Chem. Phys. 1984, 81, 3684–3690. 10.1063/1.448118. [DOI] [Google Scholar]
  46. Nosé S. A Unified Formulation of the Constant Temperature Molecular Dynamics Methods. J. Chem. Phys. 1984, 81, 511–519. 10.1063/1.447334. [DOI] [Google Scholar]
  47. Hoover W. G. Canonical Dynamics: Equilibrium Phase-Space Distributions. Phys. Rev. A 1985, 31, 1695–1697. 10.1103/PhysRevA.31.1695. [DOI] [PubMed] [Google Scholar]
  48. in ’t Veld P. J.; Ismail A. E.; Grest G. S. Application of Ewald Summations to Long-Range Dispersion Forces. J. Chem. Phys. 2007, 127, 144711 10.1063/1.2770730. [DOI] [PubMed] [Google Scholar]
  49. Hockney R. W.; Eastwood J. W.. Computer Simulation Using Particles; Adam Hilger: NY, 1989. [Google Scholar]
  50. Neumann M.; Steinhauser O.; Pawley G. S. Consistent Calculation of the Static and Frequency-Dependent Dielectric Constant in Computer Simulations. Mol. Phys. 1984, 52, 97–113. 10.1080/00268978400101081. [DOI] [Google Scholar]
  51. Caillol J. M.; Levesque D.; Weis J. J. Theoretical Calculation of Ionic Solution Properties. J. Chem. Phys. 1986, 85, 6645–6657. 10.1063/1.451446. [DOI] [Google Scholar]
  52. Sega M.; Kantorovich S.; Arnold A. Kinetic Dielectric Decrement Revisited: Phenomenology of Finite Ion Concentrations. Phys. Chem. Chem. Phys. 2015, 17, 130–133. 10.1039/C4CP04182H. [DOI] [PubMed] [Google Scholar]
  53. Flyvbjerg H.; Petersen H. G. Error Estimates on Averages of Correlated Data. J. Chem. Phys. 1989, 91, 461–466. 10.1063/1.457480. [DOI] [Google Scholar]
  54. Spencer J. Pyblock. Software available from https://github.com/jsspencer/pyblock (accessed Aug 13, 2019).
  55. Lee R. M.; Conduit G. J.; Nemec N.; López Ríos P.; Drummond N. D. Strategies for Improving the Efficiency of Quantum Monte Carlo Calculations. Phys. Rev. E 2011, 83, 066706 10.1103/PhysRevE.83.066706. [DOI] [PubMed] [Google Scholar]
  56. Barthel J.; Bachhuber K.; Buchner R.; Hetzenauer H. Dielectric Spectra of Some Common Solvents in the Microwave Region. Water and Lower Alcohols. Chem. Phys. Lett. 1990, 165, 369–373. 10.1016/0009-2614(90)87204-5. [DOI] [Google Scholar]
  57. Gereben O.; Pusztai L. On the Accurate Calculation of the Dielectric Constant from Molecular Dynamics Simulations: The Case of SPC/E and SWM4-DP Water. Chem. Phys. Lett. 2011, 507, 80–83. 10.1016/j.cplett.2011.02.064. [DOI] [Google Scholar]
  58. Elton D. C.Understanding the Dielectric Properties of Water. Ph.D. Thesis, Stony Brook University, New York, 2016. [Google Scholar]
  59. Kusalik P. G.; Svishchev I. M. The Spatial Structure in Liquid Water. Science 1994, 265, 1219–1221. 10.1126/science.265.5176.1219. [DOI] [PubMed] [Google Scholar]
  60. Buchner R.; Hefter G. T.; May P. M. Dielectric Relaxation of Aqueous NaCl Solutions. J. Phys. Chem. A 1999, 103, 1–9. 10.1021/jp982977k. [DOI] [Google Scholar]
  61. Fuoss R. M. Conductimetric Determination of Thermodynamic Pairing Constants for Symmetrical Electrolytes. Proc. Natl. Acad. Sci. USA 1980, 77, 34–38. 10.1073/pnas.77.1.34. [DOI] [PMC free article] [PubMed] [Google Scholar]
  62. Marcus Y.; Hefter G. Ion Pairing. Chem. Rev. 2006, 106, 4585–4621. 10.1021/cr040087x. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jp9b07916_si_001.pdf (225.4KB, pdf)

Articles from The Journal of Physical Chemistry. B are provided here courtesy of American Chemical Society

RESOURCES