Metamaterial Analogues of Molecular Aggregates

Abstract

Molecular aggregates are a fascinating and important class of materials, particularly in the context of optical (pigmented) materials. In nature, molecular aggregates are employed in photosynthetic light harvesting structures, while synthetic aggregates are employed in new generation molecular sensors and magnets. The roles of disorder and symmetry are vital in determining the photophysical properties of molecular aggregates, but have been hard to investigate experimentally, owing to a lack of sufficient structural control at the molecular level and the challenge of probing their optical response with molecular spatial resolution. We present a new approach using microwave analogues of molecular aggregates to study the properties of both individual meta-molecules and 1D molecular chains. We successfully replicate J- and H-aggregate behavior and demonstrate the power of our approach through the controlled introduction of structural symmetry breaking. Our results open a new area of study, combining concepts from molecular science and metamaterials.

Molecular aggregates have fascinated scientists for decades¹ and remain topical, owing to a range of interesting properties.^2,3 Aggregates of pigments are employed in nature by many photosynthetic structures used for light harvesting,^4,5 while from a synthetic standpoint, molecular aggregates are the building blocks of supramolecular science⁶ and have applications in areas such as new-generation sensors,⁷ molecular magnets,⁸ single photon sources,⁹ and nanophotonic materials.^10,11

Typically, intermolecular separations in aggregates are very much smaller than the wavelengths associated with the optical transitions they support, the interactions between molecules in an aggregate are thus dominated by near-field interactions, typically of a dipole–dipole character. Optical investigations are frequently based on far-field optical spectroscopy techniques,¹² but even near-field techniques cannot probe aggregate spatial structure at the single molecule level.⁹ These limitations make the effects of disorder and noise very difficult to investigate in a systematic way.¹³⁻¹⁷ This is unfortunate since such effects may be vital in helping to resolve the mechanisms behind exciton transport in nanowires/filaments,¹⁸⁻²¹ thereby hindering efforts to develop molecular materials. One interesting approach is to simulate aggregate behavior by making use of plasmonic particles as mimics of atoms/molecules, and much insight can be gained in this way,²² however it is still challenging to pack many such molecules within a wavelength. Furthermore, as we will see below, it is important to separate out electric and magnetic interactions if one wishes to mimic molecular aggregates, this is hard to achieve in plasmonic systems. Here we explore an alternative approach, one that involves making cm-scale analogues of molecular aggregates using microwave-domain metamaterials.

Metamaterials are synthetic structures that allow material properties to be both introduced and controlled through the inclusion of appropriate artificial (meta) molecules.²³ Electromagnetic metamaterials have been particularly well-explored in the microwave regime, where the length scales (cm) allow a range of powerful fabrication approaches to be used, including photolithography,²⁴ and 3D printing.²⁵ Importantly, the cm-length scales involved offer the prospect of investigating some of the phenomena associated with optical molecular aggregates in a way that is hard to accomplish at optical wavelengths, specifically by probing structures deep inside the near-field. In addition, the relevance goes wider than molecular systems since phenomena such as super-radiance involving arrays of Rydberg atoms are also of topical interest in a number of quantum systems, for example, those based on ion traps.²⁶

It is not a-priori clear whether employing metamaterials to explore molecular aggregation is either realistic or appropriate, but encouragement comes from recent work exploring electromagnetically induced transparency in metamaterials,²⁷ as it does from the recent use of radio frequency (RF) dipole analogues to investigate the transfer of energy between meta-molecules in a cavity.²⁸ Here we (i) establish a suitable design for individual meta-molecules, (ii) assemble 1D aggregates (chains) of these meta-molecules, where the intermolecular spacing is ≪λ, (iii) demonstrate both J- and H-type aggregation behavior, (iv) show that both electric-dipole and magnetic-dipole coupling can be employed to explore aggregation effects, and (v) take a first step in exploring some of the potential benefits of microwave metamaterial analogues. Our study thus paves the way for a new approach to explore phenomena associated with molecular aggregation, it may also yield new opportunities for metamaterials.

The optical properties of the two common types of molecular aggregates, known as J- and H-aggregates,³ are shown in Figure 1. Interaction energies between the electric dipole moments associated with excitonic transitions in neighboring dye/pigment molecules in an aggregate depend on the relative orientation of the dipole moments, see panels (a), (b), (d), and (e) in Figure 1. The dispersion of the allowed states of chains of dipoles are shown in panels (c) and (f). Also shown, in panel (g), are absorption spectra of a well-studied dye molecule, TDBC (5,6-dichloro-2-[[5,6-dichloro-1-ethyl-3-(4-sulphobutyl)-benzimidazol-2-ylidene]-propenyl]-1-ethyl-3-(4-sulphobutyl)-benzimidazolium hydroxide, sodium salt, inner salt).¹² In methanol, TDBC exists as a monomer (blue curve); however, in water, the TDBC molecules aggregate to form linear chains that display J-aggregation behavior, there is a dramatic red-shift and sharpening of the absorption (red curve). In J-aggregates the molecular dipole moments are coupled longitudinally, in H-aggregates the coupling is transverse. The changes brought about by aggregation can be dramatic, sufficient to produce a negative real part of the permittivity, allowing aggregated films to support surface waves similar to those found in plasmonics.^11,29−31 Replicating the dispersion of the H- and J-aggregate behavior seen in panels (c) and (f) of Figure 1 at microwave frequencies using meta-molecules forms the foundation of the work reported below.

Figure 1.

Optical properties of 1D molecular aggregates. Two types of aggregates may be distinguished by the nature of the coupling between the individual molecular dipole moments. Panels (b) and (e) show the configurations and relative energies of H- and J-aggregates, respectively. H-aggregates (a–c) involve transverse coupling, the highest energy state occurs when all N molecules have their dipole moments aligned, this corresponds to a zero wavenumber state; the highest wavenumber state occurs when adjacent molecules are antialigned, panel (c). J-aggregates (d–f) involve longitudinal coupling. The highest energy state occurs when all N molecules have their dipole moments antialigned, this corresponds to the highest wavenumber state; the zero wavenumber state occurs when adjacent molecules are all aligned, panel (f). Panel (g) shows the absorption spectra for TDBC dye molecules in two solutions. In methanol (blue curve) the molecules are in the monomer form and the absorption peak occurs at ∼520 nm. In water the molecules behave very differently, forming J-aggregates, and the absorption peak red-shifts, occurring at ∼585 nm. Looking at panel (e), one might expect a continuum of features to be seen in the absorption of J-aggregates for different combinations of dipole orientations, rather than just one, as seen for TDBC in panel (g). However, for J-aggregates, only the lowest energy state has a significantly nonzero net dipole moment, and it is only this state that is visible (bright), the other states have, by comparison, very small dipole moments and are not seen in far-field spectroscopy; they are dark. For H-aggregates, the situation is reversed and it is the upper state that is bright, that is, only this state has a significantly nonzero net dipole moment. Panel (g) is adapted with permission from ref (12). Copyright 1995 AIG Publishing.

Our meta-molecules are based on split-ring resonators; a schematic of a simple split-ring resonator is shown in Figure 2. This approach allows, first, powerful fabrication techniques to be employed, thereby enabling exquisite control over meta-molecule design and offering the prospect of scale-up in fabrication to larger/more complex structures; second, the split-ring resonator design is well established,³²⁻³⁴ there is thus a considerable body of knowledge upon which to draw; third, SRRs enable meta-molecule designs that simultaneously exhibit both a magnetic dipole moment, with magnetic moments arranged longitudinally with respect to the chain, and an electric dipole moment, with moments oriented perpendicular to the chain axis; SRRs thus enable designs that allow us to explore J- and H-aggregation in the same system.

Figure 2.

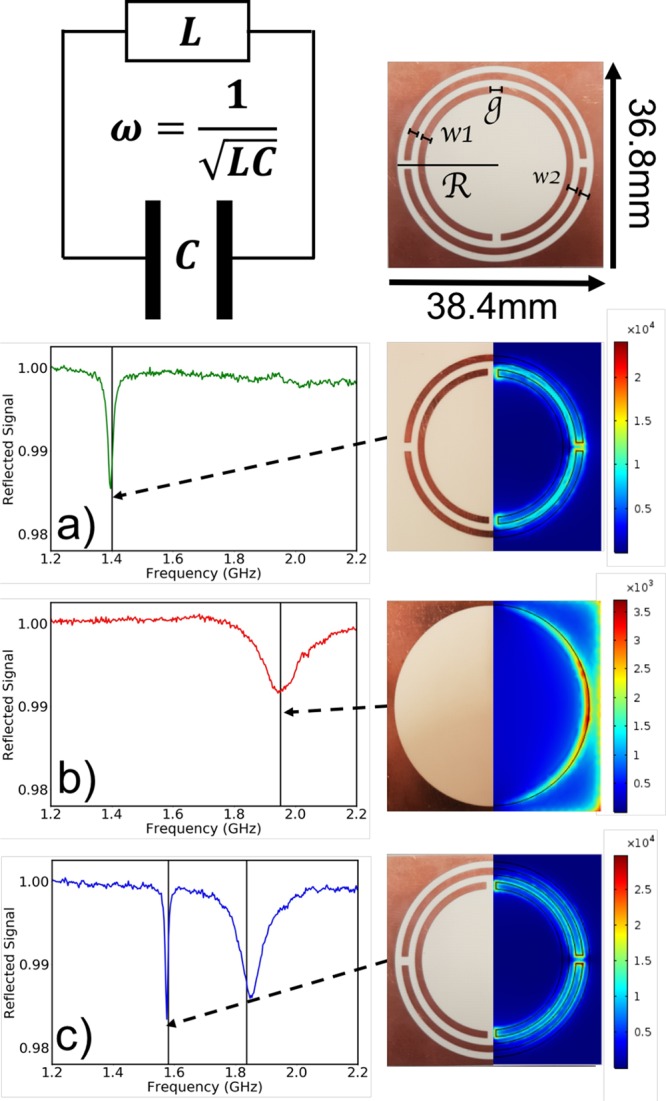
Single meta-molecules. Our meta-molecules are based on the split-ring resonator, a loop of wire with a split that acts as a resonant circuit (top-left). For such a system the resonance frequency ω is given by ω = 1/LC. Our meta-molecule design is shown top-right, dark regions correspond to copper-coated areas of a dielectric substrate, light regions to bare substrate. The structure comprises two double split-rings within a circular hole cut from a square sheet of metal, details are given in the Methods. The rows that follow are (a) double ring meta-molecule, (b) frame meta-molecule, and (c) combined double ring+frame. The experimental spectra (left column) show the power reflected back into a small antenna as a function of frequency. Black vertical lines mark the eigen-frequencies predicted using finite-element models of the meta-molecules. For the composite figures for each meta-molecule (right column), the left-half of each is a photo of the as-fabricated meta-molecule, the right-half is a color map (red indicates large magnitude) showing the numerically computed time-average of the magnitude of the electric field for the resonance frequencies predicted for each structure (see vertical lines in plots).

To explore separately the interaction of translationally and longitudinally arranged dipole moments, the electric and magnetic dipole moments of our meta-molecules need to be associated with separate meta-molecule resonances. This point is rather subtle because the simple split-ring resonator has both an electric dipole and a magnetic dipole response that can lead to somewhat complicated behavior.^35,36 This is in contrast to many pigment molecules, where an electronic dipole moment dominates the optical response. To see the origin of this problem, consider an incident electric field acting across the split of a simple split-ring resonator. Such a field may lead to charges being displaced so as to produce an electric dipole moment; as desired, however this displacement of charge induces a circulating current, the circulating current in turn inducing a magnetic dipole moment. Similarly, an incident magnetic field, oriented along the axis of the ring, will induce a circulating current in the ring, the current in turn leading to opposite charges being produced on either side of the split. This mixing of electronic and magnetic responses is known as bianisotropy.

We sought to isolate the electric and magnetic responses so as to better mimic molecular systems. We therefore selected the system shown in Figure 2 (top-right) as our meta-molecule; it comprises two concentric metallic double-split-ring resonators, we refer to this as the “double ring”, located inside a metal sheet into which a circular aperture has been cut; we refer to this last element as the “frame”. The reason for the two splits in each ring is to avoid an in-plane electric field from producing a net circulating current. The reason for two rings rather than one, where the two rings are offset in terms of their splits by 90°, is to ensure that an applied longitudinal magnetic field does not lead to a net electric dipole moment. Placing the double-ring structure within a metallic frame reintroduces the possibility for an electric dipole moment without upsetting the nonbianisotropy of the double ring.

We thus have three meta-molecule designs with which to work: the frame, exhibiting as its lowest order mode an electric dipole moment in the plane of the meta-molecule; the double ring, exhibiting a longitudinal magnetic moment perpendicular to the meta-molecule plane; and the frame+double ring, which exhibits both modes in an uncoupled manner, we refer to this latter element as the “combined” metamolecule. Details of the fabrication and design parameters for the meta-molecules we used are given in Figure 2 and in the Methods section; further details for the 1D chain are also given in the Methods section.

To establish the resonance properties of our meta-molecules we characterized the individual elements by recording their response to excitation with a near-field probe,³⁷ see Methods. Briefly, a small loop (dipole) antenna was used to excite the magnetic (electric) modes. The spectral responses were acquired using a vector network analyzer to monitor the power reflected back from the meta-molecule into the probe antenna, as shown in Figure 2. For the double ring, Figure 2a, and for the frame, Figure 2b, a single mode is seen as a dip in the reflected signal, due to power being absorbed/scattered. The origin of the modes responsible for these features is confirmed through numerical simulations using finite-element analysis, see the Methods section.

Figure 2c shows the measured response of the combined meta-molecule. Both electric and magnetic resonances are seen, their frequencies shifted somewhat (especially the magnetic (double ring) resonance) from those associated with the isolated structures, due to the change in the local environment of each resonator, that is, the resonance of the double ring is perturbed by the presence of the frame and vice versa. Comparing the right-hand panel in rows (a) and (c), we see that the presence of the frame does not alter the field pattern of the double-ring mode. This, together with an examination of the surface currents (not shown), indicate that when the frame and the double-ring are combined the magnetic and electric modes do not interact with each other.

With the individual meta-molecule designs established and their response characterized, we next set out to look at the response of 1D linear chains of such meta-molecules. A total of 90 meta-molecules were stacked axially, as shown in Figure 3 (upper), with the intermolecular separation being 3.13 mm, approximately λ/20, where λ is the wavelength in the dielectric material. To determine the collective modes supported by this chain and their dispersion, we used a near-field probe to couple to them and recorded the response (complex field) on the edge of the sample as a function of distance along the chain. An example of a recorded field distribution is shown in Figure 3 (lower), where the natural log of the time-averaged field magnitude has been plotted as a function of frequency and spatial position.

Figure 3.

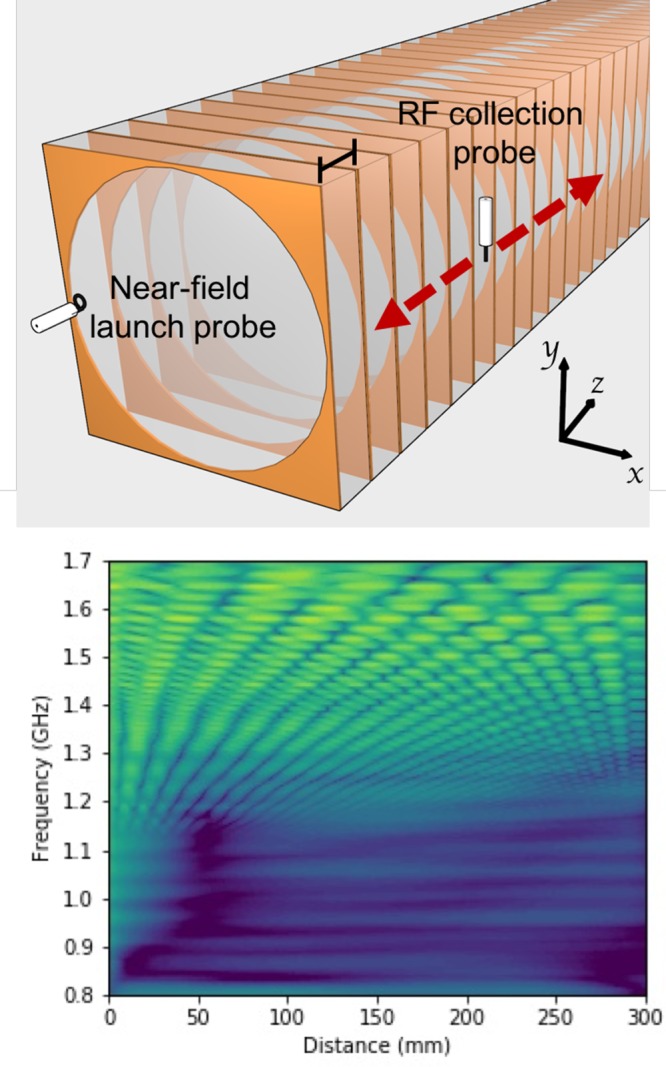
1D chain of meta-molecules. (Top) Experimental setup for a chain of meta-molecules, the period is 3.13 mm. (Bottom) Plot of the time-averaged complex electric field collected by the probe antenna for a system supporting a negative gradient mode from 1.7 to 1.1 GHz. Yellow indicates a high signal strength.

Next, we acquired data similar to those shown in Figure 3 (lower) for a range of frequencies, and for each frequency, we carried out a fast Fourier transform. By combining such data, a plot of Fourier amplitude versus both frequency and wavevector, that is, a dispersion diagram, can be produced; such data are shown in Figure 4. The double ring only data (a) show a positive gradient, that is, J-aggregate-like dispersion, due to the longitudinally coupled magnetic dipole moments. The frame only data (b) shows a negative gradient, that is, an H-aggregate-like dispersion, arising from its transversely coupled electric dipole moments. These data show that our meta-molecules are indeed capable of exhibiting J- and H-like molecular aggregate behavior, as we had set out to show (see Figure 1).

Figure 4.

Dispersion for chains of double ring meta-molecules and for chains of frame meta-molecules. Color plots of the Fourier transformed scan data from the double rings sample (a) and the frame sample (b). The weaker, higher k “echos” in the frame sample (b) are due to reflections from the end of the finite chain. The color scale represents the Fourier amplitude on a logarithmic scale; yellow indicates large amplitude. The high values (yellow regions) around k ∼ 0 are due to direct transmission between the launch antenna and the probe antenna.

Next, we used our microwave analogue system to go beyond what has been achieved in real molecular systems by combining J- and H-like behavior into one system. The dispersion of the modes on a chain of the combined, double-ring+frame meta-molecules is shown in Figure 5a; for these data we used a magnetic (loop) probe antenna because such an antenna is able to pick up fields associated with both electric and magnetic dipole modes. In this figure both positive (J-like) and negative (H-like) gradient modes are seen. Note that there are two H-like modes, these correspond to the two orthogonal (vertical and horizontal) modes in the frame; the frame is slightly rectangular, see top right panel of Figure 2, thus lifting the degeneracy of these two modes. We see both of these modes in Figure 5a rather than the single mode we saw in Figure 4b because of the use of a magnetic probe antenna for these measurements. For Figure 4, we were able to use an electric antenna, and by positioning it carefully, we were able to record the response from just one of the electric modes. The two mode crossings near 375 m^–1 and 400 m^–1 provide clear evidence for an absence of coupling between the counter propagating modes in this configuration.

Figure 5.

Dispersion for chains of double ring+frame meta-molecules. Contour plots for the symmetric combined sample (a) and the asymmetric combined sample (b). Both samples support forward and backward propagating modes but the inclusion of a symmetry breaking rotation in the asymmetric sample leads to a coupling between the J- and H-like modes, opening a band gap at 1.26 GHz. For the asymmetric sample both coupled modes have zero group velocity at 430 1/m. The high values (yellow regions) around k ∼ 0 are due to direct transmission between the launch antenna and the probe antenna.

Lastly, we sought to exploit an advantage of the superb degree of structural control available over metamaterials by introducing a modification intended to break the symmetry of our meta-molecule design. We altered the meta-molecule design by rotating the outer splits by 20°, so that the rings are now able to support a net (horizontal) electric dipole moment. The response from a chain of such meta-molecules, shown in Figure 5b, now exhibits coupling between the J- and H-type modes in the form of an anticrossing, seen at 430 m^–1 in Figure 5b. Of the two H-type modes from Figure 5a, here only one couples with the J-type mode. The H-type mode that does couple corresponds to the horizontally oriented mode; the vertical mode does not couple because it is now perpendicular to the net electric dipole created by the symmetry breaking. The data shown in Figure 5 show that we have indeed been able to explore phenomena that have not been seen in molecular systems, highlighting the power of the metamaterials approach we have developed.

In summary, we have established a number of designs of meta-molecules suitable for studying microwave analogues to molecular aggregates, based on split-ring resonators. We have shown that such meta-molecules may be assembled into 1D chains where the intermolecular separation is substantially subwavelength. Using two different designs of meta-molecules, we have separately shown J- and H-like aggregation behavior. Further, by combining two meta-molecule designs into a more complex structure, we have shown that our 1D analogue can simultaneously support both forward and backward propagating waves. Finally, by introducing an asymmetry into the design of our meta-molecule, specifically by introducing a controlled amount of bianisotropy, we have shown that forward and backward propagating modes may interact so as to anticross on a dispersion diagram, introducing a geometry-dependent stop-band in propagation along the chain. In terms of metamaterials, to the best of our knowledge, this is the first observation of simultaneous forward and backward propagating modes, one that may be of potential interest in RF applications such as power transfer.³⁸

In terms of providing an analogue for molecular aggregates, we hope this work will inspire others to investigate this area more deeply. Our meta-molecules do not mimic all of the properties of real molecules, in particular, they can not be considered the analogue of two-level systems, where electronic wave functions determine the resonance frequencies; our resonance frequencies are set geometrically. Another difference is that non-nearest-neighbor interactions are likely to be more important in meta-molecular materials than molecular ones.³⁹

We can identify a number of areas for future investigation. There is a metamaterials challenge to develop meta-molecules that go deeper into the subwavelength regime.²⁴ We achieved sufficient subwavelength aggregation by working in 1D, stacking our meta-molecules in an axial direction. It would be convenient to extend our work to higher dimensions, but even in 2D, subwavelength intermolecular separations are hard to achieve.¹⁷ Ring systems, lying between 1D and 2D might make an interesting next step and are widely found in molecular systems, both natural and synthetic.^4,40 There is a need to develop meta-molecules whose sizes in all three dimensions are significantly less than their associated resonance wavelengths.

Regarding the simulation of aggregate behavior, it should be relatively straightforward to extend the present work to investigate the effect of static disorder along the chain, important in understanding why such transport can be robust to disorder.²¹ Perhaps with the addition of suitable electronic components, it might be possible to explore the effect of noise on the propagation of energy in these systems; one might also be able to incorporate gain to explore PT symmetry breaking,⁴¹ and one could envisage programmable meta-molecules.⁴²

Methods

Finite-Element Modeling

Finite element modeling using COMSOL Multiphysics was used to design the meta-molecules. Each design was centered in a spherical air domain surrounded by a perfectly matched layer, and their resonance frequencies determined using the eigenfrequency solver within the RF module. The copper layer was described using COMSOL’s built-in material properties and an impedance boundary condition. Mesh convergence studies were undertaken to ensure the accuracy of the calculated resonance frequencies. Examples of results from finite-element modeling are presented in Figure 1.

Meta-Molecule Design

By tuning the design parameters (track widths, spacings, etc.), we ensured that the resonance frequencies of all the meta-molecule designs were such that, once incorporated into a chain, the J- and H-like dispersions would cover similar frequency bands. (Note that the frame in each meta-molecule design was intentionally made rectangular. This was to ensure that the dipolar modes in the two orthogonal directions occurred at slightly different frequencies.) Once fabricated the meta-molecule dimensions were measured and the fabrication errors incorporated into the models.

Sample Fabrication

The meta-molecules were fabricated on printed circuit board (PCB) using standard photolithography techniques. The PCB consisted of 35 μm of copper on a 3.1 mm thick Roger 4350B substrate, which has ϵ_r = 3.66 + 0.013i in the frequency range 1–20 GHz. Further details of the design are g = 1.5 mm, w1 = 1.2 mm, w2 = 1.2 mm, and R = 17.2 mm, where g is the size of all the ring splits, w1 is the width of the rings, w2 is the distance between rings, and R is the radius of the frame. It is interesting to estimate the resonance frequency of a simple split-ring with dimensions similar to those used in the present work. The inductance and capacitance can be estimated⁴³⁻⁴⁵ as 10^–8 H and 10^–12 F, respectively, giving a resonance frequency on the order of 10 GHz. Our meta-molecules are much more complex than the simple split-ring resonator, they comprise many different contributions to the overall inductance and capacitance; they are more conveniently modeled numerically. The chains consisted of 90 meta-molecules stacked axially with a period of 3.13 mm. The meta-molecules were bound with masking tape and supported on a polystyrene substrate.

RF Measurements

The resonance frequency of each meta-molecule design was measured using an Anritsu Vectorstar MS4644A vector network analyzer. A suitable antenna was placed in a region of high field (as determined from the finite element modeling) approximately 0.5 mm from the surface of each meta-molecule design and the return loss recorded (the power reflected back along the cable of the exciting antenna). These results were then normalized by measuring the return loss when the exciting antenna was placed in the same position against a blank piece of substrate (all copper removed), so as to remove the frequency dependence of the antennas. A dip in the normalized data corresponds to a resonant mode of the meta-molecule.

The exciting antennas were formed from sections of stripped coaxial cable. For the frame meta-molecule, a short straight section of stripped coaxial cable was used to couple to the dipolar electric field of the frame by placing the axis of the stripped section parallel to the plane of the frame, and over the top of one of the thin sections, that is, middle of an edge of the frame. For the split-ring meta-molecules the stripped coaxial cable was formed into a loop so as to couple to the magnetic field, the plane of the loop being normal to the plane of the meta-molecule, and located at the top of one of the outer edges of the rings, adjacent to one of the inner splits.

As for the single meta-molecule measurements, for the chains, a probe antenna was placed close to the first meta-molecule in the chain in order to excite any collective modes. A second antenna was then scanned along the chain in 0.5 mm increments, as shown in Figure 3, and the amplitude and phase of the field recorded as a function of position and frequency. For the frame sample a straight antenna orientated as shown in the upper panel of Figure 3 was used to record the field, whereas for the symmetric framed split-ring sample a loop antenna with the loop axis parallel to the direction of propagation was used. For the symmetry broken framed split-ring and unframed split-ring chains the recording antenna was a loop with its plane perpendicular to the direction of propagation. These choices were made in order to maximize the strength of the signal in each case.

The spatial complex field data for each frequency were Fast Fourier Transformed using a Tukey window to reduce artifacts arising from the finite length of the data set. Plotting the resulting Fourier spectrum for each frequency one can readily identify the dispersion relation of the collective modes of each chain, as shown in Figures 4 and 5.

The authors declare no competing financial interest.