Cooperation mitigates diversity loss in a spatially expanding microbial population

Significance

Spatially expanding populations lose genetic diversity rapidly because of repeated bottlenecks formed at the colonization front. However, the rate of diversity loss depends on the specifics of the expanding population, such as its growth and dispersal dynamics. We have previously demonstrated that changing the amount of within-species cooperation leads to a qualitative transition in the nature of expansion from pulled (driven by growth at the low-density tip) to pushed (driven by migration from the high-density region at the front, but behind the tip). Here we demonstrate experimentally that pushed waves result in strongly reduced genetic drift during range expansions, thus preserving genetic diversity in the newly colonized region.

Abstract

The evolution and potentially even the survival of a spatially expanding population depends on its genetic diversity, which can decrease rapidly due to a serial founder effect. The strength of the founder effect is predicted to depend strongly on the details of the growth dynamics. Here, we probe this dependence experimentally using a single microbial species, Saccharomyces cerevisiae, expanding in multiple environments that induce varying levels of cooperativity during growth. We observe a drastic reduction in diversity during expansions when yeast grows noncooperatively on simple sugars, but almost no loss of diversity when cooperation is required to digest complex metabolites. These results are consistent with theoretical expectations: When cells grow independently from each other, the expansion proceeds as a pulled wave driven by growth at the low-density tip of the expansion front. Such populations lose diversity rapidly because of the strong genetic drift at the expansion edge. In contrast, diversity loss is substantially reduced in pushed waves that arise due to cooperative growth. In such expansions, the low-density tip of the front grows much more slowly and is often reseeded from the genetically diverse population core. Additionally, in both pulled and pushed expansions, we observe a few instances of abrupt changes in allele fractions due to rare fluctuations of the expansion front and show how to distinguish such rapid genetic drift from selective sweeps.

Spatial population expansions occur at multiple scales, from the growth of bacterial biofilms and tumors to the spread of epidemics across the globe (1–4). Natural populations often undergo range shifts or range expansions, in response to changing climate, and increasingly, following introduction into novel geographical areas due to trade, travel, and other anthropogenic factors (5–7). The fate of these spatially expanding populations depends on their genetic diversity, which allows them to adapt to the new environment (8). The very process of spatial expansion is, however, predicted to erode the diversity of the population (9, 10), since the newly colonized territory is seeded by only a subset of the genotypes that exist in the original population. This phenomenon, known as the founder effect, greatly amplifies genetic drift in the population and leads to diversity loss and accumulation of deleterious mutations (11–13). Thus, a firm understanding of the founder effect is necessary to predict and control the fate of expanding species.

While diversity is lost during all expansions, the rate of loss is theoretically expected to be strongly influenced by the expansion dynamics, which depend on the details of dispersal and growth. Depending on the expansion dynamics, population expansions can be classified into 2 categories—pulled and pushed. In populations that do not exhibit any within-species cooperation, the growth rate is maximum at low densities and decreases monotonically as the density increases. In such populations, migrants at the low-density tip of the wave grow at the fastest rate and drive the expansion into the new area. Such expansions are called pulled waves, and their expansion velocity, also known as the Fisher velocity, depends solely on the diffusion rate of the individuals and the growth rate of the species at low density. On the other hand, pushed waves occur in the presence of cooperative growth within the population (i.e., positive density dependence of the growth rate, also known as the Allee effect) whereby the tip grows at a much lower rate than the higher-density bulk (14–17). Since the growth rate at low density in such populations is lower than in the bulk, the Fisher velocity for such populations is lower than the actual expansion velocity, while the wave fronts are steeper compared to Fisher waves with identical diffusion and low-density growth rates (14, 15, 18). This difference in the dynamics of pulled and pushed waves is predicted to have substantial genetic consequences (19–21), although they have not been fully tested quantitatively in empirical studies (22).

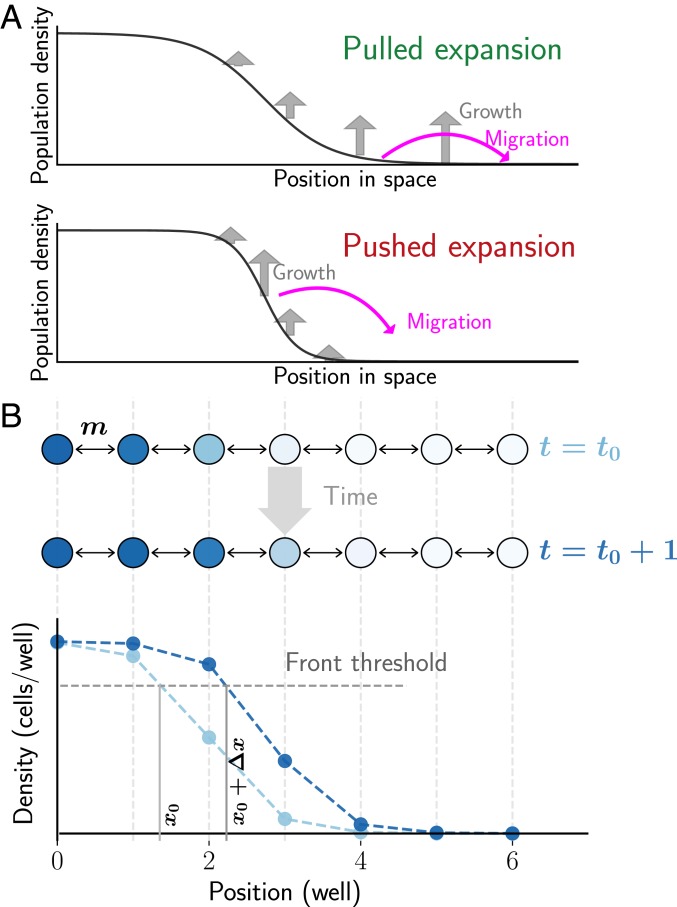
In their simplest form, range expansions can be viewed as a series of founding events, where a small subpopulation establishes a colony in a new territory, grows rapidly, and then seeds the next founder population. This series of population bottlenecks quickly erodes the genetic diversity in the population, a process aptly called the serial founder effect. The bottlenecks are less severe for species with an Allee effect because growth in the low-density founding colonies is subdued. Indeed, the slow growth of the founders provides sufficient time for the arrival of migrants from the genetically diverse population bulk. Thus, genetic diversity is predicted to persist much longer and over longer distances in populations with an Allee effect (Fig. 1A).

Fig. 1.

Experimental setup to study genetic consequences of pulled and pushed range expansions. (A) Range expansions can be broadly classified as pulled or pushed depending on the primary drivers of the expansion. In pulled expansions, the small numbers of founders from the tip of the expansion grow rapidly in the new territory (Top). This founding population contains only a small subset of the total diversity in the population. Therefore, diversity is quickly eroded as the population expands into new area. Pushed waves are driven by migration out of the bulk, because the small density of founders at the front has a subdued growth rate (Bottom). Thus, genetic diversity is maintained much longer. (B) The experimental setup consists of yeast expanding in a discrete space, discrete time 1-dimensional metapopulation landscape. Adjacent wells are connected via migration and exchange a fixed fraction of cells, m, every cycle, and then grow for 4 h (Top). This process results in an emergent wavefront of a fixed density profile moving to the right with a fixed velocity (Bottom). The location of the front is determined as the interpolated well position where the density profile crosses a predetermined threshold (Materials and Methods). Velocity is then measured as the rate of advance of the front location. The entire area to the right of the threshold location is defined as the front for subsequent computation of genotype frequencies.

This differential rate of diversity loss in pulled and pushed waves is well characterized in a wide range of theoretical models (20, 21, 23–25) and has also been observed empirically in field studies (26). However, it has been difficult to directly connect the empirical observations to theory (22, 26), in part because these natural expansions cannot be replicated, and also because numerous environmental factors cannot be well controlled. Microcosm experiments have helped address this chasm between theory and experiments by partially trading off realism for much better controlled and replicable biological systems (27–31).

Previous experiments with microbial colonies expanding on agar have demonstrated both diversity-eroding and diversity-preserving range expansions (21, 32, 33). In these experiments, a colony is inoculated with 2 genotypes, and the diversity loss manifests in the formation and coalescence of monoclonal sectors. However, this sectoring phenomenon is lost when 2 different mutualist species are inoculated together at the center instead of a single species. The sector formation in the former case and its lack in the mutualists can be well understood mechanistically for this particular system in terms of the (microscopic) demographic and geometrical properties of the expanding species. In contrast, in our current study, we explore the differential rate of diversity loss more generally as a consequence of growth demographics, independent of species-specific mechanisms.

Using the framework of pulled and pushed waves, we performed experiments to establish a general relationship between cooperativity in growth dynamics and the strength of genetic drift. Our setup is an extension of a previously developed experiment, where we demonstrated the transition from pulled to pushed waves with increasing cooperation in yeast (18). To study genetic diversity, we introduce 2 otherwise identical genotypes with different fluorescent markers, whose frequency can be tracked over time. We find that yeast populations expanding as a pulled wave undergo a drastic reduction in genetic diversity, unlike the same population expanding as a pushed wave. Moreover, we quantify the rate of diversity loss in terms of the effective population size and show that the effective population size correlates well with how pushed the expansion is (defined as “pushedness”).

We also observe a few evolutionary “jackpot” events during which one of the genotypes abruptly increases in frequency. Such events are predicted to arise naturally due to rare stochastic excursions of the expansion front ahead of its expected position (34). Our results support this theory because abrupt changes in allele frequency co-occur with substantial changes in front shape. Importantly, we show that these jackpot events can be distinguished from selective sweeps, in which a new mutant rises to high frequency due to its higher fitness compared to the ancestral population.

Results

The stepping-stone metapopulation model is widely used to describe the spatiotemporal population dynamics in patchy landscapes (35, 36). In this model, populations grow in discrete patches that are connected to nearest-neighbor patches via migration, which is reflected in our experimental setup. The budding yeast, Saccharomyces cerevisiae, expands in 1 dimension, along the rows of a 96-well plate, with cycles of growth, nearest-neighbor migration, and dilution into fresh media (Fig. 1B). At the beginning of every cycle, a fixed fraction $\left(m/2\right)$ of culture in each well is transferred into wells at adjacent locations on either side, while the remaining $\left(1-m\right)$ is transferred into the well at the same location. At the same time, the culture is also diluted into fresh media by a constant factor. After dilution, the cultures are allowed to grow for 4 h before the cycle is repeated. Starting with a steep initial spatial density profile of yeast, this process leads to a stable wavefront (defined in Fig. 1A and Materials and Methods) that moves at a constant velocity (Fig. 2A).

Fig. 2.

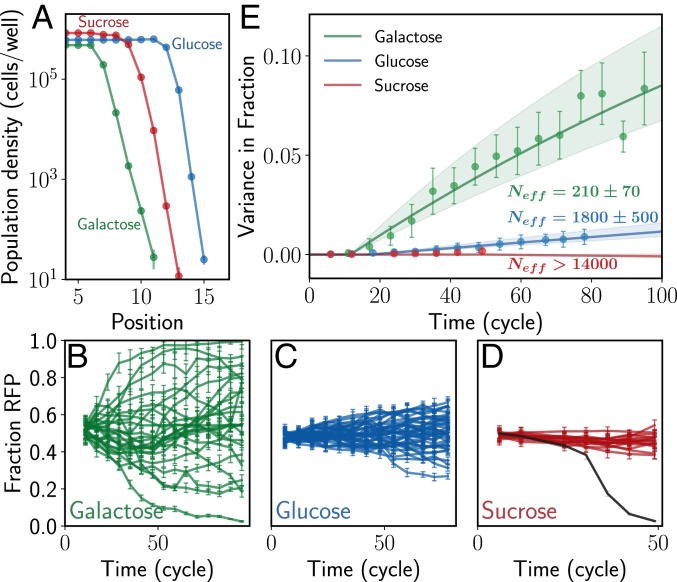
Yeast expanding in different growth media loses diversity at very different rates even though the wavefronts have similar velocity and bulk density. (A) Populations of S. cerevisiae growing in galactose, glucose, or sucrose media expand spatially as traveling waves with a constant velocity and exponentially decaying density at the front. The population-level parameters such as migration and growth rate were chosen such that the emergent wave parameters such as velocity, bulk population density, and the spatial decay exponent at the front are similar in the 3 environments. This allows for a fair comparison of effective population sizes across the conditions. Error bars represent Poisson sampling uncertainty. (B) Yeast expanding on galactose loses diversity most rapidly. Starting with equal initial frequencies of 2 genotypes that differ only in terms of a single fluorescent marker (RFP or CFP), the fraction of 1 of the genotypes in the front (RFP shown) fluctuates randomly until the genotype either reaches fixation or becomes extinct. The expansion experiments are replicated 24 times, and the dynamics of fractions vary by a large amount across replicates. (C and D) The same experiments but in different media, glucose (24 replicates) and sucrose (16 replicates), show very different rates of diversity loss. In glucose (C), the loss of diversity is much slower compared to the expansions in galactose. In sucrose (D), no significant loss of diversity is observed during the duration of the experiment (the replicate shown in black was mispipetted in cycle 30 and hence diverges from the rest [SI Appendix, Fig. S3, Top row]. This replicate is ignored in further analysis). Error bars are SD. (E) The rate of diversity loss can be quantified in terms of the variance in fractions across replicates (Eq. 1, $f_0=0.5$). In galactose and glucose, the variance increases significantly, allowing us to quantify the effective population size. In sucrose, the increase in variance is not statistically significant and we can set only a lower bound on the effective population size (Materials and Methods). The drastic loss of diversity in galactose is reflected in the effective population size of 220, over 4 orders of magnitude lower than the actual population size in the front. In contrast, effective size in sucrose is over 15,000. Error bars are SD of fractions propagated to variance.

Previous studies have shown that yeast typically do not display cooperative behavior when growing on simple sugars such as galactose or glucose, but grow cooperatively on sucrose (18, 37). Thus, we expect pulled expansions in glucose and galactose and pushed expansions is sucrose. To compare the rate of genetic drift in these different environments, we use 2 otherwise identical genotypes of the same strain, but with different constitutively expressed fluorescent markers, whose frequency can be tracked using flow cytometry. We start with a 1:1 ratio of the 2 strains in the initial density profile for the expansion experiment and observe the relative frequencies for 40–100 cycles.

In the galactose environment, the relative frequencies of the 2 genotypes in the front (see Materials and Methods for definition) change rapidly over the course of the spatial expansion, undergoing large fluctuations, occasionally leading to fixation of 1 of the genotypes (Fig. 2B). By simultaneously observing 24 replicates of the same expansion experiment, we find that while the waves are identical in terms of their velocity and wavefront shape (up to some small transients that arise due to demographic stochasticity), the internal dynamics of individual fractions are very different (Fig. 2 A and B). This can be clearly seen from the variance in fractions across replicates (Fig. 2E), which grows from 0 at the beginning of the experiment to the maximal value of 0.25. The measured variance allows us to quantify the rate of diversity loss in terms of the effective population size using the relationship

$$var\left(t\right)=f_0\left(1-f_0\right)\left(1-exp\left(\frac{-t}{N_{eff}}\right)\right),$$ [1]

where $var\left(t\right)$ is the variance in the fractions across replicates as a function of time, $f_0=0.5$ is the initial fraction at $t=0,$ and t is in units of generation time (cycles in this case, since the entire front is effectively diluted by 2× every cycle, and so each cycle corresponds to 1 generation) (10). Increase of the variance is directly related to change in other diversity metrics more commonly used in ecology. For instance, the mean Simpson’s diversity index across replicates increases linearly with variance: $\langle S\left(t\right)\rangle =2var\left(t\right)+1-2f_0\left(1-f_0\right)$ (10). For the pulled waves in galactose, the effective population size is ∼210—4 orders of magnitude smaller than the actual population size in the wavefront (Fig. 2E). We thus see that there is a tremendous loss of genetic diversity during pulled expansions.

We repeat the same experiment, but now with yeast growing on sucrose, where we expect growth to be cooperative and hence the expansions to be pushed (18). The expansion speed and bulk population density in sucrose are similar to those in galactose (Fig. 2A). Yet, while the waves are physically similar, their effect on the genetic diversity in the population is drastically different. The frequencies of the 2 genotypes, starting at an equal 1:1 ratio, remain almost unchanged at the end of the experiment for all 16 replicates (Fig. 2D). The diversity-preserving nature of these pushed expansions is reflected in the large effective population size, estimated to be higher than 15,000—at least 2 orders of magnitude larger than in pulled waves (Fig. 2E).

Drastically different effective population sizes in the simple sugar galactose and complex sugar sucrose are consistent with the theoretical expectations for pulled and pushed waves (18). Expansions in high concentrations of glucose, however, show somewhat unexpected dynamics. Because glucose is a simple sugar, we expect the expansions to be pulled and hence lose diversity quickly. However, the measured effective population size in glucose is intermediate between that in galactose and sucrose (Fig. 2 C and E); i.e., diversity is lost much faster in glucose than in sucrose, but not quite as rapidly as in galactose.

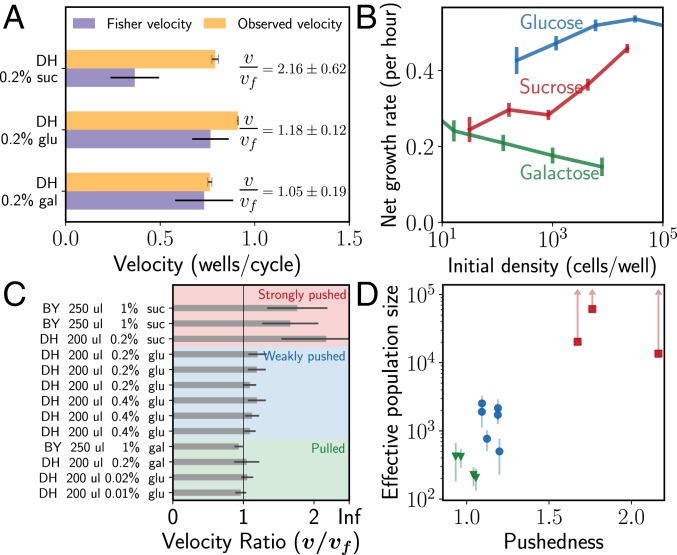
One possible explanation for this discrepancy is that expansions in glucose are weakly pushed. To test this possibility, we quantify the pulled vs. pushed nature of the expansions in all 3 media. Specifically, we measure the low-density growth rate of our strains (DH; Materials and Methods) and their expansion velocity. Pulled waves expand at the Fisher velocity, which is determined solely by the low-density growth rate and the migration rate, while pushed waves expand at a velocity greater than the Fisher velocity. We define a pushedness parameter as the ratio of the experimentally observed velocity to the Fisher velocity, so that pushedness = 1 for pulled waves and >1 for pushed waves.

For galactose, the pushedness of the expansions is observed close to 1, whereas for sucrose it is 2.2, clearly confirming that the galactose expansions are pulled and the sucrose ones are pushed (Fig. 3A). This is further supported by the complete lack of cooperativity seen in growth on galactose and the strongly cooperative growth observed in sucrose (Fig. 3B). Surprisingly, the pushedness for 0.2% glucose expansions is also greater than 1, suggesting that contrary to our naive expectation, expansions in high concentrations of glucose are in fact not pulled. More careful measurements of the growth profile of the DH strains in 0.2% glucose reveal a tiny amount of cooperative growth at very low densities (below 5 × 10³ cells per well), making them very weakly pushed (Fig. 3B and SI Appendix, Fig. S1). While this Allee effect might originate due to different mechanisms such as collective pH modulation (38), it is important to note that the emergent property of the wave, pushedness, explains the decreased rate of diversity loss without the need to understand such species-specific growth mechanisms.

Fig. 3.

The ratio of observed velocity to the Fisher velocity (termed pushedness) determines the rate of diversity loss during expansions. (A) Pulled waves expand at the Fisher velocity and hence have a pushedness of 1, whereas pushed waves have pushedness larger than 1. Consistent with the observed rates of diversity loss, the waves in galactose have pushedness = 1, and those in sucrose have a much larger pushedness of 2.2. Even though digestion of glucose is noncooperative, we found expansions in 0.2% glucose to be pushed, although not as strongly as in sucrose. Error bars are SD (Materials and Methods and SI Appendix). (B) The pushed or pulled nature of the expansions is consistent with the measured growth rates. Growth in sucrose is highly cooperative, in glucose has intermediate cooperativity, and in galactose is not cooperative at all. This explains the intermediate rate of diversity loss in glucose compared to galactose and sucrose. Error bars are SEM (Materials and Methods and SI Appendix). (C) We repeat the expansion experiments across multiple environmental conditions (different media and migration rates; see SI Appendix, Table S1 for details of experimental parameters), for 2 different pairs of yeast strains (BY and DH), and observe a wide range of pushedness values for the different expansions. Error bars are SD. (D) Effective population size is plotted against the pushedness for the strain–media combinations from C. We find that $N_{eff}$ correlates strongly with the pushedness (note the log scale on the y axis). Error bars are SD.

We probe the relationship between pushedness and the rate of diversity loss further, by repeating the expansion experiments in multiple environments using 2 different pairs of strains (DH-RFP/DH-CFP and BY-RFP/BY-YFP). The different strain–media combinations give rise to expansions spanning a broad range of pushedness values (Fig. 3C). We find that the pushedness correlates well with the effective population size during expansions (Fig. 3D). Broadly, for all instances of pulled waves, Neff was under 500, over 4 orders of magnitude below the actual population size. Within the pushed waves, we find 2 regimes with very different rates of diversity loss. In the weakly pushed regime, the effective population size ranged between 500 and 3,000. We thus see that even for pushed waves, if cooperativity is not strong enough, diversity can be lost quite rapidly. Finally, in the strongly pushed regime, we observe very little genetic drift and can therefore only set a lower bound on the effective population sizes (Materials and Methods), and the lower bounds are at or over 15,000 (Fig. 3C). Overall, for populations with approximately equal bulk densities (within a factor of 3), the rate of diversity loss is seen to be strongly modulated by the pushedness.

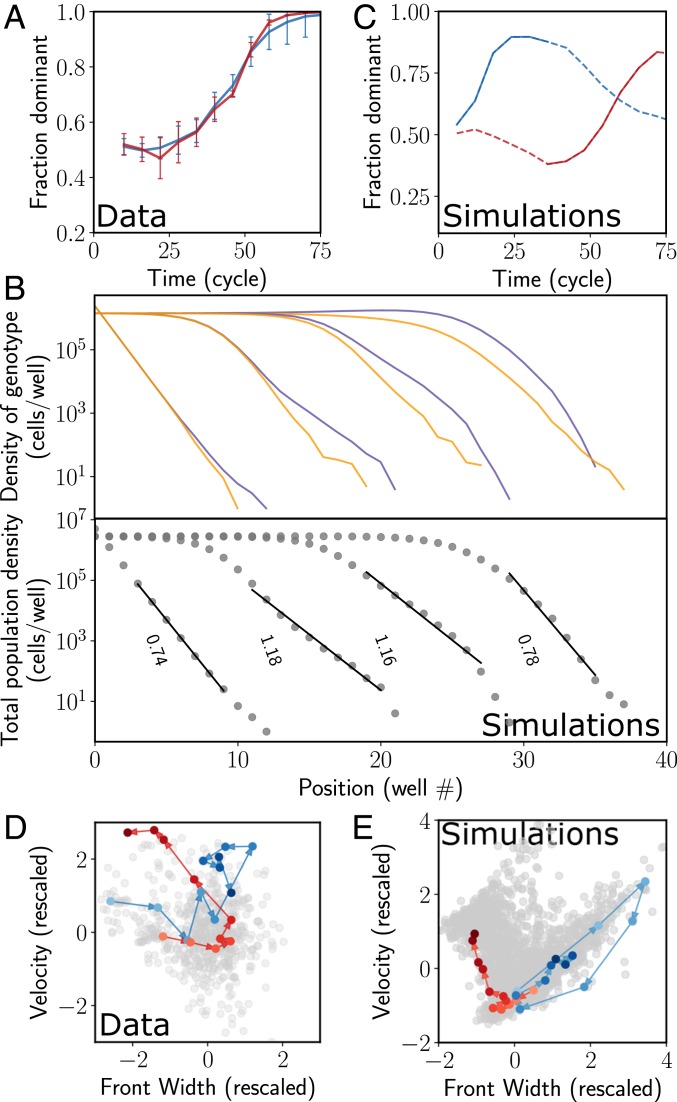
Throughout our experiments, we observe a few instances where one of the genotypes appears to take over the population very rapidly (Fig. 2D, black line). Fig. 4A shows 2 other similar rapid takeover events, which closely resemble evolutionary sweeps that might occur when a beneficial mutation arises in one of the genotypes. However, during range expansions, such sweeps can also occur purely as a consequence of a rare reproduction or dispersal event, in which case we refer to them as jackpots. In natural populations, such jackpot events can occur when a rare long-distance dispersal might establish a new population in an unoccupied territory near the front. When this clonal population merges with the expanding front, the frequency of the clonal genotype in the front suddenly increases. This process, called the “embolism effect,” has been previously proposed in theoretical literature (25), and we found one instance of it in our experiments, likely due to a droplet of culture spraying toward the front of the wave (Fig. 2D, black line and SI Appendix, Fig. S3, Top). In experiments, rapid takeovers are more likely to occur when a clump of cells of a single genotype does not break during mixing and is transferred over to the next well, leading to increased frequency of that genotype in the front. As the expansion progresses, this increased frequency propagates through the entire front (Fig. 4B, Top). Both the examples described above can be termed jackpot events that occur due to stochastic demography.

Fig. 4.

Rapid takeover by one of the genotypes due to rare fluctuations of the front and selective sweeps. (A) In some instances of the expansion experiments, the fraction of one of the species is seen to increase very rapidly. The fraction of the species that eventually dominates is plotted as a function of time for 2 such instances. Error bars are SD. (B) During spatial expansions, rapid takeovers can occur without selection, simply because of stochasticity in migration and growth or rare long-distance dispersal. Top shows the density of 2 genotypes in a simulation at different times (left to right). In an early cycle, at the very tip, stochasticity in migration led to excess colonization of the purple genotype in a well near the front (jackpot event). This fluctuation then propagated back toward the bulk as the purple genotype rapidly took over the front population. Note how this process was accompanied by a transient widening of the front (Bottom). (C) Two instances of rapid takeovers in simulations. The orange curve is from a simulation of a selective sweep during expansion, whereas the blue curve corresponds to a jackpot event. The dotted lines are the entire trajectory, and the solid sections correspond to the takeover times that are shown in D and E. (D and E) Trajectories in the space of front width and velocity for experiments (D) and simulations (E) corresponding to A and B. Each dot corresponds to the front width and velocity at a single time point for one of the replicates. The axes are rescaled so that the front width and velocity have mean 0 and SD of 1; arrows indicate increasing times. During selective sweep (orange curve in E), the trajectory initially fluctuates around the mean value of the width and velocity, but, after the mutant establishes at the front, the trajectory moves monotonically to the top left toward increasing velocity and decreasing front width. In contrast, for the jackpot event (blue), the front width and velocity transiently increase, but relax back toward their mean values at later times. Although the time series of the fractions in experiments look nearly identical in the 2 instances shown, the state space trajectories are clearly distinct and help distinguish selection from jackpots.

We can distinguish between selective sweeps and jackpot events by identifying the excess migration at the front that accompanies jackpots but not selective sweeps. In Fig. 4B, we simulate a simple model of expansion to show how the wave front widens as a consequence of the excess migration. Wider fronts expand faster, so the wave speed increases transiently as well. Importantly, both the velocity and front width return to their mean values as the front returns to equilibrium. In contrast, evolution toward a higher growth rate (migration rate is fixed in our assay and cannot be selected for) leads to increased velocity $\left(\propto \sqrt{r_0}\right),$ but decreased front width [$\propto 1/\sqrt{r_0},$ where $r_0$ is the low-density growth rate (14)]. Moreover, in the case of selective sweeps, the trajectories in the velocity-front width space do not return to the previous mean, but rather settle at the new equilibrium. These differences allow us to distinguish between the 2 processes responsible for rapid takeover by a genotype.

The differences described above are confirmed in simple simulations, where we follow the trajectory of a rapid takeover event in the state space (front width vs. velocity). For jackpots (no beneficial mutations allowed), we see the transient front widening accompanied by an increased velocity, before the trajectory returns to the mean front width and velocity (Fig. 4E). When a low rate for beneficial mutations is included in the simulations, we observe rapid extinctions of one of the neutral markers. The state space trajectories are, however, very different. After a selective sweep, they do not return to their previous locations; instead, they settle in the region of higher velocity and steeper fronts (Fig. 4E).

Among the rapid takeovers that we observe in experiments, a subset can be clearly seen to follow the selective sweep template. Fig. 4D shows the state space trajectory for one replicate that putatively evolved to a higher growth rate (red trajectory, compare to a jackpot shown in blue), corresponding to the takeover trajectories shown in Fig. 4A. We observe these putative selective sweeps only in a single growth medium among several that we used in our experiments (SI Appendix, Fig. S3). This medium was limiting in terms of an essential amino acid and thus is likely to apply a higher evolutionary pressure than the others. We also observe a few rapid takeover events that do not follow the selection template, but rather look like jackpot events. Even though the time series of allele fraction look similar for selective sweeps and jackpot events (Fig. 4A), the 2 mechanisms can be clearly distinguished based on their state space trajectories (Fig. 4D). Given the rarity of both jackpots and selective sweeps due to mutation, we do not have sufficient data to explore and contrast them in great quantitative detail. The few instances of these processes that we do observe are nevertheless fully consistent with theoretical predictions and our simulations.

Discussion

In this study, we used a well-controlled laboratory microcosm setup to probe the distinct evolutionary consequences of pulled and pushed expansions. We observed the rapid loss of diversity (small effective population size) caused by the serial founder effect when yeast expanded as a pulled wave and a much more subdued loss of diversity (large effective population size) when it expanded as a pushed wave. This ability to accurately measure both the actual and effective population sizes during expansion in our experimental setup opens the possibility for further quantitatively testing theories of eco-evolutionary feedback (22). Moreover, we explored environmental conditions that span different levels of pushedness and found that the effective population size in the front is strongly correlated with the pushedness of the expansion. Thus, our experiments suggest that pushedness is a useful measure for predicting the rate of diversity loss during range expansions.

We also observed instances of unusually rapid takeover of the populations by one of the genotypes. In the amino acid-limited media, the yeast evolved a higher growth rate, and the takeover events were driven by selective sweeps. In other conditions, rapid takeovers were instead due to rare demographic fluctuations. We were able to distinguish the two by looking at the trajectories of the wavefronts in the state space defined by velocity and front width.

The extensive theoretical work on range expansions has led to other very interesting predictions that could also be addressed using our experimental system. One prediction pertains to the quantitative dependence of the effective population size on the actual population size in the wavefront (24). It has been established that, with growth and migration held fixed, $N_{eff}$ scales linearly with $N_{bulk}$ in fully pushed expansions, and $N_{eff}\propto lo{g}^3\left(N_{bulk}\right)$ in pulled expansions ($N_{bulk},$ or the bulk density, is the carrying capacity of a single well). Moreover, in the presence of a very weak Allee effect, Birzu et al. (24) predict a third class of expansions that is intermediate between pulled and pushed, where $N_{eff}$ scales as a sublinear power of $N_{bulk}.$ We attempted to observe these different scaling relationships by varying the bulk population size in experiments in 2 different ways—by changing the total volume, and thus the population size, and by changing the amount of a limiting amino acid. Unfortunately, in the former case, the altered volume also altered the density dependence of the growth, while in the latter case, the low amino acid condition led to evolution during expansion. We speculate that the expansions in glucose, where the loss of diversity is intermediate between galactose and sucrose, might in fact belong to the newly predicted third class of expansions. Modifying our assay to modulate the bulk density without changing growth properties would help resolve this speculation.

Demographic stochasticity and environmental noise have also been predicted to cause fluctuations in the position of the expansion front (24, 34), which is well described by simple diffusion around the mean position. In pushed waves, the effects of demographic noise on front diffusion are predicted to be subdued, and front diffusion should largely reflect environmental noise. The situation is different in pulled waves, where front diffusion due to demographic noise is predicted to be much more pronounced. We observed front diffusion in both pulled and pushed waves in our experiments, where the variance in front position remains constant for some initial period before it starts increasing linearly with time (SI Appendix, Fig. S4). Contrary to expectations, we do not find a significant quantitative difference in front diffusion in pulled vs. pushed waves. This negative result could be explained by the lack of sufficiently long time series data or by the dominance of the environmental noise for both pulled and pushed expansions in our experimental setup.

The Allee effect, or the inability of organisms to grow optimally at very low densities, is often considered to have a negative impact on populations. For instance, it leads to lower expansion velocities compared to the velocity if growth were not suppressed at the low-density tip. However, in this study we demonstrate that the Allee effect can in fact have a very beneficial effect on the expanding population by helping preserve diversity as the population enters novel territories, where the diversity is especially critical for survival. Even a miniscule Allee effect at very low densities, such as what we found in the glucose expansions, can go a long way in helping mitigate diversity loss. Perhaps such tiny Allee effects pervasive in many invading species explain the lower than predicted rates of diversity loss during their expansion.

Materials and Methods

Strains.

The expansion experiments were performed using 2 pairs of strains, BY-RFP/BY-YFP and DH-RFP/DH-CFP. The BY strains were derived from the haploid BY4741 strain [mating type a, EUROSCARF (39)]. The BY-YFP strain has a yellow fluorescent protein expressed constitutively by the ADH1 promoter (inserted using plasmid pRS401 containing MET17). The BY-RFP strain has a red fluorescent protein inserted into the HIS3 gene using plasmid pRS303. This pair is auxotrophic to uracil. The DH strains are the same as those used in Healey et al. (40). They are derived from the diploid strain W303, with the RFP/CFP strains harboring constitutively expressed red and cyan fluorescent markers integrated into the URA3 gene. Both genotypes are mating type α (41), and thus we do not expect any exchange of genetic material (especially fluorescence plasmids) due to sexual reproduction.

Growth Rate Measurements and Calculation of Fisher Velocities.

Growth rates for both strain pairs were measured independently in the different media, in growth conditions identical to the final expansion experiments. Details of the measurement protocol and measurement data can be found in the SI Appendix (estimation of low-density growth rates, SI Appendix, Fig. S1), along with a detailed description of the fitting algorithm. The Fisher velocities were then obtained using the expression below as described in our previous work (18):

$$v_{lin}=mi{n}_{\lambda >0}\left\{\frac{1}{\lambda \mathrm{\Delta }t}ln\left[e^{r_0\mathrm{\Delta }t}\left(1+\frac{D_{eff}\mathrm{\Delta }t}{\mathrm{\Delta }{x}^2}\left(\cosh \left(\lambda \mathrm{\Delta }x\right)-1\right)\right)\right]\right\}.$$

Uncertainties in the Fisher velocity were obtained by bootstrapping: For each experimental condition, we sampled a growth rate from a normal distribution with the measured mean and SEM 100 times, computed the Fisher velocities by numerically minimizing the expression above, and report the mean and uncertainty based on the resulting distribution.

Expansion Experiments.

All experiments were performed at 30 °C in standard synthetic media (yeast nitrogen base and complete supplement mixture), in 200 $\text{μl}$ (or 250 $\text{μl}$ where indicated) batch culture in BD Biosciences Falcon 96-well Microtest plates. Expansions occurred along the 12-well-long rows of the plate. Migrations and dilutions were performed every 4 h using the Tecan Freedom EVO 100 robot. Plates were not shaken during growth. Optical densities were measured on the robot before every dilution cycle in the Tecan Sunrise plate reader with 600 nm light. Cell densities of fluorescent strains were measured every 6 cycles in the MacsQuant flow cytometer after dilution in PBS. All expansions started with a steep exponential initial density profile. Periodically during the expansion, the leftmost well (in the bulk of the wave, away from the wavefront) was discarded and the entire profile was shifted to the left, to create empty wells for further expansion to the right. It was ensured that the rightmost 2 wells were always at zero cell density to avoid any edge effects on the expansion.

Definition of Front.

The “front” is defined as the region of the wave density profile that falls below a threshold density, set at $0.2\times N_{bulk},$ where $N_{bulk}$ is the carrying capacity of a single well. $N_{bulk}$ is measured by taking the mean density per well in the region where cell density is approximately constant. “Fractions/frequency in the front” corresponds to the fraction of red or cyan/yellow fluorescent cells from all wells composing the front region as defined above. The location of the front is defined as the interpolated well position where the density profile crosses the threshold density.

Lower Bound on Effective Population Size.

Eq. 1, which quantifies the dependence of the effective population size on the rate at which variance in fractions across replicates increases, is used to estimate the effective population size in our analysis. However, for pushed expansions in sucrose, the variance in the measured fractions never increases significantly above zero given the uncertainties in fraction measurements. In this case, it is not possible to quantify the effective population size. However, the fact that after a given time T, the variance increases at most by an amount equal to the measurement uncertainty, defined as $V_{min},$ sets a lower bound on the effective population size:

$$N_{eff}>-T/\ln \left(1-\frac{V_{\min \left(T\right)}}{\left(f_0\left(1-f_0\right)\right)}\right).$$