Flow directionality of pristine meandering rivers is embedded in the skewing of high-amplitude bends and neck cutoffs

Significance

The bends of alluvial meandering rivers often double back on themselves, showing skewing. This skewing may be directed upstream or downstream. How skewing evolves as bends develop remains incompletely understood. Our analysis shows that, on 20 reaches of nearly pristine alluvial meandering rivers, downstream skewing dominates when the bends are relatively straight, but upstream skewing increasingly dominates as bend sinuosity increases. This provides a guide for interpreting bend evolution and offers a useful comparison with numerical models. The results suggest that rivers often carry an imprint of the direction of the flow that created them, through the shape of their high-amplitude bends and neck cutoffs. This provides a reference tool for estimating paleoflow direction on Earth and other planets.

Abstract

Information concerning the dynamics of river meandering is embedded in their planforms. Here, we focus on how bend skewing varies with increasing sinuosity, and how flow direction is embedded in bend skewing. It has often been thought that upstream-skewed bends are dominant within a sufficiently long reach. These bends may allow a reasonable inference as to the direction of flow. Here we consider this issue using 20 reaches of freely meandering alluvial rivers that are in remote locations, generally far from human influence. We find that low-amplitude bends tend to be downstream-, rather than upstream-skewed. Bends with sinuosity greater than 2.6, however, are predominantly upstream-skewed. Of particular interest are the neck cutoffs, all chosen to be relatively recent according to their position related to the main channel: 84% of these are upstream-skewed. Neck cutoffs, which have likely evolved directly from bends of the highest sinuosity, represent the planform feature most likely to have flow direction embedded in them. The field data suggest that meander bends without external forcing such as engineering works tend to evolve from downstream-skewed low-sinuosity bends to upstream-skewed high-sinuosity bends before cutoff. This process can be reproduced, to some extent, using models coupling sedimentary dynamics with flow dynamics.

Meandering rivers are common, esthetically pleasing, and of engineering importance. The planform of this ubiquitous river pattern possesses a high degree of regularity (1–5). Meandering channels are seen in a wide variety of settings, including alluvial rivers (4–8), mixed bedrock–alluvial rivers (9, 10), tidal channels (11, 12), and flows over ice (13, 14). Here we focus on alluvial meandering. Such streams have planforms with a composite of organized and irregular variation representing both autogenic and allogenic effects (1, 15–17). We ascertain to what degree flow directionality is embedded in the planforms of meandering rivers and their neck cutoffs.

The streamwise-symmetrical sine-generated curve has been proposed as an idealized description of river meander form based on the assumption of minimum variance (18). This relation is

$$\theta ={\theta }_o\sin \left(ks\right),$$ [1]

where θ = bend angle between the longitudinal (streamwise) and downvalley direction, θ_o = angle amplitude, s = centerline streamwise axis, and k = 2π/λ, where λ = arc length wavelength and k = arc length wavenumber. This planform shape is shown in Fig. 1A.

Fig. 1.

Features of bend skewing in idealized models, as well as a historical map showing several skewed bends (A) Sine-generated centerline of meander with no skewing. (B) Upstream-skewed centerline. (C) Downstream-skewed centerline. (D) Meandering Mississippi River (channel 07 near Vicksburg, MS) from a Fisk (19) map showing varying modes of skewing.

Although widely used in physical and numerical models, streamwise-symmetrical curves are a simplification of bend shape, and therefore may not be suitable for highly sinuous channels or oxbow lakes, which often show planform asymmetry (6, 19–21). Adding third-order terms allows for planforms with skewing and fattening (22):

$$\theta ={\theta }_0\sin \left(ks\right)+{\theta }_0^3\left[J_s\text{cos}\left(3ks\right)-J_f\sin \left(3ks\right)\right].$$ [2]

Here J_f = coefficient of fattening and J_s = coefficient of skewing. Fig. 1B shows a bend with a positive coefficient of skewing. The bend doubles back upon itself and points upstream (upstream skewing). Fig. 1C shows a bend that points downstream (downstream skewing). The recognition of skewing is not specifically dependent on [2]; it can be inferred from river planform. The tendency for upstream skewing was recognized as early as 1955 (23). Fig. 1D shows a Fisk (24) map of the Mississippi River; it shows both upstream and downstream skewing. We assume that while skewing may be generated by floodplain inhomogeneities (16, 17, 25), it may also be an autogenic tendency inherent to the morphodynamics of meandering alluvial rivers. Indeed, it was suggested based on empirical information that upstream skewing might predominate for meandering bends in the Ishikari River, Japan (26).

Our focus is on the tendency of bends to be skewed. It has been suggested that upstream skewing is the most natural state of alluvial meandering rivers (22, 27). The patterns predicted in refs. 22 and 27 may, however, be overly biased toward upstream skewing (28). One explanation for this limitation is that the model in question leaves out some subtle points pertaining to morphodynamics in meander loops. The authors of ref. 29 considered vegetation–river interaction in their simulations, and found that some transverse vegetation distributions along a river may reduce upstream skewing and induce downstream skewing. A more advanced model (see ref. 30 for comprehensive references) suggests that downstream skewing can occur if the channel is sufficiently wide. The difference in skewing regime is characterized in terms of subresonant (resulting in upstream skewing) or superresonant (resulting in downstream skewing) behavior. This resonance refers to the interaction of processes that form alternate bars and processes that form bend point bars.

Most models of meander migration relate the bank erosion rate to the near-bank streamwise flow velocity (e.g., refs. 22, 27, 28, and 30). A bank erosion model has also been deduced by analyzing the conservation of near-bank sediment mass (31). In this model, the bank erosion rate is assessed in terms of the gradient of the longitudinal sediment transport rate and the strength of the secondary current. The authors used this model to simulate the evolution of meandering from mildly sinuous to highly sinuous (32). In this simulation, single loops first rotate downstream and then gradually rotate back to an upstream-skewed configuration.

A recent numerical model of meander evolution (33) includes a more detailed description of erosional bank processes (natural armoring), depositional bank processes (vegetal encroachment), and self-formed width. Under unsteady flow with two cyclically alternating discharges, this model captures rich and complex meandering planforms in a train of several bends, including persistent upstream skewing, persistent downstream skewing, transition from downstream skewing to upstream skewing, and vice versa.

In addition to modeling results, field observations also show a range of behavior. An inspection of 277 bends of 15 rivers confirmed the statistical preference for upstream skewing (19). These ideas and methods have been used to interpret paleoflow direction of channels on Mars (34). In ref. 20, 57 natural stream segments were observed: these meanders tended to be skewed slightly upstream. The authors of ref. 35 examined continuous loops in 4 natural rivers (1 in a temperate region and 3 in tropical regions) and pointed out that most bends in their 3 tropical reaches did not show obvious skewing. In summary, the occurrence of, and the mechanisms behind the skewing phenomenon are not yet thoroughly documented and understood.

Here we study bend skewing by analyzing the planforms of 20 long reaches of freely migrating alluvial rivers with wide floodplains in remote locations that are in as pristine a condition as possible. This allows us to observe the planforms of self-generated by rivers with negligible anthropogenic effects. Besides natural reaches, several representative planforms from the numerical simulations of refs. 28 and 36, using a version of the theory summarized in ref. 30, are also analyzed.

Results and Discussion

We set strict criteria for data collection, as stated in Materials and Methods, to ensure that our study reaches are nearly pristine, with wide, vegetated floodplains and abundant evidence of channel migration. Of our 20 sample reaches, 8 are in South America, 7 are in North America (mostly northern Canada), 2 are in Africa, 2 are in Siberia, and 1 is in Papua New Guinea. The number of bends per reach ranges from 56 to 311, with a mean of 149. The average width ranges from 40 m to 9 times that. The reaches are summarized in Fig. 2 A and B. The width, length, and country information are listed in SI Appendix, Table S1. A subreach of an example reach, the Chulym River, a tributary of the River Ob in Russia, is shown in Fig. 2C. It flows west by south on a pristine floodplain with numerous scrolls and cutoffs.

Fig. 2.

Overview of the study reaches, and an example of the characteristic floodplain type our sample reaches flow through. (A) Planforms of all 20 reaches used in this study. (B) Location of all 20 reaches (C) Detailed view of the planform of a subreach of the Chulym River, Russia used in this study.

We detected and connected successive inflection points to divide the reaches into bends. This segmentation is described in Materials and Methods. Due to the complexity of the planforms, segmentation into individual bends was not always straightforward. As explained below, 311 bends from our initial set of 2,976 bends were discarded, leaving 2,645 bends and 411 recent neck cutoffs for analysis. (We do not consider chute cutoffs here.) Details concerning the reaches can be found in SI Appendix, Table S2.

The next step is evaluating bend-skewing angle, as described in Materials and Methods. A positive skewing angle denotes upstream skewing and a negative skewing angle denotes downstream skewing. Viewed in total, 60% of our channel bends are downstream skewed, a higher percentage than would be expected from the literature quoted above. We further organize the data into bins of increasing bend sinuosity, as measured by the inflection-to-inflection arc length to the length of the straight line connecting the inflection points.

Fig. 3 characterizes skewing in terms of percentage upstream skewed, mean, median, and 75% and 25% quartiles. The corresponding probability distributions for each sinuosity bin are given in SI Appendix, Fig. S1.

Fig. 3.

Relationships between bend skewing and bend sinuosity. (A) Number of upstream skewed bends and downstream-skewed bends in each sinuosity range (left axis) and percentage of upstream-skewed bends (right axis) vs. sinuosity (horizontal axis). Results for cutoffs are given at the far right. (B) Mean and median bend skewing angle as well as the 75% and 25% quartiles for each sinuosity bin as a function of sinuosity. Note from Materials and Methods that angle θ is negative for downstream-skewed bends and positive for upstream-skewed bends.

Fig. 3A shows 1) the number of upstream-skewed bends (dark blue), downstream-skewed bends (light blue), and total bends (dark + light) for each sinuosity bin, and 2) the corresponding percentage of bends that are upstream skewed (right axis). The corresponding numbers for neck cutoffs are shown on the far right of the plot.

According to Fig. 3A, a large proportion of our bends tend to have low sinuosity, and most of these bends are downstream skewed. This explains why downstream skewing could dominate from an overall perspective even when a superficial look suggests upstream skewing. On the other hand, the total number of bends with higher sinuosity is relatively small, but the percentage of upstream-skewed bends increases with increasing sinuosity for these bends. Downstream skewing dominates up to a sinuosity of 2.2, and upstream skewing increasingly dominates for higher sinuosity. By a sinuosity of 3.8 to 4.2, the bin of highest sinuosity, 74% of bends are upstream skewed.

It is likely that high-sinuosity bends continue to evolve to cut themselves off. In the case of the neck cutoffs, 84% of 411 cutoffs are upstream skewed. This indicates that in pristine alluvial meandering rivers, the direction of the flow can be reasonably estimated from the pattern of skewing of recent neck cutoffs, as well as the bends of highest sinuosity.

Fig. 3B shows mean and median skewing angle as a function of sinuosity. Also shown are the 25 and 75 percentiles. The lengths of the sinuosity bins on the horizontal axis vary because we calculated these statistics using the same amount of bends within each bin. Counting from the left, solid circles 1 through 9 at the center of each bin represent 250 bends, and the last solid circle represents the remaining 215 (we have 2,465 channel bends in total). The figure documents a fairly smooth transition from predominantly downstream skewed at low sinuosity to predominantly upstream skewed at high sinuosity.

The idea that upstream skewing predominates has a long history (23, 26). But, since downstream-skewed bends are not rare, we cannot say definitively that bends innately skew upstream. Indeed, different field researchers give different results (19, 20, 35). Our result that bend skewing evolves from downstream to upstream with increasing sinuosity does not necessarily contradict earlier theories. If a sufficiently long reach is evaluated, upstream and downstream-skewed bends might occur with roughly equal frequency. But, if we focus only on high-amplitude bends, or short reaches with high-amplitude bends, upstream skewing may manifest itself as dominant.

An early theory of meandering predicts that upstream skewing is an inherent tendency (22, 27, 37). This theory, however, considers only point-bar morphodynamics, and does not consider free bars. The analysis cannot be correct in general, because most of the bends analyzed here, and in particular those at low sinuosity, are downstream skewed. High-amplitude bends, however, may conform more to the conditions of the theory. A more advanced theory (e.g., refs. 30, 38, and 39) includes the effect of free bars as well as point bars. These two bar classes can go into resonance when the channel width–depth ratio β reaches a specific value β_c (dependent on other parameters such as grain size). In subresonant conditions (β < β_c), the theory predicts upstream-skewed bends, and in superresonant conditions (β > β_c) it predicts downstream-skewed bends.

In order to investigate this issue, we obtained the results of meander simulations conducted with a version of the above numerical model, under 3 different conditions (29, 36). All simulations assume that the form drag associated with hydraulic resistance is set by dunes. The planforms of the simulations are presented in Fig. 4A. The run conditions can be found in the original references.

Fig. 4.

Comparison of bend skewing patterns for different model simulations and natural reaches. (A) Representative planforms from the simulations of refs. 29 and 36. Case “chaos” (36) is an extensive subresonant simulation. Case “dune1” (29) is a subresonant simulation. Case “dune6” (29) is a fully superresonant simulation. (B) A segment of the Tana River possibly affected by bedrock. (C) Comparison of percent upstream skewed bends and cutoffs for each of the field reaches, along with the results for three numerical simulations.

Fig. 4C shows a comparison of the results for skewing versus sinuosity for the 3 model simulations and each of our 20 natural reaches. It shows that the behavior of natural reaches falls in between the subresonant and superresonant simulations. The subresonant (dune1 and chaos) cases somewhat overpredict upstream skewing compared to the field data. The superresonant case (dune6), on the other hand, substantially underpredicts upstream skewing. Overall, the subresonant simulations better approximate the observed field relation between skewing and sinuosity, with upstream skewing dominating at high sinuosity. We have plotted the natural cases so that wider lines represent wider reaches; it is seen that river width does not play a significant role in skewing. The width differences are relatively easy to quantify using remote sensing, but other differences that may be important, including bed grain size, flow depth, flow field, and bank strength must be sampled on the ground.

As seen in Figs. 3 and 4C, our field cases do not suggest that strongly superresonant behavior is common at high sinuosity. This may be because most of our reaches were chosen to be in humid areas with heavily vegetated floodplains. This condition may favor the development of narrow channels, pushing them into the subresonant regime. It is possible that downstream skewing at high amplitude may be favored in wider streams with more sparse floodplain vegetation.

Among the field data, however, there is an outsider in Fig. 4C. For this reach, the percent upstream skewed in the bin with sinuosity ranging from 3.4 to 3.8 drops below the curve of the superresonant case. This reach, in distinction to all of the other natural cases, shows predominantly downstream-skewed bends in the high-sinuosity range. It is a reach of the Tana River in Kenya, Africa. The reason for this abnormity is not clear. The climate is relatively dry (average annual precipitation is 350 to 470 mm per year), the vegetation is relatively sparse (40), and the floodplain (about 4 km wide, measured from Google Earth) is relatively narrow compared to the other reaches. The reach might be locally affected by bedrock: see Fig. 4B. Recently, a reach of the Wabash River, USA has been characterized as a bedrock–alluvial river (41). This river is mostly alluvial, but is also affected by occasional bedrock outcrops. We do not assert that bedrock must lead to downstream skewing. But, these outcrops distort the shape of the adjacent bends to varying degrees. In fact, some of our other sample reaches might also be affected by bedrock to a minor degree, but still they show subresonant behavior at high amplitude. Removing the Tana River from our database does not cause any significant change in the results of Fig. 3 (SI Appendix, Fig. S2). Meandering bedrock–alluvial streams in which bedrock is ubiquitous are briefly discussed in SI Appendix, Fig. S3.

Meanders in confined valleys have been documented in ref. 42. In contrast to our free meander reaches, these confined bend trains are remarkably upstream skewed and tend to migrate downstream as a coherent waveform. Another significant difference between these planforms and our alluvial reaches is that the former seldom generate cutoffs. Cutoffs, the dynamic processes of which are still incompletely understood, should play a vital and controlling role in the long-term planform dynamics of meandering rivers. By sporadically eliminating portions of itself, meander planform sinuosity fluctuates around a critical state (7, 43–45). Meanwhile, cutoffs generate intermittent noise that is able to influence the river both upstream and downstream (7, 46, 47). They also contribute to floodplain heterogeneity through cutoff infilling (7, 16, 17, 48). Further, ref. 21 suggests that similar cutoff geometries share similar dynamic histories, which means that early formative dynamics may be inferred to some extent from snapshots of cutoff planforms. Indeed, our result shows that at least one piece of information about flow dynamics, i.e., flow direction, is embedded in cutoff planforms.

While there have been major advances in the theory of meander migration over the years, no single theory predicts the behavior shown in Fig. 3. Here we consider 3 theories of meander migration that can be used to numerically model planform evolution, introduced above but here organized as follows for clarity: the bend theory (22, 27, 37); the bar-bend theory (17, 28, 30, 36, 49); and the bend-gradient theory (31, 32). The bend theory agrees with the data presented here in that the high-amplitude bends of our dataset tend to be upstream skewed, but it also incorrectly predicts that in the absence of floodplain inhomogeneities, all bends should be upstream skewed. The bar-bend theory captures the general trend of the data only in the subresonant case, where it somewhat overpredicts upstream skewing. And, since width is assumed to be constant in space in this theory, a reach can be either in the subresonant (narrow) regime or superresonant regime (wide), but not both simultaneously. The bend-gradient theory predicts that a bend can evolve from low-amplitude downstream skewing to high-amplitude upstream skewing, but only a single calculational example is presented. Evidently there is more progress to be made in explaining the evolution of skewing in meandering rivers, including autogenic and allogenic tendencies (16, 29, 48, 50).

Many theories use the assumption of constant channel width (50, 51). It may be that a consideration of an imposed variation of width (52) or self-formed width variation (53–55) can better explain the evolution from downstream skewed at low amplitude to upstream skewed at high amplitude. As in ref. 33, superresonant effects and subresonant effects may coexist within a reach when channel width is self-formed.

We conclude the following based on our study of 20 reaches of alluvial meandering rivers: 1) Low-sinuosity bends tend to be downstream skewed. 2) High-sinuosity bends tend to be upstream skewed, and both the frequency and mean angle of skewing increase with increasing sinuosity. 3) Recent cutoffs tend to be the most likely to be upstream skewed. These results can serve as goalposts for future modeling efforts.

Materials and Methods

Data Collection.

We used Landsat images and Google Earth Pro to collect data on pristine meandering rivers with well-vegetated, wide alluvial floodplains and a wealth of cutoffs and scrolls documenting channel migration. The Landsat Product Identifier of the images that have been used are listed in SI Appendix, Table S1. The centerline coordinates of the 20 reaches used in this study are available in Dataset S1. We chose remote locations in order to exclude the effect of human interference. (This was not always entirely possible: one reach is affected by a mine far upstream and another is affected by forestry practices). And, as discussed in Results and Discussion, the influence of bedrock cannot be totally discounted. This issue is addressed in more detail in SI Appendix.

Bend Segmentation.

To segment successive bends, we first calculate curvature as a function of streamwise channel length as

$$\text{C}=\left[\frac{dx}{ds}\frac{d^{2}y}{d{s}^2}-\frac{dy}{ds}\frac{d^{2}x}{d{s}^2}\right].{\left[{\left(\frac{dx}{ds}\right)}^2+{\left(\frac{dy}{ds}\right)}^2\right]}^{-3/2}.$$ [3]

The zero-crossing points define the inflections. Since the calculation of curvature is notably affected by noise, it is necessary to use a numerical filter to smooth out spurious bends (56, 57).

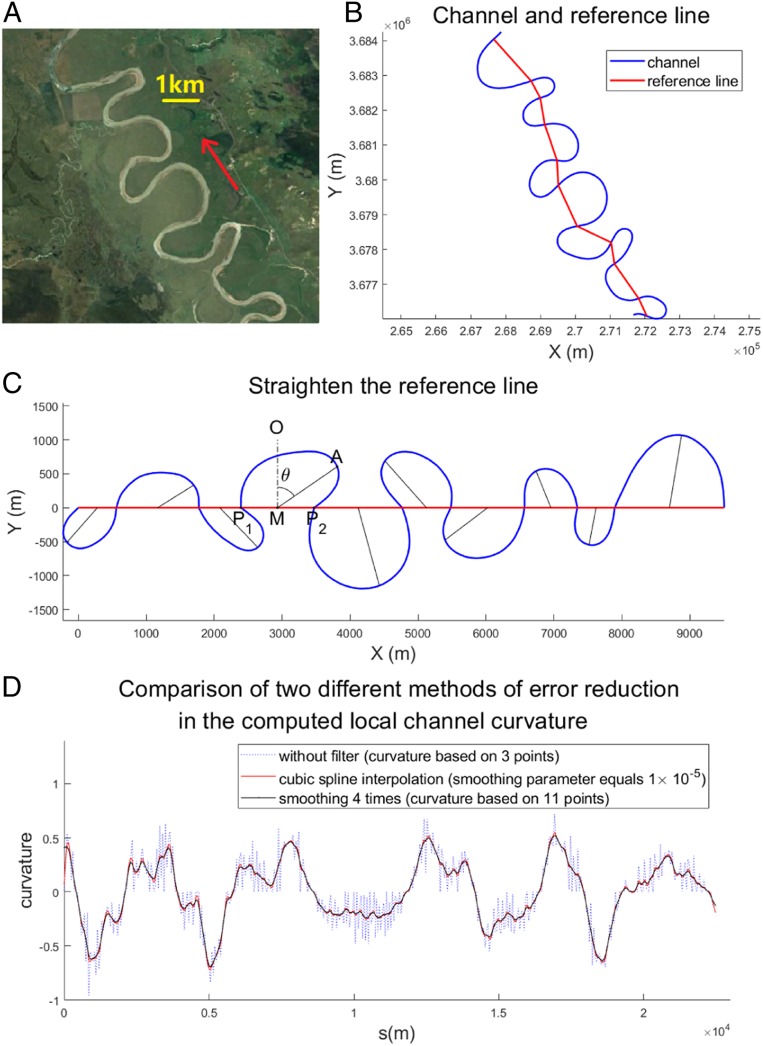
Different smoothing filters have different effects on the shape and size of developing meanders (57). We carried out a comparison of cubic spline interpolation and the curvature smoothing method in ref. 56 for a reach of the Bai River, China (Fig. 5D). The plot shows only minor differences between these two smoothing methods, which means that either method is sufficient for the purpose of determining inflection points.

Fig. 5.

Illustration of the transformation of a reach in order to extract information related to bend skewing. (A) The meandering Bai River, Sichuan Province, China. (B) Straight lines from inflection point to inflection point connect the bends. (C) The assemblage of straight lines is straightened into a single base line. The red lines from the center of the base line for each bend to the bend apex allow determining the angle of skewing. The Bai River is not included in the main compendium of bends in this analysis. (D) Comparison of cubic spline interpolation and the curvature smoothing method in ref. 56 for error reduction in the computed local curvature.

Following ref. 56, we smoothed the curvature series and identified all of the inflection points. Segmentation was done by connecting these inflection points successively. Due to the complexity of the planforms, segmentation into individual bends was not always straightforward. Some of the segments were too short or too straight for quantification. We disqualified bends whose amplitudes were less than the average channel width, as well as bends whose lengths were less than 4 times the width. Although this criterion might be somewhat arbitrary, it is appropriate here since our focus is on higher-amplitude bends.

Skewing Angle Evaluation.

The method we use to evaluate bend skewing angle is illustrated in Fig. 5C. We drew 3 straight lines. Line $P_1{P}_2$ extends from upstream inflection point to downstream inflection point of each bend. Line AM connects the bend apex, which is defined as the point of the highest curvature, to the midpoint of line $P_1{P}_2$. Line MO extends normal to line $P_1{P}_2$ from its midpoint. The angle θ from line MO to line AM defines the skewing angle. A positive value of θ corresponds to upstream skewing, and vice versa.