Ultrasound multiple scattering with microbubbles can differentiate between tumor and healthy tissue in vivo

Abstract

Most solid tumors are characterized by highly dense, isotropic vessel networks. Characterization of such features has shown promise for early cancer diagnosis. Ultrasound diffusion has been used to characterize the micro-architecture of complex media, such as bone and the lungs. In this work, we examine a non-invasive diffusion-based ultrasound technique to assess neo-vascularization. Because the diffusion constant reflects the density of scatterers in heterogeneous media, we hypothesize that by injecting microbubbles into the vasculature, ultrasound diffusivity can reflect vascular density (VD), thus differentiating the microvascular patterns between tumors and healthy tissue. The diffusion constant and its anisotropy are shown to be significantly different between fibrosarcoma tumors (n = 16) and control tissue (n = 18) in a rat animal model in vivo. The diffusion constant values for control and tumor were found to be 1.38 ± 0.51 mm² μs⁻¹ and 0.65 ± 0.27 mm² μs⁻¹, respectively. These results are corroborated with VD from acoustic angiography (AA) data, confirming increased vessel density in tumors compared to controls. The diffusion constant offers a promising way to quantitatively assess vascular networks when combined with contrast agents, which may allow early tumor detection and characterization.

Introduction

In this paper, we propose an ultrasound-based technology for the diagnosis and monitoring of cancer. This innovative technique assesses tumor-related angiogenesis in a non-invasive and quantitative manner. Angiogenesis is the formation of new blood vessels from pre-existing vessels and plays an important role in cancer. In tumors, angiogenesis has been established as one of the hallmarks of malignant transformation (Carmeliet 2005). Solid tumors need to recruit new blood vessels to grow beyond a certain size or for the hematogenous mode of metastasis (Folkman et al 1963). The morphology of such vessels resulting from tumor-related angiogenesis is abnormal. Unlike vasculature in healthy tissue, tumor vasculature is highly disorganized and isotropic (Jain 2014, Jain et al 2014). The vessels are tortuous with excessive branching and shunts (Carmeliet and Jain 2000). The microstructural properties of vascular networks, including micro-vessel density (MVD) and anisotropy are extremely relevant for distinguishing healthy tissue from multiple types of tumors (Eberhard et al 2000, Carmeliet 2005, Nico et al 2008). Various studies have linked MVD and vascular anisotropy to malignancy and overall prognosis (Weidner et al 1992, Gasparini et al 1994, Li et al 2000, Concato et al 2007, Al Murri et al 2008). MVD is commonly assessed via histopathology and has proven to be a significant and independent prognostic indicator (Weidner et al 1991, 1992).

Biopsy is the current gold standard for the diagnosis of malignancy. However, although biopsy is highly specific, it is invasive in nature and is subject to selection bias (Van Der Bij et al 2011). Thus, there is a significant interest in developing non-invasive, reliable methods to characterize the angiogenic microvasculature as a surrogate marker of malignancy. Various techniques, including ultrasound, micro-CT (Ehling et al 2014) and optical frequency domain imaging (OFDI) (Snoeks et al 2010), have been tested to characterize the microvasculature. Micro-CT scanning requires exposure to high intensity x-ray radiation in large doses, making it unsuitable for clinical use to visualize or monitor microvasculature. Optical coherence tomography (OCT) can be used to visualize the vasculature with a very good spatial resolution (typically 1–20 micron) but suffers from insufficient penetration depth (2 mm) (Fujimoto et al 2000, Vakoc et al 2012), (Yun et al 2003). Advanced OCT technologies, such as OFDI, can increase the acquisition speed, but penetration depth is still limited (4 mm) compared to ultrasound and micro-CT (Yun et al 2003). Micro-MRI imaging has shown some potential in high resolution imaging of the vasculature, but suffers from very large data acquisition time when micro resolution has to be achieved on large specimen (Uffen et al 2008).

Ultrasound is non-invasive and inexpensive compared to micro-CT and micro-MRI. Ultrasound imaging does not require any exposure to ionizing radiation, unlike micro-CT, and has much higher tissue penetration depth than OCT. However, the conventional ultrasonic imaging methods for cancer diagnosis lack specificity (Lixia et al 2016). To address this issue, methods relying on the use of ultrasound contrast agents have been developed for imaging the microvasculature (Sirsi et al 2012, Maresca et al 2014, Chong et al 2018). Current contrast agents for ultrasound are microbubbles, comprising a heavy molecular weight gas (typically a perfluorocarbon) encapsulated in a lipid shell to prolong lifetime in the circulation. The size of these agents, 1–8 μm in diameter, ensures that they act as a blood marker, since they remain confined in the vasculature. Their unique behavior under ultrasound exposure allows preferential visualization of contrast signal using non-linear imaging techniques (Simpson et al 1999, Phillips 2001). The use of contrast-enhanced ultrasound for characterization of lesions, in the kidney (Setola et al 2007), prostate (Fillon 2013), breast (Sirsi et al 2012, Maresca et al 2014), sentinel lymph nodes in breast cancer (Sever et al 2011), and pancreas (D’Onofrio et al 2012), has been demonstrated clinically with varying degrees of success. Acoustic angiography (AA) is a novel contrast-enhanced ultrasound imaging technique relying on superharmonic imaging of microbubbles that enables the 3D mapping of micro-vascular networks with a resolution of 100–200 microns (Gessner et al 2013, Lindsey et al 2014, Shelton et al 2015, 2016). In preclinical studies, it has been shown that AA is able to differentiate tumors as small as 2–3 mm from healthy tissue (Shelton et al 2015), differentiate different tumor types based on their vascularity (Dunleavey et al 2014), and detect earlier response to radiation therapy (Kasoji et al 2018). Further clinical translation for the characterization of breast lesions is ongoing (Shelton et al 2017). However, AA does not directly provide quantitative information on the micro-architecture of vascular networks, which has to be obtained via intensive offline image processing.

In the present paper, we propose an ultrasound contrast technique exploiting the diffusive properties of microbubbles circulating in angiogenic networks, to quantify the density and anisotropy of vessels. The diffusivity of ultrasound waves in a heterogeneous medium is related to the scattering power of the scatterers, as well as the density of scatterers. The diffusion constant (D) indicates the rate at which the wave diffusive halo grows in the diffusive regime. We hypothesize that measuring the diffusion constant in vessels populated with microbubbles enables the quantification of vessel density. Numerous studies have recently been conducted, quantifying parameters related to the diffusivity, such as the diffusion constant and transport mean free path, to characterize the micro-architecture of heterogeneous media (Tourin et al 2000, Derode et al 2005, Aubry and Derode 2007, 2011, Aubry et al 2008). In particular, this has been successfully exploited in bone and the lung (Du et al 2017, Mohanty et al 2017), which are both highly scattering media with highly porous structures. This makes them ideal environments for architectural quantification using diffusion parameters, an approach previously explored by Page et al (1997, 1999) and Zhang et al (1999) and further advanced by Aubry et al (Aubry and Derode 2007). It was observed that the diffusion constant was significantly different between control and edematous (fluid-filled) lungs, enabling differentiation of the two tissues (Mohanty et al 2017). This difference in diffusivity was attributed to the reduced air content of lungs in rats suffering from edema, leading to reduced scatterer density. The diffusion constant has also been used to quantify trabecular bone density and structural anisotropy (Du et al 2017).

In the present study, microbubbles are used as scatterers. Due to multiple scattering by the microbubbles, the wave travels longer and more complex paths in the vessel network. This negatively affects imaging, but is an opportunity for the wave to extract additional information from the structure. In conventional ultrasound imaging, these multiple scattered signals are commonly treated as aberration or noise. We propose to exploit them instead, to obtain quantitative information on the microstructure of angiogenesis. By isolating the incoherent contribution to the backscattered intensity, it is possible to measure the diffusion constant, which is an indicator of the density of scatterers.

We demonstrate that the diffusion constant in microbubble populations, can be used to characterize the density and anisotropy of vascular networks. In a rodent study in vivo, we show that there are significant differences in the diffusion constant measured in fibrosarcoma tumors (N = 16) versus in the healthy tissue in the contralateral flank of the animals (N = 18). To quantify the anisotropy, we measure the diffusion constant along two perpendicular orientations of transducer placement on each rat.

Methodology

Materials

Microbubble contrast agent preparation

Microbubble contrast agents were prepared following a previously published protocol (Shelton et al 2015) by combining 1,2-distearoyl-sn-glycero-3-phosphocholine (DSPC) and 1,2-distearoyl-sn-glycero-3-phosphoethanolamine-N-[methoxy (polyethylene glycol)2000] (DSPE-PEG2000) (Avanti Polar Lipids; Alabaster, AL, USA) in a 9:1 molar ratio. Lipids were dissolved in phosphate-buffered saline containing 15% (v/v) propylene glycol and 5% (v/v) glycerol for a final lipid concentration of 1.0 mg ml⁻¹. 1.5 ml aliquots of the resulting solution were then added to 3 ml glass vials. The air in the headspace of each vial was then exchanged with decafluorobutane (DFB) gas (FluoroMed; Round Rock, TX, USA). Microbubbles were formed by 45 s of mechanical agitation in a Vialmix (Lantheus Medical Imaging; North Billerica, MA, USA).

In vivo experiments

A total of 18 Female Fischer-344 rats (Charles River Laboratories, Inc.; Wilmington, MA, USA) were used in this study (approx. 180 g, 12–16 weeks old). The animals were handled according to National Institute of Health guidelines, and the study protocol was approved by the UNC Institutional Animal Care and Use Committee. Fibrosarcoma tumors were grown in the right flank of 16 animals after subcutaneous implantation of 1 mm³ tumor tissue sections from donor animals (Fix et al 2017). The left flank of all 16 animals was used as control. Two more animals, in which no tumor was implanted were also used as control.

The animals were anesthetized in an induction chamber with 5% vaporized isoflurane. A 24-gauge catheter was inserted into the animal’s tail vein for the administration of the contrast agent solution. The animal’s right flank (tumor side) and the contralateral control side were shaved, and ultrasound gel was placed between the transducer and the animal’s skin to ensure proper coupling during data acquisition. During data acquisition, the animals were placed on a heating pad, and isoflurane was maintained at 2%−2.5%. Each animal was first scanned with the Verasonics Vantage scanner to obtain the IRM for diffusivity assessment and then transferred to a Vevo 770 for B-mode and AA imaging. The size of the tumor at the time of data acquisition was estimated using the Vevo770 B-mode scanner (see Data Acquisition).

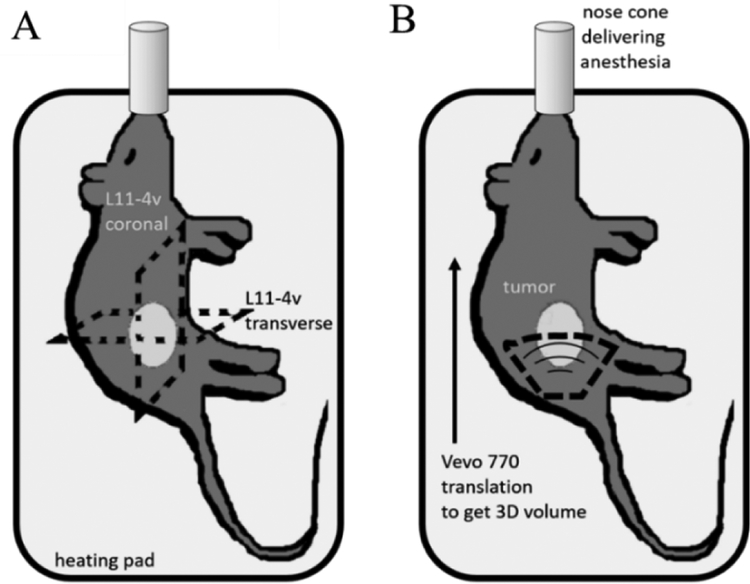
The microbubble solution was diluted with sterile saline in a ratio of 1:10 (10⁹ bubbles ml⁻¹) and 1:1 for the measurement of D and AA, respectively. The diluted microbubble solution was infused through the tail vein of each animal at a rate of 30 μl min⁻¹ using an infusion pump connected to a syringe (PHD 2000, Harvard Apparatus, Cambridge, MA,USA) (Gessner et al 2012) during data acquisition. We estimate the microbubble concentration to be around 5 × 10⁷. microbubbles ml⁻¹ for the in vivo experiments, assuming blood volume in an average rat to be approximately 20 ml for female and 30 ml for male (Lee and Blaufox 1985). It should be noted that the microbubbles were not continuously mixed in the syringe, which might have reduced the supplied bubbles. Multiple scattering acquisitions were acquired with a L11–4v transducer, placed in two perpendicular orientations (transverse and coronal) across the tumor on tumor-bearing sides (n = 16), as shown on figure 1(A). Control data was also acquired in two orientations on the contralateral control side, and on animals without tumors (n = 18). Measurements on the tumor-free, control flanks were obtained in the same anatomical region as the tumor implants. We ensured that these two planes approximately passed through the center of the tumor (largest cross-section) using B-mode imaging. Then, AA scans of both the tumor and contralateral sides were acquired as described below in the Data Acquisition section.

Figure 1.

Schematic of the experimental setup used for in vivo imaging, showing the orientations of (A) the two perpendicular planes acquired using the Verasonics for the inter-element response matrix (IRM) and (B) the B-mode and AA volumetric acquisitions using the Vevo 770.

Data acquisition

Inter-element response matrix (IRM)

A Verasonics L11–4v linear array transducer connected to a Verasonics 128 Vantage scanner (Verasonics, Inc.; Kirkland, WA, USA) operating at 7.8 MHz was used to acquire the IRM. The IRM is a 3D matrix containing the backscattered signals recorded over the entire array for signals transmitted consecutively by individual elements of the array (Aubry and Derode 2007, 2011, Aubry et al 2008, Du et al 2017, Mohanty et al 2017). All 128 elements of the array were sequentially used to transmit a two cycle Gaussian pulse with peak-to-peak pressure equal to 300 kPa. For each transmit event, all 128 elements recorded backscattered echoes simultaneously for 50 μs. The IRM was recorded using a samplingfrequency of 62.5 MHz. The acquired IRM has dimensions128 × 128 × 3125, where 3125 is the number of time points.

Acoustic angiography (AA)

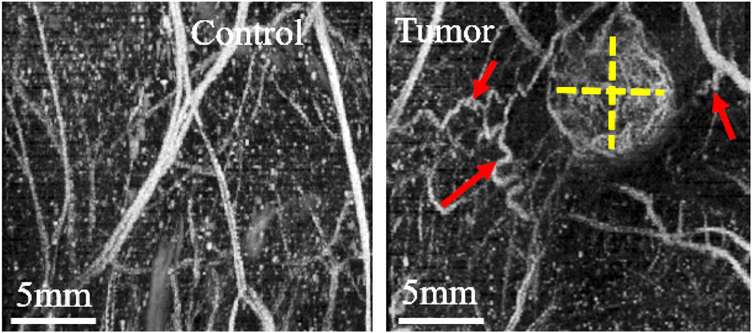
Volumetric B-mode and acoustic angiography (AA) images were acquired on a Vevo 770 scanner (VisualSonics; Toronto, ON, CA) by translating the probe in one dimension, as shown in figure 1(B). Tumor volume was calculated from B-mode as the ellipsoidal volume from sagittal and transverse planes of the largest tumor crosssection. AA was successfully acquired for 13/18 control and 14/16 tumor-bearing rats (due to our protocol’s cumulative anesthesia time constraint or probe unavailability at the end of the study, data was not acquired for all animals) using a modified 30 MHz single-element transducer (RMV 707, VisualSonics; Toronto, ON, CA) to which an added confocal 4 MHz annular element. Contrast images were acquired by transmitting with the low frequency element and receiving broadband superharmonic signals with the high frequency element during a continuous infusion of microbubbles, which were administered through the tail vein at a rate of 1.5 × 10⁸ microbubbles min⁻¹. 3D images were acquired with a step size of 100 μm, averaging two frames in every location, at a frame rate of 4 frames per second (Gessner et al 2013, Shelton et al 2015, 2016). The 3D data was then resampled to a uniform step size of 50 μm to obtain isotropic voxels. Figure 2 displays examples of sagittal maximum intensity projections (MIPs) for a control and tumor case, providing a 2D projection of the 3D volumetric data.

Figure 2.

Example of AA maximum intensity projections of control (left) and tumor-bearing regions (right, tumor size denoted with dashed yellow lines) in a rat fibrosarcoma model. Angiogenesis is clearly seen in the form of tortuous vessels (red arrows) around the periphery of the tumor and high vascular density (VD) in the tumor (more enhanced due to higher contrast agent perfusion). In contrast, control vasculature is generally more linear and directional, as shown.

Data processing

Diffusion constant measurements

The IRM data acquired using the Verasonics was processed to extract the diffusion constant. A time shift was applied to all backscattered signals in the IRM along the time dimension such that the arrival of the first backscattered echo occurs at time t = 0 for all emitter–receiver pairs. This allowed to compensate for differences in emitter-receiver distances. Each time signal of the IRM (denoted as the matrix H) can be represented by h_ij(t), where i is the emitter number and j the receiver number. The signal is then divided into overlapping time windows (each 0.5 js long with 50% overlap). The backscattered intensity I_ij(T) is calculated over each time window, where T is the time at the center of the time window, and Δ. is the width of the time window. The width of the time window was chosen based on the central frequency, such that it spans over 1 to 2 wavelengths (Tourin et al 2000, Aubry and Derode 2007, Aubry et al 2008).

$$I_{ij}(T)={\int }_{t_0(T)}^{t_0(T)+\mathrm{\Delta }}{h}_{ij}^2(t)dt$$ (1)

The average backscattered intensity I (r, T) .was calculated by averaging the backscattered intensity over transducer-receiver couples separated by the same distance (r = |i − j| × w).. Here, w is the pitch of the transducer array (w = 0.3 mm). In order to separate the coherent and incoherent contributions to the intensity, the H matrix was transformed into an antisymmetric matrix M, such that

• m_ij = h_ij for i < j,

• m_ij = −h_ij for i > j

• m_ij = 0 for i = j.

The backscattered intensity $I_{ij}^A(T)$. and the averaged backscattered intensity I^A. (r, T) was then calculated from the antisymmetric matrix following a similar procedure. The coherent I_coherent (r, T) . and incoherent I_incoherent (r, T) .intensities were extracted by respectively adding or subtracting the intensities resulting from the matrices H and M (Aubry and Derode 2007).

$$I_{\mathit{\text{coherent}}}(r,T)=\frac{I(r,T)-I^A(r,T)}{2}$$ (2)

$$I_{\mathit{\text{incoherent}}}(r,T)=\frac{I(r,T)+I^A(r,T)}{2}.$$ (3)

In the diffusive regime, the incoherent intensity can be expressed as a function of the diffusion constant, D:

$$I_{\mathit{\text{inoherent}}}(r,T)=I(T)\times \text{exp}\left(-\frac{r^2}{4DT}\right).$$ (4)

The diffusion constant was then calculated by fitting a Gaussian curve to the incoherent intensity I_inc (r, T) for multiple consecutive time windows. The variance of these Gaussian curves is plotted against time and the slope of the linear trend enables us to calculate the D. An inclusion criteria of R-squared > 0.4 was set for obtaining the D. Once the D values were obtained for the two orientations of the probe, the anisotropy ratio was calculated by taking the ratio of D along the transverse plane and coronal planes.

Vascular density (VD)

The VD corresponding to the planes used in the IRM acquisitions was calculated from AA data. This was done by following the same method as in previously published work from AA post-processing (Dunleavey et al 2014, Shelton et al 2015, Kasoji et al 2018), for regions of the data corresponding to the IRM acquisitions. In order to extract sub-volumes of AA data approximately registered to the planes of IRM data, the coordinates of the center of the tumor on the sagittal plane were used to determine the center planes used in the coronal and transverse sub-volumes. Since the animal had to be repositioned between imaging systems and different transducers used, this gives an approximate matching and should not be interpreted as being the exact same planes as used for IRM. Regions of interest (ROIs) were defined for both the coronal and transverse planes acquired as illustrated in figure 1(A). The plane thickness for each sub-volume was taken as the elevational aperture of the L11–4v (5 mm) in order to mimic the slice thickness that would correspond to the IRM acquisitions. For each sub-volume ROI corresponding to the IRM acquisition planes, the VD was calculated as the ratio of voxels above the thresholding value chosen obtained using Otsu’s method (Otsu 1979, Kasoji et al 2018), for regions of the data corresponding to the IRM acquisitions.

Data analysis and statistical methods

The diffusion constant was calculated from IRM acquisitions for both orientations in tumors and controls, and the anisotropy ratio was defined as the ratio of these values. Differences between D values obtained from control coronal plane, control transverse plane, tumor coronal plane, and tumor transverse plane were tested using the Kruskal–Wallis test with Dunn’s post-test (data was not normally distributed, so non-parametric analysis was chosen). The anisotropy ratio was also compared between tumors and controls using a Wilcoxon–Mann–Whitney test (non-normal distribution).

To confirm the hypothesis that the VD (calculated from AA sub-volumes corresponding to the IRM acquisition slices) of tumors was higher than that of controls, in both coronal and transverse orientations, a one-tailed t-test was used after confirming normality with a Kolmogorov–Smirnov test.

All data are presented as mean ± standard deviation. Statistical significance was set a priori at p < 0.05 and is graphically depicted on all figures as (*) for p < 0.05, (**) for p < 0.01 and (***) for p < 0.001, as well as (NS) to denote non-statistically-significant comparisons. Statistics were performed on GraphPad Prism version 5.01 (GraphPad Software; San Diego, California, USA).

Results

Diffusion constant and anisotropy ratio (in vivo experiments)

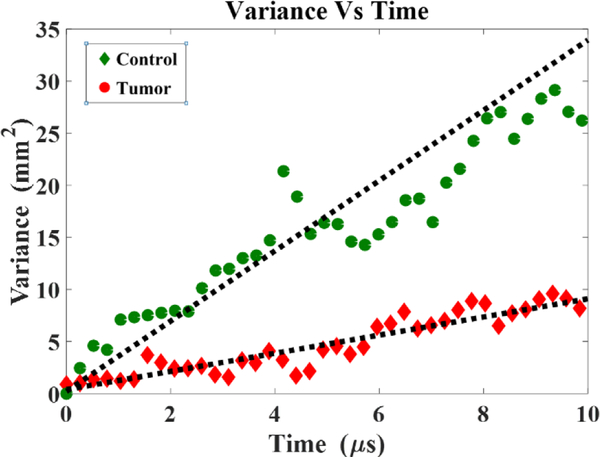
For the 16 tumor-bearing rats, the mean tumor diameter was 7.8 ± 3.4 mm, and the mean tumor volume was 360 ± 508 mm³ (range 50.9 mm³ to 2349.7 mm³). The diffusion Constant is extracted from the time evolution of the backscattered intensity as described in the methodology section. The variance of the Gaussian fit is plotted with time as shown in figure 3. These plots of the variance time-evolution are fitted with a linear model to obtain the slope, which is equal to twice the Diffusion Constant. For the tumor case, it can be clearly seen that the variance grows much more slowly than in the control μm case.

Figure 3.

Comparison of variance time evolution data for a Control and tumor case (Indicative of overall trend).

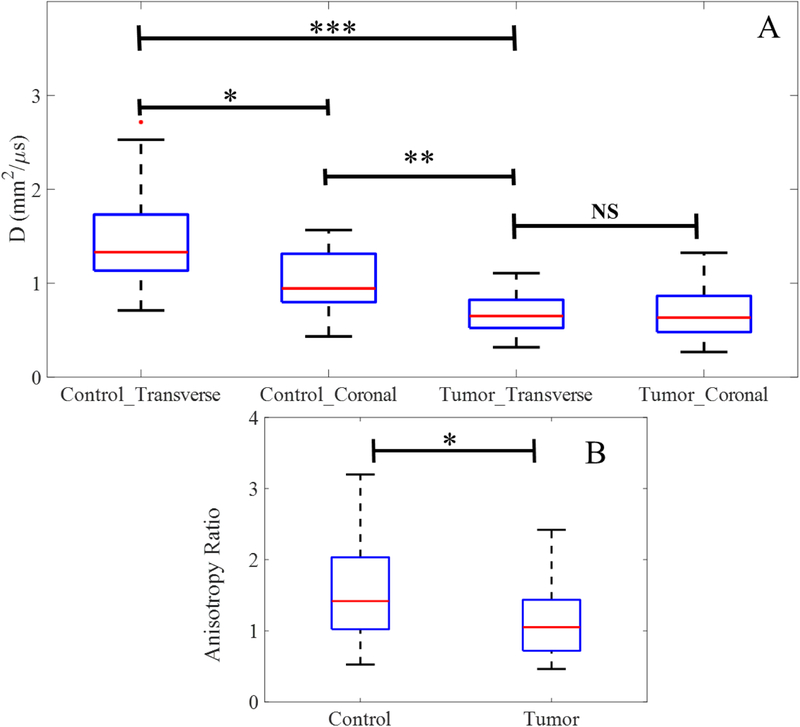
Figure 4(A) shows the D values obtained for both orientations for control and tumor flanks (n_control = 18; n_tumor = 16). Significant differences were observed for D values obtained in the transverse and coronal orientations for control regions (transverse: 1.61 ± 0.51 mm² μs⁻¹, coronal: 1.05 ± 0.31 mm² μs⁻¹, p < 0.05). However, for tumors, there was no significant difference along the two orientations (transverse: 0.67 ± 0.22 mm² μs⁻¹, coronal: 0.61 ± 0.28 mm² μs⁻¹, p > 0.05). The D values for control and tumor, combining both orientations, were found to be 1.38 ± 0.51 mm² μs⁻¹ and 0.65 ± 0.27 mm² μs⁻¹, respectively. The anisotropy ratio of control and tumor regions are compared in figure 4(B). The closer the anisotropy ratio is to one, the higher the isotropy of the tissue’s vascular network. It is evident that control tissue exhibits significantly higher anisotropy ratios than tumor-bearing tissue, with ratios of 1.62 ± 0.91 versus 1.13 ± 0.51, respectively (p < 0.05).

Figure 4.

(A) Comparison of the diffusion constant D measured along both perpendicular orientations for control and tumor, (B) and the resulting anisotropy ratios of the averaged D values.

Vascular density (VD)

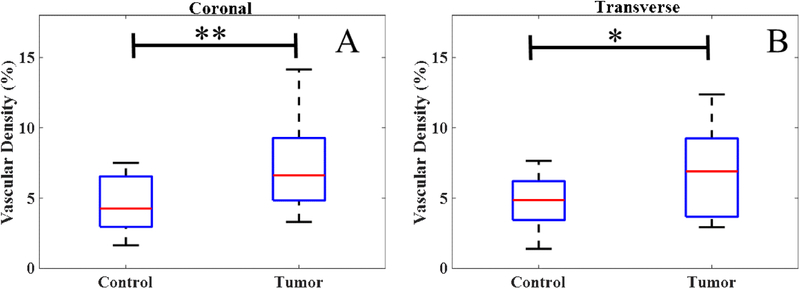
In both the coronal and transverse slices corresponding to the IRM acquisitions, the VD obtained from AA were significantly higher in tumors (n = 14) compared to controls (n = 13), as shown in figure 5. The VD for control in the transverse and coronal plane was observed to be 4.82% ± 1.87% and 4.71% ± 1.96%. Whereas, the VD for tumor in the transverse and coronal plane was observed to be 7.21% ± 3.05% and 6.59% ± 3.04%.

Figure 5.

VD was found significantly higher for tumors compared to controls, in both the coronal (A) and transverse (B) slices corresponding to the IRM acquisitions.

Discussion

We have demonstrated that the nominal values of both the diffusion constant, D, and the anisotropy of D measured using ultrasound multiple scattering by microbubbles are significantly different between tumor-bearing and control tissue in vivo. For in vivo cases, D can indeed be thought of as an indirect measure of the microvascular density. When D is measured along two different orientations and compared, it has the ability to indicate the extent of vessel anisotropy.

From the diffusion constant values, we can deduce that the degree of isotropy is much higher in tumor-bearing tissue than in control tissue. This is expected, since normal vasculature is arranged in a hierarchy of evenly spaced, directional and well-differentiated arteries, arterioles, capillaries, venules and veins, whereas in tumor proliferation, angiogenesis leads to multi-directional, chaotic and disorganized vasculature (Nagy et al 2009). Tumor-bearing tissue exhibits relatively low variability in diffusivity, and the anisotropy ratios obtained from diffusivity measurements were significantly higher in control tissue, depicting a preferred orientation of vessel growth. Comparisons between diffusion constant values and VD measurements from AA data (shown in figure 5) also support the hypothesis that diffusion constant measurements are reflective of the underlying VD of the tissue. Higher VD values for tumor-bearing tissue support the assumption that tumor vascular networks are indeed more random and have higher density.

Although the difference between the D Values for the two types of tissue (healthy and tumor) is significant, there is variability in the Diffusion Constants measured amongst individual rats is high, leading to relatively large error bars. Larger error bars are observed for control cases. This is probably due to the fact that very few vessels were captured in the healthy tissue. On the contrary, for tumor tissue, tighter error margins are observed, which may signify the homogeneity of tumor from rat to rat and within one rat for multiple readings.

The main limitation of the proposed approach is that it does not allow a local estimation of the diffusivity of the complex microbubble filled medium. The diffusion constant indicates the rate at which the wave diffuses in a scattering medium. By nature, it is a parameter that reflects multiple scattering events and diffusion through a region of interest larger than the wavelength. To obtain the Diffusion Constant, both spatial and time averaging need to be performed. Therefore, D is an quantitative parameter that reflects the vessel density of the region of interest on average. The tumor dimensions in the in vivo experiments (approx. <10 mm) are less than the length of the transducer (35 mm). Consequently, the D values measured in tumor tissue reflect a VD intermediate between the actual vessel density of tumor, and the vessel density of control tissue. Variations in tumor size might have negatively affected the value of D. for smaller tumors, the D values might have been underestimated, when averaged with values in neighboring healthy tissue. However, no correlation was found between D and tumor size. The diffusion constant for tumor cases still shows significant difference from control cases, even with this spatial averaging. This may mean that the actual diffusion constant for tumor cases would be lower when we do not account for non-tumor regions. In the future, one could combining the measurement of D to conventional ultrasound imaging and use a subset of ultrasound array elements in order to conduct localized measurement of D (Mohanty et al 2018). However, if too few elements are used, the number of points representing the incoherent backscattered intensity would be reduced, which might affect the accuracy of the Gaussian fits and a lead distorted linear variance trend. This will be the subject of future studies.

The wavelength chosen will influence the time window over which the time-dependent intensity is calculated (the time window is chosen to ensure that most windows contain a scattering event). The nonlinearity of the microbubbles is not fully exploited in the present work, but exploiting the harmonic response in the context of diffusion will be the focus of subsequent studies.

Super-resolution techniques allow imaging of angiogenic networks with outstanding spatial resolution (Errico et al 2015, Lin et al 2017). However, extracting quantitative parameters from these images requires heavy off-line post-processing. 3D ultrafast doppler tomography (UFD-T) has shown promise during preliminary studies (Alcázar 2006, Provost et al 2015) but acquisition times are currently too slow for clinical use and can take up to an hour. Although the present method does not achieve super-resolution, we propose it as an alternative that does not require any image processing, and can be used in near real-time, maybe in combination with conventional B-mode imaging, to improve the specificity of ultrasound for cancer diagnosis.

A great advantage of the measurement of the Diffusion Constant is that the information extracted is quantitative and is expected to correspond to the vessel density of individual animals. This will be tested in future studies. Combining images obtained with other contrast-enhanced imaging methods, such as AA or conventional B-mode ultrasound, with the diffusion constant and estimation of the anisotropy would provide a comprehensive set of data that has the potential to improve the specificity of ultrasound diagnosis. This combined approach could be used in the future for monitoring the response to anti-angiogenic treatments.

Conclusion

The use of microbubbles promotes multiple scattering. Multiple-scattered waves take long paths in the microstructure, and their complex backscattered signal contains information about the density and orientation of the vasculature. By extracting the incoherent backscattered contribution from the total backscattered intensity, it is possible to obtain the diffusion constant, which is a good metric of the diffusivity of the medium, i.e. the rate at which the incoherent contribution to the signal diffuses in a complex medium. In this study, we show that the diffusion constant enables the quantitatively characterization of blood vessel network, and is are related to vessel density. Significant differences are observed between control (D = 1.38 ± 0.51 mm² μs⁻¹) and tumor-bearing (D = 0.65 ± 0.27 mm² μs⁻¹) tissues. In addition to vessel density, the diffusion constant also allows characterize the existence of anisotropy in control blood vessels (1.62 ± 0.91) and confirm that tumor blood vessels (1.13 ± 0.51) are more isotropic. This approach could be utilized to non-invasively assess and quantify the microvasculature.