Abstract
Thrombin is an attractive target for antithrombotic therapy due to its central role in thrombosis and hemostasis as well as its role in inducing tumor growth, metastasis, and tumor invasion. The thrombin-binding DNA aptamer (TBA), is under investigation for anticoagulant drugs. Although aptamer binding experiments have been revealed various effects on thrombin’s enzymatic activities, the detailed picture of the thrombin’s allostery from TBA binding is still unclear. To investigate thrombin’s response to the aptamer-binding at the molecular level, we compare the mechanical properties and free energy landscapes of the free and aptamer-bound thrombin using microsecond-scale all-atom GPU-based molecular dynamics simulations. Our calculations on residue fluctuations and coupling illustrate the allosteric effects of aptamer-binding at the atomic level, highlighting the exosite II, 60s, γ and the sodium loops, and the alpha helix region in the light chains involved in the allosteric changes. This level of details clarifies the mechanisms of previous experimentally demonstrated phenomena, and provides a prediction of the reduced autolysis rate after aptamer-binding. The shifts in thrombin’s ensemble of conformations and free energy surfaces after aptamer-binding demonstrate that the presence of bound-aptamer restricts the conformational freedom of thrombin suggesting that conformational selection, i.e. generalized allostery, is the dominant mechanism of thrombin-aptamer binding. The profound perturbation on thrombin’s mechanical and thermodynamic properties due to the aptamer-binding, which was revealed comprehensively as a generalized allostery in this work, may be exploited in further drug discovery and development.
Keywords: thrombin, aptamer, generalized allostery, molecular dynamics, molecular recognition
Introduction
Abnormal blood coagulation is associated with conditions that cause numerous deaths throughout the world (Article, Steering, For, & Thrombosis, 2014; van der Spuy & Pretorius, 2012; WHO | Estimates for 2000–2012, n.d.; World Health Organization, 2014). These thromboembolic diseases are now among the principal causes of mortality in the world (Article et al., 2014), and ischemic heart disease and stroke are estimated to be the cause of 25% deaths in 2012 according to the World Health Organization (WHO | Estimates for 2000–2012, n.d.; World Health Organization, 2014). Thrombin is a key coagulation protein and serine protease that catalyzes many coagulation-related reactions (Crawley, Zanardelli, Chion, & Lane, 2007). Moreover, thrombin is also critical to the development of tumors and inducing invasion and metastasis in a variety of cancers (Nierodzik & Karpatkin, 2006; Radjabi et al., 2008). As such, understanding the molecular function of this protein and how it interacts with different binders, including existing potential therapeutics, can aid in developing further treatments against cancers and diseases associated with abnormal blood coagulation.
Blood coagulation, which leads to the formation of blood clots, is a complex process essential to hemostasis, i.e. arresting the bleeding from damaged blood vessels (Tanaka, Key, & Levy, 2009). Thrombin – as a multifunctional serine protease – performs a variety of functions during this process. Thrombin cleaves soluble fibrinogen into insoluble fibrin (Blombäck, Hessel, Hogg, & Therkildsen, 1978; Crawley et al., 2007), and activates fibrin stabilizing factor XIII (Takagi & Doolittle, 1974) and protease-activated receptors (Coughlin, 2000), which are necessary steps in forming a mesh of fibrin that eventually leads to formation of a blood clot. Thrombin is also involved in regulating the complex coagulation cascades via both positive and negative feedback (Adams & Huntington, 2006; Bajzar, Morser, & Nesheim, 1996; Di Cera, 2008). Because of its critical role of thrombin in clot formation, which is necessary for hemostasis, thrombin is an attractive target for antithrombotic therapy (Erdmann, 2010; Melnikova, 2009; Tanaka et al., 2009). Thrombin’s role in inducing tumor growth and metastasis makes it an attractive target for chemotherapeutic development (Nierodzik & Karpatkin, 2006; Radjabi et al., 2008).
The most commonly used drug that targets thrombin, heparin, is able to bind to thrombin and antithrombin, a small protein that deactivates several enzymes in the coagulation cascade including thrombin, at the same time and form an antithrombin-thrombin complex (Baglin, Carrell, Church, Esmon, & Huntington, 2002; Li, Johnson, Esmon, & Huntington, 2004). However, heparin has the potential to invoke multiple dangerous side-effects such as spontaneous hemorrhage, reduction of blood platelets, or allergic reactions (Nelson-Piercy, 1997). Other forms of therapy are in need. Short oligonucleotides – known as aptamers – are drawing more attentions in drug discovery in general. They are potentially useful in avoiding such side-effects, and are also small in size, non-immunogenic, and easy to synthesize (Keefe, Pai, & Ellington, 2010; Li et al., 2014; Ni, Castanares, Mukherjee, & Lupold, 2011; Opalinska & Gewirtz, 2002). Such a single-stranded DNA aptamer with the sequence 5′-GGTTGGTGTGGTTGG-3′ (15-Thrombin-Binding-Aptamer (15-TBA)) has good experimentally demonstrated binding (34 nM) and inhibition of human thrombin with short in vivo half-life (~2 min), which provides a benefit in fast and reversible treatment.
There are a variety of experimental studies on 15-TBA and other ligands that provide structural information and also suggest that thrombin may exhibit allosteric regulation. These studies provide the necessary inputs into molecular dynamics (MD) simulations and provide a basis for asking what the details of thrombin-15-TBA interactions are. They also suggest an allosteric response – either classical or generalized – may be involved and probe the nature of any mechanical couplings within the protein. Crystallographic studies reveal that this 15-TBA binds thrombin at the fibrinogen binding site (exosite I, as shown in Figure 1(A)) and thereby inhibit thrombin’s cleavage of fibrinogen (Padmanabhan, Padmanabhan, Ferrara, Sadler, & Tulinsky, 1993; Padmanabhan & Tulinsky, 1996; Russo Krauss et al., 2012). In addition, simultaneous binding of this 15-TBA and an RNA aptamer at exosite II (Figure 1(A)) inhibit thrombin-dependent platelet activation and procoagulant activity synergistically (Nimjee et al., 2009). That is the aptamer-binding at one of these two exosites enhances the inhibitory effect of the other aptamer at the other site. Some experiments show the affinities of ligands at these distant sites are not affected by the simultaneous ligand-binding (Colwell et al., 1998; Verhamme, Olson, Tollefsen, & Bock, 2002). However, other experimental studies demonstrate that several peptide ligands at these spatially distinct sites – exosites I and II – establish mutually exclusive binding, indicating allosteric effects (Fredenburgh, Stafford, & Weitz, 1997; Liaw et al., 1998; Petrera et al., 2009). Consequently, although thrombin has been known as an allosteric enzyme for decades, the debates on the crosstalk observed in experiments among thrombin’s functional sites, such as exosite I and II along with the active site, are not settled yet. Circular dichroism and intrinsic fluorescence spectra indicate the binding of 15-TBA does not alter thrombin’s secondary structure, but it does cause a conformational change in thrombin’s tertiary structure (Zhou, Huang, & Qu, 2010). However, how these conformational changes correlate with the functional changes is still not clear. These various experiments provide further evidence that a more detailed understanding of the thrombin’s response to binding is required and triggered our interest in studying the aptamer-thrombin complex.
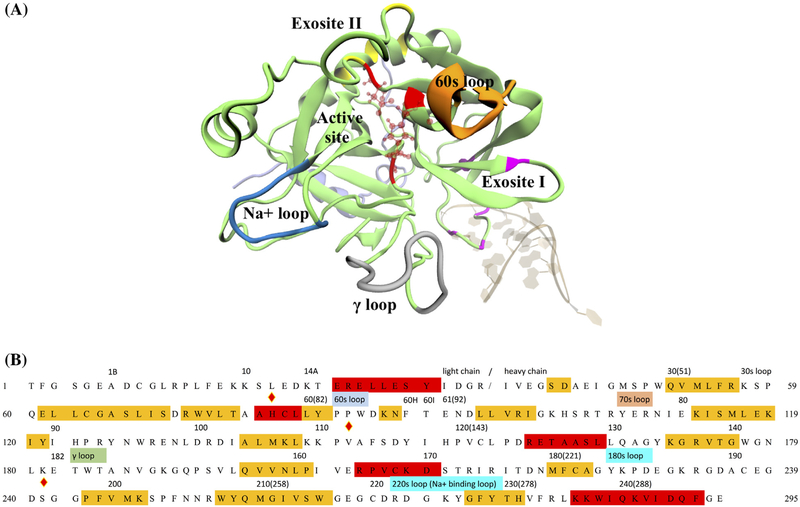
Figure 1.
Human α-thrombin and its functional sites. (A) Tertiary structure of thrombin in PDB 4DII was showed in cartoon representation. The light and heavy chains were respectively colored in light violet and lime. Several known function sites were indicated by the colors and nearby labels. The thrombin-binding aptamer in the same PDB was shown in NewRibbons representation. (B) Sequence of human α-thrombin was listed in one-letter amino acid code. The residue indices in the original PDB file and positions of several function sites were labeled above the sequence. Residues under the red and yellow stand for alpha helix and beta sheet regions. The catalytic triad was marked by the diamond signs above the letter. For the convenience of counting, a new residue number was assigned to each residue as labeled in the beginnings and ends of each row of sequence and the numbers in the parentheses.
Our primary question under investigation is which model best explains the mechanisms for thrombin’s recognition of 15-TBA; an induced-fit model or conformational selection-i.e. generalized allostery (Bosshard, 2001; Changeux & Edelstein, 2011; Motlagh, Wrabl, Li, & Hilser, 2014; Tsai & Nussinov, 2014). In the induced-fit model, the substrate causes appreciable conformational changes to adapt the substrate binding (Bosshard, 2001; Changeux & Edelstein, 2011). As such a case, we would expect pronounced changes to occur in the conformational free energy landscapes of thrombin after aptamer-binding. In the generalized allostery model, the optimal conformation for the binding events is selected from conformations of unbound thrombin (Motlagh et al., 2014; Tsai & Nussinov, 2014). Hence, we would expect more overlap of wells on conformational free energy surface, albeit with different depths, corresponding to different populations. The second question we seek to understand is how the aptamer-binding lead to an influence on the functional activities at the other sites, which may shed light on relevant macroscopic changes in above-mentioned experimental studies.
MD simulations have proven useful in studying the thermodynamic properties of biomolecules in atomic detail and revealing dynamic pictures of allosteric communications (Knaggs, Salsbury, Edgell, & Fetrow, 2007; Negureanu & Salsbury, 2012; Salsbury, Yuan, Knaggs, Poole, & Fetrow, 2012; Yuan, Knaggs, Poole, Fetrow, & Salsbury, 2010). Moreover, this computational technique provides predictive complement to experiments and benefits drug discovery (Negureanu & Salsbury, 2014; Salsbury, 2010; Salsbury, Crowder, Kingsmore, & Huntley, 2009; Vasilyeva et al., 2009). Starting from the static structures determined by experiments, atom coordinates of molecules in the biological system are updated in the MD simulations according to classical mechanics with empirical force fields with optimized parameters for biological molecules (Brooks et al., 2009; Salomon-Ferrer, Case, & Walker, 2013). The dynamic pictures of the biological system of interest are then illustrated. Quantitative analysis on the conformational ensembles of the molecules during the course of the simulations further reveals the thermodynamic properties of the biological system (Godwin, Melvin, & Salsbury, 2015; McCammon, Gelin, & Karplus, 1977). In the present work, we present a computational study using MD simulations to investigate the differences in mechanical and thermodynamic properties between the isolated thrombin (denoted as aptamer-unbound or free thrombin in the following sections) and the thrombin in complex with 15-TBA (denoted as aptamer-bound thrombin), which aims to reveal thrombin’s response to the binding of 15-TBA at exosite I (referred as aptamer-binding) and offer an insight into details of thrombin’s allostery at the atomic level.
Materials and methods
Simulation system
To study the thrombin’s response to the aptamer-binding, two types of simulations were performed. The simulations of aptamer-bound thrombin reproduce the structural ensemble of the thrombin, which is perturbed by the aptamer bound. The simulations of aptamer-unbound thrombin provide insights into intrinsic thermodynamic properties of the thrombin. We aimed to understand the effects of 15-TBA on by comparing simulations of both bound and free thrombin.
The high-resolution crystal structures of the TBA-thrombin complex in potassium and sodium buffer conditions were solved by Russo Krauss et al., 2012 and are found in the RCSB PDB with IDs 4DII and 4DIH, respectively. Russo Krauss et al’s circular dichroism measurements suggest that 15-TBA’s G-quadruplex structure is more stable in potassium environment rather than the sodium one (Russo Krauss et al., 2012). Moreover, it has been widely shown that the sodium cation binding induces significant allosteric effects on thrombin’s activity (Huntington, 2008). As the goal of this study is to reveal the effects of aptamer-binding, a potassium environment was created in silico. Therefore, in the first type of simulations, the thrombin-aptamer complex structure was extracted from PDB 4DII. The centered potassium ion was also kept to stabilize the aptamer. In the second type of simulations, instead of utilizing other available PDBs containing coordinates of aptamer-unbound thrombin (in fact most of these PDBs contains other ligands with biological functions), we used the same initial coordinates from the bound coordinates in the first complex system, perturbed by removal of the aptamer in the PDB 4DII. Usage of these initial coordinates avoids the interference from ligand and ion effects, which originates from different experimental conditions, particularly with respect to ergodicity of simulated systems. That is, beginning simulations from disparate coordinate sets would create a set of disconnected states in the simulations with a finite length, precluding the possibility of examining all trajectories together as one system. By starting all simulations from the same initial structure of thrombin and are under the same buffer condition, we are safer in an assumption of ergodicity of a concatenated trajectory from all systems than if each simulation had started from a unique set of coordinates; it is also more reasonable to infer that the thermodynamic and kinetic differences exhibiting by the thrombins under equal amount of microsecond-scaled sampling are ascribed to the aptamer-binding. The only PDB containing unliganded wild-type thrombin is PDB 3U69 (Figueiredo et al., 2012). However, this structure has a 6-residue-long truncate in the light chain compared with PDB 4DII. Performing root-mean-square-distance (RMSD) calculations on the alpha carbons show that the RMSD between the two structures is only 1.04 Å. Additionally, using the same PCA projection strategy as in Figure 6, we also verify (data not shown) that the conformation of this PDB is actually within the main well of the unbound thrombin.
Figure 6.
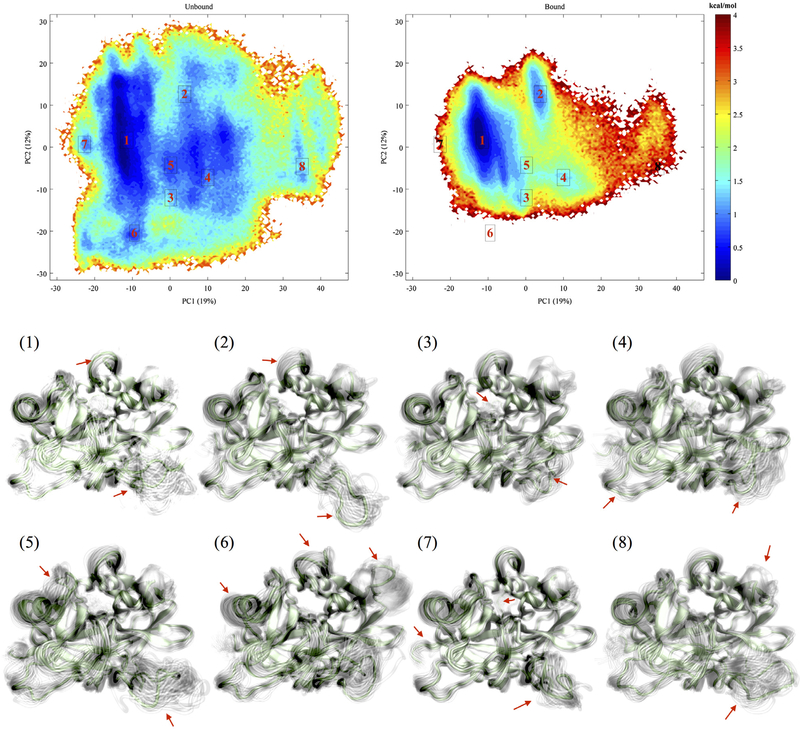
Free energy landscapes of aptamer-unbound and aptamer-bound thrombins and representative structures corresponding each labeled well.
MD simulations
Five one-microsecond-long NPT (constant particle number, temperature and pressure) MD simulations for each system, i.e. a total of 5 μs for aptamer-unbound thrombin and 5 μs for aptamer-bound thrombin respectively, were performed using the GPU-enabled ACEMD simulation package (Harvey, Giupponi, & De Fabritiis, 2009). The temperature and pressure were maintained at 300 K and 1 atm using Langevin damping (Lemons, 1997) with a damping constant of .1 and Berendsen pressure control (Berendsen, Postma, van Gunsteren, DiNola, & Haak, 1984) with a relaxation time 400 fs, respectively. As described above, the initial coordinates of the relevant molecules for the MD simulations were obtained based on the crystal structure of the thrombin-aptamer complex with PDB entry 4DII. The initial coordinates of the 18 out of 295 missing residues in the protein were modeled via the structural template-based atom fill-in tool Modeller (Šali & Blundell, 1993) and the missing hydrogen atoms were added by VMD’s psfgen package (Humphrey, Dalke, & Schulten, 1996) using default parameters. All histidine residues were assigned delta protonation. An explicit TIP3P (Jorgensen, Chandrasekhar, Madura, Impey, & Klein, 1983) water box with a 10 Å padding in all directions around the surface of thrombin, aptamer or their complex was added to mimic the aqueous environment. The system was neutralized with K+ in the form of .125mol/L- a typical experimental salt concentration in vivo. As the aptamer’s G-quadruplex structure requires a K+ ion to remain stable, the K+ ion at the center of the aptamer was initially added according to its coordinates in the PDB for the simulations with the aptamer. All simulations were performed with the CHARMM27 force field (Brooks et al., 2009). The cut-off radius of the van der Waals potential was set as 9 Å and a long-range electrostatics was calculated using a particle mesh Ewald implementation (Darden, York, & Pedersen, 1993; Harvey & De Fabritiis, 2009) with 72 evenly spaced grid points in each direction. The time step was set to 4 fs as a hydrogen mass repartitioning scheme (Feenstra, Hess, & Berendsen, 1999) was used. Bonds involving hydrogen atoms were constrained using the SHAKE algorithm (van Gunsteren & Berendsen, 1977). Each simulation was minimized using conjugate gradient minimization for 1000 steps.
Root-mean-square fluctuation and correlated motions
Root-mean-square fluctuation (RMSF) describes how far away biomolecules move from a reference in time average. In this study, alpha carbons in 500,000 conformations of aptamer-bound and aptamer-unbound thrombin in the MD simulations were picked to compute the RMSF using the following equation
| (1) |
where is the position vector of alpha carbon in residue i at frame t, is the atom’s position in the average structure over the total number of T conformations.
Correlated motion can be investigated by a covariance matrix or the normalized correlation matrix, whose elements are respectively defined as
| (2) |
| (3) |
where T, are defined the same as corresponding ones in RMSF. In this study, the correlation matrix was chosen. The matrix element with values between −1 and +1 in the correlation matrix reflects the correlation coefficient between the motions of a pair of atom to their own average positions. A correlation coefficient approaching +1 or −1 indicate the pair of atoms are strongly coupled and they tend to fluctuate about their own average positions in the same or the opposite directions. All Cα atoms in thrombin were used in this calculation.
Clustering analysis
Clustering analysis classifies data into several groups by their features (Godwin et al., 2015). In the analysis of MD trajectories, molecular conformations are classified into different groups according to their structural similarity, which is quantified by their RMSD from each other after alignment to remove center-of-mass motion and overall molecular tumbling. This classification can provide information on how the molecular structures evolve.
In this work, the aligned trajectories are clustered using our in-house implementation (R. Melvin & Salsbury, 2016) of a quality-based clustering (Quality Threshold) algorithm (Heyer, Kruglyak, & Yooseph, 1999). The QT algorithm works as follows: First, the RMSD between each conformation was used as the clustering ‘quality’, i.e. the structural similarity. Conformations within the similarity threshold were grouped as candidate clusters. Then only the candidate cluster with maximum conformations were saved as the first cluster, and conformations within it were removed from all candidate clusters for further considerations of clustering. A similar process continued to classify clustering indices for the remaining conformations until the maximum number of clusters reached. The RMSD threshold was set at 2.3 Å through trial and error. This cutoff is the smallest value that returned clustering results with almost no singleton clusters (Figure S1). This guarantees that our clustering analysis groups most conformations in both systems. For time and memory efficiency, only alpha carbons of every 10 frames (100 ps) of structures in the MD trajectories were used to perform the clustering analysis.
Markov analysis
Since conformational states can be defined in the clustering analysis, it is possible to find the transition matrix T to quantify the stability of these macrostates and their transition pathway based on a first-order Markov State Model (MSM) (Godwin et al., 2015; Häggström, 2002).
The transition matrix can then be constructed based on the trajectories in the simulations. The matrix element Tij equals the probability of transition events from conformational state i to state j under certain time steps. Thus, we can compare how stable each state is by evaluating the likelihood a state will survive after N steps using
| (4) |
where u(N) is the probability distribution that state i ends up with after N steps and u(0) is the initial distribution with vector element as
| (5) |
This part of analysis was implemented through our in-house Markov clustering analysis scripts (Melvin, Godwin, Xiao, & Salsbury, 2015).
Principal component analysis
Principal component analysis (PCA) performs linear transformation on the data-sets with high-dimensional feature information so that the main differences among the data can be illustrated using much fewer features (Abdi & Williams, 2010). In this case, PCA is performed to determine a free energy surface for aptamer-unbound thrombin and to study how this surface changes in the perturbed system, i.e. the aptamer-bound thrombin.
As it will be suggested by other analyses, the free thrombin has a more diverse range of conformations. In order to sufficiently highlight the conformational free energy surface differences in both systems, we project thrombin’s conformations into a reduced space using the basis set from the unbound simulations. In details, the covariance matrix was calculated for the aptamer-un-bound thrombin simulations. Then the eigenvectors of the covariance matrix were calculated and acted as the complete, orthonormal basis set for the reduced space. The coordinates of each structure were projected onto the new transformed space according to
| (6) |
Here, Rxyz is a vector storing xyz coordinates of each Cα atom of thrombin in the order of (x1, y1, z1, x2, y2, z2 …), vj is jth eigenvector of the covariance matrix of the atpamer-unbound thrombin and PCj is the value of the jth principal component corresponding to the original structure. Since each Cα atom has the same mass, the principal component decomposition we did here is mathematically equivalent to the mass-weighted quasi-harmonic analysis, which is used to identify low-frequency normal modes in proteins in the quasi-harmonic approximation (Hayward, Kitao, & Go, 1994; Levy, Srinivasan, Olson, & McCammon, 1984).
As the projection is bijective, each point in the principal component space is one-to-one corresponding to each structure represented in the original coordinate system. Each principal component has its weight for the corresponding mode of fluctuations. Therefore, we are able to use a few components with large weight values to illustrate the main structural characters. After projecting each structure onto the principal component space, the free energy profiles of thrombin were generated based on the probability of each point in a specific bin, i.e. ΔG = −kBT ln (p). For convenience, principal component values were shifted consistently to make the origin represent the average structure of the aptamer-unbound thrombin. These calculations were also all performed using in-house Matlab scripts (Xiao & Salsbury, 2016).
To examine the structures at different regions on the free energy surfaces, representative structures for several low free energy regions were searched by our in-house scripts too. The frames with the minimum value of free energy within interested regions were used for the visualizing structure ensembles. The conformations that are closest to the center of bin with the minimum free energy in the specified regions were highlighted as solid in the final visualization and the other conformations were illustrated as shadows or clouds (Melvin & Salsbury, 2015, 2016). Correlation matrices for each visualized ensemble were then computed for further comparisons on these identified ensembles.
Simulation comparisons
To compare the dynamics exhibiting by each run and convergence of simulations, the atomic fluctuations along each trajectory were evaluated using RMSFs. For bound and unbound systems, the Pearson correlation coefficients of RMSFs across all five runs were computed. Moreover, to quantify the extent to which the bound and unbound systems exhibit different dynamics, we calculated the inner products of the lowest six principal components using their own basis sets. The absolute values of the inner products approach to 1 if the dynamics along corresponding principal components from the unbound and bound thrombins are similar; otherwise the inner products are close to 0.
Results
Restricted atomic fluctuations after aptamer-binding
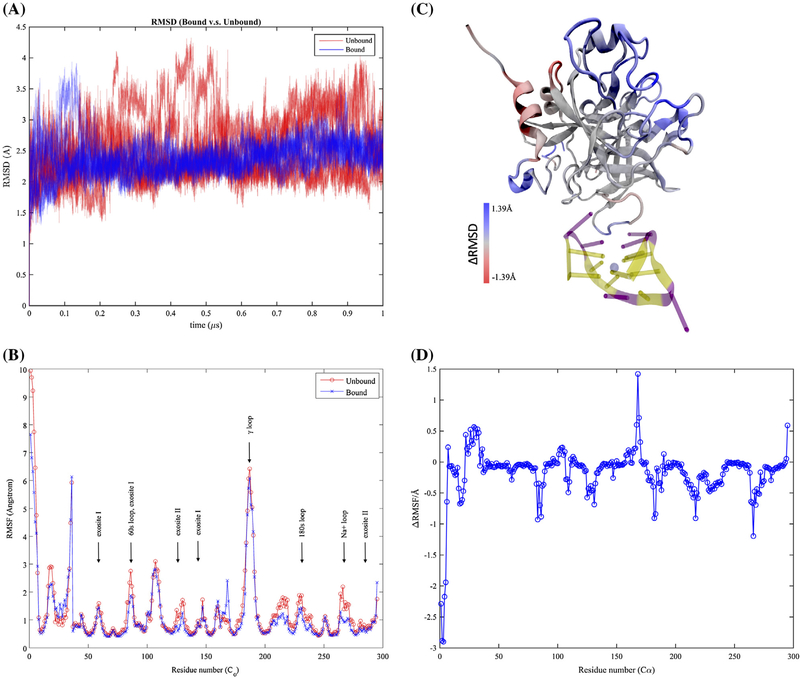
To examine the aptamer-binding effects on thrombin’s molecular properties, overall fluctuations were first evaluated using RMSD from the same initial structures. In all the simulation runs, aptamer-bound and aptamer-unbound thrombins both quickly reach equilibrium (less than 5 ns) and exhibit oscillations of RMSD around 2.4–2.5 Å in the simulations as shown in Figure 2(A). The RMSD variance range of the aptamer-bound thrombin is much smaller than the one of aptamer-unbound thrombin. This suggests thrombin has less conformational freedoms to fluctuate after aptamer-binding, which can be characterized more precisely by looking at the atomic fluctuations. For the convenience of representation, each residue was assigned a new residue index according to their orders in the amino acid sequence (Figure 1(B)).
Figure 2.
Thermodynamic fluctuations of thrombin. Free thrombin has heavier fluctuations in comparison with aptamer-bound thrombin with respect to (A) the root-mean-square distances (RMSD) to the same reference of the initial structure along simulation trajectories and (B) the root-mean-squared fluctuations (RMSF) of each alpha carbon atom. The regions with distinct fluctuations on free and aptamer-bound thrombin were also indicated by the colored regions in plot (C). The aptamer-bound thrombin has larger fluctuations in red regions and smaller fluctuations in blue regions. These fluctuation differences were further indicated via the plot of RMSF differences between aptamer-bound and aptamer-unbound thrombin in (D).
The RMSF plot (Figure 2(B)) shows, aptamer-unbound and aptamer-bound thrombins have similar atomic fluctuation patterns. In both systems, most of the alpha carbons fluctuate less than 1 Å except for the ones in surface loops and termini. However, comparisons of the atomic fluctuations indicate that binding of the 15-TBA exert a considerable influence on the fluctuations in the flexible regions, which are spatially distinct from the aptamer-binding region (residues 102–112). In Figure 2(C), the thrombin is colored according to the RMSF differences (Figure 2(D)) in the two systems. Widely spreading regions in blue (residues 1–6, 17–19, 83, 85–86, 125, 131, 182–183, 214–219, and 264–268, 270–271) exhibit more than .5 Å fluctuation decrease when the 15-TBA is bound, while equivalent amplifications of atomic functions after the aptamer-binding occur in the red regions (residues 26, 29, 30, 32, 167–169, and 295). Despite such a local-enhanced fluctuations in the alpha helix region in the light chain, aptamer-binding at exosite I mainly leads to a dramatic restraint in the flexibility of thrombin’s surface loops, including other known functional regions such as 60s loop (residues 82–91), exosite II (residues 125, 134, 281, 284, 288), γ loop (residue 182–190) and Na+ loop (residue 267–274) as labeled on Figure 1. These differences not only demonstrate the allosteric effect due to the aptamer-binding regarding atomic fluctuations, but also indicate a potentially profound effect of aptamer-binding that we will discuss in next section.
Correlated motions are altered in the presence of aptamer-binding
Comparison of correlated motions among alpha carbons allows us to examine the 15-TBA’s potential effects on thrombin’s coupled motions and intramolecular communications (Godwin et al., 2015; Salsbury, 2010; Salsbury et al., 2009). As shown in Figure 3(A) and (B), most residues of the thrombin before and after aptamer-binding share similar correlation relationships in their atomic fluctuations, and show primarily strong positive short-range correlations within secondary structures. Negative correlations are relatively moderate and usually occur within residue pairs that are separate spatially. The Pearson correlation coefficient between non-diagonal elements in the correlation matrices for aptamer-unbound and aptamer-bound thrombin is .8214, suggesting the correlated motions are actually not exactly the same in both systems. The root-mean-square averages of the correlation coefficients of all unique pairs of residues are .1845 and .1652 respectively for the aptamer-unbound and aptamer-bound systems. This quantitatively reveals that the aptamer-bound thrombin has slightly weaker strengths of overall coupling.
Figure 3.
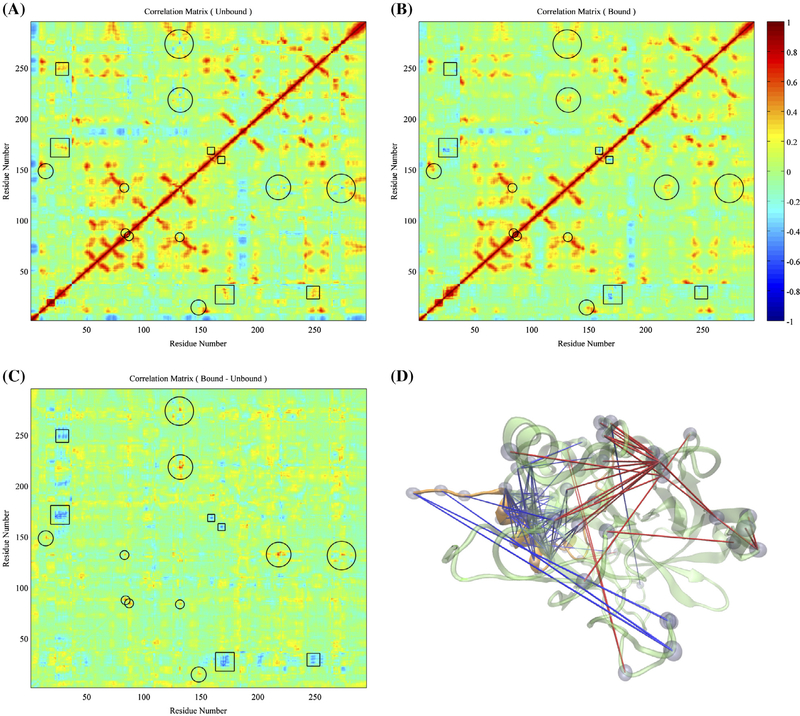
Comparisons on overall motions between the aptamer-unbound and aptamer-bound thrombin. (A) Correlations of each alpha carbon’s displacement from average position of the free thrombin. (B) Correlations of motions of each alpha carbon’s displacement from average position of the aptamer-bound thrombin. (C) Subtraction of correlation matrix of free thrombin from the one of aptamer-bound thrombin. The circles and squares highlight the regions with significant positive and negative increments of correlations, respectively. (D) Pairs of residues with significantly distinct correlated motions in both systems were highlighted via lines and beads. The blue and red lines indicate residue pairs with negative and positive subtractions of correlation matrices of aptamer-bound and aptamer-unbound thrombin respectively.
Regions with significant differences in correlation coefficients are marked based on an absolute value threshold of .40 in subtraction between correlation matrices for the aptamer-bound and aptamer-unbound thrombin (Figure 3(C) and (D)). One of the significant differences are observed in the alpha helix regions (residues 22–32) in light chain present opposite correlations with the adjacent loop region (residues 167–172), where we have seen an obvious amplification of atomic fluctuations after aptamer-binding, and the residues 247–255 behind the catalytic cleft in the heavy chain. Meanwhile, the C-terminal residues 35–36 of the light chain displays opposite coupling with the adjacent loop region (residues 167–172) and the distant γ loop. The other distinct difference is, instead of being negatively correlated as seen in the aptamer-unbound thrombin, the loop residues 131 to 134, which are adjacent to the exosite II, become weakly but positively correlated with nearby residues 217–223 after aptamer-binding. In addition, when thrombin is bound by the aptamer, motions of residues 14 and the nearby residues 148–149 become more positively correlated, while residues 131–132 and 273–275 are decoupled. As a result, our atomistic simulations indicate the allosteric effects of the aptamer-binding also include changes in long-range correlated motions.
Aptamer-binding stabilizes the conformational ground state of thrombin
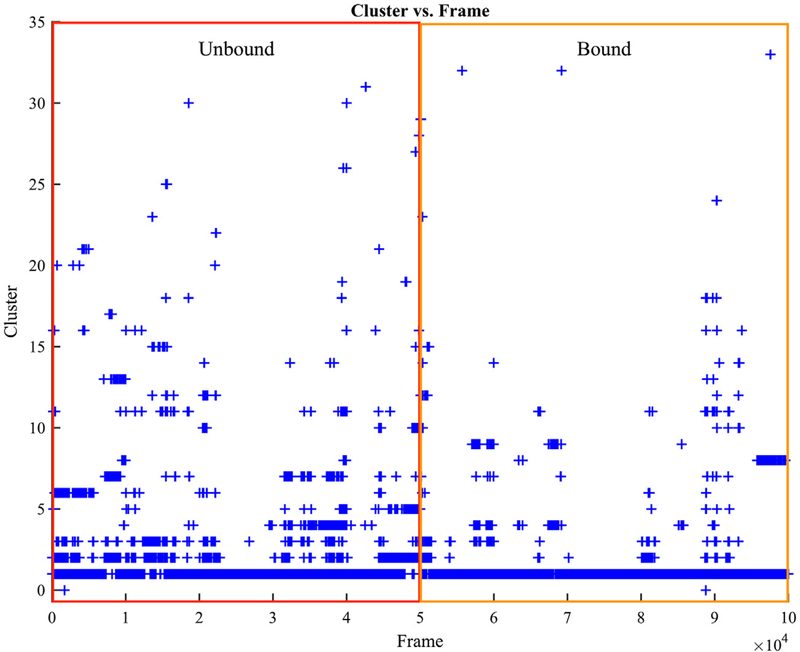
Clustering analysis was then performed to examine the structural variability of thrombin seen in our simulations. The most frequent clusters occur in all simulations regardless of the presence or absence of aptamer (Figure 4). However, their populations differ. 93% of the structures sampled in the five one-microsecond-long simulations of aptamer-bound thrombin are grouped into cluster 1 due to their structural similarities, whereas only 71% of structures in the five one-microsecond-long simulations of free thrombin belong to this cluster (Figure S2(A)). This difference indicates that without aptamer-binding, thrombin is able to adopt a more diverse range of conformations. Under the same amount of sampling in our simulations, 11 distinct conformational clusters emerge in the free thrombin but are never observed in the aptamer-bound thrombin simulations (Figure S2(B)). Although the clustering algorithm also identified three unique clusters for the aptamer-bound thrombin, considering the cluster distributions of both systems (Figure S2(A)), the clustering analysis suggests that the aptamer binding at exosite I restrict the conformational freedom of thrombin.
Figure 4.
Structure clustering evolution of thrombin in unbound and bound simulations. The red and orange regions include five 1-microsecond-long trajectories from the free thrombin and aptamer-bound thrombin simulations respectively.
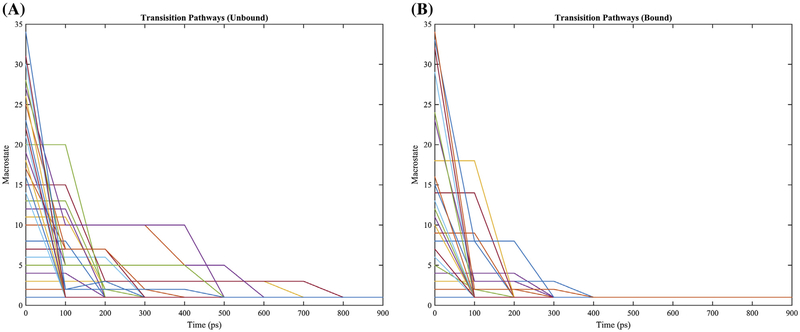
Based on the results of the clustering analysis, the transition rates among the clusters were computed under a MSM (Godwin et al., 2015; Häggström, 2002) using the clusters as states (Figure S3). According to Markov modeling (Häggström, 2002), the kinetic properties of thrombin in conformational ground and excited states are illustrated via highlights of the most likely transition path of each cluster in Figure 5. In both situations – with and without aptamer-bound – thrombin started in exited state conformations will, as expected, transition eventually back into equilibrium distributions with the ground state as the most populated state. However, as seen in Figure 5, the transitions from the exited states to the ground state are sped up in the aptamer-bound thrombin simulations. This demonstrates that the thrombin’s ground state is not just stabilized by the binding aptamer thermodynamically, but also kinetically.
Figure 5.
Transition pathways of clusters in the simulations of aptamer-unbound and aptamer-bound simulations. Only sampled clusters for each system were plotted. Every 100 ps stands for one iteration step in the transition pathway calculation.
Thrombin conformational free energy surfaces are restricted due to aptamer-binding
In order to study how thrombin’s conformational free energy landscape is changed by binding, PCA was performed to capture thrombin’s conformation in a reduced space for estimating free energy landscapes of the aptamer-bound and free thrombins. The PCA here was based on alpha carbon atoms in thrombin. This leads to a mathematical equivalence to quasi-harmonic analysis, which is used to identify low-frequency normal modes in proteins in the mass-weighted quasi-harmonic approximation (Hayward et al., 1994; Levy et al., 1984). The lowest several modes are the most deformable ones. As there are multiple flexible surface loops, five principal components are needed to cover the majority (greater than 50%) of conformation fluctuations and kinetic variance (Figure S4). Free energy surfaces based on these predominant modes were plotted (Figures 6 and S5). For each pair of principal components, aptamer-bound thrombin’s free energy surfaces are within the wider free energy surface of the aptamer-unbound thrombin. This result demonstrates that all sampled conformations of the aptamer-bound thrombin can be found in the structural ensemble of the aptamer-unbound thrombin. Additionally, under the same amount of sampling, the thrombin without aptamer-binding has more unique conformations that are not accessible after aptamer-binding.
Consistent with clustering and Markov analysis, the main free energy wells (labeled as 1 in the free energy landscapes) of aptamer-unbound and aptamer-bound thrombin overlap; though the first one is broader. In addition to the main well, there is an another well (labeled as 2) with a 2.5 kcal/mol thermodynamics barrier (indicated by the yellow ridge and color bar) to the main well in the free energy profile of the aptamer-bound thrombin. In contrast, the aptamer-unbound thrombin has several connected wells (labeled as 4 to 8) with barriers of less than 1.5 kcal/mol (indicated by the numeric value for cyan in the color bar). Therefore, the conformational transition of atpamer-bound thrombin between these wells is less favored energetically.
Thrombin’s conformations in labeled free energy wells were examined and illustrated as structural ensembles using an in-house visualization script (Melvin & Salsbury, 2015, 2016). Consistent with the experiment results in literature (Zhou et al., 2010), all of these structural ensembles share the same global structure. As expected, the aptamer-bound and aptamer-unbound thrombins share a common most populated conformational ensemble 1, which turns out to be optimal for aptamer-binding at exosite I. However, the aptamer-binding presents significant influence on the conformations of the functional sites with respect to other structural ensembles in the conformational spaces of thrombin. The structural ensembles 6 and 7, are barely accessible for the aptamer-bound thrombin as indicated on the free energy surfaces (Figure 6). These ensembles have remarkable differences with respect to the conformations and fluctuations in comparisons of the other observed structural ensembles. Most dramatically, the 60s loop is flying away from the catalytic triad and the plane of γ loop is upright and rolling up toward the catalytic cleft in structural ensemble 6. In structural ensemble 7. The γ loop also leans and collapses while the whole protein fluctuates less. In addition, the aptamer at the exosite I destabilizes the conformations 4, 5, and 8 in the aptamer-bound thrombin. These ensemble all present different conformations than ensemble 1. The γ loop in ensemble 4 tends to twist toward the exosite I, and it turns to stretch horizontally more and more in ensemble 5 and 8. On the other hand, the ensemble 2 with fairly extended γ loop is stabilized when the aptamer is bound. Ensembles 3, which has a similar pose of γ loop in ensemble 4 but more small turns, is a more significant metastable conformational state after aptamer-binding with respect to the higher thermodynamics barrier. Except for the γ and 60s loops, in different ensembles, the exosite II region and the 180s and Na+ loops also present visible diversities in local tertiary structure, pose, and ranges of fluctuations as indicated on the ensemble plots.
Such visualization of the structural ensembles is based on identifications of minima in the labeled regions on the free energy surface using principal component 1 and 2, and the shadows came from a sampling of all conformations within the free energy minima bins. However, these results are sufficient to illustrate that aptamer-binding leads to changes in thrombin’s structural ensembles and corresponding conformational free energy surfaces. These changes can produce profound influence on thrombin’s function due to the changes in the local environment, that we are about to discuss along with our previous results in the next section in details.
Discussion and conclusions
Thanks to the development of hardware and parallel programing, conventional MD simulations has been largely extended from nanosecond to microsecond scale, which offers us considerably more confidence in the validity of the results (Godwin, Gmeiner, & Salsbury, 2016). Five individual runs were performed for both the aptamer-unbound and aptamer-bound thrombins (total of 10) in order to increase sampling. While each simulation starts with the same conformation, they are not expected to exhibit identical dynamics. A comparison on the RMSFs computed from each run demonstrates that the behavior of thrombin is largely the same among all five runs for the same type of simulation (Figure S6). The minimum correlation of the RMSFs is .8246 between run 3 and run5 for bound and .8894 between run 1 and run3 for unbound. The average correlation of RMSF across five runs is .9092 and .9190 for bound and unbound simulations, respectively. This suggests our simulations tend to capture the ensemble properties of thrombins under ample sampling. The equal amount of sampling over hundreds of thousand conformations in our microsecond-scaled MD simulations is able to shed light on the differences in the thermodynamic properties of the solvated thrombin in presence and absence of the aptamer-binding at exosite I. These results suggest it is not necessary to employ any biases to the simulations to enhanced the sampling on the rare events. The above results consistently illustrate that the aptamer-binding restrains the degrees of freedom the thrombin’s conformations and stabilizes the conformational ground state. As a result, the number of possible conformations and the corresponding state lifetime is reduced when an aptamer is bound to thrombin. We hypothesize the conformational distribution of the thrombin shrinks into one that is optimal for such specific aptamer binding, which may result a general allosteric regulation on thrombin’s function.
As seen in our RMSF calculations, the aptamer-binding results in restricted fluctuations of 60s, γ and Na+ loops, which are adjacent to the catalytic site cleft. The hydrophobic 60 loop and the hydrophilic γ loop are thought to sterically restrict access of large substrates to the active site and thus play a role in thrombin’s specificity (Davie & Kulman, 2006). Along with the decreased flexibility in these functional loops due to the binding of aptamer at exosite I, we see a decrease in the number of possible conformations as illustrated via clustering analysis, which should lower the probability to find optimal orientations to fit or reject substrates. Note most of the autolytic cleavage sites of β and γ derivatives of thrombin are proximal to the surface loops (β: residues 88–89, 99–100; γ: residues 159–160, 190–191) (Bode, 2006).
In addition to the aptamer-binding effects in thrombin’s specificity, we also suspect that the autolysis rate of thrombin might become lower after aptamer’s binding, considering the correlation between autolytic degradation and stabilization of the local flexible regions (Veltman et al., 1996, 1997). On the other hand, as an enhancement of Na+ binding due to rigidification of the autolysis loop has been demonstrated experimentally (Pozzi, Chen, Chen, Bah, & Di Cera, 2011), we also suspect the less flexible Na+ loop after aptamer-binding may become easier for a sodium ion to bind and stay. Since the binding of Na+ between 180 and 220 loop (Na+ loop) allosterically improves the substrate recognition and catalytic efficiency (Huntington, 2008, 2012), the observed decreased flexibility of the Na+ loop expected may further affect thrombin’s catalytic efficiency due to a potential enhancement of Na+ binding after aptamer-binding.
Moreover, an amplification of fluctuations of regions (residues 26–32, 167–169) near alpha helix in the light chain was seen in present of aptamer binding. The biological role of thrombin’s light chain has not been revealed as much as the catalytic heavy chain, however, it interacts with the heavy chain via several salt brides, ionic, and polar interactions and is thought to probably act as an allosteric effector in thrombin’s function and structure (Carter, Vanden Hoek, Pryzdial, & MacGillivray, 2010). Some severe bleeding associate mutations on Glu8 and Glu14c (residues 16 and 27) in this light chain have been revealed as a profound perturbation on thrombin’s interaction with factor Xa (Lefkowitz et al., 2000). Deletions of Lys9 and Lys10 (residues 17–18) were also found in patients with bleeding (Akhavan et al., 2000). The ion quartet Arg4-Glu8-Asp14-Glu14c (residues 12, 15, 21, 27) has long-range effects on the Na+ site and active site (Papaconstantinou, Bah, & Di Cera, 2008). Note all of these residues in the light chain are electrically charged. We hence hypothesize that any charged residues involved in such local fluctuation amplifications after aptamer binding may result a profound influence on the intramolecular and intermolecular electrostatic interactions, which will allosterically affect thrombin’s enzymatic activity as well.
Changes in residue coupling indicate a possible allosteric effect with respect to kinetic networks and intramolecular communications. In our study, it has been shown that the aptamer-binding can slightly alter the kinetic coupling of different regions of thrombin. The regions with changes in residue coupling are mainly located around the perimeter of the catalytic pocket (Figure 3(D)). In particular, we have seen that aptamer-binding leads to changes in correlated motions near the some known functional site such as the exosite II and 60s, Na+ and γ loops. The intramolecular communication among these regions can be altered due to the different coupling of motions when the aptamer is bound. As a consequence, the specific interactions among ligands and substrates at exosite II, 60s and γ loops can be perturbed by the bound aptamer. It is also testable that, after aptamer-binding, the catalytic efficiency may be affected along with the changes in intramolecular cooperation and local environment near these important areas on thrombin. In addition, less coupled motions of the Na+ loop and exosite II should reduce allostery and make the mechanical and biochemistry properties of each local region become more biologically significant.
As indicated by Figure S7, the inner products of the principal component basis sets from the unbound and bound simulations not only suggest the thrombin exhibits different dynamics with respect to the aptamer-binding, but also show that those two basis sets are largely different. The shape of the conformational free energy surfaces thereby relies on the basis set of the reduced space. However, the basis set from aptamer-bound simulations is not as ideal for projections of both systems, as the thrombin becomes less fluctuating after aptamer-binding. It is more sufficient to use the basis set from the more fluctuating thrombin to highlight the differences in the conformational spaces of bound and unbound thrombin with a few principal components.
Although a new free energy well near (415) occurs in the aptamer-bound thrombin’s surface of PC1–PC3 (Figure S5), suggesting some element of an induced fit, other wells for the aptamer-bound thrombin can be largely found in the free thrombin’s free energy surfaces. In the process of examination free energy surfaces constructed from each pair of the predominant principal components (PC1 to 5 with more than 50% coverage), one can keep observing the same pattern of overlap in conformational ground state wells even though the aptamer-unbound thrombin has a wider conformational space. This overlap indicates the conformations that are optimal for 15-TBA binding can be selected spontaneously from the conformation space of the isolated solvated thrombin. Therefore, we conclude that conformational selection, i.e. generalized allostery, is the main mechanism for thrombin’s recognition of the aptamer instead of induced fit.
We want to emphasize that the generalized allostery not just condenses the distribution of thrombin’s conformation but also plays a role in the intramolecular communications. For example, the eight structural ensembles identified from PC1 to PC2 map (Figure 6) exhibit different correlated motions, where the differences in the visualized trends of fluctuations at different sites were more clearly quantified by correlation matrices. Each of these microstate structures has its own distinct correlated motions (Figure S8). Moreover, even though some structures from aptamer-unbound and aptamer-bound simulations are identified in the same structural ensemble due to a similar conformation, several sites including termini of the light chain, exosite I, γ loop and other nearby flexible residues can have dynamic responses upon the binding (Figure S9). Changes in the distribution of conformations due to the bound aptamer’s generalized allostery can subsequently affect the intramolecular coupling of thrombin, which results a reduced or enhanced intramolecular communication for relevant sites.
Our study provides a molecular and atomic insight into how the aptamer-binding mechanically affects the thermodynamic properties of thrombin. It has been clearly illustrated at atomic level that the aptamer-binding can lead to a general allosteric effect on thrombin through changing (1) atomic fluctuations, (2) correlated motions, (3) conformational degree of freedom and conformational transition rates and (4) conformational free energy surfaces. The combinations of these changes due to the aptamer-binding cause a profound perturbation on the local and global environment around thrombin and result an influence on thrombin’s activities. It is particularly interesting that our simulations illustrate certain excited conformations of free thrombin become inaccessible when the aptamer is bound, which might be enlightening to explain the reciprocal binding phenomena and help us understand molecular response to the aptamer therapy and possible origin of side effects. On the other hand, such conformational restrictions may lower the affinity between thrombin and other substrates at the other site if the relevant optimal conformations are barely accessible to aptamer-binding thrombin. Therefore, our knowledge of this generalized allosteric effect suggests an indirect approach to regulate relevant functions and processes of thrombin, which could be exploited in drug development.
Supplementary Material
Acknowledgements
Crystallography & Computational Biosciences Shared Resource services were supported by the Wake Forest Baptist Comprehensive Cancer Center’s NCI Cancer Center Support Grant P30CA012197. Computations were performed on the Wake Forest University DEAC Cluster, a centrally managed resource with support provided in part by the University. FRS also acknowledges a Reynolds Research leave from Wake Forest University. We thank Mr. Ryan Melvin for his help in the scripts of clustering analysis and ensemble visualization. We also thank Mr. Ryan Godwin for providing some VMD scripts of DCD trajectory processing. We thank Mr. Ryan Godwin and Mr. Ryan Melvin for their reviewing the manuscript of this work and their comments and suggestions.
Funding
This work was supported by National Cancer Institute [grant number P30CA012197].
Abbreviations and symbols
- PARs
protease-activated receptors
- MD
Molecular dynamics
- 15-TBA
15-Trhombin-Binding-Aptamer
- RMSD
root-mean-square distance
- RMSF
root-mean-square fluctuations
- MSM
Markov state model
- Na+
sodium
- K+
potassium
- KCl
potassium chloride
- PCA
principal component analysis
- PC
principal component
- NPT
isothermal-isobaric ensemble
- PME
particle mesh Ewald
- QT
quality threshold
Footnotes
Supplemental data
The supplementary material for this article is available online at http://dx.doi.org/10.1080/07391102.2016.1254682
Disclosure statement
The authors of this manuscript declare no conflicts of interest.
References
- Abdi H, & Williams LJ (2010). Principal component analysis. Wiley Interdisciplinary Reviews: Computational Statistics, 2, 433–459. doi: 10.1002/wics.101 [DOI] [Google Scholar]
- Adams TE, & Huntington JA (2006). Thrombin-cofactor interactions: Structural insights into regulatory mechanisms. Arteriosclerosis, Thrombosis, and Vascular Biology, 26, 1738–1745. doi: 10.1161/01.ATV.0000228844.65168.d1 [DOI] [PubMed] [Google Scholar]
- Akhavan H, Mannucci PM, Lak H, Mancuso H, Mazzucconi MG, Rocino H, … Perkins SJ (2000). Identification and three-dimensional structural analysis of nine novel mutations in patients with prothrombin deficiency. Thrombosis and Haemostasis, 84, 989–997. [PubMed] [Google Scholar]
- Article H, Steering H, For H, & Thrombosis H. (2014). Thrombosis: A major contributor to the global disease burden. Journal of Thrombosis and Haemostasis, 12, 1580–1590. doi: 10.1111/jth.12698 [DOI] [PubMed] [Google Scholar]
- Baglin TP, Carrell RW, Church FC, Esmon CT, & Huntington JA (2002). Crystal structures of native and thrombin-complexed heparin cofactor II reveal a multistep allosteric mechanism. Proceedings of the National Academy of Sciences, 99, 11079–11084. doi: 10.1073/pnas.162232399 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bajzar H, Morser H, & Nesheim H. (1996). TAFI, or plasma procarboxypeptidase B, couples the coagulation and fibrinolytic cascades through the thrombin-thrombomodulin complex. Journal of Biological Chemistry, 271, 16603–16608. doi: 10.1074/jbc.271.28.16603 [DOI] [PubMed] [Google Scholar]
- Berendsen HJC, Postma JPM, van Gunsteren WF, DiNola H, & Haak JR (1984). Molecular dynamics with coupling to an external bath. The Journal of Chemical Physics, 81, 3684–3690. doi: 10.1063/1.448118 [DOI] [Google Scholar]
- Blombäck H, Hessel H, Hogg H, & Therkildsen H. (1978). A two-step fibrinogen–fibrin transition in blood coagulation. Nature, 275, 501–505. doi: 10.1038/275501a0 [DOI] [PubMed] [Google Scholar]
- Bode H. (2006). Structure and interaction modes of thrombin. Blood Cells, Molecules & Diseases, 36, 122–130. doi: 10.1016/j.bcmd.2005.12.027 [DOI] [PubMed] [Google Scholar]
- Bosshard HR (2001, August). Molecular recognition by induced fit: how fit is the concept? News in Physiological Sciences : An International Journal of Physiology Produced Jointly by the International Union of Physiological Sciences and the American Physiological Society, 16, 171–173. [DOI] [PubMed] [Google Scholar]
- Brooks BR, Brooks CL, Mackerell AD, Nilsson H, Petrella RJ, Roux H, … Karplus H. (2009). CHARMM: The biomolecular simulation program. Journal of Computational Chemistry, 30, 1545–1614. doi: 10.1002/jcc.21287 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carter ISR, Vanden Hoek AL, Pryzdial ELG, & MacGillivray RTA (2010). Thrombin A-chain: Activation remnant or allosteric effector? Thrombosis, 2010, 1–9. doi: 10.1155/2010/416167 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Changeux J-P, & Edelstein H. (2011). Conformational selection or induced fit? 50 years of debate resolved. F1000 Biology Reports, 3, 19–35. doi: 10.3410/B3-19 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Colwell NS, Blinder MA, Tsiang H, Gibbs CS, Bock PE, & Tollefsen DM (1998). Allosteric effects of a monoclonal antibody against thrombin exosite II. Biochemistry, 37, 15057–15065. doi: 10.1021/bi980925f [DOI] [PubMed] [Google Scholar]
- Coughlin SR (2000). Thrombin signalling and protease-activated receptors. Nature, 407, 258–264. doi: 10.1038/35025229 [DOI] [PubMed] [Google Scholar]
- Crawley JTB, Zanardelli H, Chion CKNK, & Lane DA (2007). The central role of thrombin in hemostasis. Journal of Thrombosis and Haemostasis, 5, 95–101. doi: 10.1111/j.1538-7836.2007.02500.x [DOI] [PubMed] [Google Scholar]
- Darden H, York H, & Pedersen H. (1993). Particle mesh Ewald: An N·log(N) method for Ewald sums in large systems. The Journal of Chemical Physics, 98, 10089–10092. doi: 10.1063/1.464397 [DOI] [Google Scholar]
- Davie H, & Kulman H. (2006). An overview of the structure and function of thrombin. Seminars in Thrombosis and Hemostasis, 32, 003–015. 10.1055/s-2006-939550 [DOI] [PubMed] [Google Scholar]
- Di Cera H. (2008). Thrombin. Molecular Aspects of Medicine, 29, 203–254. doi: 10.1016/j.mam.2008.01.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Erdmann H. (2010). Engineered thrombin aims to take on heparin. Chemistry and Biology, 17, 1267–1268. doi: 10.1016/j.chembiol.2010.12.005 [DOI] [PubMed] [Google Scholar]
- Feenstra KA, Hess H, & Berendsen HJC (1999). Improving efficiency of large time-scale molecular dynamics simulations of hydrogen-rich systems. Journal of Computational Chemistry, 20, 786–798. doi: [DOI] [PubMed] [Google Scholar]
- Figueiredo AC, Clement CC, Zakia H, Gingold H, Philipp H, & Pereira PJB (2012). Rational design and characterization of D-Phe-Pro-D-Arg-derived direct thrombin inhibitors. PLoS ONE, 7. doi: 10.1371/journal.pone.0034354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fredenburgh JC, Stafford AR, & Weitz JI (1997). Evidence for allosteric linkage between exosites 1 and 2 of thrombin. Journal of Biological Chemistry, 272, 25493–25499. [DOI] [PubMed] [Google Scholar]
- Godwin RC, Melvin H, & Salsbury FR (2015). Molecular dynamics simulations and computer-aided drug discovery In Zhang Wei (Ed.), Computer-aided drug discovery (pp. 1–30). New York: Springer. doi: 10.1007/7653_2015_41 [DOI] [Google Scholar]
- Godwin H, Gmeiner H, & Salsbury FR (2016). Importance of long-time simulations for rare event sampling in zinc finger proteins. Journal of Biomolecular Structure and Dynamics, 34, 125–134. doi: 10.1080/07391102.2015.1015168 [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Gunsteren WF, & Berendsen HJC (1977). Algorithms for macromolecular dynamics and constraint dynamics. Molecular Physics, 34, 1311–1327. doi: 10.1080/00268977700102571 [DOI] [Google Scholar]
- Häggström H. (2002). Finite Markov chains and algorithmic applications (Vol. 52). Cambridge: Society. doi: 10.1017/CBO9780511613586 [DOI] [Google Scholar]
- Harvey MJ, & De Fabritiis H. (2009). An implementation of the smooth particle mesh Ewald method on GPU hardware. Journal of Chemical Theory and Computation, 5, 2371–2377. doi: 10.1021/ct900275y [DOI] [PubMed] [Google Scholar]
- Harvey MJ, Giupponi H, & De Fabritiis H. (2009). ACEMD: Accelerating biomolecular dynamics in the microsecond time scale. Journal of Chemical Theory and Computation, 5, 1632–1639. doi: 10.1021/ct9000685 [DOI] [PubMed] [Google Scholar]
- Hayward H, Kitao H, & Go H. (1994). Harmonic and anharmonic aspects in the dynamics of BPTI: A normal mode analysis and principal component analysis. Protein Science : A Publication of the Protein Society, 3, 936–943. doi: 10.1002/pro.5560030608 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heyer LJ, Kruglyak H, & Yooseph H. (1999). Exploring expression data: Identification and analysis of coexpressed genes. Genome Research, 9, 1106–1115. doi: 10.1101/gr.9.11.1106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Humphrey H, Dalke H, & Schulten H. (1996). VMD: Visual molecular dynamics. Journal of Molecular Graphics, 14, 33–38. doi: 10.1016/0263-7855(96)00018-5 [DOI] [PubMed] [Google Scholar]
- Huntington JA (2008). How Na+ activates thrombin – A review of the functional and structural data. Biological Chemistry, 389, 1025–1035. doi: 10.1515/BC.2008.113 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huntington JA (2012). Thrombin plasticity. Biochimica et Biophysica Acta, 1824, 246–252. doi: 10.1016/j.bbapap.2011.07.005 [DOI] [PubMed] [Google Scholar]
- Jorgensen WL, Chandrasekhar H, Madura JD, Impey RW, & Klein ML (1983). Comparison of simple potential functions for simulating liquid water. The Journal of Chemical Physics. doi: 10.1063/1.445869 [DOI] [Google Scholar]
- Keefe AD, Pai H, & Ellington H. (2010). Aptamers as therapeutics. Nature Reviews. Drug Discovery, 9, 537–550. doi: 10.1038/nrd3141 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knaggs MH, Salsbury FR, Edgell MH, & Fetrow JS (2007). Insights into correlated motions and long-range interactions in CheY derived from molecular dynamics simulations. Biophysical Journal, 92, 2062–2079. doi: 10.1529/biophysj.106.081950 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lefkowitz JB, Haver H, Clarke H, Jacobson H, Weller H, Nuss H, … Hathaway WE (2000). The prothrombin Denver patient has two different prothrombin point mutations resulting in Glu-300–>Lys and Glu-309–>Lys substitutions. British Journal of Haematology, 108, 182–187. doi:bjh1810[pii]. [DOI] [PubMed] [Google Scholar]
- Lemons DS (1997). Paul Langevin’s 1908 paper “On the Theory of Brownian Motion” [“Sur la théorie du mouvement brownien,” C. R. Acad. Sci. (Paris) 146, 530–533 (1908)]. American Journal of Physics,, 65, 1079–1081. doi: 10.1119/1.18725 [DOI] [Google Scholar]
- Levy RM, Srinivasan AR, Olson WK, & McCammon JA (1984). Quasi-harmonic method for studying very low frequency modes in proteins. Biopolymers, 23, 1099–1112. doi: 10.1002/bip.360230610 [DOI] [PubMed] [Google Scholar]
- Li H, Johnson DJD, Esmon CT, & Huntington JA (2004). Structure of the antithrombin-thrombin-heparin ternary complex reveals the antithrombotic mechanism of heparin. Nature Structural & Molecular Biology, 11, 857–862. doi: 10.1038/nsmb811 [DOI] [PubMed] [Google Scholar]
- Li H, Wang H, Zhao H, Yang H, Chen H, & Lan H. (2014). Development of aptamer oligonucleotides as anticoagulants and antithrombotics for cardiovascular diseases: Current status. Thrombosis Research, 134, 769–773. doi: 10.1016/j.thromres.2014.05.021 [DOI] [PubMed] [Google Scholar]
- Liaw PC, Fredenburgh JC, Stafford AR, Tulinsky H, Austin RC, & Weitz JI (1998). Localization of the thrombin-binding domain on prothrombin fragment 2. Journal of Biological Chemistry, 273, 8932–8939. [DOI] [PubMed] [Google Scholar]
- McCammon JA, Gelin BR, & Karplus H. (1977). Dynamics of folded proteins. Nature, 267, 585–590. doi: 10.1038/267585a0 [DOI] [PubMed] [Google Scholar]
- Melnikova H. (2009). The anticoagulants market. Nature Reviews. Drug Discovery, 8, 353–353. doi: 10.1038/nrd2851 [DOI] [PubMed] [Google Scholar]
- Melvin H, & Salsbury H. (2015). VisualStatistics. Figshare. doi: 10.6084/m9.figshare.1601897 [DOI] [Google Scholar]
- Melvin H, & Salsbury H. (2016). Python implementation of quality threshold clustering for molecular dynamics. Figshare. doi: 10.6084/m9.figshare.3813930.v2 [DOI] [Google Scholar]
- Melvin RL, & Salsbury FR (2016). Visualizing ensembles in structural biology. Journal of Molecular Graphics and Modelling, 67, 44–53. doi: 10.1016/j.jmgm.2016.05.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Melvin H, Godwin H, Xiao H, & Salsbury H. (2015). Markov cluster analysis in matlab. Figshare. doi: 10.6084/m9.figshare.1566809 [DOI] [Google Scholar]
- Motlagh HN, Wrabl JO, Li H, & Hilser VJ (2014). The ensemble nature of allostery. Nature, 508, 331–339. doi: 10.1038/nature13001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Negureanu H, & Salsbury FR (2012). Insights into protein – DNA interactions, stability and allosteric communications: A computational study of Mutsα-DNA recognition complexes. Journal of Biomolecular Structure and Dynamics, 29, 757–776. doi: 10.1080/07391102.2012.10507412 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Negureanu H, & Salsbury FR (2014). Non-specificity and synergy at the binding site of the carboplatin-induced DNA adduct via molecular dynamics simulations of the MutSα-DNA recognition complex. Journal of Biomolecular Structure & Dynamics, 32, 969–992. doi: 10.1080/07391102.2013.799437 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nelson-Piercy H. (1997). 6 Hazards of heparin: Allergy, heparin-induced thrombocytopenia and osteoporosis. Baillière’s Clinical Obstetrics and Gynaecology, 11, 489–509. doi: 10.1016/S0950-3552(97)80024-7 [DOI] [PubMed] [Google Scholar]
- Ni H, Castanares H, Mukherjee H, & Lupold SE (2011). Nucleic acid aptamers: Clinical applications and promising new horizons. Current Medicinal Chemistry, 18, 4206–4214. doi: 10.2174/092986711797189600 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nierodzik ML, & Karpatkin H. (2006). Thrombin induces tumor growth, metastasis, and angiogenesis: Evidence for a thrombin-regulated dormant tumor phenotype. Cancer Cell, 10, 355–362. doi: 10.1016/j.ccr.2006.10.002 [DOI] [PubMed] [Google Scholar]
- Nimjee SM, Oney H, Volovyk H, Bompiani KM, Long SB, Hoffman H, & Sullenger BA (2009). Synergistic effect of aptamers that inhibit exosites 1 and 2 on thrombin. RNA (New York, N.Y.), 15, 2105–2111. doi: 10.1261/rna.1240109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Opalinska JB, & Gewirtz AM (2002, July). Nucleic-acid therapeutics: Basic principles and recent applications. Nature Reviews. Drug Discovery, 1, 503–514. doi: 10.1038/nrd837 [DOI] [PubMed] [Google Scholar]
- Padmanabhan H, & Tulinsky H. (1996). An ambiguous structure of a DNA 15-mer thrombin complex. Acta Crystallographica Section D, Biological Crystallography, 52, 272–282. doi: 10.1107/S0907444995013977 [DOI] [PubMed] [Google Scholar]
- Padmanabhan H, Padmanabhan KP, Ferrara JD, Sadler JE, & Tulinsky H. (1993). The structure of alpha-thrombin inhibited by a 15-mer single-stranded DNA aptamer. The Journal of Biological Chemistry, 268, 17651–17654. [DOI] [PubMed] [Google Scholar]
- Papaconstantinou ME, Bah H, & Di Cera H. (2008). Role of the A chain in thrombin function. Cellular and Molecular Life Sciences, 65, 1943–1947. doi: 10.1007/s00018-008-8179-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petrera NS, Stafford AR, Leslie BA, Kretz CA, Fredenburgh JC, & Weitz JI (2009). long range communication between exosites 1 and 2 modulates thrombin function. Journal of Biological Chemistry, 284, 25620–25629. doi: 10.1074/jbc.M109.000042 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pozzi H, Chen H, Chen H, Bah H, & Di Cera H. (2011). Rigidification of the autolysis loop enhances Na+ binding to thrombin. Biophysical Chemistry, 159, 6–13. doi: 10.1016/j.bpc.2011.04.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Radjabi AR, Sawada H, Jagadeeswaran H, Eichbichler H, Kenny HA, Montag H, … Lengyel H. (2008). Thrombin induces tumor invasion through the induction and association of matrix metalloproteinase-9 and 1-integrin on the cell surface. Journal of Biological Chemistry, 283, 2822–2834. doi: 10.1074/jbc.M704855200 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Russo Krauss H, Merlino H, Randazzo H, Novellino H, Mazzarella H, & Sica H. (2012). High-resolution structures of two complexes between thrombin and thrombin-binding aptamer shed light on the role of cations in the aptamer inhibitory activity. Nucleic Acids Research, 40, 8119–8128. doi: 10.1093/nar/gks512 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Šali H, & Blundell TL (1993). Comparative protein modelling by satisfaction of spatial restraints. Journal of Molecular Biology, 234, 779–815. doi: 10.1006/jmbi.1993.1626 [DOI] [PubMed] [Google Scholar]
- Salomon-Ferrer H, Case DA, & Walker RC (2013). An overview of the Amber biomolecular simulation package. Wiley Interdisciplinary Reviews: Computational Molecular Science, 3, 198–210. doi: 10.1002/wcms.1121 [DOI] [Google Scholar]
- Salsbury FR, Crowder MW, Kingsmore SF, & Huntley JJA (2009). Molecular dynamic simulations of the metallo-beta-lactamase from Bacteroides fragilis in the presence and absence of a tight-binding inhibitor. Journal of Molecular Modeling, 15, 133–145. doi: 10.1007/s00894-008-0410-0 [DOI] [PubMed] [Google Scholar]
- Salsbury FR, Yuan H, Knaggs MH, Poole LB, & Fetrow JS (2012). Structural and electrostatic asymmetry at the active site in typical and atypical peroxiredoxin dimers. The Journal of Physical Chemistry. B, 116, 6832–6843. doi: 10.1021/jp212606k [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salsbury FR (2010). Molecular dynamics simulations of protein dynamics and their relevance to drug discovery. Current Opinion in Pharmacology, 10, 738–744. doi: 10.1016/j.coph.2010.09.016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scherer MK, Trendelkamp-Schroer H, Paul H, Pérez-Hernández H, Hoffmann H, Plattner H, … Noé H. (2015). PyEMMA 2: A software package for estimation, validation, and analysis of Markov models. Journal of Chemical Theory and Computation, 11, 5525–5542. doi: 10.1021/acs.jctc.5b00743 [DOI] [PubMed] [Google Scholar]
- van der Spuy WJ, & Pretorius H. (2012). Interrelation between inflammation, thrombosis, and neuroprotection in cerebral ischemia. Reviews in the Neurosciences, 23, 269–278. doi: 10.1515/revneuro-2012-0028 [DOI] [PubMed] [Google Scholar]
- Takagi H, & Doolittle RF (1974). Amino acid sequence studies on factor XIII and the peptide released during its activation by thrombin. Biochemistry, 13, 750–756. [DOI] [PubMed] [Google Scholar]
- Tanaka KA, Key NS, & Levy JH (2009). Blood coagulation: Hemostasis and thrombin regulation. Anesthesia and Analgesia, 108, 1433–1446. doi: 10.1213/ane.0b013e31819bcc9c [DOI] [PubMed] [Google Scholar]
- Tsai C-J, & Nussinov H. (2014). A unified view of “how allostery works”. PLoS Computational Biology, 10, e1003394. doi: 10.1371/journal.pcbi.1003394 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vasilyeva H, Clodfelter JE, Rector H, Hollis H, Scarpinato KD, & Salsbury FR (2009). Small molecule induction of MSH2-dependent cell death suggests a vital role of mismatch repair proteins in cell death. DNA Repair, 8, 103–113. doi: 10.1016/j.dnarep.2008.09.008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Veltman OR, Vriend H, Middelhoven PJ, van den Burg H, Venema H, & Eijsink VG (1996). Analysis of structural determinants of the stability of thermolysinlike proteases by molecular modelling and site-directed mutagenesis. Protein Engineering, 9, 1181–1189. [DOI] [PubMed] [Google Scholar]
- Veltman OR, Vriend H, Hardy H, Mansfeld H, van den Burg H, Venema H, & Eijsink VG (1997). Mutational analysis of a surface area that is critical for the thermal stability of thermolysin-like proteases. European Journal of Biochemistry, 248, 433–440. [DOI] [PubMed] [Google Scholar]
- Verhamme IM, Olson ST, Tollefsen DM, & Bock PE (2002). Binding of exosite ligands to human thrombin: Re-evaluation of allosteric linkage between thrombin exosites I and II. Journal of Biological Chemistry, 277, 6788–6798. doi: 10.1074/jbc.M110257200 [DOI] [PubMed] [Google Scholar]
- WHO | Estimates for 2000–2012. (n.d.). Retrieved November 29, 2015, from http://www.who.int/healthinfo/global_burden_disease/estimates/en/index1.html
- World Health Organization. (2014). WHO methods and data sources for country – Level causes of death. Retrieved from http://www.who.int/healthinfo/statistics/GlobalCOD_method.pdf
- Xiao H, & Salsbury FR (2016). A Matlab script to perform PCA on molecular dynamics trajectories. Figshare. doi: 10.6084/m9.figshare.3842877.v3 [DOI] [Google Scholar]
- Yuan H, Knaggs MH, Poole LB, Fetrow JS, & Salsbury FR (2010). Conformational and oligomeric effects on the cysteine pK a of tryparedoxin peroxidase. Journal of Biomolecular Structure & Dynamics, 28, 51–70. doi: 10.1080/07391102.2010.10507343 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou H, Huang H, & Qu H. (2010). The binding effect of aptamers on thrombin. Biochemical Engineering Journal, 52, 117–122. doi: 10.1016/j.bej.2010.07.007 [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.