Sample Size Calculation for Count Outcomes in Cluster Randomization Trials with Varying Cluster Sizes

Abstract

In many cluster randomization studies, cluster sizes are not fixed and may be highly variable. For those studies, sample size estimation assuming a constant cluster size may lead to under-powered studies. Sample size formulas have been developed to incorporate the variability in cluster size for clinical trials with continuous and binary outcomes. Count outcomes frequently occur in cluster randomized studies. In this paper, we derive a closed-form sample size formula for count outcomes accounting for the variability in cluster size. We compare the performance of the proposed method with the average cluster size method through simulation. The simulation study shows that the proposed method has a better performance with empirical powers and type I errors closer to the nominal levels.

1. Introduction

Cluster randomization trials are widely used to evaluate the effect of interventions on health outcomes, where clusters of subjects, instead of individual subjects, are randomized to different intervention groups (Eldridge and Kerry, 2012; Campbell and Walters, 2014; Hayes and Moulton, 2017). Donner and Klar (2000) discussed many advantages of cluster randomization studies, which include administrative convenience, ease of obtaining cooperation from investigators, ethical consideration, enhancement of subject compliance, avoidance of treatment group contamination, and intervention naturally applied at the cluster level. A critical feature of cluster randomization trials is the dependency among subjects within the same cluster, quantified by the intracluster correlation coefficient (ICC), denoted as ρ. Dependent observations usually correspond to a smaller effective sample size since individuals within a cluster are usually positively correlated. Suppose the research question is to investigate if there is a significant difference in mean effect between two intervention groups. Compared to an individual randomization trial, the treatment effect estimated in a cluster randomization trial of equal sample size has a larger variance, by an inflation factor of 1 + (m − 1)ρ due to the correlation among subjects within the same cluster (Eldridge et al., 2006). Here m is the fixed cluster size. This variance inflation factor is also called the design effect. The sample size under cluster randomization can be obtained by multiplying the design effect to the sample size calculated assuming individual randomization to maintain the required level of power.

Count outcomes frequently occur in cluster randomized studies. For example, Roig et al. (2010) evaluated the effectiveness of an intervention on reducing the number of cigarettes per day with a cluster randomization trial. Fairall et al. (2005) evaluated an educational outreach program for the case management of respiratory diseases with the outcome being the number of clinic visits using a cluster randomization trial. Sample size formulas have been developed for cluster randomization trials with count outcomes. For example, Amatya et al. (2013) derived the sample size formula for the count outcome in a cluster randomization trial. Hayes and Bennett (1999) provided the sample size estimate based on the coefficient of variation. One limitation of aforementioned methods is that they assume an equal cluster size in the design of cluster randomization trials. This assumption might be unrealistic because in practice clusters (formed by physician, clinic, neighborhood, etc) usually occur naturally with random variation in size due to time, logistics and budget constraint, or differences in recruitment rate, etc. Variation in cluster sizes can affect sample size estimation or the power of the study (Ahn et al., 2014; Guittet et al., 2006). A common practice has been to use the average cluster size to estimate the sample size. The resulting experimental design ignores a source of random variability (in cluster size), which might lead to under-powered trials. To address this problem, Manatunga et al. (2001) proposed a sample size formula accounting for varying cluster sizes for continuous outcomes, which adjusts traditional sample size formula by a variance inflation factor. Design parameters involved in the variance inflation factor include ICC as well as the mean and variance of cluster sizes. Along the same line, Kang et al. (2003) developed a sample size formula for dichotomous outcomes that accounts for varying cluster sizes. They compared their proposed method with the average cluster size method and the maximum cluster size method, where the cluster size is replaced by the average cluster size and the maximum cluster size, respectively. van Breukelen and Candel (2012a) proposed a correction of sample size formula to compensate for the loss of efficiency and power due to varying cluster sizes. Their approach is applicable to continuous and binary outcomes. More details can be found in van Breukelen et al. (2007, 2008); van Breukelen and Candel (2012b). To our knowledge, there has been no investigation on sample size adjustment for varying cluster sizes in the context of count outcomes.

In this study we investigate sample size calculation for cluster randomization trials under randomly varying cluster sizes, in the context of a count outcome. In Section 2, the derivation of sample size formulas under varying cluster sizes is presented. In Section 3, an empirical simulation study is conducted to investigate the performance of the proposed method compared with the average cluster size method. In Section 4, an application of the proposed method is presented. Finally, we conclude with a discussion.

2. Methods

We use k = 1/2 to indicate the treatment/control group in a cluster randomization trial. The number of clusters in each group is denoted by J_k (k = 1, 2). The cluster sizes, denoted by n_kj (j = 1, … , J_k), vary across clusters following a certain discrete distribution with mean θ and variance τ². The coefficient of variation (CV) is γ = τ/θ. We use Y_kji (i = 1, …, n_kj) to denote the count outcome observed from the ith subject in the jthe cluster of the kth group. We assume a Poisson model for Y_kji with parameter λ_k = E(Y_kji) = Var(Y_kji). Y_kji’s are assumed to be independent across clusters. We also assume a common intracluster correlation coefficient, ρ = Corr(Y_kji, Y_kji′) for i ≠ i^′ (Rutterford et al., 2015; Zou and Donner, 2004).

Suppose the hypotheses of interest are H₀: λ₁ = λ₂ versus H₁: λ₁ ≠ λ₂. For simplicity, we assume balanced randomization, i.e., J₁ = J₂ = J. An unbiased estimator of λ_k can be expressed as

$${\widehat{\mathrm{\lambda }}}_k=\frac{{\sum }_{j=1}^J{\sum }_{i=1}^{n_{kj}}{Y}_{kji}}{{\sum }_{j=1}^J{n}_{kj}}.$$ (1)

Conditional on n_kj, ${\widehat{\mathrm{\lambda }}}_k$ approximately follows a normal distribution with mean λ_k and variance

$$Var\left({\widehat{\mathrm{\lambda }}}_k|n_{kj}\right)=\frac{{\mathrm{\lambda }}_k{\sum }_{j=1}^J{n}_{kj}\left[1+\left(n_{kj}-1\right)\rho \right]}{{\left({\sum }_{j=1}^J{n}_{kj}\right)}^2}.$$ (2)

The variance of ${\widehat{\mathrm{\lambda }}}_k$ can be estimated by

$$s_k^2=\frac{{\widehat{\mathrm{\lambda }}}_k{\sum }_{j=1}^J{n}_{kj}\left[1+\left(n_{kj}-1\right)\widehat{\rho }\right]}{{\left({\sum }_{j=1}^J{n}_{kj}\right)}^2}.$$ (3)

At the design stage, ρ can be estimated from the pilot data. A summary of literatures that presents the estimates of ρ can be found in Moerbeek and Teerenstra (2016). However, the exact n_kj is usually unknown, which prevents the assessment of $\text{var}\left({\widehat{\mathrm{\lambda }}}_k\right)$ and subsequently the calculation of power. In this study, we assume that investigators have good insight about the first two moments (mean and variance) for the distribution of cluster sizes although investigators do not know the exact cluster sizes in advance. This assumption allows us to approximately marginalize with respect to n_kj and obtain $\text{var}\left({\widehat{\mathrm{\lambda }}}_k\right)$. Specifically, we assume n_kj to be independently and identically distributed with mean θ = E(n_kj) and variance τ² = Var(n_kj). Then, we have

$$Var\left({\widehat{\mathrm{\lambda }}}_k\right)=E\left[Var\left({\widehat{\mathrm{\lambda }}}_k|n_{kj}\right)\right]\approx \frac{{\mathrm{\lambda }}_{k}J\left[(1-\rho )E\left(n_{kj}\right)+\rho E\left(n_{kj}^2\right)\right]}{{(J\theta )}^2}=\frac{{\mathrm{\lambda }}_k}{J}\left[(1-\rho )\frac{1}{\theta }+\rho +\rho {\gamma }^2\right].$$

The above derivation uses the fact that $E\left(n_{kj}^2\right)={\theta }^2+{\tau }^2$, ${\sum }_{j=1}^J{n}_{kj}/J\approx \theta$ for large J, and γ = τ/θ is the coefficient of variation of cluster sizes.

With a power of 1 − β at a two-sided significance level of α, the required number of clusters in each intervention arm is

$$J=\frac{{\left(z_{1-\alpha /2}+z_{1-\beta }\right)}^2\left({\mathrm{\lambda }}_1+{\mathrm{\lambda }}_2\right)}{{\left({\mathrm{\lambda }}_1-{\mathrm{\lambda }}_2\right)}^2}\left[(1-\rho )\frac{1}{\theta }+\rho +\rho {\gamma }^2\right].$$ (4)

This sample size formula can be easily extended to accommodate unbalanced randomization. Suppose the treatment:control randomization ratio is r: 1, the number of clusters required for the control arm is

$$J=\frac{{\left(z_{1-\alpha /2}+z_{1-\beta }\right)}^2\left({\mathrm{\lambda }}_1/r+{\mathrm{\lambda }}_2\right)}{{\left({\mathrm{\lambda }}_1-{\mathrm{\lambda }}_2\right)}^2}\left[(1-\rho )\frac{1}{\theta }+\rho +\rho {\gamma }^2\right].$$ (5)

It is noteworthy that when γ = 0, i.e., no variability in cluster size so all n_kj = θ, the sample size formula becomes

$$J^{*}=\frac{{\left(z_{1-\alpha /2}+z_{1-\beta }\right)}^2\left({\mathrm{\lambda }}_1/r+{\mathrm{\lambda }}_2\right)}{{\left({\mathrm{\lambda }}_1-{\mathrm{\lambda }}_2\right)}^2}\left[(1-\rho )\frac{1}{\theta }+\rho \right].$$

Comparing J and J*, the relative change in sample size due to random variability in cluster size can be quantified by

$$R=\frac{J}{J^{*}}-1=\frac{\rho \theta }{1-\rho +\rho \theta }{\gamma }^2.$$

We have several observations about R:

• R does not depend on design parameters such as type I error α, power 1 − β, and λ₁ and λ₂.

• R is proportional to γ², the squared coefficient of variation in cluster sizes.

• Under a positive ICC, ρ > 0, which is usually the case in practice, we have R > 0. That is, the variability in cluster size always leads to a larger sample size requirement. Ignoring this source of variability at experimental design will lead to underpowered trials.

• R → 0 as ρ → 0. Actually from an equivalent expression,

  $$R=\frac{\theta {\gamma }^2}{\frac{1-\rho }{\rho }+\theta },$$

  it is obvious that R is an monotonically increasing with ρ for ρ > 0. Hence given the same coefficient of variation, the required increase in sample size is greater for trials with stronger dependence among observations from the same clusters.
• From another equivalent expression,

  $$R=\frac{\rho {\gamma }^2}{\frac{1-\rho }{\theta }+\rho },$$

  we observe that R is monotonically increasing with θ, the average cluster size. Given the same variability (γ) and ICC, a larger average cluster size is associated with a greater increase in sample size requirement.

In short, the worst scenario to ignore random variability in cluster size is for trials with high ICC and larger cluster sizes.

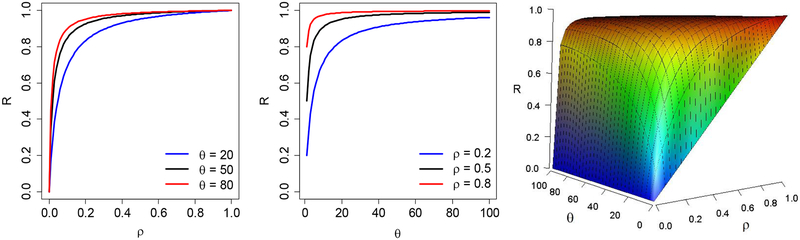
The first two plots in Figure 1 present the effects of ICC (ρ) and mean cluster size (θ) on relative change in sample size (R) with γ = 1. The relative change in sample size monotonically increases as ρ and θ increases, respectively. Figure 1 also shows the joint effect of ρ and θ on relative change in sample size. The relative change in sample size increases faster with ρ when θ is large. When θ = 1, the relative change in sample size is equal to ρ.

Figure 1:

The effect of ICC (ρ) and mean cluster size (θ) on relative change in sample size (R)

3. Simulation

We conducted simulation studies to compare the performance of the proposed method and the average cluster size method. In a cluster randomization trial with a count outcome, we assume that the cluster sizes follow discrete uniform distributions DU[5, 15] and DU[25, 85] with mean 10 and 55, variance 10 and 510, and coefficient of variation 0.32 and 0.41, respectively. We explore a wide range of ICC, ρ = 0.05, 0.15, 0.25, 0.35, 0.45, 0.55. ICC is usually less than 0.10 in cluster randomization trials in a community setting (Moerbeek and Teerenstra, 2016). However, ICC larger than 0.10 occasionally occurs in a community intervention trials. For example, in a randomization trial that assessed an educational intervention aimed at improving the management of lung disease in adults attending South African primary care clinics, the ICC takes the value of 0.32 (Amatya et al., 2013). ICC is generally larger than 0.10 in dental studies. For example, in three dental studies in which the unit of sampling was subjects and the unit of analysis was tooth (Banting et al., 1985; Donner and Banting, 1988, 1989), the ICC ranged between 0.354 and 0.432. Thus, we chose the value of ICC that ranges between 0.05 and 0.55 in our simulation. We also consider two combinations of (λ₁, λ₂): (1, 1.5) and (2.5, 2). We specify two-sided type I error α = 0.05 and power 1 − β = 0.9. Under each combination of design parameters, the required numbers of clusters per group are computed for the two methods. The empirical power and empirical type I error are evaluated according to the following algorithm:

1. For each intervention group, generate a set of cluster sizes n_kj for j = 1, … , J; k = 1, 2 from the assumed DU distribution.

2. For the (k, j)th cluster, generate a vector of correlated count observations $Y_{kj}={\left(Y_{kj1},\cdots ,Y_{kj{n}_{kj}}\right)}^{\prime }$, with mean vector 1λ_k and correlation matrix (1−ρ)I+ρ11′. Here I is the identity matrix and 1 is a vector with all elements being 1. One simple approach is to generate $Y_{kji}=Z_{kji}+Z_{kj}^{*}$, where Z_kji are random samples from a Poisson distribution with event rate λ_k(1 − ρ) and $Z_{kj}^{*}$ is generated from a Poisson distribution with event rate λ_kρ. It is easy to show that under this scheme E(Y_kji) = Var(Y_kji) = λ_k and Cov(Y_kji, Y_kji′) = λ_kρ (Mardia, 1970).

3. For k = 1, 2, obtain estimates ${\widehat{\mathrm{\lambda }}}_k$ and $s_k^2$, respectively. Reject H₀ if $\left|{\widehat{\mathrm{\lambda }}}_1-{\widehat{\mathrm{\lambda }}}_2\right|/\sqrt{s_1^2+s_2^2}>z_{1-\alpha /2}$.

Empirical power and type I error are computed as the proportion of times H₀ is rejected under the alternative and null hypothesis, respectively. All the analyses were performed with R version 3.3.3 (http://www.r-project.org). In Table 1 we present the estimated number of clusters (empirical power, empirical type I error) obtained over 10,000 iterations. Within each cell, Rows 1 and 2 corresponds to the results under the proposed method and the average cluster size method, respectively. Table 1 shows that by appropriately accounting for random variability in cluster size, the proposed method generally maintains empirical power and type I error at the nominal levels. On the other hand, the average cluster size method consistently leads to underpowered studies. Table 1 also confirms our theoretical observations that the underestimation of sample size is most severe under high ICC and larger cluster sizes. For example, under ρ = 0.55 and DU[25, 85] where θ = 55, the average cluster size approach underestimates the number of clusters by 10%. On the other hand, under ρ = 0.05 and DU[5, 15] where θ = 10, the estimated numbers of clusters are effectively the same after rounding to integer.

Table 1:

Required number of clusters per group (empirical power, empirical type I error) for the proposed method (p) and the average cluster size method (a)

	Cluster Size Distribution
	DU[5, 15]		DU[25, 85]
ρ/(λ1, λ2)	(1, 1.5)	(2.5, 2)	(1, 1.5)	(2.5, 2)
0.05	16 (90.3%, 0.055)p	29 (90.4%, 0.055)	8 (88.2%, 0.049)	14 (89.2%, 0.054)
	16 (90.5%, 0.052)a	28 (89.6%, 0.052)	8 (88.0%, 0.051)	13 (87.5%, 0.053)
0.15	27 (90.9%, 0.053)	48 (90.3%, 0.052)	20 (91.5%, 0.052)	35 (90.5%, 0.052)
	25 (88.7%, 0.053)	45 (88.7%, 0.053)	18 (88.2%, 0.054)	32 (87.9%, 0.053)
0.25	37 (90.7%, 0.508)	67 (90.4%, 0.050)	31 (90.8%, 0.055)	55 (90.1%, 0.051)
	35 (88.9%, 0.055)	62 (87.9%, 0.048)	28 (88.1%, 0.054)	50 (87.4%, 0.049)
0.35	48 (91.1%, 0.048)	86 (90.1%, 0.051)	42 (90.8%, 0.047)	76 (90.4%, 0.053)
	44 (88.3%, 0.051)	79 (88.0%, 0.046)	39 (88.4%, 0.052)	69 (87.3%, 0.050)
0.45	58 (90.8%, 0.054)	105 (90.9%, 0.049)	54 (91.2%, 0.054)	96 (89.7%, 0.054)
	54 (89.1%, 0.051)	96 (88.1%, 0.051)	49 (87.9%, 0.051)	88 (88.0%, 0.053)
0.55	69 (90.6%, 0.052)	123 (90.1%, 0.051)	65 (90.3%, 0.050)	117 (90.6%, 0.050)
	63 (88.1%, 0.053)	113 (87.3%, 0.052)	59 (87.9%, 0.053)	106 (87.1%, 0.048)

4. Example

To illustrate the application of the proposed sample size estimation method in cluster randomization studies with count data, we consider the cluster randomization trial example provided in Amatya et al. (2013). The investigators were interested in assessing an educational intervention aimed at improving the management of lung disease in adults attending South African primary-care clinics. 40 clinics were included as clusters and randomized into treatment or control group. The goal of enrollment at each clinic was 50 patients and the outcome of interest was the number of clinic visits during the 4-month study period. The analysis reported that ${\widehat{\mathrm{\lambda }}}_1=4.35$, ${\widehat{\mathrm{\lambda }}}_2=3.63$, and $\widehat{\rho }=0.32$. Suppose we want to design a new cluster randomization trial based on the estimated design parameters to achieve 90% power at a two-sided significance level of 5%. If there is no variability in cluster size (every clinic enrolls exactly 50 patients), the required number of cluster is 54. If the variability in cluster sizes is relatively small, say following DU[40, 60], the required number of clusters is 55. Under a larger variability, say DU[25, 75], required number of clusters is 59. Finally, if more patients are expected to be enrolled at each clinic where the cluster sizes follows a distribution of DU[70, 130], the required number of clusters is 55.

5. Discussion

In this paper, we present a realistic sample size estimation formula for count data in cluster randomization trials where clusters sizes are randomly varying. Under a positive ICC, which is usually the case in practice, we demonstrate that ignoring this source of variability would lead to underpowered clinical trials. A higher ICC, a larger averaged cluster size, or a larger coefficient of variation in cluster sizes, is associated with larger percentage increase in sample size requirement. We also show that the traditional sample size formula obtained under constant cluster size assumption is a special case of the proposed method with the coefficient of variation equal to zero.

Compared with traditional sample size methods for cluster randomization trials, the proposed approach requires additional information on the distribution of cluster sizes, specifically, the mean (θ) and variance (τ²) (equivalently, the coefficient of variation γ²). In practice, these parameters can be obtained from previous studies and other sources, such as pilot studies, literature, or educated guess by clinicians.

Simulation studies show that the proposed method can maintain empirical power and type I error at their nominal levels over a wide range of design configurations. However, we observe that under small sample sizes (such as when the number of clusters is less than 15), the empirical powers are slightly lower than the nominal level. This is a problem associated with poor approximation by large sample theory, which affects most sample size methods. Since the number of clusters is usually small in community intervention trials, the use of critical values z_{1− α/2} and z_{1− β} in Equations (4) and (5) instead of critical values t_{1− α/2} and t_{1− β} corresponding to the t-distribution underestimates the required sample size. To adjust for underestimation, Snedecor and Cochran (1989) suggested adding one cluster per group when the sample size is determined with a 5% level of significance, and two clusters per group with a 1% level of significance.

We also consider the sample size estimation method proposed by van Breukelen and Candel (2012a). To compensate for the loss of power due to varying cluster sizes, they adjusted the average cluster size method and derived the sample size formula for the required number of clusters per group (J_BC) as

$$J_{BC}=\frac{J^{*}}{1-\nu (1-\nu ){\gamma }^2},\text{where}\nu =\frac{\theta \rho }{\theta \rho +1-\rho }.$$

We conducted simulation studies to investigate the performance of van Breukelen and Candel’s method using the same parameter settings and algorithm as those in Section 3. Table 2 shows the required number of clusters per group based on van Breukelen and Candel’s method. The estimated numbers of clusters are slightly larger than or equal to those estimated by average cluster size method after rounding to integer, but are still generally too small to maintain the nominal power and type I error levels. It should be pointed out that van Breukelen and Candel’s method was originally developed in the context of a continuous outcome. When applying to trial design with a binary outcome, the intraclass correlation ρ has to be specially defined for a latent continuous variable on the logistic scale. For a count outcome, the appropriate definition of ρ remains unclear. In the above application the intraclass correlation ρ was defined on the scale of the count outcome, which is very likely a misuse of van Breukelen and Candel’s method to the context of a count outcome. We caution this misuse and further investigation into this important research question is warranted.

Table 2:

Required number of clusters per group (empirical power, empirical type I error) for the van Breukelen and Candel’s method

	Cluster Size Distribution
	DU[5, 15]		DU[25, 85]
ρ/(λ1, λ2)	(1, 1.5)	(2.5, 2)	(1, 1.5)	(2.5, 2)
0.05	16 (90.1%, 0.056)	29 (91.2%, 0.052)	8 (88.7%, 0.047)	13 (87.9%, 0.056)
0.15	26 (89.8%, 0.053)	46 (89.3%, 0.055)	18 (88.4%, 0.056)	32 (87.9%, 0.057)
0.25	35 (89.2%, 0.055)	63 (88.7%, 0.050)	28 (88.0%, 0.055)	51 (88.2%, 0.056)
0.35	45 (89.0%, 0.054)	80 (87.9%, 0.056)	39 (88.4%, 0.054)	69 (87.6%, 0.054)
0.45	54 (88.5%, 0.053)	97 (88.9%, 0.049)	49 (87.8%, 0.056)	88 (87.8%, 0.054)
0.55	63 (87.4%, 0.053)	114 (88.0%, 0.051)	59 (87.9%, 0.054)	106 (87.6%, 0.051)