Abstract
Sex differences in the strength of the relations between mathematics anxiety, mathematics attitudes and mathematics achievement were assessed concurrently in sixth grade (n = 1,091, 545 boys) and longitudinally from sixth- to seventh-grade (n = 190, 97 boys). Mathematics anxiety was composed of two facets, one associated with evaluations and the other for learning more generally. Girls had higher mathematics anxiety for evaluations than did boys (ds = −.30 to −.52), but not for mathematics learning. In sixth grade, the negative correlation between mathematical competence and mathematics anxiety for evaluations was stronger in girls than in boys. Longitudinally, higher mathematical competence in sixth grade was associated with lower mathematics anxiety for evaluations and better mathematics attitudes in seventh grade for girls but not for boys. The key finding is that adolescent girls’ mathematics anxiety and their attitudes toward mathematics are more reflective of their actual mathematical competence than they are for boys. One implication is that relative to boys with low mathematics achievement, girls with low achievement are at higher risk of developing mathematics anxiety and poor attitudes toward mathematics.
Keywords: sex differences, mathematics achievement, mathematics anxiety, mathematics attitudes
Sex differences in mathematical development and the sources of these differences are long-term and contentious issues, as these are thought to contribute to the underrepresentation of women in some science, technology, engineering, and mathematics (STEM) fields (Ceci & Williams, 2010; Geary, 1996; Halpern et al., 2007). Mean sex differences in mathematics achievement are generally small (Hyde, Fennema, & Lamon, 1990), although there are more males at the high end of performance (Wai, Hodges, & Makel, 2018). Independent of overall mathematical competence, several non-cognitive factors influence investment in mathematical learning and potentially contribute to the sex difference in math-intensive career choices (Eccles, Adler, & Meece, 1984; Else-Quest, Hyde, & Linn, 2010; Ceci & Williams, 2010; Richardson, Abraham, & Bond, 2012). We focused on two such factors – mathematics anxiety and attitudes (e.g., self-efficacy) – that have been shown to influence various aspects of mathematical development, such as course enrollment, and that often show sex differences (e.g., Eccles & Wigfield, 2002; Eccles et al., 1989; Hembree, 1990).
As we review below, there are many studies of sex differences in mathematics anxiety and mathematics attitudes as these relate to achievement, but the simultaneous and potentially independent contributions of sex differences in anxiety and attitudes to later mathematics achievement are not as well understood (Gunderson, Park, Maloney, Beilock, & Levine, 2018). In a sixth- to seventh-grade longitudinal study, we assessed the cross-lagged and potentially reciprocal relations between these factors and mathematics achievement, and assessed whether any such effects differed for girls and boys. We also conducted a large-scale (n = 1,091) assessment of sex differences in different facets of mathematics anxiety (associated with evaluations versus learning) and attitudes and assessed whether the strength of their relation to concurrent mathematical competence differed for girls and boys in sixth grade.
Sex Differences in Mathematics Anxiety
Mathematics anxiety manifests as apprehension or fear associated with thoughts about or actual engagement in mathematical activities (Ashcraft, 2002; Dowker, Sarkar, & Looi, 2016). This anxiety is associated with increased activity in the brain regions that are engaged during threat detection and with the expression of learned fears, and it is associated with atypical activity of brain regions that support the representation and learning of some forms of mathematics (Lyons & Beilock, 2012; Young, Wu, & Menon, 2012). The latter is consistent with disruptions in functional working memory capacity that in turn undermines mathematical performance (Ashcraft & Kirk, 2001; Maloney & Beilock, 2012), and the engagement of brain regions associated with threat detection and learned fears is consistent with the avoidance and discounting of the importance of mathematics (Hembree, 1990; Meece, Wigfield, & Eccles, 1990). Higher mathematics anxiety is associated with lower mathematical performance in boys and men as well as in girls and women (Ma, 1999), but girls and women generally have higher mean levels of mathematics anxiety and thus may suffer potentially larger consequences relative to boys and men (Hyde, Fennema, Ryan, Frost, & Hopp, 1990; Stoet, Bailey, Moore, & Geary, 2016).
Hyde et al.’s (1990) meta-analysis yielded a small overall sex difference in mathematics anxiety (d = .15), and Stoet et al.’s (2016) analysis of several large-scale data sets (total n = 761,655) yielded somewhat larger differences (ds = .23 to .28). Stoet et al.’s findings are consistent with Hembree’s (1990) early meta-analysis (ds = .19 to .31). Stoet et al. also examined sex differences in mathematics anxiety after controlling for mathematics achievement. Girls showed higher ‘excess’ mathematics anxiety than did boys (ds = .21 to .25), indicating sex differences in mathematics anxiety above and beyond the small overall sex difference in mathematics achievement (ds = .09 to .11). Other studies indicate that the sex difference in mathematics anxiety cannot be fully explained by girls’ and women’s higher levels of trait anxiety (Dowker et al., 2016). A recent study revealed the relation between mathematics anxiety and mathematics performance was stronger in adolescent girls (r = −.35) than in boys (r = −.18, p = .033 for difference; Devine, Fawcett, Szűcs, & Dowker, 2012). Even with control of test anxiety, mathematics anxiety was related to mathematics performance in girls but not in boys.
The finding of ‘excess’ mathematics anxiety in adolescent girls and a stronger relation between anxiety and performance in girls than in boys indicate that anxiety could potentially undermine girls’ mathematics performance more so than that of boys. However, the Stoet et al. (2016) and Devine et al. (2012) studies and in fact most other studies in this literature are correlational and thus the direction of the relations is unclear (Dowker et al., 2016). It is possible that girls’ higher mathematics anxiety contributes to the small sex difference in mathematics achievement, that lower performing girls develop higher levels of mathematics anxiety than lower performing boys, or there are reciprocal relations between these factors over time. Indeed, Gunderson et al. (2018) found that higher achieving first- and second-graders had lower mathematics anxiety six months later (β = −.20), and students with lower mathematics anxiety had higher mathematics achievement six months later (β = −.06). These reciprocal relations were similar for girls and boys, but have not been assessed in any other studies to our knowledge. We conducted a similar analysis with older children and assessed whether the relations between mathematics anxiety and mathematics performance were reciprocal, as found by Gunderson et al., or directional over time, and whether this relation differed across girls and boys.
Moreover, there might be different facets of mathematics anxiety that could manifest differently in boys and girls (Baloglu & Koçak, 2006; Kazelskis, 1998), but that are not always evaluated in developmental studies (Dowker et al., 2016). Wigfield and Meece (1988) found affective (e.g., at ease or not) and cognitive (e.g., worry) components to adolescents’ mathematics anxiety and a sex difference only for the affective component. Even for the affective component, there can be differences across mathematical activities. Baloglu and Koçak (2006) found that college women reported significantly higher anxiety associated with taking mathematics tests (ds = .30 to .41), men reported higher anxiety with numerical activities (ds = .14 to .25; e.g., doing multiplication), and there was no significant sex difference associated with mathematics coursework. Global assessments of mathematics anxiety might then obscure more subtle sex differences, and thus we explored the factor structure of our mathematics anxiety measure (all affective items) and identified two facets, only one of which showed sex differences.
Sex Differences in Mathematics Efficacy and Utility Beliefs
For both sexes, engagement in mathematics learning and enrollment in mathematics courses in high school and college are related to confidence or efficacy about one’s mathematical abilities, as well as to beliefs about the long-term usefulness or utility of mathematics (Crombie et al., 2005; Eccles et al., 1984; Eccles & Wang, 2016; Wigfield & Eccles, 2000). Our analyses (Methods) suggested that efficacy and utility beliefs were part of a single attitudes toward mathematics domain, but we review them independently because most prior studies have separately assessed these concepts.
Earlier studies suggested that boys had stronger mathematics utility (or value) beliefs than did girls (Eccles et al., 1984), but more recent studies are mixed, with some showing no sex difference (Crombie et al., 2005; Lauermann, Tsai, & Eccles, 2017; Petersen & Hyde, 2017; Watt, 2004) and others finding stronger utility beliefs in boys (Steinmayr & Spinath, 2008). Gaspard et al.’s (2015) study of different facets of utility may explain some of the discrepancies. Ninth-grade German boys reported higher mathematics utility as related to their future life and job (ds ~ .3) and that competence in mathematics was personally important (d = .3), whereas girls reported higher utility as related to later achievement in school (d = .15). Whatever the source of these differences, they have the potential to contribute to the sex difference in participation in math-intensive STEM coursework and fields.
Sex differences in academic self-efficacy are small (Hedge’s g = .08), but overall boys and men have higher mathematics efficacy (Hedge’s g = .18) and girls and women higher efficacy in the language arts (Hedge’s g = .16; Huang, 2013; see also Eccles & Wang, 2016; Lauermann et al., 2017; Marsh & Yeung, 1998; Watt, 2004). A meta-analysis of longitudinal studies indicated a small but reliable relation between students’ academic efficacy and their later grades or achievement, especially when the efficacy beliefs and achievement domains matched (e.g., mathematics efficacy and later mathematics achievement, β = .11; Valentine, DuBois, & Cooper, 2004). However, prior efficacy and achievement levels were not controlled in most of the studies included in the analysis and thus the direction of the relation is unclear. A recent meta-analysis of cross-lagged panel studies of academic efficacy and academic performance (across content areas, but including mathematics) found evidence for reciprocal effects in adults (Talsma, Schüz, Schwarzer, & Norris, 2018). Earlier levels of efficacy were related to later achievement (β = .085) controlling earlier achievement, and earlier achievement was related to later levels of efficacy (β = .227) controlling earlier efficacy levels. For children and adolescents (combined), earlier levels of academic achievement were related to later levels of efficacy (β = .133), but earlier levels of efficacy were unrelated to later achievement.
These relations were not moderated by sex, but the measure was the proportion of males in the sample and not separate cross-lagged assessments for males and females and thus was not a sensitive assessment of potential sex differences (Talsma et al., 2018). Lauermann et al. (2017) found reciprocal relations between mathematics efficacy and utility beliefs and math-intensive career plans through the high school years. For both sexes, career plans at the end of high school predicted employment in a STEM profession 15 years later, but men were still overrepresented in these fields. In other words, there are factors above and beyond mathematics efficacy, utility beliefs, and mathematics ability that contribute to the sex difference in STEM fields. One possibility is the sex difference in interest in people and living beings more generally as contrasted with mechanical things. The sex difference in these interests is robust (d = .93; Su, Rounds. & Armstrong, 2009) and contributes to the sex difference in occupational choices (Wang, Eccles, & Kenny, 2013). The sex difference in mathematics anxiety might be another contributing factor, but this is a feasible mechanism only if it contributes to mathematical outcomes above and beyond the influence of mathematics efficacy and utility beliefs, or mathematics attitudes more generally. We assessed this possibility.
Current Study
In all, we addressed two basic and currently unresolved issues. The first is whether mathematics anxiety and mathematics achievement are more strongly related in girls than boys, as a follow up on Devine et al.’s (2012) findings. If this is the case, then anxiety may be more disruptive to girls’ than to boys’ long-term mathematical development. The second concerns whether the longitudinal relations between mathematics achievement and mathematics anxiety and attitudes are directional or reciprocal and whether any such relations differ for anxiety and attitudes. The most relevant study suggested reciprocal relations (Gunderson et al., 2018), but the literature more generally suggests that achievement is more strongly related to later attitudes than the other way around, at least in children and adolescents (Talsma et al., 2018). The direction of these relations has implications for understanding the sources of mathematics anxiety and attitudes, including potential sex differences in these sources.
In addition to the potential importance of anxiety and attitudes, the development of mathematical competence is influenced by cognitive factors, including intelligence, working memory, and prior domain-specific knowledge (Bull & Lee, 2014; Deary, Strand, Smith, & Fernandes, 2007; Geary, Nicholas, Li, & Sun, 2017; Lee & Bull, 2016), but these are not likely to be contributors to the underrepresentation of women in STEM, given there are no substantive sex differences for these traits (Geary, 2010; Welsh, Pennington, & Groisser, 1991). The one exception is the male advantage in visuospatial abilities (Casey, Nuttall, Pezaris, & Benbow, 1995; Sokolowski, Hawes, & Lyons, 2019), but these are only modestly related to the mathematical competencies assessed in this study (Li & Geary, 2017). Nevertheless, to rule out this potential confound, we controlled for spatial abilities in the longitudinal analyses.
Method
Participants
The original sample included 1,157 students as part of an on-going longitudinal study conducted in collaboration with the Columbia Public Schools in Columbia MO and focused on predicting success in high school algebra. Twenty students did not complete one or more tests and were dropped. The basic psychometric analyses were conducted with the remaining 1,137 students. Of these, information on sex was not available for 46 students, leaving 1,091 (545 boys) students for the primary sex differences analysis. All sixth graders were invited to continue in a three-year longitudinal study through the end of high school algebra, and 190 (97 boys) of them agreed and completed all seventh-grade assessments. The longitudinal subsample was followed through the end of seventh grade and provided an assessment of longitudinal change in anxiety and attitudes (these students are currently in eighth grade).
A composite mathematics competence score was developed based on the mathematics tests administered in sixth grade (below) and indicated the students in the longitudinal component (M = 104, SD = 15) were moderately more competent (d = .33) than the students in the sixth-grade sample who did not participate in the longitudinal component (M = 99, SD = 15), t(1089) = −4.50, p < .0001. There were, however, no significant differences on the English and mathematics attitudes or mathematics anxiety measures (below, ps > .13).
Information on age was not available for the larger sample but was for the longitudinal sample. At the time of the sixth-grade testing the mean age was 12 years, 3 months (SD = 5 months) and 13 years, 0 months (SD = 5 months) at the time the standardized mathematics achievement test was administered in seventh grade. The original sample included approximately 86% of all sixth-grade students enrolled in the district. The remaining 14% of students were absent the day of the assessment or unable to participate due to other school obligations that day. For the district, sixth-graders were 61% white, 20% black, 5% Asian, 7% Hispanic, and 6% multiracial, and 43% qualified for free or reduced lunch. For the longitudinal sample, 59% of the students were white, 12% black, 4% Asian, 4% Hispanic, 8% multiracial, and 16% were native American or did not report their race.
Mathematics Tests
The tests and detailed instructions, as well as raw data for the key analyses are available at the Open Science Framework (https://osf.io/z7dju/). The assessment with the original sixth-grade sample included an Exponents and Radical Rules Test that is not reported here because of a high rate of nonresponse. The latter test appeared to be too difficult for many students. The remaining tests assess basic mathematics knowledge and skills that would be expected for a sixth grader and are used here to develop an overall mathematical competence score.
Arithmetic fluency.
The test included 24 vertically placed whole-number addition (e.g., 87 + 5), 24 subtraction (e.g., 35 – 8), and 24 multiplication (e.g., 48 × 2) problems. Students were allowed a total of 2 min to solve as many problems as possible. A composite arithmetic fluency score was based on the number correct (M = 19.29, SD = 6.57) across the three operations (α = .60).
Equality problems.
Students who do not have a mature understanding of mathematical equality have difficulties with problems presented in non-standard formats, such as 8 = __ + 2 – 3 (McNeil & Alibali, 2005; McNeil, Fyfe, Petersen, Dunwiddie, & Brletic‐Shipley, 2011). Thus, we created a 10-item test in multiple choice format (4 options) to assess competence at solving such problems. The first item was standard format and the next two were close to standard format (e.g., 7 = 2 + __), to ensure student engagement with the test. Students did not answer 3.7% of the items and these were scored as incorrect. The data were submitted to an exploratory principle components analysis with promax rotation (Gorsuch, 1983) run in SAS (2014), as well as to Parallel and minimum average parcel (MAP) analyses (R Core Team, 2017). The principle components and Parallel analyses indicated two factors and the MAP one factor but with some evidence for a second factor. Thus, we chose two factors. The first factor explained 42% of the covariance among the items and was defined (standardized loadings > .49) by the seven more difficult problems (e.g., 3 + 1 – 2 = ___ + 1). The second factor explained 12% of the covariance and was defined (standardized loadings > .54) by the three less difficult problems. Performance on the latter problems (M > 93% correct) was close to ceiling and thus these were dropped. An equality composite was based on the seven (M = 53% to 79% correct; overall 71% correct) remaining problems (α = .87).
Fractions arithmetic.
The items included sets of twelve fractions addition (e.g., 1/3 + 1/6), twelve fractions multiplication (e.g., 1/4 × 1/8), and 10 fractions division (e.g., 2 ÷ 1/4) problems. Students had 1 min for each operation to solve as many problems as possible. The score was the sum of the number of addition (M = 6.0, SD = 3.76), multiplication (M = 2.99, SD = 3.04) and division (M = 1.52, SD = 2.4) problems that were solved correctly (α = .58).
Fractions comparison.
The 48 items were an expansion of a shorter version of the fractions comparison test (Geary, Hoard, Nugent, & Bailey, 2013). For each of the 48 pairs, the student circled the larger of the two fractions and was given 90 sec to complete the test. The four item types were developed based on common problem-solving errors and strategies (Hecht, 1998; Hecht, Close, & Santisi, 2003). In the first type the numerator is constant but the denominator differs (e.g., 2/4 2/5), which assesses students’ understanding of the inverse relation between the value of the denominator and the quantity represented by the fraction. In the second type numerators have a ratio of 1.5 and denominators a ratio between 1.1 and 1.25 (e.g., 3/10 2/12), making identification of the larger magnitude easier using numerators (larger value is correct) than denominators (larger value is incorrect). The ratios were determined based on the Weber fraction for ease of magnitude discrimination for adolescents (Halberda & Feigenson, 2008). Numerators and denominators in the third type are reversed (e.g., 5/6 6/5), which requires students to choose the fraction with the larger numerator and smaller denominator. The final type involves skill at using 1/2 as an anchor for estimating fraction values (e.g., 20/40 8/9). The foils are always close to one but contain smaller numerals than the 1/2 fraction. A composite was based on performance (correct – incorrect; M = 17.55, SD = 16.29) across the four item types (α = .87).
Fractions number line.
Following Siegler, Thompson, and Schneider (2011) students were asked to place (one at a time) 10 fractions on the 0 to 5 number line; 10/3, 1/19, 7/5, 9/2, 13/9, 4/7, 8/3, 7/2, 17/4, 11/4. Target fractions were in large font and centered above the line. Students were given 4 min to complete the 10 items, and 94.4% of the lines were completed. The data for the remaining 5.6% of lines were estimated using the average of five estimates derived from the multiple imputations procedure in SAS (2014). Following Siegler et al. and procedures used in studies of whole-number lines (Geary, 2011; Siegler & Booth, 2004), the score for each item was the absolute deviation between the placement and the correct location. The overall score was the mean of the ten items (α = .85).
Equal sign.
Based on students’ poor understanding of mathematical equality (McNeil et al., 2011), two items focusing explicitly on the ‘=‘ were administered. The first asked students to identify the meaning of the symbol ‘=‘ in 3 + 4 = 7 (i.e., ‘add the numbers’, ‘solve the problem’, ‘same as’, ‘the answer’). The second asked students to identify the symbol that indicated that five pennies were the same as one nickel; the options were ‘5 cents’, ‘=‘, ‘+’, and ‘don’t know.’ Performance on the first item was close to ceiling and thus dropped (M = 88% correct). The second item (M = 29% correct) was retained.
Mathematics competence.
The scores for the arithmetic fluency, equality problems, fractions arithmetic, fractions comparison, fractions number line, and equal sign were submitted to a principle components analysis (SAS, 2014). The analysis yielded one factor with an eigenvalue greater than one, and explained 48% of the covariance among the measures. All of the standardized loadings were > .45. Next, each individual variable was standardized (M = 0, SD = 1) and a composite was created based on their mean (α = .79). To make the scores comparable to the standardized measures (below), the composite was then standardized (M = 100, SD = 15).
Academic Attitudes and Anxiety
The grade-appropriate mathematics and English attitudes measures were from the Michigan Study of Adolescent and Adult Transitions (http://garp.education.uci.edu/msalt.html) and, as noted, are designed to assess students’ self-evaluated efficacy and their beliefs about the long-term utility of competence in these areas (Eccles & Wigfield, 2002; Meece et al., 1990). The mathematics attitudes measure included seven items on a 1-to-7 Likert scale; e.g., “How much do you like doing math?” rated from 1 (“a little”) to 7 (“a lot”), and the six English items were similar. Given the importance of these measures to our study, we used three approaches to determine their factor structure. These included an exploratory principle components analysis (PCA) with promax rotation (SAS, 2014) and the number factors based on eigenvalues greater than one, as well as parallel and MAP analyses (R Core Team, 2017). As noted below, the analyses suggested that the utility and efficacy items defined single factors and thus we created overall mathematics and English attitudes measures.
Mathematics attitudes.
The eigenvalues from the PCA suggested two factors, but the parallel and MAP procedures indicated a single factor, and thus we opted for a single mathematics attitudes measure. The score was the mean of the 7 items (α = .84).
English attitudes.
All of the procedures indicated a single factor. The score was the mean of the 6 items (α = .84).
Mathematics anxiety.
The 10 items were adapted from Hopko, Mahadevan, Bare, and Hunt (2003). Each item (e.g., “Taking an examination in a math course”) was rated on a 1 (low anxiety) to 5 (high anxiety) scale. The MAP analysis suggested a single factor but the eigenvalues from the CPA and the parallel analysis indicated two factors and thus we opted for two mathematics anxiety variables. The first factor explained 43% of the covariance among items and was defined (standardized loadings > .55) by five items that involved learning mathematics (e.g., “Having to use the tables in the back of a math book”; items 1, 3, 6, 7, 9). The second factor explained 13% of the covariance among items and was defined (standardized loadings > .57) by four items that involved some type of evaluation (e.g., “Taking an examination in a math course”; items 2, 4, 5, 8). The final item (i.e., item 10; “In general, how anxious are you about math?”) loaded (> .52) on both factors but slightly better on the evaluation than learning factor and thus was included in the former. Composite scores were based on the mean of the five learning anxiety items (α = .76) and of the five evaluation anxiety items (α = .81). The factors were moderately correlated (r = .47), and consistent with the mathematics tests and mathematics coursework factors identified by Baloglu and Koçak (2006). Our measure, however, did not include items with specific numerical activities (e.g., multiplication) and thus we could not assess whether such a facet exists in adolescents.
Standardized and Cognitive Tests
Intelligence.
Students in the longitudinal cohort were administered the Vocabulary and Matrix Reasoning subtests of the Wechsler Abbreviated Scale of Intelligence (WASI; Wechsler, 1999). Based on standard procedures, scores from these subscales were used to generate an estimated full scale IQ. The intelligence of the longitudinal sample was average (M = 105, SD = 13).
Achievement.
For the longitudinal cohort, mathematics and reading achievement were assessed with the Numerical Operations and Word Reading subtests from the Wechsler Individual Achievement Test–Third Edition (Wechsler, 2009), respectively. The easier Numerical Operations items for students of this age included basic arithmetic and continued through fractions, algebra, geometry and calculus. The Word Reading assessment involved a measure of single word reading. Words begin with simple, 1-syllable items and progress to more complex vowel, consonant, and morphology types. The mathematics (M = 100, SD = 19) and reading (M = 104, SD = 13) achievement of the students in the longitudinal sample was average.
Spatial ability.
Following the work of Collaer, Reimers, and Manning (2007), the Judgment of Line Angle and Position Test (JLAP; see also Benton, Varney, & Hamsher, 1978) was administered as part of a larger assessment of cognitive abilities. The test shows a reliable sex difference (Collaer, Reimers, & Manning, 2007), and is dependent on the right parietal cortex that is often associated with mathematical learning (Dehaene, Piazza, Pinel, & Cohen, 2003). The task requires participants to match the angle of the single presented line to one of 15 line options in the array at the bottom center of the screen (see Figure 1). The task was administered on iPads using a customized program developed through Inquisit by Millisecond. There were 20 test items presented one at a time and the participant used the touch screen to select the matching angle. Each stimulus was presented for a maximum of 10 sec, and when a selection was made, a reaction time was recorded and the participant moved to a “next” screen to prepare for the next stimulus. The outcome was the number correct. Collaer and Nelson (2002) reported an adequate test-retest reliability (r = .76), and for the current sample boys (M = 13.90, SD = 2.88) outperformed girls (M = 12.44, SD = 3.20), t(188) = 3.30, p = .0012, d = .47.
Figure 1.
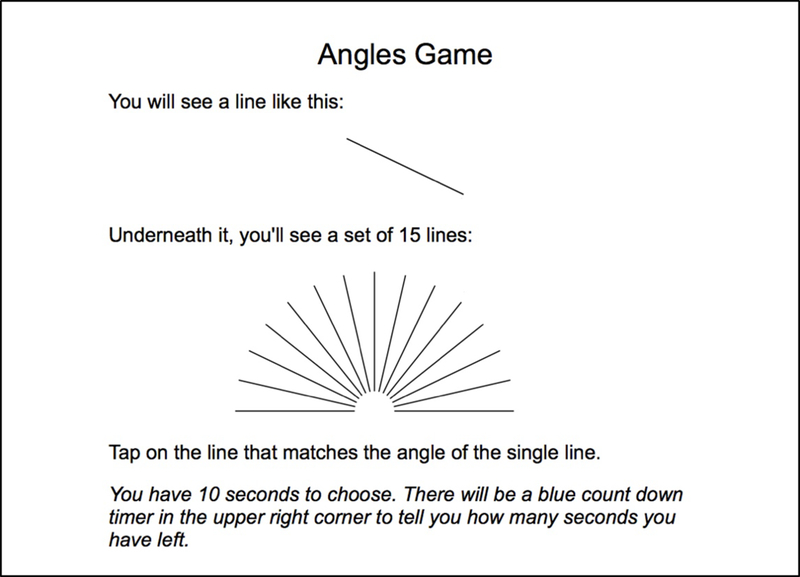
Instruction screen for Judgement of Line Angle and Position Test (JLAP).
Procedure
Assessment.
For the end of sixth-grade assessment, groups of 14 to 32 students were administered the mathematics tests and academic attitudes measures in their classroom. This assessment took about 45 min. For the longitudinal sample, students were administered the intelligence, achievement, anxiety, attitudes, and spatial measures one-on-one at a quiet location in their school. The assessments were part of three longer assessments of about 45 min each. The spatial measure was administered the first semester of 7th grade, and the intelligence, achievement, anxiety, and attitudes measures were administered in a single session the second semester of seventh grade.
Analyses.
The sixth-grade analyses focused on mean sex differences in mathematical competence and academic attitudes and anxiety, as well as sex differences in the correlations among these measures. These were conducted with the overall sample (n = 1,091) and replicated in two subsamples that were created taking the first 545 (subsample 1) and the next 546 (subsample 2) students who were assessed. Using cross-lagged panel analyses, the longitudinal component focused on sex differences in the relations between mathematics anxiety, attitudes, and mathematical competence and achievement across grades. We report effect sizes for mean sex differences as Cohen’s (1988) d [d = (Mboys – Mgirls)/pooled SD], with positive values indicating higher scores in boys and negative values higher scores in girls.
The sixth-grade sample was recruited from six schools and there was a small but significant difference in mathematical competence score across schools, R2 = .056, F(5, 1085) = 12.90, p < .0001. The mean mathematics scores ranged from 95 to 105 across schools. In order to model the nested structure of the data in the assessment of sex differences, we used multi-level models with Proc Mixed (SAS, 2014), using students as level 1 units and schools as level 2 units, allowing intercepts to vary randomly for schools.
Results
Sixth Grade
The results are presented for the overall sample and the subsamples, followed by a summary of key findings.
Overall sample.
Mean standardized mathematical competence and mean attitudes and anxiety scores are shown in Table 1 for boys (n = 545) and girls (n = 546). To control for false positives, a Bonferroni corrected p value of .0024 was used for correlations and .007 for mean sex differences. The validity of the self-reports is supported by the finding that mathematical competence was unrelated to English attitudes for either girls (r = .10, p = .0188) or boys (r = .00, p = .9744), but statistically significantly related to mathematics attitudes for both girls (r = .28, p < .0001) and boys (r = .26, p < .0001). As described below, the relation between mathematical competence and the mathematics anxiety measures sometimes differed for girls and boys.
Table 1.
Sex differences in means and correlation for the overall cross-sectional sample
| Boys | Girls | |||||||
|---|---|---|---|---|---|---|---|---|
| Measure | M (SD) | M (SD) | d | 1 | 2 | 3 | 5 | 6 |
| 1. Mathematical competence | 101. 06 (15.21) | 99.12 (14.31) | .13 | 1.00 | .10 | .28b | −.19b | −.31b |
| 2. English attitudes | 4.74 (1.15) | 5.18 (1.14) | −.38a | .00 | 1.00 | .05 | .07 | .03 |
| 3. Mathematics attitudes | 4.92 (1.07) | 4.67 (1.09) | .23a | .26b | .10 | 1.00 | −.29b | −.26b |
| 5. Math anxiety evaluation | 2.80 (0.94) | 3.11 (1.01) | −.31a | −.05 | .12 | −.15b | 1.00 | .60b |
| 6. Math anxiety learning | 1.92 (0.82) | 2.03 (0.81) | −.14 | −.23b | .08 | −.15b | .55b | 1.00 |
Note: d = (Mboys – Mgirls)/pooled SD.
= significant mean difference with Bonferroni corrected p value (.007). Correlations for boys are below the diagonal and above the diagonal for girls.
= significant with Bonferroni corrected p value (.0024).
Using the Bonferroni corrected criterion, there were no significant sex differences in mathematical competence (p = .009), or mathematics anxiety for learning (p = .018). Girls had better English attitudes (p < .0001) than did boys, and boys had better mathematics attitudes and less mathematics anxiety related to evaluations (ps < .0001) than did girls. As shown in Table 1, the correlations among the measures are remarkably similar across girls and boys. Of the correlations that were statistically significant, the largest sex differences (using Fisher’s r-to-z, 2 tailed) involved mathematics anxiety for evaluations. The relation between mathematics anxiety for evaluations and mathematical competence was stronger in girls (r = −.19, p < .0001) than in boys (r = −.05, p = .2333), z = −2.34, p = .0198, as was the relation between mathematics anxiety for evaluations and mathematics attitudes, z = −2.43, p = .0151; r = −.29, p < .0001 for girls, and r = −.15, p = .0006 for boys. The relation between mathematics anxiety for learning and mathematics attitudes was also stronger for girls (r = −.26, p < .0001) than for boys (r = −.15, p = .0004), z = −1.89, p = .0588.
These patterns suggest that girls’ mathematics anxiety for evaluations is more strongly related to their actual mathematical competence and mathematics attitudes than it is for boys. To further assess this, in a mixed model with schools as a level-2 random effect, we predicted the sex difference in mathematics anxiety for evaluations controlling for mathematical competence and estimating the interaction between sex and mathematical competence. The sex difference in mathematics anxiety for evaluations remained statistically significant, controlling for mathematical competence, F(1,1082) = 10.9, p = .001 ɳp2 = .01 . The statistically significant interaction, F(1,1082) = 6.57, p = .0105, ɳp2 = .01, indicated that the relation between mathematics anxiety for evaluations and mathematical competence was stronger in girls than in boys, with the control of overall mathematical competence. Similarly, controlling for mathematical competence, better mathematics attitudes were associated with lower mathematics anxiety for evaluations, F(1,1081) = 43.46, p < .0001, ɳp2 = .04, and the statistically significant interaction, F(1081) = 6.71, p = .0097, ɳp2 = .01, revealed a stronger relation between these measures for girls (β = −.28) than for boys (β = −.12), t = −2.59, p = .0097.
Subsamples.
To assess the robustness of these effects, we reran the analyses for each of the two subsamples. Both subsamples were average on the mathematical competence measure (M = 101, SD = 14, M = 99, SD = 15, d = .12, p = .0495). As shown in Table 2, for the first subsample (n = 545; 249 boys) and using the corrected p value (.007), there was no sex difference in mathematical competence (p = .0128). Girls had better English attitudes (p = .0001) than did boys, and boys had better mathematics attitudes (p = .0003) than did girls. Girls reported higher mathematics anxiety for evaluations (p < .0001) than did boys, but there was no sex difference for mathematics anxiety for learning (p = .0585). The pattern is identical to that found in the whole sample. As with the whole sample, the correlation between mathematics anxiety for evaluations and mathematical competence was stronger for girls (r = −.24, p < .0001) than for boys (r = −.10, p = .1278), but there was only a trend for the difference between these correlations, z = −1.67, p = .0949. The relation between mathematics anxiety for evaluations and mathematics attitudes was also stronger for girls (r = −.29, p < .0001) than for boys (r = −.23, p < .0002), but the difference was not statistically significant, z = −0.74, p = .4593. There was also a stronger correlation between mathematics anxiety for learning and mathematics attitudes for girls (r = −.25, p < .0001) than for boys (r = −.14, p = .0224), but the difference was not statistically significant, z = −1.32, p = .1868.
Table 2.
Sex differences in means and correlation for subsamples from the cross-sectional sample
| Boys | Girls | Correlations | ||||||
|---|---|---|---|---|---|---|---|---|
|
Subsample 1 (n = 545, 249 boys) | ||||||||
| Measure | M (SD) | M (SD) | d | 1 | 2 | 3 | 4 | 5 |
| 1. Mathematical competence | 102.22 (14.15) | 99.91 (13.97) | .16 | 1.00 | .06 | .27b | −.24b | −.36b |
| 2. English attitudes | 4.74 (1.18) | 5.12 (1.16) | −.32a | −.12 | 1.00 | .05 | .07 | .06 |
| 3. Mathematics attitudes | 4.97 (1.03) | 4.67 (1.08) | .28a | .30b | .07 | 1.00 | −.29b | −.25b |
| 4. Math anxiety evaluation | 2.79 (0.91) | 3.13 (1.06) | −.34a | −.10 | .08 | -23b | 1.00 | .66b |
| 5. Math anxiety learning | 1.91 (0.79) | 2.02 (0.83) | −.14 | −.23b | .04 | −.14 | .53b | 1.00 |
|
Subsample 2 (n = 546, 296 boys) | ||||||||
| 1. Mathematical competence | 100.08 (16.00) | 98.18 (14.66) | .12 | 1.00 | .16 | .29b | −.14 | −.26b |
| 2. English attitudes | 4.73 (1.13) | 5.25 (1.12) | −.45a | .09 | 1.00 | .06 | .07 | −.01 |
| 3. Mathematics attitudes | 4.88 (1.11) | 4.66 (1.11) | .20 | .24b | .13 | 1.00 | −.28b | −.27b |
| 4. Math anxiety evaluation | 2.81 (0.96) | 3.10 (0.94) | −.30a | −.02 | .15 | −.08 | 1.00 | .52b |
| 5. Math anxiety learning | 1.93 (0.84) | 2.04 (0.78) | −.14 | −.23b | .11 | −.16 | .57b | 1.00 |
Note: d = (Mboys – Mgirls)/pooled SD.
= significant mean difference with Bonferroni corrected p value (.007). Correlations for boys are below the diagonal and above the diagonal for girls.
= significant with Bonferroni corrected p value (.0024).
As shown in Table 2, the mean differences found in the first subsample were largely replicated in the second (n = 546; 296 boys). There were no significant sex differences for mathematical competence (p = .1934), mathematics attitudes (p = .0197) or mathematics anxiety for learning (p = .1307). Girls had better English attitudes (p < .0001) and higher mathematics anxiety for evaluations (p = .0004) than did boys. There was again a stronger correlation between mathematics anxiety for evaluations and mathematics attitudes for girls (r = −.28, p < .0001) than for boys (r = −.08, p = .1552), z = −2.4, p = .0164. The sex difference in the correlations between mathematics anxiety for learning and mathematics attitudes was not statistically significant (p = .1802).
Summary.
We found no substantive sex difference in mathematical competence (ds = .12 to .16) but consistent differences in academic attitudes and anxiety. Girls had consistently better English attitudes (ds = −.32 to −.45), as well as higher mathematics anxiety for evaluations (ds = −.30 to −.34) than did boys, whereas boys had consistently better mathematics attitudes (d = .20 to .28) than did girls. There were no substantive sex differences for mathematics anxiety for learning (ds = −.14). Correlational patterns suggested a stronger link between mathematical competence and mathematics anxiety for evaluations in girls than in boys.
Longitudinal
Mean scores and correlations among the key variables are shown in Table 3 for the longitudinal sample. The validity of the sixth-grade mathematical competence variable is supported by a stronger correlation with Numerical Operations (r = .76, p < .0001) than Word Reading (r = .46, p < .0001) scores, z = 4.578, p < .0001.
Table 3.
Sex differences in means and correlation for key measures for longitudinal sample
| Boys | Girls | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Measure | M (SD) | M (SD) | d | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Sixth Grade | ||||||||||
| 1. Mathematical competence | 106.53 (15.33) | 102.25 (14.01) | .29 | 1.00 | .05 | .39b | −.20 | −.31b | --- | --- |
| 2. English attitudes | 4.62 (1.14) | 5.32 (1.17) | −.59a | −.03 | 1.00 | .02 | .18 | .15 | --- | --- |
| 3. Mathematics attitudes | 4.96 (1.08) | 4.84 (1.13) | .11 | .30 | .10 | 1.00 | −.22 | −.20 | --- | --- |
| 4. Math anxiety evaluation | 2.79 (0.86) | 3.14 (1.07) | −.36 | .13 | .16 | −.06 | 1.00 | .69b | --- | --- |
| 5. Math anxiety learning | 1.88 (0.85) | 2.04 (0.86) | −.19 | −.03 | .16 | −.08 | .48b | 1.00 | --- | --- |
| Seventh Grade | ||||||||||
| 1. Numerical Operations | 100.23 (18.25) | 98.74 (19.16) | .08 | 1.00 | .00 | .33b | −.29 | −.39b | .52b | .52b |
| 2. English attitudes | 4.97 (0.99) | 5.09 (1.14) | −.11 | .10 | 1.00 | −.13 | .21 | −.03 | .13 | .31b |
| 3. Mathematics attitudes | 5.25 (0.83) | 5.01 (0.97) | .27 | .33b | .22 | 1.00 | −.48b | −.39b | .12 | −.03 |
| 4. Math anxiety evaluation | 2.34 (0.88) | 2.82 (0.93) | −.52a | −.11 | .09 | −.33b | 1.00 | .56b | −.14 | −.09 |
| 5. Math anxiety learning | 1.63 (0.59) | 1.79 (0.70) | −.25 | −.26 | .00 | −.38b | ,55b | 1.00 | −.39b | −.18 |
| 6. Intelligence | 105.44 (12.98) | 103.98 (13.94) | .11 | .46b | .16 | .20 | −.15 | −.17 | 1.00 | .58b |
| 7. Word Reading | 103.92 (12.69) | 103.81 (14.02) | .01 | .43b | .09 | .07 | −.12 | −.27 | .54b | 1.00 |
Note: d = (Mboys – Mgirls)/pooled SD.
= significant mean difference with Bonferroni corrected p value (.007). Correlations for boys are below the diagonal and above the diagonal for girls.
= significant with Bonferroni corrected p value (.0024). The correlation between girls’ mathematical competence in 6th grade and mathematics anxiety for learning (r = −31) approached the cutoff, p = .0029.
Basic sex differences.
For sixth grade, the same pattern of mean sex differences was found for the overall and longitudinal samples. Due to the smaller longitudinal sample, only girls’ better English attitudes (p < .0001) met the Bonferroni corrected criterion. Girls’ higher mathematics anxiety for evaluations met conventional significance levels (p = .0124), but no other effects did (ps > .12). In seventh grade, the only statistically significant mean difference, after the Bonferroni correction, was for mathematics anxiety for evaluations (p = .0003).
We assessed across-grade changes in English attitudes and mathematical anxiety for evaluations in a mixed model with schools as a level-2 random effect. The same results emerged when the data were analyzed with a 2 (grade) by 2 (sex) repeated measures analysis of variance. For English attitudes, there was a statistically significant main effect for sex, F(1,371) = 13.16, p = .0003, ɳp2 = .03, and a sex by grade, F(1,371) = 6.6, p = .0106, ɳp2 = .02, interaction. The main effect for grade was not statistically significant (p = .6052). The interaction emerged because girls’ attitudes about English declined from sixth- to seventh-grade, which eliminated the sex difference (Table 3). For mathematics anxiety for evaluations, there were statistically significant main effects for grade, F(1,371) = 5.65, p = .0179, ɳp2 = .02, and sex F(1,371) = 18.91, p < .0001, ɳp2 = .05, but the interaction was not statistically significant (p = .5075). Mathematics anxiety for evaluations decreased for both sexes across grades, but overall boys had lower mathematics anxiety for evaluations than did girls.
For sixth grade, the correlations among the variables were highly similar across girls and boys, as found for the prior analyses. As found for the overall sample, the relation between mathematical competence and mathematics anxiety for evaluations was higher for girls (r = −.20, p = .0512) than for boys (r = .13, p = .2188), z = −2.26, p = .0238, but neither correlation exceeded the Bonferroni cutoff. Among the correlations that did exceed the cutoff, the correlation between mathematics anxiety for evaluations and learning was stronger for girls (r = .69, p < .0001) than for boys (r = .48, p < .0001), z = 2.2, p = .0278. None of the other correlations differed across the sexes (ps > .17). For seventh grade, the correlations among the variables were again highly similar across girls and boys, and none of the correlations involving attitudes and anxiety differed for girls and boys (ps > .20).
Cross-lagged path analysis.
The analyses focused on mathematics attitudes and mathematics anxiety for evaluations, because these showed consistent sex differences. The correlations used for the whole-sample analysis are shown in Table 4 and separately for boys and girls in Table 5. If these beliefs influence mathematical development, then higher levels of anxiety and poor attitudes toward mathematics in sixth grade should be related to lower mathematics achievement in seventh grade, controlling sixth-grade mathematical competence. Alternatively, if mathematical competence influences mathematics anxiety for evaluations and mathematics attitudes, then seventh-grade outcomes in these domains should be predicted by sixth-grade mathematical competence, controlling the relation between sixth- and seventh-grade anxiety and attitudes. Moreover, if girls are more sensitive to their relative mathematical competence than are boys, as suggested by the pattern of correlations in the overall sixth-grade sample, then the relation between competence and later anxiety and attitudes should be stronger in girls than in boys. Note that we are not asking if the sex differences in anxiety or attitudes mediate the small sex difference in mathematics achievement, but rather whether the relation between within-sex variation in anxiety, attitudes, and achievement is stronger in girls than in boys.
Table 4.
Correlations used in path analyses for longitudinal sample for all students
| Correlations | ||||||
|---|---|---|---|---|---|---|
| Measure | 1 | 2 | 3 | 4 | 5 | 6 |
| 1. Mathematical competence in 6th | 1.00 | |||||
| 2. Math anxiety evaluation in 6th | −.07 | 1.00 | ||||
| 3. Mathematics attitudes in 6th | .34 | −.16 | 1.00 | |||
| 4. Numerical Operations in 7th | .76 | −.07 | .28 | 1.00 | ||
| 5. Math anxiety evaluation in 7th | −.18 | .46 | −.21 | −.21 | 1.00 | |
| 6. Mathematics attitudes in 7th | .32 | −.06 | .58 | .31 | −.39 | 1.00 |
Note: Correlations > |.27|, p < .0001. Correlations < |.14|, p > .05. JLAP = Judgment of Line Angle and Position Test
Table 5.
Correlations used in path analyses for longitudinal sample for boys and girls separately
| Correlations | |||||||
|---|---|---|---|---|---|---|---|
| Measure | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1. Mathematical competence in 6th | 1.00 | −.20 | .39 | .78 | −.31 | .37 | .30 |
| 2. Math anxiety evaluation in 6th | .13 | 1.00 | −.22 | −.14 | .47 | −.08 | .06 |
| 3. Mathematics attitudes in 6th | .30 | −.06 | 1.00 | .30 | −.24 | .49 | −.09 |
| 4. Numerical Operations in 7th | .76 | .02 | .27 | 1.00 | −.29 | .33 | .30 |
| 5. Math anxiety evaluation in 7th | .01 | .41 | −.16 | −.11 | 1.00 | −.45 | −.01 |
| 6. Mathematics attitudes in 7th | .23 | .01 | .69 | .28 | −.28 | 1.00 | .05 |
| 7. JLAP | .29 | .00 | .04 | .20 | −.04 | −.04 | 1.00 |
Note: Correlations for girls are above the diagonal and correlations for boys are below the diagonal. Correlations > |.39|, p < .0001. Correlations < |.16|, p > .05. JLAP = Judgment of Line Angle and Position Test.
To assess these alternatives, we conducted a series of path analyses using Proc Calis (SAS, 2014). We first estimated autoregressive paths for key variables, and then paths from sixth grade anxiety and attitudes to seventh grade mathematics achievement. We followed this with a model that estimated paths from sixth grade mathematical competence to seventh grade anxiety and attitudes. The best of these models was then estimated separately for girls and boys using a simultaneous analysis, with and without control of spatial ability. We estimated the fit of the various models using standard measures, that is, χ2 (non-significant effects indicate better model fit), root mean square error approximation (RMSEA, values < .08 indicate good model fit), the comparative fit index (CFI, values > .95 indicate good model fit), and the normed fit index (NFI, values > .95 indicate good model fit; Kline, 2015). The key measures were mathematical competence and achievement (Numerical Operations) in sixth- and seventh-grade, respectively, and mathematics anxiety for evaluations and mathematics attitudes in sixth- and seventh-grade.
In the baseline model (Model 1, Table 6), we estimated across-grade autoregressive paths for mathematics achievement, anxiety, and attitudes. As shown in Table 6, none of the fit indexes were acceptable, indicating significant remaining covariation among the variables. The Lagrange multiplier indicated that estimation of the correlation between the error terms for mathematics attitudes and mathematics anxiety for evaluations in seventh grade would substantively improve model fit (p < .0001), whereas estimating the correlations between the error terms for these variables and the error term for seventh-grade mathematics achievement would not improve model fit (ps > .12). Estimating the former resulted in Model 2 and a statistically significant improvement in model fit, Δχ2 = 31.42, p < .0001, as well as improvements for all of the fit indexes.
Table 6.
Fit indexes from path models from the longitudinal sample
| Model | χ2 | df | parameters | p | Models | Δχ2 | p | RMSEA (90% confidence interval) | CFI | NFI |
|---|---|---|---|---|---|---|---|---|---|---|
| Overall Sample | ||||||||||
| M1. Autoregressive paths | 45.36 | 9 | 12 | .0001 | --- | --- | --- | .15 (.11, .19) | .90 | .87 |
| M2. M1 + correlated error | 13.94 | 8 | 13 | .0832 | M2 vs. M1 | 31.42 | .0001 | .06 (.00, .12) | .98 | .96 |
| M3. M2 + att & anxiety to math | 13.58 | 6 | 15 | .0346 | M3 vs. M2 | 0.36 | .8353 | .08 (.02, .14) | .98 | .96 |
| M4. M2 + math to att & anxiety | 6.3 | 6 | 15 | .3905 | M4 vs. M2 | 7.64 | .0219 | .02 (.00. .10) | 1.0 | .98 |
| M5. M4 + att & anxiety to math | 5.94 | 4 | 17 | .2037 | M5 vs. M4 | 0.36 | .8353 | .05 (.00, .13) | .99 | .98 |
| Simultaneous Multi-sample: Boys and Girls | ||||||||||
| M6. M4 simultaneous | 8.02 | 6 | 21 | .2368 | --- | --- | --- | .06 (.00, 16) | .99 | .96 |
Note: att = mathematics attitudes; anxiety = mathematics anxiety for evaluations. RMSEA = root mean square error approximation (lower values mean a better fit); CFI = Comparative Fit Index (higher values mean a better fit); NFI = Bentler-Bonnet Normed Fit Index (higher values mean a better fit). The df for the Δχ2 is the difference in df across the two models noted in the Models column.
Model 3 provided a test of the hypothesis that anxiety and attitudes in sixth grade contributed to mathematics achievement in seventh grade. Relative to Model 2, fitting this model resulted in a non-significant change in model fit, Δχ2 = 0.36, p = .8353, a larger RMSEA value (indicating worse fit), and no improvement in fit based on the CFI and NFI. Moreover, neither of the sixth- to seventh-grade paths differed from 0 (ps > .66).
Model 4 provided a test of the hypothesis that mathematical competence in sixth grade influences mathematics anxiety and attitudes in seventh-grade. Relative to Model 2, fitting this model resulted in a statistically significant improvement in model fit, Δχ2 = 7.64, p = .0219. The RMSEA, CFI, and NFI values all indicated a better fit for Model 4 than for Model 2, and an overall excellent fit for Model 4.
Finally, we added the sixth-grade anxiety and attitudes to seventh-grade mathematics achievement paths to Model 4, creating Model 5. The latter model assesses reciprocal cross-grade relations between the anxiety, attitudes, and achievement measures. As shown in Table 6, the specification of Model 5 did not improve model fit, χ2(2) = 0.36, p = .8353, and in fact the RMSEA value indicated a worse fit than Model 4. Thus, we accepted Model 4 as the best representation of the patterns in these data. As shown in Figure 2, the individual paths for Model 4 indicated that higher mathematical competence in sixth grade was associated with lower mathematics anxiety for evaluations (β = −.14, t = −2.30, p = .0215) and better mathematics attitudes (β = .15, t = 2.34, p = .0191) in seventh grade.
Figure. 2.
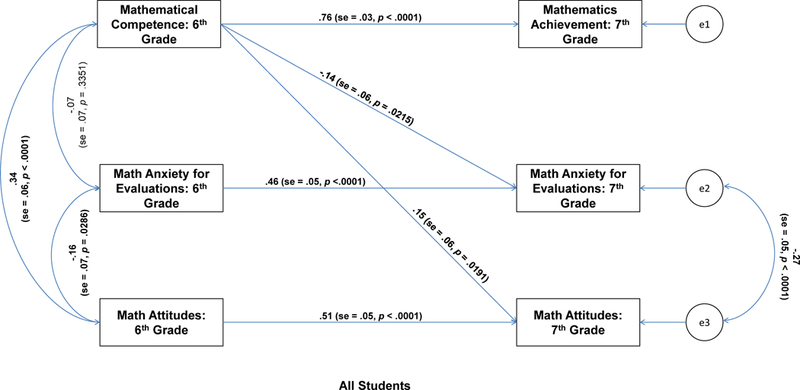
Path analysis for all students (n = 190).
To determine if the pattern of relations shown in Figure 2 differed for girls and boys, Model 4 was rerun using a simultaneous multi-sample path analysis. To reduce the number of estimated parameters and thus increase power, the three autoregressive paths were constrained to equality across girls and boys, but all other parameters were estimated separately (e.g., the correlated error for seventh-grade anxiety and attitudes) including the sixth-grade mathematics anxiety and attitudes paths to seventh-grade mathematics achievement. As shown in Table 6, all indexes indicated a good to excellent overall fit to the data. The associated paths are shown in Figure 3 for girls and Figure 4 for boys. For boys, neither the path from sixth-grade mathematical competence to mathematics anxiety for evaluations nor the path to mathematics attitudes in seventh grade were statistically significant (ps > .60). For girls, in contrast, both the path to mathematics anxiety for evaluations (p = .001) and mathematics attitudes (p < .0001) were statistically significant. A test of the equality of these estimates revealed statistically significant sex differences for the path from sixth-grade mathematical competence to seventh-grade mathematics anxiety, χ2(1) = 4.44, p = .035, and for the path from sixth-grade mathematical competence to seventh-grade mathematics attitudes, χ2(1) = 9.05, p = .0026.
Figure. 3.
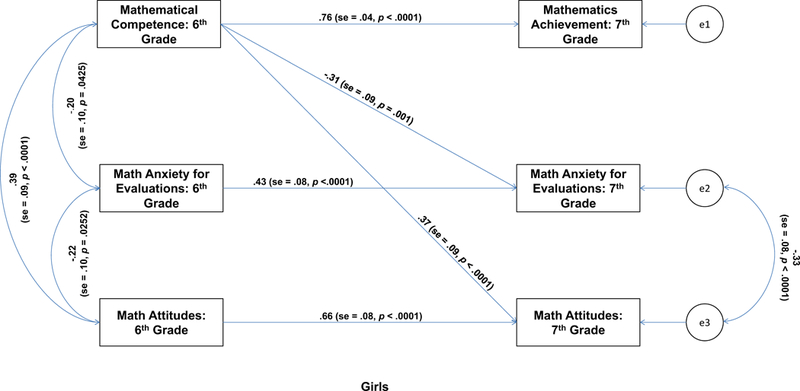
Path analysis for girls (n = 93).
Figure. 4.
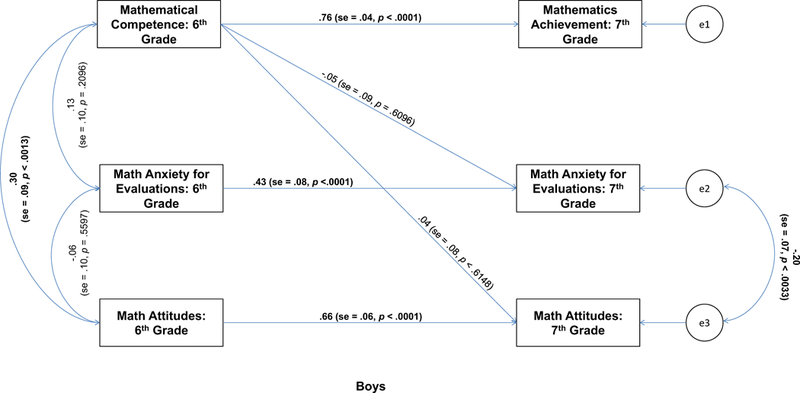
Path analysis for boys (n = 97).
To determine if the sex difference on the spatial measure (i.e., JLAP) influenced the pattern of results, we then reran the models shown in Figure 3 and Figure 4 with the addition of a direct path from the Judgment of Line Angle and Position Test to mathematical competence in sixth grade and mathematics achievement in seventh grade. These paths were constrained to equality across girls and boys and controlled for the relation between spatial ability and mathematics achievement. The path from spatial ability to sixth-grade mathematical competence was statistically significant (β = .29, t = 3.05, p = .0023), but the path to seventh-grade mathematics achievement was not (p = .76276). Critically, the basic findings were unchanged. Girls with higher mathematical competence in sixth grade had lower mathematics anxiety for evaluations (β = −.22, t = −2.53, p = .0115) and better mathematics attitudes (β = .24, t = 2.64, p = .0083) in seventh grade, whereas these paths were not statistically significant for boys (ps > .59). Moreover, the sex differences for the relation between mathematical competence in sixth grade and mathematics anxiety for evaluations, χ2(1) = 4.47, p = .0345, and for mathematics attitudes, χ2(1) = 9.27, p = .0023, in seventh grade remained statistically significant.
Summary.
In seventh grade there were no substantive sex differences in intelligence or standardized mathematics or reading achievement (ds = .01 to .11). The basic patterns found for the overall sample remained in the longitudinal sample, although some of the effects were not statistically significant due to lower power. The key findings for the overall sample were the sex difference in mathematics anxiety for evaluations and its relation to mathematical competence and this same pattern was found in the longitudinal sample. From sixth- to seventh-grade, the sex difference in English attitudes disappeared (d = −.59 and −.11, respectively, for sixth and seventh grade), but girls’ higher mathematics anxiety for evaluations was still evident in seventh grade (d = −.52). Path analyses indicated that mathematics anxiety for evaluations and mathematics attitudes in sixth grade were not related to mathematics achievement in seventh grade. However, mathematical competence in sixth grade was related to mathematics anxiety for evaluations and mathematics attitudes in seventh grade for girls but not for boys.
Discussion
The results extend our understanding of the sex differences in mathematics anxiety and attitudes (Hembree, 1990; Hyde et al., 1990; Stoet et al., 2016), and provide insights into how non-cognitive factors might differentially influence the mathematical development of girls and boys. We discuss the latter in the context of sex differences in mathematics anxiety and attitudes, but first address the more general question of whether the relations between these factors and mathematical competence is directional or reciprocal.
Cross-Lagged Relations
Independent of sex differences, our combined (across boys and girls) cross-lagged results confirmed Talsma et al.’s (2018) meta-analytic finding for children and adolescents, that is, earlier mathematical competence predicted later anxiety and attitudes, whereas earlier anxiety and attitudes were not related to later achievement. Gunderson et al. (2018) also found that earlier mathematics achievement predicted later mathematics anxiety (β = −.20) in first- and second-graders, but also that earlier anxiety predicted later achievement (β = −.06). Our Model 5 in fact showed the same pattern but both paths were smaller than those found by Gunderson et al. (βs = −14, −.02, respectively) and the path from anxiety to achievement was not statistically significant.
Nevertheless, based on Gunderson et al.’s results, Talsma et al.’s results for adults, and other findings (e.g., Ashcraft & Kirk, 2001), it is very likely that high mathematics anxiety will concurrently and prospectively undermine some aspects of mathematical performance in many individuals. Indeed, Marsh and Yeung (1998) found that the relation between earlier academic attitudes was stronger for later grades than for later test performance and thus our findings may underestimate the influence of anxiety and attitudes on some aspects of later mathematics performance. At the same time, the influence of mathematical competence on the independent development of mathematics anxiety and attitudes should not be underestimated.
Mathematics Anxiety
The first key finding is that the sex difference in mathematics anxiety was specific to evaluations, such as taking a quiz, and not all mathematical activities. The two associated facets of mathematics anxiety related to evaluations and learning are consistent with Baloglu and Koçak’s (2006) finding that women reported higher mathematics anxiety associated with mathematics tests but not mathematics coursework. Wigfield and Meece (1988) found that the sex difference in mathematics anxiety was related to negative affect and not to cognitions (e.g., worrying about mathematics class), which is consistent with our results, given the measure focused directly on affect (i.e., anxiety). Even with a focus on affect, the sex difference was specific to evaluations. This effect might be related to girls’ generally higher anxiety associated with academic evaluations (Hembree, 1988), but Devine et al.’s (2012) study indicated a sex difference in math-specific anxiety above and beyond test anxiety.
The second key finding is that the relation between mathematics anxiety for evaluations and concurrent and later mathematics achievement was stronger for girls than for boys. The pattern emerged with the overall sixth-grade sample, with the cross-lagged path analyses, and is consistent with Devine et al.’s (2012) findings for adolescents of roughly the same age as those assessed here. Girls but not boys with lower levels of mathematical competence in sixth grade had higher mathematics anxiety in sixth grade as well as a further increase in mathematics anxiety in seventh grade, controlling prior mathematical competence and the sex difference in spatial ability (Casey et al., 1995; Collaer et al., 2007). However, some other studies have found no sex difference in the relation between mathematics anxiety and mathematics performance (e.g., see Ma, 1999) or sometimes a stronger relation in males (Hembree, 1990). The difference between our results and those reviewed by Ma and Hembree might the measures used to assess mathematics anxiety. In most prior studies, the measures did not differentiate between different mathematical contexts (e.g., Meece et al., 1990). Indeed, if we would have only included our measure of mathematics anxiety for learning, we too would have found no substantive sex differences in the strength of the relation between mathematics anxiety and concurrent or later mathematical competence.
The results also differ in some ways from those of Casey, Nuttall, and Pezaris (1997) who found a relation between spatial abilities and SAT-Mathematics scores, as we found for sixth-grade mathematical competence. But, they did not find a direct relation between mathematics anxiety and SAT-M scores, once spatial abilities, geometry grades, and mathematics efficacy (confidence) were controlled. Their sample however was much higher in mathematical ability than the current sample, and mathematics anxiety generally declines as competence increases (Stoet et al., 2016). As a result, they likely had a range restriction for mathematics anxiety and mathematical competence. Moreover, the factors that influence mathematics test performance often differ for higher- and lower-ability samples (Casey et al., 1995; Geary, 1996). Our sample, unlike that of Casey et al., was of average ability and thus the results are more likely to generalize.
The key overall finding is that there is a more consistent relation between mathematical competence and mathematics anxiety for evaluations for adolescent girls than for boys, as found by Devine et al. (2012). This sex difference might compromise the mathematical development of girls more so than boys and do so in two ways. The first is through higher absolute levels of anxiety and the second through a potentially stronger relation between anxiety and later mathematics outcomes. Although we did not find a cross-lagged relation between anxiety and later achievement, Talsma et al.’s (2018) meta-analysis suggests that such a relation may eventually emerge. Even without a cross-lagged relation, higher mathematics anxiety could result in substantially more girls than boys avoiding mathematics courses and mathematical activities more generally in high school and beyond (Ceci & Williams, 2010; Eccles et al., 1989). Follow-up studies are needed, however, to further assess the specificity of the sex difference in mathematics anxiety (i.e., its primary manifestation with evaluations) and its differential relation to later outcomes. The latter in particular needs follow up with a larger longitudinal sample and with students of different ages.
Mathematics Attitudes
Unlike many previous findings (Crombie et al., 2005; Eccles et al., 1984; Eccles & Wang, 2016; Wigfield & Eccles, 2000), our results suggest that mathematics utility and self-efficacy are part of a single construct, mathematics attitudes. One potential reason (not shown in the results) is that all students rated mathematics utility highly, independent of sex (i.e., no sex differences) and independent of their actual mathematics achievement. The result was lower variation in utility beliefs than in earlier studies and a lower ability to discriminate these beliefs from self-efficacy. The pattern might reflect a secular increase in students’ beliefs about the importance of mathematics (Marsh & Yeung, 1998), or changes in the way utility beliefs and valuation of mathematics are assessed.
In any case, in keeping with prior studies girls reported more positive attitudes toward English and boys more positive attitudes toward mathematics (Eccles et al., 1984; Watt, 2004). For both girls and boys, higher mathematical competence in sixth grade was associated with more positive attitudes toward mathematics, with no sex difference in the strength of this relation. In contrast, higher mathematical competence in sixth grade was related to more positive mathematics attitudes in seventh grade for girls but not for boys, a relation that was independent of the relation between mathematical competence and later mathematics anxiety for evaluations. In contrast, Marsh and Yeung’s (1998) large-scale longitudinal study suggested the relations among mathematics affect and mathematics efficacy (self-concept), and mathematics grades and achievement were largely the same for girls and boys. Their assessments were based on high-school students and the difference between their findings and our results might be due to the age of the students. In other words, it is possible that in early adolescence girls are more accurate in their evaluations of their own mathematical competencies than are boys, and as a result form more consistent relations among anxiety, attitudes, and achievement than do boys. If so, then this sex difference may decline as students move into later adolescence. Longitudinal studies with larger samples than those used here and that cover a larger age-range than assessed by Marsh and Yeung will be needed to test this hypothesis.
Limitations and Conclusion
The primary limitation is the correlational nature of the data. Longitudinal studies enable stronger inferences about cause and effect than do correlations among concurrently collected measures but the longitudinal data are still correlational. In our sample, the cross-lagged analyses were potentially under powered for the assessment of sex differences and thus these are in need of replication. The students in the longitudinal component scored higher on our sixth-grade mathematical-competence measure than did the overall sixth-grade sample and thus we do not know if the results will fully generalize to the larger group. Still, the longitudinal students were average on nationally-normed mathematics achievement (M = 100) and intelligence (M = 105) tests in seventh grade, and thus should be representative of typical students within the United States. We chose mathematics attitudes measures that had shown sex differences in previous studies and that were found to be related to mathematical outcomes, but this does not mean that other attitudinal variables or more nuanced measures of the constructs we included would not yield different results or modify the patterns we found.
Despite these limitations, the study included a large and diverse sample of sixth graders that enabled a robust assessment of sex differences in mathematics anxiety and attitudes and their relations to concurrent mathematical competence, and a longitudinal component that indicated mathematical competence influenced later mathematics anxiety and attitudes, whereas anxiety and attitudes had little effect on later achievement, at least for adolescents (Talsma et al., 2018). The key overall finding is that in early adolescence the relation between mathematical competence and mathematics anxiety and attitudes is more consistent for girls than for boys. One implication is that lower-achieving or even average-achieving girls will develop higher levels of mathematics anxiety and worse attitudes toward mathematics than will boys with similar levels of mathematical competencies. Whether this pattern contributes to the sex difference in occupational aspirations that emerge in later adolescence remains to be determined (Eccles & Wang, 2016).
Educational Impact and Implications Statement.
Girls have higher mathematics anxiety associated with evaluations, such as quizzes and tests, than do boys, but they do not have higher anxiety in other mathematical contexts. Adolescent girls’ mathematics anxiety for evaluations and their attitudes toward mathematics are more consistently related to their actual mathematical competence than they are for boys. Thus, girls with low mathematics achievement will be more likely to develop mathematics anxiety and poor mathematics attitudes than will low-achieving boys.
Acknowledgements:
The study was supported by grants R01 HD087231 from the Eunice Kennedy Shriver National Institute of Child Health and Human Development and DRL-1659133 from the National Science Foundation. We thank Marcia Collaer for her help with the implementation of the Judgment of Line Angle Test and Position, and Amanda Campbell, Maria Ceriotti, Alexis Currie, Kaitlynn Dutzy, Amanda Evans, Jim Farley, Amy Jordan, Kelly Mebruer, Brandon Ryffe, and Logan Schmidt for their assistance with data collection and processing.
Contributor Information
David C. Geary, University of Missouri
Mary K. Hoard, University of Missouri
Lara Nugent, University of Missouri.
Felicia Chu, University of Missouri.
John E. Scofield, University of Missouri
Dana Ferguson Hibbard, Columbia Public Schools.
References
- Ashcraft MH (2002). Math anxiety: Personal, educational, and cognitive consequences. Current Directions in Psychological Science, 11, 181–185. doi: 10.1111/1467-8721.00196 [DOI] [Google Scholar]
- Ashcraft MH, & Kirk EP (2001). The relationships among working memory, math anxiety, and performance. Journal of experimental psychology: General, 130, 224–237. doi: 10.1037/0096-3445.130.2.224 [DOI] [PubMed] [Google Scholar]
- Baloglu M, & Koçak R (2006). A multivariate investigation of the differences in mathematics anxiety. Personality and Individual Differences, 40, 1325–1335. doi: 10.1016/j.paid.2005.10.009 [DOI] [Google Scholar]
- Benton AL, Varney NR, & Hamsher KD (1978). Visuospatial judgment: A clinical test. Archives of Neurology, 35, 364–367. doi: 10.1001/archneur.1978.00500300038006 [DOI] [PubMed] [Google Scholar]
- Bull R, & Lee K (2014). Executive functioning and mathematics achievement. Child Development Perspectives, 8, 36–41. doi: 10.1111/cdep.12059 [DOI] [Google Scholar]
- Casey MB, Nuttall RL, & Pezaris E (1997). Mediators of gender differences in mathematics college entrance test scores: A comparison of spatial skills with internalized beliefs and anxieties. Developmental Psychology, 33, 669–680. doi.org/10.1037/0012-1649.33.4.669 [DOI] [PubMed] [Google Scholar]
- Casey MB, Nuttall R, Pezaris E, & Benbow CP (1995). The influence of spatial ability on gender differences in mathematics college entrance test scores across diverse samples. Developmental Psychology, 31, 697–705. doi: 10.1037/0012-1649.31.4.697 [DOI] [PubMed] [Google Scholar]
- Ceci SJ, & Williams WM (2010). The mathematics of sex: How biology and society conspire to limit talented women and girls New York: Oxford University Press. [Google Scholar]
- Cohen J (1988). Statistical power analysis for the behavioral sciences (second edition). Hillsdale, NJ: Erlbaum. [Google Scholar]
- Collaer ML, & Nelson JD (2002). Large visuospatial sex difference in line judgment: Possible role of attentional factors. Brain and Cognition, 49, 1–12. doi: 10.1006/brcg.2001.1321 [DOI] [PubMed] [Google Scholar]
- Collaer M, Reimers L, & Manning S (2007). Visuospatial performance on an internet line judgment task and potential hormonal markers: Sex, sexual orientation, and 2D:4D. Archives of Sexual Behavior, 36, 177–192. doi: 10.1007/s10508-006-9152-1 [DOI] [PubMed] [Google Scholar]
- R Core Team (2017) R: A language and environment for statistical computing https://www.R-project.org/
- Crombie G, Sinclair N, Silverthorn N, Byrne BM, DuBois DL, & Trinneer A (2005). Predictors of young adolescents’ math grades and course enrollment intentions: Gender similarities and differences. Sex Roles, 52, 351–367. doi: 10.1007/s11199-005-2678-1 [DOI] [Google Scholar]
- Deary IJ, Strand S, Smith P, & Fernandes C (2007). Intelligence and educational achievement. Intelligence, 35, 13–21. doi: 10.1016/j.intell.2006.02.001 [DOI] [Google Scholar]
- Dehaene S, Piazza M, Pinel P, & Cohen L (2003). Three parietal circuits for number processing. Cognitive Neuropsychology, 20, 487–506. doi: 10.1080/02643290244000239 [DOI] [PubMed] [Google Scholar]
- Devine A, Fawcett K, Szűcs D, & Dowker A (2012). Gender differences in mathematics anxiety and the relation to mathematics performance while controlling for test anxiety. Behavioral and Brain Functions, 8, 33. doi: 10.1186/1744-9081-8-33 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dowker A, Sarkar A, & Looi CY (2016). Mathematics Anxiety: What Have We Learned in 60 Years? Frontiers in Psychology, 7, 508. doi: 10.3389/fpsyg.2016.00508 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eccles JS, Adler TF, & Meece JL (1984). Sex differences in achievement: A test of alternative theories. Journal of Personality and Social Psychology, 46, 26–43. doi: 10.1037/0022-3514.46.1.26 [DOI] [Google Scholar]
- Eccles JS, & Wang MT (2016). What motivates females and males to pursue careers in mathematics and science? International Journal of Behavioral Development, 40, 100–106. doi: 10.1177/0165025415616201 [DOI] [Google Scholar]
- Eccles JS, & Wigfield A (2002). Motivational beliefs, values, and goals. Annual Review of Psychology, 53, 109–132. doi: 10.1146/annurev.psych.53.100901.135153 [DOI] [PubMed] [Google Scholar]
- Eccles JS, Wigfield A, Flanagan C, Miller C, Reuman D, & Yee D (1989). Self concepts, domain values, and self-esteem: Relations and changes at early adolescence. Journal of Personality, 57, 283–310. doi: 10.1111/j.1467-6494.1989.tb00484.x [DOI] [PubMed] [Google Scholar]
- Else-Quest NM, Hyde JS, & Linn MC (2010). Cross-national patterns of gender differences in mathematics: A meta-analysis. Psychological Bulletin, 136, 103–127. doi: 10.1037/a0018053 [DOI] [PubMed] [Google Scholar]
- Gaspard H, Dicke AL, Flunger B, Schreier B, Häfner I, Trautwein U, & Nagengast B (2015). More value through greater differentiation: Gender differences in value beliefs about math. Journal of Educational Psychology, 107, 663–677. doi: 10.1037/edu0000003 [DOI] [Google Scholar]
- Geary DC (1996). Sexual selection and sex differences in mathematical abilities. Behavioral and Brain Sciences, 19, 229–284. doi.org/10.1017/S0140525X00042400 [Google Scholar]
- Geary DC (2010). Male, female: The evolution of human sex differences (second ed.). Washington, DC: American Psychological Association. [Google Scholar]
- Geary DC (2011). Cognitive predictors of individual differences in achievement growth in mathematics: A five-year longitudinal study. Developmental Psychology, 47, 1539–1552. doi: 10.1037/a0025510 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geary DC, Hoard MK, Nugent L, & Bailey HD (2013). Adolescents’ functional numeracy is predicted by their school entry number system knowledge. PLoS ONE, 8(1): e54651. doi: 10.1371/journal.pone.0054651 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geary DC, Nicholas A, Li Y & Sun J (2017). Developmental change in the influence of domain-general abilities and domain-specific knowledge on mathematics achievement: An eight-year longitudinal study. Journal of Educational Psychology, 109, 680–693. doi.org/10.1037/edu0000159 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gorsuch RL (1983). Factor analysis (second ed.). Hillsdale, NJ: Lawrence Erlbaum Associates. [Google Scholar]
- Gunderson EA, Park D, Maloney EA, Beilock SL, & Levine SC (2018). Reciprocal relations among motivational frameworks, math anxiety, and math achievement in early elementary school. Journal of Cognition and Development, 19, 21–46. doi.org/10.1080/15248372.2017.1421538 [Google Scholar]
- Halberda J, & Feigenson L (2008). Developmental change in the acuity of the” Number Sense”: The Approximate Number System in 3-, 4-, 5-, and 6-year-olds and adults. Developmental Psychology, 44, 1457–1465. doi: 10.1037/a0012682 [DOI] [PubMed] [Google Scholar]
- Halpern D, Benbow C, Geary DC, Gur R, Hyde J, & Gernsbacher MA (2007). The science of sex differences in science and mathematics. Psychological Science in the Public Interest, 8 (No 1, 1–52). doi: 10.1111/j.1529-1006.2007.00032.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hecht SA (1998). Toward an information-processing account of individual differences in fraction skills. Journal of Educational Psychology, 90, 545–559. doi: 10.1037/0022-0663.90.3.545 [DOI] [Google Scholar]
- Hecht SA, Close L, & Santisi M (2003). Sources of individual differences in fraction skills. Journal of Experimental Child Psychology, 86, 277–302. doi: 10.1016/j.jecp.2003.08.003 [DOI] [PubMed] [Google Scholar]
- Hembree R (1988). Correlates, causes, effects, and treatment of test anxiety. Review of Educational Research, 58, 47–77. doi.org/10.2307/1170348 [Google Scholar]
- Hembree R (1990). The nature, effects, and relief of mathematics anxiety. Journal for Research in Mathematics Education, 21, 33–46. doi: 10.2307/749455 [DOI] [Google Scholar]
- Hopko DR, Mahadevan R, Bare RL, & Hunt MK (2003). The abbreviated math anxiety scale (AMAS) construction, validity, and reliability. Assessment, 10, 178–182. doi: 10.1177/1073191103010002008 [DOI] [PubMed] [Google Scholar]
- Huang C (2013). Gender differences in academic self-efficacy: A meta-analysis. European Journal of Psychology of Education 28, 1–35. doi: 10.1007/s10212-011-0097-y [DOI] [Google Scholar]
- Hyde JS, Fennema E, & Lamon S (1990). Gender differences in mathematics performance: A meta-analysis. Psychological Bulletin, 107, 139–155. doi: 10.1037/0033-2909.107.2.139 [DOI] [PubMed] [Google Scholar]
- Hyde JS, Fennema E, Ryan M, Frost LA, & Hopp C (1990). Gender comparisons of mathematics attitudes and affect. Psychology of Women Quarterly, 14, 299–324. doi: 10.1111/j.1471-6402.1990.tb00022.x [DOI] [Google Scholar]
- Kazelskis R (1998). Some dimensions of mathematics anxiety: A factor analysis across instruments. Educational and Psychological Measurement, 58, 623–633. doi: 10.1177/0013164498058004006 [DOI] [Google Scholar]
- Kline RB (2015). Principles and practice of structural equation modeling (3rd ed.). New York: Guilford Publications. [Google Scholar]
- Lauermann F, Tsai YM, & Eccles JS (2017). Math-related career aspirations and choices within Eccles et al.’s expectancy–value theory of achievement-related behaviors. Developmental Psychology, 53, 1540–1559. doi: 10.1037/dev0000367 [DOI] [PubMed] [Google Scholar]
- Lee K, & Bull R (2016). Developmental changes in working memory, updating, and math achievement. Journal of Educational Psychology doi: 10.1037/edu0000090 [DOI]
- Li Y, & Geary DC (2017). Children’s visuospatial memory predicts mathematics achievement through early adolescence. PLoS ONE, 12(2): e0172046. doi: 10.1371/journal.pone.0172046 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lyons IM, & Beilock SL (2012). When math hurts: math anxiety predicts pain network activation in anticipation of doing math. PLoS ONE, 7(10), e48076. doi: 10.1371/journal.pone.0048076 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma X (1999). A meta-analysis of the relationship between anxiety toward mathematics and achievement in mathematics. Journal for Research in Mathematics Education, 30, 520–540. doi: 10.2307/749772 [DOI] [Google Scholar]
- Maloney EA, & Beilock SL (2012). Math anxiety: who has it, why it develops, and how to guard against it. Trends in Cognitive Sciences, 16, 404–406. doi: 10.1016/j.tics.2012.06.008 [DOI] [PubMed] [Google Scholar]
- Marsh HW, & Yeung AS (1998). Longitudinal structural equation models of academic self-concept and achievement: Gender differences in the development of math and English constructs. American Educational Research Journal, 35, 705–738. doi: 10.3102/00028312035004705 [DOI] [Google Scholar]
- McNeil NM, & Alibali MW (2005). Why won’t you change your mind? Knowledge of operational patterns hinder learning and performance on equations. Child Development, 76, 883–899. doi: 10.1111/j.1467-8624.2005.00884.x [DOI] [PubMed] [Google Scholar]
- McNeil NM, Fyfe ER, Petersen LA, Dunwiddie AE, & Brletic‐Shipley H (2011). Benefits of practicing 4= 2+ 2: Nontraditional problem formats facilitate children’s understanding of mathematical equivalence. Child Development, 82, 1620–1633. doi: 10.1111/j.1467-8624.2011.01622.x [DOI] [PubMed] [Google Scholar]
- Meece JL, Wigfield A, & Eccles JS (1990). Predictors of math anxiety and its influence on young adolescents’ course enrollment intentions and performance in mathematics. Journal of Educational Psychology, 82, 60–70. doi: 10.1037/0022-0663.82.1.60 [DOI] [Google Scholar]
- Petersen JL, & Hyde JS (2017). Trajectories of self-perceived math ability, utility value and interest across middle school as predictors of high school math performance. Educational Psychology, 37, 438–456. doi: 10.1080/01443410.2015.1076765 [DOI] [Google Scholar]
- Richardson M, Abraham C, & Bond R (2012). Psychological correlates of university students’ academic performance: A systematic review and meta-analysis. Psychological Bulletin, 138, 353–387. doi: 10.1037/a0026838 [DOI] [PubMed] [Google Scholar]
- SAS Institute. (2014). Statistical analysis system 9.2 Cary, NC: Author. [Google Scholar]
- Siegler RS, & Booth JL (2004). Development of numerical estimation in young children. Child Development, 75, 428–444. doi: 10.1111/j.1467-8624.2004.00684.x [DOI] [PubMed] [Google Scholar]
- Siegler RS, Thompson CA, & Schneider M (2011). An integrated theory of whole number and fractions development. Cognitive Psychology, 62, 273–296. doi: 10.1016/j.cogpsych.2011.03.001 [DOI] [PubMed] [Google Scholar]
- Sokolowski HM, Hawes Z, & Lyons IM (2019). What explains sex differences in math anxiety? A closer look at the role of spatial processing. Cognition, 182, 193–212.doi.org/10.1016/j.cognition.2018.10.005 [DOI] [PubMed] [Google Scholar]
- Steinmayr R, & Spinath B (2008). Sex differences in school achievement: What are the roles of personality and achievement motivation? European Journal of Personality, 22, 185–209. doi: 10.1002/per.676 [DOI] [Google Scholar]
- Stoet G, Bailey DH, Moore AM, & Geary DC (2016). Countries with higher levels of gender equality show larger national sex differences in mathematics anxiety and relatively lower parental mathematics valuation for girls. PloS ONE, 11(4): e0153857. doi: 10.1371/journal.pone.0153857 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Su R, Rounds J, & Armstrong PI (2009). Men and things, women and people. Psychological Bulletin, 135, 859–884. doi: 10.1037/a0017364 [DOI] [PubMed] [Google Scholar]
- Talsma K, Schüz B, Schwarzer R, & Norris K (2018). I believe, therefore I achieve (and vice versa): A meta-analytic cross-lagged panel analysis of self-efficacy and academic performance. Learning and Individual Differences, 61, 136–150. doi: 10.1016/j.lindif.2017.11.015 [DOI] [Google Scholar]
- Valentine JC, DuBois DL, & Cooper H (2004). The relation between self-beliefs and academic achievement: A meta-analytic review. Educational Psychologist, 39, 111–133. doi: 10.1207/s15326985ep3902_3 [DOI] [Google Scholar]
- Wai J, Hodges J, & Makel MC (2018). Sex differences in ability tilt in the right tail of cognitive abilities: A 35-year examination. Intelligence, 67, 76–83. doi: 10.1016/j.intell.2018.02.003 [DOI] [Google Scholar]
- Wang MT, Eccles JS, & Kenny S (2013). Not lack of ability but more choice: Individual and gender differences in choice of careers in science, technology, engineering, and mathematics. Psychological Science, 24, 770–775. doi: 10.1177/0956797612458937 [DOI] [PubMed] [Google Scholar]
- Watt HM (2004). Development of adolescents’ self‐perceptions, values, and task perceptions according to gender and domain in 7th‐through 11th‐grade Australian students. Child Development, 75, 1556–1574. doi: 10.1111/j.1467-8624.2004.00757.x [DOI] [PubMed] [Google Scholar]
- Wechsler D (1999). Wechsler Abbreviated Scale of Intelligence San Antonio, TX: PsychCorp, Harcourt Assessment, Inc. [Google Scholar]
- Wechsler D (2009). Wechsler Individual Achievement Test (3rd ed.). San Antonio, TX: Psychological Corporation. [Google Scholar]
- Welsh MC, Pennington BF, & Groisser DB (1991). A normative‐developmental study of executive function: A window on prefrontal function in children. Developmental Neuropsychology, 7, 131–149. doi: 10.1080/87565649109540483 [DOI] [Google Scholar]
- Wigfield A, & Eccles JS (2000). Expectancy–value theory of achievement motivation. Contemporary Educational Psychology, 25, 68–81. doi: 10.1006/ceps.1999.1015 [DOI] [PubMed] [Google Scholar]
- Wigfield A, & Meece JL (1988). Math anxiety in elementary and secondary school students. Journal of Educational Psychology, 80, 210–216. doi.org/10.1037/0022-0663.80.2.210. [Google Scholar]
- Young CB, Wu SS, & Menon V (2012). The neurodevelopmental basis of math anxiety. Psychological Science, 23, 492–501. doi: 10.1177/0956797611429134 [DOI] [PMC free article] [PubMed] [Google Scholar]


