Affect and decision making: Insights and predictions from computational models

Abstract

In recent years, interest in integrating the affective and decision sciences has skyrocketed. Immense progress has been made but the complexities of each field, which can multiply when combined, present a significant obstacle. A carefully defined framework for integration is needed. The shift towards computational modeling in decision science provides a powerful basis and a path forward, but one whose synergistic potential will only be fully realized by drawing on the theoretical richness of the affective sciences. Reviewing research using a popular computational model of choice (the drift diffusion model), we discuss how mapping concepts to parameters reduces conceptual ambiguity and reveals novel hypotheses.

Affect and Computational Models of Choice

The past three decades have seen a rapid increase in our understanding of the role of affect (see Glossary) in decision-making [1]. Yet significant challenges remain. In part, this results from the complexity of the subject matter: affective science and decision science each encompass a variety of heterogeneous, poorly understood, and sometimes vaguely defined phenomena. Their combination thus threatens to propagate and multiply these issues. Moreover, even a cursory reading of the literature presents a dizzying and often contradictory array of empirical observations regarding affect’s influence on choice, linked to a plethora of theoretical mediators and contextual moderators. Unfortunately, this has impeded the development of an integrative framework capable of linking responses across levels of analysis while arbitrating between competing explanatory mechanisms and accurately predicting behavioral effects.

Here, we argue that a paradigm shift under way in decision science towards the use of formalized mathematical and computational models of choice (such as sequential accumulator or drift diffusion models (DDM)) may represent a key step towards developing such a framework, but only if it properly incorporates the conceptual and theoretical richness of the affective sciences. First, we introduce the computational model itself, identifying key concepts and ideas to those who are new to this world. Then, we review some of the growing literature harnessing the DDM to understand the role of affective processes in decision-making. In so doing, we highlight specific ways in which these models can help to inform and arbitrate between existing theories, as well as how the full power of these models depends on making deeper contact with the rich and nuanced affective science literature. Along the way, we outline important methodological and conceptual considerations for both affective scientists and computational modelers when marrying these two approaches. Finally, we point to a number of cutting-edge developments that will shape the future of this burgeoning field and reveal novel insights into the dynamics of affect and choice.

Sequential Sampling Models of Choice

Although the DDM represents just one example from the broader family of sequential sampling models (SSMs) [2,3], we focus on it here for three primary reasons: its comparative popularity, its small but tractable number of key parameters, and the relative ease of reducing other SSMs to the DDM given certain parameter constraints [2].

Like most economic models of choice, the DDM assumes that choices result from considering evidence (E) in favor of one or another alternative that is some function of different choice attributes (e.g., gain, loss, risk) weighted by their relative importance (i.e., E =∑_a w_aAttrib_a). Where this model extends more classical approaches is its assumption that the brain computes this evidence with some noise at each moment in time (i.e., E (t) = E + σ (t)), and that choices are made by accumulating momentary evidence until the total value surpasses a subjective criterion (known as a decision threshold) associated with one or another response option.

A key strength of this model is its ability to link variables such as evidence, response caution, and response bias to choice variability, response time (RT), and even neural response, all within a single parsimonious framework [4]. For example, the model explains well-known relationships between speed and accuracy as a function of evidence strength: stronger evidence results in a faster drift rate towards one of the two decision thresholds, and is more robust to noise, yielding faster and more stable choices. The model also captures the notion that people can adjust their criterion for choosing, with a higher decision threshold resulting in slower but more accurate choices, and a lower threshold resulting in faster choices but greater error-proneness (or, in psychological terms, maximizing versus satisficing). To fully explain observed patterns of choice, most DDM models incorporate two additional parameters: non-decision time and starting point bias. The first of these embodies the assumption that perceptual processes at the beginning and motor execution processes at the end add appreciable time to any decision, but do not directly influence the evidence accumulation process or choice probabilities. Starting point bias accounts for the idea that, even before encountering a specific stimulus, a decision maker may begin with bias toward a specific response. Each of these parameters (as well as a few other less-commonly-used parameters) have characteristic effects on choices and RTs (see Box 1).

Box 1. Drift Diffusion Model: Parameters and Model Fitting.

The DDM provides a provably optimal solution to speed-accuracy trade-offs when making choices based on noisy, stationary evidence, and captures patterns of choice, RT, and neural responses remarkably accurately [2]. Familiarity with the core parameters of the DDM, as well as an understanding of the methods for identifying those parameters, is essential for affective science researchers wishing to apply this model to their own research.

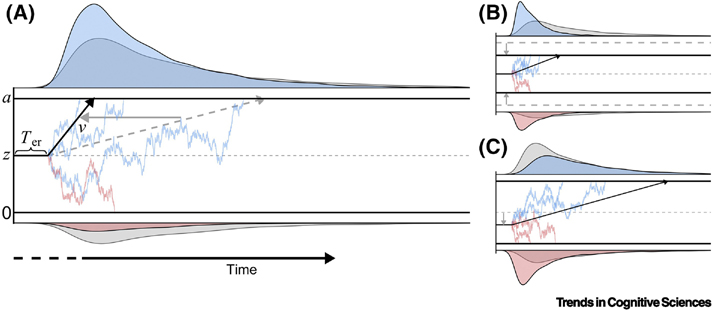
Each parameter of the DDM has a characteristic influence over the joint distribution of choices and RTs [106] (Figure I). For example, while strengthening the drift rate (v) and reducing the decision threshold (a) both reduce mean RTs, they differentially impact choice probabilities and the shape of the RT distribution. A stronger drift rate increases the relative probability of shorter RTs for the higher-value option (Figure IA). Meanwhile, reducing the threshold speeds up both the leading edge and tail of the RT distribution and increases the probability of choosing the lower-value option (Figure IB). The impact of a starting point bias (z) depends on the direction of the bias but will shift the early part of the distribution in the direction of the bias (Figure IC). Increasing or decreasing the non-decision time (T_er) will shift the overall RT distributions without changing their shape

Additional parameters beyond the core four may sometimes be warranted. For example, because a nominally equivalent stimulus (e.g., a potential $10 gain) may be processed differently on different trials, across-trial variability in parameters can be estimated (e.g., trial-to-trial variability in drift rate or starting point). Though less-studied, parameter variability has important consequences for the relative RT distributions of each alternative [107] (see also [63]). Future work should examine how concepts from affective science map to estimates of parameter variability (e.g., stimuli that elicit mixed emotions might show greater drift rate variability). Additionally, incorporating a decider’s affective goals might call for versions of the DDM that feature extra parameters (e.g., collapsing thresholds [102]).

Estimating the DDM’s parameters typically requires a large number of observations. Depending on the method and number of parameters, this can range from a bare minimum of 50–100 trials up to 1000 or more. Sometimes these observations are coded as correct versus incorrect. However, for value-based decisions where choice accuracy is difficult or impossible to define, a coding such as accept versus reject (e.g., a gamble) is often used instead. Importantly, whatever the coding, a sufficient number of each response type is necessary for estimating RT distributions (frequently at least 30 each). The number of trials required may present some issues, given affect’s often fleeting dynamics and tendency to habituate. In some cases where fatigue and habituation are a concern, it may be possible to divide trials across two or more experimental sessions. Alternatively, if individual differences are less of an interest, choice data might be pooled across participants. Moreover, depending on the complexity of the model, estimating these parameters can require extensive computational resources. For affective science researchers interested in modeling trial-to-trial shifts in affect, we recommend approaches relying on maximum likelihood estimation [8,72], or a combination of Monte Carlo simulation and Bayesian inference [108]. Experimenter ingenuity will be needed to address the challenges that arise when applying computational modeling to affective processes. For certain research questions, practical constraints for estimating a particular model might limit its use.

We view the value of this model, both for affective scientists as well as researchers more generally, as three-fold. First, values of the four computational parameters described above can be identified relatively easily from behavioral choice and RT data, and capture important patterns across a surprisingly broad variety of choices, from simple perceptual and motor decisions [3–5] to complex decisions involving morality and self-control [6–8]. Second, models like these force researchers to operationalize their theories in a more precise, mathematical way, which may help to clarify some of the conceptual ambiguities that persist in the affect and decision-making literature [9,10]. Finally, the model makes precise predictions that enable more formal arbitration between competing theories [11]. Thus, we believe that more clearly linking concepts and phenomena from the affective sciences to this model may provide a sought-after unifying framework for understanding the influence of affect on decision-making.

Building Linkages: Concepts to Parameters

Uniting two fields is like a conversation between people who speak different languages. Building a working relationship depends on finding the shared meanings underlying the terminology that each uses to organize the world. This is no trivial task as miscommunication can lead to confusion at best and dismissal at worst. So it goes when attempting to forge linkages between theoretical concepts in the affective sciences and computational parameters. In what follows, we consider how connections might be made by first highlighting two ways in which concepts from affective science might relate to parameters from the DDM: (a) direct concept-to-parameter mappings and (b) indirect mappings mediated by another psychological process (see Figure 1). Last, we discuss an example of how incorporating affective science concepts to the DDM may bring new clarity to long-standing debates (i.e., dual-systems). Throughout, we discuss ways in which computational modeling illuminates important issues in the affect and decision-making literature, while also pointing to critical ideas from the affective sciences about the moderating role of contexts and goals that modeling work should consider more carefully. Our selection of examples is not meant to be exhaustive and we hope that others will use our review as a springboard for identifying research avenues.

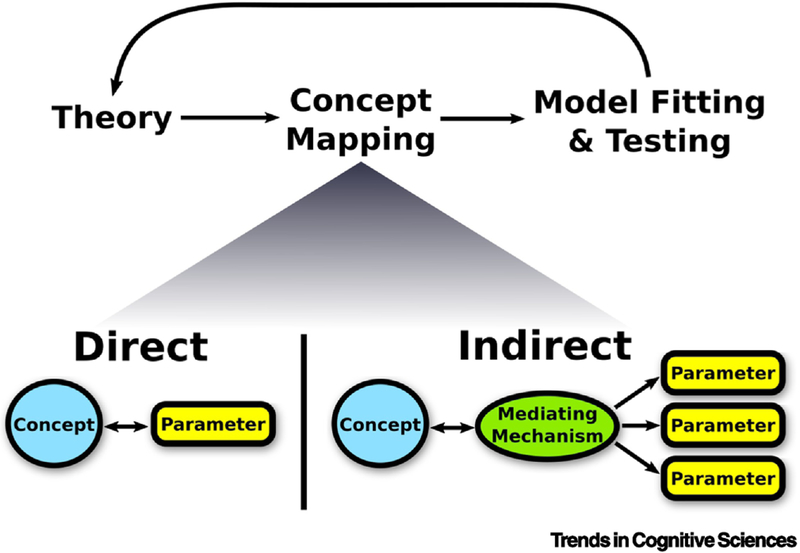
Figure 1. Mapping Affective Science Concepts to Computational Parameters.

Theories often posit the existence of hypothetical concepts. However, these concepts are frequently abstractly defined, which means they must be operationalized in order for predictions to be tested. In the context of computational models, operationalization can involve mapping a concept onto the computational parameters of the relevant model. This mapping can take at least one of two forms: direct concept-to-parameter mapping or indirect mapping through a mediating mechanism that is not directly represented in the model. Once a concept has been mapped to a parameter, the predictions can be tested, which then informs the theory.

Direct concept-to-parameter mapping

The simplest way for an affective science concept to connect to a computational parameter in the DDM is a direct concept-to-parameter relationship. Of course, linkages like these are limited by the number of parameters in the computational model. Nevertheless, direct connections likely exist. Here we discuss two such examples.

Extent of processing and decision threshold.

A considerable body of work suggests that emotions can modulate the extent of processing. Processing extent maps directly onto the role played by the decision threshold in the model. For example, a growing body of research suggests that negative affect plays a role in the phenomenon of post-error slowing (i.e., longer RTs following errors) [12]. Post-error slowing highlights a key strength of computational modeling: the ability to arbitrate between hypotheses that make highly similar predictions. Theoretically, error-induced negative affect could momentarily distract participants from choice-relevant information (reducing the drift rate), bias participants to shift their response away from an unrewarded/incorrect action (producing a starting bias), delay perceptual or motor processing (lengthening non-decision time), or produce greater caution and more extended processing of subsequent information (raising the decision threshold). Each of these explanations predicts longer RTs following an error, making it difficult to arbitrate among them.

Yet the DDM has consistently tied post-error slowing to an increase in decision threshold [13], which can endure for several trials [14]. Moreover, such slowing does not depend on the affect evoked by a specific, concrete error. Simply giving participants false feedback that they performed worse than most other participants on a perceptual color discrimination task also increased decision thresholds [15]. Negative affect’s influence also need not derive solely from errors: presentation of fearful faces (which may signal a need for caution) increased the decision threshold during a subsequent, unrelated perceptual judgment [24]. Thus, the modeling literature to date supports the simple and intuitive notion that negative affect often increases response caution, enhancing accuracy.

However, a rich vein of literature from affective science highlights important moderators of this influence (e.g., [16,17]), which computational models might benefit from incorporating. For example, not all negative emotions are alike. Some negative emotions like anger may actually produce approach-related tendencies [18], potentially reducing response caution. Indeed, prior presentation of sad facial expressions, which may also elicit approach (e.g., to comfort [19]), decreased decision thresholds during perceptual judgment [20]. Notably, sad facial expressions also increased non-decision times, canceling out the effects of the reduced threshold and yielding no overall change in mean RT. Thus, while standard analyses might have concluded that sad expression had no effect, the DDM extracted more information from the data and led to different conclusions. This case also illustrates how the DDM can push affective scientists towards more precise definitions—should “processing extent” refer to response caution or the duration of perceptual processes?

Other instances of the need to carefully consider the motivating properties of emotion abound [16,17], but have received little attention from modeling work. Most DDM research has examined extrinsically motivated tasks, but behavioral research suggests that positive affect can increase processing when people have intrinsic motives, as shown by increased deliberation times [21–23] and more careful processing [24,25]. Whether such effects act through adjustment of the decision threshold or some other mechanism like drift rate or starting bias remain unclear, but the answer has important implications: happier individuals’ reticence to process mood-threatening information may lead to costly errors.

Affect-as-information and drift rate.

A robust body of work on affect-as-information [26,27] demonstrates that affect can serve as evidence for choice in much the same way as other attributes like the size of an object in a perceptual discrimination task or the perceived healthiness of a food in a dietary decision. Put in computational terms, a weighted representation of affect may determine the drift rate along with other choice-relevant attributes (e.g., E = w_Affect * AffectMagnitude + ∑_a w_a * Attrib_a) [28]. This formulation highlights an important idea: the extent to which affect influences choices should depend not only on its valence and intensity, but also the weight it receives in the accumulation process. Yet surprisingly little modeling work has been done to directly test this important hypothesis.

What work that exists supports this idea. For example, loss aversion has been tied to affective responses behaviorally, neurally, and physiologically [29–33]. Accordingly, highly loss-averse individuals show a reduced drift rate (rather than starting bias) when accepting risky gambles [34]. Unfortunately, affect itself was not directly measured in this study, so whether this difference resulted from greater affective intensity or reduced weighting remains unclear. Supportive of the latter possibility, people with greater numerical abilities are less loss averse [35], and are also less likely to have negative affect shape their probability weighting [36].

More direct evidence of affect influencing drift rates comes from work on anxious individuals. In one study, high and low anxiety participants decided whether a priori threat-related and neutral words were “threatening” or “safe” [37], where affect elicited by the words should directly inform the choice. Indeed, both high and low anxiety participants showed a stronger drift to respond “threatening” for threat versus neutral words. Furthermore, high anxiety participants had an overall stronger drift towards “threatening”. In another study, high and low anxiety participants categorized strings of letters as “words” or “nonwords” [38]. Under these circumstances, affect elicited by threat-related words should be choice-irrelevant. As expected by affect-as-information theory, low anxiety participants showed no difference in drift rate for threat-related versus neutral words, suggesting a weight of 0 in the evidence accumulation process. However, high anxiety individuals showed a drift rate advantage for threat-related words, indicating that their affective response received weight in their choice [39].

Note that, in these studies, the DDM provides greater insight regarding the underlying decision processes than a typical logistic regression. Although strengthening the drift rate can produce higher regression weights, this need not be the case. Expanded decision thresholds will tend to produce the same effect, because increasing thresholds reduces the impact of noise during evidence accumulation, producing a tighter link between evidence and choice, and a higher regression coefficient. Thus, a standard regression has trouble distinguishing the influence of changes in drift rates from changes in decision thresholds, and can perform more poorly at uncovering what might otherwise be equally plausible explanatory mechanisms (see also [40]).

Despite the promising forays we have discussed here, numerous open questions remain about the way affect enters into the evidence accumulation process, which could be answered by a tighter marriage of affective science and computational modeling. For example, do higher drift rates in anxious individuals stem from heightened affective intensity, a greater weight, or both? Using methodological tools developed in the affective sciences to measure the intensity of affective responses (including physiology and neural responses) might help to resolve this important question. Indeed, research suggests that highly anxious people sometimes show similar physiological responses to stress to low anxiety individuals, even while reporting stronger affect [41]. Computational modeling could help reveal whether such effects derive from an increased weight on physiological signals (e.g., via increased interoceptive sensitivity [42]). Future DDM studies could use situational and dispositional moderators of affect-as-information to manipulate the underlying choice processes (e.g., choice-relevance [43–45] and emotional differentiation [46,47]; for a review, see [27]).

It will also be important to examine whether different components of affect (e.g., valence and arousal) receive independent weights, which could have different consequences for choice. For example, anxious individuals show greater risk aversion [48], whereas depressed individuals demonstrate increased loss aversion [29,49]. Computational modeling could be used to test the hypothesis that anxious and depressed individuals differ in their tendency to weight arousal or valence more highly during choice, respectively. Similarly, the mathematical observation that weights can be either positive or negative could help to explain when, why, and how people choose to avoid or approach negative emotions [17,50], or prefer high versus low arousal states [51]. Alternatively, positive and negative affect might be given separate weights [52]. Thus, future work using the DDM can draw on this literature to understand which components of affect serve as evidence and when.

Finally, it is important to note that while the DDM models choice dynamics, it is silent regarding the origins of evidence. For many perceptual decisions, the source of evidence is relatively straight-forward (e.g., light brightness), but affect is more subjective and internal. Adding to the challenge, affect is likely more dynamic than other sources of evidence, in part, because the consequences of evaluative processes [53] and even behavior [54] feed back in an iterative, regulatory loop [55,56]. Nevertheless, great progress has been made. Numerous brain regions have key roles in affective processes (e.g., amygdala, insula, ventral striatum, vmPFC), and though the specifics of their involvement in emotion have been highly debated [57,58], one possibility is that each carries different affective components for calculating overall evidence (e.g., goal-congruence, reward prediction error, etc.) [59]. Visceral sensations (i.e., interoception) may provide another important source of affective evidence. In addition to innate relationships with behavior, interoceptive signals might be transformed into evidence through learned associations and categories [57,60–62]. Thus, the same core debates in affective science will need to play out in the decision sciences in order to incorporate processes that have so far eluded computational models. Computational models may also be used to shed new light on affect’s origins [63] (also see Box 2).

Box 2. Computational Approaches to Conscious Affective Experience.

A key aspect of affect’s influence on decision making derives from conscious judgments about emotional experience. Yet the nature of such judgments has spurred foundational questions in affective science and animated rigorous, long-standing debates. Do emotions like fear, anger, and happiness represent different locations in an affective space composed of a small number of continuous dimensions (e.g., valence, arousal), or are they discrete, functional entities [57,103,109,110]? Does each emotion have a distinct biological ‘signature’ at the neural or physiological level [111,112]? What determines whether a stimulus elicits responses that rise to the level of conscious emotional experience [113,114]? One productive way to think about many of these issues might be to ask, “How do people make decisions about if they are feeling and what they are feeling?” Phrased in this way, the framework of the DDM may yield novel approaches and insights to the important problem of conscious experience [115].

For example, appraisal theories of emotion suggest that emotional experiences are differentiated via their match to different criteria or dimensions of appraisal [116]. Accordingly, research shows that the presence of one or more emotion-specific appraisals increases the likelihood of experiencing that specific emotion [117]. While research of this sort has treated appraisals in a binary present/absent manner, the weighted integration model of evidence accumulation (i.e.,E =∑_a w_aAttrib_a) suggests that different appraisals might carry different weights in determining which emotion people feel. Moreover, such weights could vary across individuals, perhaps producing important differences in how people respond to provocative events. A similar idea might be applied to physiological signals. Do changes in heartrate serve as weighted evidence of emotional states? Do the same physiological signals serve as evidence of different emotions across contexts and individuals? Computational models of this sort (perhaps combined with neural data on the activation of emotion-relevant brain regions [111]) could also help to determine whether some individuals have prepotent starting biases to experience certain emotions over others, or higher or lower thresholds for conscious experience.

Importantly, the conclusions from this work may depend on the specific decisions made by the participant: recent research has shown that continuous versus discrete affective ratings rely on separate neural processes [118] and using one scale or the other may even shape affective experience, producing differences in sensitivity and bias [119]. A recent adaption of the DDM for continuous responding could be used to compare emotion responses measured with continuous versus discrete scales [120].

Indirect concept-to-parameter mapping

Many affective science concepts imply changes in choices without directly mapping onto a single DDM parameter. In these cases, it may often be the case that the concept is best instantiated via a mechanism not directly represented in the DDM. Because there is no direct correspondence between the mechanism and a singular DDM parameter, it is likely that the mechanism can modulate multiple different decision parameters. After all, solely influencing one parameter would imply that the DDM can fully account for its effects. Even so, the DDM framework still provides utility because a careful consideration of the hypothesized mediating mechanism will often lead to clear predictions both about how affect might shape a decision and which parameters it should impact. Once identified, the DDM may be expanded by incorporating a new parameter to account for the mediating mechanism. Here we discuss two instances of indirect mapping.

Attention.

Consider the large body of work suggesting that negative information draws focus through rapid detection [64–68] and attentional capture [69–71]. When might this influence choice and how could such effects map to the DDM? Research suggests at least two distinct pathways: by influencing the drift rate or by altering non-decision times.

A number of studies now show that attending to a choice alternative or attribute increases its weighting in the evidence accumulation process [72–75]. To the extent that negative affect draws attention to a choice-relevant attribute or object, it should thus increase the weight it receives. Supporting this idea, in an emotional flanker task depressive ruminators versus non-ruminators showed a stronger drift rate for a negative target surrounded by positive distractors [76], perhaps because negative affect focused attention on the target, shielding evidence accumulation from distracting information. The same logic suggests that when negative affect draws attention to distracting, task-irrelevant stimuli [77], evidence accumulation should become less efficient (i.e., a weakened drift rate). Indeed, participants who feared failure showed reduced drift rates during a perceptual task after learning that they were performing poorly relative to other participants [15]. In this case, negative affect may have drawn attention to task-irrelevant thoughts (e.g., self-image concerns), interfering with task-related evidence accumulation.

Yet the attention-grabbing effects of affect need not influence the drift rate alone. For instance, in a dot-probe task participants must detect the location of a dot immediately following the brief presentation of a task-irrelevant stimulus that is either spatially congruent or incongruent to the dot. The more the task-irrelevant incongruent stimulus draws attention, the more it should increase the time taken to re-orient attention and encode the probe, implying an increase in perceptual non-decision time. Indeed, a spatially-incongruent, threatening stimulus increased non-decision times among clinically anxious patients, but did not affect drift rates [78]. Thus, in line with an indirect mapping, attentionally-mediated effects of negative affect can modulate different DDM parameters dependent on the context.

One way forward is to incorporate a new parameter to the DDM to account for the influence of attention. Recent work has introduced such an ‘attentional discount’ parameter to diminish the weight on unattended options during evidence accumulation [72] (see also [79]). This raises important new research questions. For instance, do emotionally evocative stimuli receive less attentional discounting when they are unattended, perhaps due to working memory intrusions? Other research has investigated when affective states will broaden or narrow attentional focus [80,81], but what “attentional focus” means is not always clear. Does breadth of attentional focus relate to the frequency of attentional shifts, the steepness of attentional discounting, or both? The computational rigor of the attentional DDM provides a route toward formally answering such questions.

Accessibility.

Another key concept from affective science with no direct mapping to a DDM parameter is the accessibility of a mental concept. This mechanism is thought to underlie affective priming, a phenomenon where affective states influence decision processes by making other information (e.g., memories, concepts, actions, etc.) more accessible [82,83]. According to priming research [84], the effect of affective priming should depend on the nature of the accessible content and its relation to the current task. Therefore, affective priming could modulate decisions through several routes, including non-decision time, starting bias, or even drift rate. Only the first two have so far been formally supported through empirical work. One study found that brief affective primes moderated non-decision times, an effect linked to the time required to encode or execute motor responses [85]. In cases where affect modulates expectations, associative mechanisms may instead produce a response bias instead: listening to happy music produced a starting point bias to categorize words as “positive” [86].

More work is needed to understand how and when affective priming, and accessibility more broadly, influences parameters of the DDM. Here again, insights from affective science will be indispensable. For instance, the relative timing of prime and choice is likely to be an important factor. Some research has found that affective priming effects are strongest when prime and choice are close in time (e.g., [87]). This may be due, in part, to rapid emotion regulation [88] that diminishes the accessibility of negatively-valenced content over time [89]. Meanwhile, other work demonstrates that the magnitude of affective priming effects can amplify with time [82,83]. When and why such differences are observed remains unclear, but one possibility is that priming sometimes influences starting point (producing diminishing effects with time) and sometimes influences drift rate (which will tend to amplify effects as more evidence accumulates), perhaps as a function of recency or duration of the prime. Future research should test these and other hypotheses.

The question of dual-systems

Incorporating computational modeling into the affective sciences can help bring clarity to important debates. For instance, dual-system models have strongly influenced the affect and decision-making literature [90]. These models generally posit the existence of a rapid, affect-driven system (e.g., System 1) and a slower, more “rational” system (e.g., System 2). This implies that the mental processes driving choice change over the time-course of a decision, and that experimentally interfering with the slower System 2 should result in more affect-driven choices. In line with such theorizing, a recent set of studies found stronger framing effects under time pressure, perhaps because affective responses (i.e., due to gain/loss frames) had a stronger influence on choice when System 2 was interrupted [91]. Yet recent DDM work also suggests that many phenomena interpreted as supporting dual-system frameworks, including RT differences and some time-pressure effects, can be explained more parsimoniously without the need to posit fast and slow processes [6–8,92]. How can we reconcile seemingly contradictory observations like these?

The idea that processing systematically varies across time is incongruent with the standard DDM but can be incorporated into a more complex model with time-varying evidence. In turn, the formal rigor of these models makes it easier to empirically differentiate competing explanations. Recent work has done precisely this [93], splitting evidence accumulation into two periods and using model-fitting to determine the nature of evidence during each period. This work reveals that early evidence accumulation more clearly reflected positive affect from a sure gain or negative affect from a sure loss. In contrast, later evidence accumulation reflected relative expected utilities of the options. In this new model, a reduction in decision thresholds increased the framing effect by enhancing the influence of evidence accumulated earlier in the process. This example nicely illustrates the mutual benefits derived from the marriage of affective science and computational modeling: theories in affective science suggest the need to modify the standard DDM, which in turn provides the mechanism for properly testing the theory.

Concluding Remarks

Computational models increasingly inform our understanding of decision processes, but the influence of affect on these computations remains in its infancy. We hope that this review lays the groundwork for integration based on the strengths of both the affective sciences and computational modeling (see Outstanding Questions). However, a conceptual framework is only one piece of the puzzle. Researchers will still be required to grapple with some of the concrete challenges that arise (see Box 3). Figuring out how best to address these issues will depend on careful theorizing that draws on all available empirical methods.

Box 3. Methodological Considerations: Self-Reported Affect.

Fitting the DDM to data requires the researcher to identify the evidence favoring one choice versus another. For perceptual judgment tasks, this is straight-forward (e.g., the square containing more white pixels is the brighter one) and involves identifying objectively correct versus incorrect choices. Identifying evidence based on an individual’s internal affective state is more challenging. Self-report is often considered the most face-valid, direct measure, but explicitly asking participants to reflect on their affective experience (sometimes repeatedly over the course of a study) may introduce confounds and limit external validity. Past work has suggested that self-report measures may lead people to attend to their current affective state, giving it greater weight in a subsequent choice (e.g., [43,121,122]). Meanwhile, prompting people to consider a potential choice-irrelevant cause of their affect can discount its potential relevance, reducing its weight (e.g., [47,122,123]). Thus, the wording and relative timing (i.e., pre- or post-choice) of a self-report measure can alter attention to internal affective states, which may in turn modulate the weight given to affect during evidence accumulation. While, it might be tempting to view many of the intricacies of affective processes and their measurement as noise to be eliminated from experimental designs, an alternative approach might occasionally capitalize on these “nuisances” and explicitly incorporate them into hypotheses to be tested with the DDM.

A similar challenge (and opportunity) arises when considering the relativity of affect. During decision making, objects must be evaluated in reference to each other. In the DDM, evidence accumulated in favor of one alternative is identical to evidence against the other. Notably, affect is also shaped by comparisons—e.g., receiving $0 is experienced positively or negatively if the alternative outcome was a $100 loss or $100 gain, respectively [124]. This has at least two important implications for research seeking to integrate affective processes within the DDM. First, it is critical to know what comparisons are contributing to affect. The available alternatives may shape affective responses to a given option, but affect can be shaped by other comparisons as well (e.g., expectations, options from previous choices, etc.). This contributes to a second important implication for researchers to keep in mind: measures of affect are likely to be more predictive of decisions when they reflect similar comparisons. This point has been demonstrated in work on loss aversion. Affective ratings correlated with loss averse behavior, but only when the affective ratings were made with a response scale that invoked similar comparisons [125].

Building clear linkages to neural and physiological mechanisms represents an important avenue for future research. There is, of course, a long history of research on the neuroscience of both decision-making [94] and affect, with many different perspectives (e.g., [57,58]). While introducing yet another field of work to the mix brings its challenges, it also provides additional methods that can inform and constrain the development of formalized models. For example, neural and physiological measures could reveal the focus of internal attention in the same way that eye gaze reveals external attention. Thus, physiological measures, such as interoceptive sensitivity [95,96], could help determine when people attend to their affective states or interoceptive information, providing a way to measure the influence of these states on evidence accumulation [27,56,97,98].

Despite these strengths, it is important to acknowledge a few limitations of computational modeling. First, caution is warranted when drawing connections between concepts, operational variables, and computational parameters. For example, measures that appear on their face to provide support for dual-systems may be inconclusive due to issues with construct validity (i.e., correspondence between a conceptual variable and its operationalization) and internal validity (i.e., confounding explanations) (e.g., [99]). A manipulation like time pressure may not solely influence the extent of processing (i.e., decision threshold), but could also influence how people allocate attention [100], which could, in turn, influence other decision processes (e.g., drift rate). Unless such processes are accounted for, the model may identify spurious effects. Therefore, computational modeling provides a powerful tool but cannot substitute for experimental ingenuity and careful observation. Second, we acknowledge, of course, that many important concepts from affective science are unlikely to be captured by a computational parameter. As Marr’s levels of analysis suggest [101], computations can be understood in terms of their purpose, algorithmic solution, and biological implementation. Computational models are best understood at the algorithmic level, but other levels of analysis are equally important. For example, the purpose of evidence accumulation (e.g. maximizing the rate of reward outcomes) can in some cases suggest important revisions to the standard DDM [102]. Computational models should be informed by work at other levels of analysis (e.g. the functions of emotions), but may not directly address important debates and issues there (see also [103,104]).

Many writers have vacillated between celebrating our progress and bemoaning the murkiness of the field of affect and decision-making [105]. We believe that melding sophisticated, formalized models like the DDM (as well as others; see Box 4) with the careful theorizing of the affective sciences can bring conceptual and empirical clarity to this exciting line of research.

Box 4. Combining Models to Understand Affect’s Impact.

Though the DDM provides a powerful model of decision processes, it does not provide a formal means of capturing all relevant facets of affect and its effects. For example, to understand the impact of affect, which evolves and persists over time [126], it is critical to account for temporal and contextual factors that extend beyond the immediate choice. Fortunately, questions pertaining to the broader affective context in which choices occur fall within the province of other computational models. Reinforcement learning models, for example, examine how temporally-extended sequences of events influence behavior. However, these models generally do not address the information-processing dynamics at play during the act of deciding. Therefore, the DDM and the reinforcement learning models each excel in addressing complementary pieces of the puzzle. Combining the two thus may lead to a fuller picture of affect’s role in choice.

For example, consider recent studies that have modeled affective states as a function of reward prediction errors [127], which may then feed back into the model to modify responses to subsequent outcomes, influencing choice [128]. In this work, positive affect from a previous experience causes subsequent rewards to be perceived more favorably whereas negative affect diminishes the perception of later rewards [128]. Accounting for this required the introduction of a ‘mood’ parameter to a reinforcement learning model that biased perception of reward prediction errors. Thus, this work explains when and why affective state might interact with previous and current rewards. But how does this biased interpretation of outcomes shape subsequent choices? Does it change the amount of evidence in favor of a given option (i.e., drift rate) or does it produce a response bias (i.e., starting point bias)? Does affective state that has been shaped by reinforcement history influence how attention is allocated during subsequent choices? Future work should consider how the DDM might be integrated with reinforcement learning models to further expand our understanding of affective processes in choice.

Figure I. Illustration of DDM Parameters and Their Effects.

The grey distributions in each panel are identical and depict the results of the same parameter settings (i.e., weak drift rate, wide decision threshold, and no starting point bias). Thus, each panel illustrates how choice probabilities and RT distributions are differentially impacted by (A) strengthening the drift rate (v), (B) reducing the decision thresholds (a), or (C) including a starting point bias (z).

Trends Box.

• There has been a paradigm shift in the decision sciences towards the use of computational models of choice. Some of these same models have begun to shed light on the role of affect in decision processes. Proper integration between computational modeling and the affective sciences holds the potential to motivate future research and enhance conceptual clarity.

• One influential model of choice, the drift diffusion model, has been successfully used to model various effects of affect on choice. Much of the research that has been conducted suggests clear connections between concepts in affective science and model parameters.

• This work is in its infancy, and the area is ripe for discovery, but requires careful theorizing on how to connect the richness of concepts and ideas from affective science to computational parameters.

Glossary

affect

a state of pleasure or displeasure stemming from visceral sensations

computational model

a mathematical model that relies on computer simulation to study the workings of a complex system

computational parameter

an entity within a computational model that, when assigned a value, determines how input to the model is transformed into output

decision threshold

the parameter of the DDM that determines the value at which evidence accumulation terminates

drift rate

the parameter of the DDM that determines rate and direction in which evidence accumulates

evidence

information from internal and/or external sources that reduces uncertainty about how to resolve a decision

non-decision time

the parameter of the DDM that accounts for time required for non-decision processes (e.g., perceptual encoding and implementing motor responses)

sequential accumulator

a structure in an evidence accumulation model that gathers evidence towards making a choice

starting point bias

the parameter of the DDM that determines the relative difference between the initial evidence value and the threshold for each choice alternative