Abstract
Analyzing count data is frequent in addiction studies but may be cumbersome, time‐consuming, and cause misleading inference if models are not correctly specified. We compared different statistical models in a simulation study to provide simple, yet valid, recommendations when analyzing count data.We used 2 simulation studies to test the performance of 7 statistical models (classical or quasi‐Poisson regression, classical or zero‐inflated negative binomial regression, classical or heteroskedasticity‐consistent linear regression, and Mann‐Whitney test) for predicting the differences between population means for 9 different population distributions (Poisson, negative binomial, zero‐ and one‐inflated Poisson and negative binomial, uniform, left‐skewed, and bimodal). We considered a large number of scenarios likely to occur in addiction research: presence of outliers, unbalanced design, and the presence of confounding factors. In unadjusted models, the Mann‐Whitney test was the best model, followed closely by the heteroskedasticity‐consistent linear regression and quasi‐Poisson regression. Poisson regression was by far the worst model. In adjusted models, quasi‐Poisson regression was the best model. If the goal is to compare 2 groups with respect to count data, a simple recommendation would be to use quasi‐Poisson regression, which was the most generally valid model in our extensive simulations.
Keywords: coverage of confidence interval, guidelines, simulation, substance use, type 1 error
1. INTRODUCTION
Count data are frequent in addiction studies, for example, when analyzing the number of drinks or cigarettes per week or a total number of criteria of addictive behaviors. These distributions typically feature a large number of zeros and small values with a long right tail corresponding to heavy users. Additionally, these distributions can vary widely, and thus the choice of a statistical model may become tricky since many are nonrobust to violations of the underlying assumptions and conditions. Contrary to continuous data for which a normal distribution often provides a reasonable fit, a single “default” distribution for count data is lacking. The Poisson or the negative binomial (NB) distributions have become classical statistical models in addiction research (Atkins, Baldwin, Zheng, Gallop, & Neighbors, 2013; Horton, Kim, & Saitz, 2007; Wagner, Riggs, & Mikulich‐Gilbertson, 2015) but have not proved successful to consistently fit a large portion of reality. Extensions of classical distributions have been proposed, such as zero‐inflated distributions to account for an excess of zeros in the data, but what should one do when facing an excess of ones instead of zeroes (eg, the number of sexual partners when investigating people in stable relationships)? In some situations, there may be outlying observations. As a result, researchers often have developed their own models when analyzing count data, which is cumbersome and time‐consuming.
This problem was pointed out years ago (Gardner, Mulvey, & Shaw, 1995), yet few studies in the addiction field investigated this question from a practical perspective and especially using simulation studies. A systematic literature review using PubMed and PsychNet with the keywords “simulation” and “count data” (June, 16, 2017) provided 254 results. A total of 8 articles were relevant for our study, after excluding articles related to longitudinal data, survival analysis, mixed‐effect models and correlated data, mediation analysis, and missing data. Table 1 summarizes the characteristics and conclusions of these articles. Overall, the studies mainly simulated Poisson distributions or distributions based on real data (6 articles). The tested models almost always include Poisson and NB regressions (7 articles) and frequently include zero‐inflated models (4 articles), while linear regression and over‐dispersed Poisson were not frequently investigated (respectively, 2 and 1 articles). It is difficult to draw a general conclusion from these studies. Poisson regression often appears as being the worse model. Indeed, Poisson distribution is not robust for over‐dispersed count data (Horton et al., 2007) because the Poisson distribution makes strong assumptions on the distribution (mean‐equal variance, resulting in an inflexible model with a single parameter), which is unrealistic when working on real health and addiction data. Thus, Poisson has long been described as causing misleading inferences (Gardner et al., 1995). More flexible count models should be used instead, such as the NB and zero‐inflated models in case of excess zeros (Horton et al., 2007; Payne et al., 2015; Preisser, Das, Long, & Divaris, 2016; Ullah, Finch, & Day, 2010) or overdispersed‐Poisson, referred to below as quasi‐Poisson (QP; Sturman, 1999). However, all these studies took into account a limited number of scenarios, varying mainly the sample size or only 1 parameter of the simulated distribution. In particular, none of these studies did consider unbalanced designs or confounding effects, which are important issues in all observational studies.
Table 1.
Systematic literature review of articles related to simulation on count data
| Authors | Year | Topic | DV | Models | Outcomes | IV | Varying Parameters | Choice |
|---|---|---|---|---|---|---|---|---|
| Sturman | 1999 | Education | Absenteeism (based on real data) | OLS, OLS with transformed DV, Tobit, P, overdispersed‐P, NB, ordered logistic, ordered probit | Type 1 error rate and no. of false positive | 10 | Sample size (n = 100, 1000), distribution of IV (normal or same as DV) | Over‐dispersed P |
| Horton et al | 2007 | Alcohol | P, NB, ZIP, over‐dispersed Poisson | P, NB, ZIP | Type 1 error rate and 99% CI | 1 binary | Variance NB (13.3, 40, 70) | All equivalent except P being worse |
| Vives et al | 2008 | Psychology | P | LS, LM, LMR I, LMR II, χ2 df test | Type 1 error rate and power | 1 | Sample size (n = 20, 50, 100, 500), lambda (0.3, 1, 5) | χ2 df test |
| Ullah et al | 2010 | Falls | Over‐dispersed falls data (based on real data) | P, NB, ZIP, ZINB | Type 1 error rate and power of model fit | 0 | No | NB |
| Roudsari et al | 2011 | Radiology | P, NB, ZINB | P, NB, ZINB, OLS | 95% CI for estimate, prediction of no. of head computed tomography | 4 | No | Unclear |
| Herbison et al. | 2015 | Falls | P | P, NB, risk ratio, hazard ratio, ratio of means, ratio of median | Estimates and variances | 1 binary | Kind of over‐dispersion (no, moderate, high) | All equivalent |
| Payne et al. | 2015 | Methodology | P | NB, P‐GLMM, NB‐GLMM | AIC, BIC, standard error of coefficients, and 95% CI | 3 | Outliers | NB and NB‐GLMM |
| Preisser et al. | 2016 | Dentistry | Dental caries (based on real data) | P, NB, marginalized ZIP, marginalized ZINB | Standard error of coefficients, 95% IC, and type I error rate | 4 | Sample size (n = 100, 200, 500, 1000) | Marginalized ZINB |
Abbreviations: CI, confidence interval; DV, dependent variable; GLMM, generalized linear mixed model; IV, independent variable; LM, Wald and Lagrange multiplier; LR, likelihood ratio; LRM I, Wald and Lagrange multiplier with Negbin I variance function; LMR II, Wald and Lagrange multiplier with Negbin II variance function; NB, negative binomial; P, Poisson; OLS, ordinary least square (linear regression); ZINB, zero‐inflated negative binomial; ZIP, zero‐inflated Poisson.
Overall, these publications and other publications not including simulations provided overly general recommendations, suggesting that one should compare and choose the best model according to the data (Gorelick & McPherson, 2015; Wagner et al., 2015). A recent study provided some guidelines for Student test use (Poncet, Courvoisier, Combescure, & Perneger, 2016), recommending Student test use for normal and symmetric distributions, the Mann‐Whitney (MW) test for strongly skewed distributions, and a robust Student test in presence of outliers. However, this study focused on continuous distributions and groups of the same size and variance, which is often not the case in addiction research. The two articles of our systematic literature review including linear regression did not conclude in favor of this model for count data (Roudsari, Mack, & Jarvik, 2011; Sturman, 1999). Additionally, several studies highlighted classical models—such as linear regression models—that provide nonoptimal analyses (Aiken, Mistler, Coxe, & West, 2015).
In the present study, we compared different statistical count models (Poisson, QP, classical, and zero‐inflated NB) in a simulation study to explore whether and to what extent it is possible to provide simple, yet valid, recommendations when analyzing count data in addiction research. We also included in our comparison classical models (linear regression and nonparametric statistics such as MW), which would considerably facilitate the statistical analyses. We considered a large number of scenarios likely to occur in addiction research, such as unbalanced designs, presence of confounding factors, and presence of outliers.
2. METHODS
We consider the statistical comparison issue of 2 samples of individuals with respect to count data using 2 simulation studies.
2.1. Design of the first simulation study
We considered combinations of 5 simulation factors as follows:
Seven classical statistical models were tested: the Poisson regression, QP regression (Ver Hoef & Boveng, 2007), NB regression, zero‐inflated negative binomial (ZINB) regression (a 2‐component model, where one combines NB regression to model the counts with a logistic regression to model an excess of zeroes, as explained, eg, in Zeileis, Kleiber, & Jackman, 2008), the linear regression (equivalent here to a Student test), a heteroskedasticity‐consistent (HC) test in linear regression (White, 1980), and the nonparametric MW test.
We generated data according to 9 population distributions: the Poisson distribution, the NB distribution (with variance equaling twice the mean), zero‐ and one‐inflated Poisson and NB distributions (obtained as mixtures with 50% of the observations generated according to a Poisson/NB distribution, and 50% of extra zeroes, respectively, of extra ones), a uniform count distribution, a left‐skewed distribution (while the Poisson and the NB distributions are right‐skewed), and a bimodal distribution (while the Poisson and the NB distributions are unimodal). All of these (noninflated) distributions were taken to have the same mean (mean = 2) and are depicted in Figure 1. We also considered the possibility to add outliers to contaminate these distributions, with 5% outliers placed around the value 20.
We tested 2 differences between population means, corresponding to a null hypothesis and an alternative hypothesis. Under the null hypothesis, we generated the data according to the same distribution in both groups (with means m1 = m2). Under the alternative hypothesis, data in the first group were generated with a mean m1 = 2 (respectively, m1 = 1 and m1 = 1.5 for zero‐ and one‐inflated distributions), and data in the second group were generated according to a distribution with a similar shape, but with a mean m2 = 4 (respectively, m2 = 2 and m2 = 3 for zero‐ and one‐inflated distributions), such that we had m2/m1 = 2 (the variance of the second group being also inflated, eg, by a factor of 2 in a Poisson or an NB distribution). For the contaminated distributions, outliers were generated identically in both groups under the null hypothesis and the alternative hypothesis.
We considered 2 sample sizes: small (n1 = n2 = 30) and moderate (n1 = n2 = 300).
Unbalanced designs were also considered for moderate sample sizes, where one group was larger than the other, with n2/n1 = 1/9, 1/2, 1, 2, or 9 (while n1 + n2 = 600). The case n2/n1 = 1 corresponded to a balanced design.
Figure 1.
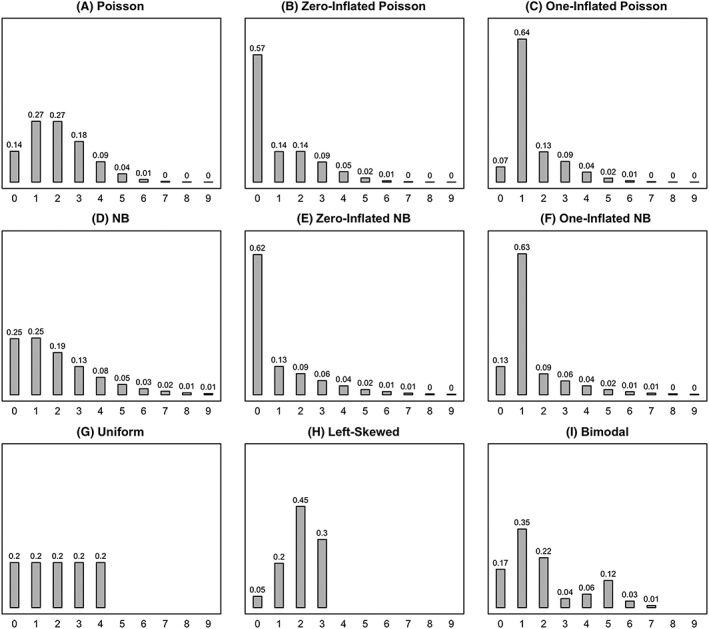
Barplots showing the nine distributions used in the first simulation study. NB, negative binomial
2.2. Design of the second simulation study
We studied situations where confounders were included as additional predictors in the models to get an adjusted comparison of the two groups. We considered combinations of 6 factors as follows:
Six statistical models were tested: the same as in study 1 except MW (for which controlling for covariates would be problematic).
We generated data according to 2 population distributions: the NB and the Poisson models (it would not be straightforward to define and generate a model including confounders according to the other distributions from Figure 1). Here also, we considered the possibility to add outliers to contaminate these distributions, with 5% outliers placed around the value 20.
We considered the same differences in population means corresponding to the null and the alternative hypothesis as in study 1. Here also, the distribution of outliers was identical in both groups under the null hypothesis and the alternative hypothesis.
We considered 2 sample sizes: small (n1 = n2 = 30) and moderate (n1 = n2 = 300), as in study 1.
We considered unbalanced designs for a moderate sample size (n1 + n2 = 600), as in study 1.
We considered 2 situations of confounding, where the unadjusted ratio between the two groups is either inflated or deflated because of confounding, compared to the adjusted ratio. We simulated 2 confounding factors—thought to be age and gender—where age was normally distributed with a standard deviation of 10 and a mean of 35 in one group, of 45 in the other group, and where we had 70% men and 30% women in one group and the other way around in the other group. An increase of 20 years was associated with a mean increase of 40%. Likewise, being a man rather than a woman was associated with a mean increase of 40%. Under the alternative hypothesis (with adjusted means m2/m1 = 2), the “inflated situation” corresponds to the case where the second group (with mean m2) was older (mean age 45 years) and with more men (70%) than the first group (35 years and 30%, respectively), while the “deflated situation” corresponds to the case where the second group was younger (mean age, 35 years) with more women (70%) than the first group (45 years and 30%, respectively). Under the null hypothesis, where the two groups are interchangeable, the inflated and the deflated situations corresponded to the same simulation setting. Examples of inflated and deflated situations are depicted in Figure 2.
Figure 2.
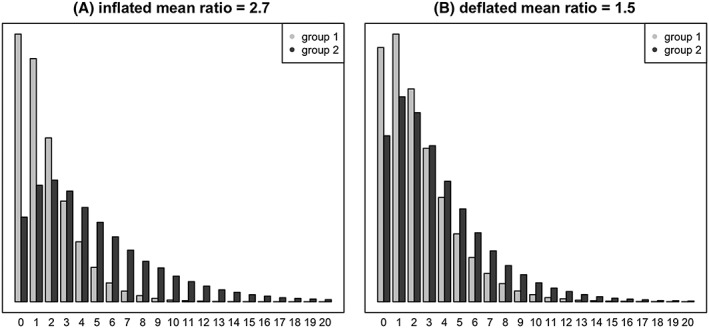
Barplots showing examples of negative binomial distributions used in the second simulation study, where the true (unconfounded) mean ratio between the two groups would be equal to 2, whereas the observed (confounded) mean ratio is equal to 2.7 (panel A, corresponding to an inflated scenario), respectively, to 1.5 (panel B, corresponding to a deflated scenario)
2.3. Implementation
For both simulation studies, we have implemented these models using the R (3.2.5) software using the following functions: the “glm” function for the Poisson regression (option “family = Poisson”), the QP regression (“family = quasi‐Poisson”), and the linear regression (default option “family = gaussian”); the “glm.nb” routine from the “MASS” library for the NB regression (with parameter “size = mu”); the “zeroinfl” routine from the “pscl” library for ZINB regression (with options “dist = negbin” and “link = logit”); the “vcovHC” routine from the “sandwich” library to get an HC test in linear regression (with the option “type = HC3,” as recommended in Long & Ervin, 2000); and the “wilcox.test” for the MW test, with options set to “exact = FALSE” and “correct = FALSE” to get the classic version of this test. Confidence intervals for the area under the curve (AUC), the association measure used in a MW test, were calculated using the “ci.auc” routine from the “pROC” library. Finally, confidence intervals for the mean ratio in a ZINB regression were obtained using the delta method via the “deltamethod” routine from the “msm” library (where a mean in ZINB regression can be estimated as the product of one minus the proportion of extra zeros, obtained via the logistic regression component of the model, and the average of the NB regression component of the model).
2.4. Outcomes considered
A total of 10 000 simulations have been run under each setting considered. All statistical tests were bilateral tests run at the nominal 5% significance level. We considered the 2 following criteria:
Type 1 error was estimated as the percentage of simulated samples under the null hypothesis in which the null hypothesis was wrongly rejected, which should be approximately 5% for a valid model. A test was considered valid if the type 1 error was below 7% and conservative if it was below 3% (Bradley, 1978).
Coverage of 95% confidence interval (CI) was estimated as the percentage of simulated samples in which the 95% CI provided by the different models contained the true mean ratio (Poisson, NB, ZINB, and QP regressions), the true mean difference (Student and HC test), or the true AUC (MW test). This was done under the null hypothesis and the alternative hypothesis. Indeed, a valid test implies a valid 95% CI under the null hypothesis. However, a model producing a valid 95% CI under the null hypothesis does not necessarily produce a valid 95% CI under the alternative hypothesis, such that (b) was a different criterion than (a). In line with the type 1 error, a 95% CI was considered valid if the coverage was above 93% and conservative if it was above 97%.
In addition, we estimated the power to be the percentage of simulated samples under the alternative hypothesis in which the null hypothesis was rightly rejected, which should be as large as possible. Such a power study is limited to our 2 sample sizes and is just reported as a useful indication. Note that for ZINB regression, we have discarded from those calculations the few samples for which this model could not be fitted due to technical problems.
3. RESULTS
3.1. First simulation study
The results of our first simulation study are summarized in Tables 2 and 3. Table 2 reports the type 1 error rate and the power estimated for the 7 models under different population distributions and with small sample sizes. One can see that the Poisson regression was nonvalid in most cases, except of course under a Poisson distribution (and under a uniform distribution, being also conservative under a left‐skewed and a one‐inflated Poisson distribution). On the other hand, the NB regression was valid (or conservative) in all settings without outliers, but not valid with outliers, whereas ZINB regression was not even valid without outliers under a zero‐ or one‐inflated NB distribution with these small sample sizes. In contrast, the remaining 4 models were valid under each setting considered, also with outliers. Among the 4 valid models, the MW test was the most powerful with outliers, whereas QP regression, linear regression, and the HC test were in general more powerful (and pretty close of each other) without outliers (except for one‐inflated distributions, where the MW test was better). Similar results were found with moderate sample sizes—also with an unbalanced design—except for ZINB regression, which became accurate under a zero‐inflated (but not under a one‐inflated) NB model, while the HC test was not valid with outliers together with n2/n1 = 1/9 or 9, whereas the statistical power gets logically much closer (and often reached) 100% in all tested settings (data not shown).
Table 2.
Type 1 error rate and power achieved by 7 statistical models to reject mean equality of 2 groups for 9 population distributions
| Statistical Model | ||||||||
|---|---|---|---|---|---|---|---|---|
| Population distribution | Outliers | Poisson | QP | NB | ZINB | Linear | HC | MW |
| Poisson | No | 4.6 | 4.6 | 4.1 | 4.2 | 4.8 | 4.8 | 5.0 |
| (99.6) | (99.5) | (99.6) | (98.0) | (99.6) | (99.6) | (99.2) | ||
| Yes | 42.3 | 6.1 | 17.1 | 15.9 | 4.1 | 4.2 | 5.3 | |
| ‐ | (44.6) | ‐ | ‐ | (48.1) | (48.4) | (96.7) | ||
| Zero‐inflated Poisson | No | 15.9 | 4.6 | 4.3 | 6.8 | 5.2 | 5.3 | 5.2 |
| ‐ | (48.8) | (38.2) | (9.5) | (47.8) | (48.0) | (25.4) | ||
| Yes | 53.6 | 6.3 | 12.4 | 14.0 | 3.7 | 3.7 | 5.0 | |
| ‐ | (17.4) | ‐ | ‐ | (16.9) | (17.1) | (20.9) | ||
| One‐inflated Poisson | No | 2.9 | 5.3 | 2.8 | 3.8 | 4.8 | 4.9 | 5.0 |
| ‐ | (98.2) | ‐ | (92.3) | (98.4) | (98.4) | (99.8) | ||
| Yes | 46.5 | 6.6 | 22.5 | 20.2 | 3.3 | 3.5 | 4.8 | |
| ‐ | (30.2) | ‐ | ‐ | (32.2) | (32.4) | (98.8) | ||
| NB | No | 16.7 | 5.3 | 6.2 | 7.1 | 5.1 | 5.3 | 5.2 |
| ‐ | (80.5) | (83.0) | ‐ | (79.9) | (80.1) | (73.9) | ||
| Yes | 44.9 | 6.0 | 13.0 | 12.5 | 4.3 | 4.4 | 5.0 | |
| ‐ | (36.4) | ‐ | ‐ | (38.2) | (38.4) | (64.3) | ||
| Zero‐inflated NB | No | 25.3 | 4.4 | 4.6 | 8.6 | 4.6 | 4.7 | 5.3 |
| ‐ | (32.3) | (28.3) | ‐ | (30.3) | (30.6) | (16.1) | ||
| Yes | 54.5 | 5.7 | 9.6 | 12.7 | 4.1 | 4.2 | 4.5 | |
| ‐ | (14.5) | ‐ | ‐ | (14.2) | (14.3) | (13.8) | ||
| One‐inflated NB | No | 10.2 | 5.3 | 6.5 | 7.7 | 4.6 | 4.7 | 5.2 |
| ‐ | (81.5) | (87.7) | ‐ | (81.7) | (81.8) | (97.8) | ||
| Yes | 47.5 | 6.6 | 20.9 | 18.8 | 3.8 | 3.9 | 4.8 | |
| ‐ | (27.6) | ‐ | ‐ | (28.9) | (29.1) | (93.7) | ||
| Uniform | No | 4.8 | 4.4 | 4.3 | 3.7 | 4.8 | 4.9 | 4.7 |
| (97.9) | (93.7) | (91.8) | (85.9) | (92.5) | (92.7) | (78.9) | ||
| Yes | 42.0 | 6.0 | 15.2 | 14.8 | 3.9 | 4.0 | 4.7 | |
| ‐ | (41.5) | ‐ | ‐ | (43.6) | (43.8) | (69.7) | ||
| Left‐skewed | No | 0.1 | 4.6 | 0.1 | 0.3 | 5.0 | 5.0 | 4.9 |
| (100) | (100) | (100) | (100) | |||||
| Yes | 39.7 | 5.9 | 20.3 | 20.3 | 2.9 | 3.1 | 4.5 | |
| ‐ | (47.2) | ‐ | ‐ | ‐ | (51.2) | (99.6) | ||
| Bimodal | No | 11.4 | 5.1 | 6.1 | 6.4 | 5.3 | 5.4 | 4.9 |
| ‐ | (82.9) | (84.5) | (67.6) | (81.3) | (81.5) | (67.0) | ||
| Yes | 43.4 | 5.8 | 14.6 | 14.0 | 4.0 | 4.1 | 4.9 | |
| ‐ | (37.2) | ‐ | ‐ | (38.9) | (39.3) | (57.3) | ||
Abbreviations: HC, heteroskedasticity consistent; MW, Mann Whitney; NB, negative binomial; QP, quasi‐Poisson; ZINB, zero‐inflated negative binomial.
Type 1 error rate for simulations under the null hypothesis is provided on the first line for each population distribution; power for simulations under the alternative hypothesis is provided under brackets on the second line for each population distribution. Power was provided only for valid models (Type 1 error rate < 7%) (hyphens for invalid models).
Distributions under the null hypothesis, m1 = m2; distributions under the alternative hypothesis, m1/m2 = 2, with sample size n1 = n2 = 30, estimation from 10 000 simulations.
Valid models and the most powerful models among the valid models are highlighted in bold.
Table 3.
95% confidence intervals for ratio for 7 statistical models under the alternative hypothesis for various population distributions
| Statistical Model | ||||||||
|---|---|---|---|---|---|---|---|---|
| Population distribution | n2/n1 | Poisson | QP | NB | ZINB | Linear | HC | MW |
| Poisson | 1/9 | 95.0 | 95.1 | 95.4 | 95.3 | 86.4 | 94.9 | 94.0 |
| 1 | 95.0 | 95.0 | 95.2 | 95.2 | 94.8 | 94.8 | 94.9 | |
| 9 | 94.8 | 94.8 | 94.9 | 96.1 | 99.0 | 94.4 | 94.3 | |
| Zero‐inflated Poisson | 1/9 | 75.5 | 90.8 | 97.9 | 94.3 | 79.7 | 94.4 | 94.4 |
| 1 | 79.9 | 96.3 | 98.5 | 95.5 | 95.3 | 95.3 | 94.7 | |
| 9 | 82.7 | 98.1 | 98.3 | 94.4 | 99.7 | 94.5 | 84.0 | |
| One‐inflated Poisson | 1/9 | 95.4 | 93.3 | 95.4 | 95.2 | 83.7 | 94.0 | 93.0 |
| 1 | 96.6 | 95.7 | 96.6 | 96.5 | 95.4 | 95.4 | 94.3 | |
| 9 | 96.7 | 96.6 | 96.7 | 95.6 | 99.3 | 94.0 | 93.1 | |
| NB | 1/9 | 75.7 | 90.8 | 94.7 | 94.1 | 79.7 | 94.0 | 94.7 |
| 1 | 79.9 | 95.9 | 95.2 | 94.9 | 94.7 | 94.8 | 94.9 | |
| 9 | 82.9 | 98.2 | 95.3 | 95.3 | 99.6 | 94.5 | 94.8 | |
| Zero‐inflated NB | 1/9 | 63.0 | 89.6 | 96.8 | 93.1 | 77.6 | 93.2 | 94.3 |
| 1 | 69.7 | 96.2 | 98.0 | 94.8 | 95.1 | 95.2 | 94.9 | |
| 9 | 73.2 | 98.4 | 97.7 | 94.1 | 99.6 | 94.4 | 94.2 | |
| One‐inflated NB | 1/9 | 81.6 | 90.1 | 89.6 | 89.4 | 78.9 | 92.4 | 93.2 |
| 1 | 86.2 | 95.6 | 92.6 | 92.7 | 94.9 | 95.0 | 95.3 | |
| 9 | 88.5 | 98.0 | 93.9 | 93.9 | 99.6 | 94.0 | 94.2 | |
| Uniform | 1/9 | 85.2 | 86.9 | 90.2 | 94.6 | 75.3 | 94.5 | 94.3 |
| 1 | 91.2 | 96.2 | 97.6 | 96.2 | 95.2 | 95.3 | 95.4 | |
| 9 | 94.6 | 99.2 | 99.1 | 96.6 | 99.9 | 95.1 | 94.8 | |
| Left‐skewed | 1/9 | 98.6 | 87.7 | 98.6 | 98.9 | 75.9 | 95.2 | 93.6 |
| 1 | 99.6 | 96.0 | 99.6 | 99.7 | 94.9 | 94.9 | 94.7 | |
| 9 | 99.9 | 99.0 | 99.9 | 99.8 | 99.9 | 95.2 | 94.3 | |
| Bimodal | 1/9 | 75.6 | 87.7 | 92.1 | 94.0 | 75.4 | 94.9 | 94.7 |
| 1 | 82.9 | 96.0 | 95.8 | 94.9 | 94.9 | 94.9 | 94.8 | |
| 9 | 87.1 | 98.9 | 97.5 | 95.5 | 99.9 | 94.7 | 94.2 | |
Abbreviations: HC, heteroskedasticity consistent; MW, Mann‐Whitney; NB, negative binomial; QP, quasi‐Poisson; ZINB, zero‐inflated negative binomial.
95% confidence intervals for the mean ratio are given for Poisson, NB, and QP: for the mean difference for linear regression and HC or the area under the curve for MW.
Distributions under the alternative hypothesis: m1/m2 = 2, with sample size n1 + n2 = 600, estimation from 10 000 simulations.
Table 3 reports the coverage of 95% CI estimated for the 4 models under the alternative hypothesis without outliers and with moderate sample sizes (to save space, cases with n2/n1 = 1/2 or 2 are not presented). Overall, the best models were the HC test and the MW test, which were valid under virtually all settings, the only exception being the MW test under a zero‐inflated Poisson distribution together with n2/n1 = 9. On the other hand, linear regression did not perform well with an unbalanced design. In fact, it was not valid when n2/n1 < 1 (ie, when the mean, and hence the variance, was higher for the smaller group) and was conservative when n2/n1 > 1 (ie, when the mean, and hence the variance, was higher for the larger group. Quasi‐Poisson regression partly showed the same behavior as linear regression, the coverage of the 95% CI increasing with n2/n1, though in a less pronounced way than for linear regression. Without being perfect, NB and ZINB were also better than linear and QP regression, while Poisson regression produced nonvalid 95% CI under most distributions except for Poisson distributed data.
We do not present the coverage of a 95% CI calculated with outliers here, since it is not clear what the true mean ratio should be—respectively, the true mean difference—in the presence of outliers.
3.2. Second simulation study
The results of our second simulation study, where confounders have been included in the model, are summarized in Tables 4 and 5. Table 4 reports the type 1 error rate estimated for the 6 models with moderate sample sizes. Again, the Poisson regression was valid in none of the settings considered except the Poisson distribution without outliers. The NB regression was valid under Poisson and NB distributions, but only without outliers, the same applying for ZINB regression. Linear regression was mostly valid, except without outliers together with n2/n1 = 1/9. Remarkably, QP regression and the HC test were valid in all situations, also with outliers and with an unbalanced design. With small sample sizes, QP regression was slightly nonvalid and the HC test was slightly conservative with outliers such that it is delicate to compare their power (data not shown).
Table 4.
Type 1 error rate achieved by 6 statistical models to reject mean equality of 2 groups for 2 population distributions adjusting for confounders
| Statistical Model | ||||||||
|---|---|---|---|---|---|---|---|---|
| Population distribution | Outliers | n2/n1 | Poisson | QP | NB | ZINB | Linear | HC |
| Poisson | No | 1/9 | 4.7 | 4.8 | 4.5 | 6.8 | 8.9 | 5.5 |
| 1/2 | 4.7 | 4.7 | 4.5 | 5.2 | 5.6 | 4.8 | ||
| 1 | 4.7 | 4.7 | 4.4 | 4.6 | 4.6 | 4.7 | ||
| 2 | 5.0 | 5.0 | 4.9 | 3.9 | 4.4 | 5.4 | ||
| 9 | 4.8 | 4.9 | 4.7 | 3.8 | 3.7 | 5.6 | ||
| Yes | 1/9 | 40.2 | 3.1 | 10.3 | 11.8 | 4.6 | 6.6 | |
| 1/2 | 40.8 | 4.5 | 14.0 | 12.4 | 5.3 | 5.2 | ||
| 1 | 41.6 | 4.6 | 15.0 | 13.6 | 4.7 | 4.6 | ||
| 2 | 42.8 | 5.7 | 17.2 | 16.0 | 5.2 | 5.0 | ||
| 9 | 43.1 | 6.3 | 20.5 | 17.6 | 4.9 | 6.7 | ||
| NB | No | 1/9 | 18.6 | 6.9 | 5.3 | 7.1 | 10.4 | 5.3 |
| 1/2 | 17.3 | 5.5 | 5.0 | 5.7 | 6.2 | 4.9 | ||
| 1 | 18.1 | 5.6 | 5.4 | 5.5 | 4.9 | 5.3 | ||
| 2 | 16.9 | 4.8 | 5.0 | 4.5 | 3.8 | 4.9 | ||
| 9 | 16.9 | 4.2 | 5.4 | 4.4 | 2.9 | 5.5 | ||
| Yes | 1/9 | 43.4 | 3.7 | 8.2 | 10.4 | 5.4 | 6.0 | |
| 1/2 | 44.1 | 4.5 | 10.5 | 9.7 | 5.2 | 5.3 | ||
| 1 | 45.4 | 4.6 | 11.4 | 10.4 | 4.6 | 4.6 | ||
| 2 | 45.0 | 5.5 | 12.4 | 11.1 | 4.9 | 5.1 | ||
| 9 | 44.9 | 5.8 | 14.3 | 11.9 | 4.4 | 5.9 | ||
Abbreviations: HC, heteroskedasticity consistent; NB, negative binomial; QP, quasi‐Poisson; ZINB, zero‐inflated negative binomial.
Type 1 error rate for simulations under the null hypothesis is provided for each population distribution.
Distributions under the null hypothesis: m1 = m2, with sample size n1 + n2 = 600, estimation from 10 000 simulations. The confounding variables were age and gender and were associated with a mean inflation of 40%. The mean age was 40 (standard deviation = 10) and the proportion of men was.5 in both groups (centered mean).
Valid models (type 1 error rate between 3% and 7%) are flagged in bold.
Table 5.
95% confidence intervals for mean ratio/difference for 6 statistical models under the alternative hypothesis for 2 population distributions, controlling for confounders
| Statistical Model | ||||||||
|---|---|---|---|---|---|---|---|---|
| Population distribution | Direction of confounding | n2/n1 | Poisson | QP | NB | ZINB | Linear | HC |
| Poisson | Inflated | 1/9 | 95.1 | 95.0 | 95.4 | 94.7 | 31.0 | 55.2 |
| 1/2 | 95.4 | 95.3 | 95.5 | 95.6 | 75.8 | 81.0 | ||
| 1 | 95.2 | 95.1 | 95.3 | 96.0 | 95.6 | 94.9 | ||
| 2 | 95.0 | 95.0 | 95.1 | 96.1 | 72.5 | 61.8 | ||
| 9 | 95.5 | 95.4 | 95.5 | 96.5 | 43.5 | 19.5 | ||
| Deflated | 1/9 | 95.1 | 94.9 | 95.2 | 95.8 | 50.1 | 60.7 | |
| 1/2 | 95.2 | 95.2 | 95.4 | 96.6 | 75.1 | 79.0 | ||
| 1 | 95.3 | 95.2 | 95.5 | 96.5 | 93.6 | 94.8 | ||
| 2 | 95.3 | 95.2 | 95.4 | 96.9 | 88.9 | 89.0 | ||
| 9 | 95.2 | 95.1 | 95.3 | 96.8 | 72.9 | 66.0 | ||
| NB | Inflated | 1/9 | 75.0 | 89.4 | 94.8 | 93.6 | 54.8 | 85.2 |
| 1/2 | 77.9 | 93.9 | 94.7 | 94.4 | 87.3 | 90.6 | ||
| 1 | 79.1 | 95.7 | 94.7 | 95.0 | 96.8 | 94.3 | ||
| 2 | 80.9 | 97.3 | 95.0 | 95.7 | 92.9 | 81.3 | ||
| 9 | 83.0 | 98.6 | 95.2 | 95.9 | 90.7 | 53.2 | ||
| Deflated | 1/9 | 77.2 | 92.5 | 95.0 | 94.4 | 68.6 | 78.3 | |
| 1/2 | 77.5 | 93.3 | 94.6 | 95.2 | 83.2 | 87.9 | ||
| 1 | 76.5 | 93.6 | 94.7 | 95.3 | 92.2 | 94.2 | ||
| 2 | 78.1 | 94.6 | 94.7 | 95.9 | 91.8 | 93.1 | ||
| 9 | 79.0 | 96.3 | 95.0 | 96.5 | 90.4 | 82.6 | ||
Abbreviations: HC, heteroskedasticity consistent; NB, negative binomial; QP, quasi‐Poisson; ZINB, zero‐inflated negative binomial.
95% confidence intervals for the mean ratio are given for Poisson, NB, and QP, for the mean difference for linear regression.
Distributions under the alternative hypothesis, m1/m2 = 2, with sample size n1 + n2 = 600, estimation from 10 000 simulations.
Confounders were age and gender and were associated with a mean inflation of 40%. For inflated mean, group 2 was older (mean age 45) and with more men (70%) than the first group (respectively, 35% and 30%), and for deflated mean, group 1 was older with more men.
Valid models (95% IC between 93% and 97%) are flagged in bold.
Table 5 reports the coverage of 95% CI estimated for the 6 models under the alternative hypothesis, with moderate sample sizes, including an inflated or a deflated situation of confounding. As usual, the Poisson regression was valid only under Poisson, not under NB distributed data. Linear regression and the HC test were not valid with an unbalanced design, while QP regression was much better, though not perfect in some settings with NB distributed data. Not surprisingly, NB and ZINB regression were valid in all these settings since we considered here only Poisson/NB distributed data without outliers (recall we did not consider the criterion of the coverage of a 95% CI with outliers).
3.3. Summary of simulations
To summarize the performance of the 7 or 6 models in the first (unadjusted comparisons) and in the second (adjusted comparisons) simulation studies, we calculated for each model the absolute difference between the estimated coverage of the 95% CI (obtained via simulation) and the target value of 0.95, averaged over the different settings considered with moderate sample sizes (in what follows the “AACE” for average absolute coverage error). We had 135 such settings in the first simulation study (90 under the null, 45 under the alternative hypothesis, the former being the pendent with moderate sample sizes of those settings described in Table 2, but including also unbalanced designs, the latter being described in Table 3), and 40 such settings in the second simulation study (20 under the null hypothesis, described in Table 4, and 20 under the alternative hypothesis, described in Table 5). Table 6 provides the rankings of the models according to this AACE criterion. In the first simulation study, the MW test was the best model, followed closely by the HC test and QP regression, the 3 models achieving an AACE below 1%. Linear regression followed at fourth position (because of its poor performance with an unbalanced design under the alternative hypothesis), still in front of ZINB and NB regression (which performed poorly with outliers), Poisson regression being by far the worst model (with an AACE of almost 20%). In the second simulation study, QP regression was ranked first, being the only model with an AACE below 1%, followed by NB and ZINB (which again suffered from outliers), the HC test and linear regression lying far behind (the HC test was not here improving linear regression with an unbalanced design under the alternative hypothesis), Poisson regression remaining at the end of the ranking. Overall, it is fair to say that QP regression was the best model, performing reasonably well in most settings considered, under the various distributions considered, with or without confounding, with or without outliers, and with a balanced or an unbalanced design.
Table 6.
Ranking of the models according to the average absolute coverage error
| First Simulation Study (Unadjusted Comparisons) | Second Simulation Study (Adjusted Comparisons) |
|---|---|
| 1. MW 0.005 | 1. QP 0.009 |
| 2. HC 0.008 | 2. NB 0.023 |
| 3. QP 0.009 | 3. ZINB 0.026 |
| 4. Linear 0.020 | 4. HC 0.092 |
| 5. ZINB 0.039 | 5. Linear 0.094 |
| 6. NB 0.043 | 6. Poisson 0.153 |
| 7. Poisson 0.193 |
Abbreviations: HC, heterosketasticity consistent; MW, Mann‐Whitney; NB, negative binomial; QP, quasi‐Poisson; ZINB, zero‐inflated negative binomial.
Average absolute coverage error is calculated with the absolute difference between the estimated coverage of the 95% CI (obtained from 10 000 simulations) and the target value of 0.95, averaged over the 135 settings with moderate sample sizes from the first simulation study, averaged over the 40 settings with moderate sample sizes from the second simulation study.
4. DISCUSSION
This study aimed to compare different statistical models to provide simple recommendations for a choice of model when analyzing count data in addiction research, including combinations of different characteristics likely to occur when real data are collected and which are present in all observational studies (ie, unbalanced designs, presence of confounders, and presence of outliers).
The study included 2 common count models in addiction research: Poisson and NB regressions (Atkins et al., 2013; Horton et al., 2007; Wagner et al., 2015). A Poisson regression was not valid in most cases, as it was already pointed out in previous studies (Horton et al., 2007). A Poisson regression resulted in an increased type 1 error rate and thus should be avoided because it causes misleading inferences (Gardner et al., 1995). This model was valid only in case of a Poisson distribution (without outliers), which is not likely to occur in addiction research, where the variance is often larger than the mean.
To our surprise, an NB regression was not the best model according to the type 1 error criterion. Indeed, it has become a classic model in addiction research (Atkins et al., 2013; Horton et al., 2007; Wagner et al., 2015), and it is widely used and recommended (Horton et al., 2007; Payne et al., 2015; Preisser et al., 2016; Ullah et al., 2010). It offered a real improvement over the Poisson distribution, which was by far the worst model in our simulations. However, even if the NB regression was valid for different population distributions and not only the NB distribution, it did not fit all population distributions. Its principal problem was that it was not robust against outliers. Outliers are almost never included in simulation studies on count data (except the article of Payne et al., 2015). Distribution with outliers is a common feature in addiction research, and thus, this was an important shortcoming for model choice.
Zero‐inflated NB regression is an extension of NB regression that has been proposed to account for a possible excess of zeros in the data. One could also propose a similar model accounting for a possible excess of ones, or of another values. Selecting a correct “inflated model” necessitates a good knowledge of the context, and this is why one cannot propose them as a simple and general recommendation to model count data. Moreover, these models typically have 4 (instead of 2) parameters, which should then be appropriately combined to get a classical summary measure of association, such as a mean ratio. Inference on this association measure is then typically produced via the delta‐method, which is not always trivial to program and which may not be accurate in small samples. Finally, one may also encounter numerical problems when fitting these models. In our simulations, we could not fit a ZINB model in about 15% of the simulated samples related to Table 5 (and in about, respectively, 4%, 5%, and 3% of the simulated samples related to Tables 2, 3, and 4).
Overall, the results showed that QP regression was the best model to detect a difference between 2 groups having a count distribution, allowing control of the type 1 error in all situations and control of the coverage of the 95% CI in most (though not in all) situations, becoming slightly less accurate with an unbalanced design. This model (QP) is not a common model in addiction research, is yet simple to use, and deserves to be better known. This conclusion is in line with the finding of the only article that tested QP regression in our systematic literature review (Sturman, 1999).
We included the linear regression in our comparison to see whether a classical model would be good enough to analyze count data, despite some obvious drawback such as the possibility to predict negative values for the count distribution (Horton et al., 2007). Previous studies suggested that the linear regression and linear regression provide nonoptimal analyses (Aiken et al., 2015) and should be used for normal and symmetric distributions without outliers (Poncet et al., 2016). This was also the conclusion of previous simulation studies using linear regression to analyze count data (Roudsari et al., 2011; Sturman, 1999). Remarkably, the linear regression was valid in all situations with respect to type 1 errors with outliers in an unbalanced design and when adjusting for confounders. Other advantages of the linear regression include popularity, simplicity of implementation (there is no problem of convergence, as it may happen with count models), and the possibility to apply it straightforwardly in a situation where count data may include noninteger values (eg, some persons reporting drinking an average of 1.5 glasses of wine per week). In spite of its resilience, its validity with respect to the coverage of 95% CI under the alternative was not as good, except possibly in the case of a balanced design. Interestingly, the validity of the linear model in the case of an unbalanced design could be much improved by performing a HC test (instead of a classical Student test), at least in the context of an unadjusted comparison. Unfortunately, there was almost no improvement in the context of an adjusted comparison.
Finally, while the MW test, using AUC as an association measure, was overall the best model (and the more powerful in the presence of outliers) in the context of an unadjusted comparison, it cannot be used in the context of an adjusted comparison (at least under current statistical methodology).
One advantage of Poisson, NB, and ZINB regression is that they produce estimate of the whole count distribution in both groups. In contrast, QP regression and the linear regression only provide a (plausible) estimate of the mean of the count distribution in both groups, where an association measure might be calculated using either a mean ratio (QP regression) or a mean difference (linear regression). Note, however, that for continuous data, one similarly summarizes a distribution with a mean and a standard deviation without the claim to provide a reliable estimate of the whole distribution.
As noted by a reviewer, a possible drawback of a mean ratio as a summary measure of association is that it is expressed in a relative scale, not in an absolute scale. For example, one would get a same mean ratio of 0.5 whether an intervention allows us to reduce an average number of symptoms or complications (compared to a situation with no intervention) from 20 to 10 or from 10 to 5, although 10 symptoms can be prevented on average in the former case against only 5 in the latter case. This is one reason why some authors prefer a mean difference rather than a mean ratio to summarize the information, eg, in the context of evaluating public health policies. It is however possible to estimate a (marginal) mean difference in a multiplicative model, such as Poisson, QP, NB, and ZINB regression, where inference on the mean difference can be conducted via the delta method. We have actually done this in our simulations for these 4 multiplicative models, and we have found largely the same results for mean difference than those reported above for the mean ratio regarding the validity of inference (data not shown).
To conclude, if the goal is not to estimate the whole distribution but just an association measure to compare 2 groups with respect to count data with a valid test and (often) valid 95% CI, a simple recommendation would be to use a QP regression, which was the most generally valid model in our extensive simulations, including situations with outliers, confounders, and unbalanced designs. Using QP regression as a “default” model to analyze count data in the addiction field would considerably simplify the practice. Researchers willing to consider an alternative or more sophisticated model could also compare their results with those provided by QP regression, where a too large discrepancy might be a suspicious indication that their findings are based on an invalid model, preventing one to draw too strong conclusions and warranting cautious progress in addiction research.
DECLARATION OF INTEREST STATEMENT
The authors have no conflicts of interest to declare.
ACKNOWLEDGMENT
This research received no specific grant from any funding agency in the public, commercial, or not‐for‐profit sectors. We are grateful to 2 anonymous reviewers, which constructive comments and suggestions led to a substantial improvement of the manuscript.
Baggio S, Iglesias K, Rousson V. Modeling count data in the addiction field: Some simple recommendations. Int J Methods Psychiatr Res. 2018;27:e1585 10.1002/mpr.1585
REFERENCES
- Aiken, L. S. , Mistler, S. A. , Coxe, S. , & West, S. G. (2015). Analyzing count variables in individuals and groups: single level and multilevel models. Group Processes & Intergroup Relations, 18(3), 290–314. 10.1177/1368430214556702 [DOI] [Google Scholar]
- Atkins, D. C. , Baldwin, S. A. , Zheng, C. , Gallop, R. J. , & Neighbors, C. (2013). A tutorial on count regression and zero‐altered count models for longitudinal substance use data. Psychology of Addictive Behaviors, 27(1), 166–177. 10.1037/a0029508 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bradley, J. V. (1978). Robustness? British Journal of Mathematical and Statistical Psychology, 31(2), 144–152. 10.1111/j.2044-8317.1978.tb00581.x [DOI] [PubMed] [Google Scholar]
- Gardner, W. , Mulvey, E. P. , & Shaw, E. C. (1995). Regression analyses of counts and rates: Poisson, overdispersed Poisson, and negative binomial models. Psychological Bulletin, 118(3), 392–404. [DOI] [PubMed] [Google Scholar]
- Gorelick, D. A. , & McPherson, S. (2015). Improving the analysis and modeling of substance use. The American Journal of Drug and Alcohol Abuse, 41(6), 475–478. 10.3109/00952990.2015.1085264 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Herbison, P. , Robertson, M. C. , & McKenzie, J. E. (2015). Do alternative methods for analysing count data produce similar estimates? Implications for meta‐analyses. Systematic Reviews, 4 10.1186/s13643-015-0144-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Horton, N. J. , Kim, E. , & Saitz, R. (2007). A cautionary note regarding count models of alcohol consumption in randomized controlled trials. BMC Medical Research Methodology, 7, 9 10.1186/1471-2288-7-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Long, J. S. , & Ervin, L. H. (2000). Using heteroscedasticity consistent standard errors in the linear regression model. The American Statistician, 54(3), 217–224. 10.1080/00031305.2000.10474549 [DOI] [Google Scholar]
- Payne, E. H. , Hardin, J. W. , Egede, L. E. , Ramakrishnan, V. , Selassie, A. , & Gebregziabher, M. (2015). Approaches for dealing with various sources of overdispersion in modeling count data: scale adjustment versus modeling. Statistical Methods in Medical Research. 10.1177/0962280215588569 [DOI] [PubMed] [Google Scholar]
- Poncet, A. , Courvoisier, D. S. , Combescure, C. , & Perneger, T. V. (2016). Normality and sample size do not matter for the selection of an appropriate statistical test for two‐group comparisons. Methodology, 12(2), 61–71. 10.1027/1614-2241/a000110 [DOI] [Google Scholar]
- Preisser, J. S. , Das, K. , Long, D. L. , & Divaris, K. (2016). Marginalized zero‐inflated negative binomial regression with application to dental caries. Statistics in Medicine, 35(10), 1722–1735. 10.1002/sim.6804 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roudsari, B. , Mack, C. , & Jarvik, J. G. (2011). Methodologic challenges in the analysis of count data in radiology health services research. Journal of the American College of Radiology: JACR, 8(8), 575–582. 10.1016/j.jacr.2011.02.002 [DOI] [PubMed] [Google Scholar]
- Sturman, M. C. (1999). Multiple approaches to analyzing count data in studies of individual differences: the propensity for type I errors, illustrated with the case of absenteeism prediction. Educational and Psychological Measurement, 59(3), 414(411). [Google Scholar]
- Ullah, S. , Finch, C. F. , & Day, L. (2010). Statistical modelling for falls count data. Accident Analysis & Prevention, 42(2), 384–392. 10.1016/j.aap.2009.08.018 [DOI] [PubMed] [Google Scholar]
- Ver Hoef, J. M. , & Boveng, P. L. (2007). Quasi‐Poisson vs. negative binomial regression: how should we model overdispersed count data? Ecology, 88(11), 2766–2772. [DOI] [PubMed] [Google Scholar]
- Vives, J. , Losilla, J.‐M. , Rodrigo, M.‐F. , & Portell, M. (2008). Overdispersion tests in count‐data analysis. Psychological Reports, 103(1), 145–160. 10.2466/pr0.103.1.145-160 [DOI] [PubMed] [Google Scholar]
- Wagner, B. , Riggs, P. , & Mikulich‐Gilbertson, S. (2015). The importance of distribution‐choice in modeling substance use data: a comparison of negative binomial, beta binomial, and zero‐inflated distributions. The American Journal of Drug and Alcohol Abuse, 41(6), 489–497. 10.3109/00952990.2015.1056447 [DOI] [PMC free article] [PubMed] [Google Scholar]
- White, H. (1980). A heteroskedasticity‐consistent covariance matrix estimator and a direct test for heteroskedasticity. Econometrica, 48(4), 817–838. 10.2307/1912934 [DOI] [Google Scholar]
- Zeileis, A. , Kleiber, C. , & Jackman, S. (2008). Regression models for count data in R. Journal of Statistical Software, 27(8), 1–25. 10.18637/jss.v027.i08 [DOI] [Google Scholar]


