Abstract
In psychiatry and psychology, relationship patterns connecting disorders and risk factors are always complex and intricate. Advanced statistical methods have been developed to overcome this issue, the most common being structural equation modelling (SEM). The main approach to SEM (CB‐SEM for covariance‐based SEM) has been widely used by psychiatry and psychology researchers to test whether a comprehensive theoretical model is compatible with observed data. While the validity of this approach method has been demonstrated, its application is limited in some situations, such as early‐stage exploratory studies using small sample sizes. The partial least squares approach to SEM (PLS‐SEM) has risen in many scientific fields as an alternative method that is especially useful when sample size restricts the use of CB‐SEM. In this article, we aim to provide a comprehensive introduction to PLS‐SEM intended to CB‐SEM users in psychiatric and psychological fields, with an illustration using data on suicidality among prisoners. Researchers in these fields could benefit from PLS‐SEM, a promising exploratory technique well adapted to studies on infrequent diseases or specific population subsets. Copyright © 2015 John Wiley & Sons, Ltd.
Keywords: epidemiologic methods, structural equation modelling, PLS‐SEM
Introduction
Structural equation modelling (SEM) has, for a long time, gained interest among psychiatry and psychology researchers (MacCallum and Austin, 2000). This general term refers to several statistical methods involving path modelling and analysis. Biomedical researchers mostly employ the covariance‐based form of SEM (CB‐SEM, also known as factor‐based SEM or LISREL, its classic software package). CB‐SEM, as introduced by Jöreskog, is a useful multivariate technique that allows to test whether a theoretical model is compatible with observed data. The representation of unobservable concepts by latent variables makes CB‐SEM especially relevant to psychiatry and related disciplines, where patients’ mental characteristics are often measured following the psychometric approach (e.g. the Hamilton Depression Rating Scale for depression). While this method is well adapted at advanced stages of the theory‐building process, it has some requirements that limit its application in some situations, in particular a relatively large sample size (the generally admitted lower limit being 200 for a standard model) but also multivariate normality of data, and some restrictions on model specification (Hair et al., 2013; Kline, 2010).
An alternative method has developed in other research fields (e.g. marketing, genetics, ecology), known as partial least squares SEM (abbreviated PLS‐SEM, also named PLS‐PM for partial least squares path modelling). It was originally conceived by Wold as an alternative to CB‐SEM for research situations that are “simultaneously data‐rich and theory‐primitive” (Wold, 1985). While both methods use similar graphical representations, there are many differences between CB‐SEM and PLS‐SEM. Essentially, the constructs used in PLS‐SEM to model unobservable concepts do not rely on the traditional psychometric perspective that is at the basis of CB‐SEM. PLS‐SEM has its own statistical properties and estimation algorithm. It is more suitable to preliminary studies, where researchers aim to develop a theoretical model and identify preeminent dependencies between concepts, and often work with smaller sample sizes. It is also better suited to studies that require estimation of individual construct scores for prediction or subsequent analyses. As it turns out, these situations are especially frequent in psychiatric research.
In this article, we aim to provide a comprehensive introduction to the PLS‐SEM method intended for CB‐SEM users in the field of psychiatric research. We briefly describe the PLS‐SEM approach in comparison to CB‐SEM, and provide rule of thumbs for its usage. We also discuss the situations in psychiatric research where the advantages of PLS‐SEM could be exploited alongside its limitations, with an illustration using data on suicidality among prisoners.
Structural equation modelling (SEM)
SEM describe and analyse structured relationships between a set of variables. Some of these variables may represent unobservable concepts (e.g. depression, quality of life) that are inferred from other directly observed variables (named indicator or manifest variables). The general term for variables representing unobserved concepts is “construct”. The relations between variables are often represented by using a diagram. Typically, squares represent observed variables, ovals or rounds represent constructs and relationships are shown as arrows (Figure 1). The hypothesized direction of causality of relationships is carried by one‐way arrows. The path model thus formed translates into to a set of equations. One of the main outcomes of both CB‐ and PLS‐SEM consists of paths parameters that quantify and test the hypothesized relationships between variables.
Figure 1.
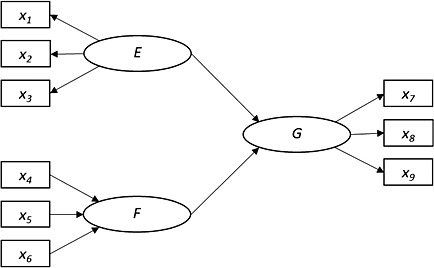
An example of path model.
The similarity between CB‐ and PLS‐SEM ends here. CB‐SEM is a factor‐based technique, where constructs behave like latent variables in a psychometric sense and are validated using the psychometric theory. Hence, measurement error issues are directly addressed by the model (Gefen et al., 2011). CB‐SEM is most useful when researchers aim to refine and organize a set of trends into a theoretical model, and test whether the obtained theory is compatible with actual data. Therefore, a very important outcome is the goodness‐of‐fit of the theoretical model to the available data. Several indices exist, the most popular being the standardized root mean square residual (SRMSR), the non‐normed fit index (NNFI) and the root mean square error of approximation (RMSEA). Statistical tests of goodness‐of‐fit are also available. However, goodness‐of‐fit tests only cannot lead to formal acceptation or rejection of a hypothesis. This way of considering the model is directly related to the underlying properties of the covariance‐based approach. Basically, parameter estimates are computed so that the theoretical covariance between variables implied by these parameters is as close as possible to the covariance between variables from the data, usually with maximum likelihood (Chin, 1998). Then, the final discrepancy between covariance matrices is measured by goodness‐of‐fit indices. As the whole method revolves around covariance, stable individual values of the intermediate variables are difficult to estimate. This point (known as “factor indeterminacy”) can be problematic when estimates of latent variable scores are needed for prediction or subsequent analyses (Rigdon, 2012). Several restrictions originate from the underlying statistical properties of the procedure: multivariate normality of data and a relatively high sample size.
By contrast, in a similar way to multiple linear regression, the objective of PLS‐SEM is the maximization of the explained variance of the dependent variables, and the model is mostly evaluated through its predictive capabilities. To model unobserved concepts, PLS‐SEM uses composites that must be considered as proxies for the factors which they replace, likewise principal component analysis in comparison to factor analysis (Rigdon, 2012). These composites are mere linear combinations of the related block of indicator variables. Hence, they are numerically defined, and are computed through a series of ordinary least squares regressions for each of the separate subparts of the path model, that are put in relation to achieve convergence. The final estimations of the constructs’ scores are then used to compute the rest of the parameters of interest (weights, loadings and path coefficients). A consequence of this sequential process is that the complexity of the full model is reduced, and has less influence on the sample size requirements. This allows PLS‐SEM to handle more complex models while staying computationally efficient, and to achieve high levels of statistical power even with smaller sample sizes (Reinartz et al., 2009). Another implication is that, as individual values of the constructs are at the core of the estimation process, these scores values can be used for predictive purposes or subsequent analyses. This supports the orientation of PLS‐SEM towards prediction instead of correlation, and the use of coefficients of determination (R 2) and other prediction‐oriented indices for validation. However, since the set of structural equations is handled sequentially instead of globally, the counterpart is that the validation procedure must cover the different subparts of the model. As of now, no available global goodness‐of‐fit index is appropriate for this task (Henseler and Sarstedt, 2012). PLS‐SEM is thus less suited for testing the adequacy of a comprehensive theory and for model selection or comparison (e.g. comparison of nested models or comparison of models on different population subsets). Furthermore, it is generally outperformed by CB‐SEM in terms of parameter consistency and accuracy when sample size is above 250 (Reinartz et al., 2009). However, this method allows researchers to identify key relationships among multiple structured variables, which can be especially useful in early‐stage exploratory or theory‐primitive situations.
Specifying a PLS‐SEM model
PLS‐SEM uses a specific language to describe the path model. The constructs are linked to a set of observed variables (also called measurement or indicator variables) which can be of continuous, scaled ordinal or binary nature and form a block. There are two main forms of measurement. The mode A (or reflective) is similar to the approach used in CB‐SEM, factor analysis and in the item response theory. It assumes that the direction of causality goes from the construct to the indicators, i.e. indicators are observable manifestations of an underlying unobservable concept. For instance in Figure 2, the construct E is measured with mode A by a block of three indicator variables (x 1, x 2 and x 3). On the contrary, a mode B (or formative) measurement model assumes that the indicators are causing the construct, e.g. F in Figure 2. However, this type of measure should be used with additional caution, as validation and interpretation of formatively measured constructs remain delicate, and in need of additional research.
Figure 2.
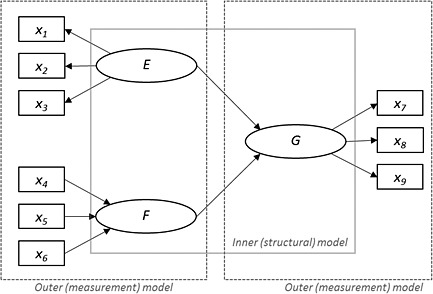
An example of diagram describing a structural equation model.
Within the path model, a distinction is made between the set of measurement blocks (called outer or measurement model) and the set of relations between the constructs (called inner or structural model). Constructs that are at the receiving end of at least one arrow (e.g. G) are called endogenous, and constructs that are connected only to outgoing arrow (e.g. E and F) are called exogenous. Some rules must be kept in mind when specifying the path model: (1) no recursive loops; (2) no unmeasured construct; (3) each indicator must appear only once and be linked to only one construct. Observable variables (that are measured directly and not through indicators) can also be directly included in the inner model (if the theory supports it) in the form of a construct measured by only one indicator.
Statistical properties
As was stated previously, the aim of the PLS‐SEM algorithm is the maximization of the explained variance of all the endogenous variables, e.g. G in Figure 2. The estimation process follows an algorithm based on a series of distinct ordinary least squares regressions, going back and forth between two ways of estimating a construct's score (by an aggregation of its indicators or by a combination of neighbouring constructs’ scores), minimizing residual variance at each step and stopping when the estimates are stabilized under a specified tolerance value (Chin, 1998). In detail, the PLS‐SEM algorithm estimates the constructs’ scores in four steps:
Initialization: The outer coefficients are fixed to one, and the indicators are centred and scaled (mean = 0 and variance = 1). Each construct's score is estimated as a weighted sum of their indicators, then scaled.
Inner approximation: The values of the initial inner coefficients depend on the weighting scheme used. Different weighting schemes are available, path weighting being the recommended approach. Each construct's score is estimated as a weighted sum of its neighbouring constructs’ scores (from Step 1), then scaled.
-
Outer approximation: The outer coefficients are now recalculated through ordinary least squares regression on the basis of the constructs’ scores (from Step 2). The computation depends on the measurement mode of the construct:
Mode A: each of the related indicators’ loadings is estimated by simple regression, with the indicator as the dependent variable.
Mode B: all of the related indicators’ weights are estimated by multiple regression, with the construct as the dependent variable.
The constructs’ scores are then recalculated using the outer coefficients (from Step 3). If convergence is achieved (according to a predefined tolerance, generally 10−5), the final estimations for the outer loadings (relevant to constructs measured with Mode A), the outer weights (relevant to constructs measured with Mode B), the path coefficients and the resulting R 2 values are computed from the construct's final scores. Otherwise, the algorithm goes back to Step 2.
Contrary to the latent variables used in CB‐SEM, the computation of the constructs’ scores in PLS‐SEM does not involve measurement error. This leads to a bias in the estimation of parameters known as “consistency at large”: theoretically, unless sample size and the number of indicators per construct become infinite, path coefficients are underestimated while outer coefficients are overestimated. However, simulation studies have shown that this bias is quantitatively low in most situations, and that CB‐SEM and PLS‐SEM estimates converge with large sample size if the CB‐SEM assumptions are respected (Barroso et al., 2010; Reinartz et al., 2009; Ringle et al., 2009). This bias should also be compared to the highly distorted estimates produced by CB‐SEM in the situations where PLS‐SEM is likely to be used: low sample size and high model complexity.
Evaluation of the model's results
Contrary to CB‐SEM, no reliable goodness‐of‐fit criterion is available to assess the global validity of the model (Henseler and Sarstedt, 2012). Hence, the model must be meticulously evaluated using a series of criteria that separately assess the quality of each part of the path model (Hair et al., 2013).
Evaluation of the measurement model
The PLS‐SEM algorithm relies heavily on the aggregation of indicators variables to infer the constructs’ scores. Moreover, the computation does not include measurement error, whereas the utilization of latent variables in CB‐SEM does. Therefore, it is essential to keep in mind that the relevance of the results is entirely subordinate to the quality of the measurement model.
Evaluation of Mode A (or reflective) measurement relies on three characteristics: (1) internal consistency; (2) convergent validity; (3) discriminant validity. (1) Internal consistency relates to the intercorrelations among the indicator variables, reflecting the reliability of the measurement. It is also close to the unidimensionality property. Internal consistency is typically assessed by scree plots, Cronbach's α or more appropriately by Dillon–Goldstein's ρ (values > 0.7 are generally considered as acceptable). (2) Convergent validity refers to the degree to which an indicator relates to the other indicators of the same construct. It is evaluated by the average variance extracted (AVE) of each construct (value > 0.5 means that the construct explains more than half of the variance of its indicators) and by the outer loading of each indicator (values > 0.7 are recommended; or > 0.4 if the indicator is theoretically important and the corresponding AVE is satisfactory, or if deletion of the indicator does not lead to an increase of the AVE of the corresponding construct). (3) Discriminant validity judges whether constructs that are not related in the model are truly distinct. It is generally assessed by examining the cross loadings (an indicator's outer loading on the linked construct should be higher than all of its loadings on the other constructs) and the Fornell–Larcker criterion (the square root of the average variance extracted of a construct should exceed its correlation with any other construct).
Evaluation of Mode B (or formative) measurement models differs from Mode A, as the underlying hypothesis of a formative measure is that the indicators represent the entirety of the construct's distinct causes (without error). In that context, interval consistency is irrelevant and the focus should be on ensuring that the indicators actually account for all (or most) of the construct's causes. This first requires an exhaustive literature review on the subject prior to the creation of the questionnaires. At the analysis stage, the evaluation involves: (1) redundancy analysis; (2) detection of collinearity issues; (3) assessment of the relevance of the formative indicators. (1) Redundancy analysis estimates the capacity of a formatively measured construct to predict an independent measure of the same unobserved concept (that can be by using a single global item representing the concept or a construct reflectively measured by a set of indicator variables). Obviously, inclusion of such redundant items must be anticipated before data collection. (2) Collinearity issues can hinder interpretation of formatively measured constructs (as in multiple linear regression), since indicators are not supposed to be highly correlated with each other (variance inflation factor values < 5 are acceptable). (3) The relevance of formative indicators is evaluated through the examination of the outer weights, which represent each indicator's relative contribution to the construct (as there is no error term, 100% of the construct is explained by its indicators). The significance of the outer weights can be tested using bootstrapping. Indicator with insignificant outer weight should be considered for deletion if its absolute contribution to the construct (measured by its outer loading) and its theoretical importance are weak. In any case, modifying a theoretical model should never be done only on the basis of statistical outcomes, and a description of the results from both full and modified models should always be reported.
Evaluation of the structural model
Once the validity of the measurement model is insured, the assessment of the structural model results allows to appreciate the predictive capabilities of the proposed model. The main criteria are: (1) the coefficients of determination of the endogenous variables; (2) the predictive relevance. (1) The coefficients of determination (R 2 values) of the endogenous constructs are the main measure of the model accuracy (acceptable values depend on the context and the discipline). (2) Predictive relevance evaluates how well the path model can predict the originally observed data. It is assessed by Stone–Geisser Q 2 values, which are obtained through blindfolding. Essentially, it is an iterative procedure that omits a part of the data and attempts to predict the omitted part using the estimated parameters (values of 0.02, 0.15 and 0.35 represent small, medium and large effects, respectively; it is not applicable to constructs measured with Mode B).
As PLS‐SEM focuses on exploration, the quantification of the hypothesized relationships within the inner model is of prime interest, and often emerge as the main result of the analysis. The main estimates are: (1) the path coefficients; (2) the effect sizes. (1) Path coefficients have standardized values from −1 to +1, and are interpreted in the same way that standardized regression coefficients. They directly quantify the hypothesized relationships within the structural model. Corresponding P‐values and confidence intervals are obtained through bootstrapping. Indirect and total effects between variables (that are combinations of the path coefficients) can also be helpful for further interpretation. (2) Effect size f 2 represents another way of quantifying the effect of a construct on another by measuring the change of the R 2 value of the endogenous variable when one of its exogenous predictor is deleted (values of 0.02, 0.15 and 0.35 represent small, medium and large effects, respectively).
Advanced topics in PLS‐SEM
Several advanced topics such as evaluation of heterogeneity in the sample, inclusion of mediating or moderating effects and higher‐order constructs are beyond the reach of this article, which aim is introductory. In particular, categorical or continuous moderating variables can be modelled with PLS‐SEM but raise some issues due to the standardization of the variables at several points of the estimation algorithm. Several methods can be used to include moderators, the most efficient apparently being the orthogonalizing and the two‐stage approaches (Henseler and Chin, 2010). This problem also exists in CB‐SEM (Lin et al., 2010). For interested readers, we recommend the well‐conceived manual by Hair et al. (2013) that provides helpful details for PLS‐SEM application.
Software
Statistical methods’ popularity and diffusion are closely linked to the availability of necessary tools. For a long time LVPLS 1.8 was the only available software for PLS‐SEM. Recent years have seen the development of several convenient software applications of PLS‐SEM: SmartPLS (Hair et al., 2013), XLSTAT‐PLSPM (Esposito Vinzi et al., 2007) and two R packages, plspm (Sanchez et al., 2013) and semPLS (Monecke and Leisch, 2012).
An example of application of PLS‐SEM
We chose to illustrate the utilization of PLS‐SEM in psychiatric research by an example on the influence of childhood adversity on suicidal behaviour in male prisoners in long‐term detention centres. Suicide is the single most common cause of death in jails and prisons, and prevention of this issue is a public health priority in many countries (World Health Organization, 2007). Risk factors of prison suicide include demographic factors (being male, being married), criminological factors (occupation of a single cell, serving a life sentence) and clinical factors (recent suicidal ideation, history of attempted suicide, current psychiatric diagnosis, psychotropic medication and history of substance abuse) (Fazel et al., 2008). Suicidality has also been linked to childhood adversity in prison (Blaauw et al., 2002; De Ravello et al., 2008; Godet‐Mardirossian et al., 2011) and in the general population (Afifi et al., 2008; Dube et al., 2001; Felitti et al., 1998). In this study, we explore the influence of childhood adversity mediated by depression and post‐traumatic stress disorder (PTSD) on suicidal behaviour in male prisoners in long‐term detention (i.e. having served 10 years or more).
Population and data
The present study is based on a subset of a larger survey of mental health in prisoners in France, commissioned in 2001 by the Ministry of Health and the Ministry of Justice. The third phase of this survey was conducted in 2005 and focused on inmates sentenced to more than 10 years of incarceration, and thus housed in separate institutions called Maisons centrales. All inmates incarcerated for at least 10 years in three of these facilities were approached by mail, and volunteers were interviewed by two clinicians (a clinician psychologist and a psychiatrist). Written informed consent was obtained prior to the interview. Collected data included socio‐demographic information, information on events during the course of the inmate's early life and incarceration time, qualitative data on the inmate's psychological state and a diagnostic interview conducted using the Mini‐International Neuropsychiatric Interview version 5.0 (MINI) (Sheehan et al., 1998). A qualitative study of the impact of long‐term incarceration on this population has already been published (Yang et al., 2009). Approval was obtained from the Comité de Protection des Personnes dans la Recherche Biomédicale Pitié‐Salpêtrière prior to the beginning of the study. Of the 135 subjects who were asked to participate in the study, 69 agreed to participate, of which only 59 were interviewed due to practical reasons. Because of the low sample size, CB‐SEM was inoperable in this situation, whereas PLS‐SEM could be used efficiently. Summary characteristics of the 59 included subjects are available in Table 1.
Table 1.
Summary characteristics for all 59 included subjects
| Variable | Missing values (n) | Count (%) or mean [range] |
|---|---|---|
| Socio‐demographic | ||
| Males (n) | 0 | 59 (100%) |
| Age (years) | 0 | 46 [30; 79] |
| Familial situation | 0 | — |
| Single | 27 (46%) | |
| Married | 8 (14%) | |
| Separated | 22 (37%) | |
| Widowed | 2 (3%) | |
| Has children | 0 | 38 (64%) |
| Education | 6 | — |
| Less than high school | 23 (39%) | |
| High school diploma | 5 (8%) | |
| Vocational qualification | 20 (34%) | |
| University diploma | 5 (8%) | |
| Incarceration | ||
| Centre | 0 | — |
| A | 24 (41%) | |
| B | 15 (25%) | |
| C | 20 (34%) | |
| Prison time (years) | 0 | 11 [10; 29] |
| Remaining sentence | 1 | — |
| <5 | 18 (31%) | |
| 5–10 | 7 (12%) | |
| >10 | 5 (9%) | |
| Lifelong sentence | 28 (47%) | |
| Childhood adversity | ||
| Separated from one parent for > 6 monthsa | 2 | 31 (53%) |
| Placement | 0 | 19 (32%) |
| Sexual abuse | 52 | 4 (7%) |
| Contact with a judge for juveniles | 0 | 19 (32%) |
| Death of a close relativea | 1 | 22 (37%) |
| Current major depression symptoms (MINI) | ||
| Depressed mood for >14 daysb | 0 | 8 (14%) |
| Anhedonia for >14 daysb | 0 | 9 (15%) |
| Weight change | 44 | 4 (7%) |
| Activity change | 44 | 8 (14%) |
| Sleep change | 44 | 0 (0%) |
| Fatigue | 44 | 9 (15%) |
| Guilt | 44 | 8 (14%) |
| Concentration trouble | 44 | 6 (10%) |
| Diagnostic of current major depression (DSM‐IV) | 0 | 12 (20%) |
| Current PTSD symptoms (MINI) | ||
| Extremely traumatic eventb | 0 | 47 (80%) |
| Painful thoughts of this eventb | 12 | 4 (7%) |
| Memory avoidance | 55 | 2 (3%) |
| Memory loss | 55 | 3 (5%) |
| Anhedonia | 55 | 2 (3%) |
| Detachment | 55 | 2 (3%) |
| Loss of emotions | 55 | 2 (3%) |
| Life disruption | 55 | 3 (5%) |
| Sleeping trouble | 55 | 4 (7%) |
| Irritability | 55 | 1 (2%) |
| Concentration trouble | 55 | 4 (7%) |
| Nervousness | 55 | 3 (5%) |
| Easily startled | 55 | 1 (2%) |
| Consequent suffering | 55 | 2 (3%) |
| Diagnostic of PTSD (DSM‐IV) | 0 | 2 (3%) |
| Current suicidality (MINI) | ||
| Death wish | 0 | 16 (27%) |
| Pain wish | 0 | 9 (15%) |
| Suicidal thoughts | 0 | 9 (15%) |
| Suicidal plan | 0 | 12 (20%) |
| Recent suicidal attempt | 0 | 1 (2%) |
| Lifelong suicidal attempt | 0 | 25 (42%) |
| Assessment of suicide risk (DSM‐IV) | 0 | — |
| Absent | 27 (46%) | |
| Low | 18 (31%) | |
| Intermediate | 1 (2%) | |
| High | 13 (22%) | |
Imputation of missing data.
Filter question.
As the MINI test contains filters, numerous missing values appear in the items concerning depression and PTSD symptoms. We have therefore resolved to measure depression symptoms with only two unfiltered items: current sadness and current anhedonia lasting for at least 14 days. Regarding PTSD symptoms, we chose to measure PTSD with a single item: the diagnostic of PTSD according the DSM‐IV. Missing values in the remaining items were imputed using multivariate imputation by chained equations (except for sexual abuse that was dismissed for having 52 missing values for 59 subjects) (van Buuren and Groothuis‐Oudshoorn, 2011).
Construction of the measurement models
As the relevance of PLS‐SEM results are highly dependent on the measurement models, it is important to ensure the quality of the measure even before constructing the path model. In this illustration, four constructs corresponding to unobservable concepts must be included in the structural model: childhood adversity (CHILD), depression (DEP), PTSD and suicidality (SUIC). Scree plots, factor analysis and Cronbach's α were used to select the appropriate indicator variables to ensure the unidimensionality of the multi‐item measures (Table 2).
Table 2.
Factor analysis of the multi‐item constructs
| Construct | Indicators’ loadings | Cronbach's α |
|---|---|---|
| Childhood adversity (CHILD) | separation: 0.561 | 0.82 |
| placement: 0.998 | ||
| sexual abuse: discardeda | ||
| judge for juveniles: 0.847 | ||
| death of a close relative: discardeda | ||
| Depression (DEP) | depressed mood: 0.891 | 0.88 |
| anhedonia: 0.891 | ||
| Suicidality (SUIC) | death wish: 0.799 | 0.90 |
| pain wish: 0.818 | ||
| suicidal thoughts: 0.859 | ||
| suicidal plan: 0.875 | ||
| recent suicidal attempt: discardeda | ||
| lifelong suicidal attempt: discardeda |
Sexual abuse was discarded because of the large number of missing values and the remaining items (death of a close relative, recent suicidal attempt and lifelong suicidal attempt) were discarded because of insufficient loadings (<0.4).
Construction of the structural model
This study explores the influence of childhood adversity on suicidal behaviour in male prisoners in long‐term detention, mediated by depression and PTSD. A simple, correspondent path model is described in Figure 3. It suggests that the influence of childhood adversity on current suicidality can be direct, or mediated by current depressive symptoms or a diagnostic of PTSD. It also implies that a diagnostic of PTSD affects current depressive symptoms.
Figure 3.

The structural model depicting the hypothetical influence of childhood adversity mediated by depression and post‐traumatic stress disorder (PTSD) on suicidal behaviour in male prisoners in long‐term detention.
Model estimation and evaluation
The full model was estimated in R 3.1.2 with package semPLS (Monecke and Leisch, 2012; R Core Team, 2013), using the path weighting scheme and a tolerance limit of 10−5. Convergence was achieved after 10 iterations. We conducted the evaluation of the results according to previously discussed, starting with the evaluation of the results of the measurement models. The model included three constructs measured with Mode A (CHILD, DEP and SUIC) and a single‐item measure (PTSD). Internal consistency was acceptable for all three measured multi‐item constructs (Table 3). Convergent validity was also satisfactory, as AVE was well above 0.5 for all three constructs and all but one outer loadings were above 0.7. The remaining item (separation) was retained as it was considered important and the AVE of the corresponding construct was above 0.5. No issue concerning discriminant validity was detected by the examination of the cross loadings nor by the Fornell–Lacker criterion (Table 4).
Table 3.
Assessment of the results of the measurement models: internal consistency (Cronbach's α and Dillon–Goldstein's ρ), convergent validity (loadings and average variance extracted [AVE]) and discriminant validity (cross loadings)
| Constructs | Internal consistency | Indicators | Outer loadings and cross loadings | AVE | ||||
|---|---|---|---|---|---|---|---|---|
| Α | ρ | CHILD | PTSD | DEP | SUIC | |||
| Childhood adversity (CHILD) | 0.82 | 0.89 | separation | 0.63 1 | 0.17 | −0.11 | 0.00 | 0.73 |
| placement | 0.98 | 0.27 | 0.07 | 0.28 | ||||
| judge for juveniles | 0.92 | 0.07 | 0.01 | 0.26 | ||||
| Depression (DEP) | 0.88 | 0.94 | depressed mood | −0.01 | −0.06 | 0.93 | 0.44 | 0.89 |
| anhedonia | 0.06 | 0.18 | 0.96 | 0.57 | ||||
| Suicidality (SUIC) | 0.90 | 0.93 | death wish | 0.14 | 0.10 | 0.48 | 0.85 | 0.77 |
| pain wish | 0.26 | 0.18 | 0.44 | 0.87 | ||||
| suicidal thoughts | 0.30 | 0.18 | 0.58 | 0.92 | ||||
| suicidal plan | 0.19 | 0.14 | 0.34 | 0.88 | ||||
*This indicator did not satisfy discriminant validity (loadings <0.7), but was retained as AVE was well above 0.5.
Table 4.
The Fornell–Lacker criterion: the square root of the average variance extracted (AVE) of a construct should exceed any of its correlation coefficient with the other constructs
| Constructs | √AVE | Inter‐construct correlation | |||
|---|---|---|---|---|---|
| CHILD | PTSD | DEP | SUIC | ||
| Childhood adversity (CHILD) | 0.86 | 1 | 0.21 | 0.03 | 0.26 |
| Depression (DEP) | 0.95 | 0.03 | 0.08 | 1 | 0.54 |
| Suicidality (SUIC) | 0.88 | 0.26 | 0.17 | 0.54 | 1 |
As the validity of the measurement models was insured, we proceeded to the assessment of the results of the structural model. The proposed model's predictive capabilities were intermediate for the suicidality (R 2 = 0.36; Q 2 = 0.13), but very weak for PTSD (R 2 = 0.05; Q 2 = −0.01) and depression (R 2 = 0.01; Q 2 = −0.11). This reflects the relatively small influence exerted by childhood adversity on depression and PTSD. Path coefficients confirmed this interpretation, as only the path coefficient between depression and suicidality indicated a strong and significant relation (β = 0.53; 95% confidence interval [CI] [0.25; 0.76] – 95% CIs were obtained by bootstrapping with 500 iterations). The other results of interest showed a significant association between childhood adversity and PTSD (β = 0.21 with 95% CI [0.06; 0.41]) and an intermediate relation, although statistically non‐significant, between childhood adversity and suicidality (β = 0.23 with 95% CI [−0.08; 0.47]). All path coefficients and outer loadings values are presented in Figure 4. Effect size confirmed this interpretation, showing a large effect of depression on suicidality (f 2 = 0.42) and a small effect of childhood adversity on suicidality (f 2 = 0.08). It appears from this exploratory study that little influence is exerted by childhood issues on suicidality in male prisoners in long‐term detention, neither directly nor mediated by depression and PTSD.
Figure 4.

Final model of the influence of childhood adversity mediated by depression and post‐traumatic stress disorder (PTSD) on suicidal behaviour in male prisoners in long‐term detention (significant coefficients are marked by a star).
Conclusion
Clinical and epidemiological research in the field of psychiatry often uses methods that assess the association between one outcome and one or several predictors, e.g. linear or logistic regression models. Such methods, sometimes called “first‐generation techniques”, are not well suited to a discipline where the ways in which risk factors may work together to influence and outcome are so complex and intricate (Kraemer et al., 2001). Models involving structural relationships between a large number of variables have been developed early on to overcome this issue, starting with Wright's path analysis (Wright, 1934). Several evolutions have followed, such as multivariate dependencies (Cox and Wermuth, 1996) and directed acyclic graphs (Greenland et al., 1999). Graphical chain model such as directed acyclic graphs (DAG) can be considered as an alternative to PLS‐SEM and even CB‐SEM. But the question of the estimation of path coefficients is secondary with DAG, which are more conceptual tools rather than numerical procedures.
Over time, the prevailing method has become CB‐SEM, a well‐tested factor‐based technique that is primarily adapted to test whether a comprehensive theoretical model is compatible with data. However, this approach raises some issues, although ongoing developments could solve some of them. For instance, CB‐SEM estimation algorithms do not converge easily, resulting in a need for larger sample sizes. Moreover, the inclusion of binary variables and the calculation of factor score estimates (i.e. “factor indeterminacy”) are possible but not straightforward (Diamantopoulos, 2011; Prescott, 2004). But fundamentally, the central role of latent variables, as defined by the traditional psychometric perspective, can be problematic. Besides the fact that the notion of latent variable is often confusing to non‐specialists, their very epistemological nature is still debated among experts (Markus and Borsboom, 2013). The near‐monopoly of reflectively measured latent variables in research involving theoretical constructs is also increasingly challenged, as other ways to conceptualize the relationship between observable variables and unobservable concepts emerge. For instance, instead of reflecting the common influence of a construct, the observable variables may determine a common effect (formative measurement), or may form a network of causal relations (Rigdon et al., 2011; Rossiter, 2011; Schmittmann et al., 2013).
In this context, PLS‐SEM can appear as a pragmatic and promising alternative. At its core, PLS‐SEM has been criticized for its use of composite‐based proxies instead of latent variables. Conceptually, the difference between CB‐ and PLS‐SEM is of the same nature than the difference between factor analysis and principal component analysis. While some authors discard principal component analysis as a convenient but inferior approximation of factor analysis, a more sensible approach would be to consider both as dimension reduction techniques, that typically yield very similar results in common practice (Steiger and Schönemann, 1978; Velicer and Jackson, 1990). The same reasoning can be applied to PLS‐SEM, which should be considered as a simpler, adaptive and complementary alternative to CB‐SEM. PLS‐SEM is especially useful in the early stage of exploratory research, i.e. when the objective is to identify key relationships among the variables, and not to quantify whether the discoveries are likely to hold in a new sample (Leek and Peng, 2015). As it has a different theoretical background, it requires the use of specifically developed standards for conception, validation and interpretation of the model, some of which are still discussed (Rigdon, 2012). Notably, it is essential to keep in mind that the relevance of the results relies largely on the high quality of the measurement models. When this condition is satisfied, known bias (i.e. “consistency at large”) become negligible in practice, and PLS‐SEM results are very close to those of CB‐SEM, with even better performance when sample size diminishes (Reinartz et al., 2009). However, further research is needed to better understand the implications of the underlying theory and to fully appreciate the extent to which PLS‐SEM can be applied, particularly regarding the use of formative measurement models and of mediating and moderating variables.
In psychiatric research, the relation between disorders and their determinants are particularly intricate. It is essential to provide researchers with methods that can reflect the complex connections between outcome and multiple risk factors that can be theorized. Additionally, a formal representation of this complexity can only reinforce the clearness of the scientific process. Formerly, this kind of method was only suitable to studies with very large sample sizes. This considerably hampered the research effort on infrequent psychiatric diseases (e.g. autism or anorexia nervosa) and on specific population subsets (e.g. prisoners). Researchers in these fields could benefit from PLS‐SEM, a promising exploratory technique well adapted to these situations. Hence, both SEM techniques could successively intervene at different stages of the theory‐building process. PLS‐SEM allows the identification of correlation trends in small‐scale studies, which can later be refined and organized as a comprehensive model in larger, more ambitious studies using CB‐SEM. Nevertheless, in order to make SEM methods more than a mere exercise of model fitting, they should be used to gather and organize insight on a particular problem for the purpose of later independent testing and confirmation. One should bear in mind that the results from SEM techniques are exploratory in nature and should be interpreted with caution even when applied correctly. Specifically, the results of SEM analysis heavily rely on the a priori model that is based on the researcher's initial hypotheses, who can omit confounding factors or important links between variables. Another source of bias can arise from interpretational confounding, i.e. the divergence between empirical and theoretical meanings (Burt, 1976). Definitive conclusions with clinical implications can only arise from repeated, well‐designed studies using fewer assumptions and more robust methods, like randomized controlled trials.
Declaration of interest statement
The authors have no competing interests.
Acknowledgements
The authors wish to thank the reviewer for many useful comments on this article, some of which were included in the final version.
Riou, J. , Guyon, H. , and Falissard, B. (2016) An introduction to the partial least squares approach to structural equation modelling: a method for exploratory psychiatric research. Int. J. Methods Psychiatr. Res., 25: 220–231. doi: 10.1002/mpr.1497.
References
- Afifi T.O., Enns M.W., Cox B.J., Asmundson G.J.G., Stein M.B., Sareen J. (2008) Population attributable fractions of psychiatric disorders and suicide ideation and attempts associated with adverse childhood experiences. American Journal of Public Health, 98(5), 946–952. DOI: 10.2105/AJPH.2007.120253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barroso C., Carrión G.C., Roldán J.L. (2010) Applying Maximum Likelihood and PLS on different sample sizes: studies on SERVQUAL model and employee behavior model In Vinzi V.E., Chin W.W., Henseler J., Wang H. (eds) Handbook of Partial Least Squares, Springer Handbooks of Computational Statistics, pp. 427–447, Springer: Berlin Heidelberg. ISBN 978‐3‐540‐32827‐8 [Google Scholar]
- Blaauw E., Arensman E., Kraaij V., Winkel F.W., Bout R. (2002) Traumatic life events and suicide risk among jail inmates: the influence of types of events, time period and significant others. Journal of Traumatic Stress, 15(1), 9–16. DOI: 10.1023/A:1014323009493. [DOI] [PubMed] [Google Scholar]
- Burt R.S. (1976) Interpretational confounding of unobserved variables in structural equation models. Sociological Methods & Research, 5(1), 3–52. DOI: 10.1177/004912417600500101. [DOI] [Google Scholar]
- Buuren S. van, Groothuis‐Oudshoorn K. (2011) mice: Multivariate Imputation by Chained Equations in R. Journal of Statistical Software, 45(3), 1–67. [Google Scholar]
- Chin W.W. (1998) The partial least squares approach for structural equation modeling In Marcoulides G.A. (ed) Modern Methods for Business Research, pp. 295–336, Lawrence Erlbaum Associates: Mahwah, NJ. [Google Scholar]
- Cox D.R., Wermuth N. (1996) Multivariate Dependencies: Models, Analysis and Interpretation, Boca Raton, FL: CRC Press. [Google Scholar]
- De Ravello L., Abeita J., Brown P. (2008) Breaking the cycle/mending the hoop: adverse childhood experiences among incarcerated American Indian/Alaska Native women in New Mexico. Health Care for Women International, 29, 300–315. DOI: 10.1080/07399330701738366. [DOI] [PubMed] [Google Scholar]
- Diamantopoulos A. (2011) Incorporating formative measures into covariance‐based structural equation models. Management Information Systems Quarterly, 35, 335–358. [Google Scholar]
- Dube S.R., Anda R.F., Felitti V.J., Chapman D.P., Williamson D.F., Giles W.H. (2001) Childhood abuse, household dysfunction, and the risk of attempted suicide throughout the life span: findings from the Adverse Childhood Experiences Study. Journal of the American Medical Association, 286, 3089–3096. [DOI] [PubMed] [Google Scholar]
- Esposito Vinzi V., Fahmy T., Chatelin Y., Tenenhaus M. (2007) PLS Path Modeling: Some Recent Methodological Developments, a Software Integrated in XLSTAT and Its Application to Customer Satisfaction Studies. Presented at the Proceedings of the Academy of Marketing Science Conference “Marketing Theory and Practice in an Inter‐Functional World”, Verona, Italy, pp. 11–14.
- Fazel S., Cartwright J., Norman‐Nott A., Hawton K. (2008) Suicide in prisoners: a systematic review of risk factors. Journal of Clinical Psychiatry, 69, 1721–1731. [PubMed] [Google Scholar]
- Felitti V.J., Anda R.F., Nordenberg D., Williamson D.F., Spitz A.M., Edwards V., Koss M.P., Marks J.S. (1998) Relationship of childhood abuse and household dysfunction to many of the leading causes of death in adults. The Adverse Childhood Experiences (ACE) Study. American Journal of Preventive Medicine, 14, 245–258. [DOI] [PubMed] [Google Scholar]
- Gefen D., Rigdon E., Detmar S. (2011) An update and extension to SEM guidelines for administrative and social science research. Management Information Systems Quarterly, 35, iii–xiv. [Google Scholar]
- Godet‐Mardirossian H., Jehel L., Falissard B. (2011) Suicidality in male prisoners: influence of childhood adversity mediated by dimensions of personality. Journal of Forensic Science, 56, 942–949. DOI: 10.1111/j.1556-4029.2011.01754.x. [DOI] [PubMed] [Google Scholar]
- Greenland S., Pearl J., Robins J.M. (1999) Causal diagrams for epidemiologic research. Epidemiology, 10, 37–48. [PubMed] [Google Scholar]
- Hair J.F., Hult G.T.M., Ringle C.M., Sarstedt M. (2013) A Primer on Partial Least Squares Structural Equation Modeling, Los Angeles, CA: Sage Publications. [Google Scholar]
- Henseler J., Chin W.W. (2010) A comparison of approaches for the analysis of interaction effects between latent variables using partial least squares path modeling. Structural Equation Modeling: A Multidisciplinary Journal, 17, 82–109. DOI: 10.1080/10705510903439003. [DOI] [Google Scholar]
- Henseler J., Sarstedt M. (2012) Goodness‐of‐fit indices for partial least squares path modeling. Computational Statistics, 28, 565–580. DOI: 10.1007/s00180-012-0317-1. [DOI] [Google Scholar]
- Kline R.B. (2010) Principles and Practice of Structural Equation Modeling, Third edn, New York: The Guilford Press. [Google Scholar]
- Kraemer H.C., Stice E., Kazdin A., Offord D., Kupfer D. (2001) How do risk factors work together? Mediators, moderators, and independent, overlapping, and proxy risk factors. American Journal of Psychiatry, 158, 848–856. [DOI] [PubMed] [Google Scholar]
- Leek J.T., Peng R.D. (2015) What is the question? Science, 347, 1314–1315. DOI: 10.1126/science.aaa6146. [DOI] [PubMed] [Google Scholar]
- Lin G.‐C., Wen Z., Marsh H.W., Lin H.‐S. (2010) Structural equation models of latent interactions: clarification of orthogonalizing and double‐mean‐centering strategies. Structural Equation Modeling: A Multidisciplinary Journal, 17, 374–391. DOI: 10.1080/10705511.2010.488999. [DOI] [Google Scholar]
- MacCallum R.C., Austin J.T. (2000) Applications of structural equation modeling in psychological research. Annual Review of Psychology, 51, 201–226. DOI: 10.1146/annurev.psych.51.1.201. [DOI] [PubMed] [Google Scholar]
- Markus K.A., Borsboom D. (2013) Frontiers of Test Validity Theory: Measurement, Causation, and Meaning, London: Routledge. [Google Scholar]
- Monecke A., Leisch F. (2012) semPLS: Structural equation modeling using partial least squares. Journal of Statistical Software, 48(3), 1–32. DOI: 10.18637/jss.v048.i03. [DOI] [Google Scholar]
- Prescott C.A. (2004) Using the Mplus computer program to estimate models for continuous and categorical data from twins. Behavior Genetics, 34, 17–40. DOI: 10.1023/B:BEGE.0000009474.97649.2f. [DOI] [PubMed] [Google Scholar]
- R Core Team (2013) R: A Language and Environment for Statistical Computing, Vienna: R Foundation for Statistical Computing. [Google Scholar]
- Reinartz W.J., Haenlein M., Henseler J. (2009) An Empirical Comparison of the Efficacy of Covariance‐Based and Variance‐Based SEM (SSRN Scholarly Paper No. ID 1462666), Rochester, NY: Social Science Research Network. [Google Scholar]
- Rigdon E.E. (2012) Rethinking partial least squares path modeling: in praise of simple methods. Long Range Planning, 45, 341–358. DOI: 10.1016/j.lrp.2012.09.010. [DOI] [Google Scholar]
- Rigdon E.E., Preacher K.J., Lee N., Howell R.D., Franke G.R., Borsboom D. (2011) Avoiding measurement dogma: a response to Rossiter. European Journal of Marketing, 45, 1589–1600. DOI: 10.1108/03090561111167306. [DOI] [Google Scholar]
- Ringle C., Götz O., Wetzels M., Wilson B. (2009) On the use of formative measurement specifications in structural equation modeling: a Monte Carlo simulation study to compare covariance‐based and partial least sqaures model estimation methodologies. Presented at the METEOR Research Memoranda RM/09/014, Maastricht University, The Netherlands.
- Rossiter J.R. (2011) Measurement for the Social Sciences, New York: Springer. [Google Scholar]
- Sanchez G., Trinchera L., Russolillo G. (2013) Package “plspm.” http://CRAN [Google Scholar]
- Schmittmann V.D., Cramer A.O.J., Waldorp L.J., Epskamp S., Kievit R.A., Borsboom D. (2013) Deconstructing the construct: a network perspective on psychological phenomena. New Ideas in Psychology, 31, 43–53. DOI: 10.1016/j.newideapsych.2011.02.007. [DOI] [Google Scholar]
- Sheehan D.V., Lecrubier Y., Sheehan K.H., Amorim P., Janavs J., Weiller E., Dunbar G.C. (1998) The Mini‐International Neuropsychiatric Interview (M.I.N.I.): the development and validation of a structured diagnostic psychiatric interview for DSM‐IV and ICD‐10. Journal of Clinical Psychiatry, 59(Suppl 20), 22–33; quiz 34–57. [PubMed] [Google Scholar]
- Steiger J., Schönemann P. (1978) A history of factor indeterminacy In Theory Construction and Data Analysis in the Social Sciences, pp. 113–178, San Francisco, CA: Sage Publications. [Google Scholar]
- Velicer W.F., Jackson D.N. (1990) Component analysis versus common factor analysis: some issues in selecting an appropriate procedure. Multivariate Behavioral Research, 25, 1–28. DOI: 10.1207/s15327906mbr2501_1. [DOI] [PubMed] [Google Scholar]
- Wold H. (1985) Partial least squares. In Encyclopaedia of Statistical Sciences, Chichester: John Wiley & Sons. [Google Scholar]
- World Health Organization (2007) Preventing Suicide in Jails and Prisons, Geneva: WHO, Department of Mental Health and Substance Abuse. [Google Scholar]
- Wright S. (1934) The method of path coefficients. Annals of Mathematical Statistics, 5, 161–215. DOI: 10.1214/aoms/1177732676. [DOI] [Google Scholar]
- Yang S., Kadouri A., Révah‐Lévy A., Mulvey E.P., Falissard B. (2009) Doing time. International Journal of Law and Psychiatry, 32, 294–303. DOI: 10.1016/j.ijlp.2009.06.003. [DOI] [PMC free article] [PubMed] [Google Scholar]


