Estimating correlations among cardiovascular patients' psychiatric and physical symptom indicators: The biplot in correspondence analysis approach

Abstract

Objectives

We employed the correspondence analysis (CA) biplot to estimate correlations between gender–age levels of cardiovascular disease patients and their psychiatric and physical symptoms. Utilization of this correlation estimation can inform clinical practice by elucidating associations between certain psychiatric or physical symptoms and specific gender–age levels.

Method

The CA biplot utilized here was designed to visually inspect row–column category associations in a 2‐dimensional plane and then to numerically estimate the category associations with correlations. To do so, we (a) estimated dimensions from row and column categories with CA; (b) verified statistical significance of dimensions with a permutation test; (c) projected row and column categories in a plan constructed with the first 2 dimensions that were statistically significant; (d) visually inspected category associations in the plane; and (e) numerically estimated category associations with correlations.

Results

Consistent with the previous results, female cardiovascular disease patients were more likely to experience psychiatric symptoms than the male patients. However, when examining the results by gender and age, both female and male patients in their 50s and 60s tended to experience elevated rates of the psychiatric symptoms.

Conclusions

The CA biplot can be useful for isolating key clinical concerns among any medical populations.

1. INTRODUCTION

Pearson's product–moment correlation is one of the most useful statistical tools to measure linear relationships between continuous random variables (Stigler, 1989) because a correlation coefficient is bounded between −1.00 and +1.00 and therefore is easy to interpret. Moreover, a squared correlation coefficient is a proportion of shared variance between two variables. Most commercialized statistical packages (e.g., SPSS or SAS) include an option for computing Pearson correlations but do not have an option to estimate correlations between category points positioned in multidimensional subspaces. If these category correlations were suspected to be clinically meaningful, investigating them would be worthwhile.

A statistically well‐known method, biplot, was first introduced by Gabriel (1971) in principal component analysis of continuous data (e.g., Gabriel & Odoroff, 1990; J. C. Gower & Hand, 1996; J. Gower, Lubbe, & le Roux, 2011). Since then, biplot has also been applied to correspondence analysis (CA) of a two‐way contingency table to visually approximate relationships between category points located, usually in a two‐dimensional map, without relying on any numerical statistics (e.g., Aitchison & Greenacre, 2002; Beh & Lombardo, 2014; Blasius & Greenacre, 2014; Gabriel, 2002; J. Gower et al., 2011; M. J. Greenacre, 2010, 2016; Le Roux & Rouanet, 2010; Lebart, Morineau, & Warwick, 1984). However, the “bi” does not necessarily refer to two dimensions but to the rows and columns of any multivariate data. CA is a statistical technique that estimates coordinates of categories (usually included in a two‐way contingency table) in multidimensional subspaces, and these estimated coordinates are used for biplotting.

Of great clinical importance, poor mental health among cardiovascular disease (CVD) patients has been linked to higher rates of mortality (Barth, Schumacher, & Herrmann‐Lingen, 2004), and therefore, understanding correlational patterns of psychiatric symptoms among CVD patients is critical for developing targeted interventions. Patients with CVD generally report high rates of depression and distress (Annunziato, Rubinstein, Sheikh, et al., 2008). These symptoms are typically measured by clinical scales such as the Beck Depression Inventory (Beck, Steer, & Carbin, 1988), the Patient Health Questionnaire (Spitzer et al., 1999), the Impact of Events Scale (Horowitz, Wilner, & Alvarez, 1979), and the Post‐traumatic Stress Disorder Checklist (Blanchard, Jones‐Alexander, Buckley, & Forneris, 1996). For the current study, we will analyze categorical data gathered from a large sample of CVD patients and create a CA biplot to visually inspect category associations and then to estimate category associations with correlations, utilizing the category coordinates estimated by CA. Therefore, we need to generate a two‐way contingency table for a CA biplot. However, our psychiatric data are multi‐way; rows include both gender and ages, and columns include multiple symptom variables (e.g., depression, distress, suicide ideation, heart attack, and diabetes). When there is a multitude of categorical variables, a multi‐way contingency table is usually constructed. However, a multi‐way contingency table is not appropriate for a CA biplot proposed in this study.

Thus, the first step in the study is to make multi‐way contingency data in the form of a two‐way table. We code the patients' gender and ages interactively to make them a single row variable with several categories (e.g., male/female age 17–39, male/female 40–49, etc.). And then, we stack the column symptom variables to make them function as a single variable as well. This enables us to create one variable for row categories and another variable for column categories for a CA biplot in order to study associations between gender–age levels (row categories) and symptom indicators of the stacked variables (column categories).

We then employ CA of the stacked two‐way table to estimate coordinates of the categories in multidimensional subspaces followed by creating a biplot of the category coordinates for visual inspection of category associations. For a CA biplot, a two‐dimensional map is usually constructed but with the first two dimensions because they account for the greatest amount of variance. However, if they were not statistically significant, interpretation of CA biplot results would be pointless. Therefore, we test statistical significance for principal inertias (or eigenvalues). Finally, we quantify the category associations with correlations; specifically, we estimate correlations of clinical symptom indicators with gender–age categories to comprehend factors associated with the CVD patients' psychiatric symptoms. We call this process a correspondence analysis biplot.

Estimating specific category correlations may confer clinically significant information. In our example, given the interactively coded row categories representing patients' gender–age levels and the columns stacked psychiatric and physical symptom indicators, clinicians can learn how well or poorly column psychiatric or physical symptom indicators are related with gender–age levels. The significance test for dimensions and the correlation estimation are novel aspects in the current study. In the biplot research utilizing CA (e.g., Beh & Lombardo, 2014; M. Greenacre & Primicerio, 2014), especially in any clinical or psychiatric domains, either testing statistical significance of dimensions or estimating correlations for category association has never been tried. This paradigm seems uniquely suited to providing clinically meaningful information from largely dichotomous patient data (e.g., often yes/no to various symptom indicators) that is common in medical and psychiatric settings.

2. METHODS

2.1. Participants

One thousand and three patients (N = 1,003) were screened between June 2005 and November 2007 at the cardiology clinic of Elmhurst Hospital Center in New York City. Patients gave verbal consent for participating in the mental health screening program, and the questionnaires were stored in their charts. Institutional Review Board approval was obtained to review screened patients' medical charts. The patients who registered for an outpatient visit in the cardiology clinic were screened for depression and post‐traumatic disorder symptoms. The two measures together took about 5–10 min for completion. The objective of the screening program was to connect patients to appropriate services. A positive screening result generated immediate evaluation by the cardiology team that consists of clinical psychologists, nurse practitioners, and physicians who decided whether to suggest a referral for a psychiatric evaluation. The patients' demographic information who participated in the study and their clinical symptom indicators are summarized in Table 1.

Table 1.

Demographic characteristics of the sample

Age	M = 61.04, SD = 14.00
Male (%)	62.1
Age 17 to 39	4.0
Age 40 to 49	8.9
Age 50 to 59	14.6
Age 60 to 69	19.3
Age 70+	15.4
Female (%)	37.9
Age 17 to 39	3.6
Age 40 to 49	4.4
Age 50 to 59	7.5
Age 60 to 69	10.4
Age 70+	12.0
Clinical categories (%)
Diabetes	20
Myocardial infraction	17
Depression	26
Distress	27
Suicide ideation	11

Note. M = mean; SD = standard deviation.

2.2. The biplot in CA of a two‐way table

Logistic regression, categorical principal components analysis (CATPCA), and multiple correspondence analysis (MCA) are often used for analysis of categorical data. Logistic regression analyzes binary data in a response variable (Y) and estimates odds ratios of a chance to get in probability of obtaining Y = 1, as every unit of predictor variables increases. In logistic regression, the predictor variables can be either categorical or continuous; however, it does not handle multiple indicator response variables simultaneously to estimate associations between the multiple response variables and predictor variables. So, logistic regression is not appropriate for the current study that aims to estimate associations between multiple indicator variables.

CATPCA and MCA are analogous to PCA of categorical variables and analyze a rectangular data matrix (which refers to the super‐indicator table) where rows represent cases and columns categorical variables; thus, they are mainly designed for analysis of column categorical variables. Because CATPCA and MCA are not designed for analysis of a two‐way contingency table, if we conduct CATPCA or MCA with the original super‐indicator table (before they are converted into a two‐contingency table), their results may estimate associations between individuals' gender–age levels and column's symptom indicators. However, all single cases are included in a biplot, and it would be too complicated to grasp comprehensive relationships between the gender–age levels and symptom indicators as shown in our current study.

On the other hand, CA is designed for analysis of a two‐way table and estimates the coordinates for rows and columns simultaneously. To estimate the most optimal row and column coordinates for a biplot, CA utilizes singular value decomposition (SVD) of a residual data matrix. The residual data matrix includes only variance occurring from row–column association, and SVD seeks row and column coordinates that fit best to the high‐dimensional cloud of profiles. This best‐fitting coordinates in the sense of least squares must pass through the centroid (or mean) of the profile points. The SVD breaks down the residual matrix into several principal inertias, from the most to least important in terms of their sizes (Beh & Lombardo, 2014; M. J. Greenacre, 2010, 2016; Lebart et al., 1984; Nishisato, 1980, 1994, 2007). When the biplot is applied to CA, it interprets a joint display of row and column categories for their associations; thus, the CA biplot fits our study goal.

The CA biplot is usually conducted in a plane constructed with the first two dimensions. However, if the dimensions were not statistically significant, the results would not be valid. Hence, we first identify the statistically significant dimensions. If several dimensions were statistically significant, it would possible to construct more than one plane.

2.2.1. A significance test for principal inertia

We conduct a permutation test to determine statistical significance of principal inertias (e.g., M. J. Greenacre, 2016; M. Greenacre & Primicerio, 2014). For a permutation simulation, 10,000 random contingency tables are generated by series of permutations of the empirical data. A contingency table consists of the cross‐tabulation matrix of row and column categories. There are several steps for obtaining random contingency tables: (a) apply the raw data related to the (original) observed contingency table with one (interactively coded) variable from rows and the other variable (that was made with several stacked variables) from columns; (b) independently permute categories from either a row or a column variable of the created raw data; (c) cross‐tabulate the permuted data to obtain a random contingency table; (d) repeat the steps (a) to (c) 10,000 times; (e) conduct CA of each random contingency table to estimate random inertias (10,000 of them) for each dimension; (f) plot 10,000 random inertias with a real observed inertia in each dimension; and finally (g) count random inertias larger than the (real) observed principal inertia to compute an empirical p value. For example, if less than 500 of the simulated principal inertias in a dimension were larger than the observed principal inertia, then its p value would be less than .05 and then the observed inertia of the dimension would be statistically significant.

2.2.2. A row (or column) isometric biplot

Our biplot can be either row or column isometric because correlation estimates will be the same irrespective of a row‐ or column‐isometric biplot. In a row‐isometric biplot, row categories are viewed as profiles that consist of column categories as their elements, and the row categories are described with principal coordinates and column categories with standard coordinates. The column standard coordinates' weighted (by masses) mean is set to be zero and variance to be one, and the column category points can also be viewed as the projections onto a plane of the unit profiles [1, 0, 0, …, 0], [0, 1, 0, …, 0], …, and so on. So, any row profile [p₁,  p₂, …, ] with elements (relative frequencies) adding up to 1 can be expressed as p₁[1, 0, …, 0] + p₂[0, 1, 0, …, 0]⋯, and it follows that the row profiles are the weighted averages of the column points, the weights being the row profile elements. This mathematical property makes the row categories projected onto the column categories, serving as the best approximation of original row profile points.

For a column‐isometric biplot, column categories are viewed as profiles that consist of row categories as their elements, and the column categories are described with principal coordinates and row categories with standard coordinates. Visual inspection of proximities among categories in the biplot allows one to understand their associations without relying on any numerical estimates, which is the most appealing feature of a biplot.

In a biplot, if the categories were in the same direction, their correlation would be positive, but if they were positioned opposite, they would be negatively correlated. Mathematically, the acute angles of cosine (less than 90°) between the vectors characterize a positive correlation, and the smaller the angles, the stronger the correlation: The cosine zero represents a perfect correlation. On the other hand, the obtuse angles of cosine (larger than 90°) refer to a negative correlation, and the cosine 180° represents a perfect but negative correlation.

2.2.3. Category contributions in a plane

To assess quality of categories, each category's contribution in a plane to total inertia is estimated, and the categories' contributions larger than the average will be interpreted. The contribution of the ith row category in a plane is computed as follows:

$$\frac{r_i\left(f_{i1}^2+f_{i2}^2\right)}{{\sum }_{k=1}^2{r}_i·f_{\mathit{ik}}^2}\times 100,$$ (1)

where r_i = the mass of the ith row category; $f_{\mathit{ik}}^2$ = the squared principal coordinate of the ith row category on dimension k (k = 1, 2). The contribution of the jth column category in a plan is $c_j\left(g_{j1}^2+g_{j2}^2\right)/\left({\sum }_{k=1}^2{c}_j{g}_{\mathit{jk}}^2\right)\times 100$, where c_j = the mass of the jth column category; $g_{\mathit{jk}}^2$ = the squared principal coordinate of the jth column category on dimension k (k = 1, 2).

2.2.4. Estimating associations between categories with correlations

To validate the visual approximation among the category relations, we estimate correlations between categories in a biplot. The biplot usually reflects chi‐squared distances among the categories to study their proximities, but these distances are not bounded, and it is hard to gauge the meaningfulness of distances until they are compared with others. Moreover, distances do not inform us as to whether the relationships are positive or negative. On the other hand, correlations are bounded between −1 and +1 and also have directions for the relationships. Therefore, we estimate correlations to confirm our visual inspection of category relationships.

2.2.5. A hypothetical biplot example

Let us assume there is a contingency table that consists of three age groups (Teens, Adults, and Elderly) as row categories and their perceived health conditions (Excellent, Neutral, and Poor) as column categories. If we plot the age and perceived health categories in a map, we can easily estimate their proximity by inspection of their locations in the map. It is sensible to expect that the Teens category would be closer to the “excellent” health category in terms of distances than the other two age groups. If we then draw lines from the origin (0, 0) to the age and health categories and examine the angles between them, the angle between the Teens and the excellent health condition would be much smaller (acute angle) than the angle between the Elderly and the excellent health condition. On the other hand, the angle between Elderly and the poor health category would be much smaller than the angles between the Teens and the same poor health category. These angles represent magnitude of correlations; the smaller the angles, the stronger the correlations.

Using this analogy, we identify a two‐dimensional map with CA that would best fit our contingency table and project both row and column categories onto this best‐fitting plane. Let us assume that there is a best‐fitting plane (1, 2) made of the first two‐dimensional axes and the principal coordinates of row category i and i^′ are defined with ${\mathbf{f}}_i=\left(f_{i1}{f}_{i2}\right)\text{and}{\mathbf{f}}_{i^{\prime }}=\left(f_{i^{\prime }1}{f}_{i^{\prime }2}\right)$. In Euclidean geometry, a scalar product between two vectors f_i and ${\mathbf{f}}_{i^{\prime }}$is denoted by ${\mathbf{f}}_i^{\mathrm{T}}{\mathbf{f}}_{i^{\prime }}$. Geometrically, the scalar product is equal to the product of the lengths of the two vectors, multiplied by the cosine of the angle between them:

$${\mathbf{f}}_i^{\mathrm{T}}{\mathbf{f}}_{i^{\prime }}=‖{\mathbf{f}}_i‖·‖{\mathbf{f}}_{i^{\prime }}‖·\text{cosθ},$$ (2)

where ‖f_i‖ denotes the length of the vector f_i. From Equation (2),

$$cos{\mathrm{\theta }}_{i{i}^{\prime }}=\frac{{\mathbf{f}}_i^{\mathrm{T}}{\mathbf{f}}_{i^{\prime }}}{‖{\mathbf{f}}_i‖·‖{\mathbf{f}}_{i^{\prime }}‖},$$ (3)

where $cos{\mathrm{\theta }}_{i{i}^{\prime }}$ is a correlation estimate between rows i and i^′. Similarly, in the given plane (1, 2), the correlation between columns j and j^′ is estimated with standard coordinates of columns j and j^′, ${\mathbf{\gamma }}_j=\left({\gamma }_{j1}{\gamma }_{j2}\right)\text{and}{\mathbf{\gamma }}_{i^{\prime }}=\left({\gamma }_{j^{\prime }1}{\gamma }_{j^{\prime }2}\right)$: $cos{\mathrm{\theta }}_{j{j}^{\prime }}={\mathbf{\gamma }}_j^{\mathrm{T}}{\mathbf{\gamma }}_{j^{\prime }}/‖{\mathbf{\gamma }}_j‖·‖{\mathbf{\gamma }}_{j^{\prime }}‖$. Likewise, we can easily estimate the correlation between row i and column j, but because our biplot is row‐isometric, the correlation is estimated with row principal and column standard coordinates:

$$cos{\mathrm{\theta }}_{\mathit{ij}}=\frac{{\mathbf{f}}_i^{\mathrm{T}}{\mathbf{\gamma }}_j}{‖{\mathbf{f}}_i‖·‖{\mathbf{\gamma }}_j‖}.$$ (4)

Equations (2)–(4) are assumed under the row‐isometric biplot. However, although the column‐isometric biplot is pursued, $cos{\mathrm{\theta }}_{i{i}^{\prime }}$ and cosθ_ij will stay the same, because $cos{\mathrm{\theta }}_{i{i}^{\prime }}={\mathbf{\varphi }}_i^{\mathrm{T}}{\mathbf{\varphi }}_{i^{\prime }}/‖{\mathbf{\varphi }}_i‖·‖{\mathbf{\varphi }}_{i^{\prime }}‖$, where ϕ is row standard coordinates; $cos{\mathrm{\theta }}_{\mathit{ij}}={\mathbf{\varphi }}_i^{\mathrm{T}}{\mathbf{g}}_j/‖{\mathbf{\varphi }}_i‖·‖{\mathbf{g}}_j‖,$ where g is column principal coordinates. In other words, an angle between two categories remains the same, irrespective of a row‐ or column‐isometric biplot.

2.3. Generating row and column categories

Patients were categorized according to age and gender. Five age categories were constructed for female and male patients: 17–39, 40–49, 50–59, 60–69, and 70+ (70 or above): “F1” and “M1” stands for female and male patients of ages 17 to 39; “F2” and “M2” for female and male patients of ages 40 to 49; “F3” and “M3” for female and male patients of ages 50 to 59; “F4” and “M4” for female and male patients of ages 60 to 69; and “F5” and “M5” for female and male patients of ages 70 or older. The age range was from 17 to 96, but we generated the age categories by considering reliable results when CA is conducted with enough counts in each category. If there were too few counts in a category, this category could emerge as an outlier and attenuate the overall analyses.

There are 10 column categories that consist of six psychiatric symptom indicators and four physical symptom indicators. The symptom indicators are recorded as a binary, “0” for absence and “1” for presence. Because individual patients were repeatedly measured over these symptoms, the patients were assigned to either absence or presence of each symptom indicator, not both. The following abbreviations are used to denote 10 binary symptom categories:

• “Sui” is for an indicator of suicide ideation (0 = absence; 1 = presence);

• “Dis” is for a screen on the Impact of Event Scales (Horowitz et al., 1979) as a measure of distress (0 = absence; 1 = presence);

• “Dep” is for a screen on the Patient Health Questionnaire as a measure of depression (0 = absence; 1 = presence);

• “Mi” is for a symptom of Myocardial Infarction (MI) or heart attack (0 = absence; 1 = presence); and

• “Dia” is for a symptom of Diabetes (0 = absence; 1 = presence).

Although the CA package is available in the R‐language domain (http://cran.r-project.org), estimating category associations with correlation is not available in the package, and we had to make a proprietary R code for correlation estimation.

3. RESULTS

3.1. Testing significance of principal inertias

Utilizing a permutation simulation, we estimated the empirical p values for the principal inertias (or dimensional eigenvalues); they were .0001, .0005, .6725, .9765, .8975, .9183, .9914, .9996, and .9809, respectively. The results show that the first two dimensions were statistically significant. We also plotted observed inertias, mean inertias from 10,000 simulated inertias, and 95th percentile from 10,000 simulated inertias over dimensions. As shown in Figure 1, the first two observed inertias were larger than the simulated inertias, and we used the first two dimensions to construct a plane for our biplot analysis.

Figure 1.

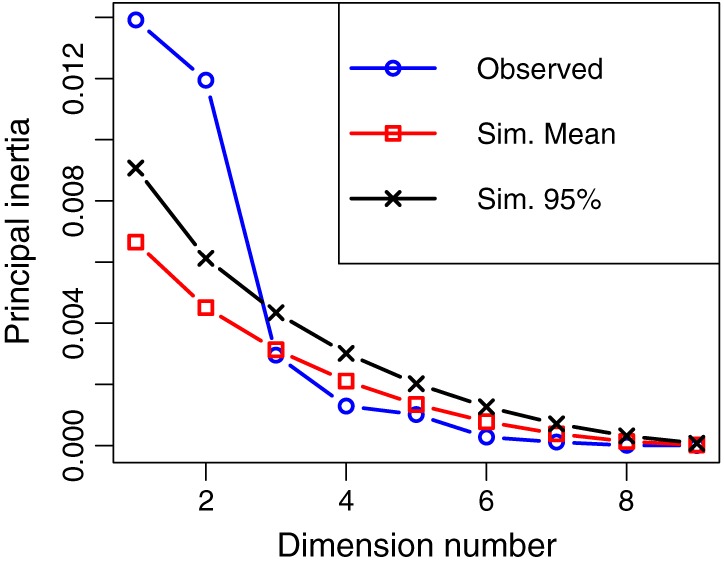
Observed inertias juxtaposed with simulated inertias from 10,000 permutations. Observed = inertias from observed data; Sim. Mean = mean of 10,000 simulated inertias with permutations; Sim. 95% = the 95th percentile of the 10,000 simulated inertias with permutations

3.2. Visual inspection of relationships and assessment of category utilities

Among nine dimensions, the first two dimensions were statistically significant. The first dimension accounted for 44.1% of total variance and the second one for 37.9%, and these two dimensions were used to construct a plan for a biplot analysis; thus, 82% of total variance was accounted for by the plane, and 18% remained as unexplained variance. With inspection of the magnitudes and directions of the dimensional coordinates, the first dimension was regarded as polarizing psychiatric symptoms against physical symptoms and the second dimension as symptom presence versus symptom absence categories. Thus, a plan consisting of these two dimensions included both dimensional information. To visually inspect associations among categories, we biplotted row and column categories as shown in Figure 2, where the row categories were viewed as points and the column categories as vectors.

Figure 2.

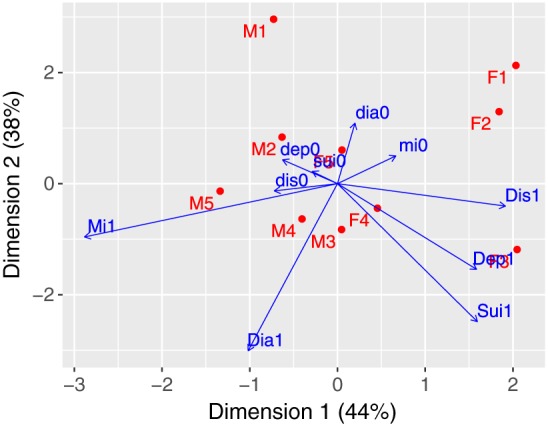
The biplot with gender–age categories and mental and clinical symptom categories projected onto a plane constructed with Dimensions 1 and 2 axes where the horizontal and vertical values represent the column standard coordinates × square root of relevant column mass. Dis1 = distress presence; dis0 = distress absence; Dep1 = depression presence; dep0 = depression absence; Sui1 = suicide ideation presence; sui0 = suicide ideation absence; Mi1 = heart attack presence; mi0 = heart attack absence; Dia1 = diabetes presence; dia0 = diabetes absence; “M” = male; “F” = female; “1” = ages between 16 and 39; “2” = ages between 40 and 49; “3” = ages between 50 and 59; “4” = ages between 60 and 69; “5” = ages of 70 or older

3.2.1. Visually approximated relationships between categories

In Figure 2, the lengths of the trajectories approximated the amount of variance, and the longer the trajectories carried more variance than the shorter ones. According to trigonometry, cos0^° represents a perfect positive correlation (+1.00); cos180^° a perfect negative correlation (−1.00); and cos90^° zero correlation. Any degree over 90^° is called obtuse, and consequently, correlation becomes negative until 180°. Let us choose two vectors, Sui1 (suicide ideation) and Dep1 (depression), which were almost overlapped. The angle between them is close to zero, and the correlation is close to be +1.00. On the other hand, the angle between Dep1 and Dia1 (diabetes) was acute but close to 90°, and the correlation is positive but close to zero. For another example, Dia1 and dia0 were in the opposite direction, with an angle between them of 180°, and therefore, the correlation would be −1.00; in other words, if Dia1 and dia0 were folded, they would be perfectly overlapped but polarized. Using this analogy, if one draws imaginary lines from the origin of (0, 0) to any two categories, one can easily approximate their associations.

3.2.2. Assessment of category utilities

To assess the utility of the categories in a biplot, the contributions of row and column categories were calculated, and then their contributions were converted into percentages. The average contribution for both row and column categories was 8.2% (=82 % /10) because of 10 categories for rows and columns. The category contributions larger than the average were included for interpretation, although all category contributions were included in Table 2.

• M1 (14.19%), M5 (12.29%), F1 (12.83%), F2 (9.33%), and F3 (17.95%) contributed more than the average contribution of 8.2%. These five gender–age categories in total accounted for 66.59% out of 82% (that was the proportion of the total variance accounted for by the biplot plane).

• All symptom presence categories, Sui1 (8.85%), Dis1 (9.99%), Dep1 (11.42%), Mi1 (15%), and Dia1 (16.99%), contributed more than 8.2%, and in total, they accounted for 62.27% out of 82%.

Table 2.

Category contributions (%) of row and column categories in the plane

Gender/age	Dim_1 (%)	Dim_2 (%)	Plane (%)	Symptoms	Dim_1 (%)	Dim_2 (%)	Plane (%)
M1 (17 to 39)	0.93	13.27	14.19	sui0	0.66	0.34	1
F1 (17 to 39)	6.62	6.22	12.83	Sui1	2.87	5.99	8.85
M2 (40 to 49)	1.54	2.35	3.89	dis0	2.82	0.01	2.90
F2 (40 to 49)	6.53	2.80	9.33	Dis1	9.61	0.38	9.99
M3 (50 to 59)	0.00	3.79	3.79	dep0	2.60	1.06	3.66
F3 (50 to 59)	13.94	4.02	17.95	Dep1	6.31	5.12	11.42
M4 (60 to 69)	1.41	2.92	4.33	mi0	3.26	1.59	4.86
F4 (60 to 69)	0.97	0.76	1.73	Mi1	13.72	1.29	15
M5 (70+)	12.17	0.11	12.29	dia0	0.26	7.09	7.35
F5 (70+)	0.00	1.67	1.67	Dia1	1.98	15.01	16.99
Total			82	Total			82

Note. The row and column category contributions (%) larger than the average 8.2% (=82 % /10) in the plane were bolded. “M” = male; “F” = female; Dis1 = distress presence; dis0 = distress absence; Dep1 = depression presence; dep0 = depression absence; Sui1 = suicide ideation presence; sui0 = suicide ideation absence; Mi1 = heart attack presence; mi0 = heart attack absence; Dia1 = diabetes presence; dia0 = diabetes absence.

However, category utility assessment does not provide any information about how they are associated to each other in a biplot. We will examine their associations in the next section.

3.3. Estimating correlations between categories in biplot configurations

The correlations (a) between clinical (psychiatric and physical) symptom indicators and (b) between the clinical symptom indicators and gender–age categories were included in Table 3. However, we mainly examined the correlations between psychiatric and physical symptom presence categories (Sui1, Dis1, Dep1, Mi1, and Dia1) and gender–age categories because their correlations are clinically most meaningful.

Table 3.

Correlations between gender–age categories and psychiatric–physical symptom categories in a plane constructed by Dimensions 1 and 2

	sui0	Sui1	dis0	Dis1	dep0	Dep1	mi0	Mi1	dia0	Dia1
sui0	1	−0.97	0.66	−0.88	1	−1	−0.32	0.56	0.43	−0.3
Sui1		1	−0.45	0.7	−0.95	0.97	0.07	−0.40	−0.64	0.62
dis0			1	−0.94	0.7	−0.6	−0.92	1	−0.39	0.51
Dis1				1	−0.90	0.85	0.89	−0.92	0.05	−0.18
dep0					1	−0.99	−0.37	0.66	0.38	−0.26
Dep1						1	0.29	−0.56	−0.5	0.43
mi0							1	−0.94	0.72	−0.81
Mi1								1	−0.44	0.6
dia0									1	−0.99
Dia1										1
M1	0.78	−0.95	0.06	−0.43	0.75	−0.85	0.39	−0.08	0.91	−0.84
M2	0.96	−1	0.45	−0.75	0.95	−0.96	0	0.32	0.68	−0.56
M3	−0.65	0.87	0.12	0.26	−0.61	0.74	−0.55	0.26	−0.97	0.93
M4	−0.08	0.42	0.68	−0.35	−0.03	0.15	−0.94	0.78	−0.93	0.97
M5	0.73	−0.45	1	−0.95	0.76	−0.65	−0.86	0.98	−0.28	0.42
F1	−0.11	−0.23	−0.81	0.53	−0.16	0	0.99	−0.88	0.84	−0.91
F2	−0.30	−0.04	−0.91	0.68	−0.35	0.16	1	−0.96	0.71	−0.82
F3	−0.99	0.89	−0.76	0.95	−1	0.97	0.39	−0.66	−0.34	0.2
F4	−0.99	0.97	−0.58	0.85	−0.99	1	0.16	−0.46	−0.56	0.43
F5	0.54	−0.79	−0.26	−0.12	0.5	−0.64	0.66	−0.39	1	−0.97

Note. The correlations equal to or larger than +0.4 in symptom presence categories were bolded here and interpreted in the text. Dis1 = distress presence; dis0 = distress absence; Dep1 = depression presence; dep0 = depression absence; Sui1 = suicide ideation presence; sui0 = suicide ideation absence; Mi1 = heart attack presence; mi0 = heart attack absence; Dia1 = diabetes presence; dia0 = diabetes absence; “M” = male; “F” = female; “1” = ages between 16 and 39; “2” = ages between 40 and 49; “3” = ages between 50 and 59; “4” = ages between 60 and 69; “5” = ages 70 or older.

3.3.1. The symptom positions differentiated in the quadrants

In our biplot, interestingly, three psychiatric symptom presence categories (Sui1, Dep1, and Dis1) were located on the second quadrant (the lower right side), and two physical symptom presence categories (Dia1 and Mi1) were located on the third quadrant (the lower left side). Thus, one can easily differentiate between psychiatric and physical symptom categories with a visual inspection. Also, in the biplot configurations, male and female CVD patients in their 60s (M4 and F4) and male patients in their 70s (M5) were adjacent to the physical symptom categories, whereas female and male CVD patients in their 50s (F3 and M3) and female patients in their 60s (F4) were adjacent to the psychiatric symptom categories. In sum, the biplot results indicate that male patients were generally more represented in the physical symptom categories but males in their 50s were quite susceptible to poor mental health. On the other hand, female patients were generally more vulnerable to mental health issues, but symptoms varied with age.

3.3.2. Estimating associations among categories with correlations

In our biplot, only positive relationships with the symptom presence categories were interpreted, because the absence category embedded in every symptom is inversely related with the presence category, and reporting them will be redundant. Although the complete correlational results were included in Table 3, only positive correlations of 0.4 or larger, which are greater than the medium effect size of 0.3 (Cohen, 1992), are reported here.

1. Irrespective of gender or age, at least one of the mental health symptom presence categories was highly correlated to another r(Sui1, Dis1) = 0.7; r(Sui1, Dep1) = 0.97; r(Sui1, Dia1) = 0.62; and r(Dis1, Dep1) = 0.85. Similarly, physical health symptom presence categories were highly related: and r(Mi1, Dia1) = 0.56.

2. Consistent with the visual configuration, female gender tended to have strong positive correlations with all psychiatric symptom presence categories. Especially, women between the ages of 50–59 (F3) and 60–69 (F4) exhibited strong relationships with distress, suicide ideation, and depression: r(F3, Sui1) = 0.89; r(F3, Dis1) = 0.95; r(F3, Dep1) = 0.97. Similarly, r(F4, Sui1) = 0.97, r(F4, Dis1) = 0.85, and r(F4, Dep1) = 1, and F4 was also positively related with diabetes: r(F4, Dia1) = 0.43. Distress was also salient for females between 17–39 (F1) and 40–49 (F2): r(F1, Dis1) = 0.53 and r(F2, Dis1) = 0.68.

3. Male patients in their 50s (M3) and 60s (M4) exhibited strong relationships with suicide ideation and depression: r(M3, Sui1) = 0.87, r(M3, Dep1) = 0.74, and r(M4, Sui1) = 0.42. Also, these age groups were highly correlated with diabetes and MI: r(M3, Dia1) = 0.93, r(M4, Dia1) = 0.97, and r(M4, Mi1) = 0.78. Male patients in their ages 70 or over (M5) were, not surprisingly, highly associated with MI and diabetes: r(M5, Mi1) = 0.98 and r(M5, Dia1) = 0.42.

4. DISCUSSION

To date, CVD patients have been considered at high risk for compromised mental health that is in turn related to poor medical outcomes. However, CVD is a broad illness, and it is unclear what specific aspects of it confer higher risk for mental health symptoms. From a clinical perspective, analyses that can isolate which patients may experience the greatest mental health morbidity would have substantial utility. Estimating relationships between characteristics of CVD patients revealed important clinical implications. The psychiatric symptom presence categories, suicide ideation and depression, were positively related with diabetes but negatively related with MI, although diabetes and MI were substantially and positively correlated. This pattern of associations with diabetes indicates that the risk complex CVD patients face for poor mental health but that is not the case for patients who have experienced an acute event such as MI. These results also imply that the mental health of CVD patients may be quite varied.

However, our analyses were able to pinpoint specific pathways, such as the prominent relationship between depression and suicidality with diabetes, especially for male patients in their 50s and female patients in their 60s. Isolating this age range is helpful from a clinical perspective; it may be that CVD male patients in this age range are most susceptible to poor mental health perhaps because of the competing roles during this time of life that could be disrupted. On the other hand, this phenomenon appeared only in the female patients in their 60s. It is unclear why the mental health burden on female patients could be more pronounced later. In general, however, women with comorbid CVD and diabetes have poorer outcomes than men (Huxley, Barzi, & Woodward, 2006); although the direction is unclear, this trajectory could be associated with more acute mental health problems.

Our results indicate that female CVD patients are generally more vulnerable to mental health difficulties than male patients and these results are consistent with the well‐established CVD literature (Keyes, 2004). However, because of the wide age range of study patients available here, we were able to determine nuances in these established patterns. Distress was ubiquitous in female patients, except for age 70 or above, but female patients in their 50s and 60s were most vulnerable to all psychiatric symptoms, distress, suicide ideation, and depression. Moreover, male patients in their 50s also displayed strong suicide ideation and depressive tendencies. The contributions of these female and male age ranges in our biplot were larger than the average contribution. Although in general, female patients tend to be more prone to these mental health issues than male patients, in the current study, we demonstrated more detailed and differentiated information in terms of patients' gender and age and had a better sense of when mental health difficulties were salient.

Comorbidity is common among CVD patients, and it may be that ones such as diabetes, which requires day‐to‐day management and many difficult side effects, are strong contributors to poor mental health. Conversely, although it was common to have diabetes and MI go hand and hand in this study, history of MI alone did not contribute to poor mental health, and this was confirmed in our correlational results (all negatively related with psychiatric symptoms), as is often expected because an MI is analogous to a traumatic experience. Taken together, these findings suggest that the elevated rates of psychiatric symptoms, especially depression and suicide ideation, among CVD patients are most common among middle age patients, regardless of gender. In addition, these symptoms are linked to diabetes, but not the experience of an MI per se. Prior literature has noted that mood symptoms are a key concern for older CVD patients with diabetes (Fenton & Stover, 2006) but our analyses were able to extend and perhaps expand this conclusion to male patients in their 50s and 60s and female patients in their 60s as well.

Such a concise pattern of findings would have been difficult to detect without the CA biplot analysis utilized here. This approach highlighted that indeed distress, depression, suicide ideation, and combinations of them impact diverse CVD patients of a wide age range. Not all CVD patients though may be at risk; those with comorbid medical conditions such as diabetes seem most vulnerable to poor mental health, especially suicide ideation and depression. Perhaps, the first priority for mental health resources in cardiology clinics should be to screen medically complex patients, especially those who require intensive disease management. The biplot in CA may be useful for isolating key clinical concerns among other similarly heterogeneous medical populations.

Kim S‐K, Annunziato RA. Estimating correlations among cardiovascular patients' psychiatric and physical symptom indicators: The biplot in correspondence analysis approach. Int J Methods Psychiatr Res. 2018;27:e1611 10.1002/mpr.1611