MULTI-SCALE SEGMENTATION USING DEEP GRAPH CUTS: ROBUST LUNG TUMOR DELINEATION IN MVCBCT

Abstract

Deep networks have been used in a growing trend in medical image analysis with the remarkable progress in deep learning. In this paper, we formulate the multi-scale segmentation as a Markov Random Field (MRF) energy minimization problem in a deep network (graph), which can be efficiently and exactly solved by computing a minimum s-t cut in an appropriately constructed graph. The performance of the proposed method is assessed on the application of lung tumor segmentation in 38 mega-voltage cone-beam computed tomography datasets.

1. INTRODUCTION

As we enter the era of precision medicine, imaging is playing an increasingly significant role with a substantially large amount of new and improved medical image data used in clinic, creating a demand for novel automated segmentation methods which can process this data faster and more thoroughly. With the recent revival of deep learning, deep networks have been used in a growing trend in medical image analysis, including deep convolutional neural networks (CNNs) based medical image segmentation. In this paper, we develop a new segmentation approach which formulates the multi-scale segmentation as a Markov Random Field (MRF) energy minimization problem in a deep network (graph), whose globally optimal solution can be achieved efficiently by graph cuts [1].

Machine learning has been widely used as a pixel classification method for medical image segmentation. Very recently, deep learning is emerging as the leading learning technique using deep networks in the imaging and computer vision field. The medical imaging community has been rapidly entering the arena, and deep learning is quickly proving to be the state-of-the-art tool for a wide variety of medical tasks, including segmentation (cf. [2, 3, 4, 5]), with the capacity of automatic discovery of relevant image features, from low-level to higher order. Deep learning is most effective when applied to large training sets, but in the medical imaging domain obtaining such a large training dataset as ImageNet (http://www.image-net.org) in computer vision poses a tremendous challenge due to the scarce and expensive medical expertise, privacy issues, funding, and the breadth of medical applications [6, 5]. In addition, training a deep learning network requires significant computational powers, especially in 3D medical imaging, and is often complicated by overfitting and convergence issues, requiring repetitive adjustment in the architecture or learning parameters. It is envisioned that semi-supervised and unsupervised learning may continuously play an important role especially for those applications where hand annotations are not available or intractable to obtain [6].

Multi-scale methods have been employed to speed up some existing segmentation methods [7, 8, 9]. These methods usually work sequentially on different scales. As an effective way of image feature extraction, they were also shown to be useful for improving segmentation accuracy [10, 11, 12]. Cour et al. [11] proposed enforcing the cross-scale constraint so that segmentation at the coarse scale should reflect a local average at the fine scales by using affinity matrices at different scales. The multi-scale segmentation is then conducted simultaneously over all scales by solving an approximate eigenvector problem. The information across different scales is propagated to reach a consistent segmentation at all scales. Their method coarsens an image based on a regular grid, which may blur details at the coarse levels. Using a data-driven coarsening scheme, such as over-segmentation, may better preserve details at the coarse levels. Kim et al. [10] used regions/supervoxels in an over-segmented image (obtained by using methods such as mean shift) as nodes in the coarse level. Each voxel at the original resolution is viewed as nodes in the fine level. A soft label consistency constraint is enforced between the nodes at the coarse level and the fine level. The segmentation is computed by a convex optimization technique on both levels simultaneously. For 3D medical image applications, the computation of eigenvector problems [11] and matrix inversions [10] are too expensive. A more efficient method is needed to take advantage of both voxel and supervoxel level information. In addition, all those multi-scale segmentation methods based on spectral graph theory or convex optimization require a heuristic rounding scheme to achieve final results, which has no guarantee of global optimality.

In this paper, inspired by the successful use of layered networks in deep learning, we develop a deep graph cut method to segment the target object in different scales simultaneously in a single optimization process to maintain the scale-wise consistency. Each scale is modeled as a separate network (graph). The image features used in each scale can be computed with different methods, such as mean shift [13], watershed [14], and other supervoxel techniques [15]. All the networks for different scales form a deep layered graph with connections introduced to enforce the segmentation consistency across all the scales. The graph cut method is then used to compute a globally optimal segmentation of the target object. Our method enables to explore diverse image features and to represent them with multiple layered networks. As the image features used in each network layer can be computed independently, it does not require a large training dataset, which alleviates the big challenge posed by the deep learning method in medical imaging. In deep learning, the image cue information flows forward and backward between multilayers by convolution/pooling and backpropagation, respectively. In our work, as the multi-scale segmentation is modeled as a deep network with each layer representing one image scale, the bidirectional information propagation between coarse and fine scales is ensured by segmenting the object over all scales simultaneously. Many previous methods (cf. [7, 8, 9, 16]) segment the object sequentially from coarse to fine scales, with image cue information propagating in just one direction.

2. METHOD

The proposed method formulates the multi-scale segmentation problem as an Markov Random Field (MRF) energy minimization problem in a layered graph, which can be optimized by computing a minimum s-t cut. We first introduce the MRF energy for the multi-scale segmentation of the target object. A novel graph transformation is then presented to encode the energy function.

2.1. Modeling the multi-scale image segmentation

This section presents a novel multi-scale segmentation energy which incorporates the voxel-wise information from the original image, as well as other scaled image information, such as region-wise information and/or a data-driven over-segmentation of the original image.

Given an image $\mathcal{I}$, denote by S₀ the finest scale of the image (i.e., $S_0=\mathcal{I}$), and by S_i (i = 1, 2, …, N) the derived image in different scales. Note that S_i’s can be computed using different methods and can be in the same level of scale. Each entity in S_i is called a supervoxel. Each supervoxel in a coarse scale level may consist of a set of (super)voxels in a fine scale. A scaled image S_i is said to be hierarchically interacted with S_j if each supervoxel in S_i consists of only supervoxels (voxels if j = 0) in S_j. Denote by $\mathcal{H}$ all hierarchically interacted image pairs (S_i, S_j). This hierarchical interaction relations among S_i’s clearly form a tree structure with S₀ being the root (Fig. 1(a)). In Fig. 1(a), S0-S3-S6-S7 represent the target object in multiple different scales, while S1-S2-S3 can be used to explore different features of the target object.

Fig. 1.

(a) The hierarchical interaction structure of an image in different scale levels forms a tree. (b) An example image in the original voxel level of scale (lower panel) and in the regional level of scale with over-segmentation (upper panel). (c) Illustrating the graph construction for two hierarchically interacted images S_i and S_j in different scale levels.

For each (super)voxel p ∈ S_i, a label $f_p\in \mathcal{L}=\left\{0,1\right\}$ is assigned. If a (super)voxel is labeled as 1, then it is assigned the “object” label in the segmentation; otherwise, it is assigned the “background” label. A scaled image S_i can be viewed as a partition of a scaled image S_j into many self-coherent regions or segments if $\left(S_i,S_j\right)\in \mathcal{H}$. For instance, a single meaningful object, such as a tumor, can be divided into multiple regions instead of being segmented as a single object. Techniques such as mean shift [13], watershed [14] can be used to generate scaled images in different levels of scale. An over-segmentation example by watershed is shown in Fig.1(b). Although the supervoxels may not directly correspond to anatomically meaningful objects, it groups portions of image into meaningful and self-homogeneous regions. For any pair $\left(S_i,S_j\right)\in \mathcal{H}$, we use R_ij(p) to denote the set of (super)voxels in S_j corresponding to each supervoxel p ∈ S_i.

The multi-scale segmentation energy takes the following form.

$$E_{MS}(f)=\sum _{i=0}^N\mathcal{E}\left(S_i\right)+\sum _{\left(S_i,S_j\right)\in \mathcal{H}}\mathcal{C}\left(S_i,S_j\right)$$ (1)

$$\mathcal{E}\left(S_i\right)=\sum _{p\in S_i}{D}_p\left(f_p\right)+{\alpha }_i\sum _{(p,q)\in {\mathcal{N}}_i}{V}_{pq}\left(f_p,f_q\right)$$ (2)

$$\mathcal{C}\left(S_i,S_j\right)=\sum _{p\in S_i}\sum _{q\in R_{ij}(p)\subset S_j}{\Theta }_{p,q}\left(f_p,f_q\right)$$ (3)

The graph-cut segmentation energy term $\mathcal{E}\left(S_i\right)$ is used for segmenting the target object in the scaled image S_i. It consists of a data term D_p(f_p) – measuring the inverse likelihood of (super)voxel p belonging to the object, and a boundary term V_pq(f_p, f_q) – penalizing the boundary discontinuity [1]. We adopt 6-neighborhood setting ${\mathcal{N}}_0$ for S₀. In general, two supervoxels p, q ∈ S_i (i = 1, 2, …, N) are said to be adjacent, i.e., $(p,q)\in {\mathcal{N}}_i$, if the Euclidean distance between their centroids is within a certain threshold. The data term D_p(f_p) for a supervoxel p can be computed from some aggregate statistics of its comprised (super)voxels, such as the average data term over them. It can also incorporate more sophisticated information such as texture description within the supervoxel. For a pair of neighboring (super)voxels $(p,q)\in {\mathcal{N}}_i$, V_pq(f_p, f_q) = 0 if f_p = f_q and V_pq(f_p, f_q) > 0 if f_p ≠ f_q. This encourages neighboring voxels to have the same label, yielding spatially more coherent segmentation. α_i is the balancing coefficient between the data term and the smoothness term for segmenting the target object in S_i.

The label consistency term $\mathcal{C}\left(S_i,S_j\right)$ (Eq.(3)) penalizes the label difference between any two corresponding (super)voxels of two hierarchically interacted image pairs $\left(S_i,S_j\right)\in \mathcal{H}$. That is, for any p ∈ S_i and q ∈ R_ij(p) ⊂ S_j, If f_p = f_q, then Θ_p,q(f_p, f_q) = 0; while if f_p ≠ f_q, then Θ_p,q(f_p, f_q) > 0. This encourages the segmentations at the coarse level and the fine level should be consistent as much as possible.

2.2. Optimization using deep graph cuts

A graph consisting of deep hierarchical subgraphs is first constructed encoding the multi-scale segmentation energy function in Eq.(1). Then, compute a minimum s-t cut in the constructed deep graph, which exactly minimizes the objective function for the segmentation.

For each scaled image S_i, a subgraph G_i = (V_i, E_i) is constructed using the graph-cut method [1]. Every (super)voxel p ∈ S_i exactly has a corresponding node v_p ∈ V_i in G_i. A common source node s and sink node t are introduced for all G_i’s. To encode the data term $\sum _{p\in S_i}{D}_p\left(f_p\right)$, we add a t-link arc from source s to each node v_p with the weight D_p(f_p = 0) and a t-link arc from each node v_p to the sink t with the weight D_p(f_p = 1). The boundary term $\sum _{(p,q)\in {\mathcal{N}}_i}{V}_{pq}\left(f_p,f_q\right)$ is enforced by introducing n-links, as follows. For each pair of neighboring voxels $(p,q)\in {\mathcal{N}}_i$, two n-link arcs are added: one from v_p to v_q and the other in the opposite direction from v_q to v_p. The weight of each arc is set as V_pq(f_p, f_q) while f_p ≠ f_q. Fig.1(c) shows an example graph construction for S_i and S_j with $\left(S_i,S_j\right)\in \mathcal{H}$ in which the red edges (in G_i) and the blue edges (in G_j) are added to enforce the boundary smoothness in the respective images.

Then, the inter-subgraph edges E_ij are introduced between G_i and G_j for each pair $\left(S_i,S_j\right)\in \mathcal{H}$ to encode the label consistency term $\mathcal{C}\left(S_i,S_j\right)$. For every (super)voxel p ∈ S_i and q ∈ R_ij(p) ⊂ S_j, an edge from node v_p in G_i to the node v_q in G_j is added with a weight of Θ_q,p(f_q = 1, f_p = 0). An edge from node v_p to node v_q is also added with a weight of Θ_q,p(f_q = 0, f_p = 1) (green arcs between two subgraphs in Fig.1(c)). When a (super)voxel q ∈ S_j has the same label as its corresponding (super)voxel p ∈ S_i according to the s-t cut, then no penalty is enforced. If a (super)voxel q ∈ S_j is labeled as object but its corresponding (super)voxel p ∈ S_i is labeled as background, then the edge (v_q, v_p) is in the s-t cut and the penalty Θ_q,p(f_q = 1, f_p = 0) is correctly enforced. Similarly, if a (super)voxel q ∈ S_j is labeled as background but its corresponding (super)voxel p ∈ S_i is labeled as object, then the arc (v_p, v_q) is in the s-t cut and the penalty Θ_q,p(f_q = 0, f_p = 1) is correctly enforced.

This completes the graph construction for the multi-scale object segmentation. The resulting graph G consists of hierarchical subgraphs G_i’s. We thus term it as a deep graph. A minimum s-t cut in G gives an optimal labeling f*. The target object is the volume of voxels p ∈ S₀ with $f_p^{*}=1$.

3. EXPERIMENT

We assess the performance of the proposed method on the application of primary lung tumor segmentation using mega-voltage cone-beam computed tomography (MVCBCT). This application is challenging because of the poor image quality (high noise), similar intensity profiles of the tumor and surrounding normal tissue, and the close proximity of the tumor to the lung boundary. Although our validation was done on two scales, the method is ready to use deep layers.

3.1. Data

Thirty-eight volumetric MVCBCT datasets were obtained to evaluate the performance of the proposed method. The datasets were acquired from patients with non-small cell lung cancer over eight weeks of radiation therapy. Each image contained 128 × 128 × 128 voxels with a voxel size of 1.07 × 1.07 × 1.07 mm³. Manual tracings of the lung tumor boundaries were obtained from an expert and were used as the reference standard when assessing the performance of the proposed approach.

3.2. Experiment Settings

The segmentation performance was assessed using two metrics: Dice similarity coefficient (DSC) and the average symmetric surface distance (ASSD). The Dice similarity coefficient is used to measure how well two volumes A and B overlap with each other, with $DSC=\frac{2\left|A\cap B\right|}{\left|A\right|+\left|B\right|}$. The larger the DSC is, the better the two volumes are aligned, with 1 indicating a perfect overlap. The average symmetric surface distance (ASSD) is used to measure how close the boundary surfaces S^A and S^B are for two objects A and B. Let d(x, S) denote the minumum distance between a point x and any point on the surface S. Then, $\mathit{\text{ASSD}}=\frac{\sum _{a\in S^A}d\left(a,S^B\right)+\sum _{b\in S^B}d\left(b,S^A\right)}{\left|S^A\right|+\left|S^B\right|}$. The smaller the ASSD is, the better the two segmented contours agree with each other.

We report the DSC’s and ASSD’s between the manually traced tumor contours and the segmentations returned by the traditional graph cut method (GC) and the proposed deep graph cut method (dGC). A two-tailed student t-test was conducted between the two methods. A p-value smaller than 0.05 is considered to be statistically significant.

For initialization, The user manually specified two concentric spheres, so that all voxels within the small sphere belong to the object, and all voxels outside the large sphere belong to the background. The segmentation was then conducted in the bounding box of the large sphere.

3.3. Energy Term Design

In this experiment, we only consider two hierarchical scales of the image: one is in the original voxel scale and the other is in the regional scale with over-segmentation.

The data term and the boundary term in the voxel scale are designed in the same way as those in the traditional graph cut method [1]. We applied the watershed method to generate the over-segmentation [14] to obtain the regional scale of the image. Two regions are defined as neighboring if the Euclidean distance between the centroids of the two regions is within 10 mm. Each region in the over-segmentation defines a supervoxel. The data term is computed based on the standard deviation of voxel intensities in each supervoxel, which serves as a rough texture descriptor about how homogeneous each supervoxel is. Suppose the mean standard deviation of all the object seed voxels is ${\overline{\delta }}_{ob}$, then the $D_p\left(f_p=1\right)\propto 1-\text{exp}\left(-\Vert {\delta }_p-{\overline{\delta }}_{ob}{\Vert }^2/{\sigma }_{\Delta }^2\right)$, where δ_p is the standard deviation of supervoxel p and σ_Δ is a parameter controlling the deviation of object intensities from ${\overline{\delta }}_{ob}$. The boundary term is defined, as follows. If f_p = f_q, then V_p,q(f_p, f_q) = 0. If f_p ≠ f_q, then $V_{p,q}\left(f_p,f_q\right)\propto \text{exp}\left(\Vert D_p\left(f_p=1\right)-D_q\left(f_q=1\right)\right){\Vert }^2/{\sigma }_R^2$. In our experiment, we use σ_Δ = 50 and σ_R = 1000.

3.4. Results

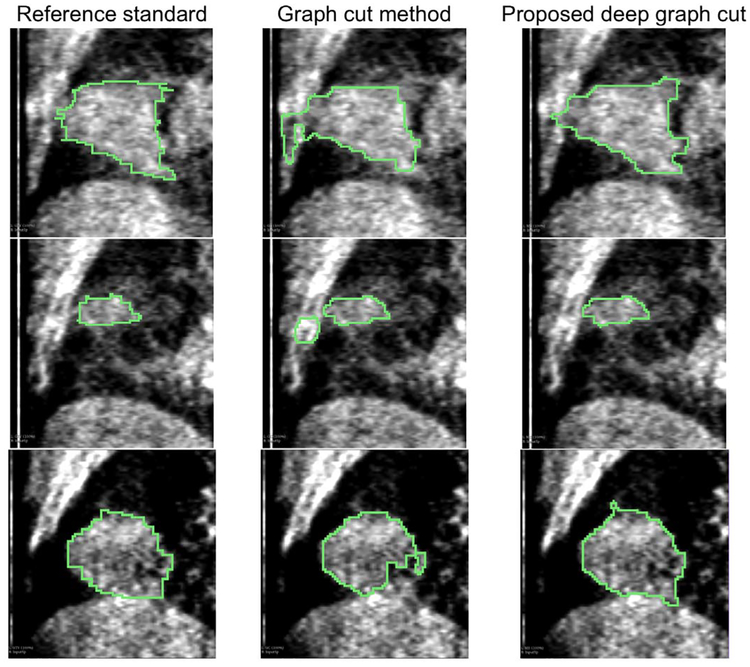
The quantitative comparisons between the proposed multiscale deep graph-cut segmentation method (dGC) and the traditional graph-cut method (GC) on the validation volumes is summarized in Table 1. For the entire validation data, the proposed dGC method produced significantly higher DSC (p < 0.01) and lower ASSD (p < 0.01), compared to the segmentation results of the traditional GC method. Illustrative results of segmentations from the proposed dGC and the traditional GC methods are shown in Fig. 2. Due to the weak boundary and similar intensity profiles of the tumor and the surrounding healthy tissues, the traditional GC method produced unsatisfying segmentation. By using the multi-scale information with the proposed dGC method, we can differentiate the tumor from the surrounding tissues, as shown in the first two rows of Fig.2.

Table 1.

Average DSC and ASSD of the proposed dGC method and the graph-cut method (GC)

	traditional GC	proposed dGC
DSC	0.76 ± 0.12	0.84 ± 0.06
ASSD (mm)	4.42 ± 3.04	2.32 ± 2.34

Fig. 2.

Illustrative segmentation results. The proposed deep graph cut method enables to use multiple scale levels of image features, thus avoiding segmentation leakage.

4. CONCLUSION

We propose a novel segmentation method in which the hierarchical image features in different scale levels can be modeled in a deep graph consisting of multiple interacting subgraphs, and the segmentation is performed with a single minimum s-t cut computation. The performance of the proposed method is assessed on 38 MVCBCT datasets to segment primary lung tumors, which is superior to the traditional graph cut method.