Incorporating Explicit Water Molecules and Ligand Conformation Stability in Machine-Learning Scoring Functions

Abstract

Structure-based drug design is critically dependent on accuracy of molecular docking scoring functions, and there is of significant interest to advance scoring functions with machine learning approaches. In this work, by judiciously expanding the training set, exploring new features related to explicit mediating water molecules as well as ligand conformation stability, and applying extreme gradient boosting (XGBoost) with Δ-Vina parametrization, we have improved robustness and applicability of machine-learning scoring functions. The new scoring function Δ_vinaXGB can not only perform consistently among the top compared to classical scoring functions for the CASF-2016 benchmark but also achieves significantly better prediction accuracy in different types of structures that mimic real docking applications.

Graphical Abstract

1. Introduction

Molecular docking is a widely used computational approach that aims to predict binding pose and affinity for a small molecule to interact with a target protein and is playing an increasingly important role in structure-based drug design.^1–3 A most critical component of molecular docking is its scoring function, and a robust scoring function should perform well across a variety of applications,^4–13 including scoring (to estimate the binding affinity between a protein and a ligand given their complex structure), ranking (to rank the known ligands for a certain target protein when precise ligand binding poses provided), docking (to determine binding site and binding mode of a ligand on a protein), screening (to screen virtual small-molecule libraries and identify bioactive lead compound for further drug development). Extensive retrospective and comparative studies^{5–9, 14–25} have clearly demonstrated that those widely used classical scoring functions, such as Autodock Vina (Vina)²⁶ and GlideScore,^27–29 perform quite well in docking and screening tasks, but their scoring power remains to be less satisfactory. Meanwhile, most efforts aiming to improve scoring power, such as the development of X-Score³⁰ and a variety of machine-learning based scoring functions,^31–47 lead to significant under-performance in docking and screening tasks compared to classical scoring functions.^{48, 49} Although one can attempt to develop task-specific scoring functions using machine learning. i. e. different machine-learning scoring functions for distinct docking tasks,^{50, 51} such strategies can easily lead to overfitting due to the data limitation.⁵² In principle, a robust protein-ligand scoring function should perform well for a variety of different applications. Thus, this remains a challenge for the scoring function development to not only improve scoring accuracy, but also enhance robustness and applicability.

In order to tackle this challenge, recently we have introduced a Δ-Vina machine learning approach,⁵³ in which machine learning is employed to parametrize corrections to the Vina scoring function.⁵⁴ By taking advantage of the excellent docking power of Vina and the strength of random forest (RF) in efficiently utilizing large training data and feature sets, our previously developed scoring function Δ_VinaRF₂₀⁵⁴ has improved scoring-docking-screening powers simultaneously and achieved superior performances in all power tests of CASF-2007,⁵ CASF-2013,^{6, 7} and CASF-2016⁹ benchmarks compared to classical scoring functions.

Here we have explored the Δ-Vina machine-learning strategy via eXreme Gradient Boosting (XGBoost)⁵⁵ in order to further enhance scoring accuracy, robustness and applicability of protein-ligand scoring functions. XGBoost is a scalable machine learning method for Gradient Boosting and has been demonstrated to achieve better performance than RF with much less computational cost.^{56, 57} Our main idea is to overcome two limitations which have not been addressed in the Δ_VinaRF₂₀ scoring function:

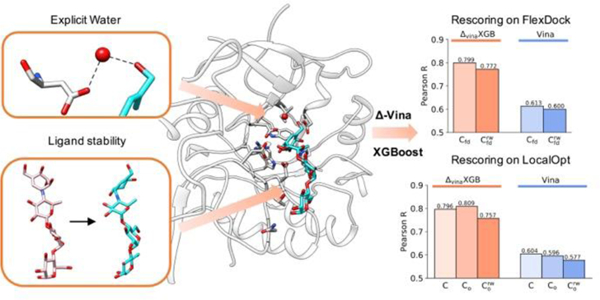
• Explicit water molecules. Receptor-bound water (also known as ordered water networks) molecules play critical roles in protein-ligand recognition. Previous studies have indicated that more than 85% protein-ligand crystal structures have at least one water molecule in ligand binding site,⁵⁸ and proper treatment of receptor-bound water molecules is beneficial for binding pose identification and binding affinity prediction.^59–74 However, both Vina and Δ_VinaRF₂₀ scoring functions were parametrized with a training set where all explicit water molecules were removed from protein-ligand complex structures, and up to now this is also the case for all other machine-learning scoring functions. In this work, in order to properly treat explicit water molecules in our Δ-Vina machine-learning, we have judiciously expanded our training set to include protein-ligand complex structures with receptor-bound water molecules and explored mediating water related features. Our newly developed scoring function, Δ_vinaXGB, has achieved superior and consistent performances in a series of tests using receptors with explicit water molecules in comparison with Vina and Δ_VinaRF₂₀, and hence it can take advantage of confident water predictions from water position analysis tools such as WaterMap^{73, 74} and WaterDock.^{62, 63}

• Ligand conformation stability. For a ligand molecule to adopt a complex-bound conformation, besides the change of intermolecular interactions and solvation, an internal free energy penalty may need to be paid, which originates from change of both ligand stability and flexibility. Previous studies have showed that the conformational energy changes of small molecules upon binding to target proteins can be in a range 0–25 kcal/mol⁷⁵ and taking the ligand conformational energies into account can significantly improve the docking performance of classic scoring functions.^{59, 76, 77} The Vina scoring function employs one ligand-dependent term, the number of rotors, to approximate the free energy change due to the ligand flexibility, but does not explicitly consider ligand conformational energy change from the global minimum of the free ligand to the docked conformation. To our best knowledge, ligand conformation stability has not been considered in machine-learning scoring functions. In this work, we have explored new features to represent ligand conformation stability and demonstrated their importance in improving the accuracy and robustness of our machine-learning scoring function.

In this article, we describe the computational details for the development of our newly released model Δ_vinaXGB, including data set preparation, feature generation, and algorithm application. Δ_vinaXGB can not only perform consistently among the top compared to classical scoring functions in CASF-2016 benchmark, but also achieves significantly better prediction accuracy with Vina local optimized and flexible docked poses that mimic real docking applications. The Δ_vinaXGB scoring function, code and data sets are freely available on the web at: http://www.nyu.edu/projects/yzhang/DeltaVina/

2. Methods

2.1. Data Preparation

Training Set.

As shown in Table 1, our training set is based on the PDBbind (v2016) database¹⁰ and CSAR data set,^{78, 79} and consists of three subsets: dry, water and decoy. For PDBbind (v2016) database, the high-quality PDBbind refined set (3<pK_d<12) as well as weak binding complexes (0.4<pK_d<3) selected from PDBbind general set (weak set) are used to construct our training set. To explore the effect of explicit water, we first analyzed the existence of receptor-bound water (RW) in these crystal structures. Water molecules in the crystal structure which are 2.0 to 3.5 Å away from protein polar atoms and possess theoretical binding affinities on receptor structure (Vina score < 0) are identified as RW. These requirements make sure that the RW are in proper positions and possess no clashes with protein. It should be mentioned that top-scored ligand poses usually adopt local minimum conformations, which might be slightly different from the conformation in crystal structure. Thus, we performed rigid local minimization of each selected complex using Vina local_search algorithm in the existence or absence of RW, which would better represent the real docking results. After removing complexes that possess distinct optimized ligand conformation compared with their native crystal structure (RMSD > 2 Å), dry subset and water subset have been built by 3264 optimized crystal structures $({\mathrm{C}}_{\mathrm{o}})$ and 3257 optimized crystal structures with RW $({\mathrm{C}}_{\mathrm{o}}^{\mathrm{r}\mathrm{w}})$, respectively. In addition, a total of 301 optimized protein-ligand complexes $({\mathrm{C}}_{\mathrm{o}})$ from the native pose of CSAR data set are also included in our dry set. The binding affinities of structures from water and dry are same as the experimental measured binding affinities (pK_d(exp)) of their corresponding crystal structures. In terms of decoy set, which serves as a negative control of binding pose and binding affinity in the whole training set, a total of 7584 structures with estimated binding affinities (pK_d(est)) are constructed using CSAR decoy set⁷⁹ and PDBbind refined set. CSAR decoys are flexible docking poses generated by Zhou’s group⁷⁹ using DOCK 4.0.1⁸⁰ based on crystal structures in CSAR-NRC HIQ benchmark release,⁷⁸ and it includes up to 500 decoys for each complex. To balance the number of decoys and native poses in our training set, we calculated Vina scores for all CSAR decoys and only selected up to 21 decoys ranking at 0%, 5%, 10%, 25%, …, 95%, 100% for each protein-ligand complex based on Vina score. PDBbind decoys are rigid docking poses generated by us using Vina based on crystal strictures from PDBbind refined set. It includes up to 5 failed docking poses, which are docking poses with RMSD lager than $2\mathrm{Å}$ and Vina scores lower than that of corresponding optimized crystal poses, for each of failed docking cases, where the top 1 docking pose is a failed docking pose. To determine the estimated binding affinity (pK_d(est)), RMSD between decoys and crystal pose was first calculated, and if the RMSD is no larger than 1 Å, which means the decoy is similar as real bound pose, pK_d(est) is assigned as the pK_d(exp) of its corresponding native pose. For decoys with RMSD larger than 1 Å, pK_d(Vina) was calculated and compared with the corresponding pK_d(exp). If the pK_d(Vina) is less than the pK_d(exp), the pK_d(est) of decoy is assigned as pK_d(Vina); otherwise, pK_d(est) is $p{\text{K}}_d(\exp )-0.5\times (RMSD-1)$, and the pK_d(est) is smaller when RMSD is larger. RMSD cutoff as 1 and 2 Å have been tested, and 1 Å can achieve better performance on Validation set. The complexes in the PDBbind (v2016) database released after 2015 as well as those overlap with the CASF (2013 and 2016) benchmark, which serve as a validation set and a test set, respectively, are excluded from our training set. With the addition of a receptor-bound water set and generation of a decoy set, our training set consists of 14406 complexes, which is significantly larger than the training set of Δ_VinaRF₂₀ (6658).

Table 1.

Data Sets.

name	subset	source	year	size	typea	BA	note
Training	dry	PDBbind (v2016) +CSAR	before 2015	3565	${\mathrm{C}}_{\mathrm{o}}$	pKd(exp)	no water
	water			3257	${\mathrm{C}}_{\mathrm{o}}^{\mathrm{r}\mathrm{w}}$		with receptor-bound waters
	decoy			7584		pKd(est)	CSAR decoys and PDBbind decoys
Validation	dry	PDBbind (v2016)	after 2015	315	${\mathrm{C}}_{\mathrm{o}}$	pKd(exp)	constructed by time-split and used to do early stop and model selection
	water			315	${\mathrm{C}}_{\mathrm{o}}^{\mathrm{r}\mathrm{w}}$
	crystal			316	C
LocalOpt	dry	CASF-2016		285	${\mathrm{C}}_{\mathrm{o}}$	pKd(exp)	constructed by Vina local minimization and used to evaluate scoring, ranking, screening power for optimized poses
	water			285	${\mathrm{C}}_{\mathrm{o}}^{\mathrm{r}\mathrm{w}}$
	decoy			1624500
FlexDock	dry	CASF-2016		5985	${\mathrm{C}}_{\mathrm{f}\mathrm{d}}$	pKd(exp)	constructed by Vina flexible docking and used to evaluate scoring and ranking power for docking poses
	water			5985	${\mathrm{C}}_{\mathrm{o}}^{\mathrm{r}\mathrm{w}}$

^aC: crystal structure, ${\mathrm{C}}_{\mathrm{o}}$: optimized crystal structure, ${\mathrm{C}}_{\mathrm{o}}^{\mathrm{r}\mathrm{w}}$: optimized crystal structure with receptor-bound water, ${\mathrm{C}}_{\mathrm{f}\mathrm{d}}$: docking poses, ${\mathrm{C}}_{\mathrm{f}\mathrm{d}}^{\mathrm{r}\mathrm{w}}$: docking poses with receptor-bound water.

Validation Set.

The validation set is constructed using structures from PDBbind (v2016) refined set and weak set that are released after 2015, which includes 316 complexes with three different structure types: C, ${\mathrm{C}}_{\mathrm{o}}$, and ${\mathrm{C}}_{\mathrm{o}}^{\mathrm{r}\mathrm{w}}$. The reasons to build the time-split holdout validation set are (1) conducting the early stopping in model training to avoid the overfitting of XGBoost on training set; (2) selecting a model that can perform well on different structure types; (3) mimicking the potential lead-compound discovery process in docking-based drug design.

Test Set.

CASF-2016 benchmark⁹ has been used to evaluate the performances of our scoring function. CASF-2016 defines four different powers (scoring power, ranking power, docking power, and screening power) and provides corresponding test sets. To further test the postdocking rescoring performance and account for the explicit water effect, two subsets, noted as LocalOpt and FlexDock (Table 1), have been generated to mimic the poses needed to be rescored in real application. In the basis of crystal structures and computer-generated cross-docking poses from CASF-2016, optimized poses of LocalOpt are obtained by Vina local optimization with different environments: without water molecules and with explicit RW. Similarly, the FlexDock set is composed of docking poses produced by Vina flexible docking using crystal structures from CASF-2016. Each complex has one crystal structure and 20 docking poses from docking situations without $({\mathrm{C}}_{\mathrm{f}\mathrm{d}})$ or with explicit RW $({\mathrm{C}}_{\mathrm{f}\mathrm{d}}^{\mathrm{r}\mathrm{w}})$. Symmetry corrected RMSD between docking pose and crystal structure is calculated using Huangarian algorithm from Dock6.^81–83

All structures from PDBbind(v2016) database are prepared using our data preparation schedule (Figure S1). The pK_a has been determined via PROPKA 3.1^{84, 85} in order to predict the protonation state of protein titratable residues.

2.2. Feature Generation

All features employed in our development of score function are summarized in Table S1. Same as Δ_VinaRF₂₀, 58 features from Vina source code are calculated, including protein-ligand interaction terms and a set of ligand property counts.⁸⁶ A total of 30 buried solvent accessible surface area (bSASA) features are computed using three different structures (complex, ligand and protein), and 10 bSASA features for each structure consist of one total bSASA term and nine pharmacophore-based bSASA terms where pharmacophore types are characterized based on SYBYL⁸⁷ atom types and DOCK⁸⁸ neighboring atoms. MSMS⁸⁹ program is used to calculate the atomic SASAs with a $1.0\hspace{0.17em}\mathrm{Å}$ probe radius and the bSASA = SASA_unbound − SASA_complex.

To explore the water effect, certain RW that mediate protein-ligand interactions are considered as bridging water (BW) molecules according to the following criteria: (1) contact with both ligand and protein, the distances between polar atoms in ligand and BW are between 2.0 and $3.5\hspace{0.17em}\mathrm{Å}$; (2) potential to form hydrogen bond networks, the angles between polar atoms in ligand, BW, and polar atoms in protein are no less than 60 degrees; (3) favorable for ligand binding, Vina score for BW are less than zero when using ligand as receptor. Finally, three BW features are calculated for the structures with RW, including the number of BW (N_BW), the Vina score between BW and protein (Vina (P, BW)), and the Vina score between BW and ligand (Vina(L, BW)).

On the other hand, our feature set contains two features related to ligand stability in order to represent the ligand conformation change during the binding process. For each ligand, a maximum of 1000 conformers were generated using RDKit,⁹⁰ and redundant conformers $(\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{D}<0.5\mathrm{Å})$ were removed on the basis of clustering analysis. The docked or crystal ligand conformer as well as newly generated conformers are minimized using MMFF^{91, 92} force filed with implicit water as solvent. The energy difference and RMSD between the conformer with lowest energy and the locally minimized docked/crystal conformer are designated as the feature ΔE_confs and RMSD_confs, which is assumed to reflect the stability of each docked/crystal ligand.

Furthermore, N_ion, which is the number of binding site ions (distances between ions and polar atoms of ligand are less than $3\mathrm{Å}$) is also included in our feature set.

2.3. Δ-Vina XGBoost Strategy

The Δ-Vina XGBoost strategy aims to correct the difference between Vina score and experimental binding affinity by XGBoost. The original Vina score with unit kcal/mol was converted to pK_d using following formula: pK_d(vina) = −0.73349E(Vina). Thus, the formula of our scoring function can be shown as the equation below:

$$\mathrm{p}{\mathrm{K}}_{\mathrm{d}}({\mathrm{\Delta }}_{\mathrm{v}\mathrm{i}\mathrm{n}\mathrm{a}}\mathrm{X}\mathrm{G}\mathrm{B})=\mathrm{p}{\mathrm{K}}_{\mathrm{d}}(\mathrm{V}\mathrm{i}\mathrm{n}\mathrm{a})+\mathrm{\Delta }\mathrm{p}{\mathrm{K}}_{\mathrm{d}}(\mathrm{X}\mathrm{G}\mathrm{B}\mathrm{o}\mathrm{o}\mathrm{s}\mathrm{t}).$$

Given a molecule i from the training set with an input feature vector $x^{(i)}=(x_1^{(i)},x_2^{(i)},\dots ,x_p^{(i)})$, a XGBoost model uses K additive trees to predict the output ${\text{y}}^{(i)}$ and each tree corrects the difference between target and predictions made by all of the previous trees. Τhus

$${\widehat{y}}^{(i)}=\varphi (x^{(i)})={\sum }_{k=1}^K\lambda f_k(x^{(i)}),f_{(k)}\in \mathcal{F}.$$

Here, $\mathcal{F}$ is the space of all possible trees and λ is a shrinkage parameter, which used to reduce the overfitting and make the sequential training meaningful. The growing of each $f_k$ is rely on a regularized objective as follows:

$$\mathcal{L}(f_k)=l({\widehat{y}}^{(i)},y^{(i)})+\Omega (f_k),\Omega (f_k)=\gamma T+\frac{1}{2}\lambda {\Vert \omega \Vert }^2.$$

where l is the loss function to compute the difference between the prediction ${\widehat{y}}^{(i)}$ and target $y^{(i)}$, and the second regularized term Ω controls the complexity of the model via the number of leaves $(T)$ in $f_k$ and the scores on leaves $(\omega )$. The feature, which can minimize this objective, will be chosen to split the terminal node of the tree into two child nodes, and only a random subset of features can be considered in each tree development to avoid the high correlation of trees. With the help of validation set, the early stopping with the patience of 50 training steps has been applied.

In our development of Δ_vinaXGB, the output y for our training set is the ΔpK_d and $\text{p}=94$ for the input feature vector x. The XGBoost package (version 0.80)⁵⁵ in Python 3 is used to build the XGBoost model. The hyper-parameters utilized in current study are n_estimators (number of trees) = 500, learning_rate (shrinkage parameter) = 0.05, subsample (subsample ratio of the training instance when constructing each tree) = 0.8, colsample_bytree (subsample ratio of features when constructing each tree) = 0.8, min_child_weight (minimum sum of instance weight needed in a tree leaf node) = 6, max_depth (maximum depth of a tree) = 10, and objective (regression type) = “reg:linear”. Because of the high variance of each XGBoost model, the final prediction of our Δ_vinaXGB model is the average of ten XGBoost models initialized with different random seed.

2.4. Evaluation Methods:

The comparative assessment of scoring functions (CASF) benchmark has been designed and updated by Wang’s group^{5–7, 9} and they defined four different powers (scoring power, ranking power, docking power and screening power) to evaluate the performance of scoring function in the CASF-2016, which is the latest version of CASF benchmark. Scoring power is aimed to evaluate the linear correlation between predicted binding affinity and experimental measured binding affinity by the classic Pearson’s correlation coefficient (R) between binding affinity and experimental measured binding affinity and the standard deviation (SD) in regression. Docking power is used to evaluate the ability of a scoring function to identify the native binding pose among computer-generated decoys and it calculates the success rate based on symmetry-corrected RMSDs between native binding pose and decoys. The top 1 docking success rate is computed as the percentage of complexes that have top-scored poses similar with native poses $(\text{RMSD}<2\mathrm{\AA })$ among all testing complexes. Ranking power is to check the ability of a scoring function to rank the activities of known ligands correctly using their predicted binding affinity. The CASF-2016 benchmark includes 57 targets and 5 known active ligands for each target. With the known active ligands for each target, ranking performances including Spearman’s rank correlation coefficient $(\rho )$, Kendall’s rank correlation coefficient $(\tau )$, and the predictive index (PI) are computed, and the overall performances for all targets (average) can indicate the ranking ability of a scoring function. Screening power is aimed to assess the ability of a scoring function to identify true binder for a given target among a pool of random molecules. The CASF-2016 provides true binders for each target and in screening power test, all ligands were cross docked to all target proteins and 100 docking poses were selected for each protein-ligand complex. Two indicators including enhancement factor and success rate are used for evaluating screening power. The enhancement factor is computed as flowing:

$$E{F}_{\alpha }=\frac{NT{B}_{\alpha }}{NT{B}_{total}\times \alpha }$$

Here, $NT{B}_{\alpha }$ is the number of true binders in top $\alpha$ ranked candidates based on predicted binding scores. $NT{B}_{total}$ is the total number of true binders for the given target protein. Meanwhile, success rate at Top1% level is calculated as the percentage of tightest true binders in 1% of top-ranked molecules.

Besides standard test sets provided by CASF-2016 benchmark, we also evaluated the postdocking rescoring performance using two additional test sets: LocalOpt and FlexDock, as shown in Table 1. Scoring power, ranking power, and screening power defined by CASF-2016 have been reevaluated in LocalOpt for Δ_vinaXGB, Δ_VinaRF₂₀, and Vina to estimate the scoring performance in local optimized poses with different water environments. Similarly, scoring correlation and ranking correlation were checked for best-scored pose from FlexDock for Δ_vinaXGB, Δ_VinaRF₂₀, and Vina to show the scoring function’s performance on real docking poses.

3. Results and Discussion

Based on a judiciously enlarged training set which consists of 14406 protein-ligand complex structures and an enlarged feature set including new features accounting for explicit water effect and ligand stability, a new scoring function Δ_vinaXGB was developed by incorporating XGBoost to Δ-Vina machine learning approach.

3.1. CASF-2016 Benchmark

The performances of Δ_vinaXGB were tested on CASF-2016 benchmark to evaluate its scoring power, ranking power, docking power as well as screening power. In the original CASF-2016 paper,⁹ Δ_vinaRF₂₀ has been evaluated and their results show that Δ_vinaRF₂₀ can achieve superior performances on all tasks. However, the training set of the published Δ_vinaRF₂₀ that they tested consists of 140 molecules that have been included in the test set of CASF-2016. To avoid the bias due to the overlap between training set and test set, we retrained the Δ_vinaRF₂₀ using training set excluding CASF-2016 structures and checked the new Δ_vinaRF₂₀ performance on CASF-2016. All of the performances of Δ_vinaRF₂₀ shown here are from the retrained Δ_vinaRF₂₀.

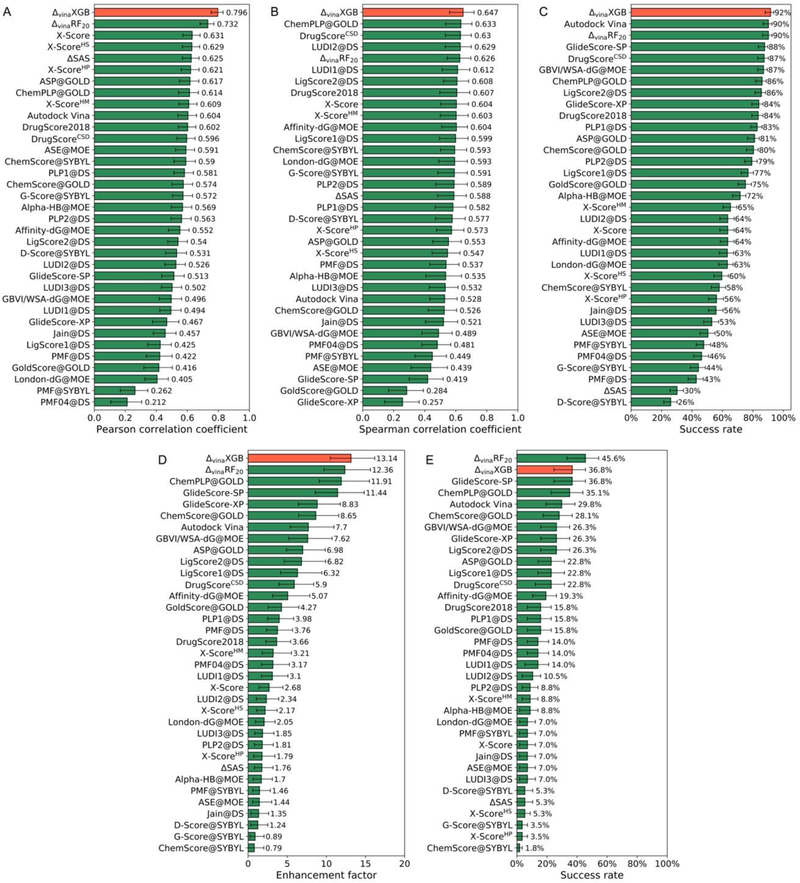
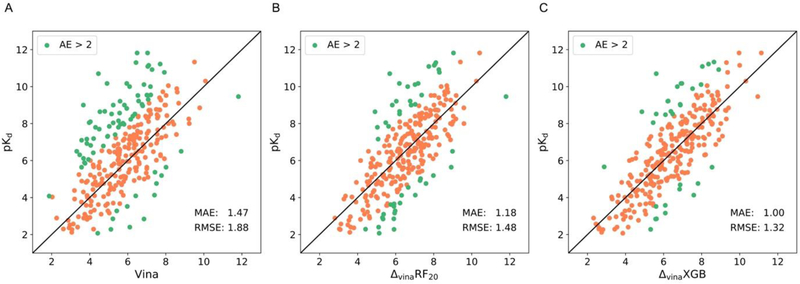
As shown in Figure 1, Δ_vinaXGB achieves Top 1 performances on scoring power, ranking power, docking power and the enhancement factor of screening power tasks. For the scoring power, the Pearson’s correlation coefficient (R) and standard deviation (SD) of Δ_vinaXGB are 0.796 and 1.32, which are both better than Δ_vinaRF₂₀ and baseline model Vina, as shown in Figure 1A. Figure 2 also indicates that Δ_vinaXGB has smallest number of cases with large errors (absolute error > 2). In ranking power, three quantitative indicators including Spearman’s rank correlation coefficient $(\rho )$, Kendall’s rank correlation coefficient $(\tau )$, and the predictive index (PI) are used to evaluate scoring functions. Similar as scoring power, Δ_vinaXGB achieves highest values on $\rho$, $\tau$, and PI, which are 0.647, 0.568 and 0.674. In docking power, the success rate of best-scored pose with crystal structures has been shown in Figure 1C, and Δ_vinaXGB’s performance is also ranked as top 1. Enhancement factor and success rate at top 1% level are calculated for screening power. As shown in Figure 1D, E, Δ_vinaXGB achieves highest enhancement factor (13.14) and second highest success rate (36.8%, same as GlideScore-SP). Best scoring function in success rate of screening power is Δ_vinaRF₂₀ at top 1% level, and Δ_vinaXGB can achieve better performance (Δ_vinaXGB: 61.4% vs. Δ_vinaRF₂₀: 59.6%) when computing the success rate at the top 10% level.

Figure 1.

Performances of scoring functions on CASF-2016 benchmark. (A) Scoring power measured by Pearson correlation coefficient, (B) ranking power in terms of spearman correlation coefficient, (C) docking power measured by success rate for best-scored poses with crystal structures, and screening power measured by (D) enhancement factor and (E) success rate at top 1% level. All scoring functions are ranked in a descending order. Δ_vinaXGB’s performances are colored as red and other scoring functions’ performances are colored as green.

Figure 2.

Scatter plots between experimental pK_d and different scoring functions: (A) Vina predicted scores, (B) Δ_vinaRF₂₀ predicted scores, and (C) Δ_vinaXGB predicted scores. The absolute error in pK_d larger than 2 are colored as green, and in other cases are colored as orange. Mean absolute errors and root-mean-square errors between predicted scores and experimental pK_d for three scoring functions have also been shown.

Based on crystal structures provided by CASF-2016, we also analyzed the performance of Δ_vinaXGB and Vina with consideration of ligand stability and flexibility. As shown in Table 2 and Figure S3, Vina performs well for relatively rigid molecules but deteriorates significantly for highly flexible molecules. On the other hand, the performance of Δ_vinaXGB is more stable which demonstrates its robustness. Furthermore, RMSD_confs and ΔE_confs, which are two features added to describe ligand stability, are ranked as top 1 and 2 among 94 features in feature importance analysis result (Figure S2). It should be noted that the accuracy of two ligand stability features is dependent on ligand conformation generation and ligand energy calculation, which may encounter difficulties for ligands with large number of rotors or large heterorings, as illustrated in Table S2, and can be improved by using deep learning methods in energy calculation.⁹³

Table 2.

Scoring Performance of Δ_vinaXGB and Vina on Different Ligand Stability and Flexibility Subsets of 285 Crystal Structures from CASF-2016.

subset	ligand stabilitya	ligand flexibilitya	number	Vina	XGB
High	$\left|\mathrm{\Delta }{\mathrm{E}}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{f}\mathrm{s}}\right|\ge 1.5 \text{kcal}/\mathrm{m}\mathrm{o}\mathrm{l}$ or $\mathrm{R}\mathrm{M}\mathrm{S}{\mathrm{D}}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{f}\mathrm{s}}\ge 2\mathrm{\AA }$	Nrot > 5	86	0.498	0.719
Medium	Structures are not in low and high subset		106	0.541	0.784
Low	$\left|\mathrm{\Delta }{\mathrm{E}}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{f}\mathrm{s}}\right|<0.5 \text{kcal}/\mathrm{m}\mathrm{o}\mathrm{l}$ and $\mathrm{R}\mathrm{M}\mathrm{S}{\mathrm{D}}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{f}\mathrm{s}}<2\mathrm{\AA }$	${\mathrm{N}}_{\mathrm{r}\mathrm{o}\mathrm{t}}\le 5$	93	0.708	0.816

^aAll complexes in each subset should satisfy both ligand stability and flexibility requirements.

3.2. Rescoring Performance

Δ_vinaXGB is mainly developed for rescoring, which needs docked poses as input. Vina is a widely used docking software and its good docking power has been validated in CASF benchmarks. To evaluate the performance of Δ_vinaXGB as a rescoring tool for complex structures that mimic real docking applications, we employed Vina local optimization and flexible docking to generate potential docked ligand poses. Here, both docked poses with and without receptor-bound water molecules are considered, and results are compared with both Vina and Δ_vinaRF_20.

3.2.1. Local Optimized Poses (LocalOpt)

LocalOpt data set has been built by Vina rigid local optimization based on crystal structures and computer-generated decoys from CASF-2016. Scoring power, ranking power, and screening power defined by CASF-2016 have been re-evaluated on LocalOpt for Δ_vinaXGB, Δ_vinaRF₂₀ and Vina. In order to accounting for explicit water effect, we also considered protein-ligand complexes which include receptor-bound water molecules.

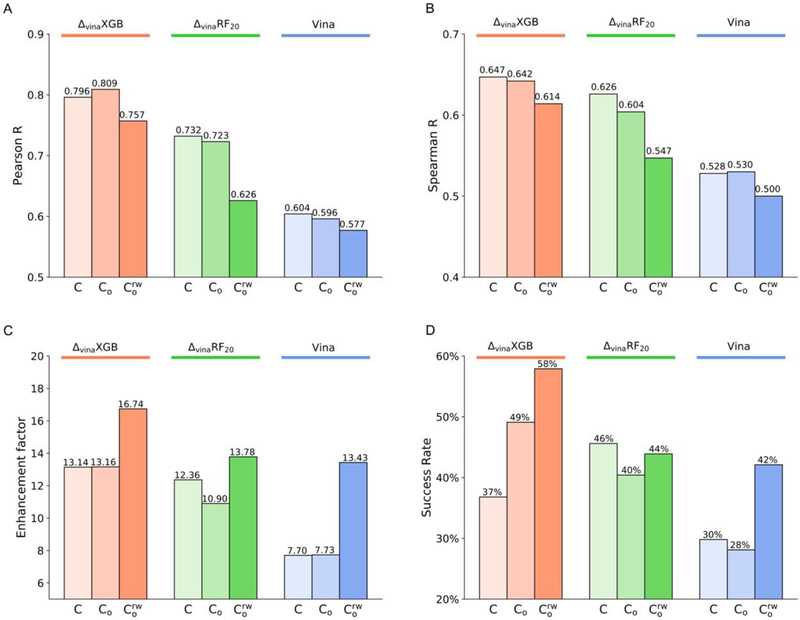
Figure 3A,B illustrates the scoring and ranking performance on LocalOpt (${\text{C}}_{\text{o}}$ and ${\text{C}}_{\text{o}}^{\text{rw}}$), together with performance on crystal structures without local optimization $(\text{C})$. For locally optimized protein-ligand structures, Δ_vinaXGB’s performance has been improved from 0.796 to 0.809 in Pearson’s R. In Spearman’s R, the performances of Δ_vinaXGB on C (0.647) and ${\text{C}}_{\text{o}}(0.642)$ are similar. When keeping explicit water molecules, Δ_vinaXGB can achieve 0.757 scoring correlation and 0.614 ranking correlation, which are close to the performances of crystal structures. However, Δ_vinaRF₂₀’s performance decreases significantly when it comes to locally optimized poses, especially for structures with water molecules, where Pearson’s R decreases from 0.732 to 0.626 and Spearman’s R decreases from 0.626 to 0.547 for ${\text{C}}_{\text{o}}^{\text{rw}}$. Both Δ_vinaXGB and Δ_vinaRF₂₀ have improved over Vina, whose performance is relatively stable on different types of structures.

Figure 3.

Performances of Δ_vinaXGB, Δ_vinaRF₂₀ and Vina on LocalOpt. (A) Pearson correlation coefficient for scoring power. (B) Spearman correlation coefficient for ranking power. (C) Enhancement factor and (D) success rate for screening power at top 1% level. Performances of Δ_vinaXGB, Δ_vinaRF₂₀, and Vina are colored as orange, green, and blue. For each scoring function, performance on crystal structures (C, shown as reference), local optimized poses $({\mathrm{C}}_{\mathrm{o}})$, and local optimized poses with receptor-bound water molecules $({\mathrm{C}}_{\mathrm{o}}^{\mathrm{r}\mathrm{w}})$ are displayed from left to right with gradually changed color.

In terms of screening power, local optimizations for computer generated cross-docking poses have been conducted with/without receptor water molecules. Similar as scoring power, Δ_vinaXGB achieves much higher enhancement factor and success rate at top 1% level after local optimization compared with Δ_vinaRF₂₀ and Vina, as shown in Figure 3C,D. One interesting thing is that all scoring functions reach the best performance on ${\text{C}}_{\text{o}}^{\text{rw}}$, except success rate of Δ_vinaRF₂₀, which is slightly worse than performance on C. Here Δ_vinaXGB achieves highest enhancement factor as 16.74 and success rate as 58%. These results suggest the importance of considering receptor-bound water molecules in virtual screening.

3.2.2. Flexible Docking Poses (FlexDock)

To further test rescoring performances on real docking poses, we conducted flexible docking using Vina for CASF-2016 test set, and 20 poses were generated for each complex. Similar as in LocalOpt, we also considered the docking environment with receptor-bound water molecules. In the evaluation process, all docking poses as well as crystal structure poses are rescored by Δ_vinaRF₂₀ and Δ_vinaXGB.

The flexible docking success rates of best-scored pose in different docking situations and RMSD cutoff have been illustrated in Figure S4. Only the best-scored pose with RMSD less than RMSD cutoff is considered as a successful docking case. It is clear that Vina always achieves best docking performance among three scoring functions when RMSD cutoff is $2\mathrm{\AA }$; however, the performances of three scoring functions are very close and the largest difference is only 2% in dry docking and 3% in docking with receptor-bound water molecules. All scoring function’s performances have been improved significantly after keeping RW, which demonstrates the importance of explicit water molecules in molecular docking. In addition, Δ_vinaXGB can achieve better docking performance than Vina and Δ_vinaRF₂₀ when RMSD cutoff is less than $0.6\hspace{0.17em}\mathrm{\AA }$.

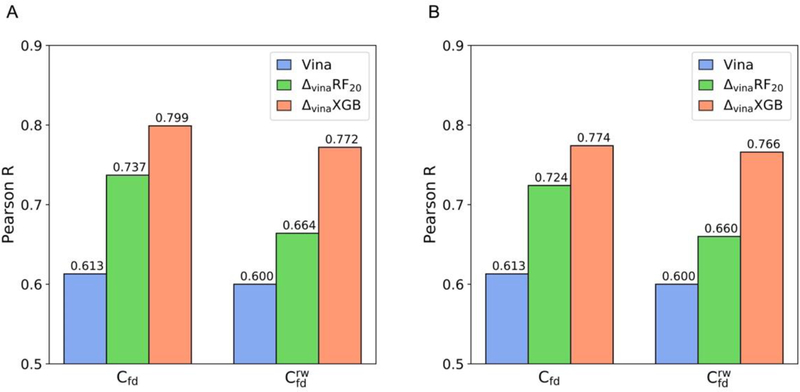
To evaluate the rescoring performance of Δ_vinaRF₂₀ and Δ_vinaXGB on flexible docking poses, we ranked docking poses based on predicted score and calculated the scoring and ranking correlation coefficient for best-scored poses. Figure 4A shows the scoring correlation, and both Δ_vinaRF₂₀ and Δ_vinaXGB improve the initial Vina performance significantly in dry and water docking situations. Δ_vinaXGB achieves the best performances, which are 0. 799 on ${\mathrm{mathvariant="normal"C}}_{\mathrm{f}\mathrm{d}}$ and 0.772 on ${\mathrm{C}}_{\mathrm{f}\mathrm{d}}^{\mathrm{r}\mathrm{w}}$ in Pearson’s R, and are close to the scoring performance on crystal structures. Rescoring using only Vina best-scored pose for each structure has also been conducted. Different from choosing best-scored poses from 20 poses generated by Vina, selecting Vina best-scored pose to rescore is an efficient rescoring method and is more convenient for Vina users. As expected, the performances of scoring have been improved a lot by Δ_vinaXGB on ${\mathrm{C}}_{\mathrm{f}\mathrm{d}}$ and ${\mathrm{C}}_{\mathrm{f}\mathrm{d}}^{\mathrm{r}\mathrm{w}}$ (Figure 4(B)). Similar performance improvements by Δ_vinaXGB have also been found in ranking correlations (Figure S5). These good performances indicate the potential application of Δ_vinaXGB in Vina-based rescoring, where using Vina to generate docking poses, and rescoring all docking poses or even top 1 pose to get more accurate binding affinity prediction using Δ_vinaXGB. Based on the script we provide, Vina docking poses can be directly used as input structures to be rescored using Δ_vinaXGB.

Figure 4.

Scoring performances of Δ_vinaXGB, Δ_vinaRF₂₀, and Vina on FlexDock. Pearson correlation coefficient for (A) best-scored docking poses and (B) Vina best-scored docking pose in dry environment $({\mathrm{C}}_{\mathrm{f}\mathrm{d}})$ and water environment $({\mathrm{C}}_{\mathrm{f}\mathrm{d}}^{\mathrm{r}\mathrm{w}})$. Here, best-scored poses are determined based on predicted scores. Performances of Vina, Δ_vinaRF₂₀, and Δ_vinaXGB are colored as blue, green, and orange.

4. Conclusion

Explicit water molecules and ligand conformation stability are two issues that have not been considered in our previous scoring function Δ_vinaRF₂₀. In this work, we have further explored the Δ-Vina machine-learning strategy via XGBoost and addressed these two limitations by judiciously expanding our training set with receptor-bound water molecules and enlarging the feature set with bridging water and ligand stability features. Our newly developed scoring function Δ_vinaXGB achieves superior performance compared with Δ_vinaRF₂₀ and Vina in two different level evaluations, including four power tests in CASF-2016 benchmark and rescoring performance for Vina optimized poses and flexible docking poses with or without explicit water molecules. This work suggests that Δ_vinaXGB significantly improved both robustness and applicability of machine-learning scoring functions and could serve as an effective rescoring tool in structure-based inhibitor design.

Supplementary Material

SI

Figure S1: Data preparation schedule for PDBbind(v2016) database.

Figure S2: Feature importance.

Figure S3: MAE of Vina and Δ_vinaXGB for structures with different number of rotors.

Figure S4: Success rates of best-scored pose in different RMSD values.

Figure S5. Ranking performances of Δ_vinaXGB, Δ_vinaRF₂₀ and Vina on FlexDock

Table S1: Feature set of Δ_vinaXGB.

Table S2: Failed conformation generation cases in CASF-2016.