Abstract
While randomized clinical trials (RCTs) should provide the basis for evidence‐based medicine, as currently designed and analyzed, they often mislead clinical decision‐making. Comparative effectiveness evaluation of two treatments [Treatment 1 (T1) versus Treatment 2 (T2)] should not be determined by the statistical effect of treatments on individual measures of outcome (benefits and/or harms), but rather on the clinical effects of treatments on individual patients who can experience both benefits and harms. Such strategies for evaluation require both methods for statistical assessment of the rates of co‐occurrence of such benefits and harms, and clinical assessment of their combined clinical impact on patients. The strategies discussed here are possible solutions to this dilemma. It is crucial to develop successful strategies to assess the effects of treatments on individual patients. Copyright © 2011 John Wiley & Sons, Ltd.
Keywords: personalized medicine, RCT, multiple outcomes, integrative outcome, harm, benefit
Introduction
Randomized clinical trials (RCTs) should provide the basis for evidence‐based medicine. However, as currently designed and analyzed, they often mislead. Concerted efforts have occurred on multiple fronts to improve this situation. For example, considerable discussion has centred around the appropriate place and relative value of efficacy (explanatory) versus effectiveness (pragmatic or practical) trials (March et al., 2005). Registration of RCTs prior to their execution has been recommended, and in some cases, required for publication of papers resulting from RCTs (DeAngelis et al., 2005; Lange and MacIntyre, 1985), to discourage the reporting of post hoc findings in place of the results of tests of a priori hypotheses. The CONSORT guidelines (Altman et al., 2001; Rennie, 1996; Schulz et al., 2010), as well as the modifications in the American Psychological Association (APA) Publication Manual (Wilkinson and The Task Force on Statistical Inference, 1999), represent key efforts to remind clinical researchers of the importance of correctly and explicitly implementing RCT methodological criteria. The fact that what results from a RCT reflects what happens to the typical member of the population sampled in the RCT, not to each individual member of that population, has been given additional emphasis, both with the growing literature about moderators of treatment (Kraemer et al, 2006; Kraemer et al., 2008), and with increased current emphasis on personalized medicine (Garber and Tunis, 2009; Lesko, 2007; Richmond, 2008). In addition, the limitations of “statistical significance” (Borenstein, 1998; Cohen, 1995; Dar et al., 1994; Hunter, 1997; Nickerson, 2000; Shrout, 1997) and its common misinterpretations, have been given wide attention, and a major effort made to encourage reporting of clinically interpretable effect sizes and their confidence intervals either in addition to, or in place of, “p‐values” indicating statistical significance.
The success of any and all these efforts, however, depends crucially on the choice of outcome measures reported from RCTs. We recently proposed that a major problem is the separate assessment of outcome in RCTs on measures of harm and measures of benefit as they affect the typical patient in a trial rather than the simultaneous assessment of benefit and harm as it accrues to individual patients in that trial (Kraemer and Frank, 2010). How to do that is the focus of this report.
In what follows, we first review the various effect sizes available for interpretation of RCT results, information needed to understand the problems with outcome measures. We then discuss the problems with both a single primary outcome and with multiple outcomes considered separately, the current accepted strategies for RCTs. After an illustration with an actual RCT to clarify the problems with the current approaches, and to demonstrate the direction in which to seek solutions, we propose several strategies to facilitate achieving the goal.
Effect sizes
Why an effect size?
As hypothesis‐testing is typically done in RCTs, a “statistically significant” result usually means only that the sample size was large enough to detect a non‐random effect. Determining whether or not that effect is of any clinical significance, requires that a clinically interpretable effect size be reported, one that can aid considerations of clinical significance, with its confidence interval as well as its “p‐value” (Kline, 2005; Kraemer and Kupfer, 2006; McGough and Faraone, 2009). Reporting such effect sizes along with the usual “p‐values” is urged both in CONSORT guidelines (Rennie, 1996; Schulz et al., 2010) and in the Publication Manual of the APA (APA, 2001), as well as by many reviewers of papers submitted for publication and by editors of journals considering those papers.
Which effect sizes are best to use in RCTs, and how to interpret the magnitude of whatever effect size is reported, remain open and contentious questions. There are many choices for an effect size comparing two treatments [Treatment 1 (T1) versus Treatment 2 (T2)], but we recommend three mathematically equivalent ones.
Area under the receiver operating characteristics (ROC) curve (AUC) is the probability that a patient in the T1 group has a response that is clinically preferable to that of a patient in the T2 group, with ties broken by a toss of a fair coin (Acion et al., 2006; Grissom, 1994; Kraemer and Kupfer, 2006; McGraw and Wong, 1992) symbolically: AUC = Prob(T1 > T2) + 0.5Prob(T1 = T2), Where “>” is here read as “clinically preferable to” and “=” as “clinically equivalent to”. AUC ranges from zero to one, with AUC = 1/2 the null value.
Success Rate Difference (SRD) (Hsu, 2004; Kraemer and Kupfer, 2006) is defined as: SRD = Prob(T1 > T2) – Prob(T1 < T2), a more convenient rescaling of AUC: SRD = 2AUC – 1. SRD ranges from −1 to +1 with SRD = 0 the null value. For a binary outcome measure (success/failure), SRD is the difference between the rates of success between T1 and T2: p 1 – p 2 (or the negative difference between the failure rates).
Finally, Number Needed to Treat (NNT) equals 1/SRD (Altman, 1998; Altman and Andersen, 1999; Kraemer and Kupfer, 2006; Wen et al., 2005). A patient is counted as a “success” if s/he has a clinically preferable response to a randomly selected patient in the other treatment group. Then NNT is the number of patients one would have to treat with T1 to find one more “success” than if the same number had been treated with T2. A negative NNT indicates the number of patients one would have to treat with T2 to find one more “success” than if the same number had been treated with T1. NNT = 1 (−1) means that every patient treated with T1 (T2) has a clinically preferable response to every patient treated with T2 (T1). NNT is never between +1 and −1, and the larger the magnitude of NNT, the more clinically equivalent the two treatments. The scale on which NNT is measured is a peculiar “wrap‐around” scale with the most extreme difference between +1 and −1, and ± infinity meaning the same thing: a random difference between T1 and T2. With its “wrap‐around” scale, NNT is inconvenient to use in computations (Altman, 1998). However, NNT, expressed in terms of the number of patients, rather than probability points, is typically easier for medical consumers to interpret.
Generally, AUC is easier to calculate, SRD has a more interpretable scale, and NNT is more meaningful to medical consumers, but a statement about any one of these three is easily translated to any other. What is unique about these effect sizes is that (unlike more commonly used Cohen's d or odds ratio) they are explicitly designed to describe the clinical impact on patients.
Why not Cohen's d for ordinal outcomes?
Cohen's d (Cohen, 1988) was originally designed for the limited circumstance where the univariate treatment responses in the two groups are normally distributed with equal variances. In that case, d is the mean difference between T1 and T2 standardized by the common standard deviation in the two groups. It can easily be shown that AUC = Φ(d/√2), where Φ() is the standard normal distribution function. Even more generally, if the responses are normally distributed with unequal variances in the two groups, and one defined d as the mean difference divided by the square root of the average variance in the two group, again AUC = Φ(d/√2). When the underlying assumptions hold, no information is lost or gained in using AUC, SRD or NNT instead of d, and well‐known methods to compute confidence intervals for d can easily be used to generate confidence intervals for AUC, SRD, or NNT (Hedges and Olkin, 1985).
However, while d is invariant under all linear transformations of the response data, AUC is invariant, more generally, under all monotonic transformations. Thus when the assumptions underlying Cohen's d are not satisfied, not only is the use of Cohen's d questionable, but the relationship between d and AUC also fails. Since normal distributions are the exception, rather than the rule, in RCTs, AUC is preferable to d, not only for its clinical interpretability, but for its statistical robustness as well.
Why not odds ratio for binary outcomes?
A stronger contrast is that with the odds ratio (OR) = p 1(1 − p 2)/[(1 − p1)p 2], where p 1 and p 2 are the success rates in T1 and T2, often used as an effect size with a univariate binary outcome measure. OR was introduced as the likelihood‐ratio test statistic for the null hypothesis that p 1 = p 2, and remains an excellent indicator of non‐equality of two proportions. However, the magnitude of OR ≠ 1 is generally non‐interpretable in terms of clinical significance (Kraemer, 2004; Newcombe, 2006; Sackett, 1996). For a binary outcome, when OR > 1, NNT ≥ (OR1/2 + 1)/(OR1/2 − 1) (Kraemer and Kupfer, 2006). Under the null hypothesis, when OR = 1, NNT = (OR1/2 + 1)/(OR1/2 − 1). But for OR = 4, for example, NNT may equal three, which might indicate a moderately strong advantage of T1 over T2, but it might also mean that NNT equals 3000 or three million, which would usually suggest clinical equivalence of T1 and T2.
How large an effect size is large enough?
How to interpret the magnitude of any effect size, including AUC, SRD or NNT, in terms of clinical significance remains a major challenge. Clearly, such interpretation must take into account the severity of the indication, the consequences of inadequate treatment, the costs and risks of treatment, the vulnerability of the population with the indication and other such factors. However, for the purpose of this discussion, we will use a translation of Cohen's standards (Cohen, 1988) “small”, “medium” and “large” effect sizes corresponding to SRD = 0.11, 0.28, 0.42 (AUC = 0.55, 0.64, 0.71, or NNT = 9, 4, 2), although we urge, as did Cohen, that these not be uncritically accepted as valid in all clinical circumstances.
Estimation of effect sizes
There are several different ways of estimating these effect sizes from the results of a RCT comparing two treatments (and thus for comparing every pair of treatments in a multi‐treatment RCT).
One can take every possible pair of patients, one from the T1 group and one from the T2 group, and, ask clinical experts (clinicians, patients, patient advocates, medical policy‐makers, etc.) blinded to group membership, to select which of the two has a clinically preferable outcome. Then AUC comparing T1 to T2 is the proportion of pairs in which T1 is preferred to T2 plus half the ties. Confidence intervals can be computed using bootstrap methods.
If one could rank order all the patients in terms of clinical preference, one could use the Mann–Whitney U‐statistic, for AUC = U/(N 1 × N 2) where N 1 and N 2 are the sample sizes in the two groups. Again, bootstrap methods could be used to generate confidence intervals.
With such a rank ordering of all the patients, one might also compute the ROC curve that graphs Prob(rank T1 > x) + 0.5Prob(rank T1 = x) against Prob(rank T2 > x) + 0.5Prob(rank T2 = x) for all possible values of x, where rank T1 and rank T2 represent the rank orders of all the patients. Then one can compute the area under the ROC curve (AUC) and, using bootstrap methods, obtain its confidence interval.
Effect sizes, power and clinical significance
A RCT is typically designed with a decision rule that specifies what configurations of outcome would lead to recommending one or another of the treatments (a statistical test). For a valid test, when the true unknown effect size is null (SRD = 0), that decision rule must be shown to lead to such a recommendation with probability less than a pre‐specified significance level (typically 5%). For adequate power, when the true unknown effect size is beyond the threshold of clinical significance (say SRD > c), the decision rule must be shown to lead to such a recommendation with probability greater than a pre‐specified level (typically 80%).
Several possible conclusions of a RCT expressed as a confidence interval on the SRD appear in Figure 1. T1 is considered “clinically superior” to T2 if the confidence interval for the effect size lies above c. T1 is considered “clinically equivalent” to T2 if it lies entirely between –c and +c. T1 is considered “non‐inferior” to T2 (T1 “statistically significantly better” than T2) if it lies above zero. It should be noted that T1 may be “clinically equivalent” to T2 as well as “statistically significantly better.” However, if T1 is shown to be “clinically superior” to T2, T1 must be “statistically significantly better” than T2.
Figure 1.
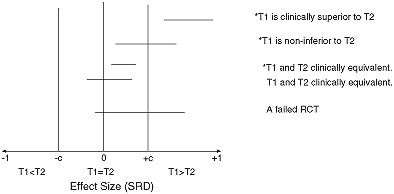
Possible different RCT results using a 95% two‐tailed confidence interval for the effect size (SRD) where c is the threshold of clinical significance, and the asterisk (*) indicates statistical significance at the two‐tailed significance level.
Finally, a “failed RCT” is one in which the confidence interval includes both the null value of zero and effect sizes of clinical significance (magnitude greater than c). A failed RCT neither establishes non‐inferiority nor equivalence, leaving the state of knowledge at the same “clinical equipoise” that existed prior to the RCT (Freedman, 1987). A well‐conceived and well‐designed RCT may fail because the research literature that formed the basis of the rationale and justification of the hypothesis of the RCT was flawed, or simply because of bad luck. In that case, combining the results (effect sizes) of that RCT with other RCTs addressing the same research question in meta‐analysis should clarify the situation. However, the most common reason for a failed RCT is poor design, poor outcome measurement, or flawed implementation, in which case such a RCT should be excluded from any subsequent meta‐analysis (Cooper and Hedges, 1994).
The crucial message is that one cannot determine the clinical impact of a treatment on patients from a “p‐value;” an effect size is needed to guide considerations of clinical significance. Such effect sizes include three mathematically equivalent ones: AUC, SRD and NNT, and these are preferred for this purpose to other more standard effect sizes such as Cohen's d or OR. All of these effect sizes are based on clinical preference; none requires univariate outcomes or imposes distributional requirements. Reporting such effect sizes and their confidence intervals conveys all the information obtainable from “p‐values” and more. With this information it is possible to begin to elucidate the major problem RCTs now have with outcome measures.
Outcome measures in a RCT: why a new approach?
Currently, the strategy most recommended by RCT methodologists (and decried by clinical researchers) is to focus on a single univariate primary outcome measure, on which the decision to recommend one treatment over the other is to be based. Almost always, this provides an incomplete picture of the clinical outcome, one reason this approach is decried by clinical researchers. However, adding more separate measures – the usual solution – does not clarify the picture. There have been many situations in recent years in which making a treatment choice because of its effect on a single outcome measure assessing severity of symptoms in some way, ignores the fact that drugs powerful enough to reduce symptoms or induce remission (Benefits), are also likely to induce serious side effects (Harms). Examples of such situations include the recommendation of rosiglitazone maleate (Avandia) for treatment of diabetes, rofecoxib (Vioxx) for treatment of arthritic pain, olanzapine (Zyprexa) for treatment of schizophrenia, and selective serotonin reuptake inhibitors (SSRIs) for treatment of depression in youth. Even now, it is not clear whether, in these situations, the benefits outweigh the harms and, if so, for whom or by how much.
What clinical researchers often do (and methodologists decry) is to use multiple outcome measures and to assess the effect of T1 versus T2 on each outcome measure separately. In the absence of adjustment of p‐values for multiple testing, false positives proliferate, which, in turn, can mislead clinicians into decision‐making that may impair patient care. However, with adjustment of p‐values for multiple testing, unless sample sizes are substantially increased, false negatives proliferate. Then, effective treatments may be withheld from clinical decision‐making for absence of scientific documentation, again impairing patient care. But even when p‐values are appropriately adjusted and sample sizes are increased, the problem is not solved, because the conclusions for multiple outcome measures considered separately often conflict with one another. For some outcome measures, T1 will be preferable to T2, for others T2 preferable to T1, with many “hung juries” (statistically non‐significant results). How, then, is any medical consumer to correctly interpret results from such RCTs for medical decision‐making?
The evaluation of the comparative effectiveness of T1 versus T2 should not depend on the relative impact of treatments on individual measures of outcome (Benefits or Harms), but on the overall clinical impact of treatments on individual patients who experience both the Benefits and the Harms. Such evaluation requires both statistical assessment of the rates of co‐occurrences of such outcomes and clinical assessment of their combined clinical impact on patients.
An illustration
The data for this demonstration are extracted from a three‐year maintenance treatment trial in 128 patients with recurrent depression who had responded to combined short‐term and continuation treatment with imipramine hydrochloride and interpersonal psychotherapy (Frank et al., 1990). For the purpose of this demonstration, we have collapsed the original five randomly‐assigned maintenance treatment conditions into three:
IMI (N = 53): those receiving active imipramine therapy with or without maintenance interpersonal psychotherapy (IPT‐M).
IPT‐M (N = 52): those receiving IPT‐M with or without a placebo tablet.
MC (N = 23): those receiving medication clinic visits, but no active treatment.
The original report of the trial specified time to first recurrence of major depression as the primary outcome measure. For the purposes of this demonstration, we define Benefit as completing the three‐year treatment trial without recurrence, while Harm was defined as reporting any of a series of somatic complaints typically associated with imipramine, but also sometimes associated with simply having depression (dry mouth, constipation, diarrhoea, sexual difficulties, clumsiness, poor coordination, difficulty speaking, or nausea or vomiting) one or more times during maintenance treatment at a level causing significant distress or incapacity. Note that since Harm was evaluated only until recurrence, those who experienced greater Benefit also had a longer opportunity to experience Harm.
Table 1 presents the results on the outcome measures specified here, the usual method of reporting following conclusion of a RCT. With IMI the probability of Benefit was 53%, for IPT‐M it was 25% and for MC, 9%. If Harm were ignored, one would clearly choose IMI over IPT‐M over MC. However, with both IMI and IPT‐M the probability of Harm was 40% while for MC it was only 17% (probably because time spent in the MC condition prior to recurrence was so much less than that spent in either the IMI or IPT‐M). If Benefit were ignored, one would clearly choose the MC over either IMI or IPT‐M. Thus, while here there are two outcome measures, each individual patient experiences one of four possible outcomes (Benefit without Harm, Benefit with Harm, No Benefit and No Harm, No Benefit, but Harm). With separate reports on Benefit and Harm (as in Table 1), a decision as to which is the preferred treatment would change dramatically depending on whether it is Harm or Benefit that is ignored. This is not an unusual situation, and it is the crux of the problem.
Table 1.
Risks of the four outcomes in three treatment groups, percentage experiencing Benefit (B: yes; b: no) and percent experiencing Harm (H: yes; h: no) by our definitions, and the correlation coefficient between Benefit and Harm
| IMI | IPT‐M | MC | |
|---|---|---|---|
| Bh (Benefit without Harm) | 0.283 | 0.154 | 0.043 |
| BH (Both Benefit and Harm) | 0.245 | 0.096 | 0.043 |
| bh (Neither Benefit nor Harm) | 0.321 | 0.442 | 0.783 |
| bH (Harm without Benefit) | 0.151 | 0.308 | 0.130 |
| Percentage benefited | 52.8 | 25.0 | 8.6 |
| Percentage harmed | 39.6 | 40.4 | 17.4 |
| Correlation coefficient | 0.147 | −0.023 | 0.266 |
Correlation between Benefit and Harm
Within each treatment group, Harm and Benefit may be uncorrelated (a patient experiencing Benefit is just as likely to suffer Harm as is a patient not experiencing Benefit), or positively or negative correlated. In Table 2, we show that for the IMI group, the correlation coefficient between Benefit and Harm was +0.15, for the IPT‐M group it was −0.02, and for the MC group it was +0.27. In this case, those in the IMI and MC groups who benefited were also somewhat more likely to experience Harm (as expected), while in the IPT‐M group, there was essentially no correlation. Again, it is not unusual that the patterns of co‐occurrence vary from one treatment to another.
Table 2.
Eleven possible rankings (clinical situations) of the four possible patient outcomes, and the effect sizes (SRD)a comparing pairs of treatment in each case
| Clinical situation | Symbol | IMI versus IPT‐M | IMI versus MC | IPT‐M versus MC |
|---|---|---|---|---|
| 1. Ignore Harm. | Bh = BH > bh = bH | 0.278 | 0.441 | 0.163 |
| 2. Ignore Benefit. | Bh = bh > BH = bH | 0.008 | −0.222 | −0.230 |
| 3. Only good result is Benefit without Harm. | Bh > BH = bh = bH | 0.129 | 0.240 | 0.110 |
| 4. Only bad result is Harm without Benefit. | Bh = BH = bh > bH | 0.157 | −0.021 | −0.117 |
| 5. Benefit outweighs Harm. | Bh > BH > bh > bH | 0.300 | 0.367 | −0.018 |
| 6. Harm outweighs Benefit. | Bh > bh > BH > bH | 0.144 | 0.011 | −0.130 |
| 7. Harm matters only when there is Benefit. | Bh > BH > bh = bH | 0.268 | 0.443 | 0.166 |
| 8. Benefit matters only when there is no Harm. | Bh > bh > BH = bH | 0.083 | −0.015 | −0.129 |
| 9. Benefit and Harm cancel each other out. | Bh > BH = bh > bH | 0.222 | 0.189 | −0.074 |
| 10. Harm matters only when there is no Benefit. | Bh = BH > bh > bH | 0.310 | 0.365 | −0.020 |
| 11. Benefit matter only when there is no Harm. | Bh = bh > BH > bH | 0.069 | −0.197 | −0.231 |
AUC can be computed by doing all pair‐wise comparisons between patients in T1 versus patients in T2 using the proportion that prefer T1 plus half the proportion of ties. AUC can also be computed by assigning to each patient the rank order of his/her outcome, using a Mann–Whitney test to compare T1 and T2. Then AUC = U/(N 1 × N 2), where U is the Mann–Whitney U‐statistic and N 1 and N 2 are the two sample sizes. AUC is also the area under the receiver operating characteristic curve (ROC) comparing the response distributions under T1 versus T2. AUC can be translated either to SRD or NNT, if needed.
Here “>” means “is clinically preferable to”, and “=” means “is clinically equivalent to”. A positive sign indicates that the first mentioned treatment is preferable to the second; a negative sign that the second treatment is preferable to the first.
The clinical situation
There are 11 possible rankings shown in Table 2. The first two lines of Table 2 are those corresponding to the usual practice of assessing Benefit ignoring Harm, and assessing Harm ignoring Benefit. In practice, we could survey clinical experts (clinicians, patients, medical policy‐makers), presenting the details defining the four possible patient outcomes, and ask them to rank order the outcomes, thus choosing one line in Table 2 as appropriate to the context.
Also listed in Table 2 are the effect sizes (SRD) comparing the pairs of treatments in the 11 possible clinical situations. Clearly, IMI is always preferred to IPT‐M (all positive SRD), but the effect sizes vary depending on the clinical situation, from Negligible (SRD = 0.008) to Moderate (SRD = 0.310). The sample size needed for adequate power to detect such an effect may be about 60 per group (in clinical situation number 10) or it may be more than 2000 per group (in clinical situation number 2). It all depends on clinicians' a priori view of the relative impact of Harm and Benefit, as here defined, on patient well‐being.
With the comparison of IMI versus MC or IPT‐M versus MC, the situation becomes more complex. In some situations the first is preferred to the second, in other situations, the reverse is true. Thus comparing IMI versus MC in clinical situation number 7, IMI is strongly preferred to MC (SRD = +0.443); in clinical situation number 11, MC is somewhat preferred to IMI (SRD = −0.197), and in clinical situations 6 or 8, they are essentially clinically equivalent (SRD = +0.011 or −0.015). Again it all depends on how clinical consumers balance Benefits against Harms.
If the outcome in question is clinically desirable, NNT has often been renamed NNB, “number needed to benefit”; if the outcome is a harmful one, negative NNT has often been renamed NNH, “number needed to harm”. It has been suggested that the overall effect of a treatment might be indicated by comparing NNB with NNH, either by subtraction or division (Nickerson, 2000). However, Table 2 demonstrates why this is not a viable suggestion. It is not possible to decide which is the preferred treatment, knowing only the separate results on Benefit and Harm alone, unless one or the other is considered clinically negligible.
Possible solutions
Strategy 1
In an actual RCT, with two binary outcome measures as in the earlier illustration, getting a panel of experts to rank order the four possible patient outcomes is an easy task. Even with three binary outcome measures resulting in eight patient outcomes, this might be feasible. In all such cases, each patient is assigned the rank order of his/her outcome, and the rank orders are compared between T1 and T2 using a Mann–Whitney test. Then AUC = U/(N 1 × N 2), which can be translated into SRD or NNT. A 95% two‐tailed confidence interval can be obtained using Bootstrap methods.
However, binary outcome measures have long been advised against in RCTs because they lack sensitivity to the differences within and among patients, resulting in reduced power to detect effects (thus requiring much larger sample sizes), and attenuated effect sizes (Cohen, 1983; DeCoster and Iselin, 2009; Kraemer and Thiemann, 1987; MacCallum et al., 2002). Yet having even one continuous outcome measure means that experts cannot possibly order all the infinite number of possible patient outcomes. Thus, this is a readily available strategy, but one of limited applicability.
Strategy 2
Suppose that in a RCT, N 1 patients were randomly assigned to T1 and N 2 to T2. After completion of the RCT, for each of the N 1 + N 2 patients, a “report card” is prepared listing the carefully selected outcomes (Benefits and Harms) that each patient experienced in the RCT. Pairs of report cards, one from the T1 group and one from the T2 group, would be submitted to evaluation by a panel of clinical experts, who would be asked which of each pair they would regard as having a clinically preferable outcome (ties permitted, and decisions “blinded” to which of the pair belonged to T1 or to T2). The proportion of all N 1 × N 2 paired decisions in which T1 was preferred to T2, plus half the proportion of ties, estimates AUC, which can then be converted to SRD or NNT. Again, confidence intervals and tests can be obtained using bootstrap methods (Efron, 1979, 1988; Efron and Tibshirani, 1995).
It should be noted that any outcomes listed that expert clinicians would not value in clinical decision‐making will not here impact pair‐wise decisions. An outcome that is valued but only after some threshold is reached (e.g. a difference in heart rates less than 5 beats/minute indicates equivalent response, while difference greater than 5 beats/minute indicate a clinical difference) would be reflected in pair‐wise decisions.
However, even with a moderate size RCT, the number of pair‐wise comparisons is daunting. For example to have 80% power to detect a moderate effect size with a 5% level two‐sample t‐test (SRD = +0.28) requires 63 subjects per group, which would mean 3969 (63 × 63) pair‐wise comparisons. Moreover this would have to be done for every RCT, and would represent an enormous investment of time, energy and money. Thus, again, this is a readily available strategy, but of limited utility.
Strategy 3
Another strategy of limited utility, but one that provides important insight into the problem, is that when B (Benefit) and H (Harm) are two continuous measures, with (B,H) having bivariate normal distributions in both the T1 and T2 groups. Without loss of generality, we can standardize the two outcome measures using the means and standard deviations from the T2 population. Then in the T2 group (B,H) has a bivariate normal distribution with means zero and variances one and a correlation between B and H equal to ρ 2. In the T1 group (B,H) has a bivariate normal distribution with means μ B and μ H, standard deviations σ B and σ H and correlation between B and H equal to ρ 1.
Now suppose that we could get clinical consensus on a simple linear preference score: B – αH (α ≥ 0) ( a clinical preference score, CPS), i.e. an agreement that one point on the standardized Harm scale offsets α points on the Benefit scale, and one could rank‐order the patients on the CPS scale. Then it can be computed that for the CPS:
and AUC = Φ(d/√2), where δ B is the Cohen's d comparing T1 and T2 on Benefit, and δ H is that comparing T1 and T2 on Harm (in both cases, positive δ indicates that T1 > T2). If α approaches zero (i.e. Harm is ignored), the AUC = Φ(δ B/√2), and as α approaches infinity (i.e. Benefit is ignored), AUC approaches Φ(δ H/√2). Once again, the effect size for each separate Benefit or Harm is meaningful only if all other Benefits or Harms are ignorable.
If α is positive and finite, it can be seen that the effect size comparing T1 and T2 depends not only on the effect sizes of Benefit (δ B) and of Harm (δ H), but also on the relative sizes of the variances in the two groups and the possibly different correlations between B and H in the two groups, as well as the weight, α, that relates the Benefit and Harm scales.
Because bivariate normal distributions in both treatment groups are rare, and because it would be difficult to elicit the weights necessary for such a CPS, this third strategy is unlikely to prove practical. However, it is useful for the following insight. If there were a linear clinical preference score, say α′X i, where α is a vector of weights and X i is a vector comprising relevant Benefits and Harms (possibly even including interactions among Benefits and Harms) for subject i, then in comparing two subjects, say i from T1 and j from T2, the outcome for i would be preferred to that for j if α′X i > α′X j, i.e. if α′(X i – X j) > 0. Thus if we could develop a linear score (CPS) based on pairwise differences that well‐predicted clinical preferences between T1 and T2, we could use that CPS to rank order all subjects to estimate the effect size comparing T1 and T2, and perhaps even in other RCTs for the same indication.
Strategy 4
To develop such a score, say, 100 “report cards” from randomly selected pairs of patients (one from T1, one from T2) would be “blindly” compared by a panel of clinical experts. Then, for example, a logistic regression analysis could be used with the preference (T1 over T2) as the dependent variable and the pair‐wise differences in the listed responses on the report card as the independent variables. The regression coefficients (weights) so derived using a stepwise‐forward procedure are then the weights to be applied to the individual scores for each patient: a CPS. Once validated on an independent sample of say, another 100 pairs of patients, these scores could then be used to rank‐order all the patients in the RCT, no matter how numerous, to compute AUC, SRD, NNT and their confidence intervals.
The expert panel would only have to do a total of about 200 pair‐wise comparisons of participants in the RCT in which the score was developed. Finally, the weights that resulted might be very informative as to how much value clinical experts place on each of the listed outcome measures, or how they balanced certain Benefits against certain Harms, augmenting the clinical relevance of the research conclusions. We might find that clinicians considered only whether or not a recurrence occurred, but not when the recurrence occurred. We might find that only certain symptoms or certain side effects are of concern, or that they are of concern only if they recur over time. We might find that the outcome measures emphasized by clinicians are not the same ones that patients emphasize. In short, a great deal can be learned about how medical decisions are made in practice.
The major reservation here is whether it is realistic to expect a panel of clinical experts to make such judgments when the “report cards” are based on a possibly long list of Benefits and Harms. To do this requires careful selection of outcome measures, each uniquely important to clinical decision‐making.
Redundant outcome measures (multiple measures of the same construct), unreliable or invalid measures, or measures insensitive to differences between and within patients, will only confuse the experts making choices. However, such redundant, unreliable, invalid or insensitive outcome measures, reported separately can also only confuse the issues as well. Clinical researchers often maintain that the more outcome measures are presented, the better the contrasts can be understood. We suggest that the opposite is true. While we agree that too few outcome measures may obscure necessary Harm/Benefit considerations, too many ill‐selected measures may confound the ability to understand results for clinical application. However, after such careful selection was done, we have, in fact, succeeded in implementing this strategy and will report the results of that effort separately.
Strategy 5
A different version of this approach is that originally suggested for CATIE (Clinical Antipsychotic Trials of Intervention Effectiveness) (Lieberman et al., 2005), variations of which might be possible in other RCTs, as well. In this approach, patients would be randomly assigned to T1 or T2, with repeated, say weekly, evaluations of response on the list of crucial Benefits and Harms. Experts blinded to the treatment group of the patient are then asked to track each patient in terms of both Benefits and Harms, and to discontinue treatment at the earliest time point at which, in their clinical judgment, Harms outweigh Benefits for that individual patient. Where in Strategy 3 a statistical integration of the clinical assessment of Benefits and Harms is used, here clinical training and intuition are directly used.
When it is decided that the treatment has failed in an individual patient, that patient is discontinued from the RCT to be otherwise treated. In this case, the single outcome measure to be used in analysis that integrates clinical evaluation of all Benefits and all Harms of clinical concern and the balance between them, is time to treatment failure [either because of lack of benefit or lack of tolerability (harm) or some combination of the two]. The AUC and NNT can then be estimated and tested from ROC comparison of survival curves (Altman and Andersen, 1999). Such an approach has appeal in that each patient can be assured that he or she will not be continued in any treatment past the point that Benefit outweighs Harm for him/her as an individual.
In CATIE, this approach arguably failed (Kraemer et al., 2009; Weiden, 2007) not because of a flaw in the approach, but because of its implementation. The discontinuation decisions were made by the individual treating clinicians at 57 sites with no central protocol defining those decision rules, rather than by a panel of clinical experts or following a common protocol defining how decisions were made. This necessitated comparison between treatments only within site, but such comparisons could not be done because no site actually completed a full replication of the complex design of the study. More important, most discontinuations were not because of failure of the drug (lack of efficacy or tolerability), but because of “patient decision” (Lieberman et al., 2005). As a result, this strategy has not yet really been put to test.
These are only a few of the simplest possible strategies that could be used to compare T1 versus T2 using the impact of treatments on patients rather than on outcome measures.
Summary
What is crucial to contributing to evidence‐based medicine, and to informing personalized medicine, is that the evaluation of the choice between treatments be based, not on examining the effects of treatments on individual response measures, but the effects of treatments on individual patients with emphasis on clinical (effect sizes), not statistical significance (p‐values).
Currently, multiple outcomes are evaluated separately, thus focusing on measures rather than patients. Despite recent advances in the design and conduct of clinical trials, statistical significance is still over‐emphasized and effect sizes not consistently reported, leading to conflicting and confusing recommendations to the clinician, patient and the medical policy‐maker. As we demonstrate here, knowing the separate results on multiple outcomes does not answer the clinically vital question of which treatment is to be preferred. Both Harms and Benefits and the balance between them within individual patients should be considered in making a recommendation of one treatment over another in the total population or in specific subpopulations when moderator effects have been detected.
Declaration of interest statement
Drs Kraemer and Kupfer have no conflicting interests that might influence this report. Dr Frank serves on an advisory board for Servier.
References
- Acion L., Peterson J.J., Temple S., Arndt S. (2006) Probabilistic index: An intuitive non‐parametric approach to measuring the size of treatment effects. Statistics in Medicine, 25(4), 591–602. [DOI] [PubMed] [Google Scholar]
- Altman D.G. (1998) Confidence intervals for the number needed to treat. British Medical Journal, 317(7168), 1309–1312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Altman D.G., Andersen K. (1999) Calculating the number needed to treat for trials where the outcome is time to an event. British Medical Journal, 319(7223), 1492–1495. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Altman D.G., Schulz K.F., Moher D., Egger M., Davidoff F., Elbourne D., Gotzsche P.C., Lang T., Consort Group (2001) The revised CONSORT statement for reporting randomized trials: Explanation and elaboration. Annals of Internal Medicine, 134(8), 663–694. [DOI] [PubMed] [Google Scholar]
- American Psychological Association (APA) (2001) Publication Manual of the American Psychological Association (5th ed.), Washington, DC, APA. [Google Scholar]
- Borenstein M. (1998) The shift from significance testing to effect size estimation In Bellak A.S., Hersen M. (eds) Research & Methods, Comprehensive Clinical Psychology, Vol. 3, pp. 319–349, Burlington, MD, Elsevier Science Publishing Co. [Google Scholar]
- Cohen J. (1983) The cost of dichotomization. Applied Psychological Measurement, 7(3), 249–253. [Google Scholar]
- Cohen J. (1988) Statistical Power Analysis for the Behavioral Sciences, Hillsdale, NJ, Lawrence Erlbaum Associates. [Google Scholar]
- Cohen J. (1995) The earth is round (p < .05). The American Psychologist, 49(12), 997–1003. [Google Scholar]
- Cooper H., Hedges L.V. (1994) The Handbook of Research Synthesis, New York, Russell Sage Foundation. [Google Scholar]
- Dar R., Serlin R.C., Omer H. (1994) Misuse of statistical tests in three decades of psychotherapy research. Journal of Consulting and Clinical Research, 62(1), 75–82. [DOI] [PubMed] [Google Scholar]
- DeAngelis C.D., Drazen J.M., Frizelle F.A., Haug C., Hoey J., Horton R., Kotzin S., Laine C., Marusic A., Overbeke A.J.P.M., Schroeder T.V., Sox H.C., VanDerWeyden M.B. (2005) Is this clinical trial fully registered? Journal of the American Medical Association, 293(23), 2927–2929. [DOI] [PubMed] [Google Scholar]
- DeCoster J., Iselin A.‐M.R. (2009) A conceptual and empirical examination of justifications for dichotomization. Psychological Methods, 14(4), 349–366. [DOI] [PubMed] [Google Scholar]
- Efron B. (1979) Bootstrap methods: Another look at the jackknife. Annals of Statistics, 7(1), 1–26. [Google Scholar]
- Efron B. (1988) Bootstrap confidence intervals: Good or bad? Psychological Bulletin, 104(2), 293–296. [Google Scholar]
- Efron B., Tibshirani R. (1995) Computer‐intensive Statistical Methods (Technical Report 174), Palo Alto, CA, Division of Biostatistics, Stanford University. [Google Scholar]
- Frank E., Kupfer D.J., Perel J.M., Cornes C., Jarrett D.B., Mallinger A.G., Thase M.E., McEachran A.B., Grochocinski V.J. (1990) Three‐year outcomes for maintenance therapies in recurrent depression. Archives of General Psychiatry, 47(12), 1093–1099. [DOI] [PubMed] [Google Scholar]
- Freedman B. (1987) Equipoise and the ethics of clinical research. The New England Journal of Medicine, 317(3), 141–145. [DOI] [PubMed] [Google Scholar]
- Garber A.M., Tunis S.R. (2009) Does comparative‐effectivenss research threaten personalized medicine? The New England Journal of Medicine, 360(19), 1925–1927. [DOI] [PubMed] [Google Scholar]
- Grissom R.J. (1994) Probability of the superior outcome of one treatment over another. Journal of Applied Psychology, 79(2), 314–316. [Google Scholar]
- Hedges L.V., Olkin I. (1985) Statistical Methods for Meta‐Analysis, Orlando, FL, Academic Press Inc. [Google Scholar]
- Hsu L.M. (2004) Biases of success rate differences shown in binomial effect size displays. Psychological Bulletin, 9(2), 183–197. [DOI] [PubMed] [Google Scholar]
- Hunter J.E. (1997) Needed: A ban on the significance test. Psychological Science, 8(1), 3–7. [Google Scholar]
- Kline R.B. (2005) Beyond Significance Testing: Reforming Data Analysis Methods in Behavioral Research, Washington, DC, American Psychological Association. [Google Scholar]
- Kraemer H.C. (2004) Reconsidering the odds ratio as a measure of 2X2 association in a population. Statistics in Medicine, 23(2), 257–270. [DOI] [PubMed] [Google Scholar]
- Kraemer H.C., Frank E. (2010) Evaluation of comparative treatment trials: Assessing the clinical benefits and risks for patients, rather than statistical effects on measures. Journal of the American Medical Association, 304(6), 1–2. [DOI] [PubMed] [Google Scholar]
- Kraemer H.C., Frank E., Kupfer D.J. (2006) Moderators of treatment outcomes: Clinical, research, and policy importance. Journal of the American Medical Association, 296(10), 1–4. [DOI] [PubMed] [Google Scholar]
- Kraemer H.C., Glick I.D., Klein D.F. (2009) Clinical trials design lessons from the CATIE study. American Journal of Psychiatry, 166(11), 1222–1228. [DOI] [PubMed] [Google Scholar]
- Kraemer H.C., Kiernan M., Essex M.J., Kupfer D.J. (2008) How and why criteria defining moderators and mediators differ between the Baron & Kenny and MacArthur approaches. Health Psychology, 27(2), S101–S108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kraemer H.C., Kupfer D.J. (2006) Size of treatment effects and their importance to clinical research and practice. Biological Psychiatry, 59(11), 990–996. [DOI] [PubMed] [Google Scholar]
- Kraemer H.C., Thiemann S. (1987) How Many Subjects? Statistical Power Analysis in Research, Newbury Park, CA, Sage Publications. [Google Scholar]
- Lange N., MacIntyre J. (1985) A computerized patient registration and treatment randomization system for multi‐institutional clinical trials. Controlled Clinical Trials, 6(1), 38–50. [DOI] [PubMed] [Google Scholar]
- Lesko L.J. (2007) Personalized medicine: Elusive dream or imminent reality? Clinical Pharmacology and Therapeutics, 81(6), 807–815. [DOI] [PubMed] [Google Scholar]
- Lieberman J.A., Stroup T.S., McEvoy J.P., Swartz M.S., Rosenheck R.A., Perkins D.O., Keefe R.S.E., Davis S.M., Davis C.E., Lebowitz B.D., Severe J.B., Hsiao J.K., Intervention Effectiveness (CATIE) Investigators (2005) Effectiveness of antipsychotic drugs in patients with chronic schizophrenia. New England Journal of Medicine, 353(12), 1209–1223. [DOI] [PubMed] [Google Scholar]
- MacCallum R.C., Zhang S., Preacher K.J., Rucker D.D. (2002) On the practice of dichotomization of quantitative variables. Psychological Methods, 7(1), 19–40. [DOI] [PubMed] [Google Scholar]
- March J.S., Silva S.G., Compton S., Shapiro M., Califf R.M., Krishnan R. (2005) The case for practical clinical trials in psychiatry. American Journal of Psychiatry, 152(5), 836–846. [DOI] [PubMed] [Google Scholar]
- McGough J.J., Faraone S.V. (2009) Estimating the size of treatment effects: Moving beyond p values. Psychiatry (Edgmont), 6(10), 21–29. [PMC free article] [PubMed] [Google Scholar]
- McGraw K.O., Wong S.P. (1992) A common language effect size statistic. Psychological Bulletin, 111(2), 361–365. [Google Scholar]
- Newcombe R.G. (2006) A deficiency of the odds ratio as a measure of effect size. Statistics in Medicine, 25(24), 4235–4240. [DOI] [PubMed] [Google Scholar]
- Nickerson R.S. (2000) Null hypothesis significance testing: A review of an old and continuing controversy. Psychological Methods, 5(2), 241–301. [DOI] [PubMed] [Google Scholar]
- Rennie D. (1996) How to report randomized controlled trials: The CONSORT statement. Journal of the American Medical Association, 276(8), 649. [PubMed] [Google Scholar]
- Richmond T.D. (2008) The current status and future potential of personalized diagnostics: Streamlining a customized process. Biotechnology Annual Review, 14, 411–422. [DOI] [PubMed] [Google Scholar]
- Sackett D.L. (1996) Down with odds ratios! Evidence‐Based Medicine, 1, 164–166. [Google Scholar]
- Schulz K.F., Altman D.G., Moher D., Consort Group (2010) CONSORT 2010 statement: Updated guidelines for reporting parallel group randomised trials. British Medical Journal, 340, 698–702. [Google Scholar]
- Shrout P.E. (1997) Should significance tests be banned? Introduction to a special section exploring the pros and cons. Psychological Science, 8(1), 1–2. [Google Scholar]
- Weiden P.J. (2007) Discontinuing and switching antipsychotic medications: Understanding the CATIE schizophrenia trial. Journal of Clinical Psychiatry, 68(Suppl. 1), 12–19. [PubMed] [Google Scholar]
- Wen L., Badgett R., Cornell J. (2005) Number needed to treat: A descriptor for weighing therapeutic options. American Journal of Health‐System Pharmacology, 62(1), 2031–2036. [DOI] [PubMed] [Google Scholar]
- Wilkinson L., The Task Force on Statistical Inference (1999) Statistical methods in psychology journals: Guidelines and explanations. American Psychologist, 54(8), 594–604. [Google Scholar]


