Abstract
This paper explored the latent class structure of the Diagnostic and Statistical Manual of Mental Disorders, 4th Edition (DSM‐IV) (assessed with the Munich Composite International Diagnostic Interview). Secondly, the screening properties of the Cannabis Abuse Screening Test (CAST) in adolescents were assessed with classical test theory using the latent class structure as empirical gold standard. The sample comprised 3266 French cannabis users aged 17 to 19 from the general population. Three latent classes of cannabis users were identified reflecting a continuum of problem severity: non‐symptomatic, moderate and severe. Gender‐specific analyses showed the best model fit, although results were almost identical in the total sample. The latent classes were good predictors of daily cannabis use, number of joints per day and age of first experimentation. The CAST showed good screening properties for the moderate/severe class (area under receiver operating characteristic curve > 0.85) and very good for the severe class (0.90). It was more sensitive for boys, more specific for girls. Although structural equivalence across gender was rejected, results suggest small gender differences in the latent structure of the DSM‐IV. The performance of the CAST in screening for the latent class structure was good and superior to those obtained with the classical DSM‐IV diagnoses. Copyright © 2013 John Wiley & Sons, Ltd.
Keywords: latent class analysis, CAST, DSM‐IV, adolescents, cannabis, psychometrics
Introduction
In recent years, many screening scales to assess cannabis‐related problems have been developed and tested. By far the most common validation method is the comparison of the screening tool against a gold standard, mainly diagnoses derived from the Diagnostic and Statistical Manual of Mental Disorders, 4th Edition (DSM‐IV) (Bashford et al., 2010; Legleye et al., 2007; Legleye et al., 2011; Martin et al., 2006b; Piontek et al., 2008; Steiner et al., 2008). A second approach uses more sophisticated statistical techniques that explore the internal structure of the instrument such as Item Response Theory (IRT) (Annaheim et al., 2010; Langenbucher et al., 2004). Both approaches are useful, but classic screening properties, such as sensitivity and specificity, render the classic validation methodology essential for public health and research purposes.
However, the validity of the DSM‐IV is challenged, especially for use among adolescents. First, most IRT analyses have not confirmed the two‐dimensional concept of abuse and dependence, with abuse reflecting less severe problems than dependence (Gillespie et al., 2007; Martin et al., 2006a; Teesson et al., 2002). Most recently, based on a comparison of different modelling techniques, it twas found that a one‐dimensional solution described best cannabis use disorders in an Australian community sample (Baillie and Teesson, 2010). Furthermore, patterns of substance use such as frequency or social contexts of use are important predictors of substance‐related disorders (Coffey et al., 2003). They are not part of the current classification system, although research suggests that their inclusion would be useful (Adamson et al., 2010; Compton et al., 2009; Piontek et al., 2011). Other problems raised in the literature concern withdrawal symptoms that are inadequately described and assessed, especially for cannabis and adolescents (Budney et al., 2004; Crowley, 2006; Vandrey et al., 2005). Also, the relevance of the diagnostic subtypes abuse and dependence has been questioned (Babor and Caetano, 2006; Hesselbrock and Hesselbrock, 2006) and there is discussion as to whether the DSM diagnoses should be categorical or dimensional (Muthen, 2006). Validations based on categorical DSM‐IV diagnoses do not enable assessment of severity in a reliable manner, which has led to a draft revision of the DSM involving a one‐dimensional structure of substance use disorders with a count of endorsed criteria defining a continuum of severity (American Psychiatric Association, 2010). Secondly, DSM‐IV and also the draft for DSM‐V have been criticized for their indifference towards gender. In fact, not only do patterns of cannabis use differ between genders: Piontek et al. (2011) found that tolerance and withdrawal showed marked differential item functioning according to gender, severity being greater in females. In addition, Martin et al. (2006a) found that hazardous use, legal problems, and physical‐psychological problems were also markedly gender‐related.
In order to address these problems related to the construct validity of the DSM, latent class analysis (LCA) or more complex modelling techniques (latent class factor analysis (LCFA)) (Magidson and Vermunt, 2001) that allow both categories and dimensions to be taken into account can be used to describe the natural distribution of cannabis use disorders in a population. The choice of the adequate technique is based on systematic comparisons (Baillie and Teesson, 2010; Muthen, 2006). The pattern of cannabis use disorders derived from these models can be used to evaluate the sensitivity and specificity of screening instruments against a challenged gold standard (Garrett et al., 2002; Hawkins et al., 2001).
Applying this approach, the aim of this article is two‐fold. First, the latent structure of adolescents’ cannabis‐related disorders based on DSM‐IV criteria will be analysed and the resulting latent class structure for girls and boys will be compared, as previous LCAs showed marked gender‐related differences (Grant et al., 2006). Second, the screening properties of the Cannabis Abuse Screening Test (CAST), which has recently been validated against the theoretical DSM‐IV diagnoses in a sample of the general adolescent population (Legleye et al., 2011) will be assessed using the latent DSM‐IV structure as the gold standard, in the same sample. To our knowledge, this is the first time that this methodology has been applied in this field.
Methods
Sample
The sample was drawn from the 2008 Survey on Health and Consumption during the Day of Defence Preparation (ESCAPAD) (Beck et al., 2006). The Day of Defence Preparation (JAPD) is a one‐day session of civic and military information that is prerequisite for registration for all public examinations in France. All adolescents reaching 17 in a given year are called up to attend this day, but it may be postponed until age 25. There are 250 civilian and military centres in France that conduct the JAPD sessions on about two days a week throughout the year. In 2008, a total of about 790,000 young people attended the JAPD. The ESCAPAD survey was conducted in a random two‐week period in December 2008 and included all adolescents attending the JAPD during this time (n = 12,570). The purpose of the survey was explained to the participants, especially its complete confidentiality and anonymity. Participation was voluntary, but none of the adolescents refused (the attractive aspect of the questionnaire and the reported boredom of the adolescents present during the day appear as the main reasons). The survey was approved by the National Council for Statistical Information (CNIS) (No. 2008X713AU) and the French Data Protection Authority (CNIL). ESCAPAD is self‐administered and takes about 30 minutes to complete.
Measures
The four DSM‐IV criteria for cannabis abuse and the seven DSM‐IV criteria for cannabis dependence in the past 12 months were assessed using the paper‐and‐pencil version of the Munich Composite International Diagnostic Interview (M‐CIDI: Lachner et al., 1998; Wittchen et al., 1995).
The CAST (Legleye et al., 2007; Legleye et al., 2011) assesses the following aspects of cannabis consumption in the past 12 months: non‐recreational use (CAST 1 “Have you smoked cannabis before midday?”, CAST 2 “Have you smoked cannabis when you were alone?”), memory disorders (CAST 3 “Have you had memory problems when you smoked cannabis?”), reproaches from family or friends (CAST 4 “Have friends or family members told you that you should reduce or stop your cannabis consumption?”), unsuccessful attempts to quit (CAST 5 “Have you tried to reduce or stop your cannabis use without succeeding?”), and problems linked to cannabis consumption (CAST 6 “Have you had problems because of your cannabis use (argument, fight, accident, poor results at school, etc.)?”). All items are answered on a five‐point scale (0 “never”, 1 “rarely”, 2 “from time to time”, 3 “fairly often”, 4 “very often”).
For comparative purposes, three cannabis‐related variables were assessed: daily use of cannabis based on the consumption during the last 30 days (yes/no), mean number of joints smoked on a typical smoking occasion during the last 12 months using a six‐point scale (less than one – coded as 0.5 – 1, 2, 3, 4, and 5 or more – coded as 5.5) and age at first cannabis experimentation (ranging from nine to 19).
Statistical analyses
Based on a previous analysis of the dimensionality of the DSM‐IV criteria in the same dataset that used confirmatory factor analysis (Piontek et al., 2011), we conclude a one‐dimensional structure of the cannabis use disorder construct. We thus ran LCA. LCA (Lazarsfeld and Henry, 1968; Wolfe, 1970) aims to identify homogenous subgroups of individuals on the basis of their responses to a specific set of categorical items. LCA assumes that item endorsement can be fully explained by an unobserved categorical latent variable with a finite number of mutually exclusive classes. It also assumes that there is no residual correlation between the items in each latent class (local independence, mixture model). The model estimates conditional item probabilities that are the probabilities that an individual from a specific class will choose a specific response category of each item, and posterior class probabilities for each individual to belong to each latent class. In our analysis, the final class membership was assigned on the basis of its maximum. To test the local independence assumption of LCA, residual correlations were inspected (Vermunt and Magidson, 2005).
LCAs were run on all DSM‐IV criteria. A multiple group LCA testing for measurement invariance across gender was performed, following a three‐step procedure (Hagenaars and McCutcheon, 2002; Lanza et al., 2007). The first step of the analysis is to find an optimal baseline model. Therefore, a series of models was fitted to the total sample (two to six classes), with no additional parameters. The model with the optimal number of classes was the one with the lowest Bayesian information criterion (BIC) and the highest entropy (Celeux and Soromenho, 1996). The Model entropy is a standardized measure of classification accuracy in the interval [0, 1] with values near one indicating greater accuracy, i.e. a good separation of latent classes.
Once the baseline latent class model was chosen, gender was introduced as a group variable. In order to test if the measurement is invariant across gender, two additional models were performed: in step 2, one model with all parameters freely estimated (unconstrained model); in step 3, a model with item response probabilities constrained across gender groups (a structural equivalence model that restricts estimation so that the parameters p are equal across gender). The best model of steps 2 and 3 was to minimize relative fit statistics, i.e. the likelihood‐ratio goodness‐of‐fit (L2) and, the BIC. But, as models in steps 2 (unconstrained model) and 3 (structural equivalence model) are nested, the difference between the corresponding G 2 can also be compared to a Chi‐square distribution (with corresponding difference in degrees of freedom). Additionally, the concordance between the model in the total sample and the two gender specific models was assessed with weighted Kappa indices according to the scale of independence judgements proposed in Landis and Koch (1977).
Latent classes were compared by computing proportions of endorsed DSM‐IV criteria and the mean numbers of endorsed DSM‐IV criteria. Additionally, we tested whether class membership could predict the three cannabis‐related variables that are not described by DSM‐IV criteria. These analyses were conducted separately by gender, and also in the total sample.
Finally, the screening properties of the CAST were assessed, separately by gender, and in the total sample, against the “severe” class, and against the combined “moderate” and “severe” classes. The optimal threshold scores on the CAST were determined by computing sensitivity and specificity and by considering the Youden index Y (Y = sensitivity + specificity – 1). The AUC (area under the receiver operating characteristic curve) was used as an indicator of the ability of the CAST to discriminate between individuals with and without a diagnosis (Rey et al., 1992). The closer the AUC value is to one, the greater is the discriminative power. In addition, the predictive power of the CAST scale was assessed. The positive predictive value (PPV) reflects the probability of a clinical diagnosis in case of a positive screening result, whereas the negative predictive value (NPV) is the probability of not having a diagnosis when the screening result is negative.
LCA was performed using SAS V9.3.2 and PROC LCA (Lanza et al., 2007) and non‐parametric AUC confidence intervals at the 95% level (95% CI) were computed with the macro %ROC procedure from SAS institute. Principal component analysis (PCA) simulation scree test was computed with the package “psy” in R (Falissard, 2009).
Results
The database comprised 3266 individuals aged 17–19 years who fully completed the CAST and the M‐CIDI, and who had smoked cannabis in the 12 months prior to the survey, 1916 boys (58.6%) and 1350 girls. Table 1 shows the distribution of the DSM‐IV criteria according to gender. Boys showed higher levels of abuse than girls; the differences between genders were smaller for the dependence criteria and there was no significant difference for withdrawal, larger/longer use than intended and impaired control. Boys had significantly higher means for abuse criteria, dependence criteria and combined abuse and dependence criteria.
Table 1.
DSM‐IV criteria according to gender , percentages and mean number of criteria with standard deviation [Mean (SD)]
| Boys (n = 1916) | Girls (n = 1350) | p‐Valuea | Total | |
|---|---|---|---|---|
| Abuse criteria | ||||
| A1 | 11.0 | 6.0 | 0.0001 | 8.9 |
| A2 | 21.9 | 4.4 | 0.0001 | 14.6 |
| A3 | 5.7 | 0.9 | 0.0001 | 3.7 |
| A4 | 25.1 | 14.0 | 0.0001 | 20.5 |
| Mean (SD) | 0.64 (0.99) | 0.25 (0.57) | 0.0001 | 0.48 (0.86) |
| Dependence criteria | ||||
| D1 | 35.2 | 26.9 | 0.0001 | 31.8 |
| D2 | 8.9 | 10.1 | 0.2678 | 9.4 |
| D3 | 35.4 | 34.8 | 0.7132 | 35.2 |
| D4 | 21.8 | 20.0 | 0.2100 | 21.1 |
| D5 | 24.4 | 18.8 | 0.0001 | 22.1 |
| D6 | 10.4 | 5.5 | 0.0001 | 27.1 |
| D7 | 19.3 | 22.5 | 0.0257 | 20.6 |
| Mean (SD) | 1.55 (1.71) | 1.39 (1.61) | 0.0039 | 1.49 (1.67) |
| Total criteria | ||||
| Mean (SD) | 2.19 (2.46) | 1.64 (1.97) | 0.0001 | 1.96 (2.29) |
A1, role impairment; A2, hazardous use; A3, legal problems; A4, social problems; D1, tolerance; D2, withdrawal; D3, larger, longer use than intended; D4, impaired control; D5, much time spent; D6, reduced activities; D7, use despite problems.
SD, standard deviation.
Chi‐squared p‐value for percentages, t‐test p‐values for means.
For step 1, the optimal number of classes in the total sample was three (BIC = −14937, entropy = 0.74), as shown in Table 2. According to this baseline model, gender was introduced as group variable for steps 2 and 3. The unconstrained model (step 2: BIC = −24025) had better fit indices than the structural equivalence model (step 3: BIC = −23989). This was confirmed by the G 2 test comparing these two models that lead to the rejection of the hypothesis of measurement invariance (p < 0.0001), i.e. the structural equivalence model did not increase model fit. This suggests that the meaning of three estimated classes differed by gender (probability of endorsing an item in each class) and that the analyses should be conducted for each gender separately. The optimal number of classes was three for each gender and the entropy was 0.75 for boys and 0.73 for girls.
Table 2.
Comparison of various LCA (BIC, L 2, classification error, entropy, and relative reduction in L 2)
| Model | L 2 | BIC | Number of parameters | Classification error | Entropy | Reduction in L 2 (%) |
|---|---|---|---|---|---|---|
| 1 class | 6000 | −10473 | 11 | 0 | 1.00 | 0 |
| 2 classes | 1841 | −14536 | 23 | 0.0539 | 0.82 | 69 |
| 3 classes | 1341 | −14937 | 35 | 0.1120 | 0.74 | 78 |
| 4 classes | 1278 | −14904 | 47 | 0.1559 | 0.70 | 79 |
| 5 classes | 1228 | −14858 | 59 | 0.1920 | 0.69 | 80 |
| 3 classes with direct effect | 1128 | −14986 | 43 | 0.1100 | 0.74 | 79 |
BIC, Bayesian information criterion.
According to Vermunt and Magidson (2005), bivariate residuals (BVR) larger than 3.84 indicate correlations that have not been captured adequately in the model. Among the 66 BVR among the 11 abuse and dependence items of the DSM, 10 were above this threshold and three were especially large: between abuse items 2 and 3 (12.26), 3 and 4 (8.37) and abuse 4 and dependence 4 (7.58). In order to account for these excessive residual associations that were not explained by the models, the local independence assumption between the corresponding items was relaxed by adding a direct effect between these variables that led to a slightly better BIC, but similar classification errors and entropy (Table 2). However, the agreement between the two classifications is very high (Kappa = 0.94) and more than 96.9% of the individuals are identically classified. So we did not change the model.
Figure 1 shows that the three‐class model had a comparable structure in boys and girls, even though the structural equivalence model could not be confirmed. The classes were ordered quantitatively; the lowest class can be named “non‐symptomatic”, the intermediate “moderate” and the upper “severe”. Boys presented a much greater likelihood of endorsing the abuse criteria (especially hazardous use) compared to girls, whereas the second and the seventh dependence criteria were more often endorsed by girls. An evaluation of the gender‐specific latent class distribution shows that boys were more numerous in the severe class than girls (10.5% versus 7.0%, p < 0.01), while girls were more numerous in the non‐symptomatic class (60.7% versus 54.8%, p < 0.01).
Figure 1.
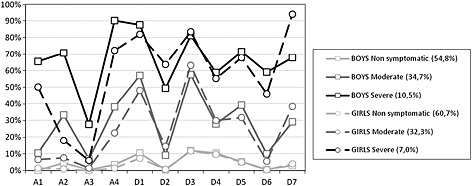
Item profiles for the three‐class model for boys and girls: conditional item probabilities of endorsing each criterion (%). Abuse (A) and Dependence (D) criteria: A1, role impairment; A2, hazardous use; A3, legal problems; A4, social problems; D1, tolerance; D2, withdrawal; D3, larger, longer use than intended; D4, impaired control; D5, much time spent; D6, reduced activities; D7, use despite problems.
Table 3 shows the comparison of the LCA for boys and girls. Overall, boys presented greater mean numbers of abuse criteria, as well as greater mean numbers of total DSM‐IV criteria in each class. With regard to dependence criteria, there was no difference between boys and girls in the non‐symptomatic group, while girls presented a higher mean in the moderate class (2.54 versus 2.40, p = 0.022) and a slightly higher (although non‐significant) mean in the severe class (5.12 versus 4.93, p = 0.17). Worthwhile to be mentioned, girls more often than boys reported four out of seven dependence criteria in the moderate class (except tolerance, much time spent and reduced activities) and two out of seven dependence criteria in the severe class (withdrawal and particularly use despite problems).
Table 3.
Comparison of the distribution of the endorsed DSM‐IV criteria by gender across latent classes, percentages and mean number of criteria with standard deviation [Mean (SD)]
| Non symptomatic | Moderate | Severe | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Boys, n = 1050 (54.8%) | Girls, n = 820 (60.7%) | Test p‐valuea | Boys, n = 664 (34.7%) | Girls, n = 436 (32.3%) | Test p‐valuea | Boys, n = 202 (10.5%) | Girls, n = 94 (7.0%) | Test p‐valuea | |
| Abuse criteria (%) | |||||||||
| A1 | 0.0 | 0.0 | — | 10.8 | 7.1 | 0.0376 | 68.3 | 53.2 | 0.0119 |
| A2 | 3.9 | 0.5 | 0.0001 | 35.1 | 8.5 | 0.0001 | 71.8 | 19.2 | 0.0001 |
| A3 | 0.4 | 0.0 | 0.0768 | 6.9 | 1.4 | 0.0001 | 29.7 | 6.4 | 0.0001 |
| A4 | 2.1 | 1.4 | 0.2193 | 40.7 | 24.1 | 0.0001 | 93.1 | 77.7 | 0.0001 |
| Dependence criteria (%) | |||||||||
| D1 | 8.8 | 6.1 | 0.0309 | 60.5 | 53.7 | 0.0240 | 89.6 | 84.0 | 0.1729 |
| D2 | 0.4 | 0.9 | 0.1847 | 9.2 | 14.7 | 0.0050 | 52.5 | 69.2 | 0.0069 |
| D3 | 10.4 | 11.0 | 0.6790 | 60.4 | 68.6 | 0.0058 | 83.7 | 86.2 | 0.5794 |
| D4 | 10.6 | 8.1 | 0.0644 | 28.0 | 34.2 | 0.0298 | 59.9 | 58.5 | 0.8206 |
| D5 | 4.4 | 5.0 | 0.5282 | 41.1 | 33.9 | 0.0167 | 73.7 | 69.2 | 0.4090 |
| D6 | 0.5 | 0.4 | 0.7168 | 9.5 | 6.0 | 0.0360 | 64.9 | 47.9 | 0.0056 |
| D7 | 2.4 | 3.2 | 0.2981 | 31.0 | 42.9 | 0.0001 | 68.8 | 96.8 | 0.0001 |
| Abuse criteria | |||||||||
| Mean (SD) | 0.06 (0.24) | 0.02 (0.13) | 0.0001 | 0.94 (0.82) | 0.41 (0.57) | 0.0001 | 2.63 (0.87) | 1.56 (0.82) | 0.0001 |
| Dependence criteria | |||||||||
| Mean (SD) | 0.37 (0.54) | 0.35 (0.50) | 0.2463 | 2.40 (1.05) | 2.54 (0.97) | 0.0248 | 4.93 (1.25) | 5.12 (0.98) | 0.1671 |
| Total criteria | |||||||||
| Mean (SD) | 0.44 (0.56) | 0.36 (0.50) | 0.0028 | 3.33 (1.17) | 2.95 (1.00) | 0.0001 | 7.56 (1.43) | 6.68 (1.23) | 0.0001 |
A1, role impairment; A2, hazardous use; A3, legal problems; A4, social problems; D1, tolerance; D2, withdrawal; D3, larger, longer use than intended; D4, impaired control; D5, much time spent; D6, reduced activities; D7, use despite problems.
SD, standard deviation.
Chi‐square p‐value for percentages, t‐test p‐values for means.
Despite these differences, the cross‐tabulation of the LCA in the total sample and the LCA for boys shows that only 0.8% (14 individuals) were not identically classified by the two analyses: Kappa was 0.989 (95% CI = 0.984–0.995), which is very good (Landis and Koch, 1977). The corresponding results for girls were also very good: only 4.1% (55 individuals) were not identically classified and Kappa was 0.931 (95% CI = 0.913–0.949).
Table 4 presents the predictive validity of class membership. It shows that for each gender separately and for the total sample, subjects in the moderate and the severe class had a higher risk of daily cannabis use, a larger number of joints smoked and a younger age at cannabis experimentation compared to the non‐symptomatic class. The confidence intervals related to the moderate and the severe class did not overlap, confirming the continuum in severity across the three classes.
Table 4.
Predictive validity of class membership for boys and girls separately and together
| Non‐symptomatic | Moderate | Severe | |
|---|---|---|---|
| OR (95% CI) | OR (95% CI) | ||
| Daily cannabis consumption a | |||
| Boys | Reference | 11.07*** (6.80–18.05) | 40.59*** (23.65–69.66) |
| Girls | Reference | 8.76*** (4.22–18.22) | 47.40*** (21.36–105.21) |
| Total | Reference | 10.82*** (7.21–16.23) | 43.32*** (27.67–67.82) |
| B (SE) | B (SE) | ||
| Number of joints per day b | |||
| Boys | Reference | 1.01*** (0.07) | 2.21*** (0.11) |
| Girls | Reference | 0.67*** (0.06) | 1.89*** (0.17) |
| Total | Reference | 0.90*** (0.05) | 2.19*** (0.08) |
| Age of first use b | |||
| Boys | Reference | −0.94*** (0.07) | −1.60*** (0.11) |
| Girls | Reference | −0.58*** (0.07) | −1.19*** (0.14) |
| Total | Reference | −0.80*** (0.05) | −1.47*** (0.09) |
All models were controlled for age, gender (for “Total” only), daily tobacco use, ≥ 10 alcohol uses in the last 30 days.
For boys (resp. girls) the latent classes were computed for boys (resp. girls) separately; for total sample, the latent classes were computed for boys and girls together without considering gender.
OR, odds ratio; CI, confidence interval; B, regression coefficient; SE, standard error.
Logistic regression models.
Linear regression models.
***p < 0.001.
The screening properties of the CAST against the severe class for boys, girls, and the total sample are presented in Table 5. According to the Y index, the optimal threshold was seven for boys (sensitivity = 0.901, specificity = 0.809), girls (sensitivity = 0.798, specificity = 0.902) and the total sample (sensitivity = 0.880, specificity = 0.848). The corresponding values of the AUC were above 0.92. At the optimal cutoff, boys presented a higher rate of false positives (19.1%) but a lower false negative rate (9.9%) than girls (9.8% and 20.2%, respectively) and a lower percentage of correctly classified subjects (81.9% versus 86.4%). The CAST was more sensitive for boys and more specific for girls, while sensitivity and specificity were more balanced in the total sample.
Table 5.
Screening properties of the CAST against the severe class
| Sensitivity | Specificity | PPV | NPV | FPR | FNR | Correct | Y = sensitivity + specificity – 1 | |
|---|---|---|---|---|---|---|---|---|
| Boys | AUC = 0.925, 95% CI = 0.910–0.940 | |||||||
| 5 | 0.965 | 0.702 | 0.276 | 0.702 | 0.298 | 0.035 | 0.730 | 0.667 |
| 6 | 0.946 | 0.756 | 0.313 | 0.756 | 0.244 | 0.054 | 0.776 | 0.701 |
| 7 | 0.901 | 0.809 | 0.358 | 0.809 | 0.191 | 0.099 | 0.819 | 0.710 |
| 8 | 0.832 | 0.848 | 0.393 | 0.848 | 0.152 | 0.168 | 0.847 | 0.680 |
| 9 | 0.787 | 0.884 | 0.445 | 0.884 | 0.116 | 0.213 | 0.874 | 0.672 |
| Girls | AUC = 0.936, 95% CI = 0.915–0.957 | |||||||
| 5 | 0.872 | 0.819 | 0.265 | 0.819 | 0.181 | 0.128 | 0.823 | 0.692 |
| 6 | 0.830 | 0.867 | 0.318 | 0.867 | 0.133 | 0.170 | 0.864 | 0.697 |
| 7 | 0.798 | 0.902 | 0.379 | 0.902 | 0.098 | 0.202 | 0.895 | 0.700 |
| 8 | 0.734 | 0.931 | 0.442 | 0.931 | 0.069 | 0.266 | 0.917 | 0.665 |
| 9 | 0.660 | 0.956 | 0.530 | 0.956 | 0.044 | 0.340 | 0.936 | 0.616 |
| Total | AUC = 0.935, 95% CI = 0.924–0.946 | |||||||
| 5 | 0.945 | 0.751 | 0.271 | 0.751 | 0.249 | 0.055 | 0.769 | 0.696 |
| 6 | 0.921 | 0.803 | 0.313 | 0.803 | 0.197 | 0.079 | 0.813 | 0.724 |
| 7 | 0.880 | 0.848 | 0.362 | 0.848 | 0.152 | 0.120 | 0.851 | 0.728 |
| 8 | 0.821 | 0.884 | 0.409 | 0.884 | 0.116 | 0.179 | 0.878 | 0.705 |
| 9 | 0.766 | 0.916 | 0.470 | 0.916 | 0.084 | 0.234 | 0.902 | 0.682 |
PPV, positive predictive value; NPV, negative predictive value; FPR, false positive rate; FNR, false negative rate; Correct, percentage of correctly classified individuals; AUC, area under receiver operating characteristic curve; CI, confidence interval; Y, Youden index.
Table 6 displays the screening properties against the combined moderate/severe class. The optimal cutoff according to the Y index was three for boys (sensitivity = 0.811, specificity = 0.774), girls (sensitivity = 0.700, specificity = 0.868) and the total sample (sensitivity = 0.775, specificity = 0.809). The corresponding AUC values were above 0.85. At the optimal cutoff, boys presented a higher false positive rate (22.6%) and a lower false negative rate (18.9%) than girls (13.2% and 30.0%, respectively), but the percentage of correctly classified subjects was similar in both gender (79.1% versus 80.2%). Again, the CAST was more sensitive for boys and more specific for girls, while sensitivity and specificity were more balanced in the total sample.
Table 6.
Screening properties of the CAST against the moderate/severe class
| Sensitivity | Specificity | PPV | NPV | FPR | FNR | Correct | Y = sensitivity + specificity – 1 | |
|---|---|---|---|---|---|---|---|---|
| Boys | AUC = 0.877, 95% CI = 0.862–0.893 | |||||||
| 1 | 0.963 | 0.479 | 0.604 | 0.479 | 0.521 | 0.037 | 0.698 | 0.442 |
| 2 | 0.880 | 0.669 | 0.686 | 0.669 | 0.331 | 0.120 | 0.764 | 0.548 |
| 3 | 0.811 | 0.774 | 0.748 | 0.774 | 0.226 | 0.189 | 0.791 | 0.585 |
| 4 | 0.733 | 0.842 | 0.793 | 0.842 | 0.158 | 0.267 | 0.793 | 0.575 |
| 5 | 0.682 | 0.890 | 0.837 | 0.890 | 0.110 | 0.318 | 0.796 | 0.573 |
| Girls | AUC = 0.853, 95% CI = 0.832–0.873 | |||||||
| 1 | 0.900 | 0.598 | 0.591 | 0.598 | 0.402 | 0.100 | 0.716 | 0.498 |
| 2 | 0.787 | 0.766 | 0.685 | 0.766 | 0.234 | 0.213 | 0.774 | 0.553 |
| 3 | 0.700 | 0.868 | 0.775 | 0.868 | 0.132 | 0.300 | 0.802 | 0.568 |
| 4 | 0.598 | 0.912 | 0.815 | 0.912 | 0.088 | 0.402 | 0.789 | 0.510 |
| 5 | 0.496 | 0.944 | 0.851 | 0.944 | 0.056 | 0.504 | 0.768 | 0.440 |
| Total | AUC = 0.869, 95% CI = 0.856–0.881 | |||||||
| 1 | 0.944 | 0.526 | 0.587 | 0.526 | 0.474 | 0.056 | 0.700 | 0.470 |
| 2 | 0.851 | 0.705 | 0.673 | 0.705 | 0.295 | 0.149 | 0.766 | 0.556 |
| 3 | 0.775 | 0.809 | 0.743 | 0.809 | 0.191 | 0.225 | 0.795 | 0.584 |
| 4 | 0.689 | 0.867 | 0.787 | 0.867 | 0.133 | 0.311 | 0.793 | 0.556 |
| 5 | 0.619 | 0.909 | 0.830 | 0.909 | 0.091 | 0.381 | 0.788 | 0.528 |
PPV, positive predictive value; NPV, negative predictive value; FPR, false positive rate; FNR, false negative rate; Correct, percentage of correctly classified individuals; AUC, area under receiver operating characteristic curve; CI, confidence interval; Y, Youden index.
Discussion
The CAST was recently validated against the DSM‐IV theoretical diagnoses (Legleye et al., 2011). In order to explore further its screening performance, our aim was to validate it against an empirical gold standard derived from the DSM‐IV criteria in the same survey sample. A previous study of the dimensionality of the cannabis use disorders construct on the same dataset (Piontek et al., 2011) led to retain only one dimension. Following this result, our LCA distinguished three latent classes for the DSM‐IV assessed with the M‐CIDI in a representative sample of French adolescents aged 17–19 years who had smoked cannabis in the previous year. The three‐class model (non‐symptomatic, moderate and severe) describes a common severity continuum represented by a single‐factor, instead of representing abuse on the one hand and dependence on the other hand. These classes were accurate predictors of daily cannabis use, of the number of joints smoked and of age of first cannabis experimentation. Boys were overrepresented in the severe class and endorsed more abuse criteria in each class but girls were overrepresented in the non‐symptomatic class and tended to report more dependence criteria in the moderate and severe classes. The differences are nevertheless rather small.
Based on the gender specific LCA gold standard, the CAST shows good discriminative power in screening for members of the severe class (AUC > 0.92) and those of the moderate/severe class (AUC > 0.85). The optimal thresholds were the same for boys, girls and the total sample: a score of seven for the severe class and a score of three for the moderate/severe class. For both classes, the CAST appeared more sensitive for boys and more specific for girls. The CAST thus appears as a short, accurate tool for screening for cannabis‐related problems in the adolescent population.
The results of the LCA support a one‐dimensional structure of the DSM‐IV with three classes that can be separated quantitatively rather than qualitatively. This is in line with an IRT analysis conducted on the same data set and also with the current proposal for DSM‐V which defines a single dimension of cannabis use disorder (American Psychiatric Association, 2010). The fact that the DSM‐IV latent classes were related to different levels of consumption frequency and quantity is also support for a continuum of problem severity. Subgroup analyses suggest that the latent structure of DSM‐IV criteria varies across gender. This lack of gender invariance is in accordance with previous research in adolescents (Martin et al., 2006a; Piontek et al., 2011) and adults (Grant et al., 2006). Our analysis showed that girls reported more often dependence symptoms than boys in the moderate class especially withdrawal, larger and longer use, impaired control, and use despite problems. Grant et al. (2006) used a lifetime span for their analyses and did not strictly exert the DSM‐IV criteria. They also found four latent classes instead of three. However, our results concerning the dependence criteria among girls are, with some exception (reduced activities is not more reported by girls in our study), in line with their results.
It is worth mentioning that although we did not find structural equivalence across gender, the three latent classes obtained separately for boys and girls and those found in the total sample were almost concordant, suggesting that gender differences with regard to the structure of DSM‐IV criteria are relatively small. This is an important feature of the DSM‐IV concept.
The present study used the latent structure of the DSM‐IV as an empirical gold standard whereas an earlier paper (Legleye et al., 2011) validated the CAST against the clinical diagnoses of dependence and cannabis use disorder with the same dataset. The comparison shows that much better screening properties were found for the empirical structure. In particular, the discriminative power of the CAST in screening for the severe class was superior to that found for dependence [AUC = 0.854 (95% CI = 0.836–0.872), sensitivity = 84.1, specificity = 71.7]. The values for the discriminative power of the CAST for screening cannabis use disorder [AUC = 0.877 (95% CI = 0.863–0.891), sensitivity = 79.5, specificity = 80.5] or the combined moderate/severe class [AUC = 0.869 (95% CI = 0.856–0.881), sensitivity = 77.5, specificity = 80.9] were very similar. The fact that the CAST accurately distinguished between the latent DSM‐IV classes suggests that it may be of significant clinical utility, not just to identify cases (i.e. screening) but also to rate problem severity. These applications would however require further testing in clinical setting.
Despite its large and representative sample, this study has certain limitations. First, the M‐CIDI was self‐administered and no information concerning psychometric properties is available. Good reliability and validity have been reported in adolescents and adult patients, respectively, using computer‐assisted interviews (Lachner et al., 1998; Reed et al., 1998). Second, there is no information available concerning test–retest reliability of the CAST, although temporal stability is an important aspect when evaluating a scale. Third, the cross‐sectional study design does not allow the identified latent classes to be interpreted as different developmental stages. Temporal progression could only be addressed in longitudinal data. Fourth, the entropy values for our three‐latent class models are below 0.8 which is usually considered a satisfactory separation of classes. This may be due to the fact that there is a real continuum in the severity of the cannabis‐related problems assessed by the DSM‐IV criteria which means class separation is difficult (Muthen, 2006; Piontek et al., 2011). More complex mixture models may be useful to take this dimensional aspect into account (Frick et al., 2012; Muthen and Asparouhov, 2006) but their utility is not always obvious when a single factor is the best solution: statistical indicators such as BIC were close for different models assessing the latent structure of alcohol and cannabis diagnostic criteria (Baillie and Teesson, 2010). Because the conditional independence assumption was not strictly verified we added direct effects. This did not change the classification substantially: the resulting classes from the model with and without direct effects overlapped almost perfectly and the screening properties of the CAST were almost unchanged. Our results are then rather robust.
Although models describing the latent structure of the DSM criteria might be improvable, the classes found in our study are easy to interpret and provide a good description of cannabis‐related problems in the adolescent population reported in other studies (Gillespie et al., 2007; Teesson et al., 2002). Further research should investigate the concordance of CAST and DSM‐IV in greater detail. One promising way is to compare their factorial structures using multiple factor analysis (Escofier and Pagès, 1998), which enables the identification of common underlying components in the concurrent sets of the CAST and the DSM‐IV items.
Declaration of interest statement
The authors have no competing interests.
Acknowledgements
The authors would like to thank the EMCDDA for its support and funding.
References
- Adamson S.J., Kay‐Lambkin F.J., Baker A.L., Lewin T.J., Thornton L., Kelly B.J., Sellman J.D. (2010) An improved brief measure of cannabis misuse: the Cannabis Use Disorders Identification Test‐Revised (CUDIT‐R). Drug and Alcohol Dependence, 110(1‐2), 137–143. [DOI] [PubMed] [Google Scholar]
- American Psychiatric Association . (2010) DSM‐5 Development. Cannabis‐use Disorder, Washington, DC: American Psychiatric Association. [Google Scholar]
- Annaheim B., Scotto T.J., Gmel G. (2010) Revising the Cannabis Use Disorders Identification Test (CUDIT) by means of Item Response Theory. International Journal of Methods in Psychiatric Research, 19, 142–155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Babor T.F., Caetano R. (2006) Subtypes of substance dependence and abuse: implications for diagnostic classification and empirical research. Addiction, 101(Suppl. 1), 104–110. [DOI] [PubMed] [Google Scholar]
- Baillie A.J., Teesson M. (2010) Continuous, categorical and mixture models of DSM‐IV alcohol and cannabis use disorders in the Australian community. Addiction, 105, 1246–1253. [DOI] [PubMed] [Google Scholar]
- Bashford J., Ross F., Copeland J. (2010) The Cannabis Use Problems Identification Test (CUPIT): development, reliability, concurrent and predictive validity among adolescents and adults. Addiction, 105, 615–625. [DOI] [PubMed] [Google Scholar]
- Beck F., Costes J.‐M., Legleye S., Peretti‐Watel P., Spilka S. (2006) L'enquête ESCAPAD sur les usages de drogues: un dispositif original de collecte sur un sujet sensible [The Escapad Survey on Drug Use: an original data collection tool on a sensitive subject] In Lavallée P., Rivest L.‐P. (eds) Méthodes d’enquêtes et sondages Pratiques européenne et nord‐américaine [Survey Methods: European and North American Practices], pp. 56–59, Paris: Dunod. [Google Scholar]
- Budney A.J., Hughes J.R., Moore B.A., Vandrey R. (2004) Review of the validity and significance of cannabis withdrawal syndrome. The American Journal of Psychiatry, 161, 1967–1977. [DOI] [PubMed] [Google Scholar]
- Celeux G., Soromenho G. (1996) An entropy criterion for assessing the number of clusters in a mixture model. Journal of Classification, (13), 195–212. [Google Scholar]
- Coffey C., Carlin J.B., Lynskey M., Li N., Patton G.C. (2003) Adolescent precursors of cannabis dependence: findings from the Victorian Adolescent Health Cohort Study. The British Journal of Psychiatry, (182), 330–336. [DOI] [PubMed] [Google Scholar]
- Compton W.M., Saha T.D., Conway K.P., Grant B.F. (2009) The role of cannabis use within a dimensional approach to cannabis use disorders. Drug and Alcohol Dependence, 100, 221–227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crowley T.J. (2006) Adolescents and substance‐related disorders: research agenda to guide decisions on Diagnostic and Statistical Manual of Mental Disorders, fifth edition (DSM‐V). Addiction, 101(Suppl. 1), 115–124. [DOI] [PubMed] [Google Scholar]
- Escofier B., Pagès J. (1998) Analyses factorielles simples et multiples: objectifs, méthodes et interprétation [Simple and Multiple Factor Analysis: Aims, Methods and Interpretation], Paris: Dunod. [Google Scholar]
- Falissard B. (2009) Various Procedures Used in Psychometry.
- Frick H., Strobl C., Leisch F., Zeileis A. (2012) Flexible Rasch mixture models with package psychomix. Journal of Statistical Software, 48, 1–25. [Google Scholar]
- Garrett E.S., Eaton W.W., Zeger S. (2002) Methods for evaluating the performance of diagnostic tests in the absence of a gold standard: a latent class model approach. Statistics in Medicine, 21, 1289–1307. [DOI] [PubMed] [Google Scholar]
- Gillespie N.A., Neale M.C., Prescott C.A., Aggen S.H., Kendler K.S. 2007. Factor and item‐response analysis DSM‐IV criteria for abuse of and dependence on cannabis, cocaine, hallucinogens, sedatives, stimulants and opioids. Addiction, 102, 920–930. [DOI] [PubMed] [Google Scholar]
- Grant J.D., Scherrer J.F., Neuman R.J., Todorov A.A., Price R.K., Bucholz K.K. (2006) A comparison of the latent class structure of cannabis problems among adult men and women who have used cannabis repeatedly. Addiction, 101, 1133–1142. [DOI] [PubMed] [Google Scholar]
- Hagenaars J.A., McCutcheon A.L. (2002) Applied Latent Class Analysis, Cambridge: Cambridge University Press. [Google Scholar]
- Hawkins D.M., Garrett J.A., Stephenson B. (2001) Some issues in resolution of diagnostic tests using an imperfect gold standard. Statistics in Medicine, 20, 1987–2001. [DOI] [PubMed] [Google Scholar]
- Hesselbrock V.M., Hesselbrock M.N. (2006) Are there empirically supported and clinically useful subtypes of alcohol dependence? Addiction, 101(Suppl. 1), 97–103. [DOI] [PubMed] [Google Scholar]
- Lachner G., Wittchen H.U., Perkonigg A., Holly A., Schuster P., Wunderlich U., Turk D., Garczynski E., Pfister H. (1998) Structure, content and reliability of the Munich‐Composite International Diagnostic Interview (M‐CIDI) substance use sections. European Addiction Research, 4, 28–41. [DOI] [PubMed] [Google Scholar]
- Landis J.R., Koch G.G. (1977) The measurement of observer agreement for categorical data. Biometrics, 33, 159–174. [PubMed] [Google Scholar]
- Langenbucher J.W., Labouvie E., Martin C.S., Sanjuan P.M., Bavly L., Kirisci L., Chung T. (2004) An application of item response theory analysis to alcohol, cannabis, and cocaine criteria in DSM‐IV. Journal of Abnormal Psychology, 113, 72–80. [DOI] [PubMed] [Google Scholar]
- Lanza S.T., Collins L.M., Lemmon D.R., Schafer J.L. (2007) PROC LCA: A SAS procedure for latent class analysis. Structural Equation Modeling, 14, 671–694. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lazarsfeld P.F., Henry N.W. (1968) Latent Structure Analysis, Boston, MA: Houghton Mifflin. [Google Scholar]
- Legleye S., Karila L., Beck F., Reynaud M. (2007) Validation of the CAST, a general population cannabis abuse screening test. Journal of Substance Use, 12, 233–242. [Google Scholar]
- Legleye S., Piontek D., Kraus L. (2011) Psychometric properties of the Cannabis Abuse Screening Test (CAST) in a French sample of adolescents. Drug and Alcohol Dependence, 113, 229–235. [DOI] [PubMed] [Google Scholar]
- Magidson J., Vermunt J. 2001. Latent class factor and cluster models, bi‐plots and related graphical displays. Sociological Methodology, (31), 223–264. [Google Scholar]
- Martin C.S., Chung T., Kirisci L., Langenbucher J.W. (2006a) Item response theory analysis of diagnostic criteria for alcohol and cannabis use disorders in adolescents: implications for DSM‐V. Journal of Abnormal Psychology, 115, 807–814. [DOI] [PubMed] [Google Scholar]
- Martin G., Copeland J., Gates P., Gilmour S. (2006b) The Severity of Dependence Scale (SDS) in an adolescent population of cannabis users: reliability, validity and diagnostic cut‐off. Drug and Alcohol Dependence, 83, 90–93. [DOI] [PubMed] [Google Scholar]
- Muthen B. (2006) Should substance use disorders be considered as categorical or dimensional? Addiction, 101(Suppl. 1), 6–16. [DOI] [PubMed] [Google Scholar]
- Muthen B., Asparouhov T. (2006) Item response mixture modeling: application to tobacco dependence criteria. Addictive Behaviors, 31, 1050–1066. [DOI] [PubMed] [Google Scholar]
- Piontek D., Kraus L., Klempova D. (2008) Short scales to assess cannabis‐related problems: areview of psychometric properties. Substance Abuse Treatment, Prevention, and Policy, 3, 25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Piontek D., Kraus L., Legleye S., Buhringer G. (2011) The validity of DSM‐IV cannabis abuse and dependence criteria in adolescents and the value of additional cannabis use indicators. Addiction, 106, 1137–1145. [DOI] [PubMed] [Google Scholar]
- Reed V., Gander F., Pfister H., Steiger A., Sonntag H., Trenkwalder C., Sonntag A., Hundt W., Wittchen H.U. (1998) To what degree does the Composite International Diagnostic Interview (CIDI) correctly identify DSM‐IV disorders? Testing validity issues in a clinical sample. International Journal of Methods in Psychatric Research, 7, 142–155. [Google Scholar]
- Rey J.M., Morris‐Yates A., Stanislaw H. (1992) Measuring the accuracy of diagnostic tests using receiver operating characteristics (ROC) analysis. International Journal of Methods in Psychatric Research, (2), 1–11. [Google Scholar]
- Steiner S., Baumeister S.E., Kraus L. (2008) Severity of Dependence Scale: establishing a cut‐off point for cannabis dependence in the German adult population. Sucht, 54, S57–S63. [Google Scholar]
- Teesson M., Lynskey M., Manor B., Baillie A. (2002) The structure of cannabis dependence in the community. Drug and Alcohol Dependence, 68, 255–262. [DOI] [PubMed] [Google Scholar]
- Vandrey R., Budney A.J., Kamon J.L., Stanger C. (2005) Cannabis withdrawal in adolescent treatment seekers. Drug and Alcohol Dependence, 78, 205–210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vermunt J.K., Magidson J. (2005) Latent GOLD 4.0 User's Guide, Belmont, MA: Statistical Innovations Inc. [Google Scholar]
- Wittchen H.‐U., Beloch E., Garczynski E., Holly A., Lachner G., Perkonigg A., Pfütze E.‐M., Schuster P., Vodermaier A., Vossen A., Wunderlich U., Zieglgänsberger S. (1995) Münchener Composite International Diagnostic Interview (M‐CIDI), Paper‐pencil 2.2, 2/95, München: Max‐Planck‐Institut für Psychiatrie, Klinisches Institut. [Google Scholar]
- Wolfe J.H. (1970) Pattern clustering by multivariate mixture analysis. Multivariate Behavioral Research, (5), 329–350. [DOI] [PubMed] [Google Scholar]


