Abstract
Objective:
Develop a high-performing algorithm to detect mesial temporal lobe (mTL) epileptiform discharges on intracranial electrode recordings.
Methods:
An epileptologist annotated 13,959 epileptiform discharges from a dataset of intracranial EEG recordings from 46 epilepsy patients. Using this dataset, we trained a convolutional neural network (CNN) to recognize mTL epileptiform discharges from a single intracranial bipolar channel. The CNN outputs from multiple bipolar channel inputs were averaged to generate the final detector output. Algorithm performance was estimated using a nested 5-fold cross-validation
Results:
On the receiver-operating characteristic curve, our algorithm achieved an area under the curve (AUC) of 0.996 and a partial AUC (for specificity > 0.9) of 0.981. AUC on a precision-recall curve was 0.807. A sensitivity of 84% was attained at a false positive rate of 1 per minute. 35.9% of the false positive detections corresponded to epileptiform discharges that were missed during expert annotation.
Conclusions:
Using deep learning, we developed a high-performing, patient non-specific algorithm for detection of mTL epileptiform discharges on intracranial electrodes.
Significance:
Our algorithm has many potential applications for understanding the impact of mTL epileptiform discharges in epilepsy and on cognition, and for developing therapies to specifically reduce mTL epileptiform activity.
Keywords: Spike detection, Epileptiform discharges, Temporal lobe epilepsy, Deep learning, Convolutional neural networks
1. Introduction
Inter-ictal epileptiform discharge (IEDs, also known as epileptiform discharges or spikes) are an EEG biomarker of epilepsy, whose physiologic role remains poorly understood. Much research is devoted to understanding the clinical relevance of IEDs and their relation with seizure generation (Hufnagel et al. 2000; Karoly et al. 2016), cognition (Kleen et al. 2010), and memory (Stein et al. 2016; Ung et al. 2017). This has motivated the development of automated algorithms for the detection of and quantification of spikes in both intracranial and scalp EEG recordings (Carrie 1972). While many approaches to spike detection have been used, including template matching (Kim and McNames 2007; Vijayalakshmi and Abhishek 2010; Lodder et al. 2013; Horak et al. 2015), wavelet analysis (Haydari et al. 2011; Le Douget et al. 2017), mimetic analysis (Boos et al. 2011; Liu et al. 2013), and power spectral analysis (Hassanpour et al. 2004; Yang et al. 2017), these detectors often suffer from a high number of false detections, which limit their utility in clinical or research applications (Halford 2009). These shortcomings highlight the difficulty of explicitly formulating the features that trained experts use to visually detect spikes on the EEG.
Deep neural networks have recently revolutionized the field of artificial intelligence, achieving unprecedented results and even surpassing human performance in many fields of applications including computer vision (Krizhevsky et al. 2012), natural language processing (Kim 2014), and bioinformatics (Sønderby et al. 2015). One of the strengths of deep neural networks is their ability to automatically learn relevant features from the input domain, bypassing the need to design handcrafted features that may or may not be relevant for the task. One type of deep neural network, the convolutional neural network (CNN), is particularly suitable for learning time-invariant morphological features from input data, and has only recently begun to be applied for IED detection, with promising results (Antoniades et al. 2016; Johansen et al. 2016; Tjepkema-Cloostermans et al. 2018).
The aim of this study was to develop a high-performing algorithm to detect mesial temporal lobe (mTL) epileptiform discharges on intracranial electrode recordings, using CNNs to extract the relevant features for detection. As the mTL is the most commonly studied brain region in patients with medication-refractory epilepsy undergoing invasive monitoring, the ability to accurately detect and quantify mTL epileptiform discharges on intracranial electrodes has many potential applications in both the clinical and research domains.
2. Methods
2.1. Patient Population
This study used data from patients who underwent monitoring with combined foramen ovale (FO) electrodes and scalp EEG electrodes at our institution between 2008 and 2017. Data was analyzed retrospectively under a protocol approved by our center’s Institutional Review Board. We selected patients with mTL epilepsy, based on semiology, neurophysiologic findings, and clinical imaging. Exclusion criteria included prior brain instrumentation or extra-temporal brain structural abnormalities.
2.2. Foramen ovale (FO) electrode recordings
Four-contact FO electrodes (Ad-Tech, Racine, WI) were placed bilaterally using fluoroscopic guidance, as described previously (Sheth et al., 2014; Wieser et al., 1985). FO electrodes are positioned to lie in the ambient cistern, directly adjacent to the mTL. As such, FO electrodes provide high-fidelity recordings of electrical activity specifically from the mTL. All recordings were acquired using XLTEK hardware (Natus Medical Inc., Pleasanton CA) with data sampled at 1024 Hz.
2.3. EEG processing and artifact detection
Preprocessing of the FO electrode data (FO-EEG), including downsampling, filtering, and artifact removal, was performed in MATLAB (Mathworks, Natick, MA), using custom and freely available scripts, including EEGLab (Delorme and Makeig 2004). Recordings were downsampled to 256Hz, then bandpass filtered from 0.5-70Hz with a Butterworth third order filter, and notch filtered at 60 Hz with a Butterworth fourth-order filter. We generated a bipolar montage for the FO channels, consisting of three channels each for the left (LFO1-LFO2, LFO2-LFO3, LFO3-LFO4) and right (RFO1-RFO2, RFO2-RFO3, RFO3-RFO4) FO electrodes. The first contacts of each electrode (LFO1, RFO1) are the deepest contacts. We also generated a common referential montage for the FO channels using a C2 reference electrode, resulting in 4 channels each for the left (LFO1-C2, LFO2-C2, LFO3-C2, LFO4-C2) and right (RFO1-C2, RFO2-C2, RFO3-C2, RFO4-C2) FO electrodes.
We used custom scripts to automate artifact and bad channel detection on the FO-EEG channels. Artifact detection was performed on one-second epochs of FO-EEG data, using the following features: maximal amplitude, area under the curve, line length, and high-frequency power. For each non-overlapping, one-second epoch in each FO-EEG channel (including bipolar and common referential channels), we calculated the features above, then normalized each feature by subtracting the median and dividing by the interquartile range (IQR, 75th percentile - 25th percentile) for all epochs within a recording (typically ~ 24 hours in length). We set thresholds for each feature and defined a channel epoch as artifactual if one of its features exceeded the set thresholds. Specifically, thresholds were set such that ~ 2% of IEDs would be removed. Additionally, we considered a channel in a one second epoch to be “flat” if its standard deviation was less than 2.5 μV.
Detection of “bad” channels (channels that showed anomalous signals for extended portions of the record) was performed on 30 second epochs of FO-EEG data. This was done on both common referential and bipolar montages. We defined a 30s epoch of a given FO-EEG channel to be “bad” if: 1) its average correlation coefficient with all other FO-EEG channels was less than 0.15; or 2) its IQR was at least three times greater than the median IQR of the other FO-EEG channels.
For an FO-EEG epoch to be used for spike detection, we required that it have at least two valid (i.e., not flagged as artifact or bad channels) common referential channels and two valid bipolar channels. Using these criteria, ~93% of the original data could be used for spike detection.
2.4. Generating a Gold Standard Dataset
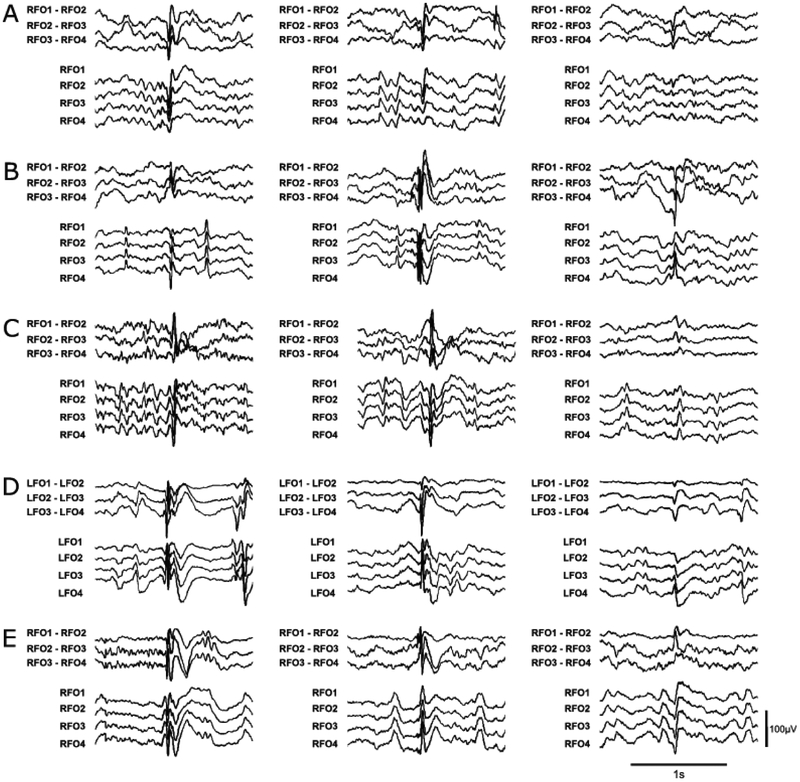
A board-certified epileptologist (ADL) annotated mTL IEDs on the FO-EEG recordings, using a custom-made graphical user interface (GUI) that displayed random 15 second epochs of FO-EEG data from each patient. The epileptologist could view both the FO-EEG and scalp EEG data, switch between different montages (including longitudinal bipolar, referential, and average montages), and adjust gain and filter settings as they typically would for clinical EEG interpretation. The epileptologist was instructed to mark at least 250 IEDs for each patient. The epileptologist indicated the level of confidence in the IED annotations by marking “definite” IEDs, including epileptiform spikes, polyspikes, and sharp waves. The epileptologist also marked “indeterminate” IEDs, which were defined as sharp transients that had location and morphology similar to “definite” IEDs within the same recording, but that themselves were not definitively epileptiform (typically due to low amplitude or failure to stand out sufficiently from the background activity). Each annotated IED was defined by a 250ms time window centered around the sample marked by the expert. All epochs that were not annotated as “definite” or “indeterminate” IEDs by the expert were defined as non-IEDs, which included baseline activity as well as artifacts not captured by our automated artifact detection algorithm. Examples of “definite” IEDs, “indeterminate” IEDs, and non-IEDs are shown in Fig. 1.
Figure 1:
Representative examples of “definite” and “indeterminate” IEDs for 5 patients, including (A) Patient #4; (B) Patient #9; (C) Patient #25; (D) Patient #26; and (E) Patient #28. The left and middle columns show “definite” IEDs, while the right column shows “indeterminate” IEDs. Amplitude and time scales for all examples are shown in the bottom right corner. Patient numbers correspond to those shown in Supplementary Table 1.
2.5. Training and Testing Data sets
We used a 5-fold cross validation scheme (described below), such that data from each patient was used either as training or as testing data, depending on the fold. For each patient, the training data and testing data were generated differently.
For training data sets, positive examples were extracted by taking a 1s window centered on each “definite” annotated spike. All other epochs, including “indeterminate” spikes, were extracted as negative examples. We used data augmentation (Krizhevsky et al. 2012) to artificially generate additional training examples. For each “definite” IED (ie, each positive training example), we created an additional 24 positive training examples, by shifting the original example by a randomly chosen time jitter of s ∈ [−125, 125] ms. This was performed for all “definite” IEDs, for all patients in the training dataset. To generate an evenly balanced training data set with an equal number of examples of IEDs and non-IEDs, we randomly discarded non-IED examples (which vastly exceed the number of IED examples) from the training set, to match the number of IED examples (including the augmented examples) and non-IED examples.
Testing datasets for each patient were generated by applying a sliding window of 1s with a step size of 250ms, across all of the patient’s data that was annotated by the expert. A 1s FO-EEG testing epoch was considered to contain an IED if at least 50% of the 250ms window in the center of that epoch was covered by a spike annotation. In the testing dataset, no data augmentation or balancing of IED and non-IED examples was applied, to more closely approximate real-world application.
The final model was trained using the entire training dataset from all patients.
2.6. Spike Detector Architecture
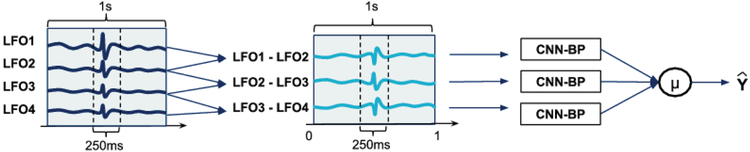
A schematic of our algorithm to detect IEDs from FO-EEG data is shown in Fig. 2 The algorithm is agnostic to laterality and can detect IEDs on either the left FO electrode (LFO) or the right FO electrode (RFO). The input to the algorithm is a 1 second epoch of FO-EEG data. Based on this 1 second input, the algorithm detects whether an IED is present within the central 250ms of this epoch. For each 1-second input, the pre-processed signal from each valid FO-EEG bipolar channel is independently fed to a CNN (CNN-BP, described below). The CNN-BP outputs for each of the valid bipolar channels are then averaged to yield a final determination of whether an IED is present in the central 250ms epoch.
Figure 2:
Outline of the IED detection scheme. Each FO bipolar channel is fed to a convolutional neural network (CNN-BP), which outputs the probability that the signal contains an IED. The 3 outputs are averaged to provide a final decision of whether an IED is present.
The architecture of CNN-BP is shown in Fig. 3. The input provided to CNN-BP is a 1 second epoch from a single FO-EEG bipolar channel. The output of CNN-BP represents the estimated probability that an IED occurred in the central 250msec of the input epoch. CNN-BP follows a typical CNN architecture, which consists of a sequence of convolutional and pooling layers followed by a series of fully connected layers (LeCun et al. 1998; Krizhevsky et al. 2012; Simonyan and Zisserman 2014). CNN-BP has three convolutional layers, which is in the typical range for applications on EEG signals (Roy et al. 2019). The first convolutional layer contains fi filters, each consisting of 32 samples which corresponds to a duration of 125ms. Of note, fi represents the number of filters for the first convolutional layer, which was a hyperparameter that was tuned during the cross-validation procedure, as described below. The second convolutional layer contains 2fi filters consisting of 16 samples each, allowing this layer to capture the subtler features of an IED. The third convolutional layer consists of 3fi filters with 8 samples each. Each convolutional layer is followed by a maxpooling layer of size = 4 and stride = 1, as well as a dropout regularization step with a dropout probability of 0.2. Following the three convolutional layers is a single fully-connected layer with 12fi neurons, followed by a logistic regression unit for final classification. We use the rectified linear unit (relu) function (Nair and Hinton 2010) as the activation function in the convolutional and fully connected layers, while the sigmoid function is used as the activation function for the final single neuron.
Figure 3:
Architecture of the convolutional neural network used to detect an IED on an individual FO bipolar channel. The input is a 1s bipolar FO signal. The output Ybp is the probability that the central 250ms of this epoch contains an IED. Further details regarding the architecture are provided in the text. The blue boxes under Conv1D represent the filters in the convolutional layer. BN = Batch Normalization; FC = Fully Connected layer
Of note, training CNN-BP to recognize IEDs from a single bipolar channel input (rather than using a combined input from all bipolar channels) permits a larger training set, as each individual IED will generate up to three positive examples (one for each ipsilateral bipolar channel) with which to train the CNN. Moreover, this simplifies the training procedure, as the CNN does not need to learn the relationship between the three bipolar channels and missing/bad channels do not need to be accounted for.
2.7. Deep Learning Methods
The neural network library Keras (Chollet François 2015) running on top of Tensorflow (Martín et al. 2016) was used to build and configure the CNN model, which was trained on two CUDA-enabled NVIDIA GPUs, running on CentOS 7. The CNN model was trained using the Adaptive Moment Estimation (Adam) optimization algorithm (Kingma and Ba 2015) with a batch-size of 128, and parameters β1, β2 and ε set to 0.9, 0.999, and 10−8, respectively. We used the log (cross-entropy) loss function. To prevent overfitting, we used dropout regularization (Srivastava et al. 2014) after each maxpool layer, with a dropout probability of 0.2.
We trained each CNN model for 5 epochs, where an epoch is defined as a complete pass over all the training data. To make the learning process more efficient, we used batch normalization (Ioffe and Szegedy 2015) and learning rate decay. The optimal learning rate α and the number of filters fi were determined by searching over the values [0.01, 0.001, 0.0001] and [16, 32] respectively, using a 5-fold cross validation scheme across patients.
For 5-fold cross-validation, patients were first partitioned into 5 folds. For a given hyperparameter pairset [αi, fi], the CNN was trained on data from 4 folds, and tested on the data from the left-out fold (testing fold). This was repeated 5 times, with each fold being used once as the testing fold. The test fold results from each iteration were aggregated across all folds to determine the performance for the [αi, fi] pair. This procedure was then repeated for each pair [αi, fi] in the grid, to find the pair with the best performance (highest AUCPR).
An unbiased estimate of the performance of this model selection process was also evaluated using a nested 5-fold cross validation. In this scheme, the patients are first partitioned into 5 outer folds. The data from 4 outer folds are further partitioned into 5 inner folds. A simple cross-validation, as described above, is carried out on these inner folds to determine the optimal pair [αi, fi]. The resulting CNN with the optimal hyperparameters is then trained on the inner folds and tested on the held-out outer fold. This is repeated 5 times, with each outer fold being used once as the testing fold. This result provides an unbiased estimate of the expected performance of the algorithm in detecting IEDs on unseen FO-EEG data from new patients.
2.8. Evaluation Metrics
A positive IED detection was defined as any detection made within 375ms of the expert annotated spike. We determined the performance of our classifier using the area under the curve (AUC) for the receiver operating characteristic (ROC) curve, as well as a standardized partial AUC (pAUC) (McClish 1989), which considers only the region of the ROC curve that corresponds to a specificity greater than 0.9. We also report the area under the curve under the Precision-Recall curve (AUCPR). To prioritize detection of “definite” IEDs, without penalizing the detection of “indeterminate” IED, we defined the sensitivity of detection as the number of correctly detected “definite” IED, divided by the total number of “definite” IED in the dataset. We defined precision, also known as positive predictive value (PPV), as the number of correctly detected “definite” and “indeterminate” IED, divided by the total number of detections made. Specificity was defined as the number of correctly identified background waveforms (non-IEDs) over the total number of these waveforms. We also report the false positive rate, as the number of false positive detections per minute of recording.
2.9. Statistical Analysis
Group results are reported as mean ± standard deviation unless stated otherwise. Intra- and inter-rater reliability for expert labeling of IEDs were assessed using Gwet’s AC coefficient (Gwet 2008). This measure provides adjustment for chance agreement and misclassification errors and has previously been used in studies assessing inter-rater agreement for IED detection (Halford et al. 2013, 2017). Agreement based on Gwet’s AC coefficient can be interpreted as follows: 0.8–1.0: ‘Very Good’; 0.6–0.8: ‘Good’; 0.4–0.6: ‘Moderate’; 0.2–0.4: ‘Fair’; <0.2: ‘Poor’ (Bagheri et al. 2017). Comparison of spike detection during seizures vs baseline was done using paired t-tests.
3. Results
3.1. Patient demographics and IED characteristics
This study used data sets generated from intracranial FO-EEG recordings from 46 patients with temporal lobe epilepsy who previously underwent evaluation in our center’s Epilepsy Monitoring Unit.Supplementary Table 1 shows the patient demographics, clinical characteristics, and details of their annotated FO-EEG data. The patient population was comprised of 19 females and 27 males, with a mean age of 40 ± 15 years. Variable IED rates across patients resulted in variability in the amount of data that the expert had to review in order to label a similar number of spikes per patient.
Altogether, the expert-annotated gold standard dataset comprised 102 hours of recording (median = 1h per patient, range = [0.1, 17.8]) and consisted of 13,959 “definite” IEDs and 8,541 “indeterminate” IEDs, with an average of 303 ± 110 “definite” IEDs and 186 ± 171 “indeterminate” IEDs per patient. This amounted to 40,942 IEDs on individual channels, after removing examples on channels that were flagged as bad or containing artifacts.
To assess the robustness and reliability of the expert-annotated gold standard dataset, the same expert (ADL) re-annotated a subset of this dataset, blinded to the previously annotated labels. This subset included data from all patients, consisted of ~ 4 hours of recording, and contained 1,061 “definite” spikes and 708 “indeterminate” spikes that were previously annotated by that expert. Gwet’s AC coefficient for intra-rater agreement based on this subset of re-annotated data was 0.586, indicating moderate agreement. In addition, a second expert (CSJ, a board-certified epileptologist) annotated the same subset of data, blinded to all previously annotated labels. Gwet’s AC coefficient for inter-rater agreement was 0.724, indicating good agreement. Among epochs labeled as non-IEDs, there was over 99% agreement between experts.
3.2. Performance of the automated IED detector
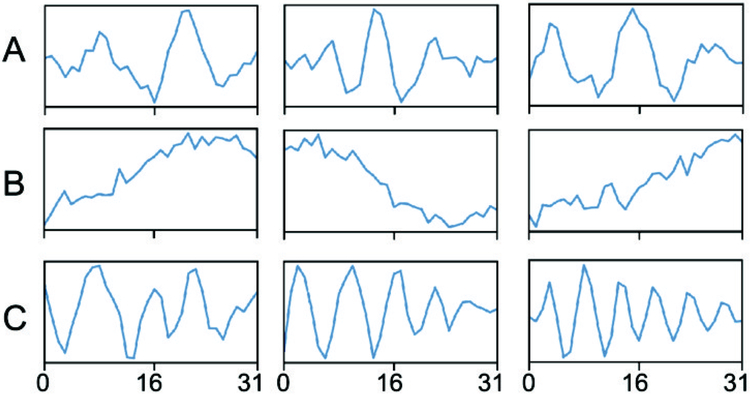
Using cross-validation, we determined that the best performing CNN-BP model used a learning rate (αi) of 0.01 and filter base number (fi) of 32. Fig. 4 shows 9 representative filters from the first convolutional layer from the best-performing model. The filters capture important morphological features of IEDs, including spikes (Fig 4A), slow-waves (Fig 4B), and polyspikes (Fig 4C), indicating that the neural network has learned salient features relevant to the spike detection task.
Figure 4:
Representative filter weights for the first convolutional layer. Each box represents a different filter, with the x-axis representing sample number and the y-axis representing the weights of the filter. The learned filters show a resemblance to salient features for IED detection, including (A) spikes, (B) slow waves, and (C) polyspikes.
Based on nested cross-validation, which provides an unbiased estimate of the expected performance of our algorithm in detecting IEDs on data from new patients, our algorithm achieved an AUC of 0.996 ± 0.002 and a pAUC of 0.981 ± 0.006. The precision-recall curve had an AUCPR of 0.807 ± 0.066. Augmentation of the training dataset (described in Section 2.5) was highly effective at improving performance of the algorithm, as the same neural network trained on the non-augmented dataset achieved a pAUC of only 0.877 ± 0.016 and an AUCPR of 0.568 ± 0.102. The algorithm’s sensitivity as a function of the false positive rate per minute is displayed in Fig. 5A. At a false positive rate less than 6/min (considered by some to be the maximum false positive rate for a spike detector to be useful (Wilson and Emerson 2002)), the algorithm achieved a sensitivity of 97.0 ± 1.0%. For a false positive rate of less than 1/min, the detector had a sensitivity of 84.0 ± 4.0%. For a PPV of 0.80, the spike detector achieved a sensitivity of 67.7 ± 11.0%. Examples of the algorithm’s true positive and true negative classifications are shown in Fig. 6, and false positive and false negative classifications in Fig. 7.
Figure 5:
Performance characteristics of the IED detection algorithm. (A) Sensitivity vs False Positive Rate; and (B) Sensitivity and PPV vs detection threshold. The line and error bars/shaded regions respectively correspond to the mean and standard deviation of each curve, across the nested cross-validation outer folds.
Figure 6:
Representative examples of correctly classified segments on nested cross validation. (A) Three examples of true positive classifications. Examples from left to right were taken from Patients 2, 6, and 23, respectively. (B) Three examples of true negative classifications. Examples from left to right were taken from Patients 31, 40, and 41, respectively. Patient numbers correspond to those shown in Supplementary Table 1.
Figure 7:
Representative examples of incorrectly classified segments on nested cross validation. (A) Three examples of false positive classifications. Examples from left to right were taken from Patients 25, 27, and 34, respectively. (B) Three examples of false negative classifications. Examples from left to right were taken from Patients 22, 29, and 36, respectively. Patient numbers correspond to those shown in Supplementary Table 1.
As an additional test of our algorithm’s performance, we assessed its output on 47 mTL seizures from 16 patients, with the reasoning that most seizures consist of repetitive spiking activity that should be detectable by our algorithm. None of these seizures were included in the training or testing datasets used in the cross-validation procedures above. We analyzed the first 60 seconds of each seizure. Not surprisingly, 37% of all seizure epochs were removed by the automated artifact detector. Using a detection threshold of 0.9, which corresponds to a PPV of 75% and sensitivity of 72%, our algorithm detected IEDs in 29% of the remaining seizure epochs. In comparison, the algorithm detected IEDs in only 3% of epochs from a 60-second pre-seizure baseline segment that spanned from 90 seconds to 30 seconds prior to each seizure’s start time. FO spike detection rates during seizures were significantly greater than during the pre-seizure baseline (p < 0.001).
3.3. Patient-specific performance of the automated IED detector
We next sought to evaluate how well the detector performed for individual patients. For each nested cross-validation fold, we set the threshold on the detector’s output to attain a PPV of 0.8 for the outer fold. We then determined the corresponding performance metrics for each patient in the outer fold (Supplementary Table 2). For a fixed PPV of 0.78 ± 0.02, patient-specific sensitivities ranged between 22.4% and 99.5%. This interpatient variability in the IED detector’s performance was likely related to differences in IED morphology and EEG background for each patient. Some patients have high amplitude IEDs with robust morphology and a relatively low-amplitude background, which makes it easier for the algorithm to detect the IEDs. Other patients have a highly active background, with abundant IED activity, or have IEDs with low amplitudes, making the IEDs more difficult to detect.
3.4. Evaluation of False Positive Detections
To better understand our algorithm’s performance with regards to false positive detections, we examined a random subset of 881 false positive detections, sampled uniformly across all patients, at a detector threshold corresponding to a PPV of 0.8. (See Figs. 6 and 7 for examples of true positive and false positive detections, respectively). These examples were closely examined by an expert epileptologist (ADL), who found that 35.9% of the algorithm’s false positive detections could be attributed to IEDs that were missed on initial expert annotation and that thus represent “false false positives”. As such, the actual false positive rate of our detector is even lower than what we have reported above. The remaining false positives were classified as follows: 10.9% were due to sharp transients that were not definitively epileptiform; 10.1% were due to artifacts that were not captured by the automated artifact detector; 23.1% were due to high-frequency, low-amplitude background activity; 3.7% were due to high-amplitude background activity; and 3.2% were due to large slow waves. An obvious cause for a positive detection was not found for 13.1% of false positives, where the expert observed only normal background activity.
4. Discussion
We have developed a high-performing algorithm for detection of mTL IEDs on intracranial electrodes, using a deep learning approach. Most machine learning algorithms require the user to pre-select specific input features that are thought to provide important information for the classification task. Using deep learning, however, we were able to input essentially raw FO-EEG signals directly to a CNN, which automatically learned the relevant features from the data, in order to detect IEDs with high sensitivity and specificity.
Few other groups have used deep learning for intracranial spike detection (Antoniades et al. 2016, 2017). One of the notable advantages of a deep learning approach to intracranial IED detection is the potential for continued improvement in performance with additional data. Unlike other classifier architectures, the performance of deep neural networks can often be continuously enhanced with larger training data sets (Sun et al. 2017). Our expert-annotated dataset of IEDs was larger than most IED datasets that have previously been used to train an intracranial IED detector. We additionally used data augmentation techniques to further expand this dataset by 24-fold, which allowed us to train a solidly performing CNN. Further modifications to the network architecture, as well as further tuning of the inputs (e.g., epoch length, different channel types) and hyper-parameters (e.g., filter size, batch size, dropout rate, number of layers) could potentially improve detector performance in the future. Additionally, the sensitivity of the detector might be improved by combining the outputs of each channel differently, particularly for IEDs that are relatively equipotential across FO electrode contacts and that may thus be poorly visible on the bipolar channels (see, for example, the false negative detections in Fig. 7). We experimented with using referential montage channels as additional inputs to our IED detector but found that they did not significantly improve performance of the detector (data not shown). We also experimented with a number of different hyper-parameters, including batch size, dropout rate, the number of convolutional and fully connected layers, but did not find these to make a meaningful difference in performance (data not shown).
Our intracranial IED detection algorithm is unique in that it specifically detects mTL IEDs from FO electrode recordings, whereas most other intracranial IED detectors have been applied to recordings from stereotactic depth and/or subdural grid electrodes and probe activity from wider and more varied regions of the brain. Given the differences between recording methods and datasets, a direct comparison of our algorithm’s performance with prior studies cannot easily be made. Noting this important caveat, however, we have nonetheless tried to summarize the results of previously published intracranial IED detectors, to give a sense of how our algorithm’s performance fits into the current landscape of intracranial IED detection. Gaspard et al utilized a dataset of 10 patients and 5,966 IEDs recorded on subdural strip, grid, or depth electrodes, to develop a spike detector based on the quantification of time–frequency properties of spikes. Their detector achieved a sensitivity of 75.6% with a false positive rate of 6 false detections per minute. Janca et al. used a dataset of 30 patients and 6,518 IEDs recorded on subdural or depth electrodes to develop a spike detector based on the modeling of the statistical distribution of the signal envelope. They reported a sensitivity of 88.9% with a false positive rate of 5.2 false detections per minute. In comparison, our IED detector achieved sensitivities of 94.05% ± 2.61% and 97.37% ± 1.18%, at false positive rates of 3 and 6 false detections per minute, respectively. Barkmeier et al. used a dataset of 10 patients and 78,743 IEDs recorded on subdural grid electrodes, and an algorithm consisting of frequency filtering and amplitude scaling and reported a mean sensitivity of 50.2% with a precision of 0.31. LeDouget et al. used a dataset of 17 patients and 3,444 IEDs recorded on subdural grid, strip, or depth electrodes, and random forest classifier with discrete wavelet transform features, and reported a sensitivity of 63% with a precision of 0.53. In comparison, our detector achieves a sensitivity of 95.74% ± 3% with a precision of 0.3 and a sensitivity of 79.76% ± 6.17% with a precision of 0.5.
In assessing our algorithm’s performance on mTL seizures that were independent from the training and testing data sets, we found that 37% of all seizure epochs were removed by the artifact detector. It is not surprising that the repetitive and high amplitude spiking activity typically seen with seizures would trigger detection of artifacts based on amplitude, line length, and other features. Notably, our algorithm (operating at a sensitivity of ~ 72%) detected 29% of the remaining seizure epochs as spikes. While it may be surprising that only 29% of the remaining seizure epochs were detected as spikes, this could be explained by the fact that our algorithm was mostly trained on individual spikes occurring on a background of relatively normal activity. As such, the algorithm is likely not optimized to detect the highly repetitive spiking without intervening normal baseline activity, as may be seen during a seizure.
The performance limiting aspect of most spike detection algorithms, including the one we have developed here, is the relatively high number of false positive detections. In trying to understand the source of false positive detections from our algorithm, we found that a substantial proportion of these false positives (35.9%) were IEDs that were missed on initial expert annotation. This is not surprising, given previous reports indicating that a high proportion of spikes are often missed on expert annotation (Barkmeier et al. 2012; Janca et al. 2014; Le Douget et al. 2017). Similarly, 10.9% of our algorithm’s false positive detections were sharp transients that were not definitively epileptiform, possibly corresponding to missed “indeterminate” IEDs. Artifacts comprised a low proportion (10.1%) of our false positive detections, which is likely due to our use of an automated artifact rejection algorithm prior to implementing the spike detection algorithm. A significant proportion of our false positive detections was comprised of high-frequency, low-amplitude background activity (23.1%), which might indicate some reliance of the spike detector on high frequency features.
A major limitation of our study is that the labels that were used for training and evaluating our spike detection algorithm were generated by a single expert epileptologist. Other spike detection algorithms have been designed based on datasets labeled by 2-3 experts, though often with poor to fair inter-rater agreement (Barkmeier et al. 2012; Gaspard et al. 2014; Janca et al. 2014) . While our dataset was labeled by only one expert, we found that both the intra- and inter-rater reliability of these labels (based on analysis of a random subset of this data) were moderate to good, indicating the robustness of the gold standard dataset for this study.
Here, we focused on detecting IEDs specifically from the mTL, as the mTL is not only one of the most epileptogenic regions of the brain, but also plays an important role in memory and cognition. Moreover, the mTL is one of the most frequently studied brain structures in intracranial investigations for epilepsy pre-surgical evaluation. Our algorithm offers an accurate and objective method for quantifying mTL IEDs on long-term intracranial electrode recordings, and therefore has many potential clinical and research applications. Examples include: quantification of the left-right distribution of mTL IEDs in patients with suspected bi-temporal epilepsy; evaluating the effect of mTL IEDs in disrupting memory encoding and/or consolidation; and assessing effects of specific medications in reducing mTL IEDs, as a potential therapeutic measure to improve cognition in patients with epilepsy. Notably, while we specifically trained our algorithm to detect mTL IEDs from FO electrode recordings, our approach, using a relatively simple CNN that takes a single FO-EEG channel as input, could easily be applied to handle data from other types of intracranial recordings (e.g., stereotactic depth electrodes) through the use of transfer learning methods (Qiang Yang and Pan 2010; Nejedly et al. 2019).
Notably, training our algorithm specifically on recordings from FO electrodes offers an additional unique benefit. FO electrodes are the least invasive modality for performing intracranial recordings in patients with epilepsy (Karakis et al. 2011; Sheth et al. 2014). Unlike other intracranial electrodes, placement of FO electrodes does not require drilling burr holes in the skull or performing a craniotomy. Rather, FO electrodes are guided into the cranium through the foramen ovale, a naturally occurring hole at the base of the skull. As such, FO electrodes offer the rare ability to concurrently record mTL activity along with scalp EEG, without concern that the scalp EEG signals will be distorted by breach artifact. This has motivated the recent use of FO electrode recordings in studies that attempt to correlate scalp EEG with mTL activity (Clemens et al. 2003; Lam et al. 2016, 2017; Spyrou et al. 2016). The algorithm developed here will provide a valuable tool to further this important line of research.
Supplementary Material
Highlights.
We developed a deep learning algorithm to detect mesial temporal lobe epileptiform discharges on intracranial EEG.
Convolutional neural networks with simple architectures deliver excellent performance in detecting epileptiform discharges.
Quantification of intracranial epileptiform activity has many research and clinical applications.
Acknowledgments
ADL was funded by NIH NINDS K23 NS01037 and R25 NS065743, and the American Academy of Neurology Institute. JJ was funded by a grant from SAGE Therapeutics. MBW was funded by NIH NINDS 1K23NS090900, 1R01NS02190, 1R01NS102574, and 1R01NS107291. SSC was funded by NIH NINDS R01 NS062092 and K24 NS088568. No funding sources had any involvement in the study design, collection, analysis, interpretation of data, writing of the report, or the decision to submit this article for publication.
Footnotes
Conflicts of Interest
None of the authors have potential conflicts of interest to be disclosed.
References
- Antoniades A, Spyrou L, Martin-Lopez D, Valentin A, Alarcon G, Sanei S, et al. Detection of Interictal Discharges With Convolutional Neural Networks Using Discrete Ordered Multichannel Intracranial EEG. IEEE Trans Neural Syst Rehabil Eng 2017;25:2285–94. [DOI] [PubMed] [Google Scholar]
- Antoniades A, Spyrou L, Took CC, Sanei S. Deep Learning for Epileptic Intracranial Eeg Data. 2016 Ieee Int Mach Learn Signal Process. 2016;13–6. [Google Scholar]
- Bagheri E, Dauwels J, Dean BC, Waters CG, Westover MB, Halford JJ. Interictal epileptiform discharge characteristics underlying expert interrater agreement. Clin Neurophysiol. 2017;128:1994–2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barkmeier DT, Shah AK, Flanagan D, Atkinson MD, Agarwal R, Fuerst DR, et al. High inter-reviewer variability of spike detection on intracranial EEG addressed by an automated multi-channel algorithm. Clin Neurophysiol. 2012;123:1088–95. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boos CF, de Azevedo FM, Scolaro GR, do Pereira MCV. Automatic Detection of Paroxysms in EEG Signals Using Morphological Descriptors and Artificial Neural Networks. Biomed Eng Trends Electron Commun Softw. 2011;387–402. [Google Scholar]
- Carrie JRG. A hybrid computer technique for detecting sharp EEG transients. Electroencephalogr Clin Neurophysiol. 1972; [DOI] [PubMed] [Google Scholar]
- François Chollet. Keras: The Python Deep Learning library. keras.io 2015. [Google Scholar]
- Clemens Z, Janszky J, Szucs A, Békésy M, Clemens B, Halász P. Interictal epileptic spiking during sleep and wakefulness in mesial temporal lobe epilepsy: A comparative study of scalp and foramen ovale electrodes. Epilepsia. 2003;44:186–92. [DOI] [PubMed] [Google Scholar]
- Delorme A, Makeig S. EEGLAB: An open source toolbox for analysis of single-trial EEG dynamics including independent component analysis. J Neurosci Methods. 2004; [DOI] [PubMed] [Google Scholar]
- Le Douget JE, Fouad A, Maskani Filali M, Pyrzowski J, Le Van Quyen M. Surface and intracranial EEG spike detection based on discrete wavelet decomposition and random forest classification. 2017 39th Annu Int Conf IEEE Eng Med Biol Soc 2017;475–8. [DOI] [PubMed] [Google Scholar]
- Gaspard N, Alkawadri R, Farooque P, Goncharova II, Zaveri HP. Automatic detection of prominent interictal spikes in intracranial EEG: Validation of an algorithm and relationsip to the seizure onset zone. Clin Neurophysiol. 2014;125:1095–103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gwet KL. Computing inter-rater reliability and its variance in the presence of high agreement. Br J Math Stat Psychol. 2008; [DOI] [PubMed] [Google Scholar]
- Halford JJ. Computerized epileptiform transient detection in the scalp electroencephalogram: Obstacles to progress and the example of computerized ECG interpretation. Clin Neurophysiol. 2009;120:1909–15. [DOI] [PubMed] [Google Scholar]
- Halford JJ, Arain A, Kalamangalam GP, LaRoche SM, Leonardo B, Basha M, et al. Characteristics of EEG Interpreters Associated With Higher Interrater Agreement. J Clin Neurophysiol. 2017;34:168–73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Halford JJ, Schalkoff RJ, Zhou J, Benbadis SR, Tatum WO, Turner RP, et al. Standardized database development for EEG epileptiform transient detection: EEGnet scoring system and machine learning analysis. J Neurosci Methods. 2013;212:308–16. [DOI] [PubMed] [Google Scholar]
- Hassanpour H, Mesbah M, Boashash B. EEG spike detection using time-frequency signal analysis. 2004 IEEE Int Conf Acoust Speech, Signal Process 2004;5(June):V-421–V-424. [Google Scholar]
- Haydari Z, Zhang Y, Soltanian-Zadeh H. Semi-automatic epilepsy spike detection from EEG signal using Genetic Algorithm and Wavelet transform. Bioinforma Biomed Work (BIBMW), 2011 IEEE Int Conf 2011;635–8. [Google Scholar]
- Horak PC, Meisenhelter S, Testorf ME, Connolly AC, Davis KA, Jobst BC. Implementation and evaluation of an interictal spike detector. Proc SPIE - Int Soc Opt Eng 2015;9600(September 2015). [Google Scholar]
- Hufnagel A, Dümpelmann M, Zentner J, Schijns O, Elger CE. Clinical relevance of quantified intracranial interictal spike activity in presurgical evaluation of epilepsy. Epilepsia. 2000; [DOI] [PubMed] [Google Scholar]
- Ioffe S, Szegedy C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. J Can Dent Assoc. 2015;70:156–7. [Google Scholar]
- Janca R, Jezdik P, Cmejla R, Tomasek M, Worrell GA, Stead M, et al. Detection of Interictal Epileptiform Discharges Using Signal Envelope Distribution Modelling: Application to Epileptic and Non-Epileptic Intracranial Recordings. Brain Topogr. 2014;28:172–83. [DOI] [PubMed] [Google Scholar]
- Johansen AR, Jin J, Maszczyk T, Dauwels J, Cash SS, Westover MB. Epileptiform spike detection via convolutional neural networks. 2016 IEEE Int Conf Acoust Speech Signal Process 2016;754–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karakis I, Velez-Ruiz N, Pathmanathan JS, Sheth SA, Eskandar EN, Cole AJ. Foramen ovale electrodes in the evaluation of epilepsy surgery: Conventional and unconventional uses. Epilepsy Behav. 2011;22:247–54. [DOI] [PubMed] [Google Scholar]
- Karoly PJ, Freestone DR, Boston R, Grayden DB, Himes D, Leyde K, et al. Interictal spikes and epileptic seizures: Their relationship and underlying rhythmicity. Brain. 2016;139:1066–78. [DOI] [PubMed] [Google Scholar]
- Kim S, McNames J. Automatic spike detection based on adaptive template matching for extracellular neural recordings. J Neurosci Methods. 2007;165:165–74. [DOI] [PubMed] [Google Scholar]
- Kim Y Convolutional Neural Networks for Sentence Classification. In: Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP) Stroudsburg, PA, USA: Association for Computational Linguistics; 2014. p. 1746–51. [Google Scholar]
- Kingma DP, Ba JL. Adam: A method for stochastic gradient descent. ICLR Int Conf Learn Represent. 2015; [Google Scholar]
- Kleen JK, Scott RC, Holmes GL, Lenck-Santini PP. Hippocampal interictal spikes disrupt cognition in rats. Ann Neurol. 2010; [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krizhevsky A, Sutskever I, Geoffrey EH. ImageNet Classification with Deep Convolutional Neural Networks. Adv Neural Inf Process Syst 2012;25;1–9. [Google Scholar]
- Lam AD, Maus D, Zafar SF, Cole AJ, Cash SS. SCOPE-mTL: A non-invasive tool for identifying and lateralizing mesial temporal lobe seizures prior to scalp EEG ictal onset. Clin Neurophysiol. 2017;128:1647–55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lam AD, Zepeda R, Cole AJ, Cash SS. Widespread changes in network activity allow non-invasive detection of mesial temporal lobe seizures. Brain. 2016;139:2679–93. [DOI] [PMC free article] [PubMed] [Google Scholar]
- LeCun Y, Bottou L, Bengio Y, Haffner P. Gradient-based learning applied to document recognition. Proc IEEE. 1998;86:2278–323. [Google Scholar]
- Liu YC, Lin CCK, Tsai JJ, Sun YN. Model-based spike detection of epileptic EEG data. Sensors (Basel). 2013;13:12536–47. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lodder SS, Askamp J, van Putten MJAM. Inter-ictal spike detection using a database of smart templates. Clin Neurophysiol. 2013;124:2328–35. [DOI] [PubMed] [Google Scholar]
- Martín A, Paul B, Jianmin C, Zhifeng C, Andy D, Jeffrey D, et al. TensorFlow: A System for Large-Scale Machine Learning. Proc 12th USENIX Conf Oper Syst Des Implement 2016; [Google Scholar]
- McClish DK. Analyzing a Portion of the ROC Curve. Med Decis Mak. 1989; [DOI] [PubMed] [Google Scholar]
- Nair V, Hinton GE. Rectified Linear Units Improve Restricted Boltzmann Machines. Proceedings of the 27th International Conference on Machine Learning, Haifa 2010; pp. 807–814. [Google Scholar]
- Nejedly P, Cimbalnik J, Klimes P, Plesinger F, Halamek J, Kremen V, et al. Intracerebral EEG Artifact Identification Using Convolutional Neural Networks. Neuroinformatics. 2019;17:225–34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang Qiang, Pan SJ. A Survey on Transfer Learning. IEEE Trans Knowl Data Eng. 2010;22:1345–1359. [Google Scholar]
- Roy Y, Banville H, Albuquerque I, Gramfort A, Falk TH, Faubert J. Deep learning-based electroencephalography analysis: a systematic review. J Neural Eng. 2019;16:051001. [DOI] [PubMed] [Google Scholar]
- Sheth SA, Aronson JP, Shafi MM, Phillips HW, Velez-Ruiz N, Walcott BP, et al. Utility of foramen ovale electrodes in mesial temporal lobe epilepsy. Epilepsia. 2014;55:713–24. [DOI] [PubMed] [Google Scholar]
- Simonyan K, Zisserman A. Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv Prepr arXiv 14091556. 2014. September 4;1–14. [Google Scholar]
- Sønderby SK, Sønderby CK, Nielsen H, Winther O. Convolutional LSTM networks for subcellular localization of proteins. Lect Notes Comput Sci (including Subser Lect Notes Artif Intell Lect Notes Bioinformatics). 2015;9199:68–80. [Google Scholar]
- Spyrou L, Martín-Lopez D, Valentín A, Alarcón G, Sanei S. Detection of Intracranial Signatures of Interictal Epileptiform Discharges from Concurrent Scalp EEG. Int J Neural Syst. 2016;26:1650016. [DOI] [PubMed] [Google Scholar]
- Srivastava N, Hinton G, Krizhevsky A, Sutskever I, Salakhutdinov R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J Mach Learn Res. 2014;15:1929–58. [Google Scholar]
- Stein JM, Lega B, Meisenhelter S, Song Y, Gross RE, Horak PC, et al. Interictal epileptiform discharges impair word recall in multiple brain areas. Epilepsia. 2016;58:373–80. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun C, Shrivastava A, Singh S, Gupta A. Revisiting Unreasonable Effectiveness of Data in Deep Learning Era. 2017 IEEE International Conference on Computer Vision (ICCV) 2017, pp 843–52. [Google Scholar]
- Tjepkema-Cloostermans MC, de Carvalho RCV, van Putten MJAM. Deep learning for detection of focal epileptiform discharges from scalp EEG recordings. Clin Neurophysiol. 2018;129:2191–6. [DOI] [PubMed] [Google Scholar]
- Ung H, Cazares C, Nanivadekar A, Kini L, Wagenaar J, Becker D, et al. Interictal epileptiform activity outside the seizure onset zone impacts cognition. Brain. 2017;140:2157–68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vijayalakshmi K, Abhishek AM. Spike detection in epileptic patients EEG data using template matching technique. Int J Comput Appl. 2010;2:5–8. [Google Scholar]
- Wilson SB, Emerson R. Spike detection: a review and comparison of algorithms. Clin Neurophysiol. 2002;113:1873–81. [DOI] [PubMed] [Google Scholar]
- Yang B, Hu Y, Zhu Y, Wang Y, Zhang J. Intracranial EEG spike detection based on rhythm information and SVM. Proc - 9th Int Conf Intell Human-Machine Syst Cybern IHMSC 2017 2017;2:382–5. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.