ADJUSTED REGULARIZATION IN LATENT GRAPHICAL MODELS: APPLICATION TO MULTIPLE-NEURON SPIKE COUNT DATA

Abstract

A major challenge in contemporary neuroscience is to analyze data from large numbers of neurons recorded simultaneously across many experimental replications (trials), where the data are counts of neural firing events, and one of the basic problems is to characterize the dependence structure among such multivariate counts. Methods of estimating high-dimensional covariation based on ℓ₁-regularization are most appropriate when there are a small number of relatively large partial correlations, but in neural data there are often large numbers of relatively small partial correlations. Furthermore, the variation across trials is often confounded by Poisson-like variation within trials. To overcome these problems we introduce a comprehensive methodology that imbeds a Gaussian graphical model into a hierarchical structure: the counts are assumed Poisson, conditionally on latent variables that follow a Gaussian graphical model, and the graphical model parameters, in turn, are assumed to depend on physiologically-motivated covariates, which can greatly improve correct detection of interactions (non-zero partial correlations). We develop a Bayesian approach to fitting this covariate-adjusted generalized graphical model and we demonstrate its success in simulation studies. We then apply it to data from an experiment on visual attention, where we assess functional interactions between neurons recorded from two brain areas.

1. Introduction.

Neurons communicate primarily through series of rapid electrical discharges known as action potentials or spikes, which take place over approximately 1 millisecond (ms); see Figure 1. Sequences of spikes (or spike trains), rather than individual spikes, encode how an animal responds to a stimulus or executes a movement. Spike trains tend to be irregular, so it is natural to model them as arising from a point process, for example a Poisson process, or to model the number of spikes in time bins as random variables that follow, for example, a Poisson distribution. In fact, modeling of spike trains was a major motivation for development of point process theory and methods (Cox and Lewis, 1972; Perkel, Gerstein, and Moore, 1967a,b). While a faculty member at the University of Chicago, Steve Fienberg interacted with one of the major figures in mathematical modeling of interacting neurons, Jack Cowan (Wilson and Cowan, 1972), and this led Steve to work on a foundational question: What simple principles can be used to generate point process models of neurons? After taking a crack at this, and publishing a short paper, Steve summarized the field in a very nice review article (Fienberg, 1974), which provides a great snapshot of the state of data analysis at that time. Back then the focus was almost entirely on analytically tractable methods, so the subject of Steve’s review was diffusion models, and their extensions, applied to spontaneously active neurons (that is, neurons recorded in vitro, having been removed from a living animal). The main results involved characterizing the stochastic process from simple assumptions and determining the resulting waiting-time distribution for boundary crossings, where, for neurons, the waiting times become times between successive spikes. Steve ended his article with a discussion of model fitting, and said, “Little in the way of statistical methodology is available to help with the problem of discriminating among intrinsically different models providing adequate fits to a set of data.” When Steve was writing this, one of the most important new ideas in statistics, generalized linear models, had just been developed and, as computer power increased and desktop computers became standard equipment in statistical research environments, resulting techniques became practical and could be applied to solve many of the problems Steve had discussed (Brillinger, 1988). It took a long time until such approaches began to be applicable to a variety of animal experiments, and to penetrate the literature in neurophysiology (Kass, Ventura, and Brown, 2005; Kass et al., 2018).

FIG 1.

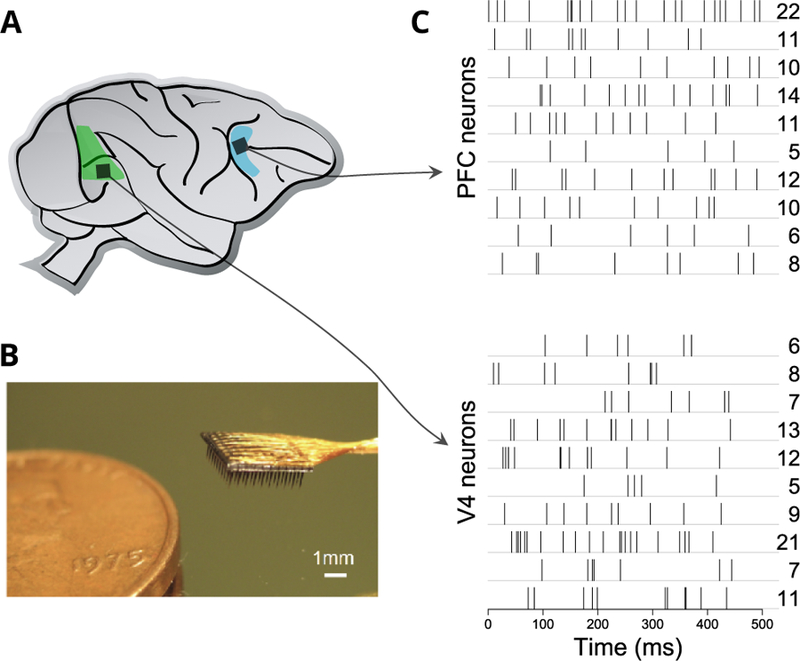
(A) Sketch of primate brain with the approximate recorded regions of prefrontal cortex (PFC) and visual area V4 indicated in blue and green, respectively. (B) Utah array with 10×10 recording electrodes shown next to a penny to compare sizes. Utah arrays implanted in each of PFC and V4 of a non-human primate recorded the spikes of neurons. (C) In each trial of the experiment, spike trains of V4 and PFC neurons were recorded simultaneously. Each row in the diagram is the spike train for one neuron in a particular trial, with spike times being indicated as vertical tick marks. The spike counts over the 500 ms are shown on the right.

As recording technologies have progressed, neurophysiology has continued to generate interesting statistical problems. Even though many studies rely on results involving individual neurons, much of the emphasis has shifted to multivariate effects in multiple-neuron data. In this paper, we analyze data from multiple neurons recorded during an experiment on the neurophysiology of attention. We all know that, when faced with a task, we are likely to perform better if we pay attention to what we are trying to do. But what are the mechanisms by which the brain allocates attention? This question has been posed with considerable experimental precision in studying visual processing by non-human primates and there is a substantial literature on the neurophysiological basis of visual attention (Maunsell, 2015). The data we consider here come from two key regions of the brain that are involved in visual processing. The first, prefrontal cortex (PFC) is generally considered to be involved with aspects of control and, in particular, control of attention. The second, area V4, is a mid-level visual region, meaning that it receives inputs from earlier visual-processing regions and sends outputs to later regions, and there is good evidence of changes in activity among neurons in V4 when a subject pays attention to a visual stimulus. What is not known are the ways the neural networks in these areas cooperate, and the extent to which there are changes in patterns of activity, both within and across areas, when the subject pays attention. Thus, the statistical challenge was to construct a framework for identifying patterns of covariation in the activity of many neurons recorded, simultaneously, from PFC and V4. As we will next explain, the methods we have developed should be useful in various contexts, but especially for studies involving spike trains among cortical neurons, meaning neurons residing within the cerebral cortex, the part of the brain most closely associated with higher-level processing.

A small subset of the data is shown in Figure 1. As illustrated there, each experimental trial consisted of multiple spike trains recorded over 500 ms: each row in the diagram is the spike train for one neuron, with the whole set of neural spike trains being recorded simultaneously on one particular experimental trial. The total number of spikes for each neural spike train, known as that neuron’s spike count, is shown on the right. Here we follow a standard simplification by analyzing the spike counts instead of the spike trains. Although the approach we report here could be extended to point processes, we chose to tackle this simpler problem first because, as we will indicate, describing multivariate interactions among the counts was itself a substantial project. In this context, typical questions of scientific interest would be, How strong is the covariation among neurons within PFC and V4, and how strong is the covariation across these two regions? How does this covariation change when the animal pays attention? We assess covariation in terms of partial correlation within Gaussian graphical models (GGMs). Partial correlation serves to identify the unique association of pairs of neurons, based on input signals that are not common to other recorded neurons. In a GGM, the d-dimensional data vector follows a multivariate Gaussian distribution having a precision matrix (inverse covariance matrix) Ω, and edges connect nodes wherever there are nonzero partial correlations. Because our data set, like many others, involves moderately large numbers of nodes (here, the neurons), i.e., d is moderately large, estimation of Ω requires some form of regularization, and it would be natural to consider the graphical LASSO and its variants, which use λ₁ regularization (Yuan and Lin, 2007; Ravikumar et al., 2011; Chandrasekaran et al., 2012). However, two major complications arise. First, the correlation across repeated trials between the spike counts of two neurons is corrupted by Poisson-like variation within the trials of each neuron, and this attenuates the estimates of across-trial correlations (Behseta et al., 2009; Vinci et al., 2016). Second, methods based on λ₁ regularization are better suited to estimate sparse networks (Rothman et al., 2008; Ravikumar et al., 2011) but in the context of spike count data, networks are not typically very sparse. In previous work we handled the first problem for pairs of neurons using bivariate hierarchical models (Vinci et al., 2016), where pairs of spike counts were assumed to be Poisson with bivariate log-normally distributed latent means; correlation between the latent means can then be thought of as a Poisson de-noised version of spike count correlation. We also handled the second problem, while ignoring the first, by allowing the LASSO penalty to vary with the pair of neurons based on informative covariates (Vinci et al., 2018a), which improved the detection of correct edges and the accuracy of partial correlation estimates. In this paper we combine those two previous strategies to provide a more comprehensive solution. The fundamental idea is that the observations (here, the spike counts) are considered to depend on latent variables (here, the logs of their Poisson means) that follow a Gaussian graphical model where partial correlations are zero with probabilities determined by covariates.

The key to our approach is the availability of informative covariates, which rests on well-documented neurophysiology concerning correlation among pairs of cortical neurons. In several studies, Pearson correlation has been shown to depend strongly on both inter-neuron distance (physical distance between the neurons) and tuning curve correlation (similarity of the two neurons’s average activities over different stimuli): the dependence is typically weaker at larger inter-neuron distance, and stronger for larger tuning-curve correlation (Smith and Sommer, 2013; Goris, Movshon, and Simoncelli, 2014; Yatsenko et al., 2015; Vinci et al., 2016). These covariates are available, but their effects may vary across brain areas, neuron types, and recording techniques. In Vinci et al. (2018a) we introduced informative covariate vectors W_ij composed of inter-neuron distances and tuning curve correlations to estimate a GGM using a Bayesian λ₁ regularization framework (the graphical LASSO with adjusted regularization, or GAR), where partial correlations between neurons i and j can be penalized differently according to a data driven function of W_ij. Through an extensive simulation study we showed that this physiologically-motivated procedure performs substantially better (in terms of correct edge detection and accuracy of partial correlation estimates) than off-the-shelf generic tools, including not only graphical LASSO but also several of its variants that have appeared in the literature, the adaptive graphical LASSO (Fan et al., 2009), the latent variable graphical model (Chandrasekaran et al., 2012), and Bayesian graphical LASSO (Wang, 2012). Improvements in functional connectivity estimation provided by auxiliary variables had previously been observed in analyses of other kinds of neural data by either using a weighted λ₁ penalty on the precision matrix, with weights taken to be inverse functions of metrics of the strength of anatomical connections (MEG data, Pineda-Pardo et al. (2014); fMRI and dMRI data, Ng et al. (2012); where the strength of anatomical connections were taken to be the fiber density and fiber count between regions, respectively), or by constraining the support of the precision matrix to reflect structural connections (fMRI data, Hinne et al. (2014); the zeros were imposed in the precision matrix where structural connections were not found). However, those studies differ from Vinci et al. (2018a) in that the dependence of the regularization on the covariates W_ij was pre-specified rather than learned from the data. In Vinci et al. (2018a), GAR used thresholding of estimated partial correlations to set edges to zero. Here, we instead use spike-and-slab priors where the probability of zero for the (i, j) partial correlation depends on W_ij, and we let the dependence on W_ij be data driven. We also include a Poisson observation model as in (Vinci et al., 2016) to avoid attenuation of correlation.

In Section 2 we provide details about our latent covariate-adjusted GGM within a Poisson-lognormal multivariate hierarchical model, and we develop Bayesian methods for estimation in Section 3. Our approach can also treat other exponential families, and thus provides a methodology for covariate-adjusted regularization in generalized graphical models. Section 3 also provides methods to infer graphs with signed edges by controlling the Bayesian false discovery and false non-discovery rates of edge detection. In Section 4 we apply our methodology to the spike count data from areas PFC and V4, and we use inter-neuron distance as the auxiliary quantity W_ij. In Sections 4.1 and 4.2, and in Appendix A (Vinci et al., 2018b), we demonstrate the benefit of our methodology compared to competing methods, and in Section 5 we add a few remarks, especially concerning opportunities for future research.

2. A Bayesian hierarchical model to include auxiliary variables.

Assume that $X^{\left(1\right)},\dots ,X^{\left(n\right)}\stackrel{\text{iid}}{\sim }N\left(\mu ,{\Omega }^{-1}\right)$ are n independent and identically distributed (iid) d-dimensional Gaussian random vectors with mean vector µ and covariance matrix Ω⁻¹. In our context, X⁽¹⁾, …, X⁽ⁿ⁾ are the latent log means of the observed spike counts Z⁽¹⁾, …, Z⁽ⁿ⁾ of d neurons in n identical experimental trials. Even though trials are identical, the neurons’ mean spike counts, also called firing rates, can vary from trial to trial due to several sources of variability, including attention, arousal, and adaptation (Churchland et al., 2011; Goris, Movshon, and Simoncelli, 2014; Vinci et al., 2016). We can therefore think of Ω⁻¹ as containing de-noised versions of spike count covariances. Goris, Movshon, and Simoncelli (2014) and Vinci et al. (2016) showed that Gamma or lognormal distributions provide adequate fits to latent firing rates, hence our choice of a multivariate normal distribution to model the joint vector of log firing rates.

To analyze the neural data in Section 4, we further assume that the d-dimensional vectors of spike counts $Z^{\left(r\right)}={\left(Z_1^{\left(r\right)},\dots ,Z_d^{\left(r\right)}\right)}^{\text{'}}$, r = 1, …, n, are distributed according to a d-dimensional Poisson-lognormal distribution:

$$\begin{gathered} Z_i^{\left(r\right)}|X_i^{\left(r\right)}~\text{Poisson}\left(e^{X_i^{\left(r\right)}}\right),\hspace{0.17em}i=1,\dots ,d \\ {X}^{\left(r\right)}={\left(X_1^{\left(r\right)},\dots ,X_d^{\left(r\right)}\right)}^{\text{'}}~N\left(\mu ,{\Omega }^{-1}\right), \end{gathered}$$ (2.1)

where the dependence structure of the observed spike counts Z^(r) is governed by the dependence structure of their latent log firing rates X^(r). Vinci et al. (2016) showed that the hierachical model in Equation 2.1 provides a good fit to the spike counts of pairs of neurons (d = 2).

In Bayesian GGMs, a prior h is assumed for the precision matrix Ω, and it is often taken to be a product of Laplace distributions over the entries ω_ij of Ω (Wang, 2012), that is:

$$h\left(\Omega |{\left({\lambda }_{ij}\right)}_{i\le j}\right)\propto \prod _{i\le j}{l}_{ij}\left({\omega }_{ij}\right)I\left(\Omega \succ 0\right),$$ (2.2)

where $l_{ij}\left(\omega \right)\propto e^{-{\lambda }_{ij}\left|{\omega }_{ij}\right|},\hspace{0.17em}I\left(\Omega \succ 0\right)$ constrains the support of the distribution h on the positive definite cone of d × d symmetric matrices, thereby ensuring ω_ii > 0 for all i = 1, …, d, and the parameter λ_ij determines the amount of shrinkage towards zero of ω_ij. In this framework, the maximum a posteriori estimator of Ω corresponds to the graphical LASSO (Yuan and Lin, 2007). Here we use a more general spike and slab type prior (George and McCulloch, 1997), replacing the Laplace distribution l_ij in Equation 2.2 by a two-component mixture composed of a point-mass at zero with mixing proportion π_ij, and a Gaussian scale mixture distribution p_ij centered at m_ij. The point-mass component allows exact zero entries in Ω (i.e. Ω can be sparse), which might induce better concentration around zero of the smaller partial correlation estimates when the graph is indeed locally sparse. Banerjee and Ghosal (2015) and Wang (2015) had previously used a spike and slab prior to estimate graphs, but they assumed the same parameters across all entries of Ω and took p_ij to be a Laplace distribution, which is centered at zero. However, allowing for non-zero mean parameters m_ij, as we do here, can be useful to better regularize locally dense precision matrices Ω, where many entries are non-zero, as might happen with neural data. The analytic expression for our spike and slab prior is:

$$h\left(\Omega |{\left({\lambda }_{ij},m_{ij},{\pi }_{ij}\right)}_{i\le j}\right)\propto \prod _{i\le j}\left\{{\pi }_{ij}{p}_{ij}\left({\omega }_{ij}\right)+\left(1-{\pi }_{ij}\right)\delta \left({\omega }_{ij}\right)\right\}\hspace{0.17em}I\left(\Omega \succ 0\right),$$ (2.3)

where δ(0) = ∞ and δ(x) = 0 for all x ≠ 0 is the Dirac delta function, ${\pi }_{ij}\in \left[0,\hspace{0.17em}\hspace{0.17em}1\right]$, π_ii = 1 for all i,

$$p_{ij}\left(\omega \right)=\int \frac{{\lambda }_{ij}}{v}\varphi \left(\frac{{\lambda }_{ij}}{v}\left(\omega -m_{ij}\right)\right)d{G}_{ij}\left(v\right),$$ (2.4)

ϕ(z) is the standard Gaussian density function, and $G_{ij}:ℝ\to \left[0,\hspace{0.17em}\hspace{0.17em}1\right]$ is a cumulative distribution function with G_ij(0) = 0 and ${\int }_0^{\infty }{v}^{-1}d{G}_{ij}\left(v\right)<\infty$ (these-conditions are necessary and sufficient for the existence of p_ij (Andrews and Mallows, 1974); see Lemma 1, Vinci et al. (2018b)). Without loss of generality, we assume ${\int }_0^{\infty }{v}^{2}d{G}_{ij}\left(v\right)=1$, which implies $\int {\left(\omega -m_{ij}\right)}^2{p}_{ij}\left(\omega \right)d\omega =1/{\lambda }_{ij}^2$ and thus allows λ_ij to be interpreted as the rate parameter of p_ij (see Lemma 1, Vinci et al. (2018b)). Equation 2.3 includes common modeling choices as special cases, where typically the prior parameters are the same for all (i, j), and m_ij = 0: for example, Gaussian/ridge (Hoerl and Kennard, 1970), Laplace/lasso (Tibshirani, 1996; Yuan and Lin, 2007; Friedman, Hastie, and Tibshirani, 2008; Rothman et al., 2008; Wang, 2012; Mazumder and Hastie, 2012), spike-and-slab with Laplace density (Banerjee and Ghosal, 2015; Wang, 2015), Elastic net (Zou and Hastie, 2005), the latent variable graphical model (Chandrasekaran et al., 2012; Yuan, 2012; Giraud and Tsybakov, 2012), as well as less explored choices; see Appendix A (Vinci et al., 2018b).

The prior distribution for Ω in Equation 2.3 has a large number of parameters, but when auxiliary variables are available, it makes sense to let them all depend on those variables and thus reduce greatly the number of effective parameters, as we now describe. Assume that q-dimensional auxiliary variables $W={\left\{W_{ij}\right\}}_{i<j}$ that carry information about the network of neurons’ firing rates are available. We incorporate that information in the prior distribution for Ω to model the neurophysiological mechanism involving W that gives rise to the neuronal correlation structure in Ω. For example, if W is inter-neuron distance, then h might produce covariance structures where two neurons are less dependent if they are farther apart. An example of a 4-dimensional dependence graph is given in Figure 2. We thus let the location, rate, and weight parameters in Equations 2.3 and 2.4 depend on W according to

$$m_{ij}={\left({\alpha }_i{\alpha }_j\right)}^{-1}f\left(W_{ij}\right),$$ (2.5)

$${\lambda }_{ij}={\alpha }_i{\alpha }_{j}g\left(W_{ij}\right),$$ (2.6)

$${\pi }_{ij}=\eta \left(W_{ij}\right),$$ (2.7)

for i ≠ j, where $f:{ℝ}^q\to ℝ,$ $g:{ℝ}^q\to {ℝ}_{+}$, and $\eta :{ℝ}^q\to \left[0,\hspace{0.17em}\hspace{0.17em}1\right]$ are flexible functions to be estimated from the data (see Figure 5), and α = (α₁, …, α_d) are parameters that ensure that f and g are on the scale of the partial correlations, ${\rho }_{ij}=-{\omega }_{ij}/\sqrt{{\omega }_{ii}{\omega }_{jj}}$, rather than on the scale of ω_ij; more details are in Appendix C.1.5 (Vinci et al., 2018b). Letting π_ij, m_ij, and λ_ij depend on W_ij models the information carried by W about Ω, which, when combined with the observed data (Z⁽¹⁾, …, Z⁽ⁿ⁾ ), can provide better inferences for Ω if W indeed contains relevant information. If no auxiliary variables are available, the model can still be used by letting f, g, and η be constants.

FIG 2.

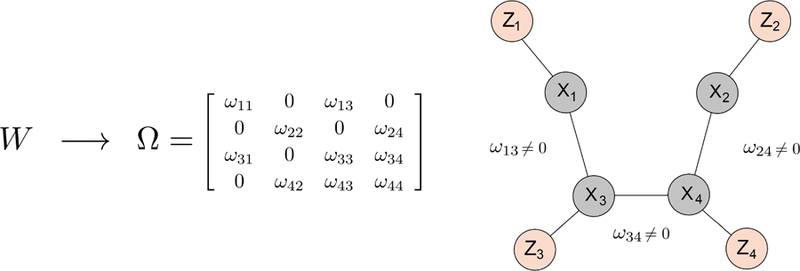
Example of a d-dimensional dependence graph specified by the hierarchical model in Equation 2.1, where d = 4 and W is inter-neuron distance, represented here as physical distance. Neuron pairs (1,2), (1,4), and (2,3) are farther apart than the other pairs, and we assume they are not functionally connected. The precision matrix Ω arises from a generative process that reflects the dependence between W and functional connectivity, and here, accordingly, the entries for the three neuron pairs that are far apart are zero. The Gaussian random vector X ~ N (µ, Ω) has dependence structure specified by Ω. The missing edges correspond to zero partial correlations. (Z₁, Z₂, Z₃, Z₄) are the observed spike counts and (X₁, X₂, X₃, X₄) their latent log means (firing rates).

FIG 5.

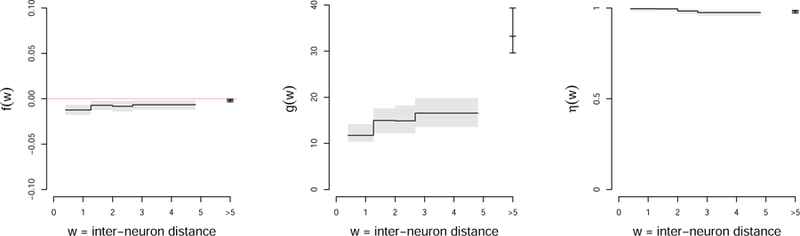
Step functions f (W ), g(W ), and η(W ) fitted to the data in condition (ϑ, ζ) = (45, 0): f ≈ 0 suggests that the partial correlations are centered around zero for all values of W, and η ≈ 1, that the shrinkage induced by g is strong enough and/or there is not a large proportion of exactly zero Ω entries; g increases with W, which means that the partial correlations are penalized more for neurons that are farther apart.

This framework generalizes the graphical LASSO with adjusted regularization (GAR) of Vinci et al. (2018a). GAR assumes that the observation model is the second line in Equation 2.1, with no Poisson hierarchy, and that the prior distribution for Ω is a product of Laplace distributions (Equation 2.2) with rate parameters λ_ij nonparametrically modulated by W_ij, as specified in Equation 2.6. Vinci et al. (2018a) applied GAR to square-rooted spike count data from macaque areas V1 and V4 with a two-dimensional W_ij composed of inter-neuron distances and tuning curve correlations; the square-root transformation was used to improve the fit to a Gaussian distribution (Georgopoulos and Ashe, 2000; Yu et al., 2009; Kass et al., 2014). The estimated rate function g in Equation 2.6 was non-linearly increasing with inter-neuron distance and decreasing with tuning curve correlation.

Next, we present Bayesian algorithms to estimate the model described above, and we fit it to multiple neuron spike data in Section 4. Estimating the Poisson-lognormal model (Equation 2.1) in high dimensions can be heavily corrupted by noise (Inouye et al., 2017), and we expect incorporation of auxiliary quantities W to improve estimation.

3. Estimating the precision matrix and the graph.

In this section we describe the Bayesian inference of Ω in the model described in Section 2. We start with full and empirical Bayes algorithms for the case when the Gaussian component X is observed (section 3.1), because they can be useful for Gaussian data, in neuroscience or other fields. We can also extend these algorithms easily when X is latent in an exponential family observation model; Section 3.2 treats the particular Poisson lognormal case in Equation 2.1. The full Bayes algorithm uses the Gibbs sampler to approximate the joint distribution of θ and Ω given Gaussian vectors ${\mathbb{X}}_n=\left\{X^{\left(1\right)},\dots ,X^{\left(n\right)}\right\}$, where θ = {f, g, η, α, m, λ}, and m = (m₁₁, …, m_dd) and λ = (λ₁₁, …, λ_dd) are the means and rates of the p.d.f. in Equation 2.4 for i = j; f, g, η, and α are defined in Equations 2.5, 2.6, and 2.7. We assume that f, g, and η are step-functions; more flexible nonparametric functions are too hard to implement at present. The empirical Bayes algorithm computes first a point estimate $\widehat{\theta }$ as the maximum of its marginal posterior, using an EM algorithm that allows f, g, and η to be of any parametric or nonparametric forms, and then estimate Ω through the posterior distribution $h\left(\Omega |{\mathbb{X}}_n,W,\widehat{\theta }\right)$.

We assign a prior density to θ of the form

$$h\left(\theta |W\right)\propto h^{\ast }\left(\theta |W\right)A{\left(\theta ,W\right)}^{-1},$$ (3.1)

where A(θ, W ) is the intractable but bounded normalizing constant of Equation 2.3 (see Lemma 2, Vinci et al. (2018b)), and h^∗(θ | W ) is a density on θ. Note that conditioning on W in Equation 3.1 means that the prior on θ depends on the auxiliary quantity W, but it is θ and W together that specify the parameters in Equation 2.3. We combine Equations 3.1 with the generative model h(Ω | θ, W ) (Equations 2.3 to 2.7), a prior distribution h(µ) on µ (e.g. h(µ) ∝ 1; see Appendix C.1.3, Vinci et al. (2018b)), and the Gaussian likelihood function $L\left(\mu ,\Omega ;{\mathbb{X}}_n\right)$, to obtain the full joint posterior distribution

$$h\left(\mu ,\Omega ,\theta |{\mathbb{X}}_n,W\right)\propto h\left(\mu \right)h\left(\Omega |\theta ,W\right)h\left(\theta |W\right)L\left(\mu ,\Omega ;{\mathbb{X}}_n\right),$$ (3.2)

which yields posterior means or maximum a posteriori estimates for θ, µ, and Ω.

3.1. Posterior computation and estimation for observed Gaussian data.

The posterior distribution in Equation 3.2 is not analytically tractable because of the positive definiteness constraint on Ω and the point-mass components in Equation 2.3 (when π_ij > 0). Instead, we use posterior simulations from the augmented quantity (µ, Ω, θ, Y, V), with posterior distribution

$$h_a\left(\mu ,\Omega ,\theta ,Y,V|{\mathbb{X}}_n,W\right)\propto h\left(\mu \right)h_a\left(\Omega ,\theta ,Y,V|W\right)L\left(\mu ,\Omega ;{\mathbb{X}}_n\right),$$ (3.3)

where V = [V_ij] and Y = [Y_ij] are nuisance parameters such that

$$h\left(\mu ,\Omega ,\theta |{\mathbb{X}}_n,W\right)=\underset{a\to 0^{+}}{\lim }\int \sum _{Y\in \mathcal{Y}}{h}_a\left(\mu ,\Omega ,\theta ,Y,V|{\mathbb{X}}_n,W\right)dV$$ (3.4)

and Ψ is the set of all 0–1 symmetric matrices with positive diagonal; in practice we take a small a, e.g. a² = 10⁻⁸. Basically, we replace the point mass component in Equation 2.3 by a Gaussian distribution with a very small variance a², so that it is highly peaked around zero.

The second term on the right hand side of Equation 3.3 is given by

$$h_a\left(\Omega ,\theta ,Y,V|W\right)\propto h_a\left(\Omega |\theta ,W,Y,V\right)h_a\left(V|\theta ,W,Y\right)h\left(Y|\theta ,W\right)h_a\left(\theta |W\right)$$ (3.5)

where

$$h_a\left(\Omega |\theta ,W,Y,V\right)=\prod _{i\le j}{\tau }_{ij}\varphi \left({\tau }_{ij}\left({\omega }_{ij}-Y_{ij}{m}_{ij}\right)\right)I\left(\Omega \succ 0\right)B\left(\theta ,W,Y,V,a\right),$$ (3.6)

with ${\tau }_{ij}=Y_{ij}{\lambda }_{ij}/V_{ij}+\left(1-Y_{ij}\right)/a$ and $Y_{ii}\equiv 1,\hspace{0.17em}\forall i$,

$$h_a\left(V|\theta ,W,Y\right)=B{\left(\theta ,W,Y,V,a\right)}^{-1}\prod _{i\le j}{g}_{ij}\left(V_{ij}\right)A\left(\theta ,W,Y,a\right),$$ (3.7)

$$h\left(Y|\theta ,W\right)=\prod _{i<j}{\pi }_{ij}^{Y_{ij}}{\left(1-{\pi }_{ij}\right)}^{1-Y_{ij}},$$ (3.8)

$$h_a\left(\theta |W\right)\propto h^{\ast }\left(\theta |W\right)A{\left(\theta ,W,Y,a\right)}^{-1},$$ (3.9)

B(θ, W, Y, V, a) is the normalizing constant of h_a(Ω | θ, W, Y, V ), A(θ, W, Y, a) is the normalizing constant of h_a(V | θ, W, Y ), h^∗ is as in Equation 3.1, and g_ij is the p.d.f. of tt_ij in Equation 2.3. In Lemma 2 (Vinci et al., 2018b) we show that the normalizing constants are finite and away from zero, that is 1 < A(θ, W, Y, a) < ∞ and 1 < B(θ, W, Y, V, a) < ∞, so that Equations 3.6, 3.7, and 3.9 are well defined distributions. Lemma 3 (Vinci et al., 2018b) shows that the quantity (µ, Ω, θ) of a sample (µ, Ω, θ, Y, V ) drawn from $h_a\left(\mu ,\Omega ,\theta ,Y,V|{\mathbb{X}}_n,W\right)$ in Equation 3.3 gets closer to a genuine sample from $h\left(\mu ,\Omega ,\theta |{\mathbb{X}}_n,W\right)$ in Equation 3.2 as a → 0⁺.

The representation prescribed by Equations 3.3, 3.6, and 3.7 is computationally convenient because it circumvents approximating intractable normalizing constants (mainly due to the positive definiteness constraint $\Omega \succ 0$ in Equation 2.3) and provides a framework where sampling (Ω | rest) does not depend on the mixing distributions G_ij’s. Using a specific Gaussian mixture in Equation 2.4 only requires a different sampling of (V_ij | rest) (Equation C.1, Appendix C.1, Vinci et al. (2018b)), which permits many different regularizations of the precision matrix Ω; more details and examples are in Appendix A (Vinci et al., 2018b).

Full Bayes estimation.

In Appendix C.1 (Vinci et al., 2018b) we describe a Gibbs sampler algorithm to draw samples from the posterior distribution of $\left(\mu ,\Omega ,\theta ,Y,V|{\mathbb{X}}_n,W\right)$ in Equation 3.3, assuming that the model components f, g, and η in Equations 2.5, 2.6, and 2.7 are the step functions

$$f\left(w\right)=\sum _{k=1}^{K_f}{\gamma }_k{I}_{A_k}\left(w\right),\hspace{1em}g\left(w\right)=\sum _{k=1}^{K_g}{\beta }_k{I}_{B_k}\left(w\right),\hspace{1em}\eta \left(w\right)=\sum _{k=1}^{K_{\eta }}{\chi }_k{I}_{C_k}\left(w\right),$$ (3.10)

where $\left\{A_1,\dots ,A_{K_f}\right\}$, $\left\{B_1,\dots ,B_{K_g}\right\}$, and $\left\{C_1,\dots ,C_{K_{\eta }}\right\}$ are partitions of the domain of the auxiliary variables W, and $I_D\left(w\right)=I\left(w\in D\right)$ is the indicator function. Hence, sampling f, g, and η reduces to sampling their coefficients $\gamma =\left({\gamma }_1,\dots ,{\gamma }_{K_f}\right)\in {ℝ}^{K_f}$, $\beta =\left({\beta }_1,\dots ,{\beta }_{K_g}\right)\in {ℝ}_{+}^{K_g}$ and $\chi =\left({\chi }_1,\dots ,{\chi }_{K_{\eta }}\right)\in {\left[0,1\right]}^{K_{\eta }}$. The numbers of steps K_g, K_f, and K_η and their locations can be chosen so that the sample partial correlations plotted against W are approximately constant within each step. We use step functions because they are flexible, if not smooth, and they allow the Gibbs sampler to run. Other functions are too difficult to implement at present. In the future we may be able to implement continuous nonparametric functions (e.g. a kernel smoother with a few degrees of freedom) as in the empirical Bayes approach.

We also assume that m_ii and V_ii in Equation 2.4 are such that m_ii ≤ 0 and $V_{ii}^2~\Gamma \left(1,1\right)$ for all i = 1, …, d. The Bayesian counterparts of several penalized MLE methods, such as the Glasso (Yuan and Lin, 2007) and the Sparse-Low rank model (Chandrasekaran et al., 2012), require the same conditions.

Empirical Bayes estimation.

Instead of jointly sampling θ and Ω given the data, we estimate θ = {f, g, η, α, m, λ} as the maximizer of the marginal posterior distribution

$$\begin{gathered} \widehat{\theta }=\underset{\theta }{\arg \max }h\left(\theta |{\mathbb{X}}_n,W\right) \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=\underset{\theta }{\arg \max }\int \int \int \sum _{Y\in \mathcal{Y}}{h}_a\left(\mu ,\Omega ,\theta ,Y,V|{\mathbb{X}}_n,W\right)dV\hspace{0.17em}d\mu \hspace{0.17em}d\Omega , \end{gathered}$$ (3.11)

and the precision matrix Ω is then inferred from the posterior distribution $h\left(\Omega |{\mathbb{X}}_n,W,\widehat{\theta }\right)$. We solve Equation 3.11 using the Expectation-Maximization algorithm described in Appendix C.2 (Vinci et al., 2018b). This simpler setting allows f, g, and η to be of any functional form, either parametric or nonparametric.

3.2. Posterior computation and estimation for latent Gaussian data.

We extend our graph estimation approach to the inference of Ω under the hierarchical model in Equation 2.1 by supplementing the previous algorithms with a mechanism to sample X given Z and the rest of the parameters and variables. Full and empirical Bayes estimation algorithms are given in Appendix C.3 (Vinci et al., 2018b) to obtain estimates of θ and Ω from the posterior distribution

$$h_a\left(\mu ,\Omega ,\theta ,Y,V,{\mathbb{X}}_n|{\mathbb{Z}}_n,W\right)\propto h_a\left(\Omega ,\theta ,Y,V|W\right)L\left(\mu ,\Omega ;{\mathbb{X}}_n\right)p\left({\mathbb{Z}}_n|{\mathbb{X}}_n\right)$$ (3.12)

where the first term on the right hand side is defined in Equation 3.5 and

$$p\left({\mathbb{Z}}_n|{\mathbb{X}}_n\right)=\prod _{r=1}^{n}p\left(Z^{\left(r\right)}|X^{\left(r\right)}\right)$$ (3.13)

is the likelihood of the observed independent random variables Z⁽¹⁾, …, Z⁽ⁿ⁾ conditioned on X⁽¹⁾, …, X⁽ⁿ⁾. Appendix C.3 (Vinci et al., 2018b) provides algorithms to fit the Poisson-lognormal model (Equation 2.1), where X | Z is sampled using rejection sampling. In Section 4 we apply this model to spike count data from macaque visual cortex using inter-neuron distance as an auxiliary variable W. Different observational distributions can be fitted in place of Poisson by just modifying the sampling step of X given Z and all other parameters. For instance, if p(z | x) is binomial or negative-binomial, then the sampling of X | rest may be performed by using rejection sampling or the data augmentation strategy based on the Pólya-Gamma distribution (Polson et al., 2013).

3.3. Graph estimation.

Once the posterior distribution of $\left(\Omega |{\mathbb{X}}_n,W\right)$ is computed, we use it to estimate the signed graph of the network, $E\left(\delta \right)=\left[E_{ij}\left(\delta \right)\right]$, where the edge between nodes i and j is defined as

$$E_{ij}\left(\delta \right)=\{\begin{array}{cc}\begin{array}{l}1,\\ -1,\\ 0,\end{array}& \begin{array}{l}{\rho }_{ij}>\delta ,\\ {\rho }_{ij}<-\delta ,\\ \left|{\rho }_{ij}\right|\le \delta \end{array}\end{array}$$ (3.14)

for some threshold δ ∈ [0, 1). Several estimates are listed below.

Definition 1.

A plug-in signed δ-graph is the signed matrix $\widehat{E}\left(\delta \right)=\left[{\widehat{E}}_{ij}\left(\delta \right)\right]$ where

$${\widehat{E}}_{ij}\left(\delta \right)=\{\begin{array}{cc}\begin{array}{l}1,\\ -1,\\ 0,\end{array}& \begin{array}{l}{\widehat{\rho }}_{ij}>\delta ,\\ {\widehat{\rho }}_{ij}<-\delta ,\\ \left|{\widehat{\rho }}_{ij}\right|\le \delta ,\end{array}\end{array}$$ (3.15)

and ${\widehat{\rho }}_{ij}$ is an estimate of ρ_ij.

Definition 2.

A posterior signed δ-graph performs a Bayesian test of the hypotheses $H_0:\left|{\rho }_{ij}\right|\le \delta$, $H_1:{\rho }_{ij}>\delta$ and $H_2:{\rho }_{ij}<-\delta$ and can be obtained as the signed matrix $\widehat{E}\left(\delta \right)=\left[{\widehat{E}}_{ij}\left(\delta \right)\right]$ where

$${\widehat{E}}_{ij}\left(\delta \right)=\underset{s\in \left\{-1,0,1\right\}}{\arg \max }{\mathbb{P}}_{ij}^{\delta }\left(s\right),$$ (3.16)

and ${\mathbb{P}}_{ij}^{\delta }\left(s\right)=\mathbb{P}\left(E_{ij}\left(\delta \right)=s|{\mathbb{X}}_n,W\right)$ is the posterior probability that E_ij(δ) = s.

Definition 3.

A posterior signed (p; δ)-graph is the signed matrix $\widehat{E}\left(p,\delta \right)=\left[{\widehat{E}}_{ij}\left(p,\delta \right)\right]$

$${\widehat{E}}_{ij}\left(p,\delta \right)=\{\begin{array}{cc}\begin{array}{l}1,\\ -1,\\ 0,\end{array}& \begin{array}{l}{\mathbb{P}}_{ij}^{\delta }\left(0\right)<1-p\hspace{0.17em}\text{and}\hspace{0.17em}{\mathbb{P}}_{ij}^{\delta }\left(1\right)\ge {\mathbb{P}}_{ij}^{\delta }\left(-1\right),\\ {\mathbb{P}}_{ij}^{\delta }\left(0\right)<1-p\hspace{0.17em}\text{and}\hspace{0.17em}{\mathbb{P}}_{ij}^{\delta }\left(1\right)<{\mathbb{P}}_{ij}^{\delta }\left(-1\right),\\ {\mathbb{P}}_{ij}^{\delta }\left(0\right)\ge 1-p.\end{array}\end{array}$$ (3.17)

3.4. Edge error detection control.

We choose the parameters δ and p of the graph estimators by controlling edge discovery errors. Let $\widehat{E}$ be an estimator of E(δ). Define the false discovery proportion

$$\text{FDP}=\frac{{\sum }_{i<j}\left|{\widehat{E}}_{ij}\right|\left(1-\left|E_{ij}\left(\delta \right)\right|\right)}{{\sum }_{i<j}\left|{\widehat{E}}_{ij}\right|},$$ (3.18)

and the false non-discovery proportion

$$\text{FNP}=\frac{{\sum }_{i<j}\left(1-\left|{\widehat{E}}_{ij}\right|\right)\left|E_{ij}\left(\delta \right)\right|}{{\sum }_{i<j}\left(1-\left|{\widehat{E}}_{ij}\right|\right)},$$ (3.19)

which are, respectively, the proportion of incorrectly detected edges out of all detections, and the proportion of missed true edges out of all non-detections. Further define the signed false discovery proportion

$${\text{FDP}}^{\ast }=\frac{{\sum }_{i<j}\left\{I\left({\widehat{E}}_{ij}>0\right)I\left(E_{ij}\left(\delta \right)\le 0\right)+I\left({\widehat{E}}_{ij}<0\right)I\left(E_{ij}\left(\delta \right)\ge 0\right)\right\}}{{\sum }_{i<j}\left|{\widehat{E}}_{ij}\right|},$$ (3.20)

which takes into account sign errors of the detected edges. Lemma 5 (Vinci et al., 2018b) shows that FDP ≤ FDP^∗, so that controlling FDP^∗ is a more stringent criterion because it also takes into account the sign of the edges. Taking the expectations of FDP, FNP, and FDP^∗ with respect to the Gaussian data ${\mathbb{X}}_n$ conditionally on the true parameters µ and Ω gives the frequentist false discovery rate

$$\text{FDR}=\mathbb{E}\left[\text{FDP}|\mu \text{,}\Omega \right],$$

false non-discovery rate

$$\text{FNR}=\mathbb{E}\left[\text{FNP}|\mu ,\Omega \right],$$ (3.22)

and signed false discovery rate

$${\text{FDR}}^{\ast }=\mathbb{E}\left[{\text{FDP}}^{\ast }|\mu ,\Omega \right].$$ (3.23)

Bounding either of these edge error metrics is a way to choose the parameters δ and p of the graph estimators given in Definitions 1, 2, and 3. These metrics are easy to compute in simulation studies, where the true graph is known, but not otherwise. For experimental data, we use instead their Bayesian counterparts, obtained by taking the expectations of FDP, FNP and FDP^∗ conditionally on the Gaussian data ${\mathbb{X}}_n$ and the auxiliary quantity W, yielding

$${\text{FDR}}_{\Pi }=\frac{{\sum }_{i<j}\left|{\widehat{E}}_{ij}\right|P\left(E_{ij}\left(\delta \right)=0|{\mathbb{X}}_n,W\right)}{{\sum }_{i<j}\left|{\widehat{E}}_{ij}\right|},$$ (3.24)

$${\text{FNR}}_{\Pi }=\frac{{\sum }_{i<j}\left(1-\left|{\widehat{E}}_{ij}\right|\right)P\left(E_{ij}\left(\delta \right)\ne 0|{\mathbb{X}}_n,W\right)}{{\sum }_{i<j}\left(1-\left|{\widehat{E}}_{ij}\right|\right)},$$ (3.25)

and

$${\text{FDR}}_{\Pi }^{\ast }=\frac{{\sum }_{i<j}\left\{I\left({\widehat{E}}_{ij}>0\right)P\left(E_{ij}\left(\delta \right)\le 0|{\mathbb{X}}_n,W\right)+I\left({\widehat{E}}_{ij}<0\right)P\left(E_{ij}\left(\delta \right)\ge 0|{\mathbb{X}}_n,W\right)\right\}}{{\sum }_{i<j}\left|{\widehat{E}}_{ij}\right|}$$ (3.26)

The posterior probability $P\left(E_{ij}\left(\delta \right)=0|{\mathbb{X}}_n,W\right)$ in Equation 3.24 can be interpreted as a local false discovery rate, so that the FDR_Π can be viewed as the global false discovery rate of the set of putative signals (here edges) in a multiple hypothesis testing problem (Efron et al., 2001; Scott et al., 2015). In simulations, FDR_Π, FNR_Π, and ${\text{FDR}}_{\Pi }^{\ast }$ appear to control their frequentist counterparts (Figure 3; see also Vinci et al. (2018a)).

FIG 3.

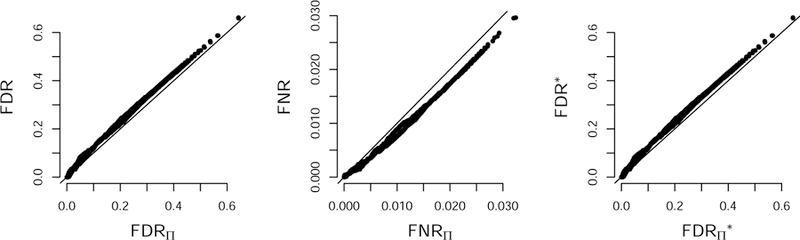
Bayesian FDR_Π, FNR_Π, and ${\text{FDR}}_{\Pi }^{\ast }$ plotted against their frequentist counterparts. Results obtained from simulated d-dimensional Gaussian vectors, d = 150, with 5580 edges and sample size n = 5000. The error rates were computed from (p, δ)-graph estimates (Definition 3).

3.5. ROC analysis.

We use Bayesian edge discovery error rates to build the graph estimates, as described above, and we evaluate their quality using sensitivity and specificity:

$$\text{SPEC}=\frac{{\sum }_{i<j}I\left({\widehat{E}}_{ij}=0\right)I\left(E_{ij}\left(\delta \right)=0\right)}{{\sum }_{i<j}I\left(E_{ij}\left(\delta \right)=0\right)},$$ (3.27)

$$\text{SENS}=\frac{{\sum }_{i<j}I\left({\widehat{E}}_{ij}\ne 0\right)I\left(E_{ij}\left(\delta \right)\ne 0\right)}{{\sum }_{i<j}I\left(E_{ij}\left(\delta \right)\ne 0\right)},$$ (3.28)

which give the proportions of true edges correctly identified and of missing edges correctly omitted, respectively. To account for sign detection performance we further define the positive and negative sensitivities:

$${\text{SENS}}^{+}=\frac{{\sum }_{i<j}I\left({\widehat{E}}_{ij}>0\right)I\left(E_{ij}\left(\delta \right)>0\right)}{{\sum }_{i<j}I\left(E_{ij}\left(\delta \right)>0\right)},$$ (3.29)

$${\text{SENS}}^{-}=\frac{{\sum }_{i<j}I\left({\widehat{E}}_{ij}<0\right)I\left(E_{ij}\left(\delta \right)<0\right)}{{\sum }_{i<j}I\left(E_{ij}\left(\delta \right)<0\right)},$$ (3.30)

which give the proportions of true positive and true negative edges correctly identified, respectively. The Receiver Operating Characteristic (ROC) curve displays (1 ‒ SPEC) versus SENS for all possible settings (e.g. values of tuning parameters) of a graph estimator. An Area Under the ROC Curve (AUC) close to one indicates good edge estimation performance, but does not account for the signs of the connections. A three-class extension of the ROC curve that accounts for connection sign is the ROC surface given by the graph of SPEC as a bivariate function of SENS⁺ and SENS⁻ over the set [0, 1]². The Volume Under the ROC Surface (VUS) is a three-class extension of the AUC that takes into account sign detection performance. A graph with signed edges assigned at random has VUS 1/6 and AUC 1/2. We thus rescale VUS to ease its interpretation, according to 1/2 + (VUS − 1/6)6/10.

4. Estimation of functional connectivity in macaque areas V4 and PFC.

Neural spike train data were recorded simultaneously from visual area V4 and PFC in the same hemisphere of a macaque monkey (Macaca mulatta) using two 100-electrode Utah arrays (Figure 1), while the animal was performing an orientation change detection task¹ (Figure 4). The visual stimuli consisted of drifting gratings, i.e., alternating light and dark bars that move in a fixed direction within a circular aperture displayed on a screen in front of the animal. Neurons in area V4 fire more rapidly when the drifting gratings are placed in a particular region of visual space, known as that neuron’s receptive field (RF). In the task, one stimulus was placed in the location of the aggregate RFs of the V4 neurons, which was in the lower left corner of the visual space, indicated by the dashed circles in Figure 4, and the other stimulus in the opposite hemifield, in the lower right corner. The animal’s task (successful completion of which resulted in a juice reward) was to make an eye movement (marked in orange) from the central blue fixation spot to the location where the grating changed orientation. The drifting gratings changed in a subtle way (a shift in orientation) that signaled the animal to respond with an eye movement, and the animal was cued in blocks of trials to attend to one of the two stimuli, either in the receptive fields of the V4 neurons being recorded (“attend in”) or the location in the opposite hemifield (“attend out”). The four experimental conditions were therefore defined by the combination of two variables:

1. ORIENTATION ϑ: a drifting grating at orientation degree ϑ = 135 or 45 was presented in the RF, and in the orthogonal orientation in the opposite hemifield.

2. ATTENTION ζ: the animal was cued to either attend towards (ζ = 1, attend in) or away from (ζ = 0, attend out) the receptive field.

FIG 4.

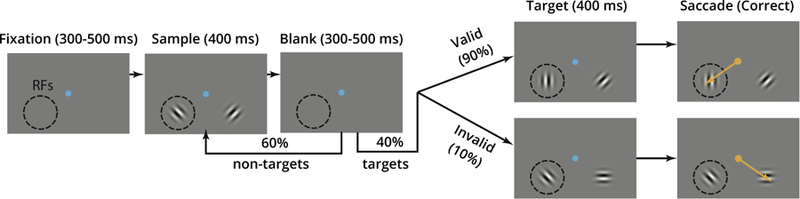
The experiment. A trial proceeded as follows: after an initial period of 300 to 500 ms of fixation on the blue central spot in the center of the visual space, a sample stimulus was presented, which consisted of two drifting gratings with orthogonal orientations appearing in the aggregate receptive field (RF) of the V4 neurons being recorded, indicated by the dashed circle in the visual space, and its opposite hemifield. The stimulus lasted for 400 ms and was followed by a blank period of 300 to 500 ms. After this blank period, there was a 40% chance that a target (a changed orientation in either the RF (“valid side”) or its opposite hemifield (“invalid side”) appeared, and a 60% chance that the sample stimulus repeated, called a “non-target”. The animal’s task was to make an eye movement (a saccade, marked in orange) from the central blue fixation spot to the location where the grating changed orientation. The animal was cued in blocks of trials to attend to (pay attention to) either the aggregate V4 RF (“attend in”) or the location in the opposite hemifield (“attend out”), while maintaining fixation on the central blue spot. We analyze the sample period, when the animal presumably prepared to detect a change in grating orientation. The animal’s attention was validated by behavioral metrics, including a decrease in response time and increase in hit rate when the target appeared at the cued location as compared to the uncued location.

This experiment was novel in that it directly investigated functional interactions among large populations of neurons in two brain areas thought to play critical roles in visual attention. A key feature of this experiment (like many others in neurophysiology) involves the substantial number of repeated observations, or trials, under identical experimental conditions. The trial-to-trial variation can provide a means of assessing cooperative activity among neurons. The questions we seek to answer are, How strongly connected, in the sense of covariation of firing rates, are the neurons within V4 and within PFC? How strongly connected are the neurons in PFC to those in V4? How does this connectivity change with attention? How does connectivity change with the orientation of the grating?

A total of 666, 759, 954, and 1077 identical repeat trials of length 500ms, starting at the stimulus onset of epoch “Sample (400ms)” in Figure 4, were recorded under the four task combinations $\left(\vartheta ,\zeta \right)\in \left\{\left(135,\hspace{0.17em}\hspace{0.17em}1\right),\hspace{0.17em}\left(45,\hspace{0.17em}1\right),\hspace{0.17em}\left(135,\hspace{0.17em}0\right),\hspace{0.17em}\left(45,\hspace{0.17em}0\right)\right\}$, respectively, and 264 candidate neuronal units were identified across the two multi-electrode arrays in one recording session. For our statistical analysis we retained only the 148 neurons (71 in V4 and 77 in PFC) that had average firing rates greater than 4 spikes per second in all four conditions. Their firing rates had maximum 67.46 spikes/s, mean 18.96, and 2.5th and 97.5th percentiles 4.78 and 56.80.

To estimate the functional connectivity between and within areas V4 and PFC we fitted the 148-variate Poisson-lognormal (PLN) model (Equation 2.1) in each of the four conditions using the full Bayes algorithm (Algorithm 1 in Appendix C.3, Vinci et al. (2018b)), which provides estimates of the conditional dependence graphs of the latent log firing rates X, with edges representing functional connections. Specifically, we let the prior distribution for Ω be Equation 2.3, with the Gaussian mixture distribution p_ij (Equation 2.4) taken to be normal with mean m_ij and rate λ_ij modulated by functions f (W_ij) and g(W_ij) (Equations 2.5 and 2.6), respectively, and point-mass weight π_ij modulated by η(W_ij) (Equation 2.7). Here, the auxiliary quantity W_ij is inter-neuron distance, measured by the distance between electrodes. Neuronal dependences have been observed to weaken when neurons are physically further apart in several cortical areas (Smith and Kohn, 2008; Smith and Sommer, 2013; Goris, Movshon, and Simoncelli, 2014; Yatsenko et al., 2015; Vinci et al., 2016, 2018a), so we expect this quantity to be useful to improve graph estimation. We let the regularizing functions f, g, and η be step functions² with five steps each, the last step modeling distances W greater than 5mm, which corresponds to pairs of neurons on different arrays; the first four steps are taken at the quartiles of the interneuron distances that are less than 5mm, corresponding to pairs of neurons on the same array. We did not consider including a low-rank covariance structure because the optimal number of factors in a factor model fitted to the square-rooted spike counts of all 148 neurons (using ten-fold cross validation; see Section 4.1 for details) was about 22 factors in each condition, suggesting that the neurons’ covariation structure was not low dimensional. Here, the animal was awake, while the very low-dimensional structure found by Ecker et al. (2014) was in data recorded under anesthesia.

Figure 5 shows the fitted functions f, g, and η in condition (ϑ, ζ) = (45, 0); fitted models in the other conditions were similar: f (W ) is close to zero, which suggests that the partial correlations are centered around zero for all values of W, and η(W ) is close to one, likely because the shrinkage induced by g(W ) is strong enough and/or there isn’t a large proportion of exactly zero Ω entries. However, g increases with W, which suggests that incorporating W in the model helped estimate the network (Vinci et al. (2018a); see also Figure 8). We drew similar conclusions by inspecting the plot of unregularized square-rooted sample spike count partial correlations versus inter-neuron distance (Figure 11, Appendix D, Vinci et al. (2018b)): although they are noisy versions of the log firing rate partial correlations, their values appear to be centered at zero and their spread to decrease with inter-neuron distance. Therefore, to avoid the excess variability that typically results from fitting non-existant or weak effects, we re-fitted the multivariate PLN model to the data, assuming f = 0 and η = 1, i.e. π_ij = 1 and m_ij = 0 for all (i, j) in Equations 2.3 and 2.4. Appendix D (Vinci et al., 2018b) contains some diagnostic plots that suggest a good model fit. Figure 6C shows the re-estimated penalty function g(W ) in the four task combinations: just as in Figure 5, g increases with inter-neuron distance W. Note that W > 5 includes all the neuron pairs that are in different brain areas, so that the penalty across areas is separate from that within areas. The fitted penalty across areas is very strong, indicating much greater sparsity (much less connectivity) across areas than within areas.

FIG 8.

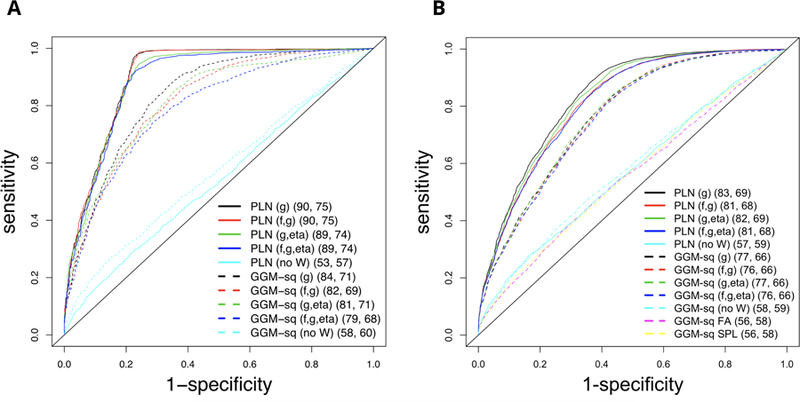
ROC curves for firing-rate graph estimation based on Poisson-lognormal (PLN) and GGM applied to square rooted spike counts (GGM-sq), averaged across repeat simulations, in the case of a fully recorded network of 50 neurons (A) and a network with 50 recorded and 10 latent neurons (B). The first set of parentheses indicates which functions of W were fitted in the adjusted regularization; the second set contains the area under the curve (AUC) and rescaled volume under the surface (VUS, Section 3.5), averaged across repeat simulations.

FIG 6.

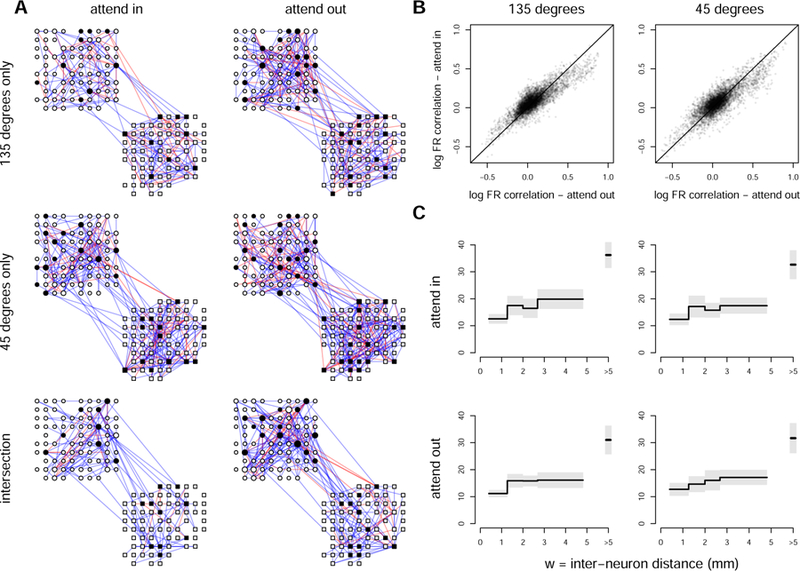
(A) Functional connectivity graphs of log firing rates of neurons in PFC (round nodes) and V4 (squared nodes); 5% Bayesian FDR^∗ (Equation 3.26, Section 3.3; (p, δ)-graphs where δ was taken to be equal to the largest of the 20th percentiles of the magnitudes of the partial correlation estimates across the four conditions). We show edges that appear only at orientation 135 degrees but not at 45 degrees, only at orientation 45 degrees but not at 135 degrees, and edges that appear for both orientations. Blue and red edges are positive and negative connections, respectively; we blackened the nodes that connect the two areas. (B) Correlations of log firing rates of the fitted PLN models under the attend in and attend out conditions, for both orientations, among pairs of neurons for which one neuron is in V4 and the other is in PFC. The magnitudes of correlations tend to be diminished for the attend in condition (95% confidence intervals for the linear regression slopes of attend in on attend out correlations are [0.74, 0.76] and [0.75, 0.77], respectively). (C) The estimated function g (Equation 2.5) with 95% posterior intervals. The function increases with inter-neuron distance W in all conditions, which implies a stronger penalization on partial correlations for pairs of neurons that are further apart.

Figure 6A displays several versions of the graphs estimated by applying 5% Bayesian FDR∗ control in the four experimental conditions. For ease of visual comparison, for both attend in and attend out conditions we have displayed edges that appear only at orientation 135 degrees but not at 45 degrees, only at orientation 45 degrees but not at 135 degrees, and edges that appear for both orientations (i.e., intersection of the two graphs under the two orientations). Table 1 contains the numbers of edges in these graphs, and the ratio (#intersection edges/#union edges) ∈ [0, 1], to quantify the similarity of functional connectivity induced by the two stimulus orientations (45 and 135 degrees) in each of the two attention conditions. There is substantial functional connectivity in pairs of neurons across regions, as well as within regions; there is somewhat diminished connectivity (in terms of number of edges) for the attend in conditions as compared with the attend out, and somewhat greater connectivity for orientation 45 degrees than for 135 degrees.

TABLE 1.

Number of edges and similarity of the graphs (135 degrees versus 45 degrees in the case of attend in or attend out) displayed in Figure 6A.

	attend in	attend out
135° only	208	284
45° only	277	325
intersection	147	251
graph similarity	23%	29%

We also observed diminished connectivity within V4 and PFC for the attend in conditions as compared with the attend out in terms of edge correlation magnitudes (not shown but similar to Figure 6B). The tendency for diminished magnitude of correlation for the attend in condition is similar to previous findings of reduced trial-to-trial pairwise correlation with attention found within single visual areas (Cohen and Maunsell, 2009; Mitchell, Sundberg, and Reynolds, 2009; Snyder, Morais, and Smith, 2016). Another report (Ruff and Cohen, 2016), however, found that spike count correlations between visual cortical areas V1 and MT increased when spatial attention was directed to the joint receptive fields of the recorded neurons. One possible explanation lies in the role of these regions in spatial attention: V1 is thought to provide feedforward input to MT neurons, while PFC has more often been implicated in sending feedback connections to visual areas, including V4. It is also of interest to examine pairwise correlation structure across areas, which we can do here because neurons were recorded simultaneously in V4 and PFC. Figure 6B displays a plot of the fitted correlations (the correlations among the latent Poisson log means, representing the log firing rates) under the attend in and attend out conditions, for both orientations, among pairs of neurons for which one neuron is in V4 and the other is in PFC. Once again we find diminished magnitude of correlation in the attend in condition.

Inverting the estimated precision matrix gives the covariance matrix, from which we may compute R² using a standard formula from multivariate analysis. In particular, we may choose a single neuron and ask how well its response (its log firing rate) may be predicted based on all the other neurons within its area, or based on all the neurons in the other area. Figure 7 displays plots of R² for all neurons in V4 and PFC, where the x-axis is R² using neurons within the same brain area, and the y-axis is R² using the neurons in the other area. These plots show two things. First, the prediction of a given neuron’s firing rate tends to be better when predicting from neurons within the same brain area than from neurons in the other area. This is not surprising. More interesting is the strong relationship between the two, and the relatively small discrepancy between these predictions. This is especially true for area V4 in the attend out condition: the blue dots in the lower left panel cluster strongly around a line that is close to the diagonal; that is, a V4 neuron whose activity is highly predictable (or much less predictable) from other V4 neurons is also highly predictable (or much less predictable) from PFC neurons. This is a striking result, suggesting that major sources of trial-to-trial covariation are shared across these two areas, especially in the attend out condition.

FIG 7.

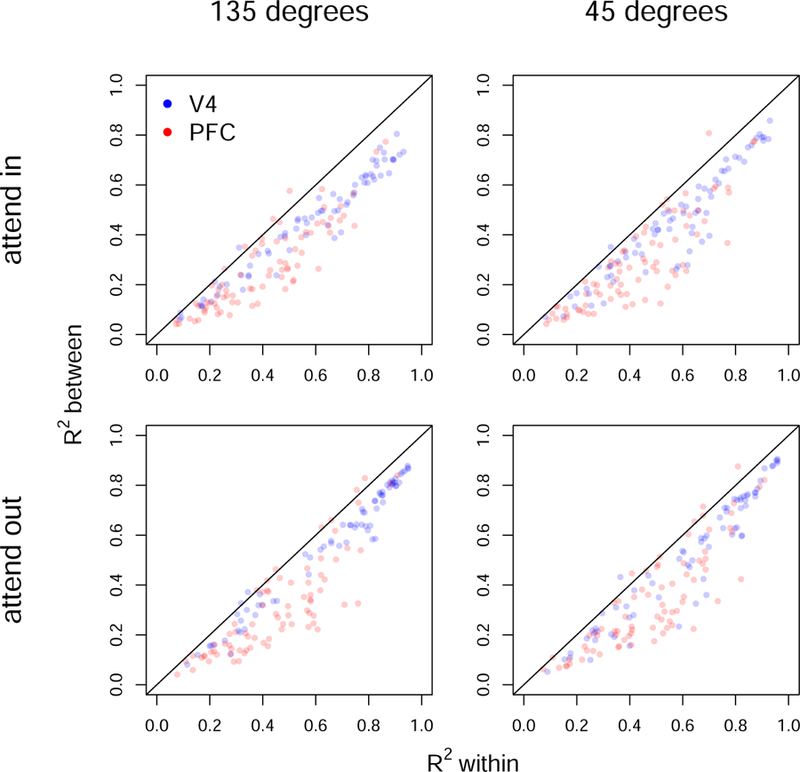
Coefficients of determinations R² of linear regressions of the log firing rate of each neuron in V4 and PFC on the log firing rates of all other neurons within the same brain area (x-axis) and in the other area (y-axis). The values of R² were determined from the fitted precision matrix.

4.1. Analyses with simpler graph estimators.

For comparison’s sake, we repeated our data analyses with related methods applied to square-rooted spike counts (the square root transformation improves the fit of a GGM to count data). The simplest estimator of the covariance matrix is the sample covariance matrix (SAM) whose inverse can be used to obtain sample partial correlations that can be thresholded to obtain a graph. Specifically we applied the Fisher-transformation to z-score the partial correlations and then applied classical 5% FDR control (Benjamini and Hochberg, 1995; Benjamini and Yekutieli, 2001) on the p-values. The graphical LASSO, Glasso (Yuan and Lin, 2007) and its adaptive variant AGlasso (Fan et al., 2009) are graph estimators based on λ₁ penalization that favor zeros in the precision matrix; graph structure can be selected via ten-fold cross-validation (CV; Fan et al. (2009)). We do not show the graphs estimated using these three methods, and instead summarize them in Table 2 in Appendix D.3 (Vinci et al., 2018b), analogously to Table 1. Although the numbers of estimated edges are different than in Table 1, the inferences drawn from these numbers are qualitatively similar to the PLN results, with the exception that Glasso suggests an increased connectivity (in terms of number of edges) for the attend in conditions as compared with the attend out, at the 45 degrees orientation.

For the R² analysis reported in Figure 7, we further considered factor analysis (FA): we let the data vector S be a noisy inflation of a latent lower dimensional vector F ~ N (0, I_q), according to S = AF + ϵ, where ϵ ~ N (0, D), A Rd×q, and D is a positive diagonal matrix; this in turn implies Ω⁻¹ = AA^T + D. If q < d/2 then the number of parameters involved (d(q + 1)) is smaller than the full dimensionality of a d × d symmetric matrix (d(d + 1)/2). For each of the four experimental conditions, we computed the maximum likelihood estimate of Ω of the d = 148 neurons assuming a factor structure with q selected via ten-fold CV. We found that about 22 factors minimized the cross-validated error in each condition. In Appendix D.3 (Vinci et al., 2018b) Figure 13 we reproduce Figure 7 with SAM, Glasso, AGlasso, and FA. Results from the first three methods appear to be noisy versions of those in Figure 7. However, because FA allows the data variables to be close to multicollinear, it produces an uninterpretable plot with all values of R² essentially equal to 1.

In the end, we have more faith in the inferences from our covariate-adjusted PLN model, because in Vinci et al. (2018a) we showed via a large simulation study that the simpler case of a covariate-adjusted GGM (GAR) applied to square rooted spike counts with no hierarchical structure in Equation 2.1 improved graph estimation, covariance structure inference, and thereby the accuracy of the results of scientific investigations, compared to related methods; and in Section 4.2 we provide additional results that show that covariate-adjusted PLN is better than GAR to extract latent firing rate network information, based on simulated data similar to the experimental data analyzed here.

4.2. Properties of the multivariate PLN model with auxiliary regularization.

We simulate spike count data from a ground truth model similar to the PLN model fitted to the experimental data (Figure 5), estimate the network of their latent firing rates using the PLN model, with and without auxiliary information, also estimate the network of observed spike counts using a GGM applied to their square-roots (GGM-sq), with and without auxiliary information, compare the fits to the ground truth using ROC curves and surfaces (Section 3.5), repeat the simulation 20 times, and report average ROC curves, AUC values, and VUS values.

For the ground truth, we set f to zero and η to one, and we let g be an increasing step function with values 10, 15, 15, 20, 30 over respective bins³ (0, 1], (1, 2], (2, 3], (3, 4], (4, 5], with W ~ Uniform(0, 5), and generate a precision matrix Ω according to Equation 2.3. Partial correlations are then set to zero for W > 4 to mimic the experimental data, since only a few edges exist between V4 and PFC in Figure 6A. We simulate n = 500 samples from a d = 50 dimensional random vector following the multivariate PLN distribution in Equation 2.1 with the generated Ω, and µ containing values observed in the experimental data. We fit the GGM-sq and PLN models with f ≡ 0, g(w) a step function, and η ≡ 1, denoted by (g) in the legend of Figure 8, f (w) and g(w) step functions, and η ≡ 1, denoted by (f, g), etc. The (no W ) fit corresponds to using a flat regularization such as the graphical lasso (Yuan and Lin, 2007; Wang, 2012), with f ≡ 0, g constant, and η ≡ 1.

Figure 8A shows that the PLN fit retrieves the firing rate network better than the GGM-sq fit, since all the PLN ROC curves are well above their GGM counterparts, and that without auxiliary information, neither PLN nor GGM-sq provides as good a fit as when W is incorporated in the estimation. Note that fitting f, g, and η as functions of W even if they do not all depend on W (only g actually depends on W in this simulation) can degrade the fit somewhat but it remains far superior to the fits that do not account for W. We provide more simulation results in Appendix A (Vinci et al., 2018b).

In any statistical investigation about dependence among variables, including graphs or multivariate regression, confounding variables are always there lurking behind the scenes. One way to capture their effects is to include as many available variables as possible in the modeling, with the hope to capture the most relevant ones. Alternatively, we may assume that a low dimensional latent quantity is present. In the context of covariance estimation, factor analysis (FA; Ecker et al. (2014); Rabinowitz et al. (2015)) and the sparse - low rank model (SPL; Chandrasekaran et al. (2012); Yuan (2012); Yatsenko et al. (2015)) have been used to model the effects of such low dimensional latent components. The simulated data here have been generated in a way that could reflect the real data we analyze, and in Figure 8A we emulated the case where all neurons in the network were recorded. We wanted then to consider also the situation where some neurons were latent, to assess how differently FA and SPL would perform compared to GGM-sq (no W ) and the methods that use the auxiliary information of W. We thus repeated the simulation, but generated count vectors for 60 neurons, and dropped 10 of them. Results are in Figure 8B. The performances of FA and SPL (with optimal oracle tuning parameter choices) are similar to the simpler GGM-sq (no W ), while our approach maintains performance robustly. We also applied FA and SPL to the case of fully recorded neurons, and conclusions about their performance were the same. However, it is possible that a covariate adjusted version of FA or SPL might produce better results; their implementation is part of our future research.

5. Discussion.

We have developed and studied a framework for estimating generalized graphical models in the presence of auxiliary variables that carry information about the graph. The graph is defined by the precision matrix for a multivariate normal distribution of a latent random vector. Here, the components of the latent random vector are logs of Poisson mean parameters, which in the context of spike counts represent log firing rates. The research we report here greatly extends previous work by combining two previously separate aspects of the model: the Poisson log-normal hierarchical aspect (which was previously considered only in the bivariate case), and the idea of using covariates to control the penalty in a sparse Gaussian graphical model. Graphs are summaries of correlation structure, and, together, Figures 6 and 7 indicate the kinds of physiological conclusions that can be drawn from the methodology we have developed: we can either examine the graph itself, as in Figure 6A, or we can look at summaries of the covariance matrix, as in Figures 6B and 7.

The approach we took here was Bayesian, and relied on a flexible and data driven covariate-adjusted spike and slab model that includes several existing types of network regularization models as special cases, e.g. ridge, lasso, and sparse - low rank decomposition, and that can readily accommodate other types of less explored network regularizations, e.g. the Elastic Net, as described in Appendix A (Vinci et al., 2018b). The fit of that model to the experimental neuron data of Section 4 suggested that ridge or LASSO-type penalties were adequate for the data we examined. Appendix A contains a toy example where the general spike and slab prior performs better than the currently available priors. Additionally, while our method and estimation algorithms were motivated by neuron spike count data, they are generally applicable to different types of data whenever auxiliary variables are available to help determine latent graphical structure; e.g. in Equation 2.1, the Poisson distribution may be replaced by others, such as binomial and negative-binomial, or continuous distributions. Because it allows for many precision matrix regularizations and data types, it may be considered a unifying framework for estimating covariate-adjusted networks. In the future, covariate-adjusted regularization could also be extended to multivariate time series and doubly-stochastic point processes.

The neurophysiological variables used as auxiliary quantities in this and previous research (Vinci et al., 2018a) were pairwise, i.e. one quantity per neuron pair (e.g. inter-neuron distance and tuning curve correlation), so it was a natural choice to introduce such information through an entrywise regularization scheme targeting the entries of the precision matrix, rather than other features (e.g. eigenvalues, factors) that do not map easily onto entrywise auxiliary information. We have provided evidence that this approach can do a good job with estimation of neuronal covariance. Furthermore, graphs provide nice interpretations of the covariance matrix. An alternative approach is to introduce latent factors, which can provide useful dimensionality reduction.

To account for the effect of unrecorded neurons and other latent factors on the dependence structure of the recorded neurons, our framework can be adapted in at least two ways. One approach is analogous in construction to the latent graphical model (Chandrasekaran et al., 2012), discussed in Appendix A (Vinci et al., 2018b). Alternatively, one could assume $X|F~N\left(\mu +AF,{\Omega }^{-1}\right)$, where $F~N\left(0,I_q\right)$ are latent factors, $q<d/2$, $A\in {ℝ}^{d\times q}$, and Ω is sparse, so that the covariance matrix of X is AA′ + Ω⁻¹, where AA′ has rank at most q. By further assuming a prior distribution on Ω as in Equation 2.3, with continuous Laplace p.d.f. components in Equation 2.4, and a prior distribution on A that constrains the model to be identifiable, we can estimate AA′ and Ω by implementing our full or empirical Bayes algorithms (Appendix C, Vinci et al. (2018b)) with additional sampling steps for F | rest and A | rest. In either case, the sparse component of the precision matrix would represent the dependence structure of the observed variables conditionally on both observed and latent variables. Implementing these approaches was beyond the scope of the work reported in this paper, but we plan to investigate them in the future.