Machine learning in human movement biomechanics: Best practices, common pitfalls, and new opportunities

Abstract

Traditional laboratory experiments, rehabilitation clinics, and wearable sensors offer biomechanists a wealth of data on healthy and pathological movement. To harness the power of these data and make research more efficient, modern machine learning techniques are starting to complement traditional statistical tools. This survey summarizes the current usage of machine learning methods in human movement biomechanics and highlights best practices that will enable critical evaluation of the literature. We carried out a PubMed/Medline database search for original research articles that used machine learning to study movement biomechanics in patients with musculoskeletal and neuromuscular diseases. Most studies that met our inclusion criteria focused on classifying pathological movement, predicting risk of developing a disease, estimating the effect of an intervention, or automatically recognizing activities to facilitate out-of-clinic patient monitoring. We found that research studies build and evaluate models inconsistently, which motivated our discussion of best practices. We provide recommendations for training and evaluating machine learning models and discuss the potential of several underutilized approaches, such as deep learning, to generate new knowledge about human movement. We believe that cross-training biomechanists in data science and a cultural shift toward sharing of data and tools are essential to maximize the impact of biomechanics research.

1. Introduction

For most of the 20th century, inference in biomedical research was predominantly based on hypothesis testing using parametric tests, such as the Student’s t test. The current surge of data, however, presents new challenges and opportunities that are shifting the data analytics landscape in many biomedical disciplines, including human movement biomechanics. Data characterizing human movement are high-dimensional, heterogeneous, and growing in volume with wearable sensing; often, they do not satisfy assumptions associated with parametric tests. Advanced analytical techniques to extract informative features from these data and model underlying relationships that cannot be modeled with traditional statistical tools could transform biomechanics research, as they have autonomous driving, speech recognition, and automated cancer detection.

Efforts to modernize biomechanical data analysis are exemplified by the use of feature extraction algorithms such as principal component analysis (PCA). The literature reflects an evolving awareness about the drawbacks of using only summary metrics (e.g., mean acceleration) or salient features (e.g., the peak knee adduction moment) to describe gait data, as summary metrics are not always the most informative with respect to outcomes of interest (e.g., disease status). PCA, which preserves the variability of multivariate datasets while reducing dimensionality to make analyses more tractable, has been used as an alternative (Deluzio and Astephen, 2007; Donoghue et al., 2008; Duhamel et al., 2006; Ryan et al., 2006). Although most biomechanics studies that employ these methods for dimensionality reduction continue to analyze the reduced data with traditional statistical tools, biomechanists are now also considering new problem formulations in which features extracted using PCA are used as inputs in machine learning models.

Two machine learning approaches, predictive modeling and data mining, serve different purposes than traditional inferential statistics. Predictive modeling is concerned with finding a function that optimally maps input data (e.g., kinematic waveforms) to a given output (e.g., disease status) with the goal of making accurate predictions in the future. One example of predictive modeling in biomechanics is myoelectric control of prostheses, where models are trained to recognize an individual’s intention based on myoelectric signals and the predicted intention is used to control the prosthesis (Oskoei and Hu, 2008). More recent efforts have centered around diagnostic and prognostic predictive models for neuromuscular and musculoskeletal pathologies (e.g., Schwartz et al., 2013), fall prediction (e.g., Wei et al., 2017), activity recognition to facilitate out-of-clinic patient monitoring (e.g., Biswas et al., 2015), and event detection to guide interventions such as deep brain stimulation (e.g., Pérez-López et al., 2016). The goal of data mining, on the other hand, is to discover new patterns in the data. Using clustering methods to identify subpopulations that exhibit different types of pathological gaits is an example of data mining (e.g., Rozumalski and Schwartz, 2009).

While applications of machine learning methods are expanding in movement biomechanics, critical evaluation of studies that apply them remains difficult. Machine learning approaches differ from the traditional statistical tools that biomechanists are trained to apply and interpret based on established reporting standards (e.g., p value for statistical significance). As the field becomes more data-intense and the use of machine learning continues to increase, good practices for conducting and reporting research at the intersection of biomechanics and machine learning are needed to ensure that conclusions are valid and reproducible. A discussion of this topic will also enable researchers to develop an intuition for the types of problems that machine learning can address more successfully than traditional statistics. Accordingly, the goal of this survey is to make machine learning efforts more visible and propose standards to increase the quality and impact of future research in this exciting area. To achieve this goal, we first review applications of machine learning that focus on neuromuscular and musculoskeletal diseases. We outline best practices for reporting the results of these analyses and common pitfalls we encountered in the literature. Finally, we offer suggestions for overcoming some of the challenges facing biomechanical data analytics and highlight opportunities where emerging techniques are likely to have great impact in upcoming years. Key terms are defined in Appendix A and our most important recommendations are summarized in the Conclusions section.

2. Methods

2.1. Literature search approach

We carried out a search for original research articles published up to December 31, 2017 using the PubMed/Medline database (1946-). Our search identified articles that used machine learning methods to study human movement biomechanics and was limited to studies of common musculoskeletal and neuromuscular diseases affecting mobility. We used search terms from three different categories to identify relevant studies: (1) movement biomechanics terms, such as gait, kinematics, and kinetics; (2) machine learning terms, such as support vector machines, neural network, and principal component analysis; (3) terms describing musculoskeletal and neuromuscular conditions, such as osteoarthritis, cerebral palsy, and stroke (Table 1). At least one term from each of these three categories had to appear in the title or abstract for the article to be considered.

Table 1.

Search terms used to identify studies that used machine learning methods to investigate movement biomechanics in populations with common musculoskeletal and neuromuscular diseases.

	Specific Terms
Machine learning method	support vector OR neural network* OR random forest* OR principal component OR linear discriminant OR lasso OR k means OR k-nn OR knn OR k-nearest* OR dimensionality reduction OR feature selection OR independent component analysis OR decision tree* OR regression model* OR logistic regression* OR reinforcement learning OR graphical model* OR Bayesian OR *fuzzy* AND
Neuromuscular or musculoskeletal condition affecting mobility	osteoarthritis OR osteoporosis OR osteonecrosis OR cerebral palsy OR running injur* OR running-related injur* OR stroke OR fracture OR Parkinson* OR polio OR carpal tunnel OR gout OR arthritis OR back pain OR fibromyalgia OR spinal cord injury OR amputee* OR joint implant OR joint replacement OR paralysis OR lumbar stenosis OR ACL tear OR meniscal tear OR muscular dystrophy OR muscular atrophy OR amyotrophic lateral sclerosis OR myopathy AND
Biomechanical outcome measure	gait OR motion OR movement OR kinematic* OR kinetic* OR accelerometer OR wearable OR IMU OR inertial measurement unit OR electromyogra* OR EMG OR force plate OR motor OR ground reaction force OR biomechanic*

2.2. Exclusion criteria

One of the authors reviewed all the titles and abstracts of articles retrieved from the database search. We excluded the following: dissertations, conference proceedings, conference abstracts, non-English articles, studies not involving human subjects, studies whose primary outcome was not one of musculoskeletal or neuromuscular function, and studies that utilized PCA for dimensionality reduction followed by traditional inferential statistics. We also excluded studies whose primary outcome or assessment of motor function was based on questionnaires, studies focusing on athletic performance that did not include injured patients, and studies focusing on myoelectric control of prostheses, because the use of machine learning in this area had been previously reviewed (Oskoei and Hu, 2008). A second author read the abstracts of the included articles to ensure that they met the inclusion criteria.

2.3. Assessed outcomes

The included articles were divided amongst four of the authors and the following information was extracted from each article: clinical condition studied, data sources (e.g., optical motion capture, electromyography, wearable devices), number of subjects, machine learning task (i.e., clustering, regression, classification), algorithms used, data shape (sample size × number of features), data purity (noise, bias, missing data, single or multiple source, inconsistencies in data collection protocol across samples), incorporation of covariates (e.g., age, sex), feature engineering approach (e.g., domain knowledge, PCA), feature selection or additional dimensionality reduction methods (e.g., forward feature selection), use of validation data for model selection and hyper-parameter tuning, evaluation of performance (use of test data and performance metrics reported), efforts to interpret the resulting model (e.g., interpretation of clusters or predictive features), and overall strengths and weaknesses. In addition to reporting these data in the Results section, we used them along with other observations made during the review to guide the discussion and recommendations of best practices.

3. Results

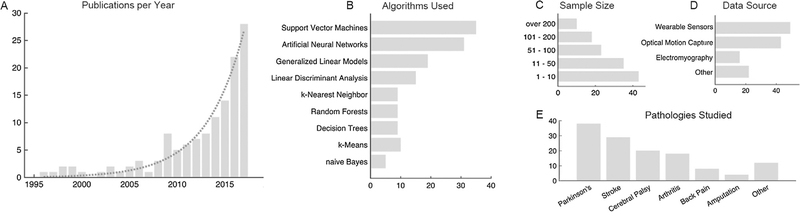
Our search yielded 3193 research articles, out of which 129, dating from 1996 to 2017, satisfied the inclusion criteria (Fig. 1A; Supplementary Table 1). The majority of studies focused on predictive tasks—classification (80.6%) and regression (11.6%)—while a few focused on data mining, in particular clustering tasks (7.8%). The most used algorithms were support vector machines, artificial neural networks, and generalized linear models (linear or logistic regression) for predictive modeling and k-means clustering for data mining (Fig. 1B). The number of subjects used in these studies varied from 4 to 2956, with the median being 40 (Fig. 1C). Movement data from wearable sensors were the most common, followed by data from traditional motion capture systems (Fig. 1D). Three studies used data collected in natural environments (Punt et al., 2016a, 2016b; Raknim and Lan, 2016; Fisher et al., 2016), while eight others used data collected outside of the laboratory, but in a controlled environment and for a short period of time (10 min–2.5 h) (Bochniewicz et al., 2017; Keijsers et al., 2003a, 2003b; Laudanski et al., 2015; O’Brien et al., 2017; Rodriguez-Martin et al., 2017; Samà et al., 2017; Yu et al., 2016). The most common subject populations were patients with Parkinson’s disease, cerebral palsy, spinal cord injury, osteoarthritis, running injuries, and stroke (Fig. 1E).

Fig. 1.

Study Characteristics. (A) The use of data science methods in human movement biomechanics studies that focus on neuromuscular and musculoskeletal pathologies has increased exponentially in recent years. (B) The mostly commonly used algorithms in the reviewed articles were support vector machines, neural networks, and generalized linear models, including linear and logistic regression. (C) The number of observations (subjects) in most studies was small to moderate. (D) Wearable sensors were the leading source of information, following by optical motion tracking. (E) The most commonly studied conditions were Parkinson’s, stroke, cerebral palsy, and arthritis.

Supplementary data associated with this article can be found, in the online version, at https://doi.org/10.1016/j.jbiomech.2018.09.009.

3.1. Areas of application

The most common area of application was classification of movement patterns, with many studies focusing on distinguishing pathological kinematics from normal kinematics. A lack of quantitative methods to assess motor symptoms associated with Parkinson’s disease has motivated the development of predictive models for automated detection of Parkinsonian gait, bradikynesia, tremor, freezing of gait, and medication-induced dyskinesia using data from accelerometers (Palmerini et al., 2011), inertial measurement units (IMUs) (Biswas et al., 2015; Buchman et al., 2014), pressure sensors (Alam et al., 2017), and digital handwriting tools (Drotár et al., 2015). Other diagnostic classifiers focused on detecting cerebral palsy in infants using data from videos (Rahmati et al., 2016) and in children using data from traditional motion capture systems (Kamruzzaman and Begg, 2006), determining cerebral palsy severity using motion capture data (Rozumalski and Schwartz, 2009; Sagawa et al., 2013; Trost et al., 2016; Zwick et al., 2004), characterizing movement patterns in post-stroke patients to inform targeted therapy (Huang and Patton, 2016; Kaczmarczyk et al., 2012, 2009; Krebs et al., 2014; Yu et al., 2016), and diagnosing osteoarthritis (Laroche et al., 2014; Levinger et al., 2009; Moustakidis et al., 2010). A few identified gait features that are discriminative of osteoarthritis status (Astephen et al., 2008; Magalhães et al., 2013; Meyer et al., 2016, 2015; Nüesch et al., 2012) or differences in muscle function between impaired and able-bodied individuals (Kuntze et al., 2015; Liu et al., 2014; Nair et al., 2010). A different set of studies focused on automated recognition of daily activities to facilitate out-of-clinic patient monitoring during rehabilitation (Biswas et al., 2015; Capela et al., 2016; Fulk et al., 2012; Fulk and Sazonov, 2011; Laudanski et al., 2015; Masse et al., 2016; O’Brien et al., 2017; Redfield et al., 2013; Roy et al., 2009; Vakanski et al., 2016).

Another area of application was predictive modeling for prognosis; this included models to assess the risk of developing a disease or estimate the effects of an intervention. For example, a few studies built models to identify factors that increase fall risk in post-stroke, Parkinson’s, and elderly patients, with the purpose of suggesting gait retraining and rehabilitation targets to mitigate risk (Kikkert et al., 2017; Punt et al., 2016a, 2016b; Wei et al., 2017), while another study built models to predict susceptibility to stroke based on features extracted from movement kinematics during writing tasks (O’Reilly et al., 2014). Finally, many studies focused on quantifying the effect of an intervention on gait and predicting which patients would benefit from interventions such as physical therapy (Duhamel et al., 2006; Jiang et al., 2017), gait modifications (Ardestani et al., 2014), orthoses prescriptions (Ries et al., 2014), and orthopedic surgery (Hicks et al., 2011; Schwartz et al., 2014, 2013).

3.2. Data characteristics

Most studies used time series data from a relatively small number of participants (median = 40 subjects), resulting in problems where the feature space was larger than the number of observations. Given that most studies were performed in controlled settings, the data did not have missing values. Noise was generally reduced using established filtering methods. Bias resulting from differences in subject characteristics was not addressed in many studies where it could have been. For example, several studies included case and control groups with unequal numbers of men and women or significantly different age groups. Generally, models were built using a single data type, but several studies integrated data from different sources (e.g., electromyography and optical motion capture) (Kamavuako et al., 2012; Moustakidis et al., 2010; Punt et al., 2017). Out of nine studies that fused data from different sources, four reported scaling or normalization of the features (Rahmati et al., 2016; Rissanen et al., 2008; Roy et al., 2013; Roy et al., 2009). For reasons pointed out in the Discussion, feature normalization is a practice we recommend when the algorithm is not scale invariant.

3.3. Feature engineering

Lower-dimensional features were most commonly engineered from time series using domain knowledge or PCA. Domain knowledge was used to extract key gait features, such as peak angles, moments, ranges of motion, muscle activity duration, cadence, and stride length. PCA was also performed to reduce dimensionality, while preserving most of the variation in the data. The number of principal components used in models was based on the percentage of variability explained, with most studies aiming to preserve at least 90% of the variability. Fewer studies derived features using Information Theory (Drotár et al., 2015), fast Fourier transforms (Ahlrichs et al., 2016), hidden Markov models (Mannini et al., 2016), wavelet decomposition (Moustakidis et al., 2010; Nielsen et al., 2011), and dynamic time warping (Zhang et al., 2016). Using the full time series in models was less common. Studies that took this approach trained models using feature spaces that were much larger than the number of observations, which is not recommended.

3.4. Model learning and performance evaluation

Model selection procedures (e.g., use of cross-validation for feature selection) and performance evaluation metrics (e.g., sensitivity and specificity, in addition to accuracy) were reported inconsistently across studies. Many studies included feature selection and hyper-parameter tuning in the model learning process. Feature selection approaches included stepwise (forward and backward) feature selection, hill climbing, and informal selection of feature combinations that led to the best model performance. Another approach was to pre-screen features and include only the ones that were significantly different between classes, using the entire dataset. Selection of hyper-parameters, such as the soft-margin constant for support vector machines or the learning rate for neural networks, was carried out using a grid-search approach in some studies, while in others selection of these parameters was not discussed. Only 8 of over 50 studies selected features or hyper-parameters using validation data, which as we point out in Section 4.3 can lead to models that do not generalize well to new data.

Model performance was assessed using held-out data, with the most common technique being k-fold cross-validation. The majority of studies reported accuracy as the primary performance evaluation metric, while fewer studies included sensitivity, specificity, F-1 score, and area under the receiver operating characteristic curve (AUC) measurements. Class imbalance was generally not discussed, even in studies that included different numbers of cases and controls, which can artificially inflate the performance of a model when only overall accuracy is assessed.

4. Discussion

The use of machine learning methods in movement biomechanics research is on the rise (Fig. 1A). From passively monitoring post-stroke patients with wearable devices to predicting outcomes of interventions in children with cerebral palsy, the range of applications where advanced analytics can improve rehabilitation research will continue to expand, particularly as wearable sensing generates vast amounts of data. The aim of this review is to bring to light machine learning efforts in movement biomechanics research and initiate a discussion of best practices and reporting standards that will maximize the impact of future work in this area.

4.1. Initial considerations

An important consideration at the beginning of a study is choosing the most appropriate statistical tool to address the research question of interest. Many research questions can be answered using traditional inferential statistics. In the literature, predictive models were often built for studies whose primary aim was to explain pathology by determining if certain gait features are discriminative with respect to disease status. Predictive modeling is not the most appropriate approach for this goal because often features are correlated, which may affect whether they are selected by feature selection approaches. The primary aim of predictive modeling is to learn a mapping function that can be used to make predictions on new data, with feature interpretation being a secondary aim.

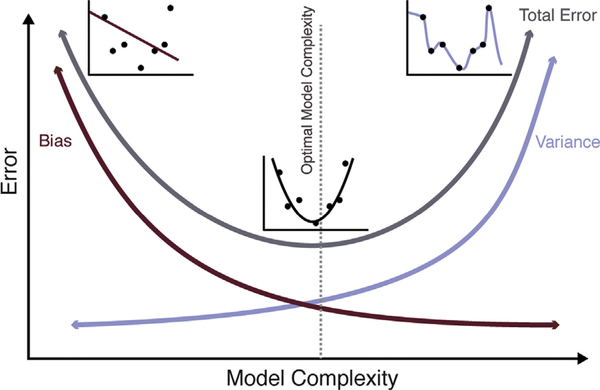
Another consideration is the size of the feature space (p) in comparison to the number of available subjects or observations (n) and its effect on the model selection process. When the number of features is larger than the number of observations (n < p), there is a high risk of overfitting a model (i.e., building a model that performs poorly on new data). The inability to learn an adequate model due to insufficient observations and a large feature space is often referred to as the curse of dimensionality. In addition to dimensionality reduction through feature engineering and feature selection, model complexity might also be considered in the context of n and p. Simple linear models, such as logistic regression, can often outperform non-linear models. Simple models are characterized by high bias and low variance, whereas complex models are characterized by low bias and high variance (i.e., complex models tend to be more accurate on training data, but less generalizable on new data; Fig. 2).

Fig. 2.

Model Complexity and the Bias-Variance Trade-off. In supervised learning tasks, bias is error that results from incorrect assumptions (e.g., fitting a linear model when the underlying relationship is not linear), causing algorithms to miss important relationships between features and labels, while variance is error that results from sensitivity to small variations, causing algorithms to model noise in the training data. The bias-variance tradeoff refers to the process of minimizing bias and variance in order to train models that can generalize well to non-training data. Simple models may be characterized by high bias and low variance (underfit to the training data), while complex models may be characterized by low bias and high variance (overfit to the training data).

4.2. Feature engineering

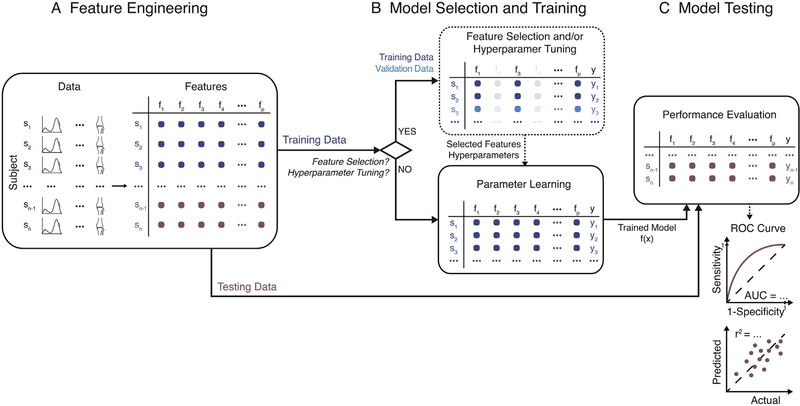
Good feature engineering (Fig. 3A) is a key step in building models from high-dimensional data, as it can lead to high model performance even with simple algorithms, such as naïve Bayes or logistic regression. Reducing data dimensionality while retaining sufficient relevant information, however, is not trivial. Discriminative information with respect to a given outcome may not always be evident and captured by features engineered using domain knowledge (e.g., stride length). Automatic feature extraction techniques, such as PCA, may capture some of the saliency in the data, but may produce features that are difficult to interpret or that are not informative with respect to a given outcome. Generally, we recommend testing a combination of automatically extracted features and ones engineered by humans. When fusing features that represent different quantities (e.g., knee angles and moments), for scale-variant algorithms it is also important to rescale features to ensure that each one contributes equally to the objective function and the optimization algorithm converges faster. Z-score normalization and min-max scaling are two common techniques used to rescale data.

Fig. 3.

Framework for Building Robust Predictive Models. (A) When the data are high-dimensional, feature engineering is first used to derive lower-dimensional representations of the data. This can be accomplished through domain knowledge (i.e., extract important gait characteristics) or automated techniques, such as principal component analysis, fast Fourier transforms, and other approaches. (B) After this step, the data are split into training and test sets, with the test set aside for performance evaluation. The model selection and training step, which uses only training data, may focus solely on parameter learning (e.g., learn regression coefficients) or may include one or two additional steps: feature selection and hyper-parameter tuning. Feature selection is performed to ensure that only relevant features are included in the model. This often improves model performance. Hyper-parameter tuning is performed to select additional parameters in complex models (e.g., select the degree of the polynomial if not a linear model). To avoid overfitting, both feature selection and hyper-parameter tuning are carried out using training data alone, which are further split into training and validation sets. (C) Last, the trained model is tested on held-out test data and comprehensive performance metrics that are more meaningful than model accuracy are reported.

4.3. Model assessment and learning

The success of a model is measured by its ability to generalize to new data. It is thus critical for model performance to be evaluated on held-out observations not used in the model selection and training process (Fig. 3B and C). If the dataset is large and representative of the underlying population, then splitting the data into a training set used to learn the model parameters and a test set used to evaluate the model’s performance is appropriate. Most commonly, however, the number of observations is too small to generate sufficient training and testing datasets, and techniques such as k-fold cross-validation, leave-one-out cross-validation (when the sample is very small), and bootstrapping are used to increase the effective size of training and testing samples. When splitting the dataset, it is important to include all the data from a given subject in only one of the sets. For example, if 10 motion capture trials are recorded for each subject, then all the trials should be part of the same set (e.g., training or test, but not both), unless the task is to train a subject-specific, rather than a generalizable model.

We recommend assessing and reporting a comprehensive set of performance evaluation metrics and ensuring that any biases in the dataset are appropriately addressed. For classification models, accuracy is the most commonly used metric, but it often provides an insufficient assessment of the model’s performance. For example, in a dataset with an unequal distribution of observations from each class (e.g., 70% versus 30%), the worst classifier—one that always predicts the majority class—would have an accuracy of 70%. Additional metrics, including the AUC, sensitivity and specificity, or the confusion matrix may be reported to enable evaluation and comparison with other models. For regression models, the mean squared error or r-squared value evaluated on test data are appropriate measures of a model’s generalizability. However, similar to classification models, these measures can be biased assessments of generalizability if the data used to train the model come from a skewed sample. In both classification and regression models, bias can be reduced by adjusting the cost function to weigh errors from different observations disproportionally. Along similar lines, including important confounders as covariates in the model and analyzing their contribution, especially when subjects from different demographic groups are represented disproportionally in different classes (e.g., cases and controls), is another step that can lead to more robust models.

Model learning—the process during which an algorithm learns from training data—is a critical step whose thorough reporting is needed to allow assessment of the model’s reliability. While for simple models this step focuses on learning model parameters, such as regression coefficients, in most cases it can include one or two additional steps: (1) feature selection and (2) hyper-parameter tuning (Fig. 3B). When these additional steps are taken, the data may be divided into three sets: a training set used to learn model parameters, a validation set used to select features or hyper-parameters, and a test set used to assess model performance, as done in a few of the reviewed studies (Palmerini et al., 2013; Rahmati et al., 2016). A common incorrect approach for feature selection is performing Student’s t tests to determine which features are significantly different between cases and controls in the entire dataset and retaining only those features for model learning. Another incorrect approach is performing step-wise regression and using the test data both for feature selection and model performance evaluation. Using the entire dataset for feature selection is plausible only if the feature selection process is unsupervised. For example, performing PCA on gait waveforms from the entire dataset and retaining features that explain 90% of the variability is acceptable because the label to be predicted by the model (e.g., disease status) is not used in the feature selection process. Model hyper-parameters should also be selected using validation data. An example is the set of kernel parameters used by support vector machines to obtain a non-linear classification boundary (e.g., width of a Gaussian kernel or degree of a polynomial kernel). Hyper-parameters are learned or tuned by sweeping through a pre-defined range, fitting different models to the training set, and tracking how the models perform on the validation set. We also recommend reporting the range of hyper-parameter sweeps, as is done by Kamruzzaman and Begg (2006). After the best model is selected, its performance is evaluated on the test set.

In unsupervised learning tasks, the model learning step may also involve selecting hyper-parameters. For example, in the case of k-means clustering, model learning involves choosing the number of clusters in addition to identifying cluster centers. The most common pitfall we encountered in the literature was the lack of rigorous approaches for selecting the number of clusters. Most studies performed clustering based on a pre-defined number. While it is appropriate to hypothesize that a dataset contains a given number of clusters, tests such as the Bayesian Information Criterion (Schwarz, 1978), Akaike Information Criterion (Akaike, 1974), Silhouette (Rousseeuw, 1987) may be used to confirm that such a model best represents the underlying structure of the data. One study, for example, used the Dunn test (Dunn, 1973) to determine that children with crouch gait exhibit distinct gait characteristics that fall into one of five subcategories (Rozumalski and Schwartz, 2009). These five categories were then related to distinct features of the underlying clinical pathology, which can guide the development of targeted treatments.

4.4. Sharing of data and tools

One of the powers of machine learning methods lies in their ability to draw insight from large, heterogeneous, noisy, and biased datasets. We found that models were nearly always trained and tested using data from a single study or laboratory, but many of the datasets could be pooled to enable the construction of more robust models. For example, pooling data from six studies that used optical motion capture data from patients with knee osteoarthritis (Astephen et al., 2008; Deluzio and Astephen, 2007; Favre et al., 2012; Levinger et al., 2009; Magalhães et al., 2013; Mezghani et al., 2017) would enable the construction of a database with 621 subjects, where protocol differences across sites could be accounted for in the model. Even if data were not pooled in the model learning phase, testing a model on data from different studies and allowing the community to improve it would increase its translational value. In recent years, a multitude of articles have called attention to a “reproducibility crisis” in biomedical research. Although a broader cultural shift toward open science is underway, sharing of data and tools has not been traditionally incentivized in biomechanics. Data curation and code documentation for public use require additional efforts and resources, and the return on investment for the researcher is not immediately apparent. Funding agencies have been promoting sharing of data and tools, but there is currently no evaluation system in place to reward researchers who contribute to open science. Despite the limitations of citation metrics such as the h-index, its increasing weight in promotion decisions makes it one of the few means through which researchers can be rewarded for open science. To that end, an internal analysis of publications from our group indicates that publications accompanied by public releases of biomechanical models (e.g., Rajagopal et al., 2016) and data (e.g., Hamner and Delp, 2013) garner higher citation counts. From 2007 to 2013, our group published 19 articles using open-source musculoskeletal modeling software OpenSim (Delp et al., 2007). Publications that included shared resources (n = 9) had an average of 30 more citations than publications without shared resources, when controlling for years since publication and journal impact factor (p < 0.05). To promote and support open science, we developed a website, SimTK.org, which hosts hundreds of projects by biomedical scientists who wish to share data, musculoskeletal models, and links to source code repositories (e.g., GitHub.com). We encourage researchers working in biomechanics and data science to contribute.

4.5. Knowing when to trust a model

A majority of the studies we reviewed focused on predictive models that could serve as valuable diagnostic or prognostic tools, but currently there is no consensus on when a model is good enough for clinical translation. Historically, conclusions drawn on p < 0.05 have driven important health decisions, but recent discussions have called into question the appropriateness of an arbitrary significance threshold that can be easily—although unintentionally—hacked by scientists who have only basic training in statistics (Leek et al., 2017; Nuzzo, 2014). Past evidence thus cautions us against the use of arbitrary thresholds to evaluate the performance of predictive models. Instead, we encourage the adoption of standards that focus on rigor and transparency. The best practices for model learning, evaluation, and reporting presented here provide a baseline for critical evaluation of the literature. Ultimately, the decision on when a model is accurate enough should be application specific, made by a team of researchers and clinicians who have enough information and training to fully understand the implications of its performance. It is also important to note that most models are intended to enhance, rather than replace, human clinical decision-making. For example, a model that automates the Fugl-Meyer assessment of sensorimotor function in post-stroke patients using data from wearable sensors would enable remote monitoring of patients to supplement sparse in-clinic assessments. Even though model estimates of the Fugl-Meyer score would be noisy and less accurate than an expert clinical assessment, the high-frequency, low-cost monitoring may be valuable supplementary information for patients and clinicians.

4.6. Interpretability

As models become more complex, they also often become more difficult to interpret. Artificial neural networks, for example, can learn highly complex nonlinear relationships from large data and outperform humans at many tasks, yet their opaqueness inspires little confidence in biomedical scientists. Lack of interpretability is particularly challenging in biomedicine, where predictive modeling is often motivated by the need to improve prevention and rehabilitation efforts. If a “black box” model predicts with high confidence that a patient will develop osteoarthritis based on his or her gait pattern, but offers no insight into the specific features of gait that are driving osteoarthritis progression, it is unclear how this knowledge could be used to improve the patient’s health. While event detection and activity recognition tasks that prioritize predictive accuracy over interpretability can be tackled with complex models, diagnostic and prognostic tools are currently better served by transparent models. Interpretability is an active area of research in machine learning, and the trade-off between accuracy and interpretability may be soon mitigated by ongoing efforts to decipher what single artificial neurons have learned and how they communicate with each other to make a prediction (Doshi-Velez and Kim, 2017).

4.7. Training in data science

Successful application of machine learning methods requires understanding of the methods that are available and how to properly apply them. An increasing interest in data science across scientific disciplines has prompted the design of massive open online courses (MOOCs) on different aspects of data analytics (e.g., Statistical Learning (Hastie, 2016) and Machine Learning (Ng, 2018)), which are practical introductory resources. As a community, investing in cross-training efforts through webinars and workshops at scientific conferences will also be critical in educating the next generation of data-savvy biomechanists.

4.8. New opportunities

Reinforcement learning is a machine learning paradigm where an agent (e.g., a musculoskeletal model) learns to perform a task (e.g., walk) by interacting with the environment and selecting actions (e.g., muscle excitations) through trial and error to maximize reward (e.g., metabolic cost) (Sutton and Barto, 1998). This approach has been used to train a program to play the game Go well enough that it can outperform any human without any input from or gameplay against other humans (Silver et al., 2017). Efforts to model neural control of movement have been ongoing in the computer science and biomechanics communities, and they are poised to be even more successful as these communities start to work together to bridge advances in reinforcement learning with physiologically accurate biomechanical models (Kidziński et al., 2018). Future research in this area promises to advance our understanding of neural control of movement and how that adapts to new perturbations, ultimately informing the development of natural human-machine interfaces for rehabilitation.

As researchers mine data from wearable sensors, where device non-wear is a common problem that results in missing data, the use of algorithms that can learn well from incomplete curves will also become more relevant. Functional data analysis, which considers the dynamic nature of curves, has already been used in studies of human movement biomechanics (Donoghue et al., 2008; Duhamel et al., 2006; Ryan et al., 2006). Building on that foundation, researchers have proposed algorithms that can learn from incomplete (sparsely sampled) curves (Bachrach et al., 1999; James et al., 2000; James and Sugar, 2003). For example, these approaches have been used to track human movement in video sequences where visual occlusions result in motion trajectories with missing data (Ormoneit et al., 2005, 2000b, 2000a).

Shrinkage methods (Copas, 1983) are a class of algorithms that can be used to reduce model complexity and improve performance. Shrinkage methods shrink the coefficients associated with each feature by adding a penalty term to the cost function that encourages coefficients to be small. Intuitively, this approach improves model generalizability because it reduces extremely high coefficients, which are likely an artifact of the available data. LASSO is an example of such a method that can achieve both shrinkage and variable selection because some of the coefficients are forced to be zero (Tibshirani, 1996). Advanced versions of LASSO can also be used for specialized variable selection. For example, group LASSO (Meier et al., 2008) can be used to select groups of features from multiple channels or sensors at once, while fused LASSO can be used to induce similar penalties to features that are spatially or temporally closer (e.g., select contiguous segments of a time series) (Tibshirani et al., 2005).

Artificial neural networks are a family of machine learning algorithms that aim to emulate the structure and connectivity of biological neural networks. They consist of an input, output, and one or more hidden layers of interconnected artificial neurons, or nodes. The number of hidden layers introduced in the model defines the depth of the network. How information flows between artificial neurons and through layers of the neural network is determined by model parameters that are learned using training data. Deep networks, defined as neural networks with multiple hidden layers, are successful at learning complex, nonlinear relationships and have already found wide use in speech recognition and image processing, where the data are high-dimensional. They also show promise in modeling movement time series data (Quisel et al., 2017), especially for applications where accuracy is more important than interpretability (e.g., event detection or activity classification). The number of model parameters to be learned grows rapidly with the depth of the network, however, requiring larger amounts of training data than are necessary for simpler models. Currently, there are no formal rules for determining the appropriate amount of data required to train a model with a desired depth. One approach to estimate if the available data are sufficient is to consider the learning curve. Typically, model performance has a logarithmic shape when plotted against sample size and eventually plateaus once the model reaches its limiting accuracy. In the latter stages of the curve, additional training data do not result in increased performance. Once pre-trained on large datasets, these networks can then be fine-tuned for tasks involving similar smaller datasets—a paradigm known as transfer learning. For example, networks such as VGG-16 have been pre-trained using millions of labeled images from the ImageNet database to recognize a multitude of different objects and are now being adapted with little effort for classification of specific types of medical images (Shin et al., 2016). Deep learning reduces the need for feature engineering, but it may only be appropriate when either a large dataset or a pre-trained network is available.

Supervised machine learning models are dependent on good feature engineering and labeled data. Most movement data being generated through mobile devices, however, are unlabeled. We have little information about what activities an individual is performing, and manual labeling of large time series is labor intensive. Semi-supervised learning is a paradigm that allows users to build models even if labels are available for only a small subset of the data (Chapelle et al., 2010). A related technique for leveraging unlabeled data is weak supervision, where a small gold-standard labeled set is used in conjunction with a large dataset with noisy labels obtained with comparatively little effort (e.g., through crowdsourcing or heuristic rules). For example, to train a supervised fall detection algorithm from several days of accelerometer data, the whole dataset must include labels on where falls occurred in the time series. Alternatively, when labels are not available, a user may take a weak supervision approach, writing a labeling function with a statement noting that if the vertical acceleration is greater than a given threshold, then the patient is likely to have experienced a fall. Since this threshold is not uniform across patients and falls, knowledge from multiple heuristics can be combined with a small set of gold-standard labels, which allows the model to learn when these heuristics agree and disagree. While the performance of weakly supervised models is partly dependent on the quality of noisy labels, these approaches have already achieved state-of-the-art performance in natural language processing applications (Ratner et al., 2017) and may find wide use in wearable sensor data analysis.

4.9. Conclusions

Research at the intersection of machine learning and biomechanics offers great promise for advancing human movement research, improving clinical decision-making, and accelerating rehabilitation programs for neuromuscular and musculoskeletal diseases. To enable appropriate use of advanced analytical techniques and stay abreast of new developments in machine learning that are galvanizing research across other biomedical disciplines (e.g., imaging, genomics, neuroscience), open data, tools, and discussions must be actively encouraged within the movement biomechanics community. We offer the following summary for biomechanists to consider as they adopt these methods and review the literature.

• When the number of observations in a dataset is smaller than the number of features, reduce the feature space through feature engineering and feature selection approaches and use a simple model for better generalizability. A deep neural network built using gait data from 10 subjects will likely not achieve good predictive performance on new data.

• As an alternative to stepwise feature selection and Student’s t tests, consider using regularization methods (e.g., LASSO) to reduce the number of features and improve model performance, especially when the feature space is very large and there is multicollinearity among features.

• Rescale heterogeneous data when using scale-variant algorithms, such as support vector machines, to ensure that each feature contributes equally to the objective function. Combining angular velocity and acceleration data from IMUs, for example, requires feature scaling.

• When developing a supervised model, use a training set for parameter selection, a validation set for hyper-parameter tuning and feature selection, and a test set for performance evaluation to ensure that the model generalizes well and the reported performance is not overestimated.

• When developing a model, include all the data from one subject (e.g., different trials) in only one set (training, validation, or test dataset) to ensure that the model generalizes well to new data.

• Include confounders as covariates in the model and analyze their contribution (e.g., regress them out). The model may be predicting a confounder rather than the outcome, if data from different classes are unbalanced in terms of that confounder. For example, if the diseased group contains a greater number of women than men compared to the normal group, a high-performing model may be predicting sex rather than disease status and will perform poorly if used to predict disease in the future.

• When classifying data into clusters, select the number of clusters using standard tests (e.g., Silhouette) to ensure that the model best represents the underlying structure of the data. Even if this number is based on a reasonable hypothesis or domain knowledge, a formal test will ensure that the model is plausible.

• Thoroughly report the feature-selection and model-learning steps, and include a comprehensive set of evaluation metrics (instead of accuracy alone). This will enable others to critically evaluate your work and place it in context with past and future studies.

• Make your data and code publicly available to allow others to reproduce and extend your models. Facilitating adoption will increase the impact of your work.

We hope that the discussion of practical guidelines, common pitfalls, and new opportunities highlighted here provide biomechanists with a scaffold upon which to build modern statistical models that enhance their research.

Appendix A

The following terms are used in the literature review and discussion of best practices.

Label (also response, dependent variable)

The output or outcome that a model learns to predict. Disease status in a diagnostic model, outcome of surgery in prognostic model, and the occurrence of tremor in an automated event detection model are examples of labels.

Feature (also predictor, attribute, independent variable)

A variable used as input to a model. For example, the peak knee flexion angle during the swing phase is a feature taken from the trajectory of knee flexion angles.

Supervised learning

Techniques used to learn the relationship between a set of independent variables (features) and one or more dependent variables (labels). Labels are used as supervisors or teachers that enable the model to learn its parameters (e.g., regression coefficients) well enough that it can make accurate predictions from new data.

Unsupervised learning

Techniques to detect patterns in input data, without using any labels to supervise learning. Clustering algorithms used to find subgroupings and principal component analysis are two of the most widely used unsupervised learning methods.

Regression

A supervised learning approach where the label is a continuous variable.

Classification

A supervised learning approach where the label is a categorical variable. Binary and multi-class classification problems are subtypes where the label encodes either two or more classes, respectively.

Class imbalance

A disproportional distribution of observations that belong to different classes (e.g., many more subjects without than with impairment), which can bias the learning process.

Clustering

An unsupervised learning approach used to discover inherent groupings in the data.

Feature engineering

The process of creating new features from existing ones to reduce data dimensionality and improve model performance. Common approaches for feature engineering from time series data include summary metrics (e.g., min, max, average of the signal), extraction of important events based on domain knowledge (e.g., peak angle), PCA, fast Fourier transforms, etc. This includes all the data, but it is blind to data labels.

Feature scaling or normalization

Practices used to standardize the range of values for each feature to facilitate convergence and prevent some features, especially those spanning different ranges, from contributing unequally to the learning process in models where the objective is not scale invariant.

Feature selection

Techniques used to select the most informative features with respect to a given label from the whole set of features. This step may not include the test data.

Model parameters

Configuration variables intrinsic to the model, which are estimated based on training data. Examples include coefficients in a linear regression, weights in artificial neural networks, the support vectors in support vector machines.

Model hyper-parameters

Additional parameters that can be used to control the complexity and learning rate of a model. Examples include the penalty coefficient in penalized linear regression, learning rate in artificial neural networks, and kernel type (e.g., Gaussian, polynomial) in support vector machines. Hyper-parameters are not learned simultaneously with the primary model parameters, but must be either selected a priori and justified or selected through a process called “hyper-parameter tuning.”

Cost function (also loss function)

A function used to estimate how well a model’s predictions fit the true labels. Model parameters are selected to minimize the cost function. A typical cost function for linear regression is the mean squared error.

Accuracy

The rate of correct predictions made by a classifier.

Sensitivity (also recall, true positive rate) = $\frac{\text{number}\text{of}\text{true}\text{positives}}{\text{number}\text{of}\text{true}\text{positives}+\text{false}\text{negatives}}$; the proportion of actual positives that are correctly identified as such (e.g., the percentage of freezing episodes that are correctly detected by the model).

Specificity (also true negative rate) = $\frac{\text{number}\text{of}\text{true}\text{negatives}}{\text{number}\text{of}\text{true}\text{negatives}+\text{false}\text{positives}}$; the proportion of actual negatives that are correctly identified as such (e.g., the percentage of normal individuals predicted as not having OA).

Precision (also positive predictive value) = $\frac{\text{number}\text{of}\text{true}\text{positives}}{\text{number}\text{of}\text{true}\text{positives}+\text{false}\text{positives}}$; the proportion of identified positives that are indeed positive (e.g., the percentage of identified falls that are actually falls).

Confusion matrix

A k × k table, where k is the number of classes, often used to describe the performance of a classifier. The rows and columns represent predicted versus true classes.

F-1 score

The harmonic mean of precision and recall. Although not as intuitive as accuracy, it can be a more informative metric of model performance when class imbalance is present.

Receiver Operating Characteristic (ROC)

A commonly used plot that visualizes the tradeoff between sensitivity and specificity as the discrimination threshold is varied for a binary classifier.

Area Under the ROC Curve (AUC)

A commonly used quantitative summary of the ROC. A random classifier has an AUC of 0.5, while a perfect classifier has an AUC of 1.

Sparsity

Generally describes an entity (e.g., a dataset or model) with few non-zero values. A sparsely sampled dataset contains many missing values. A sparse model uses only a reduced subset of the initial features, typically by imposing constraints on the objective function.

Bias

In supervised learning tasks, bias is the error that results from incorrect assumptions (e.g., fitting a linear model when the underlying relationship is not linear), causing algorithms to miss important relationships between features and labels. Even when the model assumptions are correct, the fitting method (e.g., LASO, ridge regression) can sometimes lead to bias in the estimated parameters.

Variance

In supervised learning tasks, variance is the error that results from sensitivity to small variations, causing algorithms to model noise in the training data.

Bias-variance tradeoff

The process of minimizing bias and variance in order to train models that can generalize well to nontraining data. Simple models may be characterized by high bias and low variance (underfit to the training data), while complex models may be characterized by low bias and high variance (overfit to the training data).