Abstract
NOTCH signaling regulates developmental processes in all tissues and all organisms across the animal kingdom. It is often involved in coordinating the differentiation of neighboring cells into different cell types. As our knowledge on the structural, molecular and cellular properties of the NOTCH pathway expands, there is a greater need for quantitative methodologies to get a better understanding of the processes controlled by NOTCH signaling. In recent years, theoretical and computational approaches to NOTCH signaling and NOTCH mediated patterning are gaining popularity. Mathematical models of NOTCH mediated patterning provide insight into complex and counterintuitive behaviors and can help to generate predictions that can guide experiments. In this chapter, we review the recent advances in modeling NOTCH mediated patterning processes. We discuss new modeling approaches to lateral inhibition patterning that take into account cis-interactions between NOTCH receptors and ligands, signaling through long cellular protrusions, cell division processes, and coupling to external signals. We also describe models of somitogenesis, where NOTCH signaling is used for synchronizing cellular oscillations. We then discuss modeling approaches that consider the effect of cell morphology on NOTCH signaling and NOTCH mediated patterning. Finally, we consider models of boundary formation and how they are influenced by the combinatorial action of multiple ligands. Together, these topics cover the main advances in the field of modeling the NOTCH response.
Keywords: NOTCH signaling, Mathematical modeling, Pattern formation, Lateral inhibition, Boundary formation, cis-inhibition, cell morphology, cell division, filopodia
1. Introduction
NOTCH signaling is the canonical signaling pathway used to coordinate the differentiation between neighboring cells during animal development (Artavanis-Tsakonas et al. 1999; Artavanis-Tsakonas and Muskavitch 2010; Kovall et al. 2017). Not only the molecular mechanism of NOTCH is highly conserved from worms, through flies, to humans, but also many of the developmental processes and circuits in which NOTCH is involved, are highly conserved. A classic example for such a conserved process is that of lateral inhibition patterning that describes the transition from an initially uniform field of cell to an alternating pattern of differentiation. Examples for lateral inhibition processes include the selection of sensory organ precursors (SOP, sensory bristles) in the Drosophila notum (Heitzler and Simpson 1991), hair cell patterning in the vertebrate inner ear (Daudet and Lewis 2005), the differentiation of intestinal precursors into absorptive and secretory cells (Sancho et al. 2015) and more. Other prototypical processes known to involve NOTCH signaling include asymmetric cell division (e.g. during neurogenesis), defining boundary cells (e.g. wing veins and wing margin), and coordinating synchronized oscillations (e.g. somitogenesis) (Artavanis-Tsakonas et al. 1999; Lewis 2003).
NOTCH mediated lateral inhibition has been first modeled by Julian Lewis and co-workers in 1996 (Collier et al. 1996). Since then, a large body of theoretical works have been developed to describe various aspects of NOTCH mediated patterning processes, including different types of lateral inhibition, boundary formation, wavefront propagation and synchronized oscillations (Shaya and Sprinzak 2011). Such models are used to formalize heuristic concepts into a quantitative picture that can help explaining unintuitive behaviors and generate testable predictions.
As our molecular and cellular understanding of NOTCH signaling progresses and more quantitative data is gathered, so do the modeling approaches become more refined and account for a larger variety of phenomena. In this chapter, we review the recent advances in modeling NOTCH mediated processes. Our goal is to provide a comprehensive picture of the current works in the field and represent the main approaches used to mathematically describe NOTCH mediated developmental processes. We focus here on the mathematical framework used in different approaches and provide the basic equations used to for each approach. For those who are interested in getting more practical information on performing the simulations, we refer to the practical tutorial by Formosa-Jordan and Sprinzak (Formosa-Jordan and Sprinzak 2014).
The chapter has four main sections corresponding to four topics. The first topic (section 2) is lateral inhibition and extensions of the basic model to take into account cis-inhibition, cell divisions, filopodia, and external signals. The second topic (Section 3) is modeling synchronized oscillations during somitogenesis. The third topic (section 4) is the role of cell geometry on NOTCH signaling and NOTCH mediated patterning. The fourth topic (section 5) is NOTCH signaling during boundary formation and the role of multiple ligands.
2. Models of lateral inhibition
2.1. The basic lateral inhibition model
While the general concept of lateral inhibition has been first discussed by Wigglesworth in 1940 (Wigglesworth 1940), it was not until the 1990s that these concepts were formalized into a well-defined mathematical model (Collier et al. 1996). At its core, lateral inhibition patterning is a symmetry breaking process where a group of initially identical cells differentiate into alternating patterns of cell fates. This process involves a local competition between neighboring cells, where at a certain developmental time, all cells “strive” to differentiate into one cell type and at the same time prevent their neighbors from becoming that cell type. Within each small group of cells, one cell prevails and subsequently suppresses all its direct neighbors through NOTCH signaling.
The essential symmetry breaking process during lateral inhibition patterning is achieved by an intercellular feedback loop, in which NOTCH signaling from one cell downregulates DELTA ligand activity in the neighboring cell (Fig. 5.1A). This feedback can amplify small initial differences between cells, so that one cell ends up expressing high levels of DELTA ligand while its neighbors express low levels of DELTA. This type of mechanism can in principle generate the typical checkerboard like patterns associated with lateral inhibition.
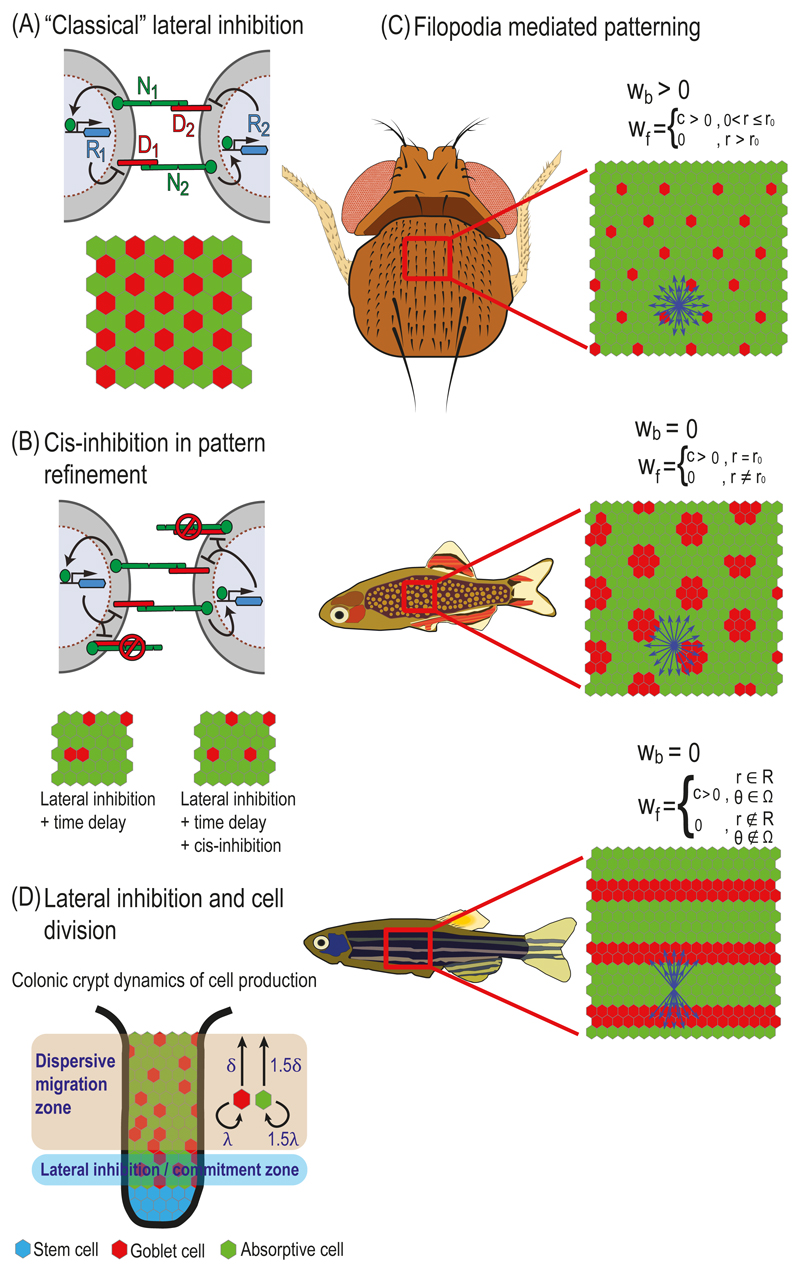
Fig. 5.1. Models of lateral inhibition.
(A) "Classical" lateral inhibition. Top – Schematic representation of a lateral inhibition circuit in two cells. In this circuit NOTCH signaling in each cell is generated by the interactions between NOTCH receptors (N1 and N2) and NOTCH ligands (D1 and D2). NoTCH signaling in each cell activates a repressor (R1 and R2) that downregulates the expression or activity of DELTA in that cell. Bottom – A typical simulation result on a hexagonal lattice of cells. Simulation starting with uniform initial conditions (plus noise) results in a salt-and-pepper like pattern where each high DELTA cell (red) is surrounded by low DELTA cells (green). (B) Cis-inhibition in pattern refinement. Top – Schematic representation of a lateral inhibition model that includes cis-inhibition between receptors and ligands. In the cis-inhibition model, a ligand on one cell binds to a receptor on the same cell leading to the formation of an inactive complex. These cell-autonomous interactions reduce the number of free ligands and receptors on the cell surface. Bottom – Cis-inhibition reduces the probability of defects (two neighboring red cells) for models of lateral inhibition that include time delays in the intracellular regulatory feedback. (C) Filopodia mediated patterning. Schematic of models that take into account long range NOTCH signaling mediated by filopodia. By controlling the relative weights of signaling through cell-cell body contacts, wb, and filopodial contacts, wf, a variety of patterns can be formed. Top – A model where signaling is mediated by both filopodia and cell body contacts. In this model filopodia are extended uniformly up to a radius r0 from the center of the cell (blue arrows). This model corresponds to the large spacing pattern of bristles on the Drosophila notum. Middle – A model where NOTCH signaling is mediated only through filopodia and not through cell body contacts. Here, the filopodia extends only to cells that are at radius r0 from the center of the cell. This model can produce a spotted pattern similar to the one observed in the skin of pearl danio fish. Bottom – A model where NOTCH signaling is limited to filopodia which are restricted to a radius range R and angular range Ω. Such a model can produce a striped pattern similar to the one observed in the zebrafish skin. (D) Lateral inhibition and cell division. A schematic model describing differentiation dynamics in the colonic crypt. Stem cells at the bottom of the crypt (blue) are differentiated into Goblet cells (red, high DELTA) and absorptive cells (green, low DELTA), which migrate towards the top of the crypt (the lumen). Stem cells divide at the bottom of the crypt (stem cells layer), causing an upward movement of the entire lattice. Lateral inhibition occurs at the layer adjacent to the stem cells layer (lateral inhibition zone or commitment zone). At this layer, cell fates are determined by the lateral inhibition process as described in (A). Once differentiated, the cells migrate from the commitment zone to the dispersive migration zone. In this zone, Goblet cells divide at a lower rate (λ) and migrate at a lower speed (δ) compared to absorptive cells (1.5λ and 1.5δ). The differences in division rates and migration speed result in a spaced salt-and-pepper like pattern in the lumen.
The first work to mathematically model this process was the work by Collier and colleagues (Collier et al. 1996). The Collier model contains differential equations describing the time evolution of two variables - activated NOTCH and DELTA in each cell. Here, we will use a slightly expanded model developed by Sprinzak et al. (Sprinzak et al. 2010) that directly accounts for NOTCH receptors, DELTA ligands and signal levels as well as for the intracellular feedback represented by a repressor which is activated by NOTCH signaling and represses DELTA production (Fig. 5.1A).
The mechanism underlying the model (Fig. 5.1A) is described by the following set of reactions between NOTCH receptors and DELTA ligands on a lattice of cells.
1. NOTCH receptors from one cell, denoted by Ni, interact with DELTA ligands on a neighboring cell, denoted by Dj, to produce a signal (representing the cleaved intracellular domain). The interaction is described by a Michaelis-Menten reaction:
| (1) |
Where the index i represents one cell in a lattice of cells, and the index j represent a neighboring cell j of cell i. [NiDj] denotes the NOTCH-DELTA complex between cell i and cell j. κ+ and κ‒ are the association and dissociation rates of NOTCH and DELTA, respectively. κs is the rate associated with conversion of the NOTCH-DELTA complex into a signal [namely, the inverse time it takes for the NOTCH intracellular domain (NICD) to get cleaved once it interacts with DELTA]. sj→i denotes the signal generated in cell i by interaction with cell j. The total signal generated in cell i is the summation over the signals generated from all of its neighboring cells:
| (2) |
2. The total signal in each cell activates a repressor, denoted by Ri, that downregulates the DELTA production in that cell:
| (3) |
The activation of the repressor by the signal and the repression of DELTA by the repressor are phenomenologically described in terms of an increasing and decreasing sigmoidal Hill functions, respectively.
3. NOTCH production rate is assumed to be constant.
4. All variables are assumed to have constant degradation rates.
These reactions are then converted into a set of ordinary differential equations for the levels of NOTCH, Ni, DELTA, Di and the repressor, Ri, in each cell i (Sprinzak et al. 2010):
| (4) |
| (5) |
| (6) |
where βN, βD and βR are the maximal production rates of NOTCH, DELTA and the repressor, respectively. γN, γD, γR, and γS are the degradation rates of NOTCH, DELTA, repressor and signal, respectively. denotes the strength of transactivation. The repression and activation reactions in equations (5) and (6) are described in terms of Hill functions, where pR and pS describe the effective Kd for the repressor and the signal, respectively, and l and m describe the Hill coefficients for the two reactions. The terms 〈D〉i and 〈N〉i are the summation of DELTA and NOTCH, respectively, over the neighboring cells j that are in direct contact with cell i:
| (7) |
The total number of differential equations is three times the number of cells.
Equations (4)-(6), can then be solved using standard ordinary differential equation (ODE) solvers. These equations can be applied to study different geometries, e.g. two cells, a line of cells, or a cell lattice. Many simulations use hexagonal cell lattices as the one shown in Fig. 5.1A, to describe epithelial like tissues. The solution of these equations provides the level of NOTCH, DELTA and the repressor over time. It can be shown (Sprinzak et al. 2011) that depending on the parameters used, these equations can lead to two classes of steady states. One class is a homogeneous steady state, in which all cells have the same concentration of all variables. This situation corresponds to an unpatterned steady state. The second class is an alternating steady state solution such as the one shown in the bottom of Fig. 5.1A. In this solution cells expressing high levels of DELTA and low levels of repressor (“high DELTA cells”, red in Fig. 5.1A) are surrounded by cells expressing low levels of DELTA and high levels of repressor (“low DELTA cells”, green in Fig. 5.1A). Several works have analyzed the types of possible patterns that can be generated from such a model and the dynamics leading to these patterns (Collier et al. 1996; Sprinzak et al. 2011; Formosa-Jordan and Sprinzak 2014). As can be seen in the examples below, the model can be expanded to include more complex situations such as taking into account additional interactions (e.g. cis-interactions), considering more complex cellular geometries (e.g. filopodia or cell shape) and including additional processes such as cell divisions.
2.2. Lateral inhibition patterning with cis-inhibition between receptors and ligands
It’s been known for quite some time that NOTCH receptors and ligands can interact not only when coming from neighboring cells (in-trans) but also within the same cell [in-cis (de Celis and Bray 1997; Klein et al. 1997; Micchelli et al. 1997). Unlike trans-interactions which lead to activation of NOTCH receptors, cis-interactions lead to inhibition of NOTCH signaling. For example, overexpressing DELTA in wing margin cells leads to suppression of NOTCH signaling in those cells (Klein et al. 1997). Several studies in recent years addressed, using mathematical modeling, the question of how cis-inhibition affects lateral inhibition (Sprinzak et al. 2010; Sprinzak et al. 2011; Formosa-Jordan and Ibanes 2014). Introduction of cis-inhibition into the model is performed by adding the following reaction to the lateral inhibition model described in equations (4)-(6):
| (8) |
Where [NiDi] denotes the inactive cis-complex of NOTCH and DELTA in cell i. are the association and dissociation rates of NOTCH and DELTA, respectively. The cis-complex is typically assumed to be removed or endocytosed at a rate of
As in the basic model, these reactions are then converted into a set of ordinary differential equations for the levels of NOTCH, Ni, DELTA, Di, and the repressor, Ri, in each cell i.
| (9) |
| (10) |
| (11) |
Where denotes the strength of cis-inhibition.
Analysis of these equations shows that cis-inhibition can contribute to several aspects of pattern formation: first, cis-inhibition increases the ability to pattern, namely, there is a larger range of parameters that supports patterning (Sprinzak et al. 2011); second, that the dynamics towards a patterned state are faster (Barad et al. 2010; Sprinzak et al. 2011). These faster dynamics turn out to be important in suppressing errors during the selection of sensory organ precursors (SOP). Barad and colleagues showed that within the equipotential group of cells there are rare cases where two SOPs can be formed instead of one [Fig. 5.1B and (Barad et al. 2010)]. They argue that a model of lateral inhibition with time delays in the intracellular feedback mechanism is expected to produce high error rates. They then show that the faster dynamics associated with cis-inhibition, can suppress the errors associated with such time delays. As predicted from their model, heterozygous mutants of NOTCH, DELTA and SERRATE, exhibit higher frequency of errors. Interestingly, a recent theoretical paper by Glass and colleagues showed that under certain conditions, time delays may actually lead to less defects in lateral inhibition patterning on cell lattices (Glass et al. 2016). Hence, it remains to be elucidated whether time delays are helpful or unhelpful for generation of ordered patterns.
In a more recent theoretical paper, Formosa-Jordan and colleagues generalized cis-interactions to include also weak cis-activation (Formosa-Jordan and Ibanes 2014). It was shown that under different parameter regimes, it is possible to get patterns that cannot be achieved using the standard lateral inhibition model. Although this result is currently theoretical, it would be interesting to check whether behaviors such as those predicted by this model may also appear in nature.
2.3. Filopodia in lateral inhibition patterning
An interesting new concept, which has emerged in recent years, is that signaling between cells can be transduced through long cellular protrusions such as filopodia or cytonemes, enabling direct communication between distant cells (Kornberg and Roy 2014). Cellular protrusions such as filopodia can have diameters as small as 0.1μm and extend dynamically over 100μm length scale. Several recent papers provided experimental evidence for situations where developmental patterns involve NOTCH signaling through protrusions. These include bristle patterns on the Drosophila notum (Cohen et al. 2010; Hunter et al. 2016), spotted skin patterns on pearl danio fish and striped skin patterns on zebrafish (Hamada et al. 2014; Eom et al. 2015).
The possibility of long-distance signaling through protrusions provide means to expand the variety of possible lateral inhibition patterns. Two recent theoretical papers explored the potential patterns that can be formed when taking long-range filopodia into account (Hadjivasiliou et al. 2016; Vasilopoulos and Painter 2016). To consider signaling through filopodia in the lateral inhibition model, we need to add additional terms representing the receptors, ligands and signals associated with filopodial signaling, which are different than signaling through cell body contacts. It is therefore useful to define the receptors and ligands contributing to the two distinct types of signaling in each cell: those from cell body contacts (b) and those from filopodial contacts (f). Following the paper form Hadjivasiliou and colleagues (Hadjivasiliou et al. 2016) we define:
| (12) |
Since the efficiency of signaling can be different between the two types of signals, relative weight factors need to be included. Thus, the dynamic equations (4)-(6) are now modified in the following way:
| (13) |
| (14) |
| (15) |
where wb and wf are the weight factors for signals received from the cell body and filopodia contacts, respectively of cells j surrounding cell i. In the case of wb = 1 and wf = 0 we get the original dynamic equations (4)-(6).
In general w can be a function of space and time, that is w = w(r, θ, t). Where r and θ are spatial polar coordinates in the two dimensions of the lattice of cells. For example, if the filopodia are a few cell diameters long and are dynamic [e.g. grow and shrink as in (Cohen et al. 2010)], the pattern generated is that of high DELTA cells with larger spacing (Fig. 5.1C, top panel). The dynamics of the filopodia in this case leads to an averaging effect which maintains equal distances between high DELTA cells. If body contact signaling is suppressed (wb = 0), then spotted patterns can be formed (Fig. 5.1C, middle panel). Finally, if the filopodia have preferred directionality a striped solution can emerge (Fig. 5.1C, bottom panel). Recent evidence shows that these two latter examples correspond to situations which arise on fish skin patterns (Hamada et al. 2014; Eom et al. 2015).
It is worthwhile noting that skin patterns were usually described in term of reaction-diffusion Turing type models (Turing 1952). Turing patterning relies on feedback interactions between morphogens (long range diffusible ligands) and it has been shown that such models can generate a variety of patterns similar to the ones shown here (Meinhardt 1996; Meinhardt 2008; Kondo et al. 2009). In fact, it can be argued that lateral inhibition with long range filopodia is mathematically equivalent to reaction diffusion models. In particular, long range signaling through filopodia, can replace the role of morphogens in Turing patterning (Hamada et al. 2014). There are two main differences between reaction diffusion models and filopodia based lateral inhibition models. On the mathematical level, there is a difference between diffusion which is a linear process (i.e. flux is proportional to concentration gradient) and signaling which is often non-linear in nature (i.e. signaling is not necessarily proportional to the expression difference between cells). On the physical level, the typical diffusion rates are often too fast to account for the time scale of patterning. For example, striped patterns in zebrafish occur over days and weeks. Explaining such patterns with morphogens would require diffusion rates that are orders of magnitude smaller than known diffusion rates for biological molecules. Hence, filopodia based lateral inhibition provides a more realistic mechanism for skin patterning than classic reaction-diffusion processes.
2.4. Lateral inhibition and cell division
In all the models described so far, it was assumed that the cellular morphology is fixed and does not change during the patterning processes. This is clearly a simplifying assumption that may be correct in some situations (e.g. when patterning is fast compared to other processes) but not always. In particular, cell division and cell growth can dynamically modify the connectivity among cells. Two recent papers discuss this issue in SOP patterning in the Drosophila notum (Hunter et al. 2016) and in patterning of secretory cells in the mammalian intestine (Toth et al. 2017).
The recent paper by Toth and colleagues (Toth et al. 2017) describes the interplay between lateral inhibition and cell divisions in the mammalian intestine. The epithelium of the intestine consists of crypts, which contain stem cells at the bottom of the crypts that continuously divide and eventually produce several types of intestinal cells including absorptive and secretory cells. Stem cell divisions yield stem cells which stay at the bottom of the crypt and progenitor cells which migrate upwards in the crypt and differentiate as they migrate. The differentiated cells keep dividing and migrating until they reach the intestine lumen. The final pattern in the lumen consists of a single secretory cells surrounded by a neighborhood of absorptive cells. Tóth et al. argued that due to the stochastic nature of cell divisions at the stem cells zone one would expect to get patched pattern in the lumen, where large groups of secretory cells and absorptive cells will be formed instead of the finely spaced salt and pepper like pattern observed. They suggest the following model for explaining this observation. In their model the authors assume that lateral inhibition takes place at a restricted zone, termed the commitment zone, right above the stem cell zone at the bottom of the crypt (Fig. 5.1D). As the progenitor cells differentiate at the commitment zone, the lateral inhibition process prevents the differentiation of two adjacent cells into secretory fates, as described in the dynamic equations (4)-(6). In this way, the lateral inhibition process induces a pattern that maintains a ratio of 1:3 between the secretory cells (DELTA expressing cells) and the absorptive cells (NOTCH expressing cells). After passing the commitment zone, cells continue to migrate and divide on their way to the lumen without being subjected to lateral inhibition. To maintain a homogeneous distribution of secretory cells in the lumen (i.e. with secretory cells separated from each other), an additional mechanism was introduced. After leaving the commitment zone, the two types of differentiated cells further divide at different rates and migrate at different speeds towards the lumen. The dispersive behavior of the division and migration reduces the variability in the final pattern and leads to the observed equispaced pattern (see Fig. 5.1D).
Coupling between lateral inhibition and cell division was also introduced to explain robust bristle patterning in the fly notum (Hunter et al.). Hunter and colleagues provided evidence that NOTCH signaling between DELTA expressing SOP and its neighbors affects cell division time and that the level of signaling is higher for direct neighbors (with cell body contacts) compared to secondary neighbors (with filopodial contacts). It was also shown that once a cell has divided, it is no longer inhibited by or inhibits other cells through NOTCH signaling. The authors then developed a lateral inhibition model that takes these observations into account. The model uses the basic dynamic equations shown in (13)-(15) and in addition includes a time-dependent probability term for cell division. This probability depends on the amount of signaling that a cell receives where a cell with higher signaling is more likely to divide. Analysis of the model showed that the coupling to cell division provides an internal clock for this process leading to a more ordered pattern.
We note that in both examples discussed here (e.g. the intestine and SOP patterning), lateral inhibition dynamics are still assumed to occur prior to cell division events. Namely, that fates which are determined by lateral inhibition on a fixed lattice are then used as an input for time dependent cell division processes. Although this makes modeling simpler, it is not clear whether this is indeed the case in all situations. Taking both processes into account at the same time may require alternative modeling approaches such as agent based modeling (as discussed in the next section).
2.5. Modulating lateral inhibition by external signals
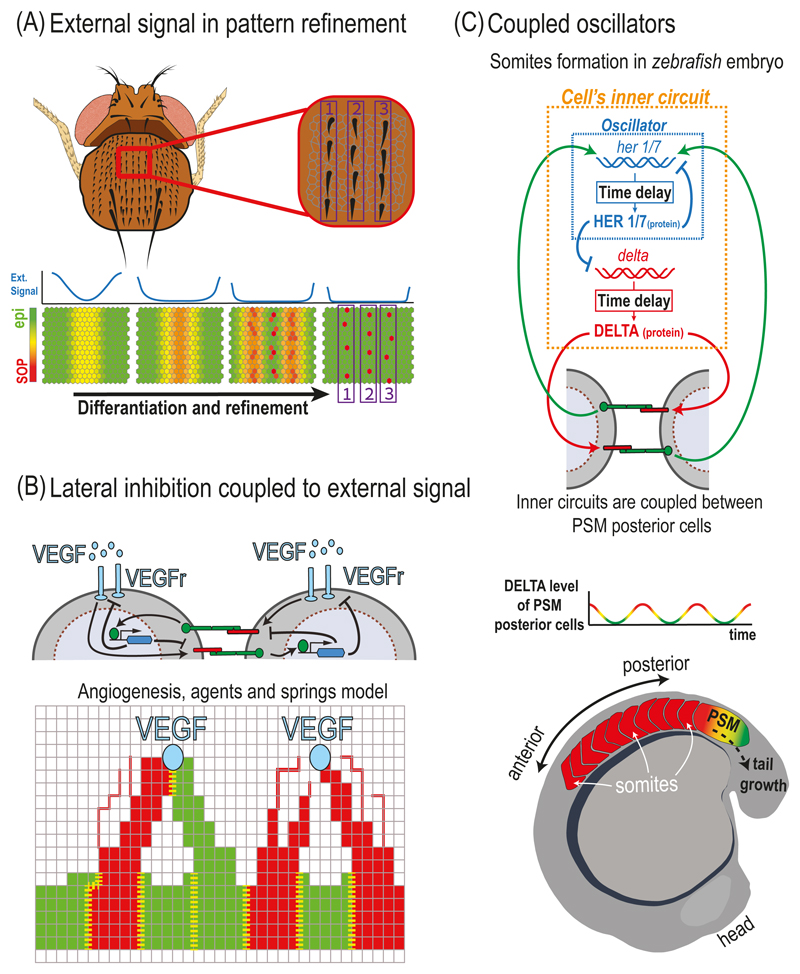
In many developmental systems, NOTCH mediated lateral inhibition is coupled to additional extracellular signals that can introduce a spatial bias, or pre-pattern, which modulate the process. An example for the effect of external pre-pattern on lateral inhibition is the organization of Drosophila bristles into organized rows on the Drosophila notum (Fig. 5.2A). A model of this process was recently described by Corson and colleagues (Corson et al. 2017). This work addresses the question of how a striped pattern of SOPs is formed in the presence of an initial pre-pattern. The initial pre-pattern in this system is generated by a spatially varying expression profile of pro-neural genes that control the expression of DELTA. The authors adopt a simplified modeling approach, where the cellular state is described by a single state variable, rather than the two variables in the lateral inhibition model described above. This state variable ranges from 0 to 1, where the value 0 corresponds to an epidermal fate and the value 1 corresponds to a SOP fate. The state variable in the model depends on signals from its neighbors (as in the lateral inhibition model above) and on an external signal which originates from the external pre-pattern of DELTA (blue lines in Fig. 5.2A). It is shown, that given the external pre-pattern, the same regulatory circuit can account for the resolution of multiple stripes and for the emergence of single SOPs in organized rows. We note that also in this model, the range of inhibition is taken to be larger than one cell diameter, potentially through the action of long-range filopodia.
Fig. 5.2. Modulation of lateral inhibition by external signals and models for somitogenesis.
(A) Lateral inhibition with external pre-pattern underlies refinement of Drosophila bristles into rows. Top – The small bristles on the Drosophila notum are arranged in distinct rows. Bottom – A model of the differentiation and refinement process of rows of bristles starting from a pre-pattern of pro-neural genes (external signal - blue lines). A continuous state variable ranges from an epidermal cell state (epi - green) and sensory organ precursor cell state (SOP - red). Pro-neural genes induce an external pre-pattern of DELTA expression which decreases at the center but remains at the edges (blue lines). The combination of lateral inhibition and external signals underlies the formation of multiple rows as well as the emergence of distinct SOPs. (B) Lateral inhibition coupled to VEGF signals in angiogenesis. Top – Schematic representation of a sprouting angiogenesis model. In this model, a gradient of vascular endothelial growth factor (VEGF, light blue circles) induces a lateral inhibition circuit in endothelial cells. Here, activated VEGF receptors (VEGFr, light blue rods) induce DELTA-LIKE-4 (red) production to promote tip cell selection and repress tip cell fate in neighboring cells. The intracellular feedback (represented by the blue hexagon) also downregulates VEGFr production, making the stalk cells less sensitive to VEGF. Bottom – Schematic of an agent-based model of sprouting angiogenesis. An external VEGF source (light blue circles) creates a VEGF gradient which induces the sprouting of endothelial cells towards the source. Each cell in the model is represented by multiple finite element agents connected by springs (red and green intersections and squares in the grid). The model captures the elongation of tip cells (red) and stalk cells (green) towards the VEGF source. Lateral inhibition between neighboring cells determines tip versus stalk fates. The boundaries between cells are marked with yellow dashed lines. Two tip cells can attach to one another as they migrate towards the source, initiating lateral inhibition at the new boundary. (C) A schematic of the zebrafish somitogenesis model. Top – An intracellular oscillator circuit (dashed blue rectangle) is coupled to an extracellular NOTCH-mediated lateral inhibition feedback (green and red arrows). Expression of her1/7 and delta genes are down-regulated by the HER1/7 protein with a time delay. In parallel, DELTA activates NOTCH signaling in the neighboring cells. Finally, NOTCH signaling activates its target her1/7 which closes the feedback loop. Bottom – DELTA levels in cells at the PSM oscillate in synchrony and in phase. As the embryo elongates, somites (white arrows) are derived from the posterior end of the PSM, at the time where the cells are at high DELTA level phase.
Another notable example for lateral inhibition coupled to external signal is angiogenesis, the process by which new blood vessels are formed. During angiogenesis, vascular endothelial growth factor (VEGF) induces sprouting of new blood vessels by converting endothelial stalk cells into tip cells that spearhead branching points (Blanco and Gerhardt 2013). NOTCH signaling regulates the selection of tip cells through lateral inhibition, where high levels of VEGF induce DELTA-LIKE-4 (Dll4) at the tip cells. Dll4 activates NOTCH signaling that downregulates VEGF receptors (VEGFr) to suppress stalk cells from becoming tip cells themselves (Hellstrom et al. 2007). This regulatory feedback is coupled to the tip cell morphology, whereby tip cells extend filopodia towards the source of VEGF signal. As one cell stretches towards the source, it starts to gain a tip cell fate and pulls with it the neighboring cells that gain a stalk cell fate. One possible scenario observed is that two emerging tip cells will meet each other as they reach the same source (Bentley et al. 2009). In this case, the two tip cells attach to each other (anastomosis) and inhibit each other (through NOTCH signaling) so that one cell ends up changing back its fate to a stalk cell. This in turn can lead to emergence of new tip cells in other nearby positions.
This dynamic process has been modeled by Bentley and colleagues in several papers (Bentley et al. 2008; Bentley et al. 2009; Jakobsson et al. 2010). To take into account the morphological aspects of these processes, the authors used a finite element agent-based modeling approach (Fig. 5.1E). Unlike the lateral inhibition models described above in which the basic element is a cell, these models split each cell’s membrane to small domains termed agents. These agents are located on a grid and are connected to each other by springs, representing the mechanical forces between them. During each time step in the simulation, the agents are free to move along the grid towards the source of the VEGF signal and retract according to a set of dynamical rules. As they move along the grid, new agents are generated at the space created between two adjacent agents, leading to extension of the membrane. This model considers dynamic extensions of the cells, where first filopodia are being extended from the membrane followed by the movement of the entire cell’s membrane - if the conditions are right. In such an agent-based model, new connections between two emerging tip cells can be formed and NOTCH mediated lateral inhibition is initiated between them. Simulations of the model capture the typical branching dynamics during angiogenesis as well as the competition between attaching tip cells described above. Hence, this approach is particularly useful in describing situations where morphological dynamics are important.
Lateral inhibition is also coupled to diffusible ligands during the development of chick retina (Formosa-Jordan et al. 2012). In this system, lateral inhibition pattern controls neurogenesis. The area of active neurogenesis spreads through non-neurogenic regions in response to external morphogens (Sonic hedgehog), giving rise to a spreading wave front behavior. Formosa-Jordan and colleagues modeled the process by introducing a secreted morphogen from the already differentiated neurons. The morphogens spread and expand the region in which lateral inhibition is permitted, hence leading to the observed neurogenic wavefront. The authors also show that in order to get a robust propagating front, they have to assume that cells outside the neurogenic region express DELTA, which impose inhibiting boundary conditions and prevent random spreading of the propagating front. Hence, the combination of lateral inhibition and secreted morphogens gives rise to a robust pattern mediated by a propagating front.
3. Modeling somitogenesis
Although NOTCH signaling is typically involved in assigning distinct fates to neighboring cells, this is not always the case. A remarkable example for a situation where NOTCH is involved in synchronizing a population of cells is that of the somitogenesis in vertebrates. During somitogenesis, the future somites are sequentially formed from the anterior side of the presomitic mesoderm (PSM) in the embryo (Kimmel et al. 1995). The model which have been proposed to describe this process, is called the 'clock and wavefront' model (Cooke and Zeeman 1976). The basic idea of the model is that the cells in the PSM exhibit oscillations in gene expression, and at the same time respond to an FGF and retinoic acid gradients. During each oscillation period, cells which are at the right phase of the oscillation stop oscillating and become the new somite (Fig. 5.2C). This whole process repeats itself as the embryo elongates. Interestingly, this process crucially depends on NOTCH signaling, as both DELTA and other NOTCH pathway components exhibit oscillations in their expression levels (Jiang et al. 2000; Holley et al. 2002).
The role of NOTCH signaling in this process was first elucidated in a seminal theoretical paper by Julien Lewis (Lewis 2003). Lewis proposed a model for zebrafish somitogenesis where each cell in the PSM contains an internal oscillator based on a delayed transactional feedback loop. He proposed that the NOTCH targets her1 and her7 (homologue to the Hes family), known to be transcriptional inhibitors, form the delayed negative feedback loop by transitionally repressing their own production (Fig. 5.2C). He then proposed that the role of NOTCH signaling is to synchronize the oscillations of the single cell oscillators and hence leading to synchronized oscillations in the whole PSM.
The mathematical description of the Lewis model thus involves an internal delayed negative feedback, and coupling between cells through NOTCH signaling. The delay in this case is attributed to the time it takes to transcribe the her1/7 mRNA and to translate the HER1/7 protein (we treat the Her1 and Her7 as a single entity in our model). The equations for the Her1/7 protein (Hi) and mRNA (mH,i) in each cell i are therefore given by:
| (16) |
| (17) |
where βH and βm are production rates of the protein and mRNA of Her1/7, respectively, and γH and γm are the degradation rates of the protein and mRNA of Her1/7, respectively. Tp and Tm are the delay times in translation and transcription, respectively. The production term in the equation of mH,i depends on a sum of two Hill functions representing the repression by H and the activation by DELTA (D) in neighboring cells, where wH and wD are the relative weights of these two contributions. We have used here a notation similar to the one in equations (4)-(6) to describe these Hill functions. For simplicity, NOTCH is not taken explicitly into account here.
The equations for Delta mRNA, mD,i, and protein, Di, in each cell i are similarly given by:
| (18) |
| (19) |
where βD and γD are the production and degradation rates of the DELTA protein, respectively.
Simulations of these equations show that under certain conditions on the parameters, a field of cells can maintain sustainable synchronized oscillations, where all the cells synchronize in phase. Out of phase oscillation are also possible for certain delay times. Interestingly, theses synchronized oscillation are quite robust to variability in the delay times and to perturbations of expression levels between neighboring cells. We note that without the delayed negative feedback these equation are reduced to the lateral inhibition model described above. More recent models of somitogenesis expanded the analysis to explain loss of global synchrony in the PSM (Riedel-Kruse et al. 2007) and the role of spatial gradients of expression within the PSM (Ay et al. 2014) on segmentation waves during somitogenesis.
4. NOTCH signaling and cell morphology
4.1. Morphology affects NOTCH signaling and NOTCH mediated patterning
Despite the fact that changes in cellular and tissue morphology occur throughout development, their role during cell fate decision processes is usually neglected. In fact, changes in cell morphology are often considered as a downstream consequence of cell fate decisions rather than an integral part of these processes. In the context of NOTCH signaling, cell morphology can affect the magnitude of signaling between cells and thereby affecting cell fate decisions. Several recent papers address this issue and highlighted the role of cell morphology on NOTCH mediated processes both experimentally and theoretically (Khait et al. 2015; Akanuma et al. 2016; Guisoni et al. 2017; Shaya et al. 2017).
One way in which cell morphology can influence NOTCH signaling is by affecting the contact area between cells. The question of how different contact geometries affect NOTCH signaling and NOTCH mediated patterning was recently addressed both theoretically and experimentally by Khait and colleagues (Khait et al. 2015) and Shaya and colleagues (Shaya et al. 2017). In the first work (Khait et al. 2015), the authors analyzed the interplay between membrane dynamics of NOTCH receptors and ligands and contact geometry. The authors developed a theoretical framework for analyzing how NOTCH signaling should depend on contact area, taking into account also membrane diffusion and endocytosis. The authors considered a simplified model of two cells, one expressing only NOTCH receptors and the other one expressing only DELTA ligands and analyzed how the membrane distribution of NOTCH and DELTA, as well as the magnitude of signaling, depend on the different parameters of the model. To take into account membrane diffusion and endocytosis, the authors used a reaction-diffusion model whose variables are the membrane concentrations of NOTCH (denoted by n), DELTA (denoted by d), NOTCH-DELTA complex (denoted by [nd]) and the total signal (denoted by S) (Fig. 5.3A). The equations for the two-cells case are given by:
| (20) |
| (21) |
| (22) |
| (23) |
where Dn, Dd and Dnd are the diffusion rates for NOTCH, DELTA and the NOTCH-DELTA complex, respectively. n0 and d0, are the concentrations of the cytoplasmic pools of NOTCH and DELTA (assumed to be constant), respectively. The rates denote endocytosis and exocytosis rates for NOTCH and DELTA, respectively. κ+ and κ‒ are the association and dissociation rates of NOTCH and DELTA, respectively. κS and γ are the rate associated with conversion of the NOTCH-DELTA complex into a signal and the signal degradation, respectively. Ir(x) is a function that describes the spatial extent of the contact area where Ir(x) = 1 for x < rcontact and zero elsewhere.
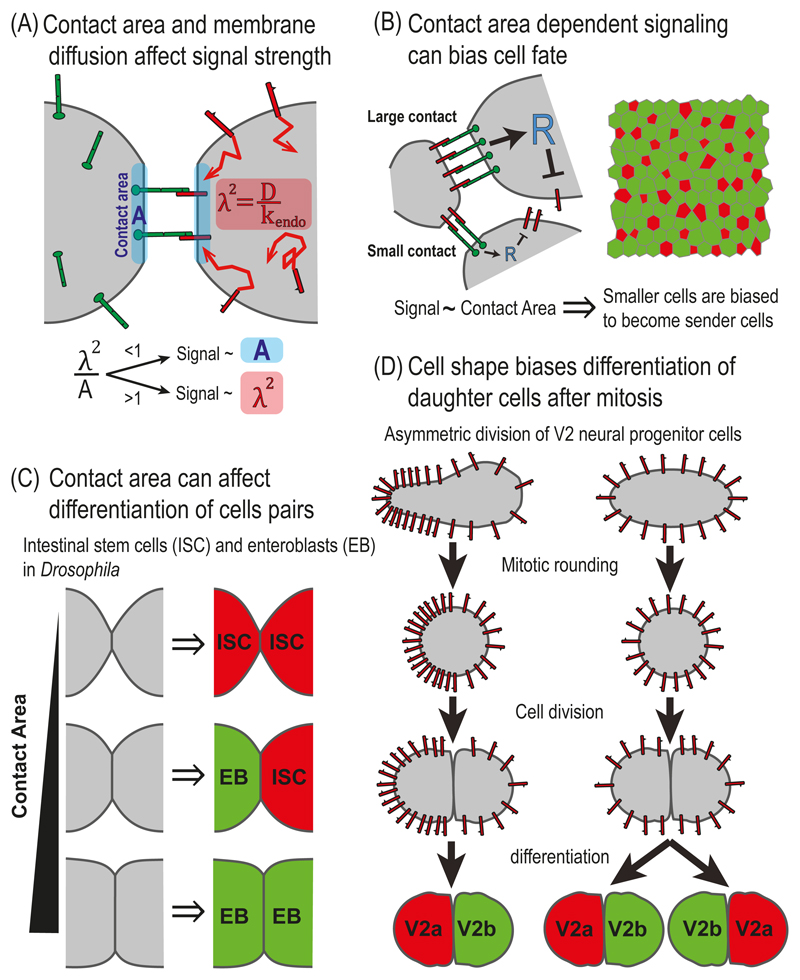
Fig. 5.3. NOTCH signaling and cell morphology.
(A) Contact area and membrane diffusion affect signal strength. Schematic representation of a two-cell reaction-diffusion model that takes into account contact area and membrane dynamics. The model identified two distinct regimes depending on the ratio between the contact area, A, and the area defined by the diffusion length scale, λ2. The diffusion length scale is defined by where D and kendo correspond to the diffusion coefficient and endocytosis rate of DELTA, respectively. While in one regime (λ2 < A), signaling depends on the contact area, in the second regime (λ2 > A), signaling is independent of the contact area. (B) Contact area dependent signaling can bias cell fate. Left - A schematic representation of a lateral inhibition model that takes into account the dependence of signaling on contact area. The model assumes that NOTCH signaling in each cell depends on the number of NOTCH-DELTA pairs formed on the boundaries with its neighbors, which is proportional to the length of the boundaries. Right – Simulations of the model over disordered cell lattices showed that smaller cells are more likely to become high DELTA cells (red). (C) Contact area can influence differentiation of cell pairs in the fly intestine. In the fly intestine, intestinal stem cells (ISC) divide and differentiate into either self-renewing ISC (red, high DELTA) or to enteroblasts (EB, green, low DELTA). The fates of the two daughter cells is determined by the lateral inhibition process and depends of the contact area between the two cells. The three possible final states are: ISC-ISC, in case of small contact area; EB-EB, in the case of large contact area; and ISC-EB, in the case of intermediate contact area. (D) Cell shape biases differentiation of daughter cells after mitosis in zebrafish neurogenesis. A schematic of a model for a lateral inhibition process which is biased by cell shape. Before mitosis, the concentration of DELTA is higher on the elongated side of the cell and lower on the round side of the cell. The asymmetry in DELTA concentration is maintained during mitosis and biases the lateral inhibition process so that the progenitor from the elongated side adopts the V2a fate (red) and the progenitor from the round side adopts the V2b fate (green).
Analysis of these equations identified two possible scenarios. For relatively large contact areas and/or slow diffusion (e.g. in epithelial contacts), signaling strength is expected to be proportional to the contact area. By contrast, for relatively small contact areas and/or a fast diffusion regime (e.g. filopodia), signaling strength should be independent of contact area but dependent on the diffusion length scale of NOTCH receptors and ligands, defined by Based on measurements of DELTA-LIKE-1 (Dll1) diffusion and endocytosis rates, the authors showed that the transition between the two regimes should occur for contact diameters on the order of 1-2μm. An interesting possibility occurs in situations where signaling is proportional to the diffusion length scale (second scenario described above). In this case, the level of signaling can actually be regulated by controlling the effective diffusion properties of NOTCH ligands or receptors. Hence, both contact geometry and membrane dynamics of NOTCH receptors and ligands can play an important role in NOTCH-dependent processes.
But does signaling indeed correlates with contact area? This question was experimentally addressed by the work of Shaya and colleagues (Shaya et al. 2017) who used micropatterned devices to measure how NOTCH signaling depends on contact area. Consistent with the prediction of the Khait model, the authors found that NOTCH signaling indeed correlates with the contact width for contact diameters ranging from 1-40μm.
Shaya and colleagues took this problem a step further and asked whether the dependence of NOTCH signaling on contact area can influence cell fate determination during lateral inhibition patterning. This was performed by expanding the lateral inhibition model to take into account the contact area and cell geometry (Fig. 5.3B). Instead of total NOTCH and DELTA levels at each cell, the expanded model followed the concentrations of NOTCH and DELTA on the cell boundaries (as in the Khait model above). For each boundary between cell i and cell j, we denote nij and dij as the concentrations of NOTCH and DELTA presented on the i-th cell. Similarly nji and dji denote the concentrations of NOTCH and DELTA presented on the j-th cell. The repressor level in each cell i, Ri, is then determined by the total signal received by cell i, from all its boundaries. Hence, the equations in this case are given by (Shaya et al. 2017):
| (24) |
| (25) |
| (26) |
Here, lij is the length of the i-j boundary and Li is the perimeter of cell i. Cell size is also taken into account by normalizing the production rate of NOTCH and DELTA by the perimeter of the cell, Li, meaning that the proteins distribute uniformly on the cell’s membrane once produced. Overall, the number of equations (24)-(26) is two times the number of boundaries plus one time the number of cells.
A major consequence derived from this model is how cell geometry affects cell fate. Simulating the model over a disordered lattice of cells revealed that smaller cells are more likely to become the high DELTA cells. This bias arises from an initial bias in inhibitory NOTCH signaling due to the differences in cell sizes across the lattice. Consistent with this prediction, Shaya and colleagues found that hair cell precursors in the developing chick inner ear are indeed smaller on average than non-hair cells (Shaya et al. 2017).
4.2. Contact area affects differentiation of cell pairs
Another interesting example for the effect of contact area on cell fate was recently reported by Guisoni and colleagues (Guisoni et al. 2017). The authors described the differentiation dynamics of intestinal stem cells in the adult Drosophila using a two-cell lateral inhibition model. In this system, the intestinal stem cells (ISCs) divide and the daughter cells can adopt one of two different cell fates – either remain in ISC fate or differentiate into enteroblasts (EBs, precursors of enterocytes). The model taken in this work is the original Collier model (Collier et al. 1996). The dependence of the contact area on NOTCH signaling is introduced by assuming that the effective Kd in the Hill function, that describes activated NOTCH, is inversely proportional to the contact area [equivalent to assuming in Eq.(6)]. By defining a threshold activity level and analyzing the parameter space, the authors identified three distinct differentiation states: (i) both cells are high DELTA cells (ISCs); (ii) one cell is a high DELTA cell (ISC) and the other is a low DELTA cell (EB); and (iii) both cells are low DELTA cells (EBs). By setting the range of parameters to fit the experimental results from the fly's intestine development, the authors showed that the outcome of differentiation crucially depends on the contact area between the cells (Fig. 5.3C). As contact area increases, there is a transition from ISC:ISC pairs [state (i)] to EB:EB pairs [state (iii)]. Consistent with their prediction, the author showed that the observed differentiation states in Drosophila intestine indeed correlate with contact areas.
4.3. Cell shape biases asymmetric cell division despite mitotic rounding
Another example for the effect of cell morphology on cell fate processes was recently reported in the context of asymmetric cell division in zebrafish neurogenesis (Akanuma et al. 2016). In this work, the authors showed that the asymmetric division of neural progenitor cells, termed V2 cells, in the developing zebrafish nervous system is affected by asymmetric cell elongation. They suggest that the DELTAC ligand is asymmetrically enriched to the more elongated side of the V2 cell, creating a bias in ligand concentration that is maintained during mitosis (Fig. 5.3D). This bias in local DELTAC concentration is translated to a bias in NOTCH signaling which is sufficient to define distinct cell fates for the two daughter cells. In order to model this process the authors coupled a lateral inhibition model to a cellular Potts model which simulates DELTAC ligands on a discrete grid representing the cell membrane [similar to the work described by Bentley and colleagues (Bentley et al. 2008)]. By running simulations in which cortical tension affects membrane dynamics of DELTAC, they show that sufficiently asymmetric cell shapes lead to asymmetry in DELTAC distributions that are sufficient to bias cell fates.
5. Boundary formation and multiple ligands
5.1. Defining sharp boundaries with NOTCH signaling
Another prototypical process known to be mediated by NOTCH signaling is that of boundary formation. Two examples where NOTCH signaling regulates boundaries are the wing margins (de Celis and Bray 1997; Klein et al. 1997; Micchelli et al. 1997) and wing veins in Drosophila (de Celis and Garcia-Bellido 1994; de Celis 1997). Although the role of NOTCH signaling in these two scenarios is to define boundary cells, the mechanism by which it operates is quite different. During vein boundary formation, NOTCH reads out a morphogen gradient to define the vein boundary. In the wing margin case on the other hand, NOTCH is used to specify boundary cells between two predefined compartments. Three recent works used mathematical models to understand the role of cis-inhibition in defining sharp boundaries and to elucidate the role of multiple NOTCH ligands in defining boundary cells (Sprinzak et al. 2010; Sprinzak et al. 2011; LeBon et al. 2014).
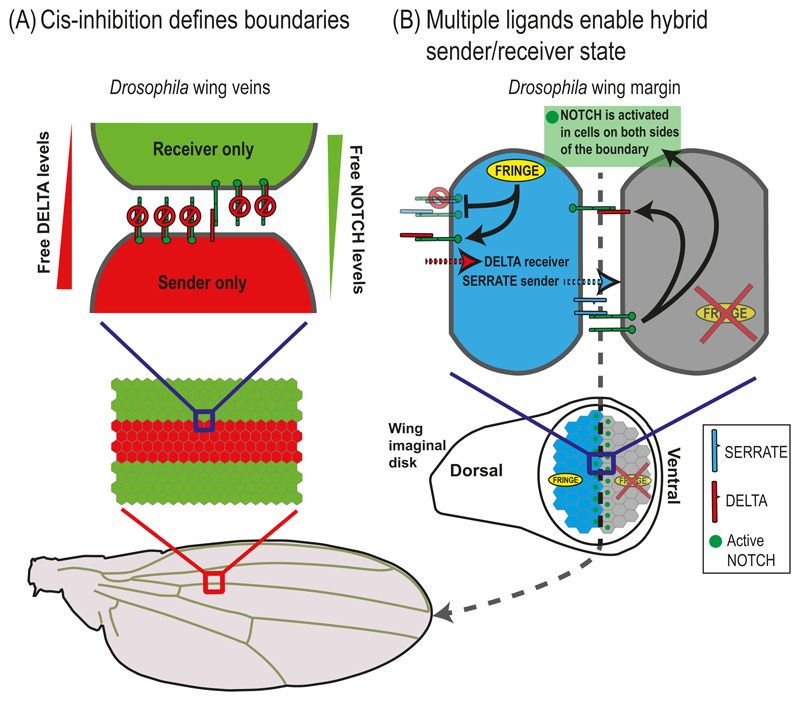
Wing vein boundaries are known to form in the wing imaginal disk through the interaction between epidermal growth factor (EGF) gradients and the NOTCH signaling. While the EGF gradients define the position of the veins, NOTCH signaling is involved in setting up the boundary between vein and inter-vein regions (de Celis 1997). One of the main questions in this process is how a graded concentration of a morphogen can be converted into a sharp all-or-none signal that defines the vein boundary. Sprinzak and colleagues used mathematical modeling to show that cis-inhibition between receptors and ligands plays a crucial role in generating the sharp response required for defining the boundary (Sprinzak et al. 2010; Sprinzak et al. 2011). The key insight obtained from the model was that cis-inhibition creates a situation where cells that express both receptors and ligands can either be in a "sender only" state or "receiver only" state, depending on the relative levels of NOTCH and DELTA that they express (Fig. 5.4A). The authors modeled the vein by assuming that DELTA production was graded (controlled by graded EGF signaling), while NOTCH production was constant (at least initially). The simulations showed that the resulting signaling profile exhibited two sharp stripes defining the vein boundaries that occurred at the positions in which the transition from sender to receiver states occurs (Fig. 5.4A). This pattern was consistent with the observed expression pattern of NOTCH transcriptional reporters [E(sp)] in the wing.
Fig. 5.4. NOTCH signaling in boundary formation.
(A) Cis-inhibition defines boundaries. A schematic overview of the cis-inhibition model for the wing vein boundary in Drosophila. In this model, wing vein boundaries are defined by the interactions between "sender" cells and "receiver" cells. The cells in the vein region (red) express more DELTA than NOTCH while the cells in the inter-vein region (green) express more NOTCH than DELTA. Due to cis-interactions between NOTCH receptors and ligands, vein cells can send but not receive signals, while inter-vein cells can receive but not send signals. (B) Multiple ligands enable hybrid sender/receiver states. A schematic model for wing margin cells in Drosophila taking into account multiple ligands and modulation by FRINGE. The cells on the dorsal side (blue) express both DELTA, SERRATE and FRINGE. The FRINGE glycosyltransferase modulates the cis- and trans-interactions between NOTCH receptors and ligands. Expression of FRINGE promotes NOTCH-DELTA interactions and suppresses NOTCH-SERRATE interactions (both in cis and in trans). The model predicts that the dorsal boundary cells (blue) can simultaneously receive signals from DELTA expressing cells and send signals to the ventral boundary cells (gray) using the SERRATE ligands. At a later stage, the ventral boundary cells activate DELTA leading to NOTCH activation in the dorsal boundary cells. This situation leads to activation of cells only on the wing margin (green dots in bottom image).
The model also provided an insight into a long-standing unintuitive observation of the system. It has been shown, that while heterozygous mutants of both NOTCH and DELTA exhibited mutant wing phenotypes (albeit different ones), the double heterozygous mutant restored the wildtype scenario (de Celis 2000). This observation is readily explained by the model, since in the double heterozygous mutant the relative levels of NOTCH and DELTA are maintained and so are the transition points between sender cells and receiver cells.
5.2. Combination of NOTCH ligands expand the repertoire of signaling states
More recently, LeBon and colleagues (LeBon et al. 2014) expanded the analysis to include multiple NOTCH ligands as well as the modulation of the receptor-ligand interactions by FRINGE glycosyltranferases. Experimental analysis in both mammalian cell culture and Drosophila showed that while glycosylation by FRINGE upregulates both cis- and trans-interactions between NOTCH1 and Dll1, it had an opposite effect on cis- and trans-interactions between NOTCH1 and JAG1. The combined effect of these interactions revealed that cells can be in different cellular states depending on the combination of ligands and FRINGE modulators they express. For example, cells that express both DELTA, SERRATE (JAG1 homolog in Drosophila), and FRINGE can receive signals from DELTA expressing cells (e.g. they are “DELTA receivers”) while at the same time they can send out signals with their SERRATE ligands (e.g. “SERRATE senders”) (Fig. 5.4B). This dual SERRATE sender/DELTA receiver cellular state can explain the bidirectional signaling observed in the wing margin cells (Fig. 5.4B). More generally, the model provided a framework for defining the possible sender/receiver states (based on the combination and levels of Notch receptors, Notch ligands, and FRINGES) as well as their ability to activate or get activated by other cellular states.
The effect of combination of multiple Notch ligands was also discussed in two other recent works by Petrovic and colleagues (Petrovic et al. 2014) and by Boreato and colleagues (Boareto et al. 2015). Petrovic and colleagues (Petrovic et al. 2014) showed that a circuit in which NOTCH signaling downregulates Dll1 but activates JAG1 can explain the transition from a lateral induction process (e.g. NOTCH signal induced higher ligand expression in the neighboring cell) that defines the chick inner ear sensory epithelium, to a lateral inhibition process that establish the alternating patterns of hair cells and supporting cells. A theoretical work by Boareto and colleagues (Boareto et al. 2015) showed that under certain conditions, when NOTCH signaling oppositely regulates DELTA and JAGGED, it is possible to obtain a three stable state solution corresponding to a full sender, a full receiver and a hybrid sender/receiver state. It remains to be seen whether such hybrid states are indeed observed experimentally. Overall, it is clear that the combinatorial action of multiple NOTCH receptors and ligands introduces another level of complexity which calls for additional theoretical and experimental works.
6. Future perspectives
Despite the significant progress in modeling NOTCH mediated developmental processes as described here, it is clear that many questions still remain open. Some of the topics that still need be elucidated include the integration of morphological, regulatory and cell division processes, the role of multiple NOTCH receptors and ligands and the combined interaction between NOTCH and other signaling pathways. As more quantitative experimental data becomes available, it is expected that novel modeling approaches and deeper refinement of existing models will follow.
Acknowledgments
This manuscript was supported by a grant from the European Research Council (grant no. 682161).
Abbreviations
- SOP
Sensory organ precursors
- NICD
NOTCH intra-cellular domain
- Dll1
DELTA-LIKE-1
- Dll4
DELTA-LIKE-4
- EGF
Epidermal growth factor
- VEGF
Vascular endothelial growth factor
- VEGFr
Vascular endothelial growth factor receptor
- ISCs
Intestinal stem cells
- EBs
Enteroblasts
- PSM
Presomitic Mesoderm
References
- Akanuma T, Chen C, Sato T, Merks RM, Sato TN. Memory of cell shape biases stochastic fate decision-making despite mitotic rounding. Nat Commun. 2016;7 doi: 10.1038/ncomms11963. 11963 ncomms11963 [pii] [DOI] [PMC free article] [PubMed] [Google Scholar]
- Artavanis-Tsakonas S, Muskavitch MA. Notch: the past, the present, and the future. Curr Top Dev Biol. 2010;92:1–29. doi: 10.1016/S0070-2153(10)92001-2. S0070-2153(10)92001-2 [pii] [DOI] [PubMed] [Google Scholar]
- Artavanis-Tsakonas S, Rand M, Lake R. Notch Signaling: Cell Fate Control and Signal Integration in Development. Science. 1999;284:770. doi: 10.1126/science.284.5415.770. [DOI] [PubMed] [Google Scholar]
- Ay A, et al. Spatial gradients of protein-level time delays set the pace of the traveling segmentation clock waves. Development. 2014;141:4158–4167. doi: 10.1242/dev.111930. 141/21/4158 [pii] [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barad O, Rosin D, Hornstein E, Barkai N. Error minimization in lateral inhibition circuits. Sci Signal. 2010;3:ra51. doi: 10.1126/scisignal.2000857. 3/129/ra51 [pii] [DOI] [PubMed] [Google Scholar]
- Bentley K, Gerhardt H, Bates PA. Agent-based simulation of notch-mediated tip cell selection in angiogenic sprout initialisation. J Theor Biol. 2008;250:25–36. doi: 10.1016/j.jtbi.2007.09.015. S0022-5193(07)00443-2 [pii] [DOI] [PubMed] [Google Scholar]
- Bentley K, Mariggi G, Gerhardt H, Bates PA. Tipping the balance: robustness of tip cell selection, migration and fusion in angiogenesis. PLoS Comput Biol. 2009;5:e1000549. doi: 10.1371/journal.pcbi.1000549. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blanco R, Gerhardt H. VEGF and Notch in tip and stalk cell selection. Cold Spring Harb Perspect Med. 2013;3 doi: 10.1101/cshperspect.a006569. a006569 [pii] cshperspect.a006569 [pii] [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boareto M, Jolly MK, Lu M, Onuchic JN, Clementi C, Ben-Jacob E. Jagged-Delta asymmetry in Notch signaling can give rise to a Sender/Receiver hybrid phenotype. Proc Natl Acad Sci U S A. 2015;112:E402–409. doi: 10.1073/pnas.1416287112. 1416287112 [pii] [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen M, Georgiou M, Stevenson NL, Miodownik M, Baum B. Dynamic filopodia transmit intermittent Delta-Notch signaling to drive pattern refinement during lateral inhibition. Dev Cell. 2010;19:78–89. doi: 10.1016/j.devcel.2010.06.006. S1534-5807(10)00296-0 [pii] [DOI] [PubMed] [Google Scholar]
- Collier JR, Monk NA, Maini PK, Lewis JH. Pattern formation by lateral inhibition with feedback: a mathematical model of delta-notch intercellular signalling. J Theor Biol. 1996;183:429–446. doi: 10.1006/jtbi.1996.0233. S0022-5193(96)90233-7 [pii] [DOI] [PubMed] [Google Scholar]
- Cooke J, Zeeman EC. A clock and wavefront model for control of the number of repeated structures during animal morphogenesis. J Theor Biol. 1976;58:455–476. doi: 10.1016/s0022-5193(76)80131-2. [DOI] [PubMed] [Google Scholar]
- Corson F, Couturier L, Rouault H, Mazouni K, Schweisguth F. Self-organized Notch dynamics generate stereotyped sensory organ patterns in Drosophila. Science. 2017;356 doi: 10.1126/science.aai7407. science.aai7407 [pii] [DOI] [PubMed] [Google Scholar]
- Daudet N, Lewis J. Two contrasting roles for Notch activity in chick inner ear development: specification of prosensory patches and lateral inhibition of hair-cell differentiation. Development. 2005;132:541–551. doi: 10.1242/dev.01589. dev.01589 [pii] [DOI] [PubMed] [Google Scholar]
- de Celis J. Notch signalling regulates veinlet expression and establishes boundaries between veins and interveins in the Drosophila wing. Development. 1997;124:1919–1928. doi: 10.1242/dev.124.10.1919. [DOI] [PubMed] [Google Scholar]
- de Celis J. The Abruptex domain of Notch regulates negative interactions between Notch, its ligands and Fringe. Development. 2000;127:1291–1302. doi: 10.1242/dev.127.6.1291. [DOI] [PubMed] [Google Scholar]
- de Celis J, Garcia-Bellido A. Roles of the Notch gene in Drosophila wing morphogenesis. Mech Dev. 1994;46:109–122. doi: 10.1016/0925-4773(94)90080-9. [DOI] [PubMed] [Google Scholar]
- de Celis JF, Bray S. Feed-back mechanisms affecting Notch activation at the dorsoventral boundary in the Drosophila wing. Development. 1997;124:3241–3251. doi: 10.1242/dev.124.17.3241. [DOI] [PubMed] [Google Scholar]
- Eom DS, Bain EJ, Patterson LB, Grout ME, Parichy DM. Long-distance communication by specialized cellular projections during pigment pattern development and evolution. Elife. 2015;4 doi: 10.7554/eLife.12401. e12401 [pii] [DOI] [PMC free article] [PubMed] [Google Scholar]
- Formosa-Jordan P, Ibanes M. Competition in notch signaling with cis enriches cell fate decisions. PLoS One. 2014;9:e95744. doi: 10.1371/journal.pone.0095744. PONE-D-13-50216 [pii] [DOI] [PMC free article] [PubMed] [Google Scholar]
- Formosa-Jordan P, Ibanes M, Ares S, Frade JM. Regulation of neuronal differentiation at the neurogenic wavefront. Development. 2012;139:2321–2329. doi: 10.1242/dev.076406. 139/13/2321 [pii] [DOI] [PubMed] [Google Scholar]
- Formosa-Jordan P, Sprinzak D. Modeling Notch signaling: a practical tutorial. Methods Mol Biol. 2014;1187:285–310. doi: 10.1007/978-1-4939-1139-4_22. [DOI] [PubMed] [Google Scholar]
- Glass DS, Jin X, Riedel-Kruse IH. Signaling Delays Preclude Defects in Lateral Inhibition Patterning. Phys Rev Lett. 2016;116 doi: 10.1103/PhysRevLett.116.128102. 128102. [DOI] [PubMed] [Google Scholar]
- Guisoni N, Martinez-Corral R, Garcia Ojalvo J, de Navascues J. Diversity of fate outcomes in cell pairs under lateral inhibition. Development. 2017 doi: 10.1242/dev.137950. [DOI] [PubMed] [Google Scholar]
- Hadjivasiliou Z, Hunter GL, Baum B. A new mechanism for spatial pattern formation via lateral and protrusion-mediated lateral signalling. J R Soc Interface. 2016;13 doi: 10.1098/rsif.2016.0484. 20160484 [pii] rsif.2016.0484 [pii] [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hamada H, et al. Involvement of Delta/Notch signaling in zebrafish adult pigment stripe patterning. Development. 2014;141:318–324. doi: 10.1242/dev.099804. dev.099804 [pii] [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heitzler P, Simpson P. The choice of cell fate in the epidermis of Drosophila. Cell. 1991;64:1083–1092. doi: 10.1016/0092-8674(91)90263-x. [DOI] [PubMed] [Google Scholar]
- Hellstrom M, et al. Dll4 signalling through Notch1 regulates formation of tip cells during angiogenesis. Nature. 2007;445:776–780. doi: 10.1038/nature05571. nature05571 [pii] [DOI] [PubMed] [Google Scholar]
- Holley SA, Julich D, Rauch GJ, Geisler R, Nusslein-Volhard C. her1 and the notch pathway function within the oscillator mechanism that regulates zebrafish somitogenesis. Development. 2002;129:1175–1183. doi: 10.1242/dev.129.5.1175. [DOI] [PubMed] [Google Scholar]
- Hunter GL, et al. Coordinated control of Notch/Delta signalling and cell cycle progression drives lateral inhibition-mediated tissue patterning. Development. 2016;143:2305–2310. doi: 10.1242/dev.134213. dev.134213 [pii] [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jakobsson L, et al. Endothelial cells dynamically compete for the tip cell position during angiogenic sprouting. Nat Cell Biol. 2010;12:943–953. doi: 10.1038/ncb2103. ncb2103 [pii] [DOI] [PubMed] [Google Scholar]
- Jiang YJ, Aerne BL, Smithers L, Haddon C, Ish-Horowicz D, Lewis J. Notch signalling and the synchronization of the somite segmentation clock. Nature. 2000;408:475–479. doi: 10.1038/35044091. [DOI] [PubMed] [Google Scholar]
- Khait I, et al. Quantitative analysis of Delta-like-1 membrane dynamics elucidates the role of contact geometry on Notch signaling. Cell Reports. 2015 doi: 10.1016/j.celrep.2015.12.040. [DOI] [PubMed] [Google Scholar]
- Kimmel CB, Ballard WW, Kimmel SR, Ullmann B, Schilling TF. Stages of embryonic development of the zebrafish. Dev Dyn. 1995;203:253–310. doi: 10.1002/aja.1002030302. [DOI] [PubMed] [Google Scholar]
- Klein T, Brennan K, Arias AM. An intrinsic dominant negative activity of serrate that is modulated during wing development in Drosophila. Dev Biol. 1997;189:123–134. doi: 10.1006/dbio.1997.8564. S0012-1606(97)98564-X [pii] [DOI] [PubMed] [Google Scholar]
- Kondo S, Iwashita M, Yamaguchi M. How animals get their skin patterns: fish pigment pattern as a live Turing wave. Int J Dev Biol. 2009;53:851–856. doi: 10.1387/ijdb.072502sk. 072502sk [pii] [DOI] [PubMed] [Google Scholar]
- Kornberg TB, Roy S. Cytonemes as specialized signaling filopodia. Development. 2014;141:729–736. doi: 10.1242/dev.086223. 141/4/729 [pii] [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kovall RA, Gebelein B, Sprinzak D, Kopan R. The Canonical Notch Signaling Pathway: Structural and Biochemical Insights into Shape, Sugar, and Force. Dev Cell. 2017;41:228–241. doi: 10.1016/j.devcel.2017.04.001. S1534-5807(17)30294-0 [pii] [DOI] [PMC free article] [PubMed] [Google Scholar]
- LeBon L, Lee TV, Sprinzak D, Jafar-Nejad H, Elowitz MB. Fringe proteins modulate Notch-ligand cis and trans interactions to specify signaling states. Elife. 2014;3:e02950. doi: 10.7554/eLife.02950. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lewis J. Autoinhibition with transcriptional delay: a simple mechanism for the zebrafish somitogenesis oscillator. Curr Biol. 2003;13:1398–1408. doi: 10.1016/s0960-9822(03)00534-7. S0960-9822(03)00534-7 [pii] [DOI] [PubMed] [Google Scholar]
- Meinhardt H. Models of biological pattern formation: common mechanism in plant and animal development. Int J Dev Biol. 1996;40:123–134. [PubMed] [Google Scholar]
- Meinhardt H. Models of biological pattern formation: from elementary steps to the organization of embryonic axes. Curr Top Dev Biol. 2008;81:1–63. doi: 10.1016/S0070-2153(07)81001-5. S0070-2153(07)81001-5 [pii] [DOI] [PubMed] [Google Scholar]
- Micchelli CA, Rulifson EJ, Blair SS. The function and regulation of cut expression on the wing margin of Drosophila: Notch, Wingless and a dominant negative role for Delta and Serrate. Development. 1997;124:1485–1495. doi: 10.1242/dev.124.8.1485. [DOI] [PubMed] [Google Scholar]
- Petrovic J, et al. Ligand-dependent Notch signaling strength orchestrates lateral induction and lateral inhibition in the developing inner ear. Development. 2014;141:2313–2324. doi: 10.1242/dev.108100. dev.108100 [pii] [DOI] [PubMed] [Google Scholar]
- Riedel-Kruse IH, Muller C, Oates AC. Synchrony dynamics during initiation, failure, and rescue of the segmentation clock. Science. 2007;317:1911–1915. doi: 10.1126/science.1142538. 1142538 [pii] [DOI] [PubMed] [Google Scholar]
- Sancho R, Cremona CA, Behrens A. Stem cell and progenitor fate in the mammalian intestine: Notch and lateral inhibition in homeostasis and disease. EMBO Rep. 2015;16:571–581. doi: 10.15252/embr.201540188. embr.201540188 [pii] [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shaya O, et al. Cell-cell contact area affects Notch Signaling and Notch dependent patterning. Dev Cell. 2017;40:1–7. doi: 10.1016/j.devcel.2017.02.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shaya O, Sprinzak D. From Notch signaling to fine-grained patterning: Modeling meets experiments. Curr Opin Genet Dev. 2011;21:732–739. doi: 10.1016/j.gde.2011.07.007. S0959-437X(11)00119-5 [pii] [DOI] [PubMed] [Google Scholar]
- Sprinzak D, Lakhanpal A, LeBon L, Garcia-Ojalvo J, Elowitz MB. Mutual inactivation of Notch receptors and ligands facilitates developmental patterning. PLoS Comput Biol. 2011;7:e1002069. doi: 10.1371/journal.pcbi.1002069. PCOMPBIOL-D-10-00231 [pii] [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sprinzak D, et al. Cis-interactions between Notch and Delta generate mutually exclusive signalling states. Nature. 2010;465:86–90. doi: 10.1038/nature08959. nature08959 [pii] [DOI] [PMC free article] [PubMed] [Google Scholar]
- Toth B, Ben-Moshe S, Gavish A, Barkai N, Itzkovitz S. Early commitment and robust differentiation in colonic crypts. Mol Syst Biol. 2017;13:902. doi: 10.15252/msb.20167283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turing AM. The chemical basis of morphogenesis. Phil Trans R Soc London Ser B. 1952;237:37–72. [Google Scholar]
- Vasilopoulos G, Painter KJ. Pattern formation in discrete cell tissues under long range filopodia-based direct cell to cell contact. Math Biosci. 2016;273:1–15. doi: 10.1016/j.mbs.2015.12.008. S0025-5564(15)00270-9 [pii] [DOI] [PubMed] [Google Scholar]
- Wigglesworth VB. The determination of characters at metamorphosis in Rhodnius prolixus. J EXP BIOL. 1940;17:201–223. [Google Scholar]