Towards whole-cortex enhancement with a ultrahigh dielectric constant helmet at 3T

Abstract

Purpose:

To present a 3T brain imaging study using a conformal prototype helmet constructed with an ultra-high dielectric constant (ε_r ~ 1000) materials that can be inserted into standard receive head-coils.

Methods:

A helmet conformal to a standard human head constructed with ultra-high dielectric constant (uHDC) materials was characterized through electromagnetic simulations and experimental work. The SNR, transmit efficiency, and power deposition with the uHDC helmet inserted within a 20-channel head coil were measured in-vivo and compared with a 64-channel head coil and the 20-channel coil without the helmet. Seven healthy volunteers were analyzed.

Results:

Simulation and in-vivo experimental results showed that transmit efficiency was improved by nearly 3 times within localized regions for a quadrature excitation, with a measured global increase of 58.21 ± 6.54% over seven volunteers. The use of a parallel transmit spokes pulse compensated for severe degradation of B₁⁺ homogeneity, at the expense of higher global and local SAR levels. A SNR histogram analysis with statistical testing demonstrated that the uHDC helmet enhanced a 20-channel head coil to the level of the 64-Channel head coil, with the improvements mainly within the cortical brain regions.

Conclusion:

A prototype uHDC helmet enhanced the SNR of a standard head coil to the level of a high density 64-channel coil, though transmit homogeneity was compromised. Further improvements in SNR may be achievable with optimization of this technology, and could be a low-cost approach for future RF engineering work in the brain at 3T.

Introduction:

New applications of functional magnetic resonance imaging (fMRI) that require higher temporal and spatial resolution¹ push the limit of image signal-to-noise (SNR) due to reduced voxel dimensions and shorter sequence repetition times. Moving to a field strength of 7 Tesla (T) or higher can offer a near-linear increase in SNR², but there are several drawbacks. Increases in static and RF field inhomogeneity³ and RF power deposition become significant issues at higher fields. Magnet and associated equipment costs increase substantially as well. These issues have limited the widespread deployment of 7T systems for both clinical and research purposes. Consequently, 3T remains the primary field strength for both clinical and fMRI use. In addition to utilizing higher field strengths, RF coil engineering technologies that can mitigate SNR losses should be developed for high spatial/temporal resolution fMRI applications. The traditional method of increasing SNR has been to design receive arrays with an ever-increasing number of elements. As the number of elements in the array increase, each individual element must be fabricated with smaller dimensions. Coil decoupling strategies⁴ and reduced penetration depth become an issue with smaller elements, leading to diminishing gains with this approach, alongside the issue of increasing costs of fabricating these types of RF coils.

An alternative solution to this problem is to incorporate high dielectric constant (HDC) materials into RF coils, which has been shown to synergistically enhance SNR for a given RF coil at a given static magnetic field strength. Prior work at 3T has explored a variety of HDC material types, each with their own strengths and limitations. Aqueous pads filled with water⁵ or barium titanate beads^6–9 have been utilized to enhance the RF field performance in the brain, heart, cervical spine, and thigh, respectively. An advantage these pads offer is ease of placement and conformation to the patients’ anatomy. The drawbacks are the maximum permittivity of the barium titanate solution is limited to approximately 515, alongside an increase of the image thermal noise due to the high conductivity of the solution^6,10. Since the displacement current as a secondary B field source is proportional to the relative electric permittivity, the SNR enhancement for 3T applications is then subsequently limited¹¹.

A solution to this problem was introduced with ultra-high dielectric constant (uHDC) materials¹². uHDC materials are comprised of monolithic ceramics and capable of reaching permittivity values of several thousand in the corresponding frequency regime of 3T. An important advantage gained with the transition to uHDC dielectric is the ability to achieve both higher relative electric permittivity with low loss. Blocks of this material have been applied to enhance both the brain¹² and spine¹³. However, enhancement of the brain cortex SNR requires a solution that encloses the head with uHDC material in a helmet-type design. Geometrically, the helmet should be made conformal to both the human head and standard receive coil geometries. Prior work has examined some performance aspects of a dielectric helmet at 3T¹⁴ and 7T^15,16, though only in simulation.

The goal of this work is to present a brain imaging study using a conformal prototype uHDC helmet with high permittivity (ε_r ~ 1000) that can be inserted into commercial receive head-coils. The SNR and transmit efficiency of this uHDC helmet inserted within a 20-Ch coil were measured and compared with a 64-Ch coil and the 20-Ch coil without the helmet.

Methods:

2.1. Theory

As described in detail previously^5,12,17,18, the uHDC enhancement mechanism can be illustrated through Ampere’s law:

$$\nabla \times \mathbf{B}=\mu (\sigma +\mathbf{i}{\epsilon }_{\mathrm{r}}{\epsilon }_0\omega )\mathbf{E}$$ [1]

The oscillating electric field produced by the RF coil induces displacement currents within the uHDC material, which then lead to the formation of a secondary magnetic field within and in the vicinity of the dielectric medium. Subsequently, the combination of the primary magnetic flux (produced by the RF coil) and the secondary flux (produced by the displacement current) yields an enhanced B distribution within the sample close to the dielectric material. This effect requires a significant contribution from the displacement current term in Eq.1, which in turn requires the dielectric material to have a high ε_r. With a typical 3T configuration of a volume transmit coil and head receive array, placement of the uHDC material within the receive array will enhance both transmit efficiency (B₁⁺) and receive efficiency (B₁⁻).

2.2. uHDC Helmet

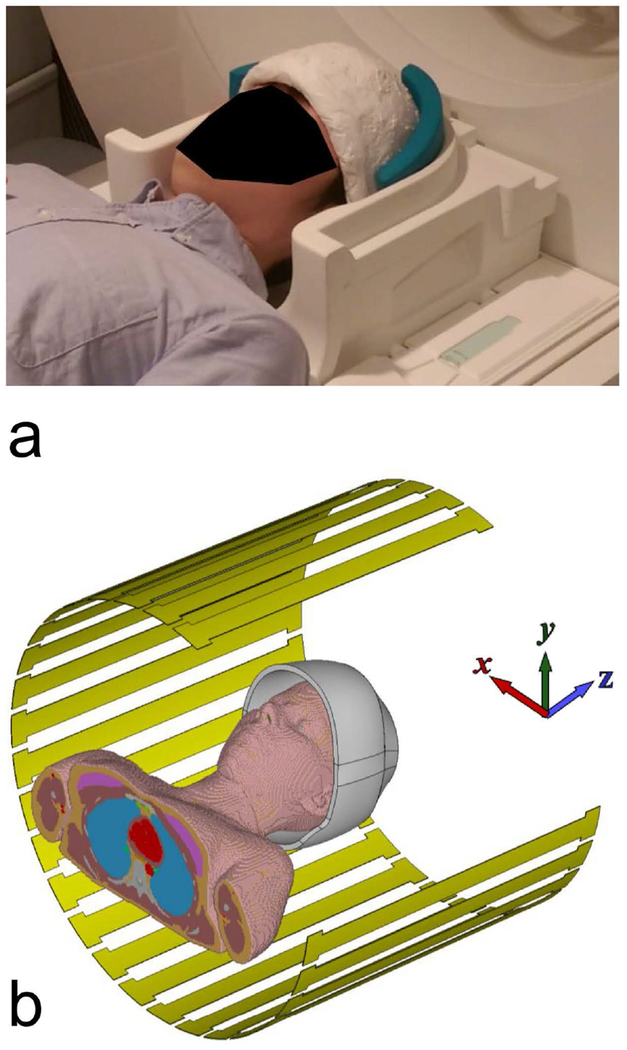
Figure 1a displays the prototype uHDC helmet (HyQ Research Solutions, LLC, State College, PA) used throughout this study, with the actual positioning utilized for scanning. The helmet fitted tightly within the Siemens 20-Ch head coil, with minimal gap between the two structures. Foam pads were placed to fill any remaining gaps and prevent head movement. The helmet opening was elliptical in shape, with dimensions of 210 by 150 mm. The helmet height was 160 mm, which included a straight 10 mm segment at the opening and a dome with height 150 mm. The thickness of the helmet was 12 mm, which was divided into a 2 mm silicone wall on each side and 8 mm of uHDC material. The helmet was utilized with two different effective permittivities of the uHDC dielectric, termed V1 (ε_r ~1000) and V2 (ε_r ~ 1200). The permittivity of the uHDC material was measured with the Hakki-Coleman method¹⁹. The conductivity of the material was determined to be approximately 0.05 S/m.

Figure 1:

(a) The uHDC helmet utilized in this study, modeling the same setup as used in experiment. Only the bottom half of the Siemens 20-Ch head coil is displayed here to permit visualization of the helmet. In experiment, both halves of the coil were utilized. (b) The configuration utilized in the electromagnetic simulations. One quarter of the transmit coil has been hidden for visualization purposes.

2.3. B₁⁺ & SNR Map Acquisition

All experiments were carried out on a Siemens PrismaFit 3T (Siemens Healthineers, Erlangen, Germany) with the standard volume coil employed for transmission. The volume coil utilized 2 independent transmit channels, and for all experiments the coil polarization was set to quadrature. Each volunteer was scanned under three different conditions for signal reception: 1) Siemens 20-Ch head/neck coil without the uHDC helmet 2) Siemens 20-Ch head/neck coil with the uHDC helmet [V1 or V2] and 3) Siemens 64-Ch head/neck coil without the uHDC helmet. For all experiments, the neck elements on these coils were disabled.

The reference voltage was calibrated with the scanner’s built-in routine under conditions 1 and 3. Under condition 2, the scanner’s built-in routine was executed followed by manual adjustment (if necessary) based upon a single slice axial B₁⁺ map. The single slice map required 28 seconds to acquire, and was placed close to isocenter around the level of the corpus callosum. After acquisition of the map, at the console a ROI was drawn over the brain and the mean B₁⁺ value calculated, which required approximately 30 seconds. If the mean value deviated from the nominal expected value, the reference voltage was then scaled by the ratio (nominal/mean) to correct the deviation.

B₁⁺ transmit efficiency maps were collected with a sequence based on the Bloch-Siegert method²⁰. Axial slices (n=9) and sagittal slices (n=3) were acquired with a 2D flow-compensated spoiled gradient echo sequence (GRE) with parameters: TR = 100 ms, TE = 10 ms, FA = 25 degrees, Voxel Size = 2 x 2 x 8 mm, FOV = 256 x 256 mm. The axial slice stack provided 100 mm of longitudinal coverage from the apex of the brain to just above the cerebellum. Additionally, a small tip angle GRE sequence with FA = 2 degrees, TE = 4 ms, Averages = 2 and otherwise identical parameters to the Bloch-Siegert sequence was utilized for SNR map calculation. Bandwidth-matched noise prescans were integrated into these sequences to acquire data for calculation of both the receive coil noise covariance and correlation matrix²¹. Subsequently, the SNR Units method²² was applied to calculate the SNR maps. These maps were divided by the acquired B₁⁺ map to remove the influence of the flip angle on the SNR value, according to the linear relationship between signal intensity and B₁⁺ at small tip angle. Data processing in this step utilized custom-built programs in IDL 8.7.1 (Harris Corporation).

Additionally, upon a single subject with the uHDC helmet in V2 configuration, the aforementioned protocols were acquired on each of the two independent transmit channels of the volume coil. This data was utilized for calculation of absolute B₁⁺ magnitude and relative B₁⁺ phase maps²³ of each transmit channel. These maps were used in an offline parallel transmit spokes calculation²⁴ designed to achieve a uniform tip angle across the slice. The optimization used some MATLAB code available from the author’s site (https://bitbucket.org/wgrissom/). The spokes pulse was designed with 5 spokes, a duration of 7.38 ms, and a target flip angle of 70 degrees. The target flip angle was close to the Ernst angle for a gradient echo scan with a TR of 2 seconds. This calculation was performed over the brain only, which was masked on the B₁⁺ maps.

Seven healthy volunteers participated in this study. All seven volunteers were scanned with the 20-Ch head coil and 64-Ch head coil, without the helmet. Five subjects were scanned with the helmet in V1 configuration, and two with the helmet in V2 configuration. All subjects provided informed consent under an IRB protocol approved by the Pennsylvania State University College of Medicine.

2.4. SNR Quantification

The SNR quantification utilized two different histogram-based methods. Prior to the application of the histogram analysis, a 2D mask was drawn on each acquired slice delineating the brain. Distance maps were calculated over these brain masks on a voxel by voxel basis. The distance metric was defined as the shortest Euclidean distance from a given voxel to the edge of the 2D brain mask.

The first histogram-based method simply sorted masked brain voxels by their SNR value into 22 different bins spaced equidistantly over the range of 0 to 282. Each bin’s count was then normalized as the number of voxels within that bin divided by the total number of voxels in all bins. The second method sorted all masked brain voxels by their distance from the surface using the predefined distance map, and calculated the mean SNR within each distance bin. The width of each bin was set to 2 mm, and a total of 22 bins were used. After calculation of these two histograms upon each subject, the mean and standard deviation across subjects were then computed on a bin-by-bin basis. Additionally, coarse histograms were calculated in the same manner that utilized 3 bins over the same SNR and distance ranges. A two-sided paired t-test was applied between the 64-Ch coil and the V1 configuration over these coarse histograms. The threshold for statistical significance was set at P < 0.05. All data processing in this step utilized custom-built programs in Matlab R2017a (Mathworks, Natick, MA).

2.5. Geometry Factor

Geometry factor maps were computed from the small tip angle GRE data utilized in the SNR calculation. The calibration region for all parallel reconstructions was defined as the central 40 k-space lines of the acquired 128 × 128 matrix. Coil sensitivity profiles were calculated from the calibration region with the ESPIRiT²⁵ method. The Berkley Advanced Reconstruction Toolbox (V4.04, https://mrirecon.github.io/bart/) was utilized in this step. Subsequently, SENSE reconstructions²⁶ with these coil sensitivity profiles were performed, at acceleration factors 2 and 4. GRAPPA ACS weights were derived from the calibration region and then used in a direct computation²⁷ of the GRAPPA geometry factor, also at acceleration factors of 2 and 4.

2.6. Electromagnetic Simulations

Prior to the electromagnetic simulation, high-resolution 3D T1w weighted images (1 mm³) of the uHDC helmet with a phantom placed in the center were acquired. These images were segmented within ITK-SNAP 3.6²⁸ to capture the exact geometry of the helmet. The segmented structure was subsequently exported as a mesh and imported to the EM field solver for simulation.

3D Electromagnetic simulations were performed with xFDTD 7.0 (Remcom, State College, PA). Figure 1b displays the simulation configuration, with one quarter of the transmit coil hidden for visualization purposes. The scanner’s transmit birdcage volume coil was modeled as a 32 rung high-pass birdcage, with a phase increment of 11.25° between capacitor gaps. Coil polarization was set to quadrature. Coil diameter and length were set to 60 cm and 50 cm, respectively. The female body model “Ella” from the virtual family²⁹ was centered in the coil for simulation. The uHDC helmet was centered upon the head, with a tilt of several degrees and offset of several mm along the Y-axis imparted to mimic experimental conditions. Helmet permittivity was set to 1000. Simulations were run at a frequency of 123.2 MHz on a 2-mm isotropic grid and convergence levels set to −40 db. The resultant B₁⁺ and electric field distributions were analyzed to calculate the transmit efficiency. The displacement current distribution was calculated in post-processing.

A spokes calculation was performed on the simulated B₁⁺ maps, with the same pulse design parameters utilized on the experimental data. Subsequently, 10-g SAR maps were computed³⁰ for all transmit scenarios: 1) quadrature polarization without the helmet 2) quadrature polarization with the uHDC helmet and 3) parallel transmit spokes with the uHDC helmet. Scenarios 1) and 2) were normalized such that the application of a single sinc pulse achieved a mean flip angle of 70 degrees over a 75 mm slab of the brain. Scenario 3) utilized five sinc pulses, each sub-pulse scaled by its respective optimization weights, to achieve a mean flip angle of 70 degrees over a single axial slice. All scenarios were time-averaged such that one excitation was applied every 100 ms. Whole body, whole head, and maximum 10-g SAR in the head were computed from the 3D maps.

Results:

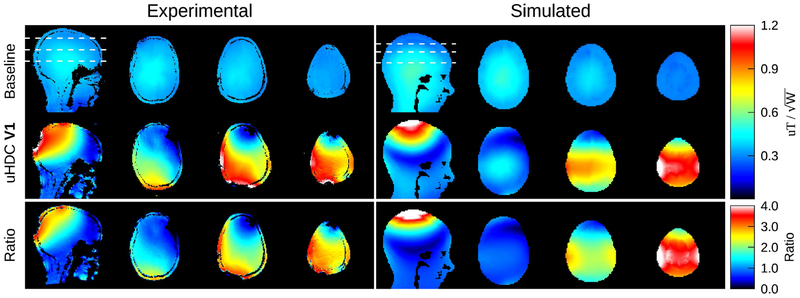
Figure 2 (left column) displays representative transmit efficiency maps (units of uT/sqrt(W)) from a volunteer acquired with the uHDC helmet in the V1 configuration. The transmit efficiency distribution was strongly enhanced by the helmet, with a ratio of up to 3 times observed in the ratio map in the bottom row. Accordingly, the reduction in RF power for the B₁⁺ mapping sequence utilized was 66% in this subject with an average reduction of 64.56% ± 7.56% relative to those without the helmet over all seven subjects. The average transmit efficiency throughout the brain increased by 58.21 ± 6.54% over all subjects. The enhancement with the helmet is inhomogeneous, however, and in some localized regions, the efficiency is decreased. The simulated transmit efficiency maps are shown in the right column of Figure 2. Compared to the experimental results, the simulation results produced a similar pattern of transmit efficiency gain, though the peak ratio reaches values close to 4. Note that the experimental results showed various degrees of asymmetry of B1+ enhancement in the left-right direction, which was likely caused by variations in the placement of the uHDC helmet with respect to the RF coil and human head.

Figure 2:

Transmit efficiency maps acquired from a subject, without (left column, top row) and with (left column, middle row) the uHDC helmet in the V1 configuration. The ratio (with/without) is displayed in the bottom row. The white dashed lines denote the location of the axial slices. The units are given in uT divided by the square root of the power delivered (forward-reflected) to the body coil, as measured by the system. The efficiency was strongly enhanced by the uHDC helmet, reaching up to 300% of the baseline value in some regions of the maps. The right column displays the simulated transmit efficiency. There is a slight rotation of the field pattern in the simulated data relative to the experimental data, and the field enhancement reached values of up to 400% of baseline.

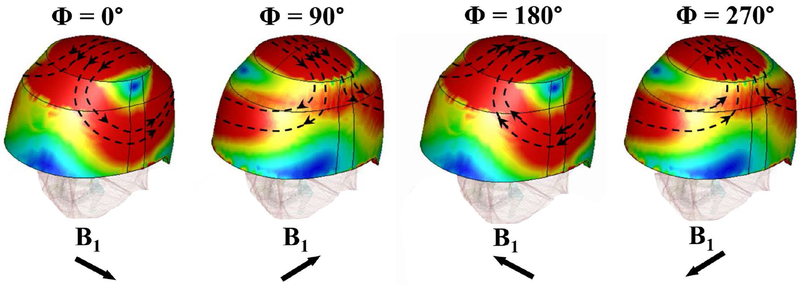
In order to understand the transmit inhomogeneity induced by the uHDC helmet observed in Figure 2, the calculated displacement current density magnitude and vector plot within the uHDC helmet at four phases over the RF cycle are displayed in Figure 3. It clearly shows that the electric field and the corresponding displacement current formed a very complex distribution and propagated as a wave over the helmet as the wavelength is greatly reduced. The total B₁+ field in the head was the superposition of the transmit field from the RF coil and the secondary field induced by the displacement current within the helmet. Thus, the contribution of the displacement current to the B₁+ at a given point in the head was not necessarily coherent to the field contribution generated by the RF coil, leading to an inhomogeneous enhancement pattern as seen in Figure 2. In addition, large displacement current loops were formed over the helmet. At the apex of the helmet, a localized region of strong displacement current magnitude over the entire RF cycle was developed by the quadrature driven RF coil. This region was coincident with the region of peak B₁⁺ in the simulated ratio map in Figure 2.

Figure 3:

Calculated displacement current magnitude and vector plot over the surface of the uHDC helmet. These field plots correspond to the induced fields of the four phases through one full RF cycle of the birdcage transmit coil in quadrature mode.

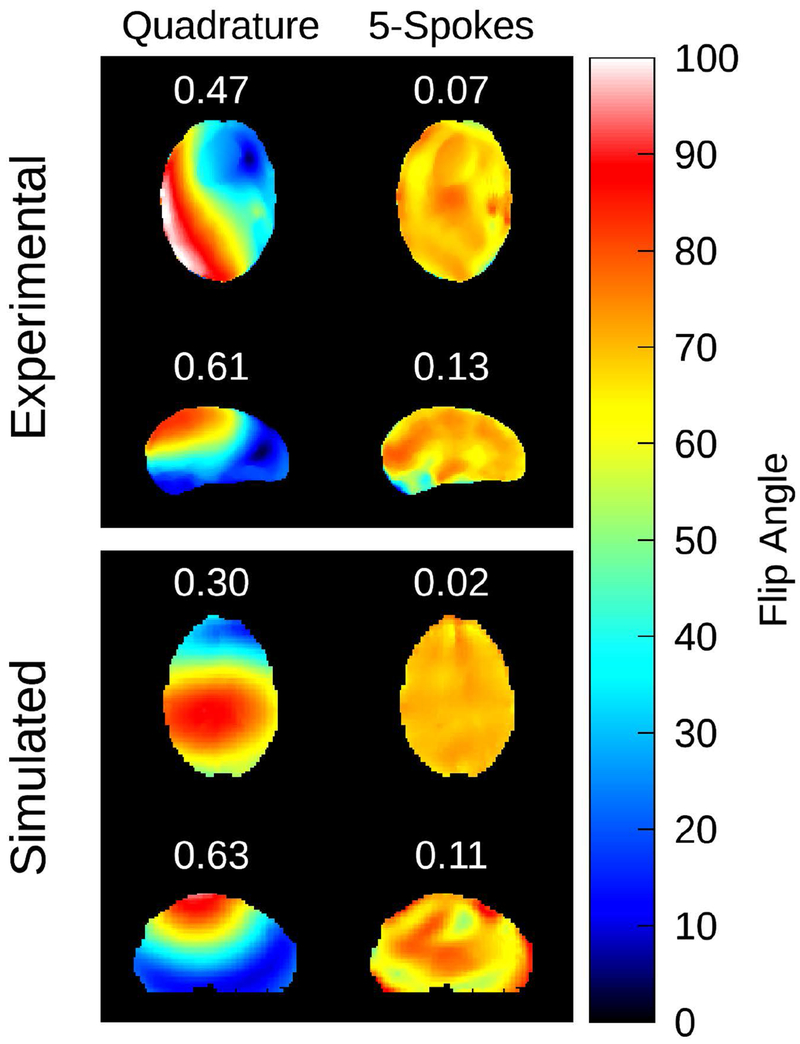
To assess the feasibility of B₁⁺ inhomogeneity compensation, Figure 4 displays the results of the offline parallel transmit spokes calculation. The optimization was performed on both an axial and sagittal slice. The left column displays a flip angle map corresponding to a quadrature excitation with the uHDC helmet present, scaled to a mean flip angle of 70 degrees. The right column displays the predicted flip angle map after application of the spokes pulse. The coefficient of variation is printed in white directly above the map. The application of the spokes pulse successfully compensated for the B₁⁺ inhomogeneity induced by the helmet, in both experiment and simulation.

Figure 4:

Results of the parallel transmit spokes RF pulse calculation. In the left column, a flip angle map corresponding to the uHDC helmet in V2 configuration and the 2 channel transmit coil set to quadrature polarization is displayed. The predicted flip angle map after application of the spokes RF pulse is displayed in the right column. The target flip angle was set to 70 degrees. The coefficient of variation is printed above each map in white text. This RF pulse calculation was applied to both experimental (top) and simulated (bottom) cases. The application of a spokes RF pulse successfully mitigated the transmit inhomogeneity induced by the uHDC helmet in both scenarios.

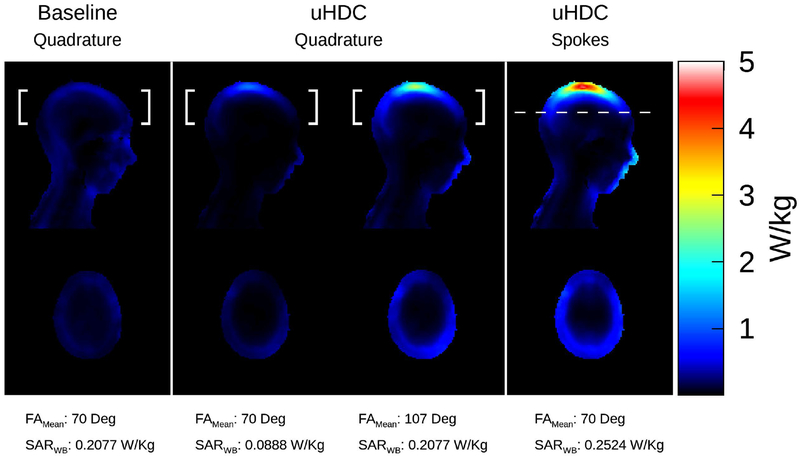
Figure 5 displays 10g SAR maps of the various transmit configurations. The white brackets indicate the region over which the mean flip angle was calculated. The spokes pulse was optimized over a single slice, thus the mean flip angle was calculated over the region indicated by the dashed white line. Supporting Information Table S1 lists the corresponding whole body, whole head, and maximum SAR in the head. When normalized by flip angle in quadrature polarization, whole body, whole head, and maximum SAR were lowered by 57.24%, 48.27%, and 28.19%, respectively, when the uHDC helmet was present. Normalization of the uHDC data by whole body SAR caused the flip angle to increase to 107 degrees. Practically, this scenario represented an overtip of the flip angle and would not be encountered under normal circumstances. The use of the spokes pulse incurred increases in all SAR quantities relative to baseline, particularly maximum SAR. All configurations with the uHDC helmet exhibited a relative SAR “hot spot” at the apex of the head.

Figure 5:

10g SAR analysis of the various transmit scenarios. The white brackets indicate the region over which the mean flip angle was calculated. For the spokes pulse (right column), this region corresponded to the optimization region, which was a single axial slice. In the left column, SAR without the helmet is displayed. In the middle column, SAR maps with the uHDC helmet are displayed, with normalization by both flip angle and whole body SAR considered. The right column displays the SAR map induced by the spokes pulse. In quadrature mode, whole body SAR was lowered significantly with the uHDC helmet present in the flip angle normalized case, though a local region of elevated SAR was observed at the top of the head. The whole body SAR increased by 21.5% relative to the case without the helmet when a spokes pulse was utilized, alongside a further amplification of the SAR at the apex of the head.

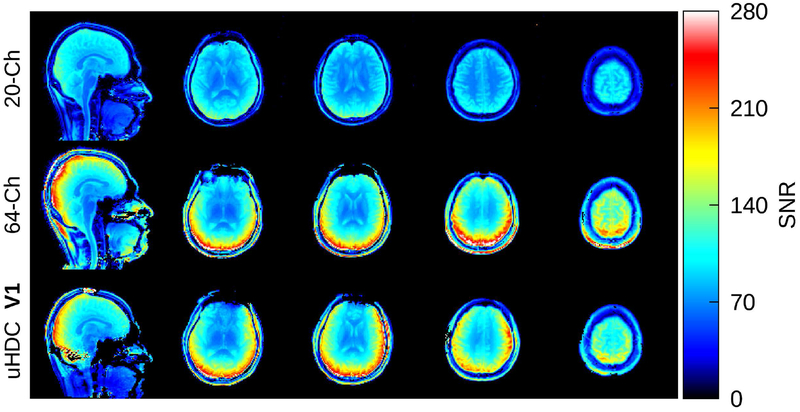
In Figure 6, SNR maps acquired on a subject from all three receive configurations are displayed. This subject was scanned with the helmet in the V1 configuration. Both the 64-Ch Coil and V1 configuration of the uHDC helmet achieved significant SNR gains relative to the 20-Ch Coil. Both cases presented a similar level of SNR enhancement around the cortical regions though regionally there were areas where each coil performed better than the other. All of the SNR maps have been divided by their corresponding acquired B₁⁺ map, which removed any dependence of the SNR upon the flip angle. SNR maps acquired on a different volunteer with the helmet in V2 configuration can be found in Supporting Information Figure S1.

Figure 6:

SNR maps from a subject, acquired with the 20-Ch head coil (top row), 64-Ch head coil (middle row), and 20-Ch coil with uHDC helmet in V1 configuration (bottom row). The SNR of the 20-Ch Coil was strongly enhanced with the uHDC helmet as compared to the baseline 20-Ch coil, and performed similarly to the 64-Ch coil. These SNR maps have been normalized by the corresponding acquired B₁⁺ map.

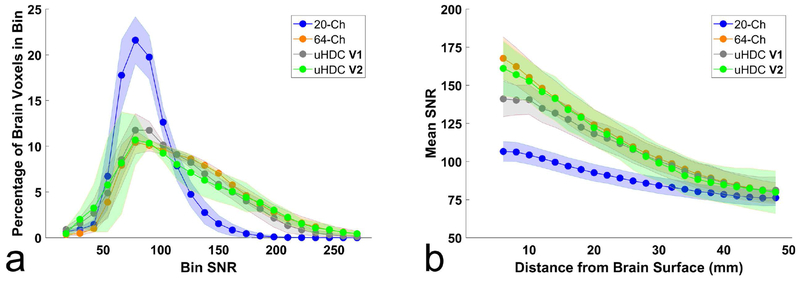
To assess the SNR enhancement over depth into the brain, Figure 7 displays the results of the SNR histogram analysis. Displayed bullets and shaded regions in Figure 7a,b represent mean and standard deviation among 7 subjects (20-Ch, 64-Ch), 5 subjects (uHDC V1), and 2 subjects (uHDC V2). In Figure 7a, voxels have been grouped into bins by their SNR value. The 64-Ch coil and uHDC configurations (V1 & V2) shift a substantial percentage of voxels into higher SNR bins, relative to the 20-Ch coil. Table 1a quantifies the percentage of voxels within three coarse SNR bins for each coil configuration. Examining the upper two bins, the uHDC V1 configuration (27.13/3.33%) and V2 (28.19/6.75%) performed slightly below the 64-Ch coil (31.75/6.77%). A paired t-test (P < 0.05) did not find significant difference between the 64-Ch coil and V1 configuration.

Figure 7:

Histogram analysis of the SNR data of each receive configuration. (a) the percentage of voxels within the brain that fall within each SNR bin. In (b), brain voxels have been grouped by the distance from the surface of the brain, and the mean SNR in each distance bin is displayed. In both plots, the 20-Ch Coil with uHDC helmet (V1 and V2 configurations) performed slightly below the 64-Ch coil. Values and shaded error bars represent mean SNR and standard deviation amongst subjects.

Table 1.

SNR Histogram Analysis

		20-Ch (n=7)	64-Ch (n=7)	uHDC V1 (n=5)	uHDC V2 (n=2)	P
a)	SNR Range	Percentage of Brain Voxels within given SNR Range
	18 to 126	94.08 ± 3.53	61.47 ± 6.02	69.53 ± 6.64	65.06 ± 11.56	0.127
	138 to 198	5.86 ± 3.45	31.75 ± 2.91	27.13 ± 4.70	28.19 ± 8.43	0.176
	210 to 282	0.05 ± 0.11	6.77 ± 3.29	3.33 ± 2.17	6.75 ± 3.15	0.131
b)	Depth Range	Mean SNR within Depth Range
	6 to 20 mm	100.35 ± 5.83	145.46 ± 11.41	132.08 ± 8.83	142.88 ± 14.31	0.172
	22 to 36 mm	85.30 ± 5.20	104.58 ± 8.29	102.50 ± 8.45	102.03 ± 12.64	0.657
	38 to 50 mm	77.38 ± 5.09	83.93 ± 6.81	83.87 ± 8.37	82.91 ± 12.85	0.986

Results of histogram analysis. (a) Percentage of voxels in the brain that fall within the SNR ranges in the leftmost column, for each of the receive coil configurations. (b) Mean SNR within the given depth range in the leftmost column. Values represent mean and standard deviation among all subjects. P values determine the likelihood of the null hypothesis μ (64-Ch) = μ (uHDC V1). Values below 0.05 indicate statistically significant differences between the mean SNR of the two coil configurations.

In Figure 7b, voxels have been grouped by their distance from the surface of the brain. At superficial distances (5 – 15 mm), the uHDC V2 configuration produced nearly the same level of SNR enhancement as the 64-Ch coil with a marginal difference observed between the 64-Ch coil and uHDC V1 configuration. All coils converged to roughly the same SNR at deeper distances within the brain. Table 1b quantifies the depth-dependent SNR within three coarse bins. At distances greater than 20 mm the 64-Ch Coil and uHDC V1 & V2 configurations were within 2% of one another. A paired t-test (P < 0.05) applied between the 64-Ch Coil and uHDC V1 did not find significant differences within any of the distance bins.

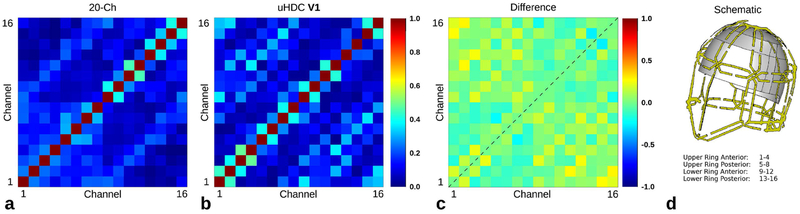
Figure 8a,b displays a sample noise correlation matrix of the 20-Ch Coil without and with the uHDC helmet. The cross-correlation of elements 1-4 were increased somewhat with the helmet present, otherwise the difference matrix in Figure 8c does not show any systematic differences between the two configurations. Averaged over the difference matrix, the correlation coefficient increased by 0.0137 with the V1 uHDC helmet.

Figure 8:

Noise correlation matrix corresponding to the same subject displayed in Fig.6. Absolute value of the noise correlation coefficient in the (a) 20-Ch head coil (b) the 20-Ch Coil with uHDC helmet in V1 configuration. The cross-correlation of elements 1-4 was increased with the uHDC helmet present, otherwise no systematic differences were observed in the difference map (c). The average increase over the difference matrix was 0.0137. A schematic of the 20-Ch Coil is displayed in (d).

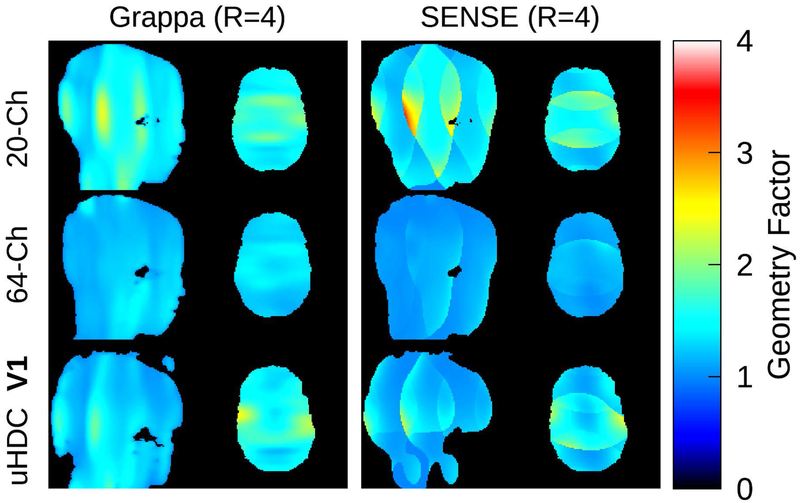
Geometry factor maps are displayed in Figure 9 for a single subject at acceleration factor 4. Supporting Information Table S2 lists the global geometry factor of the various coil configurations. All configurations achieved values close to 1 at factor 2. There was little difference between the 20-Ch Coil and uHDC V1 or V2 at GRAPPA 4, though a modest improvement was achieved at SENSE 4. The 64-Ch coil achieved significantly lower values at factor 4 compared to all other configurations.

Figure 9:

Geometry factor maps, acquired with the 20-Ch head coil (top row), 64-Ch head coil (middle row), and 20-Ch coil with uHDC helmet in V1 configuration (bottom row). Maps at acceleration factor 4 for both GRAPPA (left column) and SENSE (right column) are displayed. The geometry factor of the 20-Ch coil was modestly reduced with the uHDC helmet present, though not to the level of the 64-Ch coil.

Discussion:

The first prototype of a uHDC helmet was tested for 3T brain imaging using standard receive coils. The SNR enhancement achieved by the uHDC helmet was primarily focused in the cortical brain regions, which was similar to that achieved by the 64-Ch coil. No significant differences between the 64-Ch coil and uHDC V1 configuration were observed in SNR histograms calculated over the brain. Correlations between several elements of the 20-Ch coil close to the helmet experienced a mild increase, but otherwise were not significantly affected by the uHDC material. Geometry factor with either the uHDC V1 or V2 exhibited a modest reduction at SENSE factor 4 relative to the 20-Ch coil, but remain unchanged otherwise. Our data demonstrated the feasibility of the use of uHDC material conformal to human anatomy to significantly improve SNR of standard reception coils.

The distance between the subject and 20-Ch coil decreased when the helmet was present. Another approach to consider for increasing SNR would be to move the coil elements closer to the body. One study compared whole head 32-Ch and 64-Ch head coils, where both coils utilized the same former and physical dimensions³¹. The doubling of coil elements, without a change in distance to the body, lead to a peripheral SNR increase of 30 - 50%. Another study examined a 32-Ch coil built specifically to image the visual cortex, and compared it with a commercial 32-Ch whole head coil⁴. The visual cortex coil achieved relative gains of 50 to 100% by densely and closely packing coil elements around the back of the head only. In this work, the use of a uHDC helmet enhanced a 20-Ch head coil to the level of a 64-Ch coil. The dimensions of the 20-Ch coil were larger than the 64-Ch coil, however, simply moving the elements of the 20-Ch coil closer will not enable it to reach the performance of the 64-Ch coil. Increasing the total number and density of coil elements are necessary to reach the performance of a 64-Ch coil, thus the SNR gain from decreasing the distance to the coil only will fall below that offered by the uHDC helmet.

In comparison with previous approaches employing uHDC material^12,13, several advantages were gained with the use of a helmet for brain imaging. The SNR enhancement, as seen in Figure 3, was continuous throughout the cortex. An attempt to use discrete blocks of uHDC material would most likely yield a uneven enhancement pattern suffering from gaps between block locations. From a practical viewpoint, the structure was conformal with the human head, which permitted a snug fit and rapid placement of the insert similar to the pads used to reduce subject motion. The helmet possessed a small amount of flex, and in cases where the head nearly filled the helmet, could accommodate minor variations in head shape. A gap between the helmet and head existed when used with smaller head sizes. In this study a range of head sizes were encountered, and the effect on SNR is summarized in Figure 7 and Table 1, where the standard deviation amongst subjects is given. The variability of the 64-Ch coil (n=7) and V1 uHDC helmet (n=5) were comparable.

The transmit efficiency was strongly focused and enhanced by the uHDC helmet in all subjects. As seen in Figure 2, local gains up to three times were achieved, which also corresponded to a RF power reduction of 66% in that subject. The RF power reduction and transmit efficiency gain among all subjects was 64.56 ± 7.56% and 58.21 ± 6.54% respectively. A reduction in RF power could be useful for sequences with high power demands, such as magnetization transfer contrast³² or turbo spin-echo imaging. These values assume the use of the system’s default flip angle calibration, which attempts to maximize the integrated signal over an axial slice located at isocenter. When the uHDC helmet was present, a manual calibration that required one minute was performed to correct this system routine as necessary. Given the degree of B₁⁺ inhomogeneity induced by the helmet, a calibration based on a 2D isocenter slice may not be as accurate as a 3D calibration. Any error in the calibration that may have been present in this study would not have an effect on the results, as transmit efficiency was independent of the actual flip angle and the SNR maps were also corrected by the measured flip angle. Rapid 3D mapping sequences^33,34 could be utilized in future studies for a 3D calibration, as routine imaging sequences (MPRAGE, TSE, DTI) could be affected by global flip angle errors.

The homogeneity of the transmit field was reduced with the uHDC helmet present. The degree of inhomogeneity was observed to vary between subjects and with the material permittivity. The higher permittivity uHDC (V2) generally induced a greater degree of inhomogeneity. As demonstrated in Figure 4, this drawback could be mitigated through the use of a patient-specific pTX spokes pulse. In general, B₁⁺ shimming techniques that have been well developed at UHF (≥ 7T) can be used readily for this purpose although offline calculation is required currently. Calculations would require several minutes taking into account time for multi-channel B₁⁺ mapping, exportation and calculation in MATLAB, and importation of optimization coefficients to the scanner. Custom sequences for multi-channel B₁⁺ mapping and to apply spokes pulses are also required, which typically are not offered by the scanner vendors. Offline, MATLAB modules are needed to correctly import the B₁⁺ maps and export spokes coefficients. More work is required to integrate this technology into the typical scanner workflow to make it widely accessible to the average user.

The uHDC SAR distribution was evaluated for configurations of quadrature polarization and transmission with a spokes pulse, and compared to the baseline case. Whole body, whole head, and maximum SAR all decreased for the case of quadrature polarization with flip angle normalization (Supporting Information Table S1). A local region of elevated SAR was observed in the quadrature uHDC SAR map at the apex of the head. As seen in Figures 2 and 3, this is the region where transmit efficiency and displacement current were strongest. Even taking this “hot spot” into account, the maximum uHDC SAR in quadrature mode was still lower than the baseline case. The use of the spokes pulse incurred increases of whole body SAR (21.57%), whole head SAR (70.39%), and maximum SAR (186%) relative to baseline. These increases would require lengthening the TR to remain within IEC SAR guidelines of 3.2 W/kg (whole head) and 10 W/kg (local). The parallel transmit optimization utilized in this study applied a regularization term to limit peak power, but did not consider the electric field itself. Another approach to reduce the SAR of these pulses is to employ optimization routines that constrain global or local SAR directly.^35,36

A preferred approach to reduce the transmit inhomogeneity would be to design uHDC helmets free of such artifacts. As suggested by the computer modeling in Figure 3, the clue is that B₁⁺ inhomogeneity was the result of formation of a large displacement current loop within the continuous geometry of the helmet. The displacement current was significantly higher on the apex of the helmet over the entire phase cycle, leading to strong B₁⁺ enhancement on the top of the head. The magnitude and phase¹¹ variations will lead to uneven secondary B field generation. Regions of very low B₁⁺ were observed in experiment and simulation, most likely due to destructive interferences between the primary and secondary field. One interesting feature in simulation can be observed just below the apex of the helmet, where a vortex pattern characterized by a strong circulating displacement current and a dark eye of low magnitude was formed. According to Equation 1, this displacement current will generate a secondary B₁⁺ field perpendicular to the current. This secondary B field was coincident with the dark band observed in Figure 2, suggesting the phase of the secondary field may have opposed that of the primary field by the coil, which would lead to destructive interference in the brain. Future directions for development of uHDC helmets will include optimization of the helmet geometry and the relative permittivity (at a given static field) to produce more uniform transmission fields.

While this study provided a proof of concept that a uHDC helmet can enhance a standard head coil to the level of a high-density coil at 3T, the enhancements achieved here do not necessarily represent the upper limit possible, as this helmet was a prototype that has not been fully optimized. As demonstrated in Figure 6, the uHDC helmet with a permittivity of ~1200 (V2) attained a higher SNR than V1 with a permittivity of ~1000. Further optimization of the helmet permittivity and geometry may allow for even greater levels of enhancement with standard head coils. Development of a uHDC insert to enhance higher-density coil arrays may also be another potential approach to gain further increases in SNR.

Conclusion:

The first experimental evaluation of a prototype uHDC helmet for brain imaging at 3T was presented. This uHDC helmet strongly improved the transmit efficiency and enhanced the SNR of a commercial 20-Ch head coil to the level of a 64-Ch coil. The B₁⁺ homogeneity was greatly impaired in the prescence of the uHDC helmet. This drawback was overcome with a parallel transmit spokes pulse, at the expense of higher global and local SAR levels. Further optimizations of this design may allow for even greater SNR gains, and could be a cost-effective way of pursuing future RF engineering development for brain applications at 3T.

Supplementary Material

Supp info

Supporting Information Figure S1: SNR maps from a single subject, acquired with the 20-Ch head coil (top row), 64-Ch head coil (middle row), and 20-Ch coil with uHDC helmet in V2 configuration (bottom row). The SNR of the 20-Ch Coil was strongly enhanced by the uHDC helmet, as compared to the baseline 20-Ch coil, and performed similarly to the 64-Ch coil. In some localized regions the V2 configuration performed significantly better than the 64-Ch coil. These SNR maps have been normalized by the corresponding acquired B₁⁺ map.

Supporting Information Table S1: Results of 10g SAR analysis. FA_Mean is the mean flip angle within the normalization region displayed in Figure 5. In the flip angle normalized case with quadrature polarization, the use of the uHDC helmet lowered all SAR quantities. Normalization by whole body SAR led to increases in whole head and maximum SAR relative to baseline, and a flip angle overtip condition. The spokes pulse design incurred higher SAR for all quantities, particularly the maximum SAR.

Supporting Information Table S2: Results of geometry factor analysis. Values represent mean and standard deviation among all subjects. Each individual subject’s g-factor value was calculated by taking the mean g-factor over all acquired slices.