Dissociating effects of error size, training duration, and amount of adaptation on the ability to retain motor memories

Abstract

Extensive computational and neurobiological work has focused on how the training schedule, i.e., the duration and rate at which an environmental disturbance is presented, shapes the formation of motor memories. If long-lasting benefits are to be derived from motor training, however, retention of the performance improvements gained during practice is essential. Thus a better understanding of mechanisms that promote retention could lead to the design of more effective training procedures. The few studies that have investigated how retention depends on the training schedule have suggested that the gradual exposure of a perturbation leads to improved retention of motor memory compared with an abrupt exposure. However, several of these previous studies showed small effects, and although some controlled the training duration and others the level of learning, none have controlled both. In the present study we disambiguated both of these effects from exposure rate by systematically varying the duration of training, type of trained dynamics, and exposure rate for these dynamics in human force-field adaptation. After controlling for both training duration and the amount of learning, we found essentially identical retention when comparing gradual and abrupt training for two different types of force-field dynamics. By contrast, we found that retention was markedly higher for long-duration compared with short-duration training for both types of dynamics. These results demonstrate that the duration of training has a far greater effect on the retention of motor memory than the exposure rate during training. We show that a multirate learning model provides a computational mechanism for these findings.

NEW & NOTEWORTHY Previous studies have suggested that a gradual, incremental introduction of a novel environment is helpful for improving retention. However, we used experimental and computational approaches to demonstrate that previously reported improvements in retention associated with gradual introductions fail to persist when other factors, including the duration of training and the degree of initial learning, are accounted for.

INTRODUCTION

A critical focus of learning and memory research is the study of how training schedules can be optimized to improve retention in cognitive or motor learning tasks (Bock et al. 2005; Criscimagna-Hemminger and Shadmehr 2008; Schmidt and Bjork 1992; Smolen et al. 2016; Yin and Kitazawa 2001). Two key training schedule components include the training duration (e.g., number of trials) and the rate at which a perturbation is presented (e.g., exposure rate). Remarkably, the training schedule has been found to alter both short-term and long-term retention as well as interlimb transfer (Joiner and Smith 2008; Joiner et al. 2013; Kagerer et al. 1997; Kluzik et al. 2008; Malfait and Ostry 2004). This is in line with the idea that neural representations of learned dynamics are fundamentally influenced by the training schedule (Berniker and Kording 2008; Mandelblat-Cerf et al. 2011) and suggests that a greater understanding of how the training schedule affects the retention of motor memories can improve training paradigms for motor learning and rehabilitation.

A number of studies have attempted to manipulate training schedules to promote greater learning, in service of improving the efficacy of training paradigms. However, if long-lasting benefits are to be derived from a training session, then designing the training schedule to maximize retention should be the ultimate goal. Typically, during training, the sudden introduction of a perturbation results in large initial motor errors, which can drive fast initial learning. However, it has been suggested that gradual training paradigms, which keep motor errors small throughout training, result in greater retention of learning in a range of sensorimotor learning paradigms (Criscimagna-Hemminger et al. 2010; Hatada et al. 2006; Huang and Shadmehr 2009; Ingram et al. 2000; Kagerer et al. 1997; Klassen et al. 2005; Kluzik et al. 2008; Michel et al. 2007; Wong and Shelhamer 2011). Consequently, this idea has motivated studies to investigate how small error sizes may be harnessed to improve motor training and rehabilitation (Buch et al. 2003; Ingram et al. 2000). To date, however, the practical benefits to be gained from gradual training schedules remain unclear. In fact, the opposite approach, error augmentation, has even been promoted, where magnified error feedback is provided so that error sizes are increased compared with unmagnified abrupt training (Rozario et al. 2009; Wei et al. 2005).

Several hypotheses have been proposed to explain why gradual training might lead to better retention compared with abrupt training. One thought is based on the idea that because participants are less aware of an environmental disturbance when motor errors are kept small, the use of explicit strategies is reduced and training seems more natural. Thus gradual training would promote motor learning that is more purely implicit, which might in turn promote better retention (Hatada et al. 2006; Jakobson and Goodale 1989; Michel et al. 2007; Wong and Shelhamer 2011). Another hypothesis is based on the idea that motor adaptation is composed of slow and fast learning processes that differentially respond to error signals that drive learning (Smith et al. 2006). In line with the finding that a slow learning process is primarily responsible for both short-term and long-term retention (Joiner and Smith 2008; Sing et al. 2009b), it has been suggested that gradual training schedules lead to better retention by preferentially engaging slow learning mechanisms (Criscimagna-Hemminger and Shadmehr 2008; Torres-Oviedo and Bastian 2012; Wong and Shelhamer 2011).

However, a close examination of the evidence supporting the underlying hypothesis that gradual training leads to improved retention reveals that the studies reporting this effect have not been adequately controlled. Some of these studies have controlled the duration of the training period before retention is examined (Criscimagna-Hemminger et al. 2010; Ingram et al. 2000; Kagerer et al. 1997), whereas others have controlled the amount of learning achieved before retention onset (Huang and Shadmehr 2009; Klassen et al. 2005). Unfortunately, no study to date has simultaneously controlled for both. Thus, if the duration of training and the amount of learning can have even partially independent effects on the amount of retention, these studies would all be confounded by one or the other. Using a force-field (FF) adaptation paradigm, we studied the effect of exposure rate (abrupt versus gradual) on retention while controlling for both the amount of learning and duration of training. We accounted for the level of learning in two different ways: 1) by normalizing out the effect of differences in adaptation for our retention measures and 2) by comparing conditions using subsets of participants for whom adaptation levels could be precisely matched (<1%). Contrary to previous reports, we find no effect of exposure rate, with gradual and abrupt training schedules displaying essentially identical retention patterns for two different perturbations. In contrast, we demonstrate that long-duration training leads to markedly increased retention compared with short-duration training for both types of dynamics we studied. We then show that a computational model of multirate learning can provide a mechanistic explanation for these findings. Collectively, our results reveal that training duration has a far greater impact on retention than exposure rate.

METHODS

Participants.

Sixty-six right-handed participants (29 women; aged 23.8 ± 3.34 yr) without known neurological impairments were recruited from the George Mason University community to participate in the study. Forty-two participants performed the experiment with a position-dependent FF (experiment 1), whereas 24 participants experienced a velocity-dependent FF (experiment 2). The sample sizes used were specified in advance based on previous studies we have performed. Participants in both experiments were divided into three groups that each performed the experiment with a different training schedule (training duration and rate of FF presentation). The study protocol was approved by the George Mason University Institutional Review Board, and all participants gave written informed consent.

Experimental design.

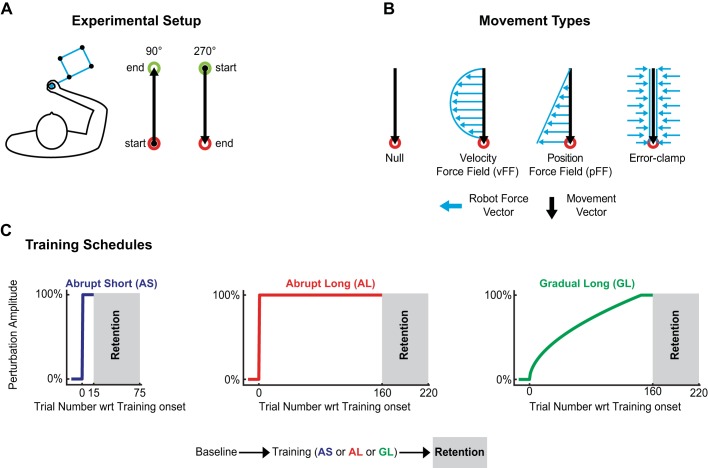
The experimental task followed the design of the standard FF adaptation paradigm (Shadmehr and Mussa-Ivaldi 1994). Participants were situated in front of a horizontal display and used the dominant hand to grip the handle of a two-joint robotic manipulandum (KINARM end-point laboratory; Fig. 1A), capable of recording the position, velocity, and force exerted all at a sampling rate of 1,000 Hz. The manipulandum is equipped with motors capable of producing forces to be applied to the hand. The xy-position of the hand was denoted by a cursor on the screen. Participants were asked to rapidly move the cursor, 0.6 mm in diameter, from the start target to the peripheral end target in a straight line. Moving in two target directions, the end target of each movement was used as the starting target for the subsequent movement (Fig. 1A). The targets, placed along the midline, were spaced 10 cm apart. Participants were allotted a range of 75–2,000 ms to initiate each movement after the appearance of the end target; otherwise, the trial was repeated. Binary visual feedback indicating the movement speed and duration was provided in the form of a changing fill color for the end target. Movements with a peak velocity between 0.25 and 0.35 m/s and durations shorter than 750 ms generated a green fill color as well as a pleasing bell sound to signify a successful trial. Alternatively, movements with peak speeds above or below this range produced end targets that filled with red or yellow colors, respectively, and were not accompanied with auditory feedback. Note that half the participants in each group experienced robot-applied forces in the 270° movement direction and the other half, in the 90° direction. Only movements in the given training direction with a peak velocity between 0.2 and 0.4 m/s were used for data analysis.

Fig. 1.

Experimental setup and paradigm. A: participants grasped the handle of a robotic manipulandum (blue) to make rapid 10-cm, point-to-point reaching movements to 1-cm circular targets in the 90° and 270° directions. B: 3 types of trials were employed. In null (no force) trials, used for task familiarization and to establish a performance baseline, the robotic manipulandum produced no forces. In force-field (FF) trials, the robot manipulandum applied forces (blue arrows) that were proportional in magnitude and perpendicular in direction to either the velocity (vFF) or position (pFF) of hand motion (black arrows). In error-clamp trials, the manipulandum steered in a virtual channel directed toward the target to minimize lateral deviations (see methods). C: after an initial baseline period, participants completed 1 of 3 training schedules (abrupt short, AS; abrupt long, AL; or gradual long, GL). These schedules varied in duration (short versus long) or exposure rate (abrupt versus gradual). All 3 training schedules were followed by a retention period consisting of 60 consecutive error-clamp trials. wrt, With respect to.

Three different types of trials were used throughout: null trials, FF trials, and error-clamp (EC) trials (Fig. 1B). During null trials, the robot motors were disabled and no external changes to the manipulandum were applied (movement of the handle was completely controlled by the participant). In FF trials, the robot motors were used to produce clockwise (CW) or counterclockwise (CCW) forces on the manipulandum to perturb hand motion. Participants in experiment 1 were presented with a position-dependent FF (pFF), whereas participants in experiment 2 were presented with a velocity-dependent FF (vFF). These FFs took the following form:

$$\left[\begin{array}{c}{F}_x\\ F_y\end{array}\right]=c_K·\left[\begin{array}{cc}0& -K\\ K& 0\end{array}\right]·\left[\begin{array}{c}x\\ y\end{array}\right]+c_B·\left[\begin{array}{cc}0& -B\\ B& 0\end{array}\right]·\left[\begin{array}{c}\dot{x}\\ \dot{y}\end{array}\right],K=45\text{N/m},B=15\mathrm{N}·\text{s/m}$$ (1)

In a vFF, c_K = 0 and c_B = ±1, whereas in a pFF, c_K = ±1 and c_B = 0. Because the above matrices are antisymmetric (where a matrix A = −A^T), the force and position/velocity vectors were orthogonal at any given point during hand motion; this results in a curl FF where the direction (CW or CCW) can be altered with a change in the sign of c, where c = +1 indicates a CW FF. Note that both experiments were balanced such that there was an equal number of participants performing the task in each movement direction (90° versus 270°) and FF direction (CW versus CCW). The values for the stiffness and viscosity parameters (K and B, respectively) were chosen to achieve relatively equal peak forces between a pFF and vFF (Sing et al. 2009a).

During EC trials, the robot motors employ a spring (6,000 N/m) and damper (150 N·s/m) system to inhibit lateral movements, obligating participants to move directly toward the target. By minimizing perpendicular displacement from a straight line toward the target, lateral movement errors are effectively reduced to zero. By minimizing lateral errors, we could measure the lateral force patterns produced by participants for compensation of the FF independently of feedback responses that might be driven by lateral errors (Scheidt et al. 2000; Sing et al. 2009a, 2013).

Task.

With the exception of the FF type and training schedule, all participants completed the same general experimental paradigm. Participants first performed four baseline blocks to ensure task comfort and familiarity. The first two baseline blocks contained 80 trials each and were entirely composed of null trials. The last two baseline blocks contained 100 trials each, where 1 in 5 trials were EC trials and the remaining trials were null trials. The EC trials were used to establish a baseline for an estimate of how the learned force-compensation patterns change throughout the experiment. Blocks were intermitted with 1-min breaks. In both experiments, the baseline blocks were followed by one of three training schedules (described below). The same FF type (vFF or pFF) and direction (CW or CCW) remained constant for each participant. The change in magnitude of the FF for each training schedule is shown in Fig. 1C. EC trials were present in the given training direction with a ratio of 5 FF:1 EC, and these trials were used to measure the force compensation patterns a participant had learned. Note that we refer to movements made in the direction opposite of the training direction as return trials (e.g., movements toward 90° when the training direction was 270°). During training and retention, participants always experienced ECs on return trials. Finally, we refer to the epoch of the experiment after training as the retention period. In this period we employed 120 consecutive EC trials (60 in the training direction) to measure the retention of motor memories acquired during the training period.

Training schedules.

In abrupt short (AS) training, participants were first presented with 15 null trials. As shown in Fig. 1C, left, the magnitude of the force then changes from 0% to 100% of the perturbation strength (between the 15th and 16th trial), which corresponds to B = 15 N·s/m for vFFs and K = 45 N/m for pFFs. As in previous studies (Joiner et al. 2013; Malfait and Ostry 2004), the training duration, during which FFs were applied, spanned 15 trials. These 30 trials were then followed by the retention period within the same block. In the abrupt long (AL) training session (Fig. 1C, middle), 15 null trials were followed by a long training period consisting of 160 trials. The magnitude of the FF was also abruptly and fully introduced between the 15th and 16th trial. Both the AS and AL FF progression rates are thus modeled as a step input, one with a much shorter duration (AS) than the other (AL). On the other hand, following Malfait and Ostry (2004), the gradual long (GL) training schedule (Fig. 1C, right) included 15 null trials followed by 160 training trials where the force smoothly transitioned from 0% to 100% of its maximum value during the first 145 trials after introduction (trial 16); the FF then remained constant at the maximum level for an additional 15 trials. The values of B and K were changed in the following nonlinear pattern for the GL training schedule:

$$\left|Q\right|=n^x,$$ (2)

where Q represents either the viscosity or stiffness FF gains (B and K), n is the trial number during the first 145 training trials, and

$$x=\frac{\log \left(s_B\cdot 15+s_K\cdot 45\right)}{\log \left(145\right)},$$ (3)

where s_B = 1 and s_K = 0 in a vFF, and s_B = 0 and s_K = 1 in a pFF. This results in 1 N·s/m (vFF) or 1 N/m (pFF) when the force is first introduced and 15 N·s/m or 45 N/m after the 145th trial. This ramp function, based on the one used in Malfait and Ostry (2004), produced the slightly nonlinear ramp illustrated in Fig. 1C. The rate of perturbation increase early in the ramp, where perturbations were small, was somewhat faster than the rate when perturbations were larger late in the ramp. As in the AS training schedule, the AL and GL training epochs were followed by the retention period.

Note that during the training period, adaptation was calculated over a window that allowed us to fairly compare the three training schedules. Based on the training duration of the AS training scheme (15 trials), the first three adaptation coefficient points during training for all training schedules represent the same trial range, and a window size of 15 trials was used afterward for the AL and GL training data. Thus the mean and standard error values are plotted as a function of the mean trial number within these different windows (Fig. 2, E and H). During the retention period, however, the mean and standard error are calculated over a two-trial window due to the increased frequency of EC trials.

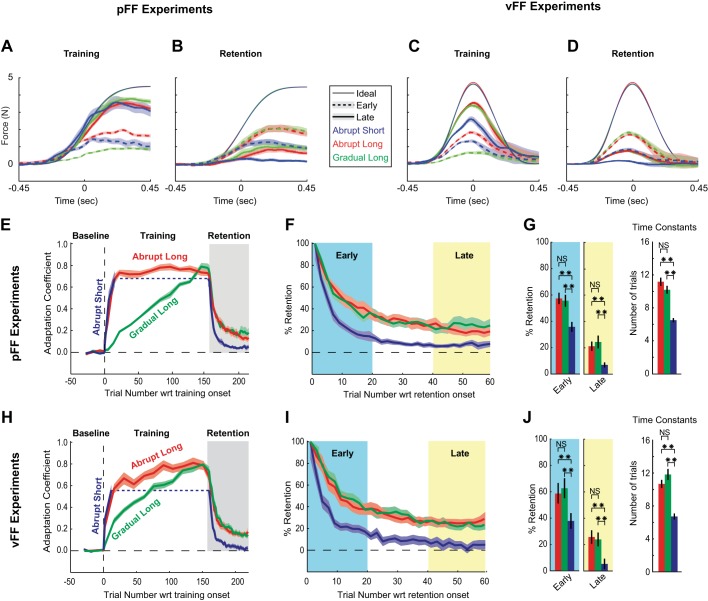
Fig. 2.

Time course of adaptation and retention for different exposure rates and training durations. A–D: population-averaged force profiles for each of the 3 training schedules (abrupt long, AL; gradual long, GL; and abrupt short, AS) and the robot-issued force pattern that participants learned to compensate for (thin traces in each panel) measured during error-clamp (EC) trials. In each panel, we plotted both the early (thick dashed traces) and the late (thick solid traces) population-averaged force patterns observed during both the training epoch (A and C) and retention period (B and D) for each training schedule (see methods). A and B display data related to experiment 1 (position-dependent force-field, pFF), and C and D display data related to experiment 2 (velocity-dependent force-field, vFF). Results suggest a stronger effect of training duration (AS versus AL) on retention compared with exposure rate (AL versus GL; see B and D) despite similar force patterns observed at the end of training (thick solid traces in A and C). E and H: learning and decay curves based on population-averaged adaptation coefficients (see methods) for each training schedule. E–G show data from experiment 1, pFF adaption, and H–J show data from experiment 2, vFF adaptation. Results show similar final adaptation levels for all 3 schedules. F and I: normalized retention curves during the retention period. The raw retention levels (gray regions in E and H) were scaled relative to final adaptation levels and thus represent %retention. Abrupt and gradual schedules display nearly identical retention when training duration is matched (AL versus GL); however, short training led to markedly reduced retention compared with long (AS versus AL). Note that trial numbers indicated on the x-axis correspond to the trial numbers for the AL and GL conditions to facilitate comparison between the AL, GL, and AS conditions. G and J, left: %retention for the early (trials 1–20; cyan regions in F and I) and late (trials 41–60; yellow regions in F and I) retention periods. Retention was significantly increased for long-duration training (AL and GL) compared with short-duration training (AS) for both early and late periods in experiments 1 and 2. However, retention was essentially identical for gradual compared with abrupt training when duration was matched (GL versus AL). Right: time constants estimated for the retention of adaptation. Results echo those for the retention level analyses at left. Shaded regions and error bars represent SE. **P < 0.01, significant differences. NS, not significant; wrt, With respect to.

Quantitative metrics.

We examined the lateral force profiles participants generated during EC trials throughout the experiment because all applied forces were perpendicular to the target direction. Because the error is reduced to near-zero levels during these trials, the lateral forces measured represent the amount of adaptive compensation participants learned to produce to counteract expected perturbations (see Fig. 2). A coefficient denoting the amount of adaptation made to compensate for the external forces can thus be computed by performing a linear regression of the lateral force profiles participants make during EC trials onto the force profiles produced by the robot, and then taking the slope of this regression. To move in a straight line, the force produced by the robot represents the ideal amount participants should compensate for. Because the robot-produced force in FF trials is proportional to the longitudinal hand position or velocity on a given trial, and the position or velocity varies from trial to trial, the amount of adaptation on a given EC trial was estimated by regressing the measured lateral force profile onto the ideal force profile that would be required for complete compensation on that specific trial. Therefore, if the ideal and applied force profiles completely overlapped, the adaptation coefficient would be 1, a completely equal but opposite force profile would result in a coefficient of −1, and no force compensation would result in an adaptation coefficient of 0 (Joiner and Smith 2008; Sing et al. 2009a; Smith et al. 2006). Note that adaptation coefficients were based on a window extending ±750 ms centered on each movement’s peak speed point. Also note that the last 12 EC trials during the baseline period were used to calculate the average baseline force pattern for each participant. The average baseline force pattern was then subtracted from the forces participants produced during the training and retention periods.

We were interested in determining how different perturbation exposure rates used during training (gradual versus abrupt) influence the retention of learning. A gradual exposure rate typically leads to small motor errors throughout training, because the perturbation strength is applied incrementally over many trials. However, an abrupt exposure rate leads to relatively larger motor errors, because the perturbation is suddenly introduced at full strength. Therefore, by studying how abrupt and gradual training schedules influence retention, we can consequently determine how the size of error influences retention. To ensure that gradual and abrupt training did in fact lead to small and large error sizes, respectively, we compared the maximal error sizes that were observed in AL and GL training. To assess error, we defined two vectors: one between the start and end targets, and the other between the start target and the hand position at the midpoint of the movement (i.e., when longitudinal displacement reached 5 cm). Errors were then calculated as the angle between these two vectors.

A key idea in this report is that it may be crucial to control both the duration of training and the amount of adaptation when examining the effect of exposure rate. Training duration was explicitly matched between AL and GL groups by the experimental design. However, it is not possible to precisely match adaptation levels in the experiment design, and differences in adaptation levels could trivially lead to differences in retention. For example, if the AL and GL groups displayed different final adaptation levels, yet both groups retained 60% of their final adaptation levels, their raw retention values would still be different. We thus employed two different methods (normalized retention analysis and matched-adaptation subsetting) of controlling the effects of final adaptation when examining the differences in the retention of adaptation between training schedules. The first method, normalized retention analysis, entailed normalizing each training schedule’s decay curve by the amount of final adaptation achieved at the end of the training period. Thus retention was expressed as a percentage of adaptation measured during the retention period to the final adaptation level achieved at the end of training for each specific training schedule, rather than as a raw retention value as in previous studies. The second method, matched-adaptation subsetting, entailed the selection of subgroups of participants for each pair of training schedules that we compared (AL versus GL, AL versus AS, GL versus AS) that were matched within 1% for final adaptation levels. Specifically, for each comparison, we selected the maximum number of participants for which a match within 1% or better could be found. This matching was performed separately for each pair of training schedules in experiment 1 (pFF training) and experiment 2 (vFF training). In experiment 1, the AL and GL adaptation-matched subgroups (n = 13 and n = 12, respectively) resulted in a 0.35% difference in final adaptation. AL and AS adaptation-matched subgroups (n = 13 and n = 12, respectively) resulted in a 0.29% difference, and GL and AS adaptation-matched subgroups (n = 12 and n = 11, respectively) resulted in a 0.31% difference. In experiment 2, AL and GL adaptation-matched subgroups (n = 8 and n = 7, respectively) resulted in a 0.90% difference in final adaptation. AL and AS adaptation-matched subgroups (n = 4 and n = 6, respectively) resulted in a 0.21% difference, and GL and AS adaptation-matched subgroups (n = 4 and n = 5, respectively) resulted in a 0.09% difference. Note that increasing the number of participants for subgroups with n = 4 participants to n = 5 participants still allows adaptation to be matched within 2% and leads to a similar pattern of results. Importantly, controlling for the level of final learning in this manner provided a second, independent evaluation of the effects of training schedule on retention.

We were interested in determining how the time constants associated with the decay of adaptation during the retention period were influenced by the effects of training duration and exposure rate. To estimate these time constants (Fig. 2, G and J, right), the entire set of the retention period data was fitted with the following equation for each participant:

$$\left(1-\alpha \right)\cdot \exp \left(-\frac{t}{\tau }\right)+\alpha ,$$ (4)

where τ corresponds to the exponential time constant for decay. This procedure was performed separately for each training schedule within both experiments and allowed us to generally compare the rate of motor memory decay.

Two-state multirate learning model.

To understand our experimental findings, we studied a two-state multirate learning model that we implemented to predict the time course of retention for all three training schedules from the learning curves that were experimentally measured during the training period (Fig. 3). We constructed one model for the pFF environment and one for the vFF environment. These two models are structurally identical, but their parameters were fit on pFF and vFF data, respectively. In both cases, the model parameters were fit to training period data combined across all three training conditions (AS, AL, and GL). Thus the model fitting procedure was blind to the experimentally measured retention data so that each model could make a naive prediction about retention for each training condition, allowing us to determine whether these two-rate models would predict the same contrasting effects of training duration and training schedule that we observed experimentally. In this model, adaptation is composed of a slow and a fast learning process. The slow learning process is not very sensitive to error but retains information well, whereas the fast learning process reacts strongly to error but has weak retention (Smith et al. 2006). The model was implemented with the following error equations and learning rules:

$$\text{FF\hspace{0.17em}trials:}\hspace{0.17em}e\left(n\right)=f\left(n\right)-x\left(n\right)$$

$$\text{EC\hspace{0.17em}trials:}\hspace{0.17em}f\left(n\right)=x\left(n\right)\to e\left(n\right)=0$$

where x(n) is motor output on trial n, f(n) is perturbation strength on trial n, and e(n) is error on trial n, and

$$x_1\left(n+1\right)=A_f\cdot x_1\left(n\right)+B_f\cdot e\left(n\right)$$

$$x_2\left(n+1\right)=A_{\text{s}}\cdot x_2\left(n\right)+B_{\text{s}}\cdot e\left(n\right)$$

$$B_f>B_s,\hspace{0.17em}{A}_s>A_f,\hspace{0.17em}x\left(n\right)=x_1\left(n\right)+x_2\left(n\right)$$

where A_f and A_s are retention factors for fast and slow processes, B_f and B_s are learning rates for fast and slow processes, and x₁(n) and x₂(n) are the individual fast and slow learning processes that contribute to the net motor output on trial n [x(n)].

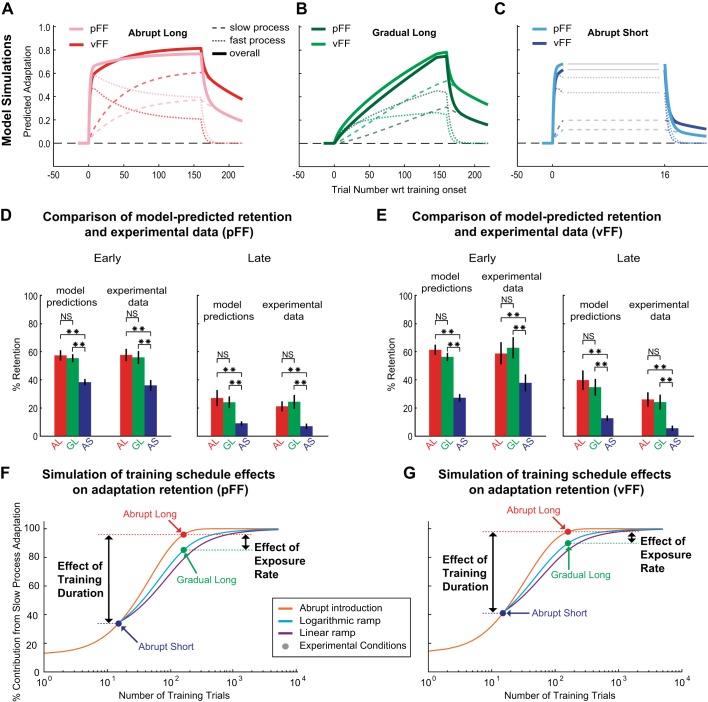
Fig. 3.

A model-based prediction of retention for different exposure rates and training durations. A–C: two-state model simulations based on position-dependent (pFF) and velocity-dependent force-field (vFF) adaptation data for the abrupt long (AL; A), gradual long (GL; B), and abrupt short (AS; C) training schedules. The models were fit solely to the training period data so that they could be used to predict retention. D and E: comparison of model predicted versus experimentally measured normalized retention for AL, GL, and AS training schedules based on pFF and vFF data sets, respectively. Note that we compared the training schedules during both the early (left) and late (right) periods of the retention epoch. Both the pFF- and vFF-based versions of the model predict little difference in retention between AL and GL, but they predict large differences in retention between AL and AS. These predictions echo the main experimental finding that training duration has a strong effect on retention, whereas exposure rate has a weak effect. F and G: simulations based on pFF and vFF adaptation, respectively. We characterized the retention predicted from a two-state multirate model for gradual and sudden exposure rates and for a wide range of training durations. Because in such a model, the fast learning process would decay very rapidly during a retention period, we used the amount of slow-process learning at the end of the training period as a proxy for retention. Specifically, we used the fraction of the final adaptation due to the slow learning process for the retention proxy shown on the y-axes of these plots, because this normalizes the retention proxy by the amount of final adaptation analogous to the experimental results based on normalized retention shown in Fig. 2. The results shown summarize the findings from ~30,000 model simulations based on the combination of 2 FFs, 3 exposure rate conditions, and training durations spanning up to 5,000 trials in the training period. Note that we simulated 2 different gradual training schedules: a logarithmically ramped schedule, such as that used in experiments 1 and 2, and a linearly ramped schedule. Also note that we included a 15-trial hold period at the end of training in both gradual conditions, and so these conditions are plotted from the 16th trial point onward, whereas the abrupt condition is plotted from the 1st trial point. Simulations of the abrupt condition from the 1st to 14th trial point can thus be interpreted as abrupt-short conditions with fewer training trials than the abrupt-short condition we experimentally tested (15 trials). The pFF- and vFF-based simulations show very similar results, as do both gradual schedules. Colored dots denote the conditions corresponding to the training schedules used in experiments 1 and 2, and black arrows illustrate the effects of training duration (AS versus AL) and exposure rate (AL versus GL) based on these conditions. For the experimental conditions, the simulations predict a percent difference of <13% between AL and GL conditions, in contrast to a difference >138% between AS and AL training. This is in line with the findings from experiments 1 and 2 demonstrating that exposure rate has little effect on retention but that training duration has a dramatic effect. Note that differences between gradual and abrupt training are <20% at all training durations and are always negative, meaning that these models consistently predict only small differences between gradual and abrupt training and that gradual training would lead to slightly reduced retention compared with abrupt across all training durations. Error bars are SE. **P < 0.01, significant difference. wrt, With respect to.

Using a least-squares approach, the model parameters were estimated separately for experiments 1 and 2. In each case, the average of each group’s training period data was concatenated, and the model was fitted onto the combined datasets. Thus the model predicted retention, since it was blind to the retention period data. To statistically compare the predicted differences in retention levels between AL, GL, and AS from the model, we made 1,000 estimates of the pFF-based and vFF-based model parameters via bootstrap. We then used these bootstrapped samples for estimates of the standard error of the predicted early and late retention for each of the training schedules (Fig. 3, D and E).

Previous studies have shown that the slow process is directly responsible for both short-term and long-term retention (Joiner and Smith 2008; Sing et al. 2009b). Therefore, we also used the two-state model to characterize how exposure rate and training duration influence retention by using slow-process learning as a proxy. Specifically, we simulated adaptation using three different exposure rates: an abrupt condition where the perturbation is introduced suddenly, a gradual condition where the perturbation is introduced linearly, and another gradual condition where the perturbation is introduced logarithmically (employed in the current study). The linear ramp was included because it is a popular gradual ramping procedure used in motor adaptation studies (Huang and Shadmehr 2009; Hussain and Morton 2014; Klassen et al. 2005; Schlerf et al. 2012; Wang et al. 2011; Wong and Shelhamer 2011). In addition, we included a 15-trial period at the end of both gradual training conditions in which the perturbation was at its maximum value (i.e., hold period). We included a hold period in our simulations so that they were consistent with the gradual condition used in the experimental design. Also note that a hold period was used in a vast majority of studies we are aware of employing a gradual training schedule (Criscimagna-Hemminger et al. 2010; Gibo et al. 2013; Huang and Shadmehr 2009; Joiner et al. 2013; Klassen et al. 2005; Kluzik et al. 2008; Malfait and Ostry 2004; Wang et al. 2011; Wong and Shelhamer 2011). Therefore, the very first training schedule simulated for the gradual conditions has a 16-trial training duration, whereas the first simulation for the abrupt condition begins with a 1-trial training duration. In these simulations, we calculated the fraction of total adaptation that is accounted for solely by slow-process learning over a range of 5,000 trials; this provided enough trials for all three exposure rates to elicit near-steady-state slow-process contribution. Slow-process contribution was subsequently normalized by the value found on the 5,000th trial of the abrupt condition, allowing us to express each quantity as a percentage of total contribution possible (Fig. 3, F and G). Note that these simulations were performed for model parameters derived separately from the pFF data set (Fig. 3F) and the vFF data set (Fig. 3G). The simulations demonstrate how different training schedules lead to distinct patterns of slow-process contribution to total learning, which may act as a proxy for differences in retention between the training schedules.

Statistical analysis.

To examine differences in the magnitude of retention, we operationally defined an early and a late period during the retention epoch of the experiments as the first (1–20) and last (41–60) group of 20 EC trials in the measured movement direction. We compared the retention found in each training schedule within these periods and determined if statistically significant differences were present. Note that the early and late periods during the training epoch, however, were defined as the first and last 10% of training trials in each training schedule to facilitate comparisons between them (Fig. 2, A and C). When we compared the final adaptation levels and the retention levels between the three training schedules, we used ANOVAs and subsequently determined which training schedule was significantly different with post hoc analysis. For example, two-tailed t tests were used between the training schedule groups to compare the final adaptation levels. We also used ANOVAs followed by t tests to determine if significant differences were present between the time constants associated with the decay of adaptation found in the retention period of each training schedule. Note however that the entire set of retention period data was used to estimate the time constants. When comparing a pair of training schedule groups in our matched-adaptation analyses, we used two-tailed t tests. In all cases, the significance level (alpha) was set to 0.05, and a Kolmogorov–Smirnov test was performed to verify that the data were normally distributed.

RESULTS

We studied how two key features of the training schedule, training duration and exposure rate, influence the retention of motor memories. In particular, we compared retention of the trained adaptation for the three different training schedules —abrupt long (AL), gradual long (GL), and abrupt short (AS)— so that we could examine the specific effects of exposure rate (AL versus GL) and training duration (AL versus AS). We made these comparisons in two different force-field (FF) adaptation paradigms, one based on a position-dependent FF (pFF) and one based on a velocity-dependent FF (vFF), to determine whether the findings would be consistent for different physical dynamics. Critically, we exerted control over both the training duration and the amount of learning before retention was assessed. The experimental design allowed us to match the training duration across conditions, and the analytical methods allowed us to match the final level of learning across conditions. Specifically, we accounted for the final level of learning in two different ways to analyze retention: 1) normalizing out differences in adaptation and 2) subsetting the data so that subgroups of participants with matched adaptation levels could be compared.

Participants were instructed to make rapid 10-cm point-to-point reaching movements while grasping the handle of a robotic manipulandum with the right hand as diagrammed in Fig. 1A. Experiment 1 began with a 360-trial baseline period in which no FF perturbation was present. Next, in the training period, participants were randomly assigned to one of three training schedules: AS, where the full FF was suddenly introduced and continued for 15 trials; AL, where the FF was suddenly introduced and continued for 160 trials; and GL, where the FF was incrementally introduced (see methods) for 145 trials and remained at full strength for an additional 15 trials. Retention was then assessed in a 60-trial period that followed training (Fig. 1C). This retention period consisted entirely of error-clamp (EC) trials in which motor errors that promote learning were essentially eliminated. Experiment 2 was identical to experiment 1, except that, during training, a vFF was used rather than a pFF.

Note that throughout the present study, we operationally defined the retention of motor memories as its ability to withstand the passage of time and recurring memory retrievals that take place during the retention period. In animal conditioning studies, decay of adaptation from memory retrieval is generally assessed during an extinction period, in which the stimulus driving an adaptive response is no longer provided (Cohen et al. 2004; Medina et al. 2002; Pavlov 1927). Analogously, we used EC trials to assess memory stability during extinction, but the EC also allowed us to essentially eliminate the possibility for motor errors to systematically drive either unlearning or further learning (see methods). Note that the use of EC trials to study memory retention has been widely adopted in many FF adaptation and visuomotor-rotation studies (Huang and Shadmehr 2009; Joiner et al. 2013; Scheidt et al. 2000; Shmuelof et al. 2012; Smith et al. 2006).

Final adaptation levels and error sizes for each schedule during the training period.

All three training schedules resulted in substantial levels of motor adaptation in both experiments 1 and 2 throughout the training and retention epochs as demonstrated in Fig. 2. The level of adaptation was quantified based on an adaptation coefficient (Joiner et al. 2013; Sing et al. 2009a; Sing and Smith 2010; Smith et al. 2006), which corresponds to the coefficient for the linear regression between the lateral force pattern that a participant produced on a particular EC trial and the ideal compensatory force for that movement. The final adaptation level was defined as the adaptation level found on the last EC trial in the training period. In experiment 1, we found final adaptation values that were within 6% for all three training schedules and not significantly different from one another [F(2, 41) = 0.32, P = 0.73; ANOVA]. The final adaptation levels were 0.73 ± 0.049, 0.77 ± 0.016, and 0.68 ± 0.067 (means ± SE) for the AL, GL, and AS schedules, respectively (Fig. 2E). In experiment 2 (Fig. 2, H–J), where we used a paradigm identical to experiment 1 except that the FF perturbation was velocity dependent rather than position dependent, the three training schedules led to final adaptation values that were within 17% of each other (0.68 ± 0.055, 0.72 ± 0.051, and 0.55 ± 0.50 for the AL, GL, and AS schedules, respectively). However, here we found that there was a slight significant difference among the training schedules [F(2,23) = 3.4, P = 0.044; ANOVA]. Specifically, AS training resulted in a significantly lower adaptation amount than the other schedules [t(14) = 1.82, P = 0.038; t(14) = 2.78, P = 0.004 for AL versus AS and GL versus AS, respectively; 2-tailed t tests]. Thus gradual and abrupt exposure rates led to similar levels of final adaptation when training duration was matched, and there were no significant differences between AL and GL in both experiments 1 and 2. When we decreased the training duration (15 versus 160 trials), final adaptation was only mildly reduced, with the reduction being statistically significant in experiment 2 but not in experiment 1.

Note that, as expected, abrupt training led to consistently larger error sizes than gradual training. In both experiments 1 and 2, the largest errors observed in the AL group were two- to threefold higher than those observed in the GL group [31.4 ± 2.6° and 13.6 ± 1.3° of directional error (see methods) for AL and GL groups in experiment 1, and 29.8 ± 3.9° and 11.9 ± 2.1° for AL and GL groups in experiment 2]. This is in line with the approximately two- to threefold increases in error size observed for abrupt versus gradual training in several previous studies (Criscimagna-Hemminger et al. 2010; Kluzik et al. 2008; Malfait and Ostry 2004; Wang et al. 2011).

Normalized retention analysis reveals that retention is insensitive to exposure rate yet highly sensitive to training duration.

The final adaptation levels were similar across experiments and training schedules; however, these levels were not precisely matched across groups, and in one case (AS in experiment 2) the differences from other groups were even statistically significant. Because differences in the level of final adaptation would propagate into differences in retention even if the rates of decay were identical, raw measurements during the retention period do not provide a clean measure of the ability to retain motor memories formed during training. To obtain a clean measure of retention that prevents this propagation, we normalized the raw retention levels measured during the retention period by the final adaptation level. Specifically, we used the adaptation coefficient (AC) measured on the last EC trial in the training period for this normalization.

Figure 2E shows the raw decay curves measured during the retention epoch for experiment 1, and Fig. 2F shows the normalized decay curves. To assess how the training schedule influenced retention, we first focused our analysis on the early (trials 1–20) and late (trials 40–60) periods of the retention epoch (Fig. 2, F and G). Throughout both the early and decay periods, we detected significant differences between the training schedule groups [early period: F(2,41) = 6.7, P = 0.0032; late period: F(2,41) = 6.02, P = 0.0053; ANOVA]. Interestingly, we found that both long-duration training groups (AL and GL) displayed nearly identical retention in the early part of the retention period (Fig. 2, F and G); however, the short-duration group displayed significantly less retention [57.3 ± 4.3% and 55.6 ± 4.4% for AL and GL, respectively, compared with 35.8 ± 3.7% for AS; t(26) = 15.4, P = 0.788 for AL versus GL; t(26) = 3.76, P = 8.68 × 10⁻⁴ for AL versus AS; t(26) = 3.32, P = 0.0026 for GL versus AS; 2-tailed t tests]. In the late part of the retention period (Fig. 2, F and G), we also found nearly identical retention for AL and GL groups but reduced retention for AS [20.6 ± 3.4% and 24.2 ± 5% for AL and GL, respectively, compared with 6.7 ± 1.9% for AS; t(26) = −0.595, P = 0.557 for AL versus GL; t(26) = 3.51, P = 0.0016 for AL versus AS; t(26) = 3.24, P = 0.0032 for GL versus AS; 2-tailed t tests].

Experiment 2 (vFF training) echoed the results from experiment 1 (Fig. 2, H–J). We found significant differences throughout the retention period [early period: F(2,23) = 17.4, P = 3.52 × 10⁻⁵; late period: F(2,23) = 21.8, P = 7.47 × 10⁻⁶; ANOVA]. With post hoc analysis, we found no difference between early or late retention for AL versus GL training [early period: retention levels of 59.3 ± 5.4% and 62.5 ± 4.8% for AL and GL, respectively; t(14) = −0.444, P = 0.66; late period: 25.8 ± 3.3% and 23.6 ± 3.4% for AL and GL, respectively; t(14) = 0.459, P = 0.65; 2-tailed t tests]. In contrast, AS training led to reduced retention in both the early and late periods of the retention block [early period: 37.6 ± 3.29%; t(14) = 3.26, P = 0.0021 for AL versus AS; t(14) = 4.02, P = 2.16 × 10⁻⁴ for GL versus AS; late period: 5.1 ± 3.8%; t(14) = 4.11, P = 1.6 × 10⁻⁴ for AL versus AS; t(14) = 3.64, P = 6.8 × 10⁻⁴ for GL versus AS; 2-tailed t tests]. In both experiments 1 and 2, long-duration training displayed retention during the late period that was at least four times larger than during short-duration training, but late-period retention was nearly identical when the training schedule only differed in exposure rate. In summary, this analysis suggests that for both pFF and vFF adaptation, the exposure rate has little effect on the retention of adaptation (AL versus GL). In contrast, training schedules with longer durations lead to significantly improved retention (AL versus AS and GL versus AS).

We next examined whether the time constants associated with the decay of adaptation during the retention period varied depending on the training schedule. In particular, we estimated the exponential time constants for decay for each individual by fitting the entire set of the retention period data with a single exponential plus offset (see methods). The time constants determined from this fitting procedure are presented in Fig. 2, G and J, right, for experiments 1 and 2, respectively. In experiment 1, we found time constants of 11.2 ± 1.89, 9.9 ± 1.65, and 6.5 ± 0.95 trials for AL, GL, and AS, respectively. In experiment 2, we found time constants of 10.7 ± 1.4, 11.9 ± 1.90, and 6.78 ± 1.05 trials for AL, GL, and AS, respectively. We found a significant difference in estimated time constants between the training schedules [experiment 1: F(2,41) = 16.6, P = 6.53 × 10⁻⁶; experiment 2: F(2,23) = 10.9, P = 0.0006; ANOVA]. However, we specifically found that exposure rate has no effect on the time constants when training duration is matched [t(26) = −0.477, P = 0.64; t(14) = −0.54, P = 0.59 for AL versus GL in experiments 1 and 2, respectively; 2-tailed t tests]. In contrast, decreased training duration for AS resulted in time constants for decay during the retention period that were reduced by 34–42% in experiment 1 and by 37–43% in experiment 2, indicating that retention decays more rapidly than for long-duration training groups [experiment 1: t(26) = 7.95, P = 1.9 × 10⁻⁹; t(26) = 9.72, P = 1.7 × 10⁻¹⁰ for AL versus AS and GL versus AS, respectively; experiment 2: t(14) = 2.93, P = 0.0052; t(14) = 3.98, P = 2.42 × 10⁻⁴ for AL versus AS and GL versus AS, respectively; 2-tailed t tests]. These findings echo the results from the early and late period analysis; together, they demonstrate that when differences in final adaptation are accounted for by normalizing the raw retention data, there is little effect of gradual versus abrupt exposure rates if training duration is matched. In contrast, increased training duration leads to significantly improved retention measured in either early or late retention periods or by a time constant analysis based on data from the entire retention period for both vFF and pFF training.

Matched-adaptation analysis shows that retention is insensitive to exposure rate yet highly sensitive to training duration.

The normalized retention analysis presented in Fig. 2, F and G, and Fig. 2, I and J, takes into account the differences in final learning levels between individuals (and thus between groups) by measuring retention relative to final learning. However, it is possible that higher levels of learning might lead to disproportionately high levels of retention, making the normalization imperfect. To address this possibility, we devised a second method for controlling final adaptation that would not be affected by a potential nonlinear scaling between final adaptation and retention. Using this method, we attempted to precisely match the final adaptation levels between training schedules in experiments 1 and 2 by selecting a subset of participants from each group (AL, GL, and AS) in each experiment that could be almost identically matched in terms of final learning across groups. We did this matching separately for each group comparison (AL versus GL, AL versus AS, and GL versus AS) in experiment 1 and for each group comparison in experiment 2. In particular, we found that the subgroups could be matched to the extent that the differences in final adaptation were consistently less than 1%; note that here final adaptation is defined as the adaptation measured on the last EC trial during training. We found that for pFF training, the adaptation-matched AL and GL subgroups contained 13 and 12 participants, respectively. These subgroups displayed retention levels during the early period (trials 1–20) that were nearly equal to one another [59 ± 5.1% and 63 ± 4.4%, respectively; t(23) = 0.146, P = 0.88 for AL versus GL; 2-tailed t test], in line with the findings from the normalized retention analysis showing that exposure rate had little effect on retention. In contrast, the adaptation-matched AS and AL subgroups, which contained 12 and 13 participants, respectively, displayed significantly different levels of retention during the early period, with long-duration training leading to higher retention [retention amounts of 55 ± 4.6% and 34.5 ± 4% for the adaptation-matched AL and AS subgroups, respectively; t(23) = 3.45, P = 0.0022; 2-tailed t test]. The adaptation-matched GL and AS subgroups contained 12 and 11 participants, respectively, and we observed retention patterns that mirrored those of the AL and AS subgroups [retention levels of 54 ± 5% and 38 ± 5% for the adaptation-matched GL and AS subgroups, respectively; t(21) = 2.32, P = 0.0034; 2-tailed t test]. During the late period (trials 41–60), AL and GL subgroups continued to display retention levels that were nearly identical to one another, whereas the AS subgroups led to substantially smaller retention compared with the AL and GL subgroups [t(23) = −0.502, P = 0.62; t(23) = 3.27, P = 0.0066; t(21) = 2.62, P = 0.016 for AL versus GL, AL versus AS, and GL versus AS, respectively; 2-tailed t tests]. The time constant analysis based on exponential fitting of each individual’s decay curve (trials 1–60) also demonstrated that short-duration training led to a significantly smaller rate of decay in these adaptation-matched subgroups [t(23) = −2.32, P = 0.014; t(21) = 2.46, P = 0.011 for AL versus AS and GL versus AS, respectively; 2-tailed t tests]. However, we found no evidence for an effect of exposure rate on these time constants [t(22) = 1.14, P = 0.26 for AL versus GL; 2-tailed t test].

We repeated the adaptation-matched analysis for experiment 2 and found that it led to the same pattern of results we found after matching adaptation in experiment 1. During the early period, the AL and GL subgroups (n = 8 and n = 7, respectively) displayed retention levels of 59 ± 5% and 63 ± 4.4%, respectively [t(13) = −0.607, P = 0.55; 2-tailed t test], the AL and AS subgroups (n = 4 and n = 6, respectively) showed retention amounts of 64 ± 4.1% and 39 ± 4.7%, respectively [t(8) = 5.06, P = 0.0019; 2-tailed t test], and the GL and AS subgroups (n = 4 and n = 5, respectively) showed retention levels of 62.6 ± 5% and 38 ± 3%, respectively [t(7) = 3.78, P = 0.0138; 2-tailed t test]. Late-period retention continued to indicate no significant difference between the long-duration subgroups but significantly reduced retention for short-duration subgroups [t(13) = 0.362, P = 0.72; t(8) = 4.53, P = 0.0038; t(7) = 3.36, P = 0.024 for AL versus GL, AL versus AS, and GL versus AS, respectively; 2-tailed t tests]. Correspondingly, the time constants we found supported the notion that training duration significantly increases retention, whereas exposure rate has little effect [t(13) = 0.563, P = 0.58; t(8) = 2.72, P = 0.017; t(7) = 2.72, P = 0.013 for AL versus GL, AL versus AS, and GL versus AS, respectively; 2-tailed t tests]. Taken together, these results mirror the findings of the normalization-based retention analysis. That is, we found retention to be almost equal for abrupt and gradual exposure rates when both the training duration and the final learning levels were controlled for. In contrast, long-duration training led to greater retention compared with short-duration training when both the exposure rate and final learning levels were controlled for. Thus the finding that long- and short-duration training led to different amounts of retention but that gradual and abrupt exposure rates resulted in essentially identical retention held for both pFF and vFF adaptations and for both methods of controlling the final learning level.

A multirate model of motor learning predicts the experimental findings.

We next attempted to determine whether a computational model of motor adaptation could explain the pattern of results we observed. In particular, to explain why training duration might have a far greater effect on retention than exposure rate, we examined a model in which the interaction between two adaptive processes with different timescales underlies motor adaptation (Joiner and Smith 2008; Sing and Smith 2010; Smith et al. 2006). In this model, a fast learning process quickly reacts to error but has poor retention, whereas a slow learning process reacts slowly to error but has strong retention. There is clear evidence that the slow process is what primarily leads to both short- and long-term retention, since fast-process adaptation decays quite rapidly (Joiner and Smith 2008; Sing et al. 2009b). Therefore, we hypothesized that the similarities and differences between slow-process adaptation for abrupt versus gradual exposure rates and for long- versus short-duration training would explain the pattern of retention we observed experimentally.

We began by estimating the parameters of this model for pFF and vFF adaptation in the current data set. We then ran simulations of different training durations and different exposure rates to determine whether the differences in final adaptation levels for slow-process learning might explain our experimental findings. We estimated the parameters of the model separately for the experiment 1 (pFF adaptation) and experiment 2 (vFF adaptation) data. In both cases, we used only the training period data from all three training schedules (AS, AL, and GL) so that the fitting procedure had no access to the retention period data. Thus both the pFF- and vFF-based models make unfettered predictions for retention for all training schedules, leading to a total of six predictions for retention data to which the models were not fit. For the pFF data in experiment 1, the estimated model parameters were A_s = 0.9886, B_s = 0.0199, A_f = 0.8337, and B_f = 0.2825. For the vFF data in experiment 2, the estimated model parameters were A_s = 0.9919, B_s = 0.0287, A_f = 0.7905, and B_f = 0.2322. The model simulations for slow process, fast process, and overall adaptation, based on both the pFF and vFF parameter estimates, are shown in Fig. 3, A–C, for the three training schedules.

We first sought to determine whether the simulations of the two-state model presented in Fig. 3, A–C, could predict the experimentally observed pattern of retention for the training schedules we studied, to assess the validity of this model. Because the model parameters were estimated using only the training period data, the models make specific predictions for retention for the three vFF and three pFF training conditions: AL, GL, and AS. More specifically, we compared the experimental data and model predictions for the early- and late-period retention as defined in Fig. 2, G and J, for all three training schedules in pFF and vFF environments. This comparison is shown for both the pFF (Fig. 3D) and vFF (Fig. 3E) data sets. We found that both the pFF- and vFF-based versions of the model predict marked differences in retention between long- and short-duration training, but only subtle differences in retention between abrupt versus gradual training. Specifically, we found that the models predict that the difference in early normalized retention between long- and short-duration training is severalfold larger than the difference between abrupt and gradual training [pFF: 57 ± 3.66%, 55 ± 2.84%, and 38 ± 2.27% for AL, GL, and AS, respectively; t(26) = 3.08, P = 0.0048 for AL versus AS; t(26) = 4.68, P = 5 × 10⁻⁵ for GL versus AS; t(26) = 0.43, P = 0.67 for AL versus GL; vFF: 61 ± 3.6%, 56 ± 2.9%, and 27 ± 2.7% for AL, GL, and AS, respectively; t(14) = 7.57, P = 1 × 10⁻⁵ for AL versus AS; t(14) = 7.32, P = 4 × 10⁻⁴ for GL versus AS; t(14) = −1.08, P = 0.2975 for AL versus GL]. We found that the stronger effect of training duration compared with exposure rate predicted by the models during the early period was also maintained during the late period [pFF: 27 ± 5.65%, 24 ± 4.13%, and 9 ± 1.45% for AL, GL, and AS, respectively; t(26) = −4.41, P = 2 × 10⁻⁴ for AL versus AS; t(26) = 3.43, P = 0.002 for GL versus AS; t(26) = 0.43, P = 0.67 for AL versus GL; vFF: 40 ± 6.87%, 35 ± 5.32%, and 13 ± 2.03% for AL, GL, and AS, respectively; t(14) = 3.77, P = 0.0021 for AL versus AS; t(14) = 3.86, P = 0.0007 for GL versus AS; t(14) = −0.58, P = 0.575 for AL versus GL]. These predictions echo our primary experimental finding that short-duration training leads to substantially reduced retention compared with long-duration training but that gradual and abrupt training lead to essentially identical retention levels. Thus the two-rate models of pFF and vFF adaptation both successfully predict the pattern of retention seen in the experimental data.

Differences in the amount of slow-process learning accrued during training predict the effects of exposure rate and training duration on retention.

The construction of a quantitative model allows for analysis of the internal dynamics that account for learning phenomena. In particular, analysis of the multirate model that we simulated allows us to go beyond the relationship between the experimentally observed learning and forgetting curves and examine the slow and fast adaptive processes that underlie the adaptive response. Thus we examined, in the model, how the exposure rate and training duration determine the extent to which the slow and fast learning processes contribute to the final adaptation accrued before retention was tested for the training schedules we studied. Examination of the modeling results for the AL and GL training schedules reveals that although these schedules lead to learning curves during the training period that have markedly different shapes, they still result in very similar levels of final adaptation not only for overall learning but also for the fast and slow processes, as well. Specifically, overall adaptation was within 4% for GL and AL schedules in both pFF- and vFF-based simulations (pFF-based simulations: 0.76 and 0.75 for AL and GL; vFF-based simulations: 0.81 and 0.78 for AL and GL). Similarly, slow-process adaptation was within 12% in both pFF- and vFF-based simulations, and fast-process adaptation was within 13%. Correspondingly, as reported above, these simulations predicted very similar retention levels for AL and GL training for both types of FFs in both the early and late retention periods (Fig. 3, D and E). The similarity between the retention levels observed, both early and late, with AL and GL training results from the similarity between the amount of slow-process adaptation accrued by the end of the training, because the modeling shows little persistence of fast-process adaptation in the retention period.

The critical importance of the amount of slow-process learning at the end of the training period is also supported by comparison of the modeling results for the AS and AL training schedules (Fig. 3, A and C). Although the simulations for AS and AL learning led to similar overall adaptation levels by the end of the training period, the way that this overall adaptation was composed, in terms of slow- and fast-process contributions, was very different. With the use of both sets of parameters (pFF and vFF data), the slow-process level at the end of the training period in the AL training schedule was nearly three times as large as in the AS schedule. In contrast, the fast-process level at the end of the training period in the AS training schedule was 50–100% higher than that in the AL schedule. In accordance with the difference in slow-process levels at the end of the training period, short-duration training (AS) consistently led to decreased retention, both early and late, compared with long-duration training (AL), despite higher fast-process learning for AS during the training period (Fig. 3, D and E). In summary, our modeling results show very similar levels of slow-process adaptation for gradual and abrupt long-duration training (GL and AL) resulting in similar levels of retention, whereas short-duration training leads to markedly reduced levels of slow-process adaptation resulting in reduced levels of retention. Taken together, these observations provide a possible mechanistic explanation for why the retention of adaptation is improved for long-duration training versus short-duration training but largely unaffected by exposure rate.

We next used the two-state model to simulate adaptation in gradual and abrupt training schedules over a large span of training durations to gauge the effects of exposure rate at different training durations. In particular, we used the two-state model to analyze the fraction of learning that results from the slow process (i.e., slow-process contribution) not only for our own experimental conditions but also for every possible training duration between 1 and 5,000 trials (see methods). We compared abrupt training with logarithmically ramped gradual training (employed in the current study) and linearly ramped gradual training. Note that both gradual training paradigms incorporated 15-trial hold periods at the full perturbation level at the end of the training period, because hold periods are used in both the current experiments and a vast majority of gradual training studies we are aware of (Criscimagna-Hemminger et al. 2010; Gibo et al. 2013; Huang and Shadmehr 2009; Joiner et al. 2013; Klassen et al. 2005; Kluzik et al. 2008; Malfait and Ostry 2004; Wang et al. 2011; Wong and Shelhamer 2011). Figure 3 shows the results of these simulations for the parameters derived both from our pFF data (Fig. 3F) and from our vFF data (Fig. 3G). To facilitate comparisons between different cases, the results shown in Fig. 3 express final slow-process adaptation as a fraction of that achieved on the 5,000th abrupt training trial, where this adaptation was maximal. Note that because the gradual conditions included hold periods, these conditions are plotted from 16th trial point onward, whereas the abrupt condition is plotted from the 1st trial point. Simulations of the abrupt condition from the 1st to 14th trial point can thus be interpreted as abrupt-short conditions with fewer training trials than the abrupt-short condition we experimentally tested (15 trials).

These simulations reveal that slow-process contribution is substantially more sensitive to training duration than exposure rate. Note that we used logarithmic scaling for the trial number axis of these plots, and the sigmoidal shape present is because of this scaling; i.e., on a linearly scaled representation, the slope of the plotted relationship is instead monotonically decreasing. Also note that the black arrows illustrate the effects of training duration (AS versus AL) and exposure rate (AL versus GL). Both pFF- and vFF-based modeling predict a strong effect of training duration but a weak effect of exposure rate, echoing our experimental findings (note the difference in black arrow sizes; pFF-based modeling led to differences of 183.7% and 12.6% in slow-process contribution for AS versus AL and AL versus GL conditions, respectively, whereas vFF-based modeling led to differences of 138.8% and 8.9%). When any two training schedules are compared, the effect of training duration will clearly depend on the specific number of training trials chosen for long- and short-duration training. However, over the entire range of training trials, the simulations predict an ~86% improvement in slow-process contribution. In contrast, exposure rate leads to a substantially smaller maximal improvement of ~19% in slow-process contribution, and this effect declines with further training trials (pFF-based: <10% slow-process contribution is found after 328 trials for both logarithmic and linear conditions; vFF-based: <10% slow-process contribution is found after 224 trials for both logarithmic and linear conditions).

Interestingly, the simulations predict that the sudden condition consistently leads to greater slow-process contribution compared with either gradual condition, suggesting that gradual training might lead to lower retention compared with abrupt training. Therefore, the two-state model predicts that differences in exposure rates, and accordingly error size, cannot provide an explanation for studies reporting retention advantages for gradual training (Huang and Shadmehr 2009; Klassen et al. 2005). The discrepancy between gradual and abrupt exposure rates may arise because with abrupt exposure rates, the perturbation is at full level for the entirety of the training period, whereas gradual training only leads to complete exposure of the perturbation toward the end of training. However, the effect is small because gradual training schedules include a number of trials at the end of training during which the perturbation is at full strength. In summary, although our simulation results should not be expected to fully account for how retention can be predicted under all training schedules, we find that a simple, if imperfect, model can capture the essence of our experimental findings. The discrepancy between the AS versus AL and AL versus GL conditions found in our simulations, as well as the results from experiments 1 and 2, provide demonstrable evidence that error size has little impact on retention.

As detailed in methods, the parameters for the two-state learning model we used in the simulations were obtained by simultaneously fitting the learning curves of the mean data for all three experiments (AL, GL, and AS). However, the modeling results presented in Fig. 3 were not dependent on the details of this fitting procedure. We obtained very similar simulation results when we instead determined the model parameters from fitting our data sets individually or from averaging the parameters obtained from individual data set fits. In particular, we compared the results from obtaining model parameters from fitting the AL data alone, from fitting the GL data alone, and from averaging the parameters from these two individual fits (we did not use parameters obtained from fitting AS alone because the short time course of the AS learning curves does not allow the slow-process coefficients to be determined with sufficient confidence). In both cases we obtained results that were qualitatively similar to the results obtained when all data sets were used. After fitting the model onto the data from the AL group alone, we found that training duration has a marked impact on slow-process contribution and that exposure rate has little impact (pFF-based: slow-process contributions of 98.5%, 89.3%, and 40% for AL, GL, and AS, respectively; vFF-based: slow-process contributions of 91.6%, 80.4%, and 29.2% for AL, GL, and AS, respectively). Fitting the model onto the data from the GL group alone led to a similar pattern of results (pFF-based: slow-process contributions of 94.3%, 85.8%, and 35.8% for AL, GL, and AS, respectively; vFF-based: slow-process contributions of 98.4%, 91.4%, and 44% for AL, GL, and AS, respectively). Last, we still found that training duration has a much larger effect on slow-process contribution compared with exposure rate when the parameters obtained from fitting the AL data alone and the parameters obtained from fitting GL data alone were averaged (pFF-based: slow-process contributions of 96.9%, 88.1%, and 37.3% for AL, GL, and AS, respectively; vFF-based: slow-process contributions of 96.3%, 87.4%, and 37.1% for AL, GL, and AS, respectively). For both the pFF- and vFF-based simulations, the training duration led to an increase in slow-process contribution of >87%, whereas the exposure rate only led to an increase of <17% across all training durations.

DISCUSSION

In the current study we compared the retention of motor adaptation for different training durations and exposure rates and examined these effects for two different types of force-field (FF) perturbations. The rationale for examining two different FF perturbations was to assess the generality of our findings. That is, we wanted to see if there were consistent effects of training duration and exposure rate for different types of physical dynamics. When we controlled for both the final amount of adaptation achieved during training and the duration of the training period, we found that gradual and abrupt training led to essentially identical retention. This held for both position-dependent and velocity-dependent FF adaptation (pFF and vFF, respectively) and for two different methods of controlling the final adaptation: 1) normalizing the raw retention data by the amount of final learning and 2) subsetting the experimental groups so that final adaptation levels could be matched within 1%. In contrast, we found that training duration had a profound effect on retention. This also held for both pFF and vFF adaptation and for the two different methods of controlling the final adaptation.

We then performed a secondary analysis and examined a two-state model of motor adaptation to understand why the retention of motor learning is more strongly influenced by training duration rather than exposure rate or error size. The model was fit only to the adaptation period data and therefore was used to predict retention. Although we cannot use this model to precisely predict retention for all possible training schedules, we considered that the model might provide insight into our results given that it has been used previously to explain long-term retention behavior in a FF adaptation paradigm (Joiner and Smith 2008). We found that slow-process learning, which predicts retention because fast-process learning rapidly decays away, was highly sensitive to training duration but only mildly sensitive to exposure rate (training duration led to a >85% increase in slow-process learning for the abrupt condition and for both types of gradual conditions studied, whereas exposure rate led to a <20% increase). This echoes our experimental results suggesting that the effects of training duration and exposure rate can be explained by a simple two-rate model of adaptation. Thus we find little evidence for improvements in retention associated with gradual training compared with abrupt, yet we find that retention of adaptation can be dramatically improved if training duration is increased.

Previous work examining the effects of the training schedule on motor learning.

A number of previous studies have compared the retention following gradual and abrupt training (Criscimagna-Hemminger et al. 2010; Huang and Shadmehr 2009; Ingram et al. 2000; Kagerer et al. 1997; Klassen et al. 2005; Kluzik et al. 2008; Michel et al. 2007; Wong and Shelhamer 2011), and two of these used the same FF adaptation paradigm that we employed (Huang and Shadmehr 2009; Klassen et al. 2005). Both these studies were also based on point-to-point reaching movements perturbed by velocity-dependent curl FFs like the vFF we used in experiment 2. Given these similarities, it may seem surprising that our findings are at odds with those of these previous studies. In particular, both studies reported that a gradual training schedule (with linear ramping) leads to increased retention compared with an abrupt schedule, whereas we found no advantage. Unfortunately, there are methodological and analytical issues with both previous studies that call their claims into question. Both studies attempted to experimentally match the level of learning achieved in each training schedule, but they did so by increasing the training duration for the gradual training groups. This training duration mismatch would lead to greater retention for the gradual groups even if gradual training per se had no effect, suggesting that the findings resulted from a conflation of exposure rate and training duration.

In the Huang and Shadmehr (2009) study, gradual training was more than twice as long as abrupt training (50 versus 20 trials). This is in line with the idea that the experimental finding was due to a mismatch in training duration rather than a difference in exposure rate. In addition, the simulations we represent in Fig. 3, F and G, may provide an explanation for this finding. Specifically, the simulations based on our vFF data predict that a gradual group with 50 training trials would lead to slow-process contribution that is 28.5% higher compared with an abrupt group with 20 training trials (48.4% and 62.2% predicted slow-process contribution for abrupt and gradual training, respectively). This suggests that the data from the Huang and Shadmehr study are in agreement with our own results.

One experimental condition in the Huang and Shadmehr (2009) study (abrupt exposure for 50 training trials) provided a control for training duration. However, inspection of the data suggests that the duration-matched gradual and abrupt training groups displayed similar levels of retention, and, oddly, the authors failed to test whether a significant difference was present between the amount of retention that was observed in these groups. Instead, the authors reported a significant interaction between the effects of training schedule and epoch and argued that the gradual training schedule thus led to a slower rate of decay. Unfortunately, the authors failed to account for differences in final adaptation between the two training schedules, and the effect was relatively weak (P = 0.039). Therefore, because gradual training, as expected, led to lower final adaptation, a significant interaction is exactly what should be expected with nonnormalized retention data if both groups displayed the same relative exponential decay, because lower adaptation would lead to less decay. Thus the findings are entirely consistent with identical normalized decay and retention for gradual and abrupt groups, underscoring the importance of the normalization we used when examining retention.

Klassen et al. (2005) also compared abrupt and gradual training, but in this study the authors examined long-term retention after 24 h. In particular, the authors used a vFF task where participants were instructed to move toward one of eight potential targets. To control for the final level of adaptation, the duration of gradual training was made greater than that for abrupt training (280 versus 240 total trials), and retention on day 2 was greater for the gradual condition. Thus this increased retention might be due to an increased training duration rather than the gradual nature of the training (e.g., smaller error sizes). It also should be noted that the authors assessed retention by averaging the amount of relearning during the second and third blocks on day 2. This retention metric conflates true retention, the memory that would remain at the beginning of the second day, with savings, which depends on the rate of relearning during the day 2 training. In addition, the authors performed a second experiment based on visuomotor rotation (VMR) learning and found no effect of gradual versus abrupt training.

In summary, neither Huang and Shadmehr (2009) nor Klassen et al. (2005) simultaneously controlled the training duration and level of final adaptation before measuring retention. In the former study, the gradual training condition in the main experiment included more than double the amount of training than the abrupt condition, and when the amount of training was matched in the control experiment, retention levels were not directly compared across conditions, and differences in final learning arose but were not accounted for. In the latter study, only one of the two experiments was in line with the idea that gradual training leads to improved retention, and in that experiment, training duration was greater for gradual training and retention was not assessed independently of savings. Other studies investigating how abrupt versus gradual training affects retention matched the training duration but unfortunately left the amount of learning uncontrolled (Ingram et al. 2000; Kagerer et al. 1997; Michel et al. 2007). These studies analyzed raw retention instead of retention relative to the amount of learning, which the normalization procedure we used determines. In addition to normalizing retention, we also matched adaptation levels between abrupt and gradual training groups to within 1% and consistently found no significant difference in retention levels.

Effects of awareness and strategization associated with gradual versus abrupt training.

One of the ideas that has motivated the proposition that gradual training may be advantageous compared with abrupt training is that the gradual introduction of a perturbation can lead to small errors that escape conscious detection. Thus participants would adapt while unaware that a perturbation has been levied (Michel et al. 2007; Taylor et al. 2011; Wang et al. 2011). A lack of awareness precludes explicit strategization, and thus a number of studies have suggested that gradual training favors more “natural” learning, meaning more predominantly implicit learning, which might promote increased aftereffects and improved retention (Hatada et al. 2006; Michel et al. 2007; Wong and Shelhamer 2011). This line of thought seems quite reasonable, and there is other evidence, independent of training schedule manipulations, demonstrating that increased implicit and decreased strategic learning can lead to stronger aftereffects and improved retention (Fernández-Ruiz et al. 2000; Richter et al. 2002; Weiner et al. 1983). However, this general argument depends on the assumption that strategic learning can act as a substitute for implicit learning in improving motor performance so that lower levels of implicit learning are called for. Clearly, the extent to which explicit strategies can effectively substitute for implicit adaptation varies widely from one motor task to another. For visuomotor learning, including VMR and saccade adaptation, explicit strategies can be very effective in substituting for implicit learning (in terms of performance) because high levels of both directional and end-point accuracy can be obtained by strategically choosing an aim point that is displaced from the target location (Herman et al. 2009; Mazzoni and Krakauer 2006; Taylor et al. 2014). However, effective adaptation to a FF requires the production of a novel motion-dependent force pattern, which must be learned incrementally. Accordingly, several studies that attempted to associate the learning of different FFs with distinct cognitive cues have failed to yield substantial cue-dependent adaptation. In contrast, motor cues such as motion direction, limb position, and even the geometry of a preceding motion or of the motion of another limb can readily elicit robust cue-dependent adaptation (Gupta and Ashe 2007; Howard et al. 2012, 2013; Nozaki et al. 2006; Yokoi et al. 2011). Thus the available evidence suggests that FF learning is unlikely to be amenable to cognitive strategization. Therefore, the increased awareness associated with sudden rather than gradual FF training may not promote increased strategy. Correspondingly, we find little effect of gradual versus abrupt training when final adaptation is controlled. In summary, our results suggest that training schedules that inhibit the awareness of a perturbation do not generally lead to improved retention compared with training schedules that elicit greater conscious awareness.

Effects of gradual and abrupt training on cerebellum-dependent motor adaptation.

A key difference between gradual and abrupt exposure rates is that they may lead to differences in credit assignment for errors. The idea is that gradual training results in small errors that would likely be assigned as due to self-generated rather than environmental changes. However, abrupt training results in large errors that would likely be assigned to environmental rather than endogenous causes (Berniker and Kording 2008; Schlerf et al. 2013). Accordingly, several studies have suggested that the difference in error sizes between gradual and abrupt training lead to differences in credit assignment and engage distinct neural mechanisms (Berniker and Kording 2008; Boyden et al. 2006; Criscimagna-Hemminger et al. 2010; Robertson and Miall 1999). The cerebellum is widely believed to be critical for error-driven motor learning, including FF adaptation (Diedrichsen et al. 2005; Maschke et al. 2004; Smith and Shadmehr 2005), and error size selectivity in cerebellar plasticity has been reported. The error signals that drive learning in the cerebellum are thought to be encoded by complex spikes, which drive neural plasticity in the form of long-term depression (LTD) (Boyden et al. 2006; Kitazawa et al. 1998). Interestingly, Soetedjo et al. (2008) found that complex spike probability was higher for small compared with large error sizes in saccade adaptation, suggesting that the cerebellum may be primarily responsible for learning from the small errors that arise from endogenous sources. However, Boyden et al. (2006) found that retention of vestibuloocular reflex adaptation was only dependent on cerebellar LTD when large error sizes were administered. Thus the details of error size selectivity in the cerebellum remain controversial.

Recently, Criscimagna-Hemminger et al. (2010) reported that gradual training led to greater FF adaptation and retention in patients with cerebellar degenerations, compared with abrupt training. This might suggest that cerebellum-independent learning mechanisms are responsible for learning from small errors, which would imply that the cerebellum is specifically tuned to learning from large error signals. However, a subsequent study from the same authors pointed out that the experimental design conflated exposure rate with FF direction (CW versus CCW), found that cerebellar patients were biased for improved adaptation in CCW versus CW FFs, and demonstrated that there was little effect of gradual versus abrupt training in an experimental design that balanced out FF direction in examining exposure rate (Gibo et al. 2013). This latter finding is in agreement with another recent study that reported no difference between gradual and abrupt VMR adaptation in patients with cerebellar degeneration (Schlerf et al. 2013). Together, these findings suggest that the distinction between large and small errors may not be critical for understanding how motor adaptation depends on cerebellar function.

However, recent work has suggested that the retention of motor memories is critically dependent on the cerebellum. Motor adaptation can be partitioned into a component that is temporally labile with a time constant of ~20 s and a temporally stable component that persists for much longer; these components map onto fast and slow learning processes for FF adaptation, respectively (Sing et al. 2009b). A recent reanalysis of several studies examining FF adaptation deficits in individuals with cerebellar degeneration suggests that temporally stable slow-process learning is specifically impaired by cerebellar damage (Hadjiosif et al. 2014). Taken together with the current findings, this suggests that the increased retention due to improvements in slow-process learning that accrue from prolonged training durations are critically dependent on cerebellar function. This is somewhat at odds with the idea that the cerebellum may specifically contribute to the rate of motor adaptation rather than the retention of it, based on the effect of cerebellar transcranial direct current stimulation (tDCS) on VMR learning (Galea et al. 2011). However, a recent attempt to replicate this result by the same author failed to find any consistent effects of cerebellar tDCS (Jalali et al. 2017). Moreover, it has been shown that inhibitory (cathodal) stimulation of the cerebellum during FF learning using tDCS impairs both the initial learning rate and 24-h retention (Herzfeld et al. 2014).

Error augmentation.

Given that error signals are known to drive motor adaptation, several recent studies have sought to promote increases in motor adaptation by increasing the size of error signals. These studies have been motivated by the possibility of increasing the rate of motor adaptation to facilitate rehabilitation following neurological insults, and the idea has been termed error augmentation. Interestingly, training with larger errors via error augmentation is, at its essence, opposite the idea of gradual training, which introduces a perturbation incrementally to avoid large errors during training. Several error augmentation studies have reported modest to large increases in the rate of adaptation (Emken and Reinkensmeyer 2005; Rozario et al. 2009; Patton et al. 2006; Wei et al. 2005). However, significant increases even in raw retention levels have not been observed (Wei et al. 2005). The current findings suggest that improved adaptation levels observed in these error augmentation paradigms might be harnessed to improve retention if increased training durations were incorporated.

GRANTS

This work was supported by National Institutes of Health (NIH) Grant EY021252 (to W. M. Joiner), National Science Foundation Grant 1553895 (to W. M. Joiner), and NIH Grant R01 AG041878 (to M. A. Smith).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

L.A., E.A.H., M.A.S., and W.M.J. conceived and designed research; L.A. and K.P.N. performed experiments; L.A., E.A.H., M.A.S., and W.M.J. analyzed data; L.A., M.A.S., and W.M.J. interpreted results of experiments; L.A. prepared figures; L.A. drafted manuscript; L.A., M.A.S., and W.M.J. edited and revised manuscript; L.A., M.A.S., and W.M.J. approved final version of manuscript.