Role of paroxysmal depolarization in focal seizure activity

Abstract

We analyze the role of inhibition in sustaining focal epileptic seizure activity. We review ongoing seizure activity at the mesoscopic scale that can be observed with microelectrode arrays as well as at the macroscale of standard clinical EEG. We provide clinical, experimental, and modeling data to support the hypothesis that paroxysmal depolarization (PD) is a critical component of the ictal machinery. We present dual-patch recordings in cortical cultures showing reduced synaptic transmission associated with presynaptic occurrence of PD, and we find that the PD threshold is cell size related. We further find evidence that optically evoked PD activity in parvalbumin neurons can promote propagation of neuronal excitation in neocortical networks in vitro. Spike sorting results from microelectrode array measurements around ictal wave propagation in human focal seizures demonstrate a strong increase in putative inhibitory firing with an approaching excitatory wave, followed by a sudden reduction of firing at passage. At the macroscopic level, we summarize evidence that this excitatory ictal wave activity is strongly correlated with oscillatory activity across a centimeter-sized cortical network. We summarize Wilson–Cowan-type modeling showing how inhibitory function is crucial for this behavior. Our findings motivated us to develop a network motif of neurons in silico, governed by a reduced version of the Hodgkin–Huxley formalism, to show how feedforward, feedback, PD, and local failure of inhibition contribute to observed dynamics across network scales. The presented multidisciplinary evidence suggests that the PD not only is a cellular marker or epiphenomenon but actively contributes to seizure activity.

NEW & NOTEWORTHY We present mechanisms of ongoing focal seizures across meso- and macroscales of microelectrode array and standard clinical recordings, respectively. We find modeling, experimental, and clinical evidence for a dual role of inhibition across these scales: local failure of inhibition allows propagation of a mesoscopic ictal wave, whereas inhibition elsewhere remains intact and sustains macroscopic oscillatory activity. We present evidence for paroxysmal depolarization as a mechanism behind this dual role of inhibition in shaping ictal activity.

INTRODUCTION

In clinical recordings of focal seizure activity it is common to observe a sequence of events with an initiation phase that gradually evolves into synchronized, sustained high-amplitude oscillatory activity. This activity then eventually terminates, usually abruptly, marking the end of the electrographic seizure. Here our principal focus is on the component of the seizure activity where oscillatory electrical activity is sustained, specifically on the two properties, hyperexcitation and hypersynchrony, that are often employed to characterize this type of activity (e.g., Fisher et al. 2005). In this context, “hyperexcitation” refers to excessive neural activity associated with large deflections in the EEG signal and high neuronal firing rates, whereas “hypersynchrony” refers to synchronous activity across neural populations, resulting in high-amplitude fluctuations in the EEG as well as synchrony across multiple signals. These properties seem somewhat contradictory since “hyperexcitation” indicates that the imbalance between excitation (E) and inhibition (I) is in favor of E (Fig. 1A), whereas the term “hypersynchrony” is typically used to describe the large-amplitude fluctuations observed in EEG recordings and suggests that the balance alternates between dominant E and I effects (Fig. 1B).

Fig. 1.

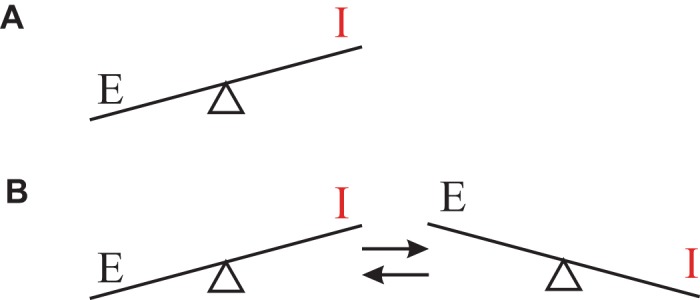
Simplified representation of 2 (seemingly contradictory) roles of excitatory (E) and inhibitory (I) activity ascribed to clinical seizure activity (e.g., Fisher et al. 2005). A: hyperexcitation is a disturbed balance in favor of excitation. B: hypersynchronous oscillation that is often characteristic for clinical recording of ongoing seizures requires back and forth switches between dominant excitation and inhibition.

Recent studies describing key observations at a microelectrode array scale and associated cortical activity at a macroscopic scale have provided compelling evidence and a possible explanation for the simultaneous presence of both hyperexcitation and hypersynchrony during human focal seizure activity (Eissa et al. 2017; Schevon et al. 2012). The advantage of recording at this scale is that, in contrast with the standard clinical recording, the action potential activity generated by a small population of (individual) neurons can be recorded. Schevon et al. (2012) showed how, at the mesoscopic scale of the microelectrode array, an ictal wave front of hyperexcitation that borders an ictal core area propagates slowly (at ~1 mm/s), thereby recruiting the surrounding penumbra into the ictal core. The next surprising finding by Eissa et al. (2017) showed how this millimeter-sized mesoscopic process of the propagating wave of hyperexcitation affected a much larger centimeter-sized oscillating macroscopic cortical network. These observations provided evidence that during a seizure a small mesoscopic ictal wave front perturbs a larger macroscopic network and that this larger network responds with a strong, hypersynchronous oscillation seen in clinical measurements of human focal seizure activity. The oscillations propagate at a speed that is orders of magnitude higher than the speed of the ictal wave (Liou et al. 2017; Smith et al. 2016). Here, it is of interest to note that the slowly propagating ictal wave, and not the faster-propagating oscillation, is consistent with the speed of the clinically observed Jacksonian march first described by Hughlings Jackson in 1870 (e.g., Extercatte et al. 2015).

Data analyses of microelectrode arrays and modeling of human focal seizure activity suggest that neural excitation dominates at a local millimeter-sized mesoscale network and inhibition fails to restrain it (Meijer et al. 2015; Schevon et al. 2012; Trevelyan et al. 2006). In contrast, we propose that excitation and inhibition coexist in the centimeter-sized macroscale network to produce oscillatory activity in response to the perturbation provided by the ictal wave (Eissa et al. 2017, 2018). Thus inhibition plays a dual role, both permitting seizure expansion by its failure and shaping cortical activity at distant locations (Eissa et al. 2017; Liou et al. 2018; Wenzel et al. 2017). The above findings demonstrate that multiple spatial scales should be considered simultaneously to more fully understand focal seizure activity (Eissa et al. 2017; Schevon et al. 2019). In the context of the specific call to which this article responds, it is of interest that modeling components in Eissa et al. (2017, 2018) and Meijer et al. (2015) are based on the Wilson–Cowan (W-C) equations that were introduced almost half a century ago (Wilson and Cowan 1972, 1973). The W-C formalism is capable of representing a plethora of neural behavior ranging from resting state, limit cycles, chaos, to hyperchaos (e.g., Destexhe and Sejnowski 2009; H. R. Wilson, unpublished observations).

The purpose of this article is to explore mechanisms that may be involved in the dual role of inhibition: 1) local failure of inhibitory restraint at the millimeter-sized mesoscale to allow propagation of hyperexcitation and 2) the ability of inhibition at the macroscopic (centimeter) scale to promote hypersynchronous oscillatory activity. We review and present clinical, experimental, and theoretical evidence for the scale-dependent role of inhibition and the resulting dynamics underlying the focal seizure. In this context, we evaluate the role of paroxysmal depolarization (PD) at the level of cell populations as a contributor to the complicated phenomenon of the focal seizure.

METHODS

Terminology

Hyperexcitation and hypersynchrony are typically used to characterize seizure activity (e.g., Fisher et al. 2005). The term “hyperexcitation” refers to excessive neural activity reflected in large deflections in the EEG and/or the high firing rates in neural populations observed during seizures. “Hypersynchrony” refers to synchronous activity across neural populations resulting in high-amplitude compound signals seen in the EEG as well as synchrony across multiple recording channels.

We separate neuronal effects into meso- and macroscales. Mesoscale is the scale captured by the microelectrode array, i.e., a millimeter-sized neural network. Macroscale is the scale seen in clinical EEG records, i.e., centimeter-sized neural networks.

Core, ictal wave, and penumbra are cortical territories with distinct activity patterns observed at a mesoscopic scale during microelectrode array recordings and first defined in Schevon et al. (2012). The ictal wave is a hyperactive front that surrounds the core area and that propagates at a velocity of ~1 mm/s. The front is surrounded by penumbra that is recruited into the core as the wave propagates.

Perturbator and oscillator are macroscopic cortical territories. The perturbator is the functional area formed by core/ictal wave/penumbra activity to which a large oscillator area responds by oscillation. These cortical domains are based on electrocorticogram (ECoG) signals that are time locked with the perturbator activity described by Eissa et al. (2017).

“Paroxysmal depolarization” (PD), “paroxysmal depolarization shift waveform” (PDS), and “depolarization block” (DB) are terms that describe a depolarized state of a neuron during which action potentials cannot be generated. This state has been observed experimentally and can be modeled with the standard Hodgkin–Huxley equations (Hodgkin and Huxley 1952).

E and I represent the excitatory and inhibitory neuronal populations in a network. The dynamics of these populations can be employed to model different types of neuronal network activity as first described by Wilson and Cowan (1972, 1973).

Patient Data

Study participants at Columbia University Medical Center consisted of patients with pharmacoresistant focal epilepsy who underwent chronic ECoG studies to help identify the epileptogenic zone for subsequent removal. Procedures were approved by the internal review board committees at Columbia University Medical Center and The University of Chicago, Comer Children’s Hospital, and written informed consent was obtained before the procedure. Patients were implanted with a 96-channel, 4 × 4-mm microelectrode array (Utah array; Blackrock Microsystems, Salt Lake City, UT) along with subdural electrodes (ECoG). The Utah array recordings, sampled at 30 kHz/channel with a 0.3 Hz to 7.5 kHz band-pass filter and a ±8-mV range, used a skull peg (pedestal) reference selected on the basis of daily assessment of recording quality. The reference for ECoG recording was an epidural upside-down strip placed distant to the coverage area. The two data streams were aligned by a digital pulse-coded signal and seizure recordings were categorized as core or penumbra with previously described methods (Schevon et al. 2012). Single-unit data were obtained from filtered multiunit activity (FIR1, 1,000th order, 300–5,000 Hz) with a template matching technique developed by our group to track units in noisy data undergoing gradual waveshape alterations induced by seizures (Merricks et al. 2019; E. M. Merricks, E. H. Smith, R. G. Emerson, L. M. Bateman, G. M. McKhann, Jr., R. R. Goodman, S. A. Sheth, B. Greger, P. A. House, A. J. Trevelyan, and C. A. Schevon, unpublished observations). Briefly, spikes from the peri-ictal period were extracted from the multiunit activity using a negative threshold of 4 times the median absolute deviation in the signal divided by 0.6745 (Quian Quiroga et al. 2004). Spikes were then compressed in feature space with principal components and clustered with k means (Merricks et al. 2015). Templates from the peri-ictal units were then calculated in order to track units through ictal recruitment. Hoops were defined at voltage inflections and expanded to allow for waveshape changes. The Mahalanobis distance in principal component space of spikes that passed through all hoops was calculated, and those with <1% chance of occurring in a χ² distribution were discarded. Units were subclassified as putative fast-spiking (FS) interneurons versus other cell types, predominantly pyramidal cells, based on the full width at half-maximum of each unit’s mean waveform and the cell-intrinsic mean autocorrelation lag, as per Csicsvari et al. (1998). FS interneurons have been shown to exhibit briefer action potentials due to the fast opening of K⁺ channels creating a strong, brief afterhyperpolarization, whereas the burst firing of pyramidal cells versus the high firing rate of FS interneurons results in a longer mean lag in the cell’s autocorrelation (Merchant et al. 2012). These metrics have previously been shown to correspond to the anticipated network dynamics of their putative cell types in similar neocortical recordings in humans (Peyrache et al. 2012).

Animal Models

All experimental procedures involving animals were reviewed and approved by and were in compliance with the Institutional Animal Care and Use Committee at The University of Chicago.

Embryonic rat hippocampal neurons were isolated and maintained in vitro according to previously published methods (Shelat et al. 2013; Suresh et al. 2016). Briefly, hippocampi from embryonic day 18 Sprague-Dawley fetuses were dissociated into single cells with trypsin (0.25%) and mechanical trituration. Cells were seeded onto polyethylenimine-coated coverslips to record single-cell activity. The seeded neurons were maintained in Neurobasal medium containing B27 supplement and GlutaMAX (all from Life Technologies) in a humidified atmosphere (5% CO₂-95% atmospheric air at 37°C). Cultures were maintained by replacing half of the medium volume with freshly made culture medium every 4–5 days.

The effect of saturation of the parvalbumin interneurons on propagation of activity was examined in neocortical mouse slices. The mice used in these experiments were created as follows: PV-Cre knockin mice that express Cre recombinase in parvalbumin-positive inhibitory neurons (PVn) (B6 PV^cre mice; JAX stock: 017320; B6.129P2-Pvalb^tm1(cre)Arbr/J) were mated with mice that express channelrhodopsin TdTomato fusion protein in the presence of Cre recombination [JAX stock: 012567; Ai27(RCL-hChR2(H134R)/tdT)-D]. Briefly, postnatal day 30 (P30) mice were deeply anesthetized under isoflurane and decapitated, and the brain was quickly removed and placed into ice-cold artificial cerebrospinal fluid (ACSF) containing (mM) 118 NaCl, 25 NaHCO₃, 1 NaH₂PO₄, 1 MgCl₂·6H₂O, 3 KCl, 30 d-glucose, and 1.5 CaCl₂. Neocortical (450 μm) brain slices were made with a Leica VT1000s tissue slicer (Wetzlar, Germany). The slices were incubated for 12 min in oxygenated brain slice recovery solution containing (mM) 93 N-methyl-d-glucamine, 2.5 KCl, 1.2 NaH₂PO₄, 30 NaHCO₃, 20 HEPES, 25 glucose, 5 sodium ascorbate, 2 thiourea, 3 sodium pyruvate, 10 MgSO₄·7H₂O, and 0.5 CaCl₂·2H₂O, pH adjusted to 7.4 with 10 N HCl (https://www.brainslicemethods.com/recipes). Slices were then maintained in oxygenated ACSF at room temperature (22°C) for 1–2 h before use.

Electrophysiology

Electrophysiological recordings were obtained from the coverslips by a whole cell current-clamp technique under the visual guidance of an Axioskop 2 plus microscope (Carl Zeiss, Thornwood, NY) connected to a Nikon CoolSnap HQ2 camera (Nikon, Tokyo, Japan) and imaged with Nikon Imaging Software (NIS Elements AR; Nikon USA). Patch electrode pipettes were fabricated from filamented borosilicate glass capillaries (Warner Instruments, Hamden, CT) with a P-97 micropipette puller (Sutter Instrument, Novato, CA). The electrodes were filled with pipette solution containing (in mM) 140 K gluconate, 10 HEPES, 2 MgCl₂, 4 Na₂ATP, 1 CaCl₂, and 10 EGTA (pH 7.3–7.4) with a resistance between 3 and 5 MΩ. The extracellular ACSF solution contained (in mM) 118 NaCl, 25 NaHCO₃, 1 NaH₂PO₄, 1 MgCl₂·6H₂O, 3 KCl, 30 d-glucose, and 1.5 CaCl₂ bubbled with 95% O₂-5%CO₂ at 31°C. Neuronal activity was recorded with a MultiClamp 700B amplifier (Molecular Devices, Sunnyvale, CA) and digitized and acquired at 25 kHz with a Digidata 1440A interface (Molecular Devices).

Extracellular signals were obtained with an ACSF-filled micropipette on the slice surface. The signals were amplified 10,000 fold, filtered between 0.25 and 1.5 kHz, and integrated with a 50-ms time constant to obtain an index of activity (van Drongelen et al. 2003). Recordings were made from brain slices submerged in a recording chamber (6 mL) and perfused with oxygenated ACSF (31°C; flow rate 17 mL/min). The ACSF was saturated with 95% O₂-5% CO₂, pH = 7.4.

Simulation

To simulate distinct excitatory and inhibitory activity patterns, we used the persistent sodium plus potassium (I_Na,p + I_K) model described by Izhikevich (2007). Briefly, the cell model’s membrane potential V is governed by the following pair of coupled first-order ordinary differential equations (ODEs):

$$\begin{array}{c}C\dot{V}=I_{\text{s}}-g_{\text{L}}\left(V-E_{\text{L}}\right)-g_{\text{Na}}{m}_{\infty }\left(V\right)\left(V-E_{\text{Na}}\right)-g_{\text{K}}n\left(V-E_{\text{K}}\right)\text{ and}\\ \dot{n}=\raisebox{1ex}{$\left[n_{\infty }\left(V\right)-n\right]$}\!\left/ \!\raisebox{-1ex}{${\tau }_n$}\right.\end{array}$$ (1)

In these equations, the dot in $\dot{y}$ denotes the time derivative of y. Furthermore, V is the membrane potential, n is a recovery variable, and I_s is the postsynaptic current. All other symbols are defined in Table 1. This model can be considered to be a simplified two-dimensional version of the Hodgkin–Huxley (H-H) model (using only V and n), where, in addition to the leak current, an inward current activates instantaneously and membrane repolarization is created by an outward current. Using different parameters, this model generates the regular-spiking (RS)/class I or the FS/class II profiles and exhibits the two bifurcations leading to neural firing and paroxysmal saturation, respectively.

Table 1.

Cellular and synaptic parameters in Eqs. 1 and 2 used in simulations in Figs. 5 and 6

Cellular Parameters	Name	Unit	Regular-Spiking Neuron	Fast-Spiking Neuron
C	Membrane capacitance	μF/cm2	1	1
EL	Leak Nernst potential	mV	−80	−78
ENa	Sodium Nernst potential	mV	60	60
EK	Potassium Nernst potential	mV	−90	−90
gL	Leak conductance	mS/cm2	8	8
gNa	Sodium conductance	mS/cm2	20	20
gK	Potassium conductance	mS/cm2	10	10
m∞(V)	Index m equilibrium value		1/{1 + exp[−(20 + V)/15]}	1/{1 + exp[−(20 + V)/15]}
n∞(V)	Index n equilibrium value		1/{1 + exp[−(25 + V)/5]}	1/{1 + exp[−(45 + V)/5]}
τn	Time constant for n update	ms	1	1

Synaptic Parameters	Name	Unit	Excitatory Synapse	Inhibitory Synapse
α	Constant of alpha function	μA	25	−3
β	Constant of alpha function	ms−1	0.3	0.1

V, membrane potential (mV).

To evaluate network effects we modeled synaptic connectivity between the cells with a so-called alpha function, αβte^−βt for t ≥ 0, corresponding to the following pair of coupled first-order ODEs (e.g., van Drongelen 2018):

$$\begin{array}{c}{\dot{I}}_{\text{s}}=z\text{\hspace{0.17em}and}\\ \dot{z}=\alpha \beta x-2\beta z-{\beta }^2{I}_{\text{s}}\end{array}$$ (2)

in which I_s is again the postsynaptic current, x is the presynaptic spike train, z is a variable used to convert the second-order ODE into a pair of first-order ODEs, and α and β are synapse-specific constants, related to the maximal current amplitude and (inverse) time constant, respectively. The sign of α indicates whether the synaptic current is excitatory (positive) or inhibitory (negative). The dots denote the time derivative.

Simulation models were implemented in MATLAB (MathWorks, Natick, MA). The parameters of Eqs. 1 and 2 and their values we used in the simulations are summarized in Table 1.

REVIEW AND RESULTS

To facilitate the description of distinct dynamics across neuronal network scales, we use the terms “core,” “ictal wave,” and “penumbra” as defined in Schevon et al. (2012) for ictal mesoscale dynamics and we introduce the terms “perturbator” and “oscillator” for the macroscale processes associated with hyperexcitation and hypersynchrony, respectively. Here, the mesoscopic (millimeter sized) perturbator is the hyperactive area formed by the core and penumbra separated by the propagating ictal wave. The oscillator is the macroscopic (centimeter sized) network that responds to the perturbator’s activity by generating synchronous oscillations that are time locked with the perturbator’s activity. The oscillator’s behavior during the seizure is different from its interictal activity, and because of its spatial extent as well as its strong correlation with perturbator activity (Eissa et al. 2017, 2018), it is also different from physiological oscillatory brain activity such as alpha or gamma rhythms. In the following, we review seizure-related processes at the meso- and macroscales and present evidence that supports the role of PD in sustained seizure activity.

Mesoscale (Perturbator)

At the mesoscale, ictal hyperactivity is not restrained by inhibitory action and propagates across the network (Schevon et al. 2012). There are several candidate mechanisms that may contribute to combined failed inhibition and hyperexcitation at the ictal wave, including the candidate mechanisms depicted in Fig. 2A.

Fig. 2.

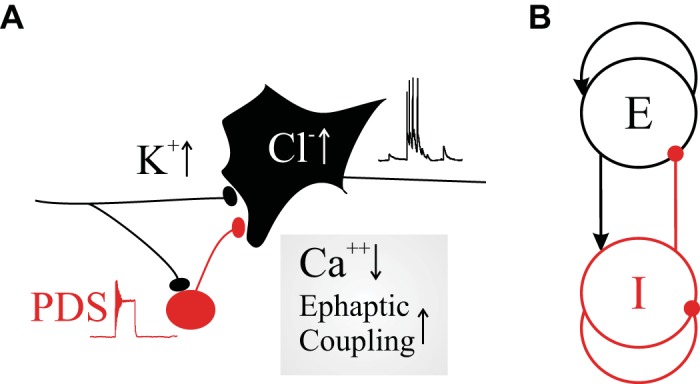
Candidate mechanisms leading to hyperexcitation, failure of inhibition, and hypersynchrony. A: a diagram of an inhibitory cell (red) connected to an excitatory cell (black), both stimulated by external input. Reduced inhibitory efficacy can be caused by saturation of the inhibitory cell leading to paroxysmal depolarization shift (PDS) and increased Cl⁻ concentration in the excitatory neuron. The overall activity of both cells can be increased by increasing K⁺ levels in the extracellular space. The components in the box at bottom right represent that ephaptic effects may increase when synaptic transmission fails because of a low Ca²⁺ concentration. B: a Wilson-Cowan type macroscopic population model that is capable of generating sustained oscillations when inhibitory function is intact. E, excitatory; I, inhibitory.

During excessive neural activity during an ongoing seizure, the extracellular K⁺ concentration may increase, causing further depolarization and resulting in a further increase of excitability. In fact, increased extracellular K⁺ (with and without the GABA_A blocker bicuculline) was introduced as an in vitro seizure model (Rutecki et al. 1985). Obviously, high extracellular K⁺ levels would increase excitability of both inhibitory and excitatory neurons, and it remains to be seen how this would lead to a disturbed balance in favor of the excitatory population. A similar effect would be expected with the 4-aminopyridine seizure model (e.g., Avoli et al. 1996).

A second potential source creating a hyperexcited network is increase of the intracellular Cl⁻ concentration in the excitatory neurons that might occur for various reasons including failure of cation-chloride transporters and/or increased Cl⁻ influx due to GABA_A synaptic activity at high levels of inhibitory cell activity (e.g., Ben-Ari et al. 2012). This change in chloride gradient reduces the hyperpolarizing effect of the GABA_A receptors (Alfonsa et al. 2015), and a few experimental studies have even found evidence for an excitatory effect of the GABA transmitter (e.g., Fujiwara-Tsukamoto et al. 2007). The chloride effect also depends on the ${\text{HCO}}_3^{-}$ gradient across the neural membrane, and the details of this effect were recently modeled by Lombardi et al. (2019). In sum, the above change in the chloride Nernst potential toward more depolarized values is consistent with reduced inhibitory efficacy possibly resulting in a disturbed balance toward excitation (Fig. 1A). Obviously this effect would occur in the inhibitory cells as well, and careful analysis at the network level will be required to assess its possible effects.

A third mechanism leading to excessive excitation or synchrony is a strong rebound of excitatory activity following a sudden synchronized burst of inhibitory action (Chang et al. 2018). This mechanism could therefore play a role, but it requires an additional explanation on how such synchronous inhibitory burst would be evoked.

A fourth possible mechanism was reported in multiple studies using ion-sensitive electrodes in experimental seizure models that showed low local extracellular Ca²⁺ concentrations at or even before seizure onset (e.g., Jefferys and Haas 1982; Pumain et al. 1985). This is rather surprising since these low Ca²⁺ levels impede or even abolish the very synaptic transmission often considered critical for sustaining seizure activity! Therefore propagation via alternative interaction was proposed. And since disabling gap junctions does not prevent seizure activity under low-Ca²⁺ conditions, viable alternative explanations include propagation of excitation via the ephaptic process and/or via diffusion of extracellular K⁺ (Chiang et al. 2018; Dudek et al. 1998; Durand et al. 2010; Jefferys and Haas 1982; Zhang et al. 2016). We emphasize that in this possible ictal mechanism in which Ca²⁺ decreases in combination with ephaptic transmission and/or K⁺ diffusion, there is no distinction between the effects of inhibitory and excitatory population activities!

A fifth candidate mechanism involved in failure of inhibition, and the focus of this article, is associated with the paroxysmal depolarization shift (PDS; Fig. 2). When a neuron is stimulated it initially transitions from its resting potential to action potential firing. This is a well-accepted fact in the neuroscience community, and it is also widely acknowledged that this phenomenon of excitability is governed by a bifurcation in the ion channel dynamics as described by the H-H equations (Hodgkin and Huxley 1952). A less well-known phenomenon is that when stimulus levels are further increased these same H-H equations undergo a second bifurcation that predicts cessation of action potential firing and the neuron’s transition into a fixed, depolarized state. Importantly, this saturation effect is not only a mathematical modeling result of the H-H equations but a phenomenon that can be observed when real neurons are strongly stimulated by either injected or synaptic current. Since the smaller interneurons are most susceptible to this effect, as we will show, this phenomenon may lead to failed inhibition at high levels of activity.

It may be stating the obvious, but to support generation of any network activity, including seizures, neurons must have voltage-sensitive and ligand-sensitive ion channels that support cellular inward and outward currents. Thus, in addition to the possible ictal trigger mechanisms listed above, we must have multiple working ion channels to carry the network activity. For example, important inward currents that are capable of supporting burst activity include the voltage-sensitive persistent sodium current (Suresh et al. 2016; van Drongelen et al. 2006).

In sum, although the candidate mechanisms reviewed above may affect the E-I balance in favor of excitation, they all have different points of action: the K⁺ and/or ephaptic effects act on both excitatory and inhibitory cells, the Cl⁻ effect acts postsynaptically to inhibitory synapse, and the PDS effect acts presynaptically to this synapse. Since these candidate mechanisms may act independently on different processes, there is no reason to assume that they might not occur simultaneously and enhance each other’s effect on creating and sustaining hyperexcitation.

Macroscale (Oscillator)

Macroscopically, the seizure’s electrical activity is commonly dominated by a repetitive bursting pattern. This pattern is well known from clinical recordings that use centimeter-sized electrodes on the scalp or directly on the cortical surface. Eissa et al. (2017) showed that the oscillation in the centimeter-sized seizing network is time locked with the action potential activity in and around the ictal wave. These data suggest that local spiking activity in the millimeter-sized ictal wave front perturbs the neurons in the wider surrounding network. Hence we use the term “perturbator” for the core-wave-penumbra domain to describe its macroscopic effect.¹ Thus, at the macroscopic oscillator level, there is a mechanism such that the oscillator responds to the perturbator’s action by generating oscillations. From a theoretical perspective, the level of hyperexcitability can be explained with a single parameter (dimension) in a deterministic scenario (Fig. 1A). To explain oscillation, however, one needs at least two dimensions (van Drongelen 2018). To account for these two dimensions, a simple assumption is that both E and I functions are present across the larger oscillator network (Fig. 1B).

Thus the processes at work at the mesoscale (i.e., failed inhibition and hyperexcitation) seem far different from those at work at the macroscale (i.e., functional inhibition and hypersynchronous network oscillation). Eissa et al. (2018) demonstrated that the contributions of E and I activity can generate oscillatory, seizurelike activity in a simplified, linearized version of the W-C version of a population model (Fig. 2B) (Wilson and Cowan 1972, 1973). Therefore, we wanted to identify possible mechanisms generating focal seizures that can explain the apparent discrepancy that exists across scales: 1) failure of inhibition within the perturbator and 2) the presence of inhibition to sustain oscillatory activity in the oscillator. With this in mind, we examine in the following section how the PD phenomenon may be behind this duality in inhibitory action.

The Paroxysmal Depolarization Shift

Here we refer to PD as the neuronal saturation effect governed by the dynamics of the ion channels (Fig. 3). The waveforms in Fig. 3 were obtained by simulation of the standard Hodgkin and Huxley dynamics (Hodgkin and Huxley 1952) for two different cell sizes: one related to the size of cortical excitatory neurons (Fig. 3, top) and one to the size of inhibitory cells (Fig. 3, bottom). This simulation predicts that PD effects will be size dependent, i.e., smaller neurons saturate at lower current intensities than larger ones. In the following we do not distinguish whether the neuronal saturation occurs within a particular waveform but instead focus on the postsynaptic consequences of the neuronal saturation itself. Given our interest in the transition from neural firing to a depolarized saturation state during high input levels (associated with cessation of action potential generation), we use the common terminology associated with this phenomenon: i.e., “paroxysmal depolarization” (PD) is a term that describes the saturated depolarization state of the neuron during epileptiform activity, “paroxysmal depolarization shift” (PDS) usually refers to a waveform that includes a significant portion of a saturated state (e.g., Fig. 4, A2 and B2), and “depolarization block” (DB) describes the saturated neuronal state and the “block” refers explicitly to the neuron’s inability to fire action potentials during that state.

Fig. 3.

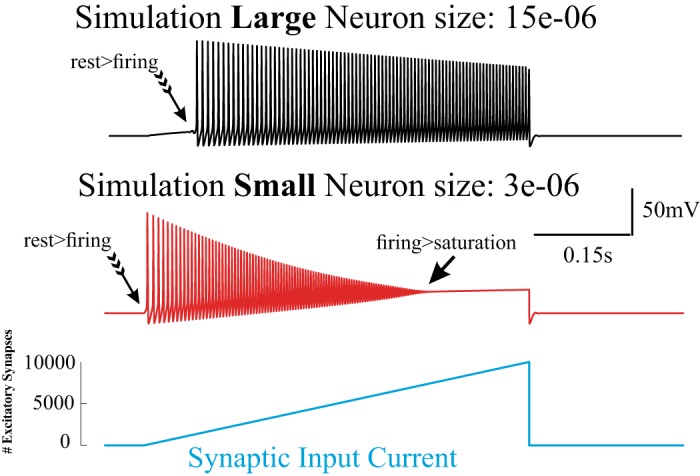
Size effect of the neuronal response to synaptic input simulated with the Hodgkin–Huxley formalism. Two model neurons of different sizes with identical ion channel dynamics show different susceptibility for saturation. The larger neuron (top) starts responding (generating action potentials, rest > firing) at higher input levels than the smaller neuron representing an interneuron (middle). Also, saturation (firing > saturation) occurs at lower levels in the smaller neuron. Note that at the input levels used her, the larger neuron does not reach saturation levels. The synaptic input current for each neuron is plotted at bottom.

Fig. 4.

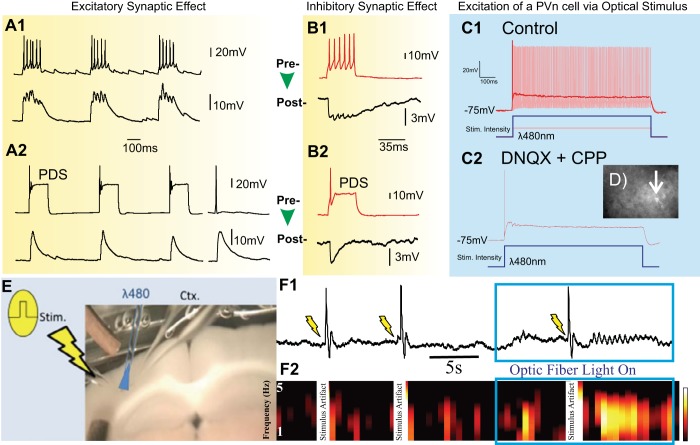
Experimental data gathered in cortical neurons on effects of paroxysmal depolarization on synaptic transmission and propagation. A: dual patch-clamp recording of coupled rat cortical neurons showing the effect of paroxysmal depolarization shift (PDS) on synaptic transmission between 2 excitatory neurons. B: dual patch-clamp recording of coupled rat cortical neurons showing effects between a presynaptic inhibitory cell (red traces) and a postsynaptic excitatory one (black traces). The recordings in A and B show that the postsynaptic output (bottom trace of each pair) and synaptic transmission is reduced when the presynaptic neuron (top trace of each pair) transitions from normal bursting (A1 and B1) to PDS activity (A2 and B2). A2 shows that the postsynaptic effect of PDS (3 bursts on left) is similar to that of a single presynaptic action potential (traces on right). Both the bursts in A1 and B1 were evoked with 20-pA injections; the injections to evoke the PDS in A2 and B2 were 80 pA and 45 pA, respectively. C: saturation effects shown with patch-clamp measurements in a red fluorescence identified parvalbumin-positive (PVn) inhibitory neuron upon optical stimulation in a brain slice from PVn-hChR2 mice ([postnatal day 30). C1: 2 superimposed responses at different light intensities: the lower intensity (150 μW delivered at slice surface) evoked rapid firing (light red) whereas the highest intensity (520 μW delivered at slice surface) resulted in a PDS (red). C2 depicts the same PDS response as in C1 and is obtained upon the same optical stimulation (520 μW) after the neuron was synaptically isolated from network excitation with 6,7-dinitroquinoxaline-2,3-dione (DNQX) and 3-(2-carboxypiperazin-4-yl)propyl-1-phosphonic acid (CPP). This demonstrates that the PDS behavior is an intrinsic property and not evoked via the network. D: image of fluorescent neocortical PVn neuron in brain slice from PVn-hChR2 mice (arrow) with micropipette. E: setup for the optical stimulation of the inhibitory PVn neurons. Electrical stimulation is indicated by the pulse and lightning flash on left; optical stimulation of the PVn neurons at the blue symbol at a wavelength (λ) of 480 nm. The extracellular measurement (Ctx) in the cortex is positioned right from the optical stimulus. F: the first 2 trials show how electrical stimuli alone do not result in propagation at the extracellular recording site: the responses in the integrated extracellular cortical signal (F1) and the associated spectrogram depicting frequencies 1–5 Hz (F2). The large deflections are stimulus artifacts. Interestingly, at the third stimulus given during strong optical activation of the inhibitory population, neural activity does propagate. The intensity of the optical stimulus in F is 520 μW, the same as used in C2. Color scale in F2: −35 to −20 dB/Hz.

PDS in experimental seizures was first observed more than half a century ago (Goldensohn and Purpura 1963; Matsumoto and Marsan 1964). With this discovery, investigators attempted to interpret this finding by primarily investigating the cause of the saturation and how it correlates with discharges in clinical recordings (Moraidis et al. 1991; Segal and Furshpan 1990; Silva-Barrat et al. 2005; Speckmann and Walden 1993; Stiglbauer et al. 2017; Straub et al. 1994; Traub et al. 1993). The main emphasis of research pertaining to the role of PDS activity has been on the relationship between the PDS in the excitatory population and epileptiform discharges in the clinical recordings, such as the interictal spike (Hotka and Kubista 2019). Although PDS activity has been observed in human experimental seizures evoked in resected cortical tissue from patients with epilepsy (e.g., Marcuccilli et al. 2010), clinical interpretation of the PDS has been hampered by the fact that it can only be observed directly in intracellular measurements that are not available in a clinical context. Furthermore, several extracellular studies in humans failed to find evidence of PD (Stead et al. 2010; Truccolo et al. 2011), and only indirect evidence was found in two studies in humans using microelectrode arrays (Ahmed et al. 2014; Merricks et al. 2015). Because of these challenges, the effects of the paroxysmal saturation have been, by necessity, examined only in experimental seizures and theoretical models. In addition to investigating the mechanisms governing PD, we have a strong interest in understanding the consequences of the neural saturation in network dynamics. In the following, we summarize both previously reported and novel findings on paroxysmal saturation mechanisms and effects.

Experimental Data

The concept of failed inhibitory constraint in experimental seizures was published by Wong and Prince (1990) and more recently described by Trevelyan et al. (2006, 2007). These studies clearly show that seizures can propagate after failure of inhibition, but the mechanism(s) underpinning these observations remain poorly understood. Two relatively recent studies demonstrated that propagation of local hyperexcitation due to failed inhibition in both neocortex and archicortex (hippocampus) can be attributed to PDS in the inhibitory component of the cortical network (Cammarota et al. 2013; Ziburkus et al. 2006). Although these studies provide compelling support for the significance and/or role of PDS in propagation of excitatory activity, they also raise a few questions. First, it is unclear how synaptic inhibitory efficacy is reduced during the PDS—specifically, how the PDS in the inhibitory cell affects the inhibitory postsynaptic current evoked in the pyramidal neuron it connects to. Second, the experiments do not explain why saturation would occur primarily in the inhibitory cells. This motivated us to measure the pyramidal cell’s inhibitory postsynaptic signal during PDS activity of the inhibitory neurons and examine the susceptibility of E and I neurons to saturation. Finally, we investigated whether local saturation of the inhibitory population is capable of promoting propagation of neuronal excitation across a mesoscopic network involving multiple synaptically connected neurons.

Our initial findings with respect to the above questions are summarized in Fig. 4. To record synaptic effects, we performed intracellular measurements of connected cell pairs in cultures made from rat hippocampal neurons (10–15 days in vitro): pairs of excitatory cells (n = 5; Fig. 4A) and inhibitory-excitatory cell pairs (n = 2; Fig. 4B). We evoked activity in the presynaptic neuron of each pair by current injection and recorded from the pre- and postsynaptic cells. In both excitatory and inhibitory synapses we observed that burst-related postsynaptic currents consist of compound effects evoked by the series of action potentials in the presynaptic burst (Fig. 4, A1 and B1). However, postsynaptic currents are significantly reduced when the presynaptic neuron is in the PDS mode (Fig. 4, A2 and B2). The right pair of traces in Fig. 4A2 shows the pre- and postsynaptic measurements of a single presynaptic action potential. Comparing the measurements in Fig. 4A, one can see that during a PDS burst evoked postsynaptic currents are on the same order as that evoked by a single action potential rather than a postsynaptic effect similar to one evoked by a presynaptic burst of action potentials. Thus, at high input levels of depolarization, presynaptic bursting transitions into PDS activity and the postsynaptic current is reduced! In addition, our experiments showed a size effect for a transition from bursting to PDS mode. Bursts in Fig. 4, A1 and B1, were evoked with 20-pA injections. The injections to evoke the PDS in Fig. 4, A2 and B2, were 80 pA for the pyramidal cell and 45 pA for the inhibitory neuron. This finding confirms the size effect of the PDS phenomenon, i.e., the predicted simulation result shown in Fig. 3.

Next, we measured the network consequences of the synaptic transmission effects in acute coronal neocortical brain slices made from a P30 mouse that express both excitatory channelrhodopsin and TdTomato fluorescent protein in parvalbumin-positive inhibitory neurons (PVn) (methods). The adult P30 mouse was used to avoid possible depolarizing GABA_A postsynaptic potentials as observed in younger rodents (e.g., Brown et al. 2016; Owens et al. 1996). Using the PVn-hChR2 mouse, we identified PVn cells and selectively excited/activated the TdTomato-labeled PVn neurons by illuminating them with 480-nm (blue) light delivered on the surface of the slice via a fiber-optic cable.

A whole cell patch-clamp recording of a PVn cell was made to examine the required intensities to evoke action potential and PDS activities as a function of illumination (Fig. 4, C1 and D). To demonstrate the intrinsic nature of this effect, we showed that the PDS response sensitivity in the PVn cell did not change after isolation from excitatory synaptic input (Fig. 4C2). Next, we evaluated the network propagation effect of PDS activity across the PVn population by electrically stimulating the neocortex and measuring the effect of the stimulation at a distance of 300 μm while 520-μW, 480-nm illumination in between stimulus and recording electrode was either on or off (Fig. 4E). With the light off, functional inhibition is present, and the electrical stimulus did not result in propagation toward the recording electrode. However, propagation was observed when the light was turned on to depolarize the inhibitory PVn population at the level shown to evoke PDS saturation in the inhibitory cells (Fig. 4F).

Modeling

The goal of our modeling approach is to evaluate the dual role of inhibition at the cellular scale by simulating the activities of a set of neurons with feedback and feedforward motifs, embedded in two distinct seizure territories: one network located inside the perturbator and another one in the much larger oscillator. In the remainder of this section we first describe the role of PD at the single-neuron scale, followed by the details of its effect on network activity.

Excitatory and inhibitory cell properties.

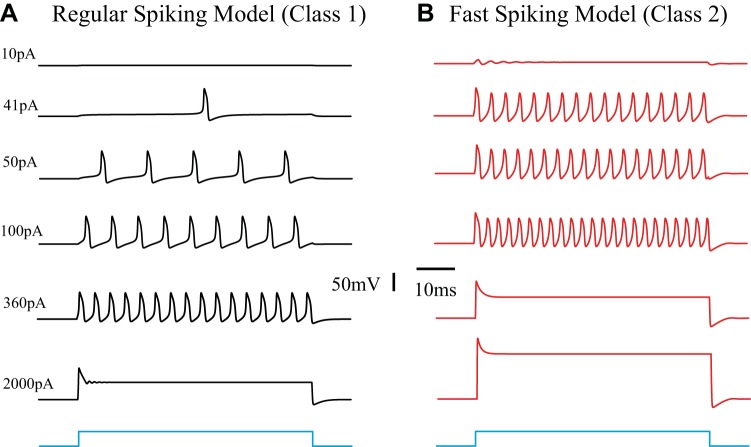
We employed the I_Na,p + I_K model developed by Izhikevich (2007) to simulate the different excitability profiles of cortical E and I neurons (methods). Whereas E neurons commonly show a RS-type response, I cells are mostly characterized as the FS type (e.g., Connors and Gutnick 1990). These two types of neurons not only fire at different rates but also have different input-output relationships. Following the classification by Hodgkin (1948), the inhibitory cells commonly show a class II response characteristic and the excitatory cells show a class I characteristic (Fig. 5).

Fig. 5.

Response characteristics of the regular-spiking (RS) and fast spiking (FS) models. Neuronal response profiles are frequently grouped into 3 classes, as first defined by Hodgkin (1948). The underlying nonlinear dynamics and bifurcations can be described by using different parameter sets in Eq. 1. The parameters used for this figure are summarized in Table 1. A: an excitatory pyramidal cell model of the RS type with Class I properties. B: an inhibitory cell model of the FS type with class II excitability. In addition, it can be seen that saturation at high input levels occurs at a much lower level for the inhibitory cells than for the larger pyramidal neurons (360 pA vs. 2,000 pA).

We want to emphasize again that experimental and modeling data show that cell size matters (Figs. 3, 4, and 5). When a neuron is stimulated it transitions from resting state into firing action potentials. With further increased input the neuron undergoes a second transition, i.e., the firing state transitions into the DB state with cessation of action potential generation. Thus DB is just as much part of the neuronal repertoire as resting state and firing. The size effect of the neural response to input is critically important because cortical inhibitory neurons are on average smaller than the excitatory ones.

Network simulation.

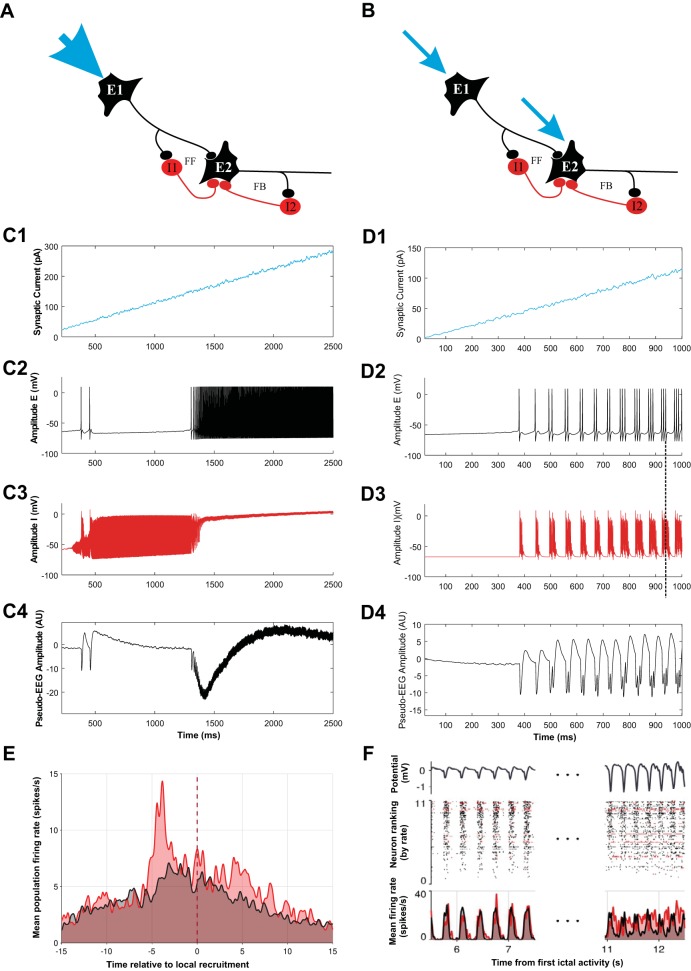
At the core-penumbra interface there is a narrow well-defined ictal wave (Schevon et al. 2012). Interestingly, this wave affects a large area across cortex (Eissa et al. 2017). This effect must be due to a combination of intra- and intercortical long-range and randomlike/short-range connections. We now assume that this long-range effect results in propagation of the ictal wave whereby it becomes broader and lower in amplitude—similar to a combined convection and diffusion process. In our analysis of neural activity across the different seizure territories, we focus on a motif that includes both feedback and feedforward inhibition under two different conditions (Fig. 6): one condition that mimics the network in the perturbator condition with input from a strong narrow wave of excitation (Fig. 6A) and another that mimics the oscillator scenario with more spatially distributed and weaker inputs (Fig. 6B). The important and interesting consequence of the two scenarios shown in Fig. 6, A and B, is the distinction between the inhibitory feedback experienced by the excitatory cells. In the perturbator scenario the activities of E1 and E2 differ because the narrow ictal wave arrives first at E1. Because of this difference, the feedforward and feedback inhibition experienced by E2 is also different. In the oscillator scenario in Fig. 6B, activities of E1 and E2 are similar because of the broader activation of the wave. As a result, the activities of I1 and I2 will also be similar and the difference of the feedback and feedforward inhibition experienced by E2 vanishes! Importantly, the responses of these motifs are also dramatically different. The perturbator network responds by a failing inhibitory process and propagation of excitation (Fig. 6C), whereas the neuronal response in the oscillator network is oscillatory (Fig. 6D).

Fig. 6.

A motif with feedback and feedforward connections, modeling the activity, and recorded activity during human focal seizure activity: part of a network with excitatory neurons (E1 and E2) and inhibitory neurons (I1 and I2). Neuron E2 can be inhibited via neuron I1 in a feedforward loop (FF) and via neuron I2 in a feedback loop (FB). The circuit is excited with a strong external input (blue arrows). A depicts a detail within the perturbator with a slowly propagating ictal wave (1 mm/s) starting at the arrow at top left. As the ictal wave propagates, neuron E2 will eventually get excited so that it experiences both FF and FB inhibition. B depicts the situation of the same circuit within the oscillator. The network now receives input from the small and far-away perturbator. Via long-range excitatory connections, the perturbator excites the neurons in the oscillator, E1 and E2. Compared with the scenario in A, the input at the oscillator is weaker and broader, thereby creating similar relatively strong inputs to both neurons (blue arrows). As a result both excitatory cells will simultaneously exhibit similar activities. In this case, the inhibitory effect of both inhibitory cells on neuron E2 will be also similar, in both strength and delay. As a result, a clear distinction between the effect of inhibition via FF and FB on E2 vanishes, and FF now resembles FB. C and D depict the response of networks in A and B, respectively. C1 and D1 depict the input function (note the different vertical calibrations in C1 and D1). C2–C4 depict responses of E2 (black, C2) and I1 (red, C3) and the associated extracellular pseudo-EEG evoked by the neural activity (C4) for the scenario in A. Note that inhibitory activity precedes the excitatory activity. D2–D4 are the same as in C but for the network scenario shown in B. Note that once the oscillation is established the inhibitory activity persists after offset of excitation (vertical dashed line across D2 and D3). E depicts the spike sorting result of extracellular activity during a human focal seizure at the passage of an ictal wave at time 0 indicated by the vertical dashed line. Putative inhibitory neural firing (red) is reduced substantially before the increase in putative excitatory firing (black) as the wave front passes. F depicts the spike sorting result of the activity in an area away from the wave front during oscillatory activity of the local field potential (top). Spike sorting shows that putative excitation and inhibition are, on average (bottom), synchronized with the oscillation and that here putative inhibition is active after offset of the putative excitation. Note the similarities between the recordings in E and F and the simulations shown in C and D, respectively. In E, where FF inhibition dominates, the inhibitory activity peak precedes the excitatory one. In contrast, in F, where feedback inhibition rules to create oscillations, the inhibitory activity persists after the excitatory activity peaks (data from Merricks et al. 2018). AU, arbitrary units.

Clinical Data

Although data obtained from experimental and theoretical epilepsy models are useful and may lead to important insight into the ictal mechanisms, the critical test is to confirm findings and predictions with clinical observations of seizures in patients with epilepsy. For that reason we describe and evaluate such observations at both meso- and macroscales.

Mesoscale observation at the ictal wave.

Microelectrode data of activity during human focal seizures revealed a slowly moving wave of action potential activity (Schevon et al. 2012). Spike sorting results of the activity from an example focal seizure recorded around this wave’s propagation showed differing contributions of putative inhibitory (n = 19; 17.1%) and excitatory (n = 92; 82.9%) neurons to the activity pattern (Fig. 6E). Similar findings across small patient populations have been reported in Ahmed et al. (2014) and Merricks et al. (2018, 2019, and unpublished observations). Our result demonstrates that 1) effective inhibition is reduced as the ictal wave front approaches a given microelectrode recording site (time = 0 in Fig. 6E) and 2) this reduction is at least in part due to a marked decrease in the inhibitory firing rate, i.e., an effect that is presynaptic to the GABA_A synapse from the inhibitory to excitatory neurons. These aspects of the observation agree well with our PDS hypothesis, and accordingly they agree well with the simulation in Fig. 6C, where in a local cell pair the inhibitory activity precedes the excitatory activity.

Activity in the oscillator.

Although microelectrode data in Schevon et al. (2012) show recruitment of the penumbra territory into the ictal core, it does not reveal how this relates to oscillatory behavior seen in macroscale clinical data. Spike-triggered averages, using the action potentials in the ictal wave area as a trigger, demonstrated a surprisingly large, centimeter-sized area that will not be recruited in the core but is significantly affected by these spikes (Eissa et al. 2017) (Fig. 7). To distinguish this large area from the mesoscale penumbra, we use the term “oscillator.” Bifurcation analysis using a combined W-C-type neural field and neural mass model in Eissa et al. (2017) demonstrated that neural inhibition in the oscillator is crucial for distinct dynamical pathways for the on- and offset of oscillatory seizure activity. Furthermore, results presented by Eissa et al. (2018), using a linearized W-C neural mass model for the oscillator, suggested that inhibitory activity is essential for sustaining the observed properties of the oscillatory component in ongoing focal seizures.

Fig. 7.

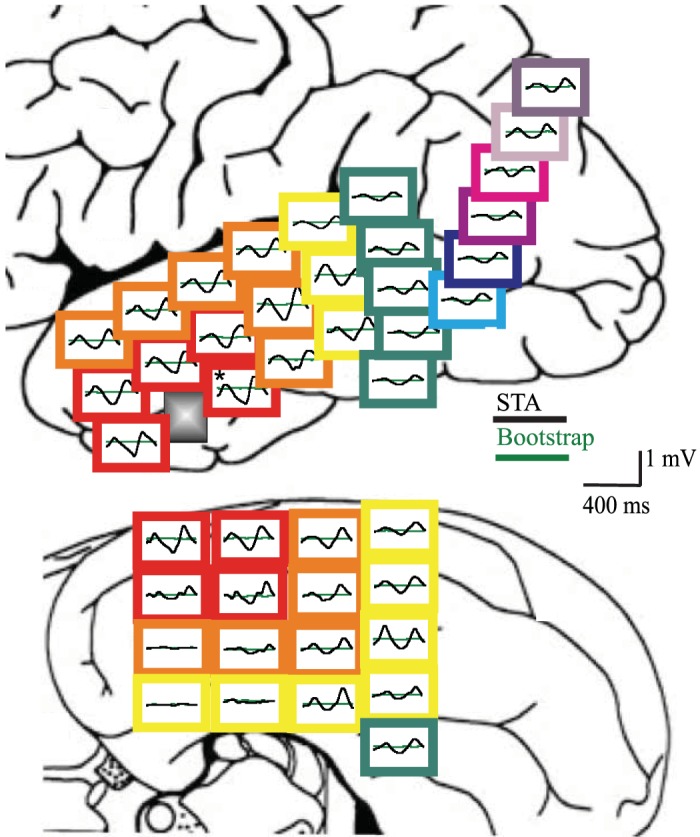
Macroscopic effect of the perturbator located at the gray square close to the temporal tip: lateral view (top) and basal view (bottom) showing the spike triggered averages (STAs) arranged spatially. At each location, the average (black) and its noise estimate (green) are depicted. It can be seen that the effect of the ictal wave activity ranges across a macroscopic centimeter-sized area (reproduced from Eissa et al. 2017).

Although the above-described macroscopic observations and associated models of the behavior in the oscillator explain observations, it is of interest to link these to underlying behaviors at the mesoscale. As we described in the previous modeling section, the perturbator’s neural behavior is determined by feedforward inhibition and its failure, whereas the oscillator neural activity is dominated by feedbacklike inhibition because the distinction between feedforward and feedback vanishes (Fig. 6, A–D). Microelectrode array data recorded away from the ictal core confirm that the neurons oscillate (Fig. 6F). Considering the spike sorting results for this data, another interesting difference between the excitatory-inhibitory timing (Fig. 6F, bottom) in the perturbator and the oscillator is that now inhibitory activity peaks after excitatory activity, similar to the simulated activity of the oscillator cell pair in Fig. 6D. Furthermore, as can be seen in the spike rasters in Fig. 6F, the oscillatory activities of the individual neurons are not perfectly synchronized, similar to oscillatory activity in a stochastic version of the W-C formalism (Wallace et al. 2011).

DISCUSSION

We explored the coexistence of hyperactivity and hypersynchrony during focal seizures and summarized evidence for a dual role of inhibitory function. We propose PD as a possible mechanism behind this dual role, i.e., failure of inhibition in front of the ictal wave allows propagation, whereas inhibition elsewhere remains intact and contributes to oscillatory activity (Fig. 6, C–F). We argue that the simultaneous inhibitory failure at the ictal wave and intact inhibitory function in the oscillator are not contradictory phenomena (Eissa et al. 2017, 2018). Because there are different territories of vastly different size, distinct dynamics can interact and coexist during seizures (Fig. 6) (Eissa et al. 2017). We present compelling evidence that PD can be responsible for the duality of inhibitory action in the seizing network (Figs. 3–6). At the mesoscale, PD causes synaptic transmission from smaller inhibitory cells to fail because of strong excitation from the approaching ictal wave (Figs. 3–5). In contrast, traveling waves originating from the ictal wave front (Smith et al. 2016) are lower in amplitude and more spread within the oscillator territory, and this enables the inhibitory-excitatory interactions that promote macroscopic network oscillatory activity (Fig. 6). In this context, we want to acknowledge that network oscillatory activity can be observed under physiological conditions as well, but the widespread oscillatory response that is highly correlated with the activity in the small perturbator is pathological. In sum, we conclude that the body of evidence presented here supports that PD is not only a cellular marker or epiphenomenon but is an active contributor to the seizure itself.

The saturation of neurons at high levels of input and its dependence on cell size form the basis of the complicated multiscale dynamics seen during ongoing seizures (Fig. 6) (e.g., Eissa et al. 2017). As shown in experimental and computational models of synaptically isolated neurons, the saturation of the action potential generation process exhibits a sudden transition (bifurcation) in the voltage-sensitive channel dynamics in response to high current input levels (e.g., Figs. 3, 4C, and 5). The phenomenon hinges on the presence of inward and outward currents governed by nonlinear voltage sensitivity. Although important from a physiology point of view, the presence of the saturation phenomenon is independent of the ion species involved in the voltage-sensitive inward and outward currents. At a given current level, the saturation effect is more dramatic in smaller neurons (Figs. 3–5). However, in networks these current inputs originate from synaptic activity. Thus saturation of the action potential generator occurs via the interplay of voltage-sensitive dynamics (intrinsic) and synaptic (network) function.

We are aware that the multidisciplinary evidence we present here is compelling but does not fully confirm our hypothesis on the relevance of PDS in sustaining focal seizure activity. We want to discuss one critique we frequently receive, namely, that although PDS is considered a cellular hallmark of epileptiform activity, it has not been observed in the inhibitory activity involved in many seizure models (e.g., Miri et al. 2018). This fact is clearly of interest, but we want to point out that this is not surprising because the territory of the perturbator’s PDS phenomenon in the inhibitory population is rather small relative to the large oscillator network involved in the seizure where inhibition is functional (e.g., Fig. 7). Hence, if one does not specifically look for the inhibitory PDS phenomenon in front of the mesoscopic ictal wave, the likelihood to observe it is extremely low. Nonetheless, even though it is unlikely to observe the role of the PDS phenomenon in the inhibitory population, its action in promoting propagation of experimental seizure activity has been shown to work in animal models (Cammarota et al. 2013; Ziburkus et al. 2006) (Fig. 4).

Another question that arises from the idea that an ictal wave propagates at ~1 mm/s and causes the larger network to respond by having seizure oscillatory activity is how can this process explain seizures that last several minutes requiring an (unrealistic) large cortical area to be recruited in the core territory? One probable scenario is that the ictal wave front not only propagates but also eventually spawns new ictal wave fronts via long-range connections. A snapshot around t = 00:14 of the movie by Schevon et al. (2012) (https://media.nature.com/original/nature-assets/ncomms/journal/v3/n9/extref/ncomms2056-s6.mov) shows such a spawning process, possibly via the 1-mm long-range intracortical connections. In this particular case the spawned activity fails to propagate, but it is easy to imagine that there will be cases in which such a spawned front will continue to exist and propagate, thereby taking over the perturbator role of a vanishing wave.

Finally, how might the present insight help us understand how anticonvulsant therapies work: do they act directly on the mechanisms feeding in the ictal wave front locally, or do they interact with the global response of the oscillator? This might help target drug development, inform stimulation paradigms, etc. First, the dynamical picture sketched by the evidence presented does not lead to a simple answer to this question. However, the idea that an ictal wave is the culprit for keeping the seizure activity going leads to the idea that prevention or destruction of this ictal wave should be the target of anticonvulsant therapy. On the other hand, a successful approach may result from mitigating the response of the oscillator. In this case, the clinical problems resulting from the ictal wave’s hyperexcitation would not be addressed, but the effects of involvement of the larger cortical oscillator area would be limited. It is important therefore to set the goal of a clinical intervention. If the idea is to obstruct the ictal wave as the source of the seizure activity, one has to increase efficacy of surround inhibition. Within our PDS hypothesis, this obviously cannot be done by increasing the strength between E-I connectivity since this would only promote the saturation we already see in the inhibitory neurons and that leads to the very ictal wave one wants to prevent from occurring. Other tactics such as enhancing the I-E connectivity or controlling the activity profile of the inhibitory population might work in this case. Also, since the ictal wave propagation is a phenomenon associated with inhibitory failure due to hyperexcitation, it is not surprising that overall reduction of neuronal excitation often works as an anticonvulsant. Finding therapeutic approaches to prevent the downstream oscillatory activity may be more difficult since both excitation and inhibition play a role in this case. Therefore this situation resembles the physiological state, and any therapeutic change in this state may result in more severe side effects.

GRANTS

A. K. Tryba, E. M. Merricks, S. Lee, T. L. Eissa, C. A. Schevon, and W. van Drongelen were supported by NIH Grants R01 NS-095368 and R01 NS-084142.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

A.K.T., C.A.S., and W.v.D. conceived and designed research; A.K.T., E.M.M., R.R.G., R.G.E., and C.A.S. performed experiments; A.K.T., E.M.M., S.L., T.P., S.C., T.L.E., R.G.E., C.A.S., and W.v.D. analyzed data; A.K.T., E.M.M., D.R.N., R.R.G., C.A.S., and W.v.D. interpreted results of experiments; A.K.T., E.M.M., T.L.E., and W.v.D. prepared figures; A.K.T. and W.v.D. drafted manuscript; A.K.T., E.M.M., S.L., T.P., S.C., D.R.N., T.L.E., R.R.G., R.G.E., C.A.S., and W.v.D. edited and revised manuscript; A.K.T., E.M.M., S.L., T.P., S.C., D.R.N., T.L.E., R.R.G., R.G.E., C.A.S., and W.v.D. approved final version of manuscript.