White matter tracing combined with electric field simulation – A patient-specific approach for deep brain stimulation

Highlights

• •Novel workflow for combined tractography and patient-specific DBS simulations.
• •Accurate tissue segmentation is essential for DBS electric field simulation.
• •The tissue model is of higher importance for current controlled DBS.
• •Directional leads require a precise targeting to tailor the electric field.
• •DRT overlapped the isovolume in Zi for all patients.

Abstract

Objective

Deep brain stimulation (DBS) in zona incerta (Zi) is used for symptom alleviation in essential tremor (ET). Zi is positioned along the dentato-rubro-thalamic tract (DRT). Electric field simulations with the finite element method (FEM) can be used for estimation of a volume where the stimulation affects the tissue by applying a fixed isolevel (V_DBS). This work aims to develop a workflow for combined patient-specific electric field simulation and white matter tracing of the DRT, and to investigate the influence on the V_DBS from different brain tissue models, lead design and stimulation modes. The novelty of this work lies in the combination of all these components.

Method

Patients with ET were implanted in Zi (lead 3389, n = 3, voltage mode; directional lead 6172, n = 1, current mode). Probabilistic reconstruction from diffusion MRI (dMRI) of the DRT (n = 8) was computed with FSL Toolbox. Brain tissue models were created for each patient (two homogenous, one heterogenous isotropic, one heterogenous anisotropic) and the respective V_DBS (n = 48) calculated from the Comsol Multiphysics FEM simulations. The DRT and V_DBS were visualized with 3DSlicer and superimposed on the preoperative T2 MRI, and the common volumes calculated. Dice Coefficient (DC) and level of anisotropy were used to evaluate and compare the brain models.

Result

Combined patient-specific tractography and electric field simulation was designed and evaluated, and all patients showed benefit from DBS. All V_DBS overlapped the reconstructed DRT. Current stimulation showed prominent difference between the tissue models, where the homogenous grey matter deviated most (67 < DC < 69). Result from heterogenous isotropic and anisotropic models were similar (DC > 0.95), however the anisotropic model consistently generated larger volumes related to a greater extension of the electric field along the DBS lead. Independent of tissue model, the steering effect of the directional lead was evident and consistent.

Conclusion

A workflow for patient-specific electric field simulations in combination with reconstruction of DRT was successfully implemented. Accurate tissue classification is essential for electric field simulations, especially when using the current control stimulation. With an accurate targeting and tractography reconstruction, directional leads have the potential to tailor the electric field into the desired region.

1. Introduction

Deep brain stimulation (DBS) is an established therapy for symptom relief in several movement disorders such as Parkinson's disease (PD), essential tremor (ET) and dystonia (Hariz et al., 2013; Benabid et al., 2009a; Benabid et al., 2009b). For ET and tremor-dominant PD the electrodes are most commonly placed in the ventral intermediate nucleus of the thalamus (VIM) or in the zona incerta (Zi) (Blomstedt et al., 2012; Blomstedt et al., 2011; Flora et al., 2010).

Anatomical studies have shown that both the VIM and Zi are in the vicinity of the same neuronal tract, the dentato-rubro-thalamic tract (DRT) (Gallay et al., 2008; Hassler et al., 2013), which has been suggested as a potential target for tremor reduction (Coenen et al., 2011a; Coenen et al., 2011b). The DRT originates the deep cerebellar nuclei, primarily in the dentate nucleus, and extends via the superior cerebellar peduncle to the contralateral red nucleus, where a minority of the fibres are terminated. The majority of the fibre bundle is projected to the thalamus and thereafter to cortex, where the tremor network extends to the primary motor cortex.

To investigate the result of the clinical stimulation settings in reference to the anatomy the finite element method (FEM) can be used, where the electrical spread around the active contact is simulated using the patient-specific tissue to determine the conductivity in the model (Åström et al., 2009; McIntyre et al., 2004; Chaturvedi et al., 2010). With the concept by Åström et al. (2009), the electric field is visualized by using a fixed isolevel (Åström et al., 2015; Alonso et al., 2016; Latorre and Wårdell, 2019) together with the patients preoperative MRI data where anatomical evaluation can be made. This methodology has also been used in further studies by the Linköping group (Alonso et al., 2016; Åström et al., 2010) and other groups (Mädler and Coenen, 2012; Akram et al., 2018). Recent advances in DBS technology includes using current control stimulation and directional leads which has the possibility to steer the electric field. Alonso et al. (2016) showed that there are differences in model behaviour depending on the stimulation mode when investigating different lead designs, including voltage and current stimulation and directional leads where it is possible to steer the electric field. With the development of diffusion MRI (dMRI), it would in a similar way as for the electric field be possible to superimpose the white matter tracts, and to estimate the anisotropy of the tissue conductivity. The latter is possible since both water diffusion and brain tissue conductivity is higher along the axons compared to the perpendicular direction (Nicholson, 1965; Tuch et al., 2001), and this information can be used as input to the FEM simulation (Chaturvedi et al., 2010; Åström et al., 2012).

In the late nineties and early 2000, dMRI was introduced to develop a methodology to reconstruct neuronal pathways (Mori et al., 1999; Peled et al., 1998; Westin et al., 2002). The first methods were based on estimating a diffusion tensor in each voxel and propagating a streamline representing the path of a nerve tract by following the principle direction of diffusion. However, to be able to handle multiple direction regions like crossing, kissing and branching fibres, more advanced models have been developed (Malcolm et al., 2010; Qazi et al., 2009; Behrens et al., 2007; Tournier et al., 2012; Pujol et al., 2015). In DBS research, several groups have applied different tractography methods to evaluate the anatomy in the deep brain structures and estimate the effect of the DBS lead. Pujol et al. (2017) have explored the use of tractography for mapping complex white matter anatomy in the vicinity of the subthalamic nucleus. Coenen et al. (2014) used a single tensor model to reconstruct the DRT and study the distance from the centre of the tract to the active DBS contact. Akram et al. (2018) used a probabilistic tractography approach to perform group analysis of the estimated brain region affected by the stimulation. Few studies have however combined advanced methods for white matter tracing with patient-specific electric field simulations based on tissue specific conductivity in the vicinity of the DBS lead.

The aim of this study was to develop a workflow which combines tractography reconstruction and patient-specific electrical field simulations in DBS. Information from dMRI was used for reconstruction of white matter tracts and modelling anisotropic conductivity. The method was exemplified for Zi-DBS and reconstruction of the dentato-rubro-thalamic tract (DRT), and the electric field was evaluated for different brain tissue model complexities and DBS lead designs.

2. Material and methods

2.1. Clinical data

2.1.1. Patients

Patients (n = 4, 3 female, age 77 ± 11.2) with ET were referred for DBS surgery in Zi (Fig. 1(a)) to the Department of Neurosurgery at Linköping University Hospital. All patients gave their written informed consent before the surgical procedure and the study was approved by the Local Ethics Committee (No. 2012/434-31 and 2018/143-32). Three patients were implanted with the conventional lead (3389, Medtronic Inc, USA), and one patient with the directional lead (6172, Abbott In. USA). The different electrode designs are shown in Fig. 2. All patients were evaluated before and three months after surgery using item 5 in part A and items 10–14 in part B of the essential tremor rating scale (ETRS). The stimulation pulse width was 60 µs for all patients with a repetition frequency of 140 Hz, except for Patient 2 who was programmed with a frequency of 150 Hz. For patient overview information see Table 1.

Fig. 1.

View of the region of interest for the analysis. (a) Pre-operative coronal T₂ slice where Red nucleus (RN), Zona incerta (Zi) and the subthalamic nucleus (STN) is highlighted and (b) post-operative CT where the artefact from the DBS lead is visible.

Fig. 2.

Schematic view of the different DBS leads. The directional lead has the possibility to steer the electric field by only activate one of the different segments (a, b and c). Contact notations for the conventional lead; Left side: 0–3 (distal to proximal), Right side: 8–11 (distal to proximal). Contact notations for the directional lead; Left side: 1–4 (distal to proximal), Right side: 9–12 (distal to proximal).

Table 1.

Patient information; demographics, ETRS-score before and after surgery, implanted lead including active contact and side (Left = L, Right = R) and clinical stimulation amplitude. ETRS score evaluated for item 5 in part A and items 10–14 in part B (maximum score = 32 points, high score indicates more severe symptoms).

No.	Sex	Age	Lead	Side (contact)	Amplitude	ETRS
						Pre-op	Post-op	Improvement
1	F	86	Medtronic 3389	L (2)	L: 3 V	19	4	79%
2	M	83	Medtronic 3389	L (3)	L: 2.1 V	22	8	64%
3	F	61	Medtronic 3389	L (3) R (10)	L: 1.6 V R: 1.1 V	14	3	79%
4	F	78	Abbot 6172	L (2a) R (10a)	L: 1.3 mA R: 1.0 mA	22	5	77%

2.1.2. Imaging and surgical procedure

Prior to surgery, dMRI images were acquired for all patient (Ingenia 3T, Philips Healthcare, the Netherlands). Each dMRI dataset was retrieved applying 32 diffusion sensitizing gradients distributed over a half sphere with a b-value of 800 s/mm², one b0 volume, TE 100 ms, TR 8530 ms, and a voxel size of 1.75 × 1.75 × 2 mm³. On the day of surgery, pre-operative T₂ images (Fig. 1(a)) were acquired on the same MRI system (TE 80 ms, TR 8000 ms, voxel size 0.5 × 0.5 × 2 mm³) using the Leksell® Stereotactic System (G frame, Elekta instrument AB). The T₂ images were used to identify the Zi target and trajectory during preoperative planning with SurgiPlan® (Elekta Instrument AB, Sweden) (Blomstedt et al., 2012). The DBS leads were implanted in the Zi according to the clinical protocol (Wårdell et al., 2016) with the patients under general anaesthesia. Fluoroscopy (Philips BV Pulsera, Philips Medical Systems, the Netherlands) was used to verify position of the leads during the surgical procedure. Postoperative CT (GE Lightspeed Ultra, GE Healthcare, UK) was performed within 24 h after surgery (Fig. 1(b)) to verify electrode position and exclude haemorrhage.

2.2. Processing workflow

The imaging data and stimulation parameters for each patient were processed according to the developed workflow as presented in Fig. 3. This includes tractography reconstruction, brain conductivity modelling, FEM simulation, visualization and data analysis.

Fig. 3.

An overview of the processing workflow starting with patient clinical data which is used for tractography and electrical field simulation. The combined results are visualized together. All data has been analysed to evaluate the intersection of the electric stimulation with the reconstructed DRT, and performance of different brain tissue models.

2.2.1. Diffusion model

The dMRI and pre-operative T₂ datasets were processed in NifTI format (Li et al., 2016) using FSL v5.0 FDT toolbox (FMRIB Analysis Group, University of Oxford, UK). A brain mask was created with the bet function based on the b0 volumes. The converted files were then corrected for eddy currents and motion artefacts using eddy. Two diffusion models were used for this workflow. The first diffusion model was computed with bedpostX (Behrens et al., 2007; Behrens et al., 2003), with two possible fibres per voxel, and used as input to the tractography. The second diffusion model was a diffusion tensor estimation using DTIFIT. This model was further used for the brain model computation.

2.2.2. Tractography

The preoperative T₂ images were co-registered with the dMRI, using FLIRT (Jenkinson et al., 2002). Seed mask, waypoint masks and the exclusion mask were manually delineated based on the diffusion images and T₂ images. Probabilistic tractography reconstruction was performed with the default setting of probtrackx2 (Behrens et al., 2007; Behrens et al., 2003) (number of samples = 5000, curvature threshold = 0.2). The precentral gyrus was used as seeding region, and the posterior subthalamic area (PSA), superior cerebellar peduncle (SCP) and dentate nucleus (DN) were used as waypoints. Projections to contralateral cerebrum or ipsilateral cerebellum were excluded. The resulting tracts were transformed to T₂ image space for analysis and visualization. All transforms of directional volumes were made with the vecreg function to correct for the directional information.

2.2.3. Brain conductivity models

For each patient, four brain models were created as input to the electrical field simulations. The first two models, assuming a bulk of homogenous and isotropic tissue, were created by applying conductivities (σ) corresponding to grey matter (Model I, σ_GM = 0.123 S/m) and white matter (Model II, σ_WM = 0.0754 S/m) respectively. A heterogenous isotropic model (Model III) was created, according to previously described method (Åström et al., 2009), to include the effect of varying conductivity properties in the brain using an inhouse developed MATLAB software, ELMA (Johansson et al., 2019). The software performs a tissue segmentation based on the intensities in the T₂ images. The different tissues were assigned conductivity according to tabulated values (Åström et al., 2009; Gabriel et al., 1996; Andreuccetti et al., 1997) for grey matter (σ_GM), white matter (σ_WM) based on the stimulation pulse width and frequency and the cerebrospinal fluid (CSF) (σ_CSF = 2.0 S/m) and blood (σ_blood = 0.7 S/m) which in the range of DBS therapy is frequency independent (Wårdell et al., 2013). Conductivity values for voxels with mixed tissues were assigned using a linear interpolation function. An anisotropic brain model (Model IV) was created to include the effect of tissue structure in the simulation using Eq. (1).

$$\mathit{\sigma }=\frac{{\sigma }_e}{d_e}*\mathit{D}$$ (1)

where σ is the conductivity tensor, D is the diffusion tensor, σ_e is the effective extracellular conductivity and d_e is the effective extracellular diffusivity. The tissue classification and conductivity assignment from the heterogeneous isotropic model was used as an estimate of σ_e in each voxel. The mean diffusivity of the diffusion tensor was used to estimate d_e according to Eq. (2) and (3).

$$d_e=\frac{\mathit{trace}\left(\mathit{D}\right)}{3}$$ (2)

$$\mathit{trace}\left(\mathit{D}\right)=D_{\mathit{xx}}+D_{\mathit{yy}}+D_{\mathit{zz}}={\lambda }_1+{\lambda }_2+{\lambda }_3$$ (3)

where λ₁, λ₂ and λ₃ are the eigenvalues and D_xx, D_yy and D_zz are the diagonal element of the diffusion tensor. For the two patient specific models (Model III and Model IV), a peri-electrode space (PES) of 250 µm was included to represent the tissue electrode interface (Alonso et al., 2016). The PES is assumed to consist of fibrous tissue (Nielsen et al., 2007) and was therefore assigned conductivity as σ_WM.

2.2.4. DBS lead models and FEM simulation

The brain models were used as input to FEM simulation in Comsol Multiphysics (version 5.3 Comsol AB, Stockholm, Sweden). The geometry of the DBS leads were modelled (Alonso et al., 2016) for the FEM simulations and placed in the brain models based on the lead artefact as seen in the post-operative CT, Fig. 1(b). For all simulations the clinical parameters (amplitude, frequency, pulse length) at the chronic state (at least 1 month after surgery) were used, Table 1. For the patients with the conventional lead (3389), simulations were performed in voltage mode for each brain model using the clinical contacts (n = 16). For the patients with the directional lead (6172), simulations were performed in current mode for each brain model using clinical contacts both in ring mode, spitting the nominal current equally between the three segments, and for each of the three segments separately (n = 32).

The electric field distribution around the active contact was calculated using the equation of continuity for steady currents (Eq. (4))

$$\nabla ·J=-\nabla ·\left(\sigma \nabla V\right)=0$$ (4)

where J is the current density (A/m²), σ is the electrical conductivity (S/m) and V the electric potential (V). During simulation, the active contact was considered as a voltage or current source, the non-active contacts were set to floating potential and non-conductive surfaces were set to insulation. To reduce the computational time to approximately 5 min, the tissue was modelled as a box, 100 × 100 × 80 mm³, where the outer surfaces were set to ground potential. Each FEM simulation was performed with approximately 3000,000 degrees of freedom using a physics-controlled tetrahedral mesh, mesh density is finest closest to the electrode, with approximately 2000,000 elements.

2.2.5. Visualization

The electric field and tractography reconstruction were visualized together with the patient's pre-operative MRI data using 3DSlicer (Fedorov et al., 2012). Global connectivity was visualized with a threshold set at 10% of the total number of generated tracts within the inclusion/exclusion criteria. For anatomical evaluation of the tracts in the region of interest, i.e., the PSA, a 20% threshold was used. This threshold was derived using the distance between RN and STN and the width of RN at the axial slice 3 mm below AC-PC line. The width of DRT at its thinnest and thickest part should be in the range of the distance between RN and STN and the width of RN respectively. The result from the FEM simulations was superimposed on the image using an electrical field isolevel of 0.2 V/mm, corresponding to activating neurons with axon diameter of approximately 3–4 µm according to single cable neuron model simulations (Åström et al., 2015; Johansson et al., 2018). Visualization of the result was made in 2D slices (axial, sagittal and coronal) and in 3D views.

2.3. Data analysis

The tissue of the reconstructed DRT was characterized using the mean value (m) and standard deviation (sd) of the fractional anisotropy (FA) and mean diffusivity (MD). For all simulations the volume within the 0.2 V/mm isosurface (V_DBS) was calculated using Comsol's volume integration function. To investigate the effect of the stimulation on the DRT common volumes (CV) for the DRT and all different V_DBS were calculated according to Eq. (5) (vertical bars indicating summation of included voxels).

$$CV=\left|V_{DBS}\cap V_{DRT}\right|$$ (5)

The common volume with the DRT was also calculated as the percent of the V_DBS (Eq. (6)).

$$CV\%=\frac{CV}{V_{DBS}}$$ (6)

Dice coefficient (DC) was used to evaluate the differences in simulation outcome between brain models using Model III as reference (Eq. (7)).

$$DC=2\frac{\left|V_{DB{S}_{ModelIII}}\cap V_{DB{S}_{ModelY}}\right|}{\left|V_{DB{S}_{ModelIII}}\right|+\left|V_{DB{S}_{ModelY}}\right|},Y=I,II,IV$$ (7)

DC was also used to evaluate the difference in ring mode and directional mode for the directional lead (Eq. (8)).

$$\mathit{DC}=2\frac{|V_{\mathit{DB}{S}_{\mathit{r}\mathit{i}\mathit{n}\mathit{g}\mathit{m}\mathit{o}\mathit{d}\mathit{e}}}\cap V_{\mathit{DB}{S}_{\mathit{d}\mathit{i}\mathit{r}\mathit{e}\mathit{c}\mathit{t}\mathit{i}\mathit{o}\mathit{n}\mathit{a}\mathit{l}\mathit{m}\mathit{o}\mathit{d}\mathit{e}}}|}{\left|V_{\mathit{DB}{S}_{\mathit{r}\mathit{i}\mathit{n}\mathit{g}\mathit{m}\mathit{o}\mathit{d}\mathit{e}}}\right|+\left|V_{\mathit{DB}{S}_{\mathit{d}\mathit{i}\mathit{r}\mathit{e}\mathit{c}\mathit{t}\mathit{i}\mathit{o}\mathit{n}\mathit{a}\mathit{l}\mathit{m}\mathit{o}\mathit{d}\mathit{e}}}\right|}$$ (8)

For evaluation of the anisotropy in the region surrounding the active contact, the FA values of the voxels within the isosurface was calculated and presented as m ± sd. The results were compared to two reference tissues, CSF which represents isotropic tissue and internal capsule (IC) which represents highly anisotropic tissue. The anisotropic information from CSF and IC was retrieved by placing a ROI in each tissue type for all patients.

3. Results

The suggested workflow, Fig. 3, for combining tractography reconstruction with patient specific electric field simulation was successfully implemented. DBS leads were implanted for all patients in the Zi, which all had a substantial improvement in the ETRS score, Table 1.

3.1. Dentato-rubro-thalamic tract and electric field visualization

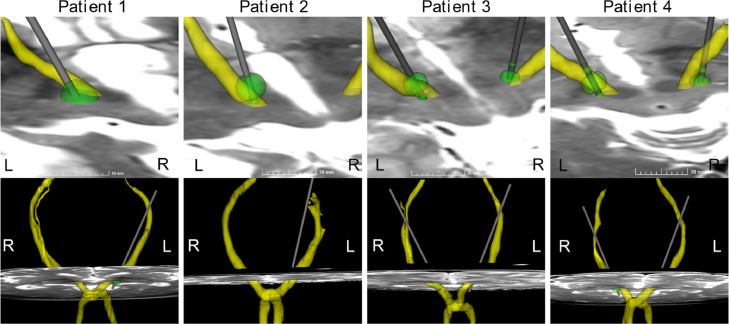
The DRT was computed for 8 paths, and the crossing of the fibres were successfully reconstructed for all patients (FA 0.55 ± 0.16, MD 0.8 ± 0.4∙10⁻³mm²/s). Fig. 4 show a visualisation of the respective patients with the combined tractography and FEM simulation superimposed on the preoperative T₂ MRI. A 3D visualization with 360° rotation for Patient 4 is shown in Fig. 5.

Fig. 4.

Visualization with V_DBS (green) and reconstructed DRT (yellow) superimposed on pre-operative T₂ MRI for each patient using the clinically active contact. The V_DBS is from simulation using Model III, for Patient 4 in ring mode. The top row is a zoomed in visualization of the region of interest seen from above, and the lower row show a global visualization of the DRT in a front view. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Fig. 5.

3D visualization with 360° rotation for patient 4 including DRT (yellow) and V_DBS (green) for Model III in ring mode. The video file is anvailible online. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

3.2. Common volume between DRT and electric field

Fig. 6 visualize the electric field from Model III and Model IV together with the reconstructed DRT. Calculated CV from all simulations is found in Fig. 7. For all models and stimulation modes part of DRT was within the electric field volume (V_DBS). For ring mode, the CV between V_DBS and the DRT was in the range 3.6–33.7 mm³ (5–51% of the V_DBS). The brain models result in different CV, this is most prominent for Patient 4 and Model I (Fig. 7(a)). However, the difference is not as distinct when the data is normalized with the V_DBS (Fig. 7(b)). Patient 4, who had a directional lead (Fig. 2(b)), was evaluated using the clinical contact both in ring mode and each segment separately. The CV was in the range 4.1–28.5 mm³ and 1.0–16.1 mm³ for the left and right side respectively. The largest CV was retrieved using segment 2a and segment 10c for right and left side respectively, and the smallest CV using segment 2b and segment 10a respectively independent on which brain tissue model that was used, Fig. 7(c) and (d).

Fig. 6.

Contours visualizing V_DBS for Model III (green) and Model IV (orange) together with the reconstructed DRT. Left to right includes a 3D view and axial, sagittal and coronal slices. The slices were chosen where the extension of the electric field was as largest. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Fig. 7.

Common volume for all simulated V_DBS and reconstructed DRT. (a) includes all simulations in ring mode, (b) values from (a) in percentage of total V_DBS, (c) common volume for all simulations with directional lead and (d) values from (c) in percentage of total V_DBS. The plots include simulations using all models.

3.3. Impact of brain model complexity

The electric field distribution was evaluated for the four different brain models. Isocontours at 0.2 V/mm from all patient simulations are displayed in axial, coronal and sagittal slices (Fig. 8). The isocontours of the electric field show a small difference perpendicular to the contact (axial direction), except for Patient 4 Model I where the axial difference is larger, but is more pronounced in the coronal and sagittal direction. For voltage control, the homogenous models (Model I and II) present equal result, as expected according to the theory. A summary of analysed volumes, DC and tissue anisotropy is found in Fig. 9(a)–(c). In voltage control mode (Patients 1–3), the influence of the brain models was relatively low indicated by a high DC (0.95–0.98, Fig 9(b)). For current control stimulation (Patient 4), however, the variation in DC was larger with values down to 0.67 (Fig. 9b). Homogenous grey matter (Model I) differed most (DC 0.67–0.69) from the patient specific isotropic model (Model III) in current control stimulation. For Model II and IV the agreement was similar to voltage control DBS, DC 0.93–0.98. Independent on stimulation mode, Model III consistently generated a slightly smaller V_DBS than the anisotropic model (Model IV). Fig. 9(c) shows a comparison of the estimated anisotropy within the V_DBS and the ROIs in CSF and IC. Comparison between the anisotropy within the V_DBS and the ROIs indicates that the tissue in the stimulated region is neither highly anisotropic nor highly isotropic (Fig. 9(c)).

Fig. 8.

Isocontours (0.2 V/mm) for all simulations in ring mode using the clinical stimulation parameters. The visualization on axial, sagittal and coronal slices were chosen where the extension of the isocontours were largest. Note: results from Model I and Model II cannot be separated for voltage control (Patients 1, 2 and 3).

Fig. 9.

Plots of (a) the V_DBS for all simulation in ring mode, (b) DC comparing Model III with the other models and (c) the anisotropy within the V_DBS compared to information from internal capsule (IC) and cerebrospinal fluid (CSF).

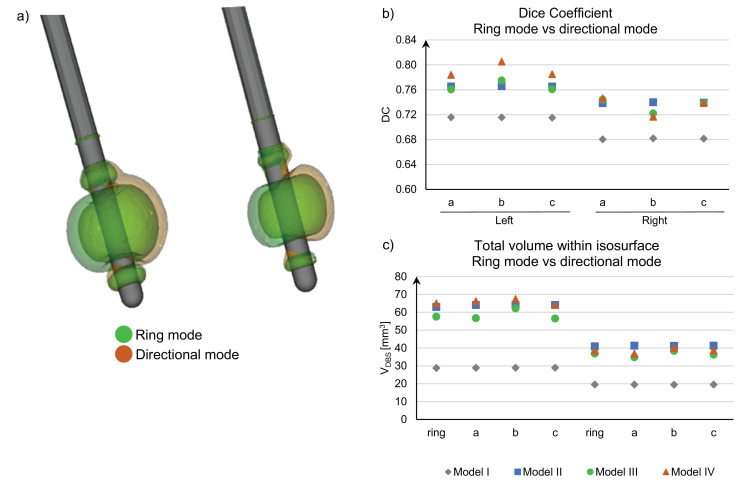
3.4. Directional vs. ring mode

Visualization of the electric fields for Patient 4 (current mode, Model III) in ring- and directional mode are presented in Fig 10(a). The directional mode has a moderate but evident steering effect, also verified by the calculated DC values, Fig 10(b). The higher stimulation amplitude on the left side reduces the steering effect and thus generating larger DC values. For the homogenous brain tissue models (Model I and Model II), the V_DBS is very similar in ring mode and directional mode, Fig 10(c). However, Model III and Model IV have a difference in the integrated volume which is an effect of the considered tissue heterogeneity and anisotropy.

Fig. 10.

V_DBS comparing ring mode and directional mode in Patient 4, (a) Visualization of the isosurface (0.2 V/mm) in ring mode (green) and using directional mode (segment a, orange) from simulation with Model III, (b) DC comparing ring mode and each segment and (c) plots the total volume of the V_DBS. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

4. Discussion

A workflow has been developed to combine DBS patient-specific electrical field simulations with tractography reconstruction, Fig. 3. The novelty lies within the combination of individual patient components including tracing of the DRT, FEM simulations with conductivity and anisotropy data, conventional and directional DBS lead designs as well as stimulation settings in voltage and current control modes.

4.1. Dentato-rubro-thalamic tract

For all patients it was possible to generate a reconstruction from cortex to contralateral dentate nucleus, fibres crossing in pons (Fig. 4), using the probabilistic method implemented in FSL. Previous work comparing this method with a two-tensor streamline method indicate that the probabilistic method has a tendency to leak into unexpected regions (Qazi et al., 2009). Therefore, a cut-off value was used in this work for visualization of the DRT, similar to other studies (Calabrese et al., 2015; Akram et al., 2018; Jbabdi et al., 2013). The two thresholds in this study were based on the percentage of the total number of reconstructed tracts, not a defined number of reconstructed tracks per voxel as implemented by other groups (Akram et al., 2018; Calabrese et al., 2015). The threshold for the analysis in the PSA region was selected based on evaluation of the cross sectional size of the reconstructed DRT and the individual T₂ MRI compared to the histology work reported by Gallay et al. (2008). The second threshold was selected to generate a reconstruction spanning from DN to cortex. To use a percentage threshold reduces the impact of the total number of reconstructed tracts, which can be an effect of e.g., seeding region size and the MR acquisition. Some groups have used high angular resolution diffusion imaging (HARDI) acquisition, including a high number of diffusion sensitizing gradient directions and multi-shell acquisition with higher b values (Akram et al., 2018; Howell and McIntyre, 2016) while others uses clinically available sequences similar to this study (Fenoy et al., 2016; Mädler and Coenen, 2012). As previously reported (Tuch et al., 2002), higher angular resolution and larger b-values increase the possibility to resolve multiple fibre direction in areas with orientational heterogeneity. Wilkins et al. (2015) studied the effect on number of diffusion sensitizing directions at clinical b-values (b = 1000 s/mm²) and showed that the orientational error and false negative detection decreased with increased number of directions. Future work will focus in improving the dMRI acquisition protocol, including multi-shell acquisition and gradient distribution, with the aim at introducing the workflow for intraoperative evaluation during DBS implantations.

While numerous approaches have been developed to reconstruct the trajectory of white matter pathways using diffusion MRI data, the presence of false-negative and false-positive tracts still pose limitations to the use of tractography for clinical decision-making (Schilling et al., 2019; Pujol et al., 2015). For this work the probabilistic method implemented in FSL was chosen to manage the complex anatomy, which also comes with the risk for more false positive tracts compared to the single tensor approach. To manage this risk, the threshold for analysis in the region of interest was based on previous anatomical studies. However, as Schilling et al. (2019) states, to get an accurate tracking result one might have to seek other modalities or strategies to overcome the limitations in currently available methods.

4.2. Common volume between DRT and electric field

To evaluate the electrical field in relation to the DRT, the intersection of both volumes was computed, i.e., CV. As the selection of cut-off value will impact the calculation of the CV, there is a risk of over- or underestimation of the CV in relation to the chosen threshold. However, investigations of different cut-off values showed that all CV will change similarly, i.e., the relationship in which simulation model that generated a larger CV is independent of the cut-off value, see supplementary material for information on CV for several threshold values. This indicates that the relative differences between the models still holds, but care should be taken before doing any quantitative analysis of clinical outcome based on the CV. Coenen et al. (2014) did a correlation analysis of the distance from the active DBS contact to the centre of the reconstructed DRT which failed to meet significance. According to the authors this was due to the limited number of patients (n = 11). An advantage of our approach is that the extension of the electric field which depends on the stimulation amplitude is considered. On the other hand, from a tractography point Coenen et al. approach would reduce the effect of false positive or negative reconstructions in the outer part of the tract since only the centre point is used. Akram et al. (2018) compared the averaged simulation volumes of two groups with good (n = 6) and poor (n = 3) clinical response using a total group averaged DRT reconstruction. By analysing the images, they found that the poor responders resulted in a stimulation volume adjacent to the DRT while the good responders had a high overlap with DRT. Both these studies together with present work has the limitation with the number of samples for performing any statistical analysis of the clinical outcome. Therefore, any quantitative approach will be difficult to apply, and visual analysis might be more suitable.

As all data is spatially evaluated on the pre-operative MRI, it is important to be aware of the spatial error that originates from co-registration. In this study the error comes from two sources; the diffusion data, which has higher distortion levels that anatomical MRI, and the postoperative CT which are registered to the pre-operative MRI. To avoid part of these errors, it would be preferable to do all scans with the stereotactic frame using the same scanner and acquisition sequence (Hyam et al., 2015). Future work will investigate methods to improve the anatomical accuracy of the reconstructed tracts based on new data acquisition and processing and will include additional data for performing statistical analysis.

4.3. Comparison of different brain models

During this project, four different brain tissue models were used to evaluate the effect of tissue conductivity and model complexity on the FEM simulation result, Fig 8. In voltage control mode, Patients 1–3, there were only a small difference in electric field distribution between all models (DC > 0.95, Fig 9(b)), which is due to the fact that the tissue close to the DBS lead was quite homogenous in the segmentations. Even if the difference was small, it is also important to note that the homogenous models overestimate and underestimate the V_DBS for different patients, Fig 9(a). This provides a difficulty using homogenous models as one cannot assume the same error when comparing several patients. In contrast, current control stimulation (Patient 4) presented a larger variation, which was most pronounced for homogenous grey matter (Model I, DC > 0.67). This implies that in current stimulation the choice of brain model and segmentation accuracy is of high importance. It has previously been shown by FEM simulation that the presence of cystic cavities filled with CSF, Virchow-Robin spaces, have a high influence of the outcome as is can deform the shape of the electric field also in voltage control stimulation (Åström et al., 2006). This concludes that for implantation areas with high tissue homogeneity a simple homogenous model with right selection of tissue material could generate a relatively good result, but with difficulty to perform inter patient comparisons. However, with increasing heterogeneity the difference in result will increase.

It was also found that simulation with the heterogenous anisotropic model (Model IV) consistently generated larger electric field extension compared to the heterogeneous isotropic model (Model III), consistent with previous work (Åström et al., 2012). The high similarity between the models (DC > 0.95) can be overestimated due to the PES, which is modelled as homogeneous white matter closest to the electrode. Another aspect that influences the result is the level of anisotropy in the brain region. As shown in Fig 9(c), the level of anisotropy in the stimulated area is not very high. In another part of the brain, with higher level of tissue anisotropy, an increased difference between the models would be expected.

When designing the anisotropic brain model it was assumed that existing tabulated values for the conductivities (Gabriel et al., 1996; Andreuccetti et al., 1997) are correct as a net effective conductivity. Another approach was described by Tuch et al. (2001) who empirically derived a linear fit between the conductivity tensor and the diffusion tensor (σ = k∙D, k = 0.844) which have been used in several other publications (Åström et al., 2012; Butson et al., 2006; Chaturvedi et al., 2010). Howell and McIntyre (2016) compared that model with three other models and conclude that Tuch relationship is overestimating the conductivity of brain tissues while it gives a good prediction of the conductivity of CSF. In this study it was chosen to scale the conductivity tensor to generate a net effective conductivity as tabulated values while preserving the anisotropy from the diffusion tensor. Unfortunately, the measured conductivity values from literature are not completely consistent, and the sources are difficult to compare since measurements are made using different frequencies. The uncertainty of the true conductivity will remain a limitation when trying to fit a correct conductivity tensor.

In order to perform relative comparisons between simulations, a fixed isolevel was applied as in previous studies (Åström et al., 2015, 2010; Latorre and Wårdell, 2019; Alonso et al., 2016; Wårdell et al., 2013, Hemm et al., 2016) based on single cable neuron model simulation (Åström et al., 2015; Latorre and Wårdell, 2019). Other studies are taking a different approach on evaluating the differences in model design by applying neuron model simulation based on the output from FEM simulation (Howell and McIntyre, 2016). With Howells and McIntyre's approach the output from different models is compared by using the threshold voltage for stimulation of axons located up to 3 mm from the electrode surface. While their method is good for comparing different computer models an advantage with our approach is the possibility to visualise the electric field together with the pre-operative MR images. Hemm et al. (2005) was one of the first to use a fixed isolevel. Other groups have recently adapted this concept (Coenen et al., 2014; Akram et al., 2018), but applies it together with homogenous tissue models. The present study however, stress the importance to have an appropriate tissue model when applying a fixed isolevel for the anatomical analysis.

4.4. Effect of directional leads

The patient implanted with directional leads, Fig. 2(b), was clinically programmed for one of the three segments of the active contacts. As the true rotation of the leads could not be determined, simulations were made for all segments separately and in ring mode. The results show that there is a clear steering effect in directional mode (DC < 0.81) which indicate that one segment can generate a more optimal inclusion of the DRT whereas another segment can steer the electric field away from the DRT. If the assumption that the DRT is important for clinical effective tremor reduction holds (Coenen et al., 2011b) then the directional lead has a potential to tailor the electrical field to include as much as possible of the DRT. This requires that the anatomy of the DRT can be defined with high accuracy and the rotation of the lead correctly retrieved. On the other hand the steering effect will be reduced with higher amplitude (Alonso et al., 2016), as also seen in Fig. 10(b), where the left side had both higher amplitude (Table 1) and a higher DC. Therefore, to get most benefit out of a directional lead, the targeting must be made with high accuracy to make low amplitude stimulation possible.

5. Conclusion

This study presents a workflow for combining patient-specific electric field simulation and tractography data to evaluate the effect of DBS. When evaluating the result of the electric field simulation together with the white matter tracing, it is important to consider the reliability of the brain conductivity model and the limitation of the tractography methods in terms of anatomical representation. With a precise targeting and accurate tractography reconstruction, the directional leads can tailor the electrical field to focus the stimulation on the tract of interest and decrease the impact of other surrounding tissue.

Declaration of Competing Interest

None.