Estradiol Enhances the Depolarizing Response to GABA and AMPA Synaptic Conductances in Arcuate Kisspeptin Neurons by Diminishing Voltage-Gated Potassium Currents

Synaptic and intrinsic properties interact to sculpt neuronal output. Kisspeptin neurons in the hypothalamic arcuate nucleus help convey homeostatic estradiol feedback to central systems controlling fertility. Estradiol increases membrane depolarization induced by GABA_A receptor activation in these neurons.

Abstract

Synaptic and intrinsic properties interact to sculpt neuronal output. Kisspeptin neurons in the hypothalamic arcuate nucleus help convey homeostatic estradiol feedback to central systems controlling fertility. Estradiol increases membrane depolarization induced by GABA_A receptor activation in these neurons. We hypothesized that the mechanisms underlying estradiol-induced alterations in postsynaptic response to GABA, and also AMPA, receptor activation include regulation of voltage-gated potassium currents. Whole-cell recordings of arcuate kisspeptin neurons in brain slices from ovariectomized (OVX) and OVX+estradiol (OVX+E) female mice during estradiol negative feedback revealed that estradiol reduced capacitance, reduced transient and sustained potassium currents, and altered voltage dependence and kinetics of transient currents. Consistent with these observations, estradiol reduced rheobase and action potential latency. To study more directly interactions between synaptic and active intrinsic estradiol feedback targets, dynamic clamp was used to simulate GABA and AMPA conductances. Both GABA and AMPA dynamic clamp-induced postsynaptic potentials (PSPs) were smaller in neurons from OVX than OVX+E mice; blocking transient potassium currents eliminated this difference. To interrogate the role of the estradiol-induced changes in passive intrinsic properties, different Markov model structures based on the properties of the transient potassium current in cells from OVX or OVX+E mice were combined in silico with passive properties reflecting these two endocrine conditions. Some of tested models reproduced the effect on PSPs in silico, revealing that AMPA PSPs were more sensitive to changes in capacitance. These observations support the hypothesis that PSPs in arcuate kisspeptin neurons are regulated by estradiol-sensitive mechanisms including potassium conductances and membrane properties.

SIGNIFICANCE STATEMENT Kisspeptin neurons relay estradiol feedback to gonadotropin-releasing hormone neurons, which regulate the reproductive system. The fast synaptic neurotransmitters GABA and glutamate rapidly depolarize arcuate kisspeptin neurons and estradiol increases this depolarization. Estradiol reduced both potassium current in the membrane potential range typically achieved during response to fast synaptic inputs and membrane capacitance. Using simulated GABA and glutamate synaptic inputs, we showed changes in both the passive and active intrinsic properties induced by in vivo estradiol treatment affect the response to synaptic inputs, with capacitance having a greater effect on response to glutamate. The suppression of both passive and active intrinsic properties by estradiol feedback thus renders arcuate kisspeptin neurons more sensitive to fast synaptic inputs.

Introduction

Homeostatic feedback, a key aspect of physiology, regulates both intrinsic and synaptic properties of neurons. Reproduction is driven by central gonadotropin-releasing hormone (GnRH) secretion, which is sculpted by sex steroid feedback. Estradiol feedback can suppress GnRH neuron activity and hormone release via negative feedback, or increase GnRH neuron activity via positive feedback, producing a surge of release as the central signal for ovulation (Sarkar et al., 1976; Moenter et al., 1991). Estradiol feedback is mediated by estrogen receptor α (ERα; Couse and Korach, 1999; Christian et al., 2008), which is typically not detectable in GnRH neurons (Hrabovszky et al., 2000). Afferents thus likely communicate estradiol feedback signals to GnRH neurons. Kisspeptin neurons of the hypothalamic arcuate and anteroventral periventricular (AVPV) nuclei express ERα, and produce the neuromodulator kisspeptin, which excites GnRH neurons (Liu et al., 2008; Pielecka-Fortuna et al., 2008; Oakley et al., 2009; Lehman et al., 2010). In rodents, kisspeptin mRNA expression is differentially regulated by estradiol in arcuate (decreased) versus AVPV (increased) neurons (Smith et al., 2005), thus, these regions have been postulated to convey negative versus positive feedback (Oakley et al., 2009).

In ovariectomized (OVX) mice supplemented with a constant physiologic estradiol level (OVX+E), negative and positive feedback occur in a time-of-day- and estradiol-dependent manner, with GnRH neuron activity suppressed in the morning and increased in late afternoon (Christian et al., 2005). Similar changes in GnRH neuron firing rate, responsiveness to current injections and GABA inputs are observed between negative and positive feedback states in this daily surge model and during the estrous cycle (Christian and Moenter, 2007; Silveira et al., 2017; Adams et al., 2018a,b). In the daily surge model, estradiol feedback and time-of-day also regulate GABA input to arcuate kisspeptin neurons and response to GABA_A receptor (GABA_AR) activation (DeFazio et al., 2014). Activation of GABA_ARs depolarizes the membrane potential of arcuate kisspeptin neurons. Neither estradiol nor time-of-day alter reversal potential of GABA-induced currents or baseline membrane potential. Despite the consistent electrochemical driving force, depolarization in response to exogenous GABA was suppressed in arcuate kisspeptin neurons from OVX relative to OVX+E mice. These cells also receive substantial estradiol-regulated glutamate input mediated by AMPA receptors (Wang et al., 2018); it is unknown whether estradiol modulates response to AMPA receptor activation.

It is challenging to test hypotheses regarding membrane potential response to synaptic inputs with standard electrophysiology methods. Postsynaptic currents (PSCs) recorded in voltage-clamp mode reveal underlying synaptic conductances, but clamping the membrane potential removes the influence of alterations in voltage-gated conductances that shape the membrane potential response in the postsynaptic neuron. In current clamp, the membrane potential is free to vary in response to synaptic input resulting in postsynaptic potentials (PSPs), and the passive and active properties of the postsynaptic cell are able to sculpt the PSP. With this approach, the difficulty is the lack of control over the timing and amplitude of the synaptic events as the underlying conductances driving PSPs (and PSCs) vary with presynaptic factors, and synapse variability within and among cells.

Dynamic clamp is a variation of current-clamp that overcomes these limitations by allowing the introduction of simulated synaptic conductances, such as those underlying GABA and AMPA PSCs, while simultaneously monitoring the membrane potential response (Sharp et al., 1993; Milescu et al., 2008; Adams et al., 2019). Changes in the membrane potential response to identical simulated synaptic conductances can thus be studied across experimental groups and during pharmacological manipulation of postsynaptic voltage-gated conductances. Because both GABA and glutamate induce depolarizing PSPs in arcuate kisspeptin neurons, the membrane potential response to fast synaptic transmission may be subject to modulation by voltage-gated potassium conductances (Hoffman et al., 1997). We quantified estradiol regulation of voltage-gated potassium currents and action potential firing properties. We then used dynamic clamp and computational modeling to test the hypothesis that potassium currents mediate estradiol enhancement of the membrane potential response to fast synaptic transmission in arcuate kisspeptin neurons.

Materials and Methods

All chemicals were acquired from Sigma-Aldrich unless noted.

Animals.

Arcuate kisspeptin neurons were visualized in brain slices from Tac2-enhanced green fluorescent protein (GFP) BAC transgenic mice [015495-UCD/ STOCK Tg (Tac2-EGFP)381Gsat, Mouse Mutant Regional Resource Center; Ruka et al., 2013] and kisspeptin-hrGFP transgenic mice (Cravo et al., 2013). Arcuate kisspeptin neurons are distinguished by the coexpression of three peptides: kisspeptin itself, dynorphin, and neurokinin B (encoded by Tac2; Oakley et al., 2009). Because of this coexpression, these cells are often referred to as KNDy neurons. Single-cell PCR demonstrates that fluorescently-identified cells in the relatively thick brain slices used for recording in Tac2-GFP mice also express kisspeptin and/or dynorphin at high percentages in support of their identity as KNDy neurons (Ruka et al., 2013). All mice had ad libitum access to Harlan 2916 chow and water and were held on a 14/10 h light/dark cycle with lights on at 04:00 Eastern Standard Time. Vivarium temperature was 21–23°C. Adult female mice 60–90 d old were ovariectomized under isoflurane anesthesia with bupivacaine as a local analgesic; some mice (OVX+E) received a subcutaneous SILASTIC implant that contained 0.625 μg of estradiol in sesame oil in the scapular region also with bupivacaine treatment; these implants produce a physiologic level of estradiol (DeFazio and Moenter, 2002; Nunemaker et al., 2002; Christian et al., 2005). Studies were performed 2–4 d after surgery. The Institutional Animal Care and Use Committee of the University of Michigan approved all procedures (PRO00006816; PRO00008797).

Brain slice preparation.

All extracellular solutions were bubbled with 95% O₂/5% CO₂ throughout the experiments and for at least 30 min before exposure to tissue. Coronal brain slices (300 μm) were prepared through the hypothalamus with a Leica VT1200S using modifications of previously described methods (DeFazio and Moenter, 2002). All slices were prepared during the negative feedback (A.M.) phase of the daily surge model (brain slicing 9:00–10:00 A.M. Eastern Standard Time; recording 10:00 A.M.–1:30 P.M.). The brain was rapidly removed and placed in ice-cold sucrose saline solution containing the following (in mm): 250 sucrose, 3.5 KCl, 26 NaHCO₃, 10 D-glucose, 1.25 Na₂HPO₄, 1.2 MgSO₄, and 3.8 MgCl₂ (350 mOsm). Slices were incubated for 30 min at room temperature (∼21–23°C) in 50% sucrose saline and 50% artificial CSF (ACSF) containing the following (in mm): 135 NaCl, 3.5 KCl, 26 NaHCO₃, 10 d-glucose, 1.25 Na₂HPO₄, 1.2 MgSO₄, 2.5 CaCl_2, 315 Osm, pH 7.4. Slices were then transferred to 100% ACSF solution at room temperature for 0.5–5 h before recording. One to three recordings were obtained per mouse with a minimum of two mice studied per group; variation within a mouse was not less than that within a group. For experiments with control and drug treatment within the same cell, only one cell per slice was studied.

Recording solutions and data acquisition.

The pipette solution consisted of the following (in mm): 130 K gluconate, 15 KCl, 10 HEPES, 5 EGTA, 0.1 CaCl₂, 4 MgATP and 0.4 NaGTP, 305 mOsm, pH 7.2 with NaOH; this solution is based on the native intracellular chloride concentration in arcuate kisspeptin neurons determined using gramicidin perforated-patch recordings. (DeFazio et al., 2014). A 15 mV liquid junction potential was negated before each recording (Barry, 1994). During all recordings, slices were continuously superfused at 2 ml/min with ACSF bubbled with 95% O₂ 5% CO₂ and kept at 30–31°C with an inline-heating unit (Warner Instruments). GFP-positive cells were visualized with a combination of infrared differential interference contrast and fluorescence microscopy on an Olympus BX50WI microscope. Recordings were made with an EPC-10 patch-clamp amplifier and a computer running Patchmaster software (HEKA Elektronik). For dynamic clamp experiments, membrane voltage was filtered at 10 kHz and digitized at 20 kHz for data analysis. For voltage-clamp recordings of GABA and AMPA PSCs and potassium currents, membrane current was digitized at 10 kHz and filtered at 7 kHz. Input resistance, series resistance, baseline current, and capacitance were monitored throughout experiments from the membrane current response to a 20 ms, 5 mV hyperpolarizing voltage step to monitor recording quality. All recordings with input resistances (R_in) <0.5 GΩ series resistances (R_s) >20 MΩ, or unstable membrane capacitance (C_m) were rejected; stricter series resistance criteria were used for some studies, as specified in the Voltage-gated potassium current characterization section.

Experimental design.

The following parameters were characterized in GFP-identified arcuate kisspeptin neurons in brain slices prepared from OVX and OVX+E mice: input resistance; capacitance, potassium currents; action potential properties; on-cell membrane response to glutamate; mPSC conductance and time course; and dynamic-clamp recordings of membrane response to simulated GABA and AMPA receptor-mediated conductances. Specifics for measuring these parameters are in the next sections followed by how statistical comparisons were made. In addition, the effects of different Markov models of potassium currents from OVX and OVX+E neurons on the postsynaptic response were compared in silico.

Voltage-gated potassium current characterization.

Potassium currents were isolated pharmacologically during whole-cell voltage-clamp recordings by blocking fast sodium and calcium currents as well as ionotropic GABA and glutamate receptor-mediated currents [(in μm) 2 tetrodotoxin (TTX and d-APV are from Tocris), 200 CdCl₂, 20 d-APV, 10 CNQX, and 100 picrotoxin]. Cells were held at −75 mV between protocols. Series resistance was monitored before compensation using the current response to a 5 mV hyperpolarizing step. Cells with R_s > 15 MΩ without compensation were discarded. Two types of potassium currents, transient and sustained, were distinguished based on voltage dependence. Preliminary studies showed that a 100 ms prepulse from −75 to −40 mV inactivated the transient component, and that a 100 ms prepulse at −110 mV completely removed inactivation. A family of voltage steps was thus applied in combination with these two prepulses, to isolate and characterize the transient and sustained components. To evoke both currents, a 100 ms prepulse at −110 mV was first applied to remove the inactivation of the transient component, and then followed by test steps (200 ms, 10 mV intervals) from −60 to +50 mV. To isolate the sustained component, the same step protocol was applied but with the 100 ms prepulse set at −40 mV, which inactivates the transient component but leaves the sustained component mostly unchanged. The transient component was then isolated by subtracting the family of currents obtained with the −40 mV prepulse from the currents obtained with the −110 mV prepulse. To quantify the activation of the transient component, the peak current reached during each voltage step was extracted and plotted as a function of step voltage. For the sustained component, we used the steady-state value reached at the end of each voltage step. Current density was calculated by dividing current by the cell's capacitance. To assess the voltage dependence of activation, both transient and sustained currents were divided by the driving force derived from the Goldman–Hodgkin–Katz current equation (Clay, 2000, 2009):

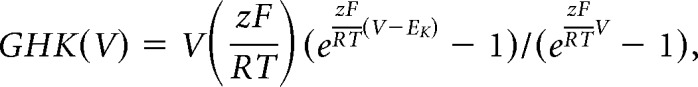where V is the step potential and E_K was calculated to be −92.6 mV after activity corrections (Kielland, 1937). In this derivation GHK(V) is unitless, thus the current divided by GHK(V) has units of picoamperes (pA) and is proportional to the permeability of the membrane to potassium. The potassium current is described by the following relationship in which Perm_maxWC assumes the role of the maximum conductance (g_max) used in linear driving force models [e.g., I = g_max (V − E_K)]:

In the Markov models and in silico assessment section, the maximum of this permeability factor (Perm_maxWC) divided by the capacitance of the cell is referred to as Perm_maxD and is used to scale the model current to match those obtained in whole-cell recordings. Perm_maxWC and Perm_maxD can be thought of as the current and current density when the driving force GHK(V) = 1. To estimate V_{0.5activation}, the peak and sustained currents were divided by GHK(V), normalized to the maximum value, plotted as a function of step potential and fit with the Boltzmann equation:

V is the command potential of the step, V_0.5 is the potential at half-maximum, and k is the “slope factor” (k has no units attributable to the F/RT factor).

Inactivation of the transient component was characterized using a variable prepulse (−110 to −40 mV, 10 mV steps, 200 ms) followed by a −10 mV test pulse. As above, the fully inactivated sweep (−40 mV prepulse) was subtracted from the other traces to isolate the transient component. The peak of this isolated current during the test pulse was normalized by the maximum value, plotted as a function of the prepulse potential, and then fit with the Boltzmann equation to provide an estimate of k and V_{0.5inactivation} for each cell. The time course of inactivation was characterized by stepping the membrane potential to −110 mV for 100 ms to remove inactivation, then stepping to the inactivation potential (−40 mV) for 0, 2, 4, 8, 16, 32, 64, 128, 256, and 512 ms, followed by a test pulse to −10 mV to assess the peak current. The non-inactivating component during the test pulse after 512 ms inactivation was subtracted from each of the other traces to isolate the transient current. Similarly, the time course of recovery from inactivation was characterized by stepping the membrane potential to −40 mV for 100 ms to fully inactivate the transient current, and then stepping to −70 mV for the durations above, followed by a test pulse to −10 mV to assess the peak current. The non-inactivating component at 0 ms recovery was subtracted from each of the other traces to isolate the transient current. V_0.5 parameters and k are reported as means of values obtained from fits to data from each cell. After normalization to the peak value, inactivation and recovery time course [tau, (τ)] curves for each cell in each group were fit with single exponential decay or recovery equations.

It was not possible to quantify all parameters from every cell, because not all cells remained within our quality control standards long enough for inclusion in the analysis of the time dependence of activation and inactivation. The OVX groups thus contained 9 cells for voltage dependence, 6 for recovery from inactivation and 5 for inactivation time course; the OVX+E groups contained 12, 9, and 9 cells, respectively.

Action potential properties.

To characterize action potential properties, current-clamp recordings were obtained in the presence of antagonists of receptors for fast synaptic transmission (in μm: 20 d-APV, 10 CNQX, 50 picrotoxin). Cells were maintained at −75.9 ± 0.3 mV by current injection (<50 pA) in current-clamp after bridge compensation of series resistance by at least 95%. Current steps (5 pA increments, 500 ms, −10 pA to +60 pA) were delivered to test the membrane potential response. The first current step to display an action potential was defined as the rheobase and the first spike analyzed in detail. Action potential threshold was defined as the potential at which the membrane potential slope exceeded 2 V/s. Action potential latency was defined as the time from start of the current injection to threshold. Rate of rise was defined as the maximum of the voltage trace derivative from threshold to peak. Full-width at half-maximum (FWHM), and afterhyperpolarization (AHP) time and amplitude were measured relative to threshold.

On-cell measurement of the response to activation of AMPA receptors.

On-cell measurement of membrane potential (OCVm) was accomplished with minor modifications of the approach used in (Verheugen et al., 1999; DeFazio et al., 2002, 2014). On-cell recordings were made with 2–3 MΩ pipettes and a minimum seal of 1.5 GΩ in ACSF containing 0.5 μm TTX. The patch was held at +100 mV pipette potential for 100 ms, exposing the patch to hyperpolarized potential [V_patch = V_m − (+100 mV)], removing inactivation from voltage-gated potassium channels. The patch was then ramped to −200 mV [V_patch = V_m − (−200 mV)] over 50 ms to activate transient currents in the patch. To measure membrane potential response to activation of AMPA receptors, NMDA (40 μm d-APV), GABA_A (100 μm picrotoxin), Group 2 and 3 metabotropic glutamate receptors (mGluRs; 20 μm LY341495, Tocris Bioscience) and Group 1 mGluRs [0.5 mm (S)-MCPG, Tocris Bioscience] were blocked. A pipette containing 100 μm glutamate in a solution containing the following (in mm): 150 NaCl, 3.5 KCl, 2.5 CaCl₂, 1.3 MgCl₂, 10 HEPES, and 10 d-glucose was positioned 10–50 μm from the cell. A baseline measure of membrane potential was obtained, then a 10–40 ms, 4–20 PSI pressure application of glutamate was triggered 50 ms before a second ramp was initiated. Data were analyzed as described previously (DeFazio et al., 2014).

Determination of synaptic conductances and time courses for dynamic-clamp studies.

The decay time constant of GABA PSCs is relatively independent of membrane potential in the range (−60 to −75 mV) used in these studies, but is strongly dependent on the pipette chloride concentration (Houston et al., 2009). It is thus important to use a physiologic chloride concentration to determine the conductance time course for use in dynamic clamp studies. Whole-cell voltage-clamp recordings of miniature GABA or AMPA receptor-mediated PSCs were obtained using a physiologic 15 mm Cl⁻ pipette solution at a holding potential of −75 mV in ACSF containing 1 μm TTX. To isolate GABA_A receptor-mediated miniature PSCs (GABA mPSCs), 20 μm d-APV, 10 μm CNQX were added to block NMDA and AMPA receptors, respectively. To isolate AMPA receptor-mediated miniature PSCs (AMPA mPSCs), 20 μm d-APV, 100 μm picrotoxin were added to block NMDA and GABA_A, receptors, respectively. After detection and visual verification of each event using custom software in Igor Pro (WaveMetrics), conductance was calculated from the mean PSC amplitude and the maximum PSC amplitude for each recording by dividing current by the driving force, V − E_rev. The decay time constant was estimated using a monoexponential fit from 80 to 20% of the peak of the averaged mPSC for each cell. As expected, the decay time constant observed with 15 mm Cl⁻ (τ; Table 1) was faster than that observed with using 140 mm Cl⁻ (15 mm: 8.64 ± 0.52, n = 12 cells from 6 mice; 140 mm: 11.05 ± 0.69, n = 18 cells from 13 mice; p = 0.014; two-tailed, unpaired Student's t test, t = 2.623 df = 26, OVX and OVX+E groups were combined; 140 mm data from DeFazio et al., 2014). Using the 15 mm Cl⁻ pipette solution, there was no difference between cells from OVX and OVX+E mice in GABA mPSC decay time constant (p = 0.645, OVX: n = 5 from 2 mice, OVX+E: n = 7 from 4 mice, two-tailed, unpaired Student's t test, t = 0.474 df = 10) or conductance (p = 0.876, Mann–Whitney U test, U = 16, df = 10). We did not detect a difference in GABA mPSC amplitude between OVX and OVX+E as reported (DeFazio et al., 2014). This is likely attributable to the decreased signal-to-noise ratio using physiologic 15 mm Cl⁻ versus 140 mm Cl⁻. Each experimental approach has benefits and limitations that must be balanced by the specific hypothesis. In the present work, determining the shape of the synaptic conductance for dynamic clamp was the goal, which necessitates using physiologic chloride. Similarly, no differences were detected between cells from OVX and OVX+E mice in AMPA mPSC decay time constant (Table 1; p = 0.687, OVX: n = 5 cells from 5 mice, OVX+E: n = 7 cells from 5 mice, two-tailed, unpaired Student's t test, t = 0.415, df = 10) or conductance (p = 0.343, Mann–Whitney U test, U = 11, df = 10).

Table 1.

Properties of mPSCs in arcuate kisspeptin neurons from OVX and OVX+E mice recorded with 15 mm Cl⁻ pipette solution

	mPSC conductance, mean ± SEM, nS	max mPSC conductance range, nS	Median mPSC conductance (range), nS	tau, ms mean ± SEM
GABA
OVX
(n = 5, 2 mice)	1.30 ± 0.31	1.34–5.82	1.06 (0.87–2.42)	8.34 ± 0.58
OVX +E
(n = 7, 4 mice)	1.27 ± 0.14	1.22–4.55	1.02 (0.83–1.62)	8.86 ± 0.82
AMPA
OVX
(n = 5, 5 mice)	0.34 ± 0.07	0.67–1.23	0.25 (0.20–0.60)	2.33 ± 0.21
OVX +E
(n = 7, 5 mice)	0.28 ± 0.04	0.40–2.40	0.21 (0.14–0.36)	2.19 ± 0.24

Synaptic conductances in dynamic clamp.

The dynamic-clamp system consisted of a separate computer (Marquis C733-T with dual Intel Xeon E5–2667v2 Ivy Bridge-EP 3.3 GHz, 8-core processors, 8x16Gb DDR3–1866 SDRAM, ASLabs) and data acquisition system (PCIe-6361 Multifunction DAQ card with a BNC interface, National Instruments) interacting with the Patchmaster EPC10 patch-clamp amplifier system as described. Dynamic clamp was implemented using freely available QuB software (MLab edition, https://milesculabs.biology.missouri.edu/QuB.html), as described previously (Milescu et al., 2008). The digital outputs of the EPC10 were used to trigger independent GABA and AMPA synaptic conductances in the dynamic-clamp system.

The time course of the GABA and AMPA receptor-mediated postsynaptic conductances (g_syn) was modeled based on the mPSC data in Table 1 using a monoexponential of 9 and 2.3 ms, respectively. The input to the dynamic clamp system is the membrane potential of the cell (V_m), read from the EPC10 patch-clamp amplifier in current-clamp mode; the output from the system is the computed command current (I_dc), which drives the current command input of the EPC10. This input/output cycle was repeated at ∼50 kHz. To implement the synaptic conductance model in dynamic clamp mode, I_dc was calculated from the postsynaptic conductance (g_syn) as a function of time after a trigger and the linear driving force: I_dc = g_syn × (V_m − E_rev), where E_rev is the reversal potential (E_GABA = −55 mV; E_AMPA = 0 mV).

For dynamic-clamp recordings, holding current was adjusted to keep the baseline membrane potential near −75 mV. During these experiments, fast synaptic response to endogenous GABA and glutamate release was blocked with 20 μm d-APV, 10 μm CNQX, 100 μm picrotoxin to prevent interference with the analysis of PSPs generated by dynamic clamp (dcPSPs). Action potentials were blocked with 1 μm TTX to block nonlinear influence of sodium currents near action potential threshold. To test the effect of blocking voltage-dependent potassium and calcium channels, some experiments included 4AP (0.5 mm) and/or Ni²⁺ (300 μm) as detailed below. Before each acquisition series, series resistance (R_s < 20 MΩ) was estimated as above and compensated 95% using the C_slow and R_s compensation circuitry of the amplifier. Bridge balance was confirmed in current-clamp mode by manually adjusting the bridge to cancel the fast transient voltage deflection in response to a 5 ms duration 5 pA hyperpolarizing current step. In most cases, R_s estimated in voltage clamp from the peak current in response to a 20 ms, 5 mV hyperpolarizing step in voltage-clamp, corresponded well with R_s estimated by the automatic C_slow compensation circuitry of the EPC10/Patchmaster software. In rare cases of discrepancy, we considered the manual bridge balance in current-clamp mode to be more accurate.

Membrane response to dcPSPs in cells from OVX versus OVX+E mice.

Using the monoexponential conductance models, GABA and AMPA conductances were applied and the GABA or AMPA dcPSPs recorded. Conductances near and above the physiologic range of mPSCs were used (1, 2, 5, 10 nS for GABA; 0.5, 1, 2, 3 nS for AMPA; Table 1). These values span a similar range of conductances based on the range of physiologic values observed in the mPSC studies, as well as the possibility of larger conductance events under in vivo conditions. To test whether any difference in postsynaptic response was attributable to transient potassium currents, these studies were repeated during bath-applied treatment with a low concentration of 0.5 mm 4AP. To quantify the amount of current blocked at this concentration, voltage-clamp recordings were made of arcuate kisspeptin neurons in brain slices from OVX mice, comparing control slices and slices exposed to 0.5 mm 4AP. Based on the voltage-dependent inactivation of the transient current characterized above, we used a shortened protocol to record the combined transient and non-inactivating currents (−110 mV for 200 ms, followed by a −10 mV test pulse), then isolated the transient component by subtracting the non-inactivating component (−40 mV for 200 ms, followed by a −10 mV test pulse). The peak transient current density at −10 mV was reduced by 38% (control: 0.20 ± 0.02 nA/pF; 4AP: 0.13 ± 0.02 nA/pF; n = 6 per group, p = 0.0134, t = 2.998, df = 10). At this concentration, no difference in input resistance was detected (control: 0.74 ± 0.07 GΩ; 4AP: 0.86 ± 0.06 GΩ, p = 0.1987, t = 1.375, df = 10).

Markov models and in silico assessment.

To model the transient K⁺ current, three Markov model structures were selected from the literature: one modeling a Hodgkin–Huxley-type mh current (Mendonça et al., 2018), one modeling pure open-state inactivation (OSI), and one modeling pure closed-state inactivation (CSI; Fineberg et al., 2012). Kv models were assembled in QuB using the Eyring formalism: k = k₀ × exp(k₁V) for transitions between states, with model-specific scaling of rates between states. The output of these models is open probability, P_open(V, t). During optimization, P_open was converted to current using the following relationship:

where Perm_max is a parameter optimized in parallel with the k₀ and k₁ for each rate, and is analogous to the maximum conductance (g_max) when using a linear driving force. The maximum open probability (P_{open_max}) is related to the Perm_maxWC measured during the whole-cell voltage-clamp characterization of the potassium current by the following relationship:

Where P_{open_max} is the maximum value of P_open(V, t). Optimization revealed Perm_max was different for each model and always greater than Perm_maxWC. This is because P_{open_max} < 1 for models with inactivation states and depends on the rate of inactivation (Holmqvist et al., 2002; Kaulin et al., 2008). The rate constant parameters (k₀, k₁) and Perm_max were optimized to representative transient potassium currents of a single arcuate kisspeptin neuron from the OVX and OVX+E groups measured as described. Specifically, normalized voltage dependence of activation and inactivation, normalized time course of inactivation and recovery from inactivation, peak permeability as a function of voltage, and the kinetics of the macroscopic current as a function of step voltage and time were selected from one cell in each group that was most representative of the median for that group.

Using a numerical approach in QuB (Milescu et al., 2008; Navarro et al., 2018; Salari et al., 2018), each Kv model type (mh, OSI, and CSI) was optimized to the OVX and OVX+E datasets separately resulting in six models. During optimization, the same voltage protocols used in the potassium current characterization studies were run through each Kv model, and resulting open probability was converted to current using the I_Kv equation in the previous paragraph. For each model optimization, errors for different parameters (e.g., V_{1/2 activation} curve) were weighted. As the optimization proceeded, the weighted sum of squares differences between the model and data for each parameter were summed to make a single error for that model. This weighted sum of errors was minimized by iteratively altering the model parameters (Milescu et al., 2008). The Davidon–Fletcher–Powell (DFP) algorithm was used to search for minima in the parameter set.

Optimized Kv models for each of the OVX and OVX+E datasets were tested in silico using experimentally-determined mean R_in (OVX: 0.78 GΩ, OVX+E: 0.87 GΩ) modeled as a leak conductance with a reversal potential of −75 mV, and C_m (OVX: 14.5 pF, OVX+E: 11.8 pF), as well as the overall mean R_in and C_m (OVX: 0.83 GΩ, OVX+E: 13.2 pF). These values were the means of the passive properties of cells in the dcPSP experiments without 4AP plus those of cells in the action potential study. Because the Kv models had a non-zero open probability near −75 mV, the leak conductance and holding current (<1.6 pA) were adjusted to maintain the apparent input resistance at the above values and the initial membrane potential at −75 mV for each Kv model. To test the effect of Kv models on the amplitude of in silico GABA and AMPA PSPs, the same conductance waveforms and four conductance values used for the dynamic clamp studies were delivered to the model cell defined above. QuB was used to solve the following differential equation for membrane potential as a function of time, V(t):

The components on the right side of the equation are defined as follows.

I_command allows manipulation of the membrane potential.

I_syn = g_syn(t)(V − E_syn), where g_syn and E_syn reflect the GABA or AMPA conductance and reversal potential, respectively (as defined in the dynamic clamp methods).

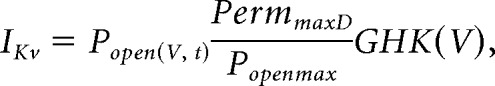where P_open is the output of the Kv model as a function of V and time, Perm_maxD is defined in the Voltage-gated potassium current characterization section.

I_leak = g_leak(V − E_leak), where g_leak is the linear leak conductance expressed as density and E_leak is −75 mV.

To establish control PSP values, Perm_maxD was set to 0 to eliminate the influence of the Kv model. For each Kv model, the leak conductance and holding current were adjusted to set the initial conditions of simulation at −75 mV and R_in for OVX or OVX+E. Input resistance was confirmed in silico for each model using a 100 ms, −5 pA current injection via I_command.

Statistics.

Data are reported as mean ± SEM with individual values shown where practical. Statistical comparisons were made using Prism 7 or Prism 8 (GraphPad Software). Data were tested for normal distribution with Shapiro–Wilk. Tests were chosen appropriate for the experimental design and data distribution as specified in the results. V_0.5 parameters, slope, and time course of inactivation and recovery parameters estimated from individual curve fits from each cell were compared with a two-tailed, unpaired Student's t test (with Welch's correction as appropriate), or two-tailed Mann–Whitney U test depending on the data distribution. For two-way ANOVA, the Bonferroni post hoc is considered sufficiently robust to use with non-normally distributed data (Underwood, 1996). Significance was set at p < 0.05.

Results

Voltage-gated potassium currents are diminished in neurons from OVX+E mice

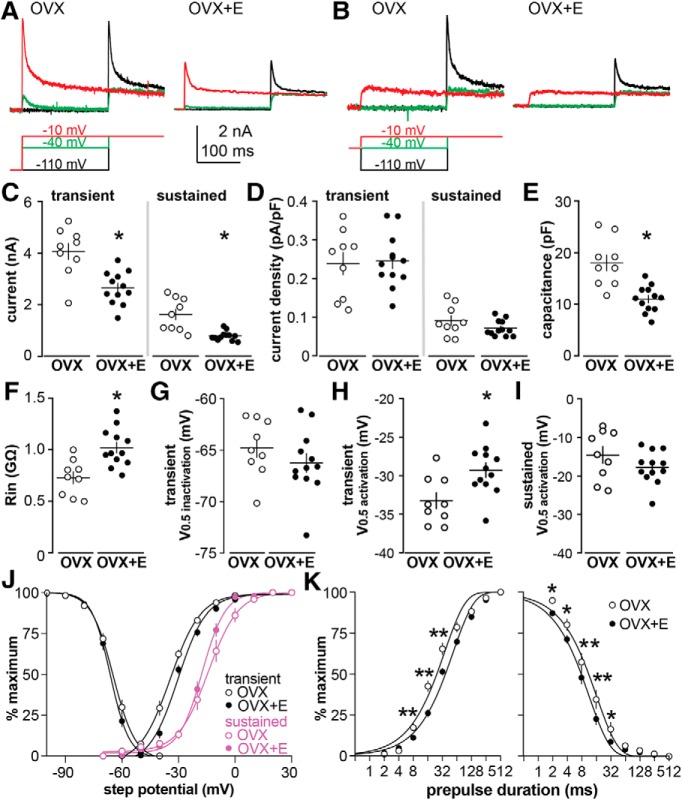
Estradiol enhances the membrane depolarization of arcuate kisspeptin neurons in response to GABA (DeFazio et al., 2014). We postulated that the effects of estradiol on the postsynaptic response to GABA are mediated by intrinsic conductances of the arcuate kisspeptin neuron. Voltage-gated potassium currents can be activated near the baseline membrane potential and their activation would tend to resist membrane depolarization. We thus tested the hypothesis that estradiol diminishes voltage-gated potassium currents. Representative potassium currents in cells from OVX versus OVX+E mice are shown in Figure 1, A and B. Both transient (p = 0.0006, t = 4.123, df = 19) and sustained (p = 0.0041, t = 3.828, df = 8.973) currents were suppressed by estradiol (Fig. 1C; OVX n = 9 cells from 6 mice, OVX+E n = 12 cells from 9 mice, two-tailed, unpaired Student's t test, with Welch's correction for sustained current). Current density was not different between groups (Fig. 1D; peak t = 0.202, df = 19; sustained t = 1.351, df = 11.20) as estradiol treatment reduced capacitance (Fig. 1E; p = 0.0003, two-tailed, unpaired Student's t test, t = 4.428, df = 19) as reported (Frazão et al., 2013). Under these recording conditions, estradiol also increased input resistance (Fig. 1F; p = 0.0016, two-tailed, unpaired Student's t test, t = 3.697, df = 19).

Figure 1.

Changes in voltage dependence reduce potassium channel availability in arcuate kisspeptin neurons from OVX+E mice. A, Top, Selected traces of potassium currents generated following the −110 mV prepulse; bottom, voltage protocol. The activation pulses shown are from −110 mV (black), −40 mV (green) and −10 mV (red), before a test pulse at −10 mV. B, Top, Selected traces of potassium currents generated following the −40 mV prepulse; bottom, voltage protocol. C, D, Individual values and mean ± SEM for peak transient (left) and sustained (right) current (C) and current density (D). E–I, Individual values and mean ± SEM for capacitance (E), input resistance (F), transient V_{0.5inactivation} (G), transient V_{0.5activation} (H), and sustained V_{0.5activation} (I). C–I, *p < 0.05, two-tailed, unpaired Student's t test (with Welch's correction as appropriate; Tables 3,4). J, Mean ± SEM normalized inactivation/activation and nonlinear regression fits for the transient current (black lines) and activation for the sustained current (magenta lines). K, Log base 2 plots of mean ± SEM and nonlinear regression fits of normalized time course of inactivation (left) and recovery from inactivation (right). Some error bars are within the symbols in J and K. K, *p < 0.05, **p < 0.01, two-way ANOVA/Fisher's LSD.

Voltage dependence parameters and statistical parameters are presented in Table 2. The V_{0.5inactivation} (Fig. 1G,J) of the transient current was not altered by estradiol but estradiol increased the slope of the voltage dependence, indicating that these channels inactivate over a narrower voltage range when the steroid is present. The V_{0.5activation} of the transient potassium current was depolarized in neurons from OVX+E mice (Fig. 1H,J), but the slope was not different. Estradiol also accelerated the time course of inactivation, indicating that the channels inactivated more rapidly at the −40 mV test potential, and it delayed recovery from inactivation of the transient current (Fig. 1K; Table 3). Although current density was unchanged, changes in voltage dependence suggest diminished efficacy of the transient potassium current in arcuate kisspeptin neurons from OVX+E mice.

Table 2.

Voltage-dependence of activation and inactivation, and statistical parameters

	OVX, mean ± SEM	OVX+E, mean ± SEM	p	t or U statistic (df)
Transient activation
V0.5, mV	−33.2 ± 1.0 (n = 9)	−29.3 ± 0.9 (n = 12)	0.01	t = 2.86 (19)
Slope factor, k	0.0039 ± 0.0002 (n = 9)	0.0041 ± 0.0003 (n = 12)	0.808	U = 50 (19)
Transient inactivation
V0.5, mV	−64.8 ± 0.9 (n = 9)	−66.2 ± 0.9 (n = 12)	0.287	t = 1.09 (19)
Slope factor, k	−0.0051 ± 0.0002 (n = 9)	−0.0060 ± 0.0001 (n = 12)	0.003	t = 2.89 (19)
Sustained activation
V0.5, mV	−14.5 ± 2.1 (n = 9)	−17.7 ± 1.2 (n = 12)	0.187	t = 1.37 (19)
Slope factor, k	0.0036 ± 0.0001 (n = 9)	0.0045 ± 0.0001 (n = 12)	0.0002	t = 4.67 (19)
Transient maximum permeability
PermmaxWC, pA at driving force = 1	157.8 ± 12.8 (n = 9)	106.9 ± 8.3 (n = 12)	0.0026	t = 3.472 (19)
PermmaxD, pA/pF at driving force = 1	9.4 ± 3.6 (n = 9)	9.9 ± 2.7 (n = 12)	0.713	t = 0.373 (19)

Table 3.

Time course of activation and inactivation, and two-way ANOVA parameters

Inactivation time course (OVX: n = 5, OVX+E: n = 9)
Interaction	F(9,126) = 2.593	p = 0.089
Prepulse duration	F(9,126) = 772.7	p < 0.0001
Estradiol	F(1,14) = 5.189	p = 0.039
Recovery time course (OVX: n = 6, OVX+E: n = 9)
Interaction	F(9,99) =7.941	p < 0.0001
Prepulse duration	F(9,99) =1277	p < 0.0001
Estradiol	F(1,11) =11.72	p = 0.0057

Estradiol modifies action potential properties of arcuate kisspeptin neurons

Changes in potassium currents are likely to result in changes in neuronal firing properties. We thus compared action potential properties between cells from OVX and OVX+E mice (Fig. 2; Table 4). The holding current was manually adjusted to set the membrane potential to ∼−75 mV, and the resulting baseline membrane potential was not different between groups (OVX n = 22 cells from 13 mice, −76.2 ± 0.4 mV; OVX+E n = 18 cells from 10 mice, −75.5 ± 0.5 mV, p = 0.236, two-tailed, unpaired Student's t test, t = 1.205, df = 38). Current steps (5 pA increments, 500 ms) were applied until the cell initiated firing. The properties of the first action potential were quantified, with representative traces shown in Figure 2, A and B. Less current was needed to induce firing (rheobase) in cells from OVX+E mice (Fig. 2C; p = 0.005, two-tailed Mann–Whitney U test) and action potential latency was shorter (Fig. 2D; p < 0.0001, two-tailed Mann–Whitney U test), consistent with the weaker transient potassium current in arcuate kisspeptin neurons from OVX+E mice. Estradiol also hyperpolarized the action potential threshold (Fig. 2E; p = 0.008, two-tailed, unpaired Student's t test) and reduced the rate of rise of the action potential spike (Fig. 2F; p = 0.009, two-tailed Mann–Whitney U test). Action potential amplitude was also reduced in the OVX+E group (Fig. 2G; p = 0.030, two-tailed, unpaired Student's t test). No differences were observed in action potential full width at half maximum or afterhyperpolarization time between groups (Fig. 2H,I), but the AHP amplitude was reduced (Fig. 2J; p = 0.005 two-tailed, unpaired Student's t test) in cells from OVX+E mice. The difference in AHP amplitude may be primarily driven by the hyperpolarization of threshold in OVX+E mice because this was the reference for the measurement. In these current-clamp studies, there was no statistically detectable effect of estradiol on capacitance (OVX: 13.7 ± 0.7 pF, OVX+E: 12.1 ± 0.7 pF) or input resistance (OVX: 0.847 ± 0.054 GΩ, OVX+E: 0.934 ± 0.054 GΩ). Throughout the studies within this paper, the effects of estradiol on capacitance (reducing) and input resistance (increasing) are in the same direction and similar magnitude, but vary with regard to achieving the p < 0.05 standard set for significance. P values for these parameters range between 0.03 and 0.14 for two-sample tests. Based on this range, it would be difficult to exclude effects of passive properties when the p value is mildly over the standard while considering effects when the p value is mildly under the standard. Because of the potential impact of passive properties on many of the variables being assessed, we have incorporated both overall and group (OVX vs OVX+E) means as detailed below.

Figure 2.

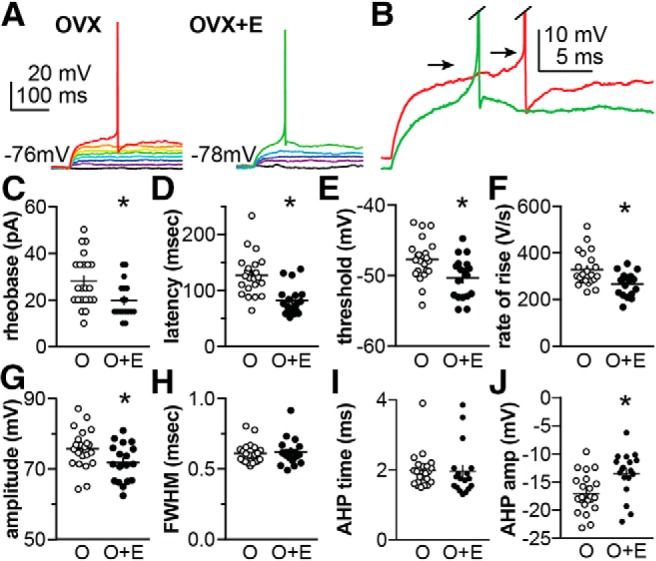
Estradiol alters action potential properties in arcuate kisspeptin neurons. A, Representative current-clamp recordings of kisspeptin neurons from OVX (left) and OVX+E (right) mice. Current steps (5 pA increments) were applied until the cell initiated firing; action potential properties of the first spike were characterized. B, Expanded axis view of the onset of the spikes in A; arrows mark threshold and spikes were truncated. C–J, Individual values and mean ± SEM values of action potential properties of cells from OVX (O; white circles) and OVX+E (O+E; black circles) mice; C, minimum current to induce firing (rheobase); D, latency; E, action potential threshold; F, action potential rate of rise; G, action potential amplitude; H, FWHM of action potential spike; I, time of AHP; J, AHP amplitude (amp). *p < 0.05 two-tailed unpaired Mann–Whitney U test (C, D, F) or two-tailed unpaired Student's t test (E, G, J). Note some graphs do not include the origin. Mann–Whitney U test did not detect differences between groups in H and I (both p > 0.15).

Table 4.

Statistical parameters for action potential properties of cells from OVX (n = 22) versus OVX+E (n = 18) mice (Fig. 2)

Parameter	p	t or U, df = 38
Rheobase, pA	0.005*	U = 97
AP latency, ms	0.0001*	U = 59
AP amplitude, mV	0.030*	t = 2.25
Threshold, mV	0.008*	t = 2.80
AP FWHM, ms	0.798	U = 188
AP rate of rise, V/s	0.009*	U = 103
AHP min time, ms	0.182	U = 148.5
AHP amp, mV	0.005*	t = 3.02
Baseline mV	0.236	t = 1.21
Input resistance, G	0.142	U = 143.5
Capacitance, pF	0.114	U = 139.5

*p < 0.05 two-tailed, unpaired Student's t test or two-tailed Mann–Whitney U test.

Response of arcuate kisspeptin neurons to activation of AMPA receptors is not increased by estradiol in on-cell measurements

In addition to GABA, these cells also receive substantial glutamatergic transmission that is regulated by cycle stage and estradiol feedback (Wang et al., 2018). To attempt to isolate responses mediated by AMPA receptors, mGluRs, NMDA, and GABA_A receptors were antagonized and membrane potential estimated before and during brief, local application of 100 μm glutamate using an on-cell method as described previously (DeFazio et al., 2014). As reported (DeFazio et al., 2014), estradiol did not affect baseline membrane potential of arcuate kisspeptin neurons (OVX: −78.7 ± 2.0, OVX+E: −81.9 ± 1.0, both n = 9 cells from 4 mice, two-tailed unpaired Student's t test, p = 0.1597, t = 1.475, df = 16). The change between baseline membrane potential and that following glutamate application was not different between groups (OVX: 30.3 ± 3.2 mV, OVX+E: 24.5 ± 1.9 mV, p = 0.144, two-tailed, unpaired t test with Welch's correction, t = 1.555 df = 13.14). The apparent lack of effect of estradiol on membrane response to glutamate may be attributable to robust activation of AMPA receptors overwhelming the estradiol-dependent difference in potassium currents, perhaps because of the more depolarized reversal potential for AMPA-mediated currents, and/or the shorter time course of AMPA versus GABA receptor-mediated currents. These limitations would increase the influence of two caveats of this on-cell approach: (1) only a single measurement can be obtained during transmitter treatment, and (2) the exogenous transmitter application has a higher amplitude and longer duration than levels achieved via synaptic release. To test these responses under more physiologic conditions, we used dynamic clamp.

Dynamic clamp reproduces postsynaptic responses

GABA and AMPA synaptic conductances were simulated in dynamic clamp using a monoexponential curve with a decay time constant based on measurements of endogenous PSCs obtained under physiologic chloride conditions. NMDA receptor-mediated postsynaptic conductances were not simulated because the nonlinear magnesium block <−50 mV limits their activation in the membrane potential range-of-interest (Nowak et al., 1984). The process for obtaining the synaptic conductance waveform from the experimental data is outlined in Figure 3 using GABA_A receptor-mediated PSCs. GABA postsynaptic potentials (dcPSPs) generated using dynamic clamp were similar to endogenous PSPs (Fig. 3C).

Figure 3.

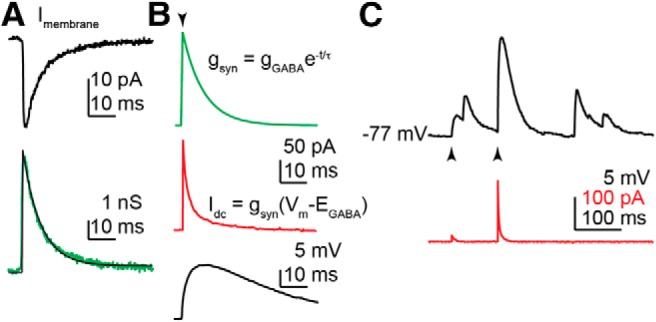
A, Averaged GABA PSC (top, black) recorded at −75 mV using 15 mm Cl⁻ pipette solution (E_GABA = −55 mV). The current trace was converted to conductance (bottom, green), by dividing by the driving force of −20 mV, and fit with a monoexponential function (bottom, black) to determine tau, which was used in the rest of the studies. B, The simulated GABA conductance (top, green) constructed from the monoexponential function derived from the fit in A. During a triggered event (arrowhead), the dynamic clamp current is calculated from the conductance waveform, scaled by g_GABA, and the driving force (V_m − E_GABA), updated at ∼50 kHz with real-time measurement of the membrane potential (V_m). I_dc (middle, red) is the analog output of the dynamic clamp system. The response to this stimulus signal in current-clamp mode is shown in the black trace (bottom). C, Membrane potential response (dcPSPs; black) to simulated GABA conductances (g_GABA = 1 and 10 ns; arrowheads) is similar to spontaneous GABA PSPs in the trace; the current injected by dynamic clamp (I_dc) is shown in red.

Simulated GABA and AMPA conductances generate smaller PSPs in neurons from OVX mice

Dynamic clamp was used to introduce consistent and repeatable simulated synaptic conductances. Membrane potential during dcPSP experiments was not different among groups (Table 5). For GABA, four test conductances at 1, 2, 5, and 10 nS with a reversal potential of −55 mV were delivered to cells (Fig. 4A). Representative examples of dynamic clamp-induced GABA postsynaptic potentials (dcPSPs) are shown in Figure 4B for OVX and OVX+E groups. Amplitude of GABA dcPSPs relative to baseline membrane potential was calculated and plotted as a function of conductance (Fig. 4E). At all conductances tested, GABA dcPSPs were smaller in neurons from OVX mice (n = 16 cells from 13 mice; Tables 6, 7) than those from OVX+E mice (n = 18 cells from 11 mice). This is consistent with previous observations using the OCVm technique (DeFazio et al., 2014).

Table 5.

Membrane potential (mV) during dcPSP experiments and statistical parameters

	OVX	OVX+E
GABA
Control	−75.7 ± 0.2 n = 16	−76.2 ± 0.1 n = 18
4AP	−75.8 ± 0.2 n = 14	−75.8 ± 0.2 n = 9
AMPA
Control	−75.5 ± 0.1 n = 12	−75.6 ± 0.2 n = 11
4AP	−75.3 ± 0.2 n = 9	−74.3 ± 0.3 n = 7
GABA; two-way ANOVA, df = 53
Interaction	F(1,53) = 0.9973	p = 0.3225
4AP	F(1,53) = 0.7313	p = 0.3963
Steroid	F(1,53) = 1.404	p = 0.2413
AMPA; two-way ANOVA, df = 35
Interaction	F(1,35) = 0.1140	p = 0.73676
4AP	F(1,35) = 1.268	p = 0.2679
Steroid	F(1,35) = 0.0009263	p = 0.9759

Figure 4.

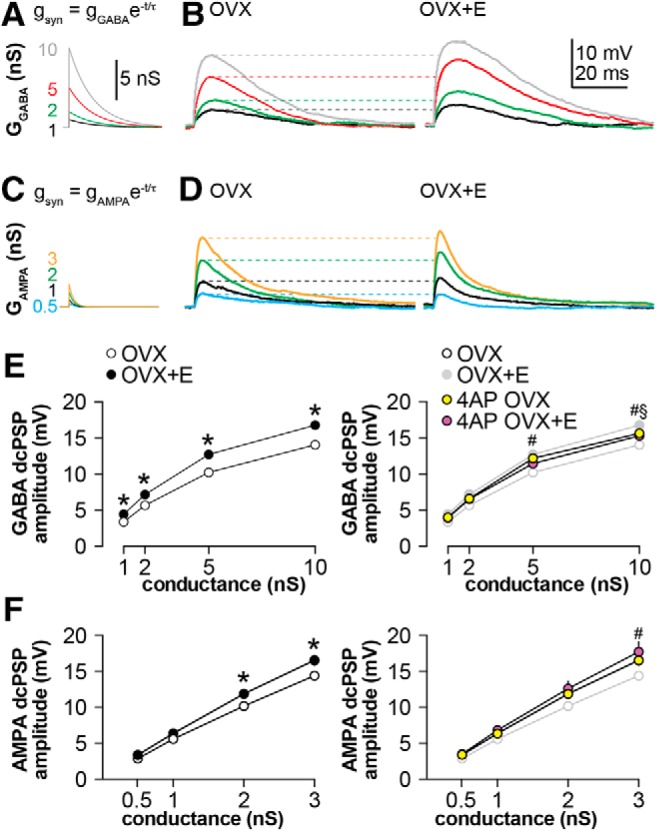
Estradiol enhances membrane depolarization in response to simulated conductances. A, Family of GABA conductances studied: 1 nS (black), 2 nS (green), 5 nS (red), or 10 nS (gray). B, Representative raw traces showing dcPSPs produced in response to the simulated GABA conductances in cells from OVX (left) and OVX+E (right) mice. C, Family of AMPA conductances studied: 0.5 (teal), 1 (black), 2 (green), and 3 (yellow). D, Representative raw traces showing dcPSPs produced in response to the simulated AMPA conductances in cells from OVX (left) and OVX+E (right) mice. E, F, Left, GABA (E) or AMPA (F) dcPSP amplitude in neurons from OVX mice was diminished compared with that from OVX+E mice. Right, Blocking part of the transient potassium current with 0.5 mm 4AP restored the depolarization in cells from OVX mice to the level observed in cells from OVX+E mice. Data from the left graph are replotted in gray on the right; some error bars are within the symbols. Statistics in E and F: two-way repeated-measures ANOVA/Bonferroni including all four treatments, *p < 0.05 OVX versus OVX+E, #p < 0.05 OVX versus 4AP OVX, §p < 0.05 OVX + 4AP versus OVX+E.

Table 6.

Statistical parameters for GABA dcPSP studies (two-way, repeated-measures ANOVA/Bonferroni)

	post hoc p values
	10 nS	5 nS	2 nS	1 nS
OVX vs OVX+E	<0.0001	<0.0001	0.0020	0.0483
OVX vs OVX + 4AP	0.0021	0.0001	0.1365	0.5442
OVX + 4AP vs OVX+E	0.0376	>0.9999	>0.9999	>0.9999

GABA, interaction: p = 0.0004, F_(9,159) =3.60; conductance: p < 0.0001, F_(3,159) = 2463; treatment: p < 0.0001, F_(3,53) =9.327.

Table 7.

Statistical parameters for AMPA dcPSP studies (two-way, repeated-measures ANOVA/Bonferroni)

	post hoc p values
	3 nS	2 nS	1 nS	0.5 nS
OVX vs OVX+E	0.0058	0.0427	0.7049	>0.9999
OVX vs OVX + 4AP	0.0210	0.0865	0.9346	>0.9999
OVX + 4AP vs OVX+E	>0.9999	>0.9999	>0.9999	>0.9999

AMPA, interaction: p = 0.0015, F_(9,99) = 3.286; conductance: p < 0.0001, F_(3,99) = 1542; treatment: p = 0.0426, F_(3,33) = 3.041.

To test whether the estradiol modulation of membrane response was specific to GABA dcPSPs, four test conductances based on AMPA-mediated PSCs with a reversal potential of 0 mV were delivered: 0.5, 1, 2, and 3 nS (Fig. 4C; Tables 6, 7). Similar to GABA dcPSPs, cells from the OVX+E group exhibited greater membrane potential depolarization in response to the 2 and 3 nS synaptic conductances (Fig. 4F; Tables 6, 7; OVX: n = 12 cells from 7 mice, OVX+E: 11 cells from 10 mice). This is in contrast to the above results obtained using the OCVm technique. It is likely this disparity reflects the increased rigor provided by the dynamic clamp method in terms of a more physiologic (shorter) duration of the applied synaptic conductances compared with slower and more prolonged activation of AMPA receptors with local application of glutamate. The differences in conductance time course (longer for GABA) and driving force (greater for AMPA) between GABA_A and AMPA receptors likely also play a role in the physiologic response. No statistical difference in input resistance was detected in these groups but estradiol reduced capacitance (Table 8).

Table 8.

Input resistance and capacitance (mean ± SEM) and ANOVA parameters for dynamic clamp studies in Figure 4

	Input resistance, GΩ		Capacitance, pF
	OVX	OVX+E	OVX	OVX+E
GABA
Control	0.740 ± 0.057 n = 16	0.844 ± 0.058 n = 18	15.20 ± 1.07*	11.46 ± 0.62
4AP	0.977 ± 0.070 n = 14	0.788 ± 0.043 n = 9	12.22 ± 0.98	11.95 ± 0.79
Two-way ANOVA parameters
Interaction	F(1,53) = 5.402	p = 0.0240	F(1,53) = 3.511	p = 0.0665
4AP	F(1,53) = 2.05	p = 0.1581	F(1,53) = 1.799	p = 0.1856
Estradiol	F(1,53) = 0.4564	p = 0.5023	F(1,53) = 4.689	p = 0.0349,
				Bonferroni post hoc
				OVX vs OVX+E, p = 0.013
AMPA
Control	0.719 ± 0.075 n = 12	0.813 ± 0.047 n = 11	15.02 ± 0.76*	12.07 ± 0.95
4AP	0.797 ± 0.028 n = 9	0.704 ± 0.049 n = 7	12.87 ± 1.23	11.46 ± 1.25
Two-way ANOVA parameters
Interaction	F(1,33) = 1.613	p = 0.2129	F(1,33) = 1.293	p = 0.4634
4AP	F(1,33) = 0.001431	p = 0.9700	F(1,33) = 4.189	p = 0.1907
Estradiol	F(1,33) = 0.1304	p = 0.7203	F(1,33) = 10.44	p = 0.0424,
				Bonferroni post hoc
				OVX vs OVX+E, p = 0.193

*p < 0.05 main effect of estradiol on capacitance two-way ANOVA.

Decreasing 4AP-sensitive currents increases the membrane potential response to simulated synaptic conductances in neurons from OVX mice

Voltage-gated potassium currents, which are elevated in cells from OVX mice, are poised to modulate response to synaptic input because they can activate at subthreshold membrane potentials (Segal et al., 1984; DeFazio et al., 2002). We tested the hypothesis that blocking a portion of transient potassium channels increases the response to simulated GABA and AMPA synaptic conductances. Since these cells have substantial transient currents, fully blocking this current could have strong effects on input resistance. We thus chose to partially block the transient with a low concentration (0.5 mm) of 4AP Gustafsson et al. (1982), which blocked ∼38% of the transient current in these cells. Treatment with 4AP increased amplitude of GABA dcPSPs in neurons from OVX mice to levels observed in OVX+E mice (Fig. 4E, right; 5 and 10 nS conductances, OVX vs OVX+4AP, n = 14 cells from 8 mice; Tables 6, 7; two-way, repeated-measures ANOVA/Bonferroni). AMPA dcPSPs in cells from OVX mice were similarly enhanced by this 4AP treatment (Fig. 4F, right; 3 nS conductance). Of note, the low concentration of 4AP used did not alter passive properties (Table 8). Together these observations suggest that transient potassium currents play a role in shaping the membrane potential response to fast PSCs, and that this action is reduced by estradiol.

Postsynaptic voltage-gated calcium channels do not shape dcPSPs

An interesting question is whether or not activation of other voltage-gated conductances, such as calcium channels, might boost or prolong the membrane response to synaptic conductances. To begin to test whether calcium channels shape the membrane potential response, we applied 300 μm Ni²⁺ during dcPSP recordings in cells from OVX+E mice under the same conditions used in Figure 4, E and F (left; TTX, APV, CNQX, and picrotoxin). OVX+E mice were chosen as estradiol has been reported to increase T-type calcium currents in both arcuate and AVPV kisspeptin neurons (Wang et al., 2016; Qiu et al., 2018). Representative traces in response to 10 nS (GABA) or 3 nS (AMPA) conductances are shown in Figure 5A; summary data in 5B–E. This high concentration of Ni²⁺ was used to provide broad-spectrum blockade of voltage-gated calcium channels. Under these conditions, Ni²⁺ had no effect on GABA or AMPA dcPSP amplitude or time course; further studies with blockers of specific calcium channel subtypes were thus not pursued.

Figure 5.

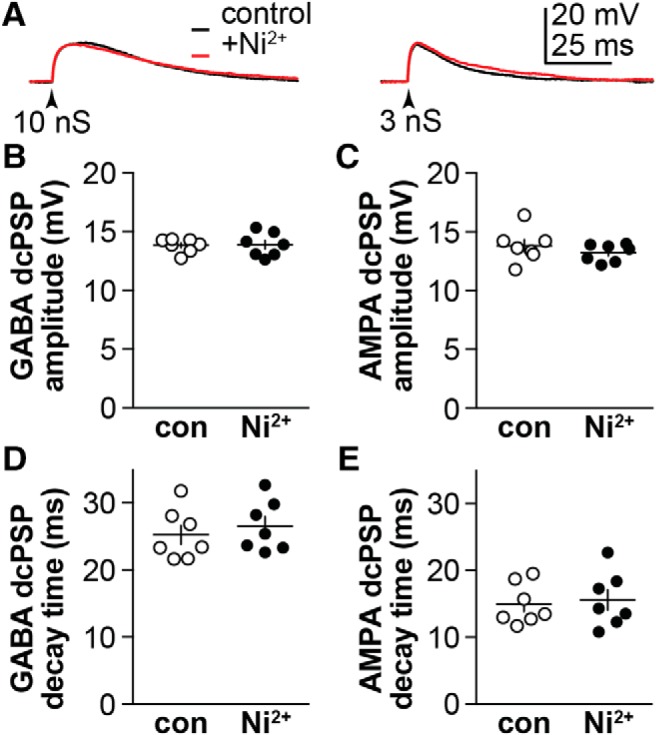
Voltage-gated calcium currents do not sculpt membrane response in cells from OVX+E mice during triggered GABA (10 nS) or AMPA (3 nS) dcPSPs (arrowheads). A, Representative traces under control conditions (black) and 300 μm Ni²⁺ (red) for GABA dcPSPs (left) and AMPA dcPSPs (right). B, C, Individual values and mean ± SEM of GABA and AMPA dcPSP amplitude. D, E, Individual values and mean ± SEM of GABA and AMPA dcPSP decay time constant. Two-tailed, paired Student's t test. GABA peak: p = 0.8845, t = 0.1515, df = 6; GABA tau: p = 0.1852, t = 1.496, df = 6; AMPA peak: p = 0.3670, t = 0.9754, df = 6; AMPA tau: p = 0.4053, t = 0.8949, df = 6.

In silico analysis of the interaction of PSP and passive cellular properties

These results suggest that estradiol-dependent suppression of a transient potassium current leads to an increased response to synaptic conductances. Passive properties of these cells were also altered and the possible contribution of these changes needed to be considered. To test this we used an in silico approach. For this, we combined the input resistance and capacitance values from the action potential and dcPSP studies to increase the statistical power as both studies were conducted under similar conditions. In this combined dataset, estradiol increased input resistance (OVX: n = 50, 0.78 ± 0.25 GΩ vs OVX+E: n = 47, 0.87 ± 0.23 GΩ, Mann–Whitney U test, p = 0.0188, U = 850.5) and reduced capacitance (OVX: 14.50 ± 3.52 pF, OVX+E: 11.84 ± 2.91 pF, two-way t test, p = 0.0001, t = 4.043). To compare the effects of Kv models without this difference in passive properties, we also calculated the overall mean input resistance and capacitance (n = 97, 0.83 ± 0.24 GΩ and 13.2 ± 3.5 pF, respectively).

The cell was modeled in silico as a single compartment with OVX, OVX+E group means or the overall mean capacitance and resistance; synaptic conductances of identical size and shape used for the dynamic clamp experiments were applied. Mean values of passive properties from the OVX versus OVX+E groups did not alter in silico GABA PSPs (Fig. 6A), which were similar in amplitude to GABA dcPSP recordings from OVX+E mice (Table 9). The difference in passive properties between groups was thus not sufficient to generate the difference in OVX versus OVX+E dcPSP amplitudes observed. In silico AMPA PSPs, however, were more sensitive to the differences in passive properties, specifically their amplitude was increased when the passive properties from OVX+E mice were used (Fig. 6B; Table 9). This selective effect on the response to AMPA is likely attributable to the greater driving force and the briefer stimulus. This suggests the experimentally observed difference in AMPA dcPSPs could be explained in part by the difference in passive properties. An additional role for voltage-gated potassium currents cannot be eliminated, however, as 4AP modified the dcPSP without changing passive properties.

Figure 6.

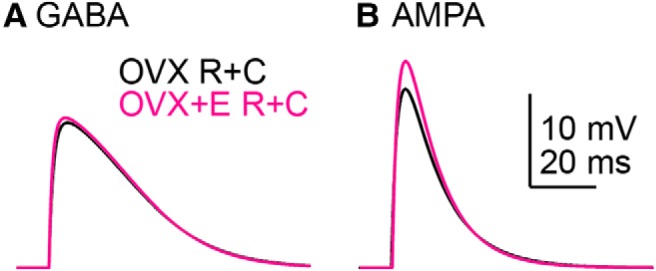
In silico analysis of the interaction between input resistance and capacitance (R+C) to shape the response to GABA (A; 10 nS) and AMPA (B; 3 nS) synaptic conductances.

Table 9.

In silico PSP amplitudes (mV) and the effects of Kv models with different input resistance (R) and capacitance (C) combinations

	Corresponding group R + C		Overall R + C
	OVX	OVX+E	OVX	OVX+E	OVX 38% Kv block
GABA, 10 nS
dcPSP	14.11 ± 0.51	16.77 ± 0.35
In silico R + C only	16.12	16.67	16.39
+mh	14.87	16.41	15.17	16.12	15.56
+OSI	14.24	15.85	14.58	15.73	15.02
+CSI	15.53	16.48	15.80	16.24	16.02
AMPA, 3 nS
dcPSP	14.55 ± 0.62	16.57 ± 0.62
In silico R + C only	19.87	22.93	21.26
+mh	17.32	21.83	18.28	20.40	19.06
+OSI	17.12	20.22	18.15	19.43	18.83
+CSI	18.43	21.75	19.44	20.60	19.95

In silico analysis of interaction between PSPs and voltage-gated potassium currents

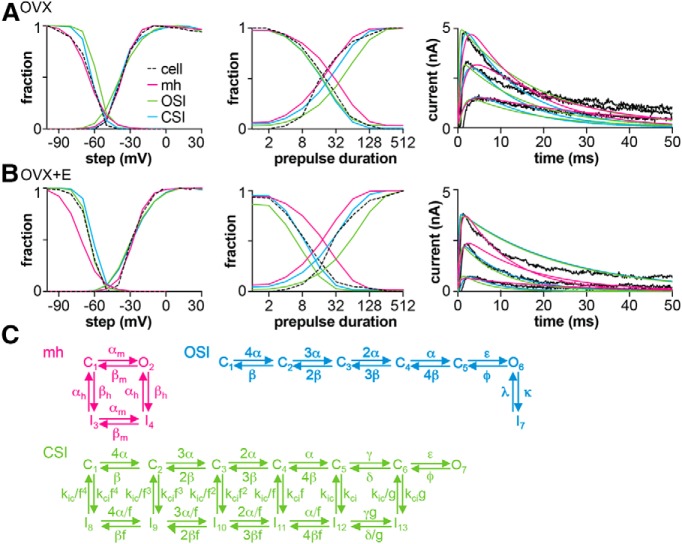
Estradiol-induced shifts in the voltage dependence of activation, the time course of inactivation and recovery, as well as the peak conductance are hypothesized to suppress the transient potassium current during a postsynaptic potential, resulting in larger PSPs in neurons from OVX+E mice. This hypothesis was evaluated in silico by optimizing three Markov models (Kv models; Fig. 7) to the potassium current characteristics from a representative cell from each group, OVX and OVX+E: mh Hodgkin–Huxley-equivalent model (similar to Mendonça et al., 2018), and OSI and CSI models (Fineberg et al., 2012). As is typical, none of the Kv models perfectly reproduced the currents measured in cells, and some models fit certain features better than others. Each of the models reproduced the basic voltage dependence and shape of the potassium currents from the representative OVX and OVX+E datasets (Fig. 7; Table 10).

Figure 7.

Optimization of Kv models to whole-cell voltage-clamp data. A, B, Kv model kinetics in response to the potassium current voltage-clamp protocols from Figure 1 with representative datasets from OVX (A) and OVX+E (B) groups. Left, Activation and inactivation; middle, time course of inactivation and recovery from inactivation; right, current traces in response to voltage steps to −30, −10, and +10 mV. The black traces are data from the representative cell from each group used for optimization. C, Markov model structures tested: mh Hodgkin–Huxley (Mendonça et al., 2018), OSI, and CSI (Fineberg et al., 2012). C, Closed state; I, inactivated state; O, open state.

Table 10.

Kv model rates

	OVX		OVX+E
	k0	k1, mV−1	k0	k1, mV−1
mh
αm	6.49E+2	1.67E−2	1.24E+3	1.84E−2
ßm	1.98E+0	−1.49E−1	1.35E+1	−1.50E−1
αh	7.66E−3	−1.16E−1	9.28E−3	−1.08E−1
ßh	5.79E+1	2.20E−2	7.62E+1	1.82E−2
OSI
α	4.54E+3	3.32E−2	4.28E+3	9.50E−3
ß	1.14E+3	−3.00E−2	1.29E+3	−5.74E−2
ϵ	4.65E+7	−1.76E−1	4.62E+7	−1.66E−1
φ	1.38E+7	−1.59E−1	1.31E+7	−1.54E−1
λ	6.08E−2	−8.22E−2	5.41E−2	−7.83E−2
κ	8.17E+1	−8.84E−3	9.54E+1	−4.88E−2
CSI
α	2.02E+1	−2.62E−1	2.03E+1	−2.49E−1
ß	3.26E−3	−2.67E−1	3.28E−3	−2.56E−1
γ	1.07E+3	3.41E−2	1.04E+3	3.85E−2
δ	8.82E−1	−2.19E−1	8.49E−1	−2.10E−1
ϵ	1.15E+4	−3.04E−2	1.11E+4	−3.77E−2
φ	7.21E+2	−3.15E−2	7.18E+2	−6.55E−2
kic	2.47E+1	*	2.51E+1	*
kci	1.09E+1	*	1.08E+1	*
f	4.15E−1	*	4.18E−1	*
g	1.41E+2	*	1.40E+2	*

*k_ic, k_ci, f, and g are voltage-independent parameters thus lack k₁.

These Kv models were next combined in silico with the single-compartment model cell representing an arcuate kisspeptin neuron with OVX, OVX+E, or overall mean capacitance and input resistance and a −75 mV baseline membrane potential as above. Because some of the Kv models had non-zero open probabilities at −75 mV, leak conductance and holding current were adjusted to set the input resistance and baseline membrane potential at the specified values before testing the response to the synaptic conductance (Table 11). The time course of the PSPs and the resulting potassium currents are shown in Figure 8; PSP amplitudes with different combinations of passive and Kv models are shown in Table 9. When synaptic conductances were delivered to the model cell, each of the Kv models reacted differently to the change in membrane potential. The mh model reacted more quickly but had a smaller peak current during the GABA PSP, compared with the OSI model, which activated more slowly but produced a larger amplitude current. Both of these Kv models blunted the largest GABA PSP by >1 mV and AMPA PSP by >2 mV (Table 9). The amplitudes of the GABA and AMPA PSPs as a function of synaptic conductance for these different conditions are plotted in Figure 9 for the different Kv models. In contrast, the CSI Kv model produced a minimal potassium current in response to the synaptic conductances and correspondingly minimal effect on the PSPs (<0.5 mV GABA and <1.5 mV AMPA). More transient potassium current was activated during AMPA than GABA synaptic conductances (Fig. 8, compare A, C). This was additive with the amplifying effects of OVX+E passive properties on AMPA PSPs. A similar pattern was observed in that Kv models optimized to OVX+E Kv data were less effective at blunting the AMPA PSP (Fig. 9). These effects of Kv persisted when differences in passive properties between OVX and OVX+E groups were neutralized (Figs. 8B,D, 9B,D). Finally, we confirmed the Markov models reproduced the expected effects of a 38% reduction in Kv amplitude as was observed in recordings of cells from OVX mice with 4AP (Table 9). These in silico results are consistent with a role for estradiol-mediated amplification of GABA and AMPA PSPs via decreased capacitance, increased input resistance, and suppression of Kv properties.

Table 11.

In silico Kv simulation parameters

	Popen_max	Corresponding group R + C		Overall R + C
		I_inj, pA	G_leak, nS	I_inj, pA	G_leak, nS
OVX
mh	0.77	0.570	0.082	0.519	0.086
OSI	0.69	1.603	0.070	1.461	0.074
CSI	0.49	0.056	0.088	0.050	0.091
OVX+E
mh	0.79	0.078	0.096	0.087	0.091
OSI	0.70	0.156	0.094	0.131	0.090
CSI	0.47	0.009	0.096	0.008	0.091

Figure 8.

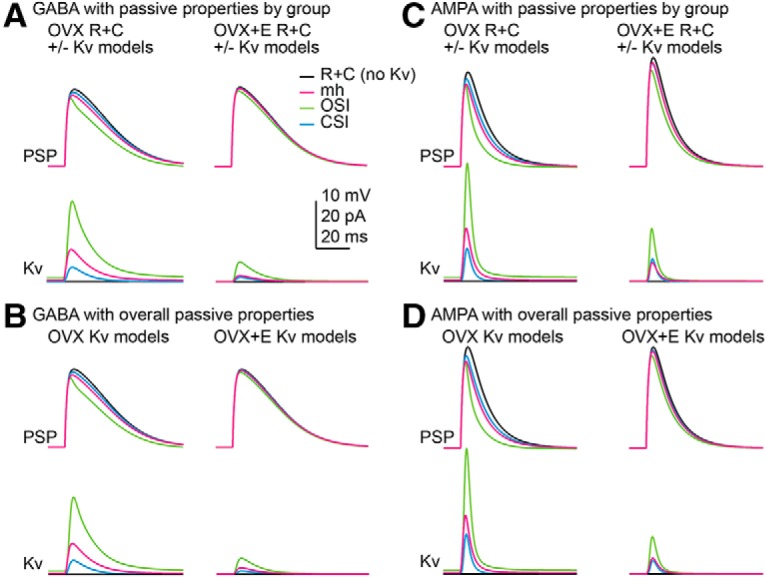
In silico analysis of the interaction between passive properties (R+C) and voltage-gated potassium channels (Kv) in shaping the response to GABA and AMPA synaptic conductances. A, C, In silico PSPs (top) and Kv model current (bottom) for GABA (A; 10 nS) and AMPA (C; 3 nS) using the OVX and OVX+E group passive properties and the three Kv models optimized to the respective group properties. B, D, In silico PSPs (top) and Kv model current (bottom) for GABA (B; 10 nS) and AMPA (D; 3 nS) using the overall mean passive properties and the three Kv models optimized to the respective group properties.

Figure 9.

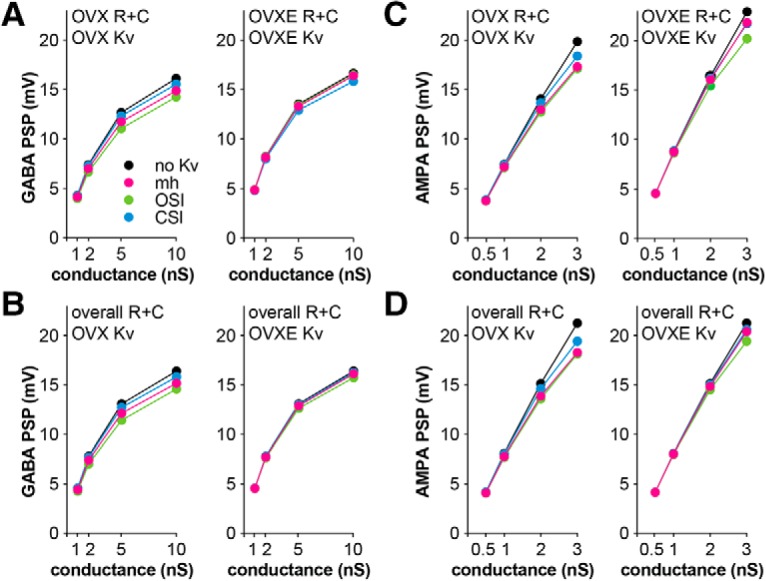
PSP amplitude induced by GABA (A, B) and AMPA (C, D) conductances with the different Kv models. Kv models are deterministic thus there are no error bars. A, C compare the combined effects of R+C and Kv models; B, D illustrate the effect of Kv models when R+C is held constant between groups.

Discussion

GnRH release, the final central output regulating fertility, is sculpted by steroid feedback. Estradiol feedback is conveyed to GnRH neurons at least in part via ERα-expressing kisspeptin neurons of the arcuate nucleus, which may play a role in GnRH pulse generation and its regulation by steroid feedback (Qiu et al., 2016; Clarkson et al., 2017; Vanacker et al., 2017; Wang et al., 2018, 2019). We examined estradiol-sensitive intrinsic mechanisms, demonstrating that estradiol-sensitive passive properties and potassium conductances directly shape the membrane potential response to fast synaptic input in these neurons.

Other studies have investigated the interactions between transient potassium channels and postsynaptic response. For example, in dendrites of CA1 and cortical layer V pyramidal cells these channels affect synaptic plasticity and dendritic integration (Hoffman et al., 1997; Losonczy et al., 2008; Harnett et al., 2013; Hall et al., 2015). Blocking a higher proportion of transient potassium current than in the present work directly increased membrane potential response to glutamatergic inputs (Hoffman et al., 1997). The present work is consistent with these findings but, importantly, extends these concepts in at least three important ways. First, the use of dynamic clamp ensured the incoming “synaptic” stimulus does not vary among groups. Second, transient potassium currents were shown to interact with depolarizing GABA and AMPA PSPs. Third, a known systemic homeostatic input to these cells (estradiol) modified this interaction.

Estradiol-induced increases in the depolarization response to exogenous GABA to near the theoretical maximum (E_GABA; DeFazio et al., 2014) led to the hypotheses that voltage-gated conductances intrinsic to these cells are estradiol-sensitive, and that these changes enhance the membrane potential response to synaptic inputs. The present work supports both hypotheses. Sustained and transient voltage-gated potassium currents were reduced by estradiol. Potassium current density was not affected as estradiol also reduced the size of cell (capacitance), suggesting an alternative mechanism, such as posttranslational modifications of existing channels, may underlie these estradiol-induced changes (DeFazio and Moenter, 2002). Despite the similar current density, rheobase and latency to fire, action potential properties that can be altered by subthreshold transient potassium current activation, were decreased by estradiol. It is unlikely that the relatively small changes in passive properties are sufficient to drive these changes in action potential properties, but may synergize with the estradiol-induced decrease in transient potassium current function to give rise to increased excitability in the OVX+E group.

In addition to GABA, arcuate kisspeptin neurons receive AMPA-mediated fast synaptic inputs that are regulated by estradiol and cycle stage (Wang et al., 2018). On-cell analysis of the membrane potential response to AMPAR activation did not reveal a similar estradiol-dependent increase in responsiveness. To extend these observations with a more physiologic approach that permits continuous monitoring of membrane response, we used dynamic clamp to deliver model GABA and AMPA conductances. Both GABA and AMPA dcPSPs were enhanced by estradiol, attributable at least in part to decreased activation of the transient potassium current. Blocking 38% of this current with 4AP restores dcPSP amplitude in cells from OVX mice to levels observed in cells from OVX+E mice, consistent with blunting of both AMPA and GABA dcPSPs by the more robust transient potassium current in the OVX group.

To parse the estradiol-induced changes in active versus passive properties, in silico modeling was used. In a model cell containing only passive properties, there was a minor influence on the response to GABA. In contrast, the AMPA response was sensitive to the small difference in capacitance. These observations suggest the estradiol-induced increased GABA response requires mechanisms other than the estradiol-dependent change in passive properties, whereas the increased AMPA response is likely attributable in part to passive changes.

To overcome the challenges of studying potassium currents in the subthreshold range where they are likely to sculpt response to synaptic input, we optimized and tested three different Kv models of representative transient potassium currents from OVX and OVX+E mice using the current density determined in our studies. The estradiol-dependent decrease in capacitance not only increased the passive responsiveness of the cell, but also reduced the magnitude of the potassium current. In silico studies of the interaction between these Kv models and synaptic conductance-induced PSPs revealed that both the type of the Kv model (mh, OSI, CSI) and optimization to OVX versus OVX+E parameters affected the outcome. mh and OSI models optimized to the OVX dataset reproduced the blunting of PSPs observed in the dynamic clamp study, whereas the CSI model had a smaller effect. This was reflected in the size and timing of the Kv current: the mh and OSI models produced faster and larger currents in response to PSPs. The failure of Kv models optimized to the OVX+E dataset to blunt the PSPs was associated with smaller, slower model currents during the PSPs. These in silico conditions neutralized the effects of cell-to-cell variation in input resistance and capacitance observed in the dynamic-clamp studies and the influence of other voltage-gated channels. Together, these observations further support the hypothesis that estradiol-dependent functional suppression of transient potassium currents drives the increased response to both GABA and AMPA synaptic conductances, and revealed an additional role for passive properties in regulating response to AMPA. These studies also emphasize the importance of assessing multiple Markov model structures when testing hypotheses in silico, as model structure had as much effect on the output of the system as the experimental data to which the models are optimized.

The present work focused on voltage-gated potassium currents as an estradiol-sensitive active property. There was little effect of voltage-gated calcium currents on dcPSPs under the conditions examined, suggesting that the transient potassium current counteracted any potential boosting effect of calcium channels. It is also unlikely that the observed estradiol-enhanced response to GABA and AMPA dcPSPs is attributable to boosting by sodium channels, because TTX was used to avoid contamination of recordings with action potentials. The possibility cannot be excluded, however, that sodium currents, or calcium currents, play additional roles in shaping the membrane potential response to synaptic input in vivo (Carter et al., 2012; Branco et al., 2016). In this regard, estradiol-induced modification of sodium channels in these cells is suggested by its hyperpolarization of action potential threshold (Kress et al., 2010) and reduction of action potential rate-of-rise, estradiol also enhances T-type calcium currents in kisspeptin neurons (Wang et al., 2016; Qiu et al., 2018).

Our findings support recent work showing a transient potassium current in arcuate kisspeptin neurons from male mice contributes to firing irregularity by interacting with a persistent sodium current independent of fast synaptic input (Mendonça et al., 2018). The present findings extend that work by demonstrating potassium currents in these cells are diminished by estradiol, an important modulator of these cells, and optimizing the Kv models to the properties of the Kv current of the arcuate kisspeptin neurons from OVX and OVX+E mice. Our in silico work revealed that small differences in Kv properties can affect the response of the model to synaptic input. Together these studies suggest voltage-gated potassium currents in these cells interact with other intrinsic properties (e.g., capacitance, sodium channels) and extrinsic properties (e.g., synaptic input) to modify firing output. These complex interactions are of interest with regard to the perhaps paradoxical finding in the present study of an effect of estradiol in an animal model of negative feedback that would tend to activate, rather than suppress, these cells. Of note, estradiol also reduces GABA PSC amplitude (Frazão et al., 2013; DeFazio et al., 2014), and reduces a neuropeptide-induced depolarization (Qiu et al., 2016). Knockdown of ERα specifically in these cells increases the percentage of high-firing cells and glutamatergic transmission while disrupting cycles, which depend on functional negative feedback (Wang et al., 2019). This raises the intriguing possibility of a role for estradiol in multiple aspects of network homeostasis affecting these cells.

The conductance range used for these dcPSP studies was carefully considered. The mean conductance for GABA_A and AMPA mPSCs was similar to the smallest conductances tested using dynamic clamp. mPSCs with a maximum synaptic conductance approaching the size of the largest conductances tested with dynamic clamp were observed, but rare. In vivo, when presynaptic activity is not blocked and when the full presynaptic network is intact, even larger PSCs may occur. Standard experimental conditions for recording PSCs in brain slices facilitate analysis of the shape of the synaptic conductance by isolating the transmitter receptor-of-interest, but they necessarily alter the pattern of presynaptic activity.

Transient voltage-gated channels and fast synaptic inputs represent functionally broad targets for physiologic regulation. Potassium channels play established roles in action potential firing and dendritic integration. The present work directly demonstrates an additional role for these conductances in sculpting response to depolarizing synaptic transmission. The estradiol sensitivity of this response further indicates it helps shape the output of arcuate kisspeptin neurons in response to systemic feedback. How these features are integrated with changes in GnRH neuron properties to give rise to the varied patterns of GnRH release necessary for fertility remains an experimental target.