Dentate Gyrus Mossy Cells Share a Role in Pattern Separation with Dentate Granule Cells and Proximal CA3 Pyramidal Cells

The complementary processes of pattern completion and pattern separation are thought to be essential for successful memory storage and recall. The dentate gyrus (DG) and proximal CA3 (pCA3) regions have been implicated in pattern separation, in part through extracellular recording studies of these areas. However, the DG contains two types of excitatory cells: granule cells of the granule layer and mossy cells of the hilus.

Abstract

The complementary processes of pattern completion and pattern separation are thought to be essential for successful memory storage and recall. The dentate gyrus (DG) and proximal CA3 (pCA3) regions have been implicated in pattern separation, in part through extracellular recording studies of these areas. However, the DG contains two types of excitatory cells: granule cells of the granule layer and mossy cells of the hilus. Little is known about the firing properties of mossy cells in freely moving animals, and it is unclear how their activity may contribute to the mnemonic functions of the hippocampus. Furthermore, tetrodes in the dentate granule layer and pCA3 pyramidal layer can also record mossy cells, thus introducing ambiguity into the identification of cell types recorded. Using a random forests classifier, we classified cells recorded in DG (Neunuebel and Knierim, 2014) and pCA3 (Lee et al., 2015) of 16 male rats and separately examined the responses of granule cells, mossy cells, and pCA3 pyramidal cells in a local/global cue mismatch task. All three cell types displayed low correlations between the population representations of the rat's position in the standard and cue-mismatch sessions. These results suggest that all three excitatory cell types within the DG/pCA3 circuit may act as a single functional unit to support pattern separation.

SIGNIFICANCE STATEMENT Mossy cells in the dentate gyrus (DG) are an integral component of the DG/pCA3 circuit. While the role of granule cells in the circuitry and computations of the hippocampus has been a focus of study for decades, the contributions of mossy cells have been largely overlooked. Recent studies have revealed the spatial firing properties of mossy cells in awake behaving animals, but how the activity of these highly active cells contributes to the mnemonic functions of the DG is uncertain. We separately analyzed mossy cells, granule cells, and pCA3 cells and found that all three cell types respond similarly to a local/global cue mismatch, suggesting that they form a single functional unit supporting pattern separation.

Introduction

The hippocampus is essential for the storage and retrieval of spatial and episodic memories (Eichenbaum, 2004; Squire et al., 2004). Due to the extensive recurrent collateral system in CA3, this region is often proposed to be involved in pattern completion, the process of retrieving a full pattern of activity from partial or degraded inputs (Marr, 1971; McNaughton and Morris, 1987; McClelland and Goddard, 1996), or the related computational functions of generalization and error correction. The dentate gyrus (DG) has been proposed to be involved in the complementary computation of pattern separation, which is thought to minimize interference between similar experiences by reducing overlap between similar input patterns before storage (Marr, 1969; McNaughton and Nadel, 1990; Yassa and Stark, 2011). Neunuebel and Knierim (2014) provided direct evidence for DG pattern separation and CA3 pattern completion in a local/global cue mismatch (“double rotation”) task: the DG population response to cue mismatch was less correlated than its entorhinal inputs (pattern separation), whereas there was a coherent population response in CA3 (pattern completion) (Knierim and Neunuebel, 2016).

CA3 is often modeled as a homogeneous auto-associative network; however, there is increasing evidence for anatomical and functional gradients along the CA3 transverse axis (Claiborne et al., 1986; Ishizuka et al., 1990, 1995; Li et al., 1994; Witter, 2007; Hunsaker et al., 2008; Nakamura et al., 2013; Marrone et al., 2014; Lee et al., 2015; Lu et al., 2015; Sun et al., 2017; Flasbeck et al., 2018). These gradients indicate that proximal CA3 (pCA3) may be better considered as a functional component of the DG circuit than as part of CA3 (Scharfman, 2007; Hunsaker et al., 2008). Although Neunuebel and Knierim (2014) found evidence of pattern completion in CA3, most of these cells were from intermediate and distal CA3. More recently, the response to cue rotation in pCA3 cells was shown to resemble the DG response (Lee et al., 2015), further suggesting that pCA3 and DG may work as a coordinated, functional unit (Hunsaker et al., 2008).

While most cells in the DG are granule cells (Amaral et al., 1990), the hilus of the DG contains excitatory mossy cells, which receive inputs from, and project back to, granule cells, both directly and through interneurons (Amaral, 1978; Scharfman, 2016). Mossy cells also receive backprojections from CA3, creating a feedback loop from CA3 to DG (Scharfman, 2007). Although the computational role of mossy cells in the DG circuit is relatively unknown, they may support pattern separation, perhaps by regulating granule cell sparseness (Myers and Scharfman, 2009); consistent with this notion, loss of mossy cells causes context discrimination deficits (Jinde et al., 2012). There are very few studies of the in vivo firing properties of mossy cells, but they appear to be highly active relative to the sparse firing of granule cells, and often have multiple place fields and fire in multiple environments (Danielson et al., 2017; GoodSmith et al., 2017; Senzai and Buzsáki, 2017). Although the soma of mossy cells are located in the hilus, their spikes can be recorded extracellularly on tetrodes located in pCA3 and throughout the DG hilus and granule cell layer (Henze and Buzsáki, 2007; Neunuebel and Knierim, 2012; GoodSmith et al., 2017).

To determine how mossy cells may contribute to the pattern separation functions of the hippocampus, we analyzed previous data from tetrodes located in pCA3 or DG (Neunuebel and Knierim, 2014; Lee et al., 2015). Using a random forests classifier, we separated putative mossy cells, granule cells, and pCA3 cells (GoodSmith et al., 2017) and examined their responses in the double rotation task. The population response of mossy cells to cue mismatch resembled the granule cell and pCA3 cell responses. These results implicate mossy cells in pattern separation and add further support to the notion that pCA3 cells are more appropriately considered as part of a pCA3/DG pattern separation circuit than as part of the auto-associative CA3 network responsible for pattern completion.

Materials and Methods

Subjects and surgery

In total, cells from 16 male Long–Evans rats (Charles River Laboratories, 4–7 months old) were analyzed in the present study. Data from two previous papers were analyzed (Neunuebel and Knierim, 2014; Lee et al., 2015), consisting of cells from 14 rats. Cells that were recorded on tetrodes located in the DG of the rats from Lee et al. (2015) (not analyzed in that study) and recordings from 2 additional rats were also analyzed. All rats were individually housed on a 12 h reversed light/dark schedule with ad libitum access to water. Custom-built recording drives consisting of 15–20 independently movable tetrodes were implanted over the right hippocampus, and tetrodes were slowly lowered over many days into the DG and/or CA3. Recordings were performed during the surgery to find the lateral edge of CA3, which was used as a landmark for drive placement; the most lateral tetrode ranged from 3.2 to 4.9 mm lateral to bregma and 3.2 to 4.4 mm posterior to bregma. All animal care, surgical, and housing protocols were approved by the Institutional Animal Care and Use Committee at Johns Hopkins University or the University of Texas Health Science Center at Houston and complied with National Institutes of Health guidelines.

Training and behavior

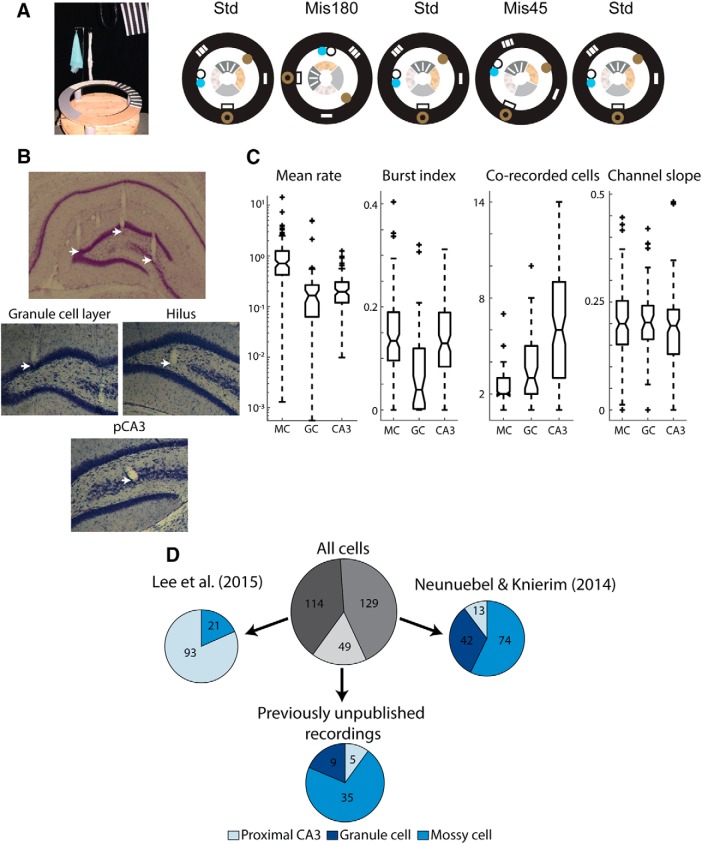
Following recovery from surgery, rats were food restricted to 80%–90% of their free feeding weight and trained in a “double rotation task” (Knierim, 2002) (see Fig. 1A). Rats were trained to run in a clockwise direction around a circular track (76 cm outer diameter, 56 cm inner diameter) for arbitrarily placed chocolate sprinkle rewards. The track was divided into four segments by distinct texture cues on the track (local cues). Six large cues (global cues) were placed around the periphery of the black-curtain encircled room, and white noise was played through a white noise generator. Once rats were trained and tetrodes were in the DG or CA3, the double rotation experiment was conducted over 4 d, typically during the dark portion of the light/dark cycle. To ensure recording stability throughout the experiment, baseline sessions (each 15–30 min) were recorded at the start and end of each recording day while the rat rested in a small dish on a pedestal. Each day, recording sessions with the standard cue configuration (STD), in which local and global cues were in the same configuration as during all training sessions, were interleaved with mismatch sessions (MIS), in which local cues were rotated counterclockwise and global cues were rotated an equal amount in the clockwise direction for a total cue mismatch of 45°, 90°, 135°, or 180°. For example, in a 180° mismatch, local cues were rotated 90° counterclockwise and global cues were rotated 90° clockwise. Each day consisted of five recording sessions, beginning and ending with a STD session, with two MIS sessions chosen pseudo-randomly so that each mismatch angle was experienced two times over the course of the 4 d of recording (once in days 1–2 and once in days 3–4). In some rats, an additional STD session was recorded at the start of the recording, but these sessions are not analyzed here. For recordings from Neunuebel and Knierim (2014), rats were recorded as they foraged for food in an open 135 cm × 135 cm square box after the final double rotation session each day. Two rats (227 and 232) were excluded in that study from analysis of this foraging session due to poor behavioral coverage of the arena, and we have excluded them from our analysis of the foraging (but not double rotation) session as well.

Figure 1.

Double rotation task and cell classification. A, Left, The double rotation track. Right, Schematic of an example double rotation recording day. B, Nissl-stained brain sections showing tetrode tracks. Mossy cells can be recorded on tetrodes located throughout the DG and pCA3. Top, An example section showing tetrodes located in the granule cell layer, hilus, and pCA3 pyramidal cell layer (white arrows, left to right, respectively). Bottom, High-magnification images of Nissl-stained sections, showing tetrodes ending in the granule cell layer, hilus, and pCA3 cell layer. C, Firing properties used for cell type classification. Box plots represent the distributions (from left to right) of the mean firing rate (log scale), burst index, number of cells recorded on the same tetrode, and channel slope for classified mossy cells (MC), granule cells (GC), and pCA3 cells (CA3). For each plot, dashed line indicates the range of data (except for outliers, denoted by + signs). Horizontal lines indicate the median, 25th percentile, and 75th percentile. Notches indicate the 95% CI of the median. D, Source and classification of all 292 cells analyzed. From Neunuebel and Knierim (2014), 74 cells were classified as mossy cells, 42 were classified as granule cells, and 13 were classified as pCA3 cells. From Lee et al. (2015), 93 cells were classified as pCA3 cells and 21 were classified as mossy cells. An additional 49 cells that were not previously analyzed were also classified and analyzed here. Of these 49 cells, 35 were classified as mossy cells, 5 were classified as pCA3 cells, and 9 were classified as granule cells.

Electrophysiological recordings

Electrophysiological recording procedures were described previously (Neunuebel and Knierim, 2014; Lee et al., 2015). Tetrodes were made from 12.5 μm nichrome wires or 17 μm platinum-iridium wires (California Fine Wire). Nichrome tetrodes were electroplated with gold to reduce the impedance to ∼200 kOhms, and unplated platinum-iridium tetrodes had an impedance of ∼700 kOhms. Neural signals were recorded using a Cheetah Data Acquisition System (Neuralynx). A subset of rats from Lee et al. (2015) was recorded using a 64-channel wireless system (Triangle Biosystems International) that transmitted the signal to the Cheetah acquisition system. The signals were amplified 1000–5000 times and filtered between 600 Hz and 6 kHz (for units) or between 1 and 300 or 475 Hz (for local field potential). Spike waveforms above a threshold of 30–70 μV were sampled for 1 ms at 32 kHz, whereas local field potentials were continuously sampled at 1 kHz.

Histological procedures

Rats were deeply anesthetized and perfused with 4% formaldehyde. Coronal brain sections were sliced (40 μm) with a freezing microtome and stained with cresyl violet. Images of the brain slices were acquired using a Moticam 2000 camera (Motic Instruments) or IC Capture DFK 41BU02 camera (The Imaging Source) attached to a Motic SMZ-168 stereoscope. Tetrode tracks were identified, and the lowest point of the track was used to determine the recording location.

Unit isolation

Single units were isolated offline based on multiple waveform characteristics (i.e., spike amplitude peak, area under the waveform, and valley depth) using custom-written manual cluster-cutting software (WinClust, J.J.K.). The isolation quality of each unit was rated on a subjective scale from 1 (very good) to 5 (poor), depending on separation of the cluster from other clusters and background noise. Isolation was judged independent of behavioral firing correlates, and only cells rated as fair or better (categories 1, 2, and 3) were included in the analysis.

Random forests classification

Cells were classified using a random forests classifier (Breiman, 2001). Random forests is an ensemble learning method where the mode of a large number of decision tree classifiers defines the ensemble classifier output. Each decision tree is generated through random subsampling of the data and random feature selection, creating an ensemble classifier that is less susceptible to overfitting than other supervised learning methods. The classifier was previously trained to distinguish between putative granule cells, mossy cells, and proximal CA3 cells based on the firing properties of the cells during a postbehavior baseline sleep session (GoodSmith et al., 2017). The postbehavior sleep session was used to train the classifier because most granule cells are silent during behavior, and they often do not fire spikes unless the animal is sleeping (Jung and McNaughton, 1993; GoodSmith et al., 2017). Therefore, recording periods of sleep is essential to record enough spikes to isolate the activity of granule cells and classify them. In addition, prior studies had indicated that the number of cells on a tetrode during sleep may be a good predictor of cell type, based on the dense packing of cells in the granule layer compared with the sparse packing in the hilus (Neunuebel and Knierim, 2012). Using sleep recordings to classify DG cells also makes it easier to apply the classifier in different studies that use different behavioral tasks (assuming a sufficient period of sleep is recorded).

The features used to train the classifier were the mean firing rate, burst index (proportion of all interspike intervals that were ≤ 6 ms), number of well-isolated putative excitatory cells recorded on the same tetrode, and channel slope (slope of best fit line through peaks of normalized and sorted waveforms on the four tetrode wires). An additional feature, whether the tetrode tip was closer to the granule cell layer or proximal CA3 cell layer based on histology, was included to better separate granule cells from CA3 cells, as there was more overlap in firing properties and minimal histological ambiguity between these cell types. The classifier was trained using cells recorded on the same day that the animal was killed (thus minimizing potential drift of the electrode tip between the time of recording and the time of brain perfusion). Furthermore, only cells recorded from tetrodes that ended clearly in the granule cell layer, hilus, or CA3 based on tetrode track reconstructions (i.e., the tetrode tip was not located near the boundary between the hilus and the granule cell layer or between the hilus and the CA3 pyramidal cell layer) were included in the training data. The classifier had an “out of bag” error rate (an estimate of the classifier's generalization error) of 5.7%. The spatial firing properties of classified cells from earlier recording days and tetrodes located near layer boundaries were also shown to resemble the results from the training data, further indicating the accuracy of the classifier (GoodSmith et al., 2017). Finally, juxtacellular recordings from identified granule cells and mossy cells were consistent with the observed spatial firing properties of classified DG cells (GoodSmith et al., 2017). More detail about the methods used to select features and measures taken to validate the model can be found in GoodSmith et al. (2017).

Data analysis and statistical tests

Rate maps and place fields.

An overhead camera recording red and green LEDs on the rat's head at 30 Hz was used to track the rat's position and head direction during recording sessions. Spikes that occurred while the rat's head was outside of the track boundaries or when the rat's speed did not meet a 3 cm/s speed threshold were excluded from analysis. Linear rate maps were created by converting the rat's Cartesian position into degrees along the track. The mean rate for each 1° was calculated, and the linear rate map was smoothed with a Gaussian filter (σ = 3°). The spatial information score (Skaggs et al., 1996) and mean firing rate were calculated from this linear rate map. A p value was determined for the spatial information score of each cell by a shuffling procedure, in which the spike train and position train were shifted relative to each other by a random time (minimum of 30 s), and the spatial information was recalculated. This procedure was repeated 1000 times, and the cell was considered significant at p < 0.01 if the observed spatial information was greater than the shuffled score 990 of 1000 times. Cells were considered to be active and have a place field if they met the following activity criteria: (1) the cluster isolation score was ≤ 3; (2) the spatial information score was > 0.75 bits/spike; (3) the spatial information score was significant (p < 0.01); (4) the cell fired ≥ 20 spikes on the track; and (5) the mean firing rate on the track was < 10 Hz (to exclude interneurons).

Population correlation matrices.

Two population correlation matrices were generated for each rotation angle: one for the MIS session and the preceding STD session (STD1 vs MIS; termed the MIS matrix) and another for the STD session before and after the MIS session (STD1 vs STD2; termed the STD matrix). See Neunuebel et al. (2013) for description of correlation matrix generation procedures. Each correlation matrix was generated using cells that were active in at least one of the two sessions being compared. To generate the correlation matrices, normalized firing rate vectors were created for each 1° bin along the track from the sample of active cells. Each of the 360 firing rate vectors contains the firing rate of each of the cells in the sample at that location along the track. The vectors were created from recordings across all animals and recording days (i.e., they were not restricted to simultaneously recorded cells). The Pearson correlation for each pair of firing rate vectors was calculated, giving a 360 × 360 matrix of correlation values. In these matrices, high correlation along the main diagonal represents stable and coherent firing between sessions (as the population firing rate vector at matching track locations is similar). A coherent shift of population activity with local cues would cause the band of correlation to shift down, whereas coherent rotation with global cues would cause the correlation band to shift up. To generate polar plots for statistical quantification, the average correlation value along each of the 360 diagonal correlation bands was calculated and plotted at the rotation angle that generated that correlation (Neunuebel et al., 2013). The highest mean correlation value (the peak value of the polar plot) was determined for the STD (Peak_STD) and MIS (Peak_MIS) matrices. This value was used to compare STD to MIS matrices and to calculate the peak correlation difference index (PCDI) and Euclidean distance (defined below).

To compare the STD and MIS matrices, the average Peak_STD and Peak_MIS values across rotation angles were calculated for each cell type and significance was tested using a bootstrapping procedure (Neunuebel and Knierim, 2014). Because 45° mismatch angles do not appear to cause as strong a decorrelation of the population response as the other mismatch amounts, in any cell type studied here or previously (Neunuebel and Knierim, 2014; Lee et al., 2015; Knierim and Neunuebel, 2016), this rotation mismatch was excluded from this analysis. In addition, due to the very sparse firing of classified granule cells, there were not enough active granule cells for the 90° mismatch to compare using the bootstrapping procedure (too few unique bootstrap samples were possible). We therefore calculated the average value of only the larger (135° and 180°) mismatch angles. Including the 90° mismatch for mossy cells and pCA3 cells did not alter the results. For each correlation matrix, the sample of cells used to generate that matrix was sampled with replacement until a new bootstrapped sample of the same sample size was obtained. A correlation matrix was created using the bootstrapped sample, and the peak correlation values were calculated. If Peak_STD is significantly higher than Peak_MIS due to an overall difference in the population response, the Peak_STD of the bootstrap sample would be higher than the Peak_MIS bootstrap value regardless of the subset of cells used. If the observed differences between Peak_STD and Peak_MIS were due instead to the activity of a small subset of cells, then some bootstrap samples would exclude these cells and the Peak_MIS would be larger than Peak_STD. We created 100 bootstrap samples, and the p value was defined by the number of bootstrap samples where Peak_MIS > Peak_STD. The 2.5 and 97.5 percentiles of the Peak_STD and Peak_MIS bootstrap values were used to generate 95% CIs of the correlation value.

For both the PCDI difference and Euclidean distance measures, the correlation matrices were normalized so that the values ranged from 0 to 1, thus controlling for differences in the total distribution of correlation values between cell types (Lee et al., 2015). The PCDI value was defined as (Peak_STD − Peak_MIS)/(Peak_STD + Peak_MIS), which allows more direct comparison between cell types by controlling for the different Peak_STD values in the different cell types. The Euclidean distance was calculated by creating a vector of the correlation values along the diagonal that generated the peak average correlation in a correlation matrix. The Euclidean distance was calculated between this vector for the STD matrix and the MIS matrix.

For both PCDI and Euclidean distance measures, to compare between cell types, the difference in the PCDI or Euclidean distance value was calculated between each pair of cell types (granule cell–mossy cell, pCA3 cell–mossy cell, and granule cell–pCA3 cell). A shuffling procedure was used to determine statistical significance (Lee et al., 2015). Cells were randomly assigned to one of the two cell types being compared so that the number of active cells of each type matched the observed data. The Euclidean distance and PCDI difference values were calculated from the shuffled data, and the procedure was repeated 1000 times. The p value was the number of times that the absolute value of the shuffled PCDI or Euclidean distance difference values exceeded the actual values observed.

It is possible that a small number of misclassified cells could bias our results. To address this issue, we separately analyzed a subset of cells that are less likely to have been misclassified. The random forests classifier consists of multiple individual decision tree classifiers. When classifying cells, the cell's firing properties are run through each decision tree, and the output of that decision tree is one “vote” toward the final random forests classification. The cell type with the most votes is the output of the random forests classifier. The percentage of decision tree classifiers that have the same output can be viewed as one measure of confidence in the classification. For example, if 80% of decision trees labeled a cell as a mossy cell, that cell is less likely to be a misclassified pCA3 or granule cell than if only 50% of the decision trees had classified it as a mossy cell. We split our data into the top 50th percentile and bottom 50th percentile based on the percentage of “votes” that the final classification received. For the top 50th percentile of cells, >76% of the votes were for the same cell type; the bottom 50th percentile ranged from 44% to 75% of votes. Due to the limited number of granule cells, further subsampling of granule cell data would not produce easily interpretable results. We therefore restricted this analysis to pCA3 and mossy cells. We repeated the PCDI and Euclidean distance difference analyses separately for the top 50th percentile and bottom 50th percentile of cells.

Downsampling of mossy cells and pCA3 cells.

Due to the extremely sparse firing of granule cells in behaving rats, small numbers of active granule cells were recorded, which may complicate the comparisons of granule cells with other cell types. To investigate how the number of cells can affect the appearance of correlation matrices and polar plots, we created new plots using a random subsample of the mossy cell and pCA3 populations. For each rotation angle, we created new STD and MIS matrices. Random mossy cells and pCA3 cells were selected so that the number of cells used to generate each plot was equal to the number used to generate the corresponding granule cell plots. Polar plots were then generated from these downsampled correlation matrices.

Rotational and stability analyses.

The rotation between rate maps that generated the highest correlation was determined for all cells that met the activity criteria in both the STD and MIS sessions (see Fig. 2, rotate cells). The rate map of the STD session was correlated with the rate map of the MIS session as the MIS session rate map was shifted in 5° increments. The angle of rotation that led to the peak correlation value was assigned as the rotation angle of that cell.

Figure 2.

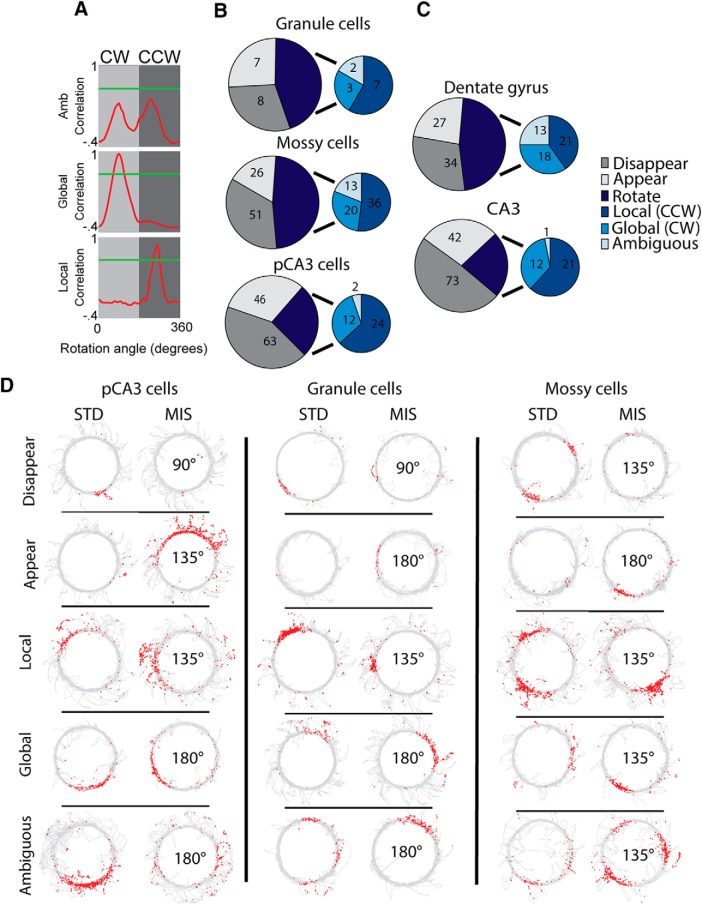
Rotation and remapping of individual cells. A, For cells that met place-field criteria for both STD and MIS sessions, rate map correlations were calculated as one of the rate maps was rotated in 5° increments. The correlation value is plotted against the angle of rate map rotation. Green line indicates a correlation threshold of 0.6. Following Neunuebel et al. (2013), any cell that did not pass this threshold for any rotation angle was considered to be an ambiguous rotation (top). Remaining rotate cells were classified as clockwise rotations (middle, rotation with global cues) or counterclockwise rotation (bottom, rotation with local cues) based on the direction of rotation that generated the peak correlation. B, C, Number of cells that rotated or remapped following cue rotation. Cells that were active in only the MIS session (appear) or only the STD session (disappear) were designated as remapping cells. Rotating cells were further divided into counterclockwise (CCW), clockwise (CW), or ambiguous rotations as described in A. Only cue rotations > 45° are included in these plots. B, Results from classified granule cells, mossy cells, and pCA3 cells. C, Results from all cells on anatomically localized DG and pCA3 tetrodes (before separation of mossy cells). D, Example recording sessions. One example of each of the different response types is shown for each cell type. For each cell, a pair of consecutive sessions (STD, MIS) is shown. The mismatch angle is indicated in the center of the MIS session plot. Each plot represents the trajectory of the rat in gray. Red dots represent the location of individual spikes of the cell.

Only cells that met the activity criteria in all three STD sessions were used for STD session stability plots. Place cells were ordered based on the locations of their peak firing on the track in the first STD session, and this order was preserved for the second and third STD session plots.

Statistical tests.

Statistical tests were calculated in MATLAB (The MathWorks) and R. Data represent the mean ± SEM, and p values indicate the results of two-tailed tests. Wilcoxon rank-sum tests were used to compare the distance from the proximal edge of CA3 for mossy cells and pCA3 cells recorded on pCA3 tetrodes and to compare the number of mossy cell and granule cell place fields in foraging sessions. When comparing the responses of all three cell types, Kruskal–Wallis one-way ANOVA or χ² tests were used to test the null hypothesis that the responses from all three cell types came from the same distribution. Post hoc pairwise χ² tests were then calculated and considered significant if the p value was < 0.017 (using Bonferroni correction for multiple comparisons).

Results

Classification of cells recorded in the DG and proximal CA3

We analyzed a total of 292 well-isolated, active cells recorded from 16 rats as they performed a double rotation task (Fig. 1). In this task, standard (STD) cue configuration sessions were alternated with mismatch (MIS) sessions in which local and global cues were rotated in opposite directions for a total cue mismatch of 45°, 90°, 135°, or 180°. Two MIS sessions a day were chosen so that each mismatch angle was experienced twice over the 4 d of recording (Fig. 1A). Of these 292 cells, 129 cells from Neunuebel and Knierim (2014) were recorded on tetrodes in the DG hilus or granule cell layer. These 129 cells represent all cells that met the defined activity criteria (Neunuebel and Knierim, 2014) in at least one recording session (double rotation or foraging). Of the remaining 163 cells, 114 cells were recorded on proximal CA3 tetrodes in Lee et al. (2015), and a further 29 cells were recorded in the granule cell layer or hilus (16 cells from tetrodes in the hilus, 13 from tetrodes in the granule cell layer) of the rats from Lee et al. (2015) but were not analyzed in that paper (Fig. 1B,D). An additional 20 active cells were recorded on tetrodes in the DG or pCA3 of 2 rats not included in either study. The cutoff between proximal and intermediate CA3 in Lee et al. (2015) was chosen to maintain a similar number of tetrodes in proximal, intermediate, and distal CA3. We have maintained this division here, and all tetrodes from ∼0% to 40% of the length of the transverse axis of CA3 are included as proximal CA3. Notably, only cells that had a place field in at least one recording session were included in our analysis; the large majority of granule cells and pCA3 cells recorded during sleep were silent during behavior (Jung and McNaughton, 1993; Skaggs et al., 1996; Neunuebel and Knierim, 2012; GoodSmith et al., 2017), and these silent cells were not analyzed or included in the total count here.

We previously developed a random forests classifier that was able to accurately sort recordings from DG and proximal CA3 tetrodes into putative mossy cells, granule cells, and proximal CA3 pyramidal cells based on firing properties recorded during a baseline/sleep session (GoodSmith et al., 2017). The features used for classification were mean firing rate, burst index, the number of cells recorded on the same tetrode, and channel slope (see Materials and Methods). An additional feature, whether the tetrode tip was closer to the granule cell layer or CA3 pyramidal cell layer based on histology, was used to improve classification between granule cells and pCA3 cells. Using this classifier, we separately analyzed the mossy cells, granule cells, and pCA3 cells from Lee et al. (2015) and Neunuebel and Knierim (2014). The distributions of classification features for classified cells are plotted in Figure 1C. From these plots, it is apparent that mean rate was an important factor in segregating mossy cells from granule cells and pCA3 cells, burst index was an important factor in segregating granule cells from mossy cells and pCA3 cells, and the number of corecorded cells was useful in segregating each cell type from the others. Channel slope was not as useful for segregating cell types, but removal of this feature slightly increases the classifier's error rate (GoodSmith et al., 2017). While there was overlap in all the firing properties used for classification, the random forests classifier is able to separate the cell types based on relationships among features.

In total, 104 of 169 cells (62%) recorded on tetrodes in DG and 26 of 123 cells (21%) recorded on tetrodes in pCA3 were classified as mossy cells. Of the 123 cells recorded on proximal CA3 tetrodes, 85 were recorded in the portion of CA3 that extends into the DG (classically defined as CA3c) (Lorente de Nó, 1934) where mossy cells are located. For tetrodes located in CA3c, 25 of 85 cells (29%) were classified as mossy cells, while only 1 of 38 cells (2%) recorded in pCA3 but outside of CA3c was classified as a mossy cell. Anecdotally, tetrodes on which mossy cells were recorded often had tracks that ended near the boundary between CA3 and the hilus. Finally, mossy cells tended to be recorded on tetrodes that were closer to the most proximal end of CA3, where the CA3 layer is less tightly packed (distance from proximal CA3 end: mossy cells 0.60 ± 0.06 mm; pCA3 cells 0.75 ± 0.03 mm; rank sum test z = 2.64, p = 8.3 × 10⁻³).

Neunuebel and Knierim (2014) made no attempt to distinguish between granule cells and mossy cells, and instead analyzed all putative principal cells recorded throughout the DG granule cell layer and hilus (although they estimated that approximately half of the recorded DG cells may have been mossy cells). Cells classified as mossy cells from DG recordings were more often located on tetrodes that ended in the hilus and near the boundary between the granule cell layer and hilus than in the granule cell layer (59 mossy cells in hilus, 36 near boundary, 6 in granule cell layer). It is possible that some cells recorded at the boundary between the hilus and granule cell layer were adult-born granule cells. However, of all 130 classified mossy cells analyzed in the present study, 88 (67%) were recorded on tetrodes located clearly in the hilus or pCA3 pyramidal cell layer (away from the subgranular zone and granule cell layer), indicating that the observed responses of classified mossy cells were not likely driven by adult-born granule cells (although we cannot completely rule out this possibility).

For DG recordings, following the five double rotation sessions, rats foraged for random food rewards in a 135 cm × 135 cm box. Classified mossy cells were more likely than granule cells to be active in this foraging session (35 of 52 mossy cells and 14 of 41 granule cells active; χ² = 10.11, p = 0.0015). Of the active granule cells, the majority (9 of 14) were only active in the foraging session (silent in all double rotation sessions). The number of place fields in the box was also significantly higher for mossy cells than granule cells (mossy cells: mean 3.5, median 3, range 1–9; granule cells: mean 1.5, median 1, range 1–3; rank sum test z = 3.57, p = 3.64 × 10⁻⁴). These foraging results resemble our previous results from mossy cells and granule cells (GoodSmith et al., 2017; see also Danielson et al., 2017; Senzai and Buzsaki, 2017) and indicate an accurate classification of granule cells and mossy cells in the present study.

Remapping and rotation of individual cells in the DG/CA3 circuit

We first investigated whether there were any differences in the proportion of active cells (see Materials and Methods) that rotated or remapped in response to cue mismatch. For each MIS session and its preceding STD session, a cell that was active in only the MIS session (appear) or only in the STD session (disappear) was considered to be a “remap” cell. Cells that were active in both the STD and MIS sessions were considered “rotate” cells. The rate map of the MIS session was rotated in 5° increments relative to the STD session map, and the angle that resulted in the peak correlation between maps was calculated. To be consistent with previously used criteria (Neunuebel and Knierim, 2014; Lee et al., 2015), if the peak correlation value was <0.6, the rotation was considered to be “ambiguous” (Fig. 2A, top). The remaining “rotate” cells were separated into clockwise (global cue-dominated; Fig. 2A, middle) and counterclockwise (local cue-dominated; Fig. 2A, bottom) rotations based on the direction of rotation that resulted in the highest rate map correlation.

In both DG and pCA3 recordings, 45° rotations caused significantly less remapping than larger rotation amounts (Neunuebel and Knierim, 2014; Lee et al., 2015). For this reason, we excluded 45° rotations in our analysis of rotation and remapping proportions. Proximal CA3 cells were more likely to remap than mossy cells (Fig. 2B; remap vs rotate cells: granule 15 vs 12, mossy 77 vs 69, pCA3 109 vs 38; χ₍₂₎² = 15.0, p = 5.4 × 10⁻⁴; pairwise χ²: granule vs mossy χ₍₁₎² = 0.07, p = 0.79; mossy vs pCA3 χ₍₁₎² = 14.5, p = 1.4 × 10⁻⁴; granule vs pCA3 χ₍₁₎² = 3.85 p = 0.05). The remapping in mossy cells and granule cells both resembled the overall results from all cells recorded in the DG (Fig. 2C, top), whereas the proximal CA3 cells resembled the proximal CA3 data before removal of mossy cells (Fig. 2C, bottom).

For cells active in at least one double rotation session, there was a significant difference across cell types in the proportion of sessions with place fields, but no pairwise comparisons were significant after adjusting for multiple comparisons (active sessions vs silent sessions: granule 67 vs 58; mossy 366 vs 199; pCA3 323 vs 222; χ₍₂₎² = 6.95, p = 0.03; granule vs mossy χ₍₁₎² = 5.47, p = 0.02; mossy vs pCA3 χ₍₁₎²= 03.58 p = 0.06; granule vs pCA3 χ₍₁₎² = 1.34, p = 0.25). In active sessions, there was no significant difference between cell types in mean firing rate (mossy 1.05 ± 0.07 Hz; granule 0.96 ± 0.19 Hz; CA3 0.92 ± 0.06 Hz; Kruskal–Wallis test, χ₍₂₎² = 3.84, p = 0.15) or peak firing rate (mossy 9.83 ± 0.72 Hz; granule 10.04 ± 2.48 Hz; CA3 9.24 ± 0.62 Hz; Kruskal–Wallis test, χ₍₂₎² = 2.55, p = 0.28). While mossy cells have been shown previously to have higher firing rates in behavior than granule cells or pCA3 cells (GoodSmith et al., 2017; Senzai and Buzsáki, 2017), this difference is not apparent in the present data. This discrepancy from previous results may be due in part to the limited number of granule cells and/or differences in the task (open field vs circular track). Thus, this negative result should be treated with some caution. For each cell type, example recording sessions are shown for each response type in Figure 2D.

The majority of mossy cells, granule cells, and pCA3 cells “remapped” (i.e., a place field was detected in either the STD or MIS session, but not both) following cue mismatch. While there are more “rotate” responses in mossy cells than pCA3 cells, the proportion of unambiguous rotations that followed local cues was ∼60% for all cell types (local cue cells vs global cue cells: granule 7 vs 3; mossy 36 vs 20; pCA3 24 vs 12; χ₍₂₎² = 0.15, p = 0.93; pairwise χ²: granule vs mossy χ₍₁₎² = 0.12, p = 0.73; mossy vs pCA3 χ₍₁₎² = 0.05 p = 0.81; granule vs pCA3 χ₍₁₎² = 0.04, p = 0.84). The increased number of “rotate” responses in mossy cells is largely due to the fact that mossy cells fire in almost all environments (GoodSmith et al., 2017; Senzai and Buzsáki, 2017) (i.e., they rarely turn on or shut off between environments), which by our classification criteria would place them more in the rotate category than the remap category.

Population responses in the DG/pCA3 circuit

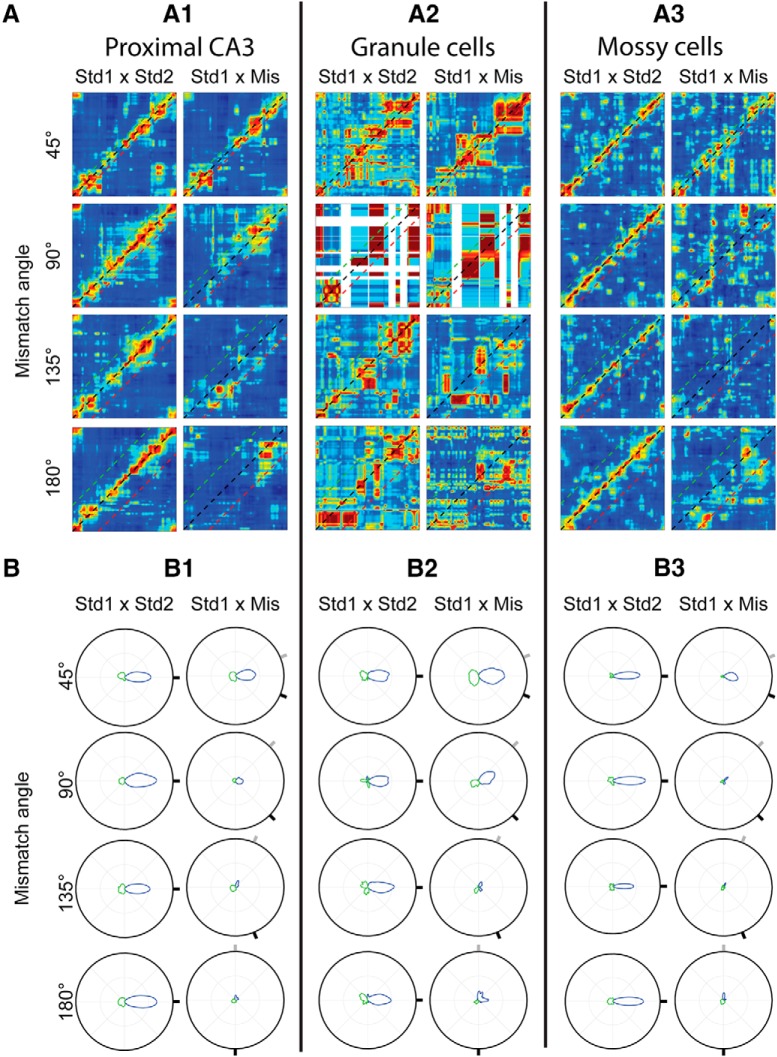
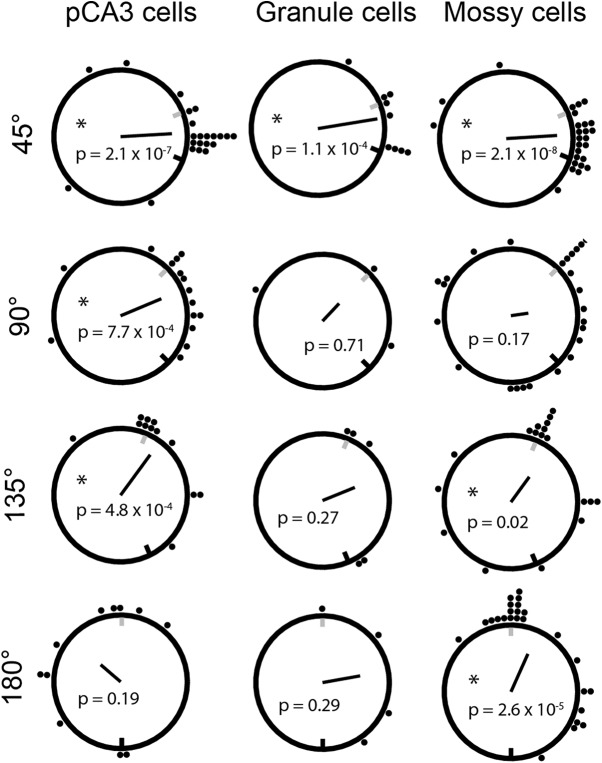
While cells were slightly more likely to rotate in the direction of local cues than global cues, it is unclear whether this represents a coherent shift of the place cell population or whether different cells rotated by different amounts. We therefore examined the population responses of active granule cells, mossy cells, and pCA3 cells to determine whether there was a coherent response to cue mismatch (Lee et al., 2004). Population firing rate vectors were created at each location of the circular track, and spatial correlation matrices were made from these firing rate vectors (see Materials and Methods; Fig. 3A). For putative granule cells, mossy cells, and pCA3 cells, there was a band of high correlation along the main 45° diagonal in the STD1 versus STD2 plots for all angles (although the band is less clear for granule cells; see below), indicating stable population firing at corresponding locations in repeated standard sessions. In STD1 versus MIS plots, there was a broader band of high correlation centered on the main diagonal following 45° rotations, but there were no clear high correlation bands following rotation amounts ≥ 90°. To better visualize the correlation values, polar plots were created by calculating the average rotation angle along each of the 360 diagonals in the correlation matrix (Fig. 3B). In these figures, a peak at 0° indicates that the highest mean correlation in the correlation matrix was along the main diagonal, while a rotation of the peak from 0° indicates a shift of the population response. For example, in a 90° mismatch session, a large peak of the polar plot that was rotated 45° counterclockwise would indicate that the population of active cells followed local cues. The magnitude of the peak indicates how coherent the population response was, with small and/or broad peaks indicating a largely decorrelated population response and large, narrow peaks indicating a highly coherent population response.

Figure 3.

Population responses of granule cells, mossy cells, and pCA3 cells to cue rotation. A, Correlation matrices between STD1 and STD2 sessions (left) or between STD1 and MIS sessions (right) for pCA3 cells (A1), granule cells (A2), and mossy cells (A3). For reference, black, green, and red lines are plotted along the main diagonal, at the rotation amount of global cues and at the rotation amount of local cues, respectively. For all cell types, there is a band of correlation in all STD1 × STD2 plots near the main diagonal, representing stable spatial firing of the cell population in repeated standard sessions. There is a correlation band in the STD1 × MIS matrix following 45° rotations, but there are no coherent bands of high correlation for larger rotations. B, Polar plots of average correlation values for pCA3 cells (B1), granule cells (B2), and mossy cells (B3). For each of the 360 diagonal bands in the correlation matrix, the average correlation value was determined and plotted here. Green lines indicate angles where the average correlation value was negative. Black circle represents a correlation value of 1. Due to the small number of granule cells, the correlation matrices in A were not as clear for these cells; but in the polar plots, the similarity of response patterns of all three cell types is clearer. There is a peak of correlation at 0° rotation for all STD plots (marked by a black tick mark at the edge of the circle). In MIS plots, the gray and black tick marks around the circle represent the angle of local and global cue rotations, respectively. There is a broader peak centered on 0° in the 45° MIS plot, but a very low peak correlation value following all larger cue rotations.

Due to the extremely sparse firing of granule cells (Jung and McNaughton, 1993; Chawla et al., 2005; Neunuebel and Knierim, 2012; Danielson et al., 2016; Diamantaki et al., 2016a,b; GoodSmith et al., 2017; Hainmueller and Bartos, 2018), there were very few active granule cells in any given session (even though many more cells were recorded during the baseline sleep sessions) (Neunuebel and Knierim, 2012, 2014), and thus very few cells were available to generate each correlation matrix. While each pCA3 and mossy cell plot was generated using 37–57 active cells, the 90° granule cell plots were generated from only 4 and 5 cells, and white bands in these plots represent regions of the track on which no active cells fired any spikes. The remaining granule cell matrices were made from 10–13 active granule cells. The small numbers of cells cause the granule cell correlation matrices to appear less structured, even in STD1 versus STD2 plots. However, the same response pattern seen in mossy cells and pCA3 cells is clearly visible in the granule cell polar plots (Fig. 3B). In all three cell types, there was a peak correlation at 0° in all STD1 versus STD2 polar plots, indicating stable population firing between standard sessions. There was no large correlation peak following any rotation > 45° in STD1 versus MIS plots, indicating that there was not a coherent population response to cue mismatch in any cell type (Fig. 3B).

To determine how the appearance of granule cell correlation matrix and polar plots could be affected by the small number of granule cells used to generate each plot, we next created new plots using downsampled mossy cell and pCA3 cell populations (Fig. 4). Cells were randomly selected so that the number of cells used to generate each correlation matrix plot matched the number used to generate the corresponding granule cell plot. The correlation matrix and polar plots for these downsampled populations (Fig. 4) resemble the granule cell results (Fig. 3A2,B2). In both downsampled mossy cell and pCA3 cell populations, a coherent correlation band is still apparent between STD sessions, but there is not a coherent population response following any cue mismatch > 45°. While each plot in Figure 4 is generated from a single representative downsampled population, the same response pattern was apparent consistently when the downsampling procedure was repeated 10 times.

Figure 4.

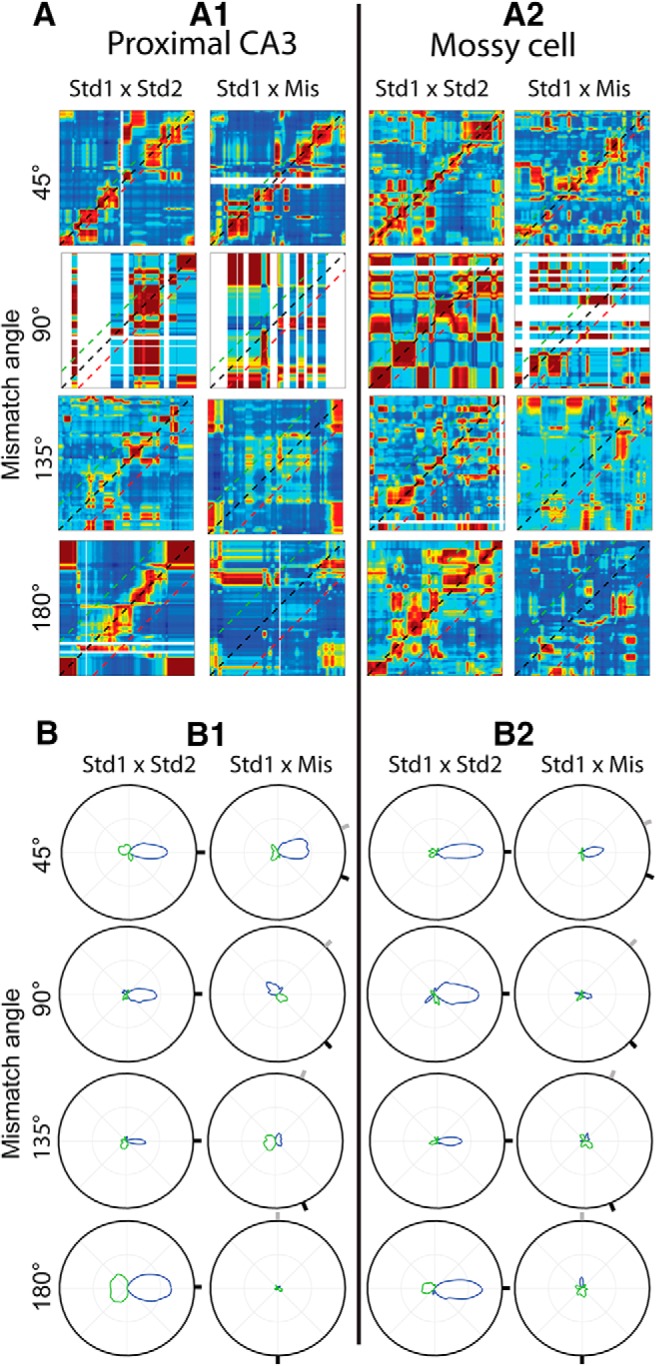
Responses of downsampled pCA3 and mossy cell populations to cue rotation. A, Correlation matrices of downsampled pCA3 cell (left) and mossy cell (right) populations (plotted as in Fig. 3A). Correlation matrices were generated using the same number of cells used to generate the corresponding granule cell plots (Fig. 3A3). B, Polar plots of correlation matrices in A (plotted as in Fig. 3B).

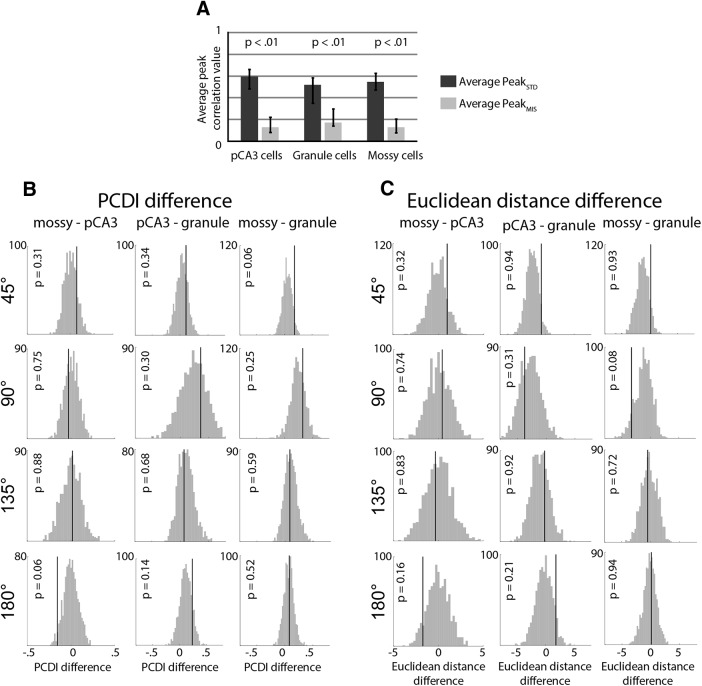
To quantify the reduction in population correlation following cue rotations, we compared the peak value of the polar plot from the STD matrix (Peak_STD) to the MIS matrix (Peak_MIS), using the full dataset from Figure 3. The average of these correlation values for the 135° and 180° mismatch angles was calculated so that there was one average Peak_STD and one average Peak_MIS value for each cell type (for justification of exclusion of 45° and 90° mismatch angles, see Materials and Methods). For all cell types, the average Peak_MIS value was less than the average Peak_STD value (Fig. 5A; mossy cell, p < 0.01; pCA3 cell, p < 0.01; granule cell, p < 0.01; bootstrapping tests, see Materials and Methods).

Figure 5.

Comparison of population responses. A, The highest average correlation band value (peak value on the polar plot) was calculated for each correlation matrix. The average of this value for the 135° and 180° rotation angles was calculated for each cell type in the STD and MIS matrices (one value for each column in Fig. 3B; for more detail, see Materials and Methods). The average of the 135° and 180° value is plotted here, and a bootstrapping procedure was used to determine 95% CIs (black bars). p values for the difference between the STD and MIS correlation values were defined as the number of bootstrap samples in which the average Peak_STD value was less than the average Peak_MIS value. In all three cell types, the correlation was significantly higher between STD sessions than between STD and MIS sessions. B, PCDI difference values. The PCDI value was calculated for each cell type and rotation angle, and the difference was calculated between each pair of cell types. The actual difference value (black line) was compared with the values obtained by a shuffling procedure, and the p value was defined as the number of times that the absolute value of the shuffled value exceeded the observed value. There were no significant differences between any cell types for any rotation angles. C, Same as in B, but using the Euclidean distance measurement (Lee et al., 2015).

A direct comparison of Peak_MIS values between cell types would not be appropriate, due to differences in the Peak_STD values and the number of cells used to generate each plot between the different cell types. To correct for these differences, each correlation matrix was first normalized so that the correlation values ranged from 0 to 1, and the PCDI was calculated as previously described (Lee et al., 2015) (see Materials and Methods). The PCDI reflects the magnitude of the reduction in the average value of the peak correlation band between the STD1 versus STD2 matrix and the STD1 versus MIS matrix. To compare between cell types, the difference between the PCDI values was calculated between each pair of cell types, and this value was compared with a distribution of PCDI difference values generated by a shuffling procedure (Fig. 5B). The shuffling procedure generates random correlation matrices while preserving the relative number of cells used to make each correlation matrix. For all cell type pairs and rotation angles, the observed PCDI difference value (Fig. 5B, black line) was not significantly larger than the values obtained through shuffling (Fig. 5B, histogram), indicating that there were no statistically significant differences among the cell types. As an alternative measure, we calculated the Euclidean distance difference between cell types (Lee et al., 2015) (see Materials and Methods). The Euclidean distance was calculated between the peak correlation bands of the normalized correlation matrices to compare the similarity of the correlation values along those diagonal bands. The Euclidean distance measure reflects the similarity of all correlation values along the peak correlation band (rather than the average value reflected in the PCDI value). As with the PCDI difference, there was no significant difference between any pair of cell types for any rotation angle (Fig. 5C).

It is possible that the similar responses to cue mismatch across all three cell types were due in part to a small number of misclassified cells. To address the possible contributions of misclassified cells to our results, we separately analyzed cells in the top and bottom 50th percentiles of classification “confidence” (see Materials and Methods). If our results were driven by a small number of misclassified cells, removing the cells with the lowest classification confidence should produce different results. Due to the limited number of active granule cells, we focused this analysis on mossy cells and pCA3 cells. For both the top and bottom 50th percentile of cells, there was no coherent response to cue mismatch for either cell type. We calculated the PCDI and Euclidean distance difference values separately for the top and bottom 50th percentiles and found no significant difference between mossy cells and pCA3 cells for any rotation angle (top 50th percentile: PCDI: 45° p = 0.49, 90° p = 0.18, 135° p = 0.83, 180° p = 0.45; Euclidean distance: 45° p = 0.32, 90° p = 0.20, 135° p = 0.16, 180° p = 0.08; bottom 50th percentile: PCDI: 45° p = 0.53, 90° p = 0.76, 135° p = 0.55, 180° p = 0. 29; Euclidean distance: 45° p = 0.47, 90° p = 0.72, 135° p = 0.75, 180° p = 0.89). These results suggest that the similar responses to cue mismatch observed throughout the DG/pCA3 circuit are not driven by a small number of misclassified cells.

Peak rotation amount of individual cells

Of the cells classified as rotating cells, ∼65% of granule cells, mossy cells, and pCA3 cells rotated in the direction of local cues. In the initial analysis (Fig. 2), any rotation in the clockwise or counterclockwise direction that resulted in a peak rate map correlation ≥ 0.6 was considered a clockwise or counterclockwise rotation. Notably, the angle of place field rotation did not need to match the cue rotation amount to be considered a rotation. Cells that had place fields at random locations in both sessions could still generate a high correlation and be considered a clockwise or counterclockwise rotation. As mossy cells tend to be active in most contexts, with place fields moving to new locations in distinct contexts (GoodSmith et al., 2017; Senzai and Buzsáki, 2017), these cells could be particularly susceptible to this kind of error. To determine which place field rotations were directly controlled by either the local or global cues, we next identified the peak correlation angle for each place cell that was active in both the STD and MIS session (all rotate cells from Fig. 2).

As seen previously in DG and pCA3, more cells rotated their place fields following a 45° rotation than larger rotation amounts, and the peak rotation angle tended to be centered at ∼0° but spread in both the local and global directions (Fig. 6, top). Granule cell rotation amounts were only significantly nonuniformly distributed following the 45° rotation (Fig. 6, middle), while mossy cells reached significance for all but the 90° rotation (Fig. 6, right), and pCA3 cells reached significance for all mismatch angles <180° (Fig. 6, left).

Figure 6.

Peak rotation amount of individual cells that passed activity criteria in both STD and MIS sessions under comparison (remapping cells were not analyzed here). As in Figure 2, correlations between STD and MIS rate maps were calculated following 5° shifts of one rate map. Each black dot represents one “rotate” cell (as defined for Fig. 2). The location of the dot represents the rotation angle that generated the peak correlation value. Black line indicates the direction and magnitude of the mean vector of the distribution of rotation angles (the black unit circle is provided for scale), and p values are results of Rayleigh tests (asterisks mark significant results). Gray and black tick marks along the black circle represent the rotation angle of the local and global cues, respectively. All three cell types reach significance following the 45° rotation. At larger rotation angles, there is an overrepresentation of the rotation amount that corresponds to the counterclockwise rotation of the local cues, causing a number of rotation angles to reach significance in the Rayleigh test for mossy cells and pCA3 cells. While granule cells do not have a significant overrepresentation of local cues in larger rotation angles, this difference may be due to the relatively small number of active granule cells per plot. The proportion of cells that rotated within ±10° of the actual local cue rotation amount is not significantly different between any of the cell types.

Notably, although the majority of cells do not appear to have rotated to the location predicted by either local or global cues, a subset of the active cells rotated their fields with the local cues (Fig. 6). A similar proportion of granule cells, mossy cells, and pCA3 cells rotated their fields within ± 10° of the local cue rotation (for all mismatch rotations > 45°; cells with peak rotation within ± 10° of the local cue rotation vs cells with peak rotation > 10° from local cue rotation: granule 4 vs 8; mossy 26 vs 43; pCA3 12 vs 26; χ₍₂₎² = 0.42, p = 0.81; pairwise χ²: granule/pCA3 χ₍₁₎² = 0.01, p = 0.91; pCA3/mossy χ₍₁₎² = 0.40, p = 0.53; mossy/granule χ₍₁₎² = 0.08, p = 0.77). Although there does not appear to be a coherent rotation with local cues at the level of the entire population (Fig. 3), there is an overrepresentation of the local cue rotation amount in all three cell types, as previously observed in pCA3 and DG (Neunuebel and Knierim, 2014; Lee et al., 2015).

Stable firing in repeated standard sessions

Although the correlation matrices show a band of high correlation at corresponding locations between standard sessions for all cell types, the peak correlation band for granule cells is less clearly defined than pCA3 and mossy cells in the correlation matrix plots (Fig. 3). While this difference may be due to the low number of active granule cells, it could also indicate that the firing of granule cells is less stable in repeated standard sessions than mossy cells or pCA3 cells. To determine and compare the stability of firing in repeated STD sessions for granule cells, mossy cells, and pCA3 cells, we first compared the subset of cells that were active in at least one of the three standard sessions throughout the recording day. There was no significant difference in the correlation between STD1 and STD3 rate maps in the three cell types (mossy cells: 0.55 ± 0.04; granule cells: 0.61 ± 0.08; CA3 cells: 0.62 ± 0.04: Kruskal–Wallis test, χ₍₂₎² = 2.20, p = 0.33; Fig. 7A). For all cell types, if a cell was active in one standard session, it had a similar probability of being active in all three standard sessions (9 of 19 granule cells, 64 of 100 mossy cells, 51 of 89 pCA3 cells; χ² test, χ₍₂₎² = 2.18, p = 0.34). We next focused on the cells that were active in all three standard sessions, and looked at how stable the firing positions of these cells were through the recording day. In Figure 7B, the cells that were active in all three STD sessions are shown for each cell type. The cells are ordered so that their peak firing position in STD1 is in sequential order along the track from top to bottom, and this order is maintained for the STD2 and STD3 plots. The relative locations of the place fields are maintained through the STD2 and STD3 sessions, suggesting stability in repeated STD sessions for all cell types. Finally, as in Figure 6, we plotted the rotation angle that resulted in the peak rate map correlation between STD1 and STD3 (Fig. 7C). For all three cell types, there was a significantly unimodal distribution of peak rotation angles (Rayleigh test; pCA3 cells: z = 45.86, p = 1.2 × 10⁻³⁰; granule cells: z = 8.89, p = 3.3 × 10⁻⁶; mossy cells: z = 50.97, p = 1.0 × 10⁻³⁰), and a rotation of 0° resulted in the highest rate map correlation, further indicating stable firing though all three STD sessions. These results appear consistent with previous studies, which have indicated that granule cell place field locations are very stable between repeated exposures to a familiar environment (Hainmueller and Bartos, 2018).

Figure 7.

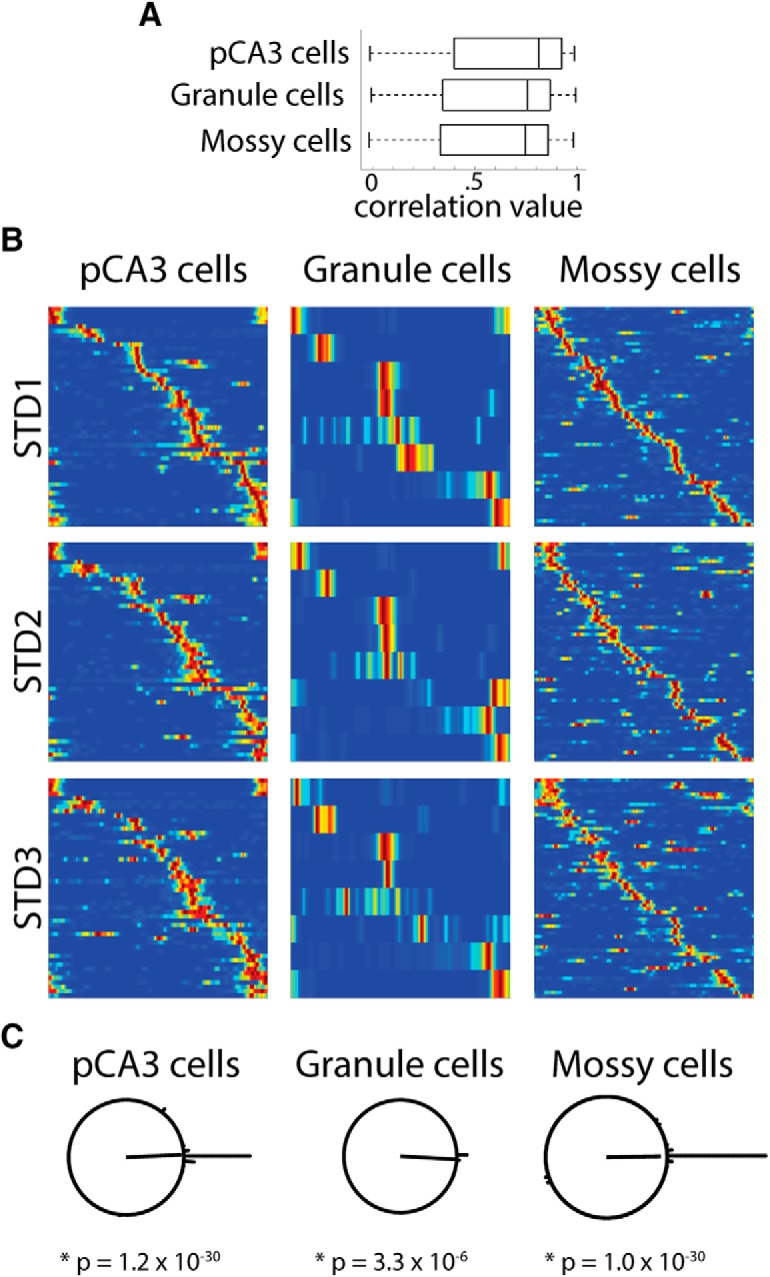
Stable firing in repeated standard sessions. A, Correlation between the first STD session (STD1) and third STD session (STD3) linear rate maps for all cells that were active in at least one STD session. Box plots of the correlation values for pCA3 cells, granule cells, and mossy cells are shown. There were no significant differences between the distributions of correlation values for any of these cell types. B, The subset of cells that were active in all three standard sessions is plotted for pCA3 cells, granule cells, and mossy cells. The firing of each cell is ordered based on the location of its peak firing along the track in STD1, and that cell order is preserved for in the plots for STD2 and STD3. For all three cell types, the relative firing positions are preserved through all three STD sessions. Mossy cells have more firing outside of the main place field (i.e., firing away from the diagonal band), as expected based on the high activity and multiple place fields of mossy cells. C, As in Figure 6, the peak rotation angle was calculated between STD1 and STD3 for each cell type. The majority of cells in all areas have a peak rotation angle of 0° (44 of 48 pCA3 cells, 8 of 9 granule cells, and 50 of 57 mossy cells had a peak rotation amount within 10° of a 0° rotation).

Discussion

In addition to the more numerous granule cells, mossy cells are the second excitatory cell type in the DG. Mossy cells occupy a key node in the anatomical circuitry of the DG, as (1) they are part of a disynaptic recurrent feedback loop through which granule cells influence other granule cells (Scharfman and Myers, 2013); (2) they are the recipient of feedback from CA3 to the DG (Scharfman, 2007); and (3) they form the projection to the contralateral DG, thus integrating the processing between the right and left DG (Buckmaster et al., 1996). In contrast to granule cells, very few studies have targeted mossy cells to investigate their firing correlates in freely moving animals. Recent studies have shown that prior literature reporting behavioral correlates of putative granule cells have instead recorded from a mixture of granule cells and mossy cells (Diamantaki et al., 2016a; GoodSmith et al., 2017; Senzai and Buzsáki, 2017).

In the present study, we found that a large proportion of active cells recorded extracellularly on tetrodes in both DG and pCA3 were mossy cells. Similar to granule cells and pCA3 pyramidal cells, mossy cells had stable firing between repeated standard sessions, but there was no coherent population response after cue mismatches > 45°. This pattern of activity was previously seen in the DG (Neunuebel and Knierim, 2014) and pCA3 (Lee et al., 2015), but it was not known the extent to which the results were affected by the inclusion of mossy cells. The present results indicate that the lack of a coherent response to the cue mismatch is shared throughout the DG/pCA3 circuit and may suggest a common role in pattern separation among all three excitatory cell types (although the small number of active granule cells analyzed here, due to the extremely sparse firing of these cells, warrants some caution in this interpretation).

The DG/pCA3 circuit

A number of recent studies have found evidence of functional similarities between DG and pCA3 (Hunsaker et al., 2008; Nakamura et al., 2013; Marrone et al., 2014; Lee et al., 2015; Lu et al., 2015). Due to the high degree of connectivity between DG and pCA3 (Claiborne et al., 1986; Ishizuka et al., 1990, 1995; Scharfman, 2007; Witter, 2007), it has been proposed that the pCA3 and DG form a single functional unit to perform pattern separation, with distal and intermediate CA3 performing the pattern completion computation typically associated with CA3 (Hunsaker et al., 2008; Lee et al., 2015; see also Lu et al., 2015).

The role of mossy cells in the DG/CA3 circuit is uncertain. Mossy cells receive excitatory inputs from granule cells and CA3 backprojections, and activation of mossy cells may regulate the sparse firing of granule cells required for pattern separation (Myers and Scharfman, 2009, 2011). Mossy cells also receive a number of neuromodulatory inputs (Amaral and Campbell, 1986; Swanson et al., 1987; Prince et al., 2016; Scharfman, 2016). By modulating mossy cell activity and excitability (Harley, 2007; Hofmann and Frazier, 2010; Etter and Krezel, 2014; Nozaki et al., 2016), these neuromodulatory inputs could influence DG pattern separation and the strength of mossy fiber outputs to CA3 based on task demands. Mossy cells also project to the contralateral DG (Buckmaster et al., 1996), and the multiple place fields of individual mossy cells (GoodSmith et al., 2017; Senzai and Buzsáki, 2017) may represent an efficient way of encoding the pattern separation output of the DG in a minimal number of fibers that must travel the long distance across hemispheres.

Using the double rotation task, it is possible to directly assess pattern separation in the DG/pCA3 circuit by comparing the population response of DG/pCA3 cells to the previously reported responses of entorhinal inputs to DG (Neunuebel et al., 2013; Knierim and Neunuebel, 2016). The medial entorhinal cortex (MEC) population correlation gradually decreases with increasing mismatch angle, but there is a significant population response (rotating with global cues) for all mismatch angles. The lateral entorhinal cortex (LEC) population shows a weak spatial signal that rotates with local cues, although the population correlation is low, even between STD sessions. Pattern separation is evidenced by a circuit that produces outputs that are less correlated than its inputs (Yassa and Stark, 2011); the population responses of granule, mossy, and pCA3 cells to cue mismatch are more decorrelated (relative to repeated STD sessions) than the entorhinal inputs to the DG (Knierim and Neunuebel, 2016), consistent with a shared pattern separation function for DG/pCA3 cells.

Granule cells have traditionally been proposed as the cell type responsible for orthogonalizing overlapping entorhinal inputs (McNaughton and Morris, 1987; McNaughton and Nadel, 1990; Rolls and Treves, 1998). However, mossy cells have also been implicated in pattern separation, with degradation of mossy cells causing granule cell hyperexcitability and context discrimination deficits (Jinde et al., 2012). The response patterns observed here do not necessarily demonstrate an active pattern separation computation occurring in mossy cells, since both the inputs (from granule cells and pCA3 cells) and outputs of mossy cells show similar decorrelated patterns of activity following cue mismatch. However, the similar responses of granule cells and mossy cells are consistent with the proposed role of mossy cells in dynamically regulating pattern separation and granule cell activity (Myers and Scharfman, 2009). In some situations, granule cells may remap less than mossy cells or CA3 cells (Senzai and Buzsáki, 2017; Hainmueller and Bartos, 2018) and in these situations, mossy cells may have a more active pattern separation role.

We found that all cell types showed a similar proportion of “rotate” cells that followed the local cues. This subset of local cue cells had previously been seen in the DG and pCA3 (Neunuebel and Knierim, 2014; Lee et al., 2015) and could reflect inputs from LEC or from more distal regions of CA3, both of which have been shown to be controlled by local cues in the double rotation task (Neunuebel and Knierim, 2014; Lee et al., 2015). This subset of cells may also reflect the influence of immature adult-born granule cells, which appear to receive preferential input from LEC over MEC (Vivar et al., 2012; Woods et al., 2018) and are more active than mature granule cells (Ge et al., 2007; Danielson et al., 2016). Further experiments will be required to determine how adult-born granule cells contribute to the DG response to cue mismatch.

Although the present results suggest a shared pattern separation function for the DG/pCA3 circuit, future studies will be required to determine precisely how the components of this circuit interact to support pattern separation and hippocampal function as a whole. Recent work has revealed how subsecond interactions between DG cells may support memory discrimination (van Dijk and Fenton, 2018). Simultaneous recordings from a large number of DG and pCA3 cells may allow for a direct examination of how information is processed at the millisecond timescales of neural computation within the DG/pCA3 circuit to support DG functions in the double rotation task. Further, while pattern separation is one function often ascribed to the DG, the DG has also been suggested to be important for the conjunctive encoding (Kesner, 2013) or “binding” (Lee and Jung, 2017) of medial and lateral entorhinal inputs into a combined sensory/spatial representation (Knierim et al., 2006). Recent studies of the egocentric reference frame of LEC representations (Wang et al., 2018) and temporal coding in LEC (Tsao et al., 2018) suggest that the DG may be a key structure in integrating egocentric with allocentric spatial reference frames and temporal context representations with spatial context. It is unlikely that the DG has one single function, and pattern separation and conjunctive encoding may be concurrent and complementary functions of the DG. In future studies, pairing simultaneous DG/pCA3 recordings with manipulation of individual cell types or input regions during cue mismatch or discrimination tasks may provide additional information about how the DG/pCA3 circuit is organized, and how it interacts with the recurrent system in distal CA3 to support proposed DG functions.

Prevalence of mossy cells in DG/CA3 recordings

In the present analysis, the majority of cells recorded in DG (62%) and many cells recorded in pCA3 (21%) were mossy cells. Anatomically, mossy cells are greatly outnumbered by granule cells and pCA3 cells; however, if one considers only cells active during behavior, a disproportionate number of cells may be mossy cells, as they fire much less sparsely than granule cells and pCA3 cells. For example, in previous recordings, ∼10% of granule cells recorded during long sleep sessions were active in a given recording environment compared with ∼80% of mossy cells (GoodSmith et al., 2017). Given these approximate activity levels, if 100 DG cells were recorded in sleep and only 10% of those cells were mossy cells, nearly half of the active cells in a given environment (9 of 90 granule and 8 of 10 mossy cells) would be mossy cells. Most cells recorded in previous DG extracellular studies were assumed to be granule cells (Jung and McNaughton, 1993; Skaggs et al., 1996; Shen et al., 1998; Leutgeb et al., 2007; Alme et al., 2010). However, the present analyses indicate that a large majority of the DG cells recorded in these studies were actually mossy cells. Any future DG recordings or evaluation of prior DG studies must therefore be particularly cognizant of the significant number of mossy cells in extracellular DG recordings.

Assessing activity in the DG is difficult relative to other hippocampal subfields in part because of the close proximity of mossy cells, granule cells, and pCA3 cells. This is even more problematic when techniques have a low spatial resolution. Local field potential recordings and fMRI imaging studies are not capable of reliably distinguishing between activity in the DG and pCA3 or between granule cells and mossy cells within the DG. However, our results indicate that this distinction may not be essential when evaluating pattern separation, since the population responses of all cells within the boundaries of the DG (including pCA3) were similar. Our results may help to explain why fMRI data from DG/CA3 tend to be biased toward pattern separation rather than pattern completion (Lacy et al., 2011; Yassa et al., 2011). Although it is possible that the BOLD signal in DG/CA3 is primarily driven by DG activity, some influence of CA3 pattern completion would be expected due to the sparse activity in DG relative to CA3 (Yassa and Stark, 2011). However, CA3c represents a much larger proportion of CA3 in humans than in rodents (Lim et al., 1997), and our results suggest that changes in DG/CA3 BOLD activity following small input changes would be driven predominately by pattern separation in both DG and pCA3, overshadowing the influence of distal CA3. In future studies, it will be essential to focus not solely on the anatomical divisions between DG and CA3, but on the functional division between pattern completion in the recurrent system of intermediate/distal CA3 and pattern separation in the DG/pCA3 circuit.